Classe prima Liceo Scientifico
Triangoli: confronto di angoli e di segmenti
(applicazione del primo teorema dell’angolo esterno per un triangolo)
Problema_1-Sia ABC un triangolo qualsiasi e P un punto interno allo stesso. Considerata la semiretta di
origine B e passante per P, sia D il punto in cui essa interseca il lato AC. Congiungere P con il vertice C.
Dimostrare che l’angolo BPC è maggiore dell’angolo BAC.
Dimostrazione
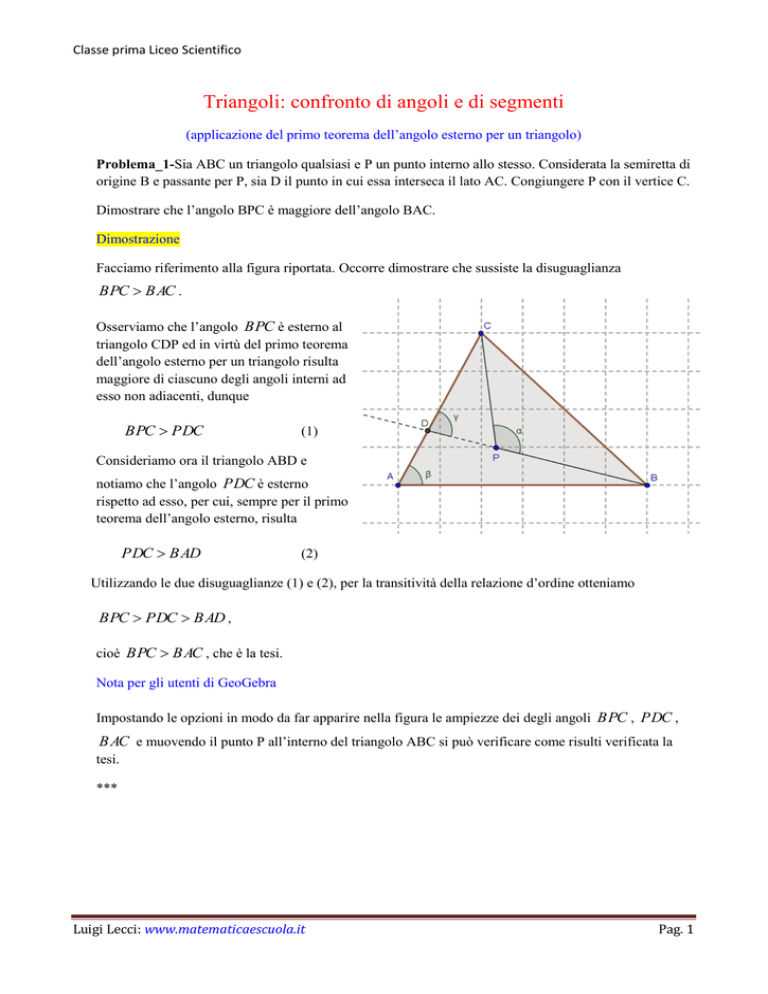
Facciamo riferimento alla figura riportata. Occorre dimostrare che sussiste la disuguaglianza
BPC BAC .
Osserviamo che l’angolo BPC è esterno al
triangolo CDP ed in virtù del primo teorema
dell’angolo esterno per un triangolo risulta
maggiore di ciascuno degli angoli interni ad
esso non adiacenti, dunque
BPC PDC
(1)
Consideriamo ora il triangolo ABD e
notiamo che l’angolo PDC è esterno
rispetto ad esso, per cui, sempre per il primo
teorema dell’angolo esterno, risulta
PDC BAD
(2)
Utilizzando le due disuguaglianze (1) e (2), per la transitività della relazione d’ordine otteniamo
BPC PDC BAD ,
cioè BPC BAC , che è la tesi.
Nota per gli utenti di GeoGebra
Impostando le opzioni in modo da far apparire nella figura le ampiezze dei degli angoli BPC , PDC ,
B AC e muovendo il punto P all’interno del triangolo ABC si può verificare come risulti verificata la
tesi.
***
Luigi Lecci: www.matematicaescuola.it
Pag. 1
Classe prima Liceo Scientifico
Problema_2-Considerata nel piano una retta r sia P un punto non appartenente ad r ed M la proiezione
ortogonale di P su r. Fissare su r due punti A e B da parti opposte rispetto ad M, con MA<MB e unire P
con A e B. Dimostrare che PA<PB.
Dimostrazione
Facciamo riferimento alla figura riportata a
lato.
Consideriamo il punto A simmetrico di A
rispetto ad M e notiamo che dall’ipotesi
MA<MB si deduce che MA<MB, pertanto
A si trova tra M e B.
Osserviamo che i due triangoli AMP,
AMP, rettangoli in M, sono congruenti
perché hanno i cateti ordinatamente
congruenti (PM r per ipotesi è lato
comune ed MAMA perché A è
simmetrico di A rispetto ad M), dunque
risulta anche PAPA , cioè il triangolo PAA è isoscele sulla base AA. Ricordiamo che gli angoli alla
base di un triangolo isoscele sono congruenti tra loro ed acuti per cui l’angolo P A 'B essendo adiacente
all’angolo acuto P A 'A sarà ottuso e quindi è il maggiore degli angoli del triangolo PAB. Poiché in un
triangolo all’angolo maggiore si oppone il lato maggiore, nel triangolo PAB il lato maggiore è PB, da
cui, PB>PA. Ricordato che PAPA, segue immediatamente la tesi PB>PA.
***
Luigi Lecci: www.matematicaescuola.it
Pag. 2
Classe prima Liceo Scientifico
Problema_3-Si consideri nel piano un angolo acuto rOs e sia P un qualsiasi punto interno all’angolo.
Indicato con A il punto sulla semiretta r tale che OAOP, tracciare la semiretta t di origine A e passante
per P.
i)
ii)
Dimostrare che la semiretta t interseca il secondo lato s dell’angolo rOs .
Detto B il punto di intersezione tra t ed s, dimostrare che OB>OA
Dimostrazione
Facciamo riferimento alla figura riportata a lato.
i)
Notiamo subito che il triangolo OAP è
isoscele per costruzione sulla base AP e
quindi l’angolo O AP è acuto. Proviamo che
la semiretta t avente origine in A e passante
per P deve necessariamente intersecare il
secondo lato Os dell’angolo acuto rOs .
Infatti, se t non intersecasse s sarebbe ad essa
parallela e gli angoli O AP , rOs , formando una coppia di angoli coniugati interni rispetto a
dette parallele tagliate dalla trasversale r dovrebbero essere supplementari, quindi la somma
delle loro ampiezze sarebbe 180°. Ciò però non è possibile perché entrambi gli angoli sono acuti
ii)
( rOs lo è per ipotesi e O AP perché angolo alla base di un triangolo isoscele). Dunque t
incontra s. Sia B il punto di intersezione.
Abbiamo precisato nella dimostrazione del precedente punto che il triangolo OAP è isoscele su
AP e dunque, ribadiamo, gli angoli adiacenti alla base AP sono acuti. Osservato che l’angolo
OPB è esterno rispetto al triangolo OAP e che è adiacente all’angolo acuto OPA , si deduce
che OPB è ottuso e quindi il triangolo OPB è ottusangolo e OB è il lato maggiore perché
opposto all’angolo maggiore: OB>OP; dall’essere OP OA segue la tesi OB>OA. C.V.D.
Luigi Lecci: www.matematicaescuola.it
Pag. 3












