Fisica generale II, a.a. 2012/2013
ESERCITAZIONE A: ELETTROSTATICA
LA FORZA DI COULOMB
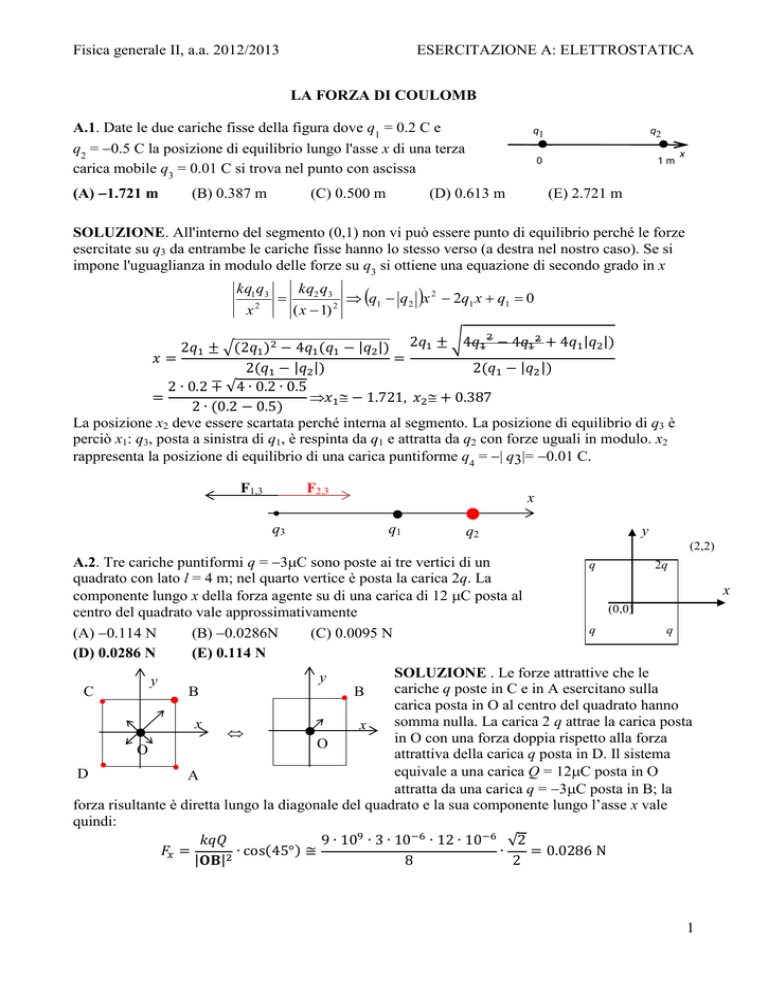
A.1. Date le due cariche fisse della figura dove q1 = 0.2 C e
q2 = 0.5 C la posizione di equilibrio lungo l'asse x di una terza
carica mobile q3 = 0.01 C si trova nel punto con ascissa
(A) 1.721 m
(B) 0.387 m
(C) 0.500 m
q1
q2
0
(D) 0.613 m
1m
x
(E) 2.721 m
SOLUZIONE. All'interno del segmento (0,1) non vi può essere punto di equilibrio perché le forze
esercitate su q3 da entrambe le cariche fisse hanno lo stesso verso (a destra nel nostro caso). Se si
impone l'uguaglianza in modulo delle forze su q3 si ottiene una equazione di secondo grado in x
kq1 q3
kq2 q3
q1 q 2 x 2 2q1 x q1 0
2
2
x
( x 1)
√
| |
√
| |
| |
√
| |
La posizione x2 deve essere scartata perché interna al segmento. La posizione di equilibrio di q3 è
perciò x1: q3, posta a sinistra di q1, è respinta da q1 e attratta da q2 con forze uguali in modulo. x2
rappresenta la posizione di equilibrio di una carica puntiforme q4 = | q3|= 0.01 C.
F1,3
F2,3
q3
x
q1
q2
y
(2,2)
A.2. Tre cariche puntiformi q = 3C sono poste ai tre vertici di un
q
2q
quadrato con lato l = 4 m; nel quarto vertice è posta la carica 2q. La
componente lungo x della forza agente su di una carica di 12 C posta al
(0,0)
centro del quadrato vale approssimativamente
q
q
(A) 0.114 N
(B) 0.0286N
(C) 0.0095 N
(D) 0.0286 N
(E) 0.114 N
SOLUZIONE . Le forze attrattive che le
y
y
cariche q poste in C e in A esercitano sulla
C
B
B
carica posta in O al centro del quadrato hanno
S
S
S
somma nulla. La carica 2 q attrae la carica posta
x
x
in O con una forza doppia rispetto alla forza
O
O
attrattiva della carica q posta in D. Il sistema
S
S
equivale a una carica Q = 12C posta in O
D
A
attratta da una carica q = 3C posta in B; la
S
S
forza risultante è diretta lungo la diagonale del quadrato e la sua componente lungo l’asse x vale
quindi:
√
| |
1
x
Fisica generale II, a.a. 2012/2013
ESERCITAZIONE A: ELETTROSTATICA
A.3. Agli estremi A, B di un segmento lungo 100 cm sono
qA
vincolate due cariche positive con qA = 1 nC e qB = 3 nC. Una
terza carica positiva q = 6 nC è libera di muoversi lungo il
A
segmento AB e all’equilibrio raggiunge un punto C compreso tra
A e B. La distanza CB vale circa (arrotondare)
(A) 50 cm
(B) 59 cm
(C) 69 cm
(D) 76 cm
C
qB
q
B
(E) 63 cm
SOLUZIONE. La posizione di equilibrio della carica q è quella in cui essa subisce da qA e qB forze
repulsive uguali in modulo. Essendo |AB|= 1m, detta x la distanza (espressa in metri) tra q e qB si ha
√
La posizione x2 è esterna al segmento e non corrisponde a una posizione di equilibrio. Dunque
CB 0.63 m= 63 cm.
NB. Viene naturale assumere A come origine dell’asse delle ascisse; in questo caso però la x è la
distanza |AC| mentre il problema chiede (in metri) |CB|=1x. Anche se il procedimento è corretto,
scambiare x con 1x è una disattenzione molto costosa.
A.4. Una carica q = 4.1(106)C è nell’origine. Se si vuole che su una carica Q = 1.6(107)C si
eserciti una forza di intensità 6.3(106) N nella direzione positiva dell’asse x questa carica deve
essere posta nel punto di ascissa
(A) 3.14 m
(B) 30. 6 m
(C) ________
(D) 18. 4 m
(E) 30.6 m
SOLUZIONE. Tra le due cariche, concordi, si esercita una forza repulsiva; Q deve quindi stare a
destra di q (ascissa positiva) a una distanza x tale che
√
A.5. Una carica Q1 = 1 C è posta su di una sferetta metallica di
massa m = 30 g appoggiata a un estremo di una bacchetta isolante
lunga L = 30 cm. All’altro estremo della bacchetta è incollata una
seconda sferetta, identica alla prima, con una carica di Q2 = 0.1 C.
Se la bacchetta ruota in un piano orizzontale attorno all’asse
verticale p della figura, per quale periodo di rotazione la prima
sferetta si staccherà dalla bacchetta?
(A) 1.40 s
(B) 2.43 s
(C) 3.15 s
(D) 5.44 s
p
Q1
Q2
5 cm
25 cm
(E) _____
SOLUZIONE. La sferetta con carica Q1 subisce, oltre alla forza coulombiana attrattiva FCoulomb
dell’altra sferetta distante L = 0.3 m, la forza centrifuga Fcentr dovuta al moto circolare piano a
distanza di 0.05 m dall’asse p. La condizione di distacco è quindi
|
|
√
2
Fisica generale II, a.a. 2012/2013
ESERCITAZIONE A: ELETTROSTATICA
A.6. Secondo il modello atomico di Bohr, l’elettrone dell’atomo d’idrogeno (con massa
me 9.11 1031 kg, carica q = e 1.6 1019 C) percorre un’orbita circolare di raggio
r 5.3 1011 m attorno al suo nucleo con frequenza pari a circa
(A) 107 Hz
(B) 13.5 1012 Hz (C) 6.6 1015 Hz (D) 3.0 108 Hz
(E) 9.0(1016)Hz
SOLUZIONE. Secondo il modello di Bohr, l’elettrone ruota attorno al nucleo su un’orbita di
raggio tale che la forza attrattiva coulombiana uguagli in modulo la forza centrifuga repulsiva:
√
√
IL CAMPO ELETTRICO
E2
A.7. Due cariche Q1 = 3.5 C e Q2 = 1.2 C sono tenute fisse su due punti
diametralmente opposti di una circonferenza mentre la carica q = 1.1 C è
libera di muoversi solo sulla stessa circonferenza. Nel punto in cui la carica
q è in equilibrio l’angolo 1 della figura vale circa
(A) 55°
(B) 35°
(C) 74°
Q1
(D) 16°
(E) 45°
E1
q
d1
d2
1
Q2
C
SOLUZIONE. La carica q è in equilibrio se e solo se il campo risultante
E1+E2 ha componente tangenziale nulla lungo la circonferenza (cioè è
diretto come la retta qC). Poiché il triangolo Q1qQ2 è inscritto in una semicirconferenza, esso è
rettangolo; 1 e 2 sono angoli complementari e d2 = tan(1) d1.
E2
E1
Osservando che i triangoli qCQ1 e qCQ2 sono isosceli e utilizzando
1
l’uguaglianza di angoli opposti al vertice si ricavano le relazioni
q
angolari rappresentate nella figura. Uguagliando il modulo delle
d1
d
2
componenti tangenziali di E2 e di E1 si ha:
1
Q1
Q2
C
√
(√ )
A.8. Nei vertici A e B di un triangolo equilatero sono state poste le cariche QA e
QB. Nel terzo vertice C si trova che il campo elettrico è normale a CB e diretto
nel verso indicato. Se la carica QA vale +1 C, la carica QB vale
(A) 1 C
(B) 0.5 C
(C) 0.87 C
EA
(D)0.87 C (E) non esiste
E
A
Etot
C
C
EB
SOLUZIONE. Poichè il campo totale ha componente nulla
lungo la retta CB, QB deve essere tale che
| |
| |
| | | |
|
|
B
|
|
Perciò la carica in B è negativa e pari alla metà di quella in A: QB = 0.5 C.
A
B
3
Fisica generale II, a.a. 2012/2013
B
A
C
C
A
B
ESERCITAZIONE A: ELETTROSTATICA
A.9. Sui sei vertici di un esagono di lato d = 0.25 nm sono collocati tre ioni
ossigeno (cerchi neri, O2; carica 2e = 3.21019 C) e tre ioni cesio (cerchi
bianchi, Cs+; carica e = 1.61019 C). Se la distanza massima tra gli atomi di
ossigeno vale 3 d e la minima d, il modulo del campo elettrico nel centro
dell’esagono vale (k = costante elettrica =1/40)
27 ke
3ke
(A) 0
(B) 2
(C)
d
d2
6ke
(D) 2
(E)_____
d
SOLUZIONE. Il campo creato al centro dell’esagono dalla coppia di ioni ossigeno-cesio B-B è la
somma dei campi equiversi creati dai singoli ioni: è diretto lungo la diagonale B-B e di modulo
Le altre due coppie di ioni creano al centro dell’esagono campi uguali in modulo a EBB e formanti
con esso angoli di 60°. Il campo risultante è quindi diretto da B a B e pari in modulo a
E1+E2
E1
E2
P
d1
Q1
d2
Q2
A.10. Due cariche Q1 = 0.3 C e Q2 = 0.4 C si trovano agli estremi
di un diametro di una circonferenza di raggio 0.5 m. Il punto P
della circonferenza dove il campo elettrico è normale al diametro
ha ascissa x (vedi figura) pari a
(A) 0.10 m
(B) 0.20 m
(C) 0.36 m
(D) 0.64 m
(E) 0.80 m
SOLUZIONE. Poichè il triangolo Q1PQ2 è inscritto in una
semicirconferenza, esso è rettangolo; e sono complementari e
tan() = d2/d1. Inoltre, esso è simile al triangolo rettangolo avente per cateti E2 ed E1:
0
xP
1 x
Dalle relazioni precedenti ricaviamo
(
)
e per x si ha
A.11. Un grammo di idrogeno atomico viene separato in NA 6.02(1023) protoni, ciascuno con
carica e = 1.6(1019) C e in altrettanti elettroni (con uguale carica negativa); i protoni vengono
portati al polo Nord e gli elettroni al polo Sud. Se il raggio terrestre è RT 6340 km, il campo
elettrico al centro della Terra vale (in N/C)
(A) 98
(B) 0
(C) 43
(D) 4(107)
(E) ___________
SOLUZIONE. Il campo elettrico al centro della Terra è la sovrapposizione dei due campi elettrici,
uguali in modulo, direzione e verso, creati da una coppia di cariche opposte pari in modulo a
poste a distanza RT dal centro della Terra. Il verso del campo è dal Polo Nord al Polo Sud e la sua
intensità è pari a
4
Fisica generale II, a.a. 2012/2013
ESERCITAZIONE A: ELETTROSTATICA
A.12. Il campo elettrico nel terzo vertice P di un triangolo equilatero di lato r = 0.2 m, in cui gli altri
due vertici sono occupati ciascuno da una carica q = 15 nC (positiva), vale in modulo
(A) 3375 V/m
(B) 5846 V/m
(C) 10125 V/m
(D) 17537 V/m
(E) ______
EB
C
A
SOLUZIONE. Se A eB sono i vertici occupati dalle cariche, il campo in C è
verticale e pari in modulo a
EA
A
B
A.13. Una carica q1 = 5.5 (108) C è nell’origine dell’asse x e una carica q2 = 3.3(108) C si trova
in x2= 0.58 m. A che punto dell’asse x il campo è nullo?
(A) 2.58 m
(B) 1.38 m
(C) 0.28 m
(D) 0.95 m
(E) 0.11
SOLUZIONE. Nel segmento compreso tra le due cariche esse producono campi con lo stesso
verso; l’ascissa corrispondente al punto in cui il campo si annulla sarà quindi esterna al segmento e
sarà soluzione dell’equazione:
| |
| |
|
|
√
| | | |
L’unica soluzione accettabile è xB. xA corrisponde al punto in cui il campo sarebbe nullo se q1 e q2
fossero cariche concordi.
TEOREMA DI GAUSS
A.14. Calcolare il campo elettrico a distanza r di un filo infinitamente lungo, posto lungo l’asse x,
caricato con una densità lineare di carica lin (in C/m).
E
SOLUZIONE. Per considerazioni di simmetria, il campo
r
elettrico generato da un filo di lunghezza infinita:
r
a) deve avere direzione perpendicolare al filo
b) deve avere lo stesso modulo in punti equidistanti
dal filo.
Per il calcolo del campo, applichiamo la legge di Gauss a
h
un cilindro di altezza h e di raggio r, che ha per asse il
E
r
filo. Per la considerazione a) il flusso di E è diverso da
zero solo attraverso la superficie laterale Slat = (2rh); poiché linh è la carica contenuta nel cilindro
si ha
h
(E) 2rhE( r ) lin E ( r ) lin
0
2 0 r
5
Fisica generale II, a.a. 2012/2013
ESERCITAZIONE A: ELETTROSTATICA
A.15. Due fili paralleli e distanti D = 1.25 m portano la stessa carica positiva con una densità lineare
lin = 3.8∙106 C/m. Il campo in un punto P distante d1 = 0.75 m dal primo filo e d2 = 2 m dall’altro
vale in modulo
(A) 5.7104 V/m (B) 1.25105 V/m (C) 8.55104 V/m (D) 4.56104 V/m (E)3.14104 V/m
SOLUZIONE. Per il principio di sovrapposizione, il campo in P è
la somma dei contributi dei due fili:
|
|
(
(
Filo 1
Filo 2
P
)
d1
D
)
EP
A.16. Calcolare il campo elettrico E(r) in un generico punto P posto a distanza r dal centro di un
sfera isolante di raggio R, caricata con carica Q e densità di carica , funzione della distanza r dal
r
centro della sfera, secondo la relazione: = 0 .
R
SOLUZIONE. Per il calcolo del campo per r < R utilizziamo la legge di Gauss applicata a una
superficie sferica di raggio r. La carica interna a questa superficie è pari a
∫
∫
∫
si trova per 0 l’espressione
Poiché deve essere
e l’espressione precedente può essere scritta come
( )
Il campo E(r) vale
( )
Per r R,
e
Per r R, quindi, il campo è quello che una carica puntiforme Q posta al centro della sfera
genererebbe a distanza r.
2R2
2R1
A.17. Una carica elettrica Q = 10 C è distribuita uniformemente, cioè a
densità costante, nel volume di una sfera di raggio RS = 10 cm. Il rapporto
tra il campo elettrico a R1 = 5 cm dal centro e il campo elettrico a R2 = 15 cm
dal centro, E(R1)/E(R2), vale circa
(A) 1/9
(B) 4/9
(C) 3/2
(D) 1.66
(E) 1.125
SOLUZIONE. Per R > RS, il campo è quello di una carica puntiforme Q
posta al centro della sfera:
E1
E2
2RS
6
Fisica generale II, a.a. 2012/2013
ESERCITAZIONE A: ELETTROSTATICA
Per il calcolo del campo per R< RS utilizziamo la legge di Gauss applicata a una superficie sferica di
raggio R1. La carica interna a questa superficie è pari a
(
)
e il campo E(R1) vale
(
)
Dunque
z
a
y
E
A.18. Si consideri la superficie chiusa del cubo di lato a
mostrato in figura. Il flusso del campo elettrico attraverso tale
superficie quando è presente un campo elettrico E = E0i
(costante e diretto come l’asse delle x) vale
(A) E0a2
(B) 2 E0a2
(C) 6E0a2
(D)
(E) 0
x
SOLUZIONE. Il flusso di E è diverso da zero solo attraverso
le facce A e B del cubo perpendicolari al campo. Il versore normale alla faccia B (nB) ha verso
opposto a quello del campo; il versore normale alla faccia A (nA) ha lo stesso verso del campo e si
ha:
Si può giungere alla stessa conclusione applicando la legge di Gauss e considerando che il cubo non
contiene cariche in quanto il campo uniforme ha divergenza ovunque nulla.
A.19. Con riferimento al problema precedente, se il campo elettrico è diretto come l’asse delle x e
vale E = (C∙x) i, con C = costante positiva, la carica contenuta nel cubo vale
(A) 0Ca
(B) 0C/a3
(C) 0Ca3
(D)
(E) 0
SOLUZIONE. Il flusso di E è diverso da zero solo attraverso le facce A e B del cubo
perpendicolari al campo.
Per il teorema di Gauss,
Si arriva alla stessa conclusione considerando che
∫
A.20. Su una barra cilindrica di alluminio lunga L = 2 m e avente diametro d = 3 cm viene posta una
carica Q = 5 C. Il campo elettrico alla superficie della barra a distanza uguale dagli estremi vale in
modulo
(A) 0.54 MV/m (B) 3.0 MV/m
(C) 5.4 MV/m
(D) 13.5 MV/m (E) 25 MV/m
SOLUZIONE. La densità lineare di carica sulla barra conduttrice vale lin = Q/L. Per simmetria, in
ogni punto P equidistante dagli estremi della barra il campo E è perpendicolare alla superficie
cilindrica della barra stessa come nel caso del cilindro conduttore indefinito.
7
Fisica generale II, a.a. 2012/2013
ESERCITAZIONE A: ELETTROSTATICA
Utilizzando l’espressione del campo elettrico generato da un cilindro conduttore in un punto P a
distanza r si ha
|
|
Sostituendo i dati del problema con r = d/2 si ottiene
|
|
A.21. Il modulo del campo elettrico immediatamente sopra il punto centrale di una piastrina
metallica carica a forma di quadrato di lato L = 20 cm e 0.1 mm di spessore è di 150 V/cm. La
carica elettrica complessiva della piastrina vale circa
(A) 2.6 nC
(B) 5.1 nC
(C) 5.8 nC
(D) 10.6 nC
(E) 15.4 nC
SOLUZIONE. Per simmetria, il campo elettrico immediatamente sopra il punto centrale di una
piastrina metallica carica è perpendicolare alla piastra stessa come nel caso della lastra conduttrice
infinitamente estesa, e per distanze sufficientemente piccole dalla lastra, indipendente dalla
distanza. Utilizzando l’espressione del campo elettrico generato da una lastra conduttrice
infinitamente estesa (vedi lezione I) si ha:
| |
A.22. Il rivelatore di un contatore Geiger è costituito da un filo lungo L = 0.1 m e diametro
d = 0.1 mm in asse con un cilindro metallico vuoto con diametro interno D = 1 cm. Filo e cilindro
sono sotto vuoto e portano cariche di segno opposto e uguali in valore assoluto. Se il modulo del
campo elettrico in prossimità della superficie interna del cilindro è |E1| = 3(104) V/m, il campo E2 in
prossimità del filo vale in modulo
(A) 6(104) V/m
(B) 3(104) V/m
(C) 3(106) V/m (D) 3(107) V/m
(E) 3(104) V/m
SOLUZIONE. Il campo elettrico tra filo e cilindro metallico conduttore, diretto
orizzontalmente nella figura per ragioni di simmetria, è dovuto unicamente al
filo. Il filo carico produce un campo pari in modulo a
|
L
|
dove lin è la densità lineare di carica e r la distanza dal filo. Si ha pertanto:
|
( )|
|
( )|
|
D
( )|
A.23. Un cubo di spigolo a ha un vertice nell’origine O di un
sistema di riferimento cartesiano ortogonale ed è disposto come in
figura. Si calcoli il flusso del campo elettrico attraverso la superficie
del cubo e la carica Q contenuta nel volume delimitato dal cubo, nei
casi in cui il campo elettrico E sia dato da (, costanti):
a) E = x2 i;
b) E = (x i + y j ).
z
y
x
8
Fisica generale II, a.a. 2012/2013
ESERCITAZIONE A: ELETTROSTATICA
SOLUZIONE. Nel caso a), il campo elettrico è diretto lungo l’asse x e il flusso di E attraverso la
superficie del cubo è quello attraverso le facce del cubo perpendicolari a tale asse: poiché tuttavia il
campo è nullo in corrispondenza alla faccia del cubo posta sul piano yz (x = 0) si ha
Per la legge di Gauss:
Nel caso b), il flusso di E attraverso la superficie del cubo è quello attraverso le facce del cubo
perpendicolari all’asse x e all’asse y: di nuovo, il campo è nullo in corrispondenza alla faccia del
cubo posta sul piano yz (x = 0) e attraverso alla faccia del cubo posta sul piano xz (y = 0) e quindi
Per la legge di Gauss:
A.24. Un parallelepipedo di spigoli a = 10 cm, b = 15 cm, c = 20 cm, ha un vertice nell’origine O di
un sistema di riferimento cartesiano ortogonale e gli spigoli coincidenti con gli assi cartesiani. Nella
regione è presente un campo elettrico E = (5x i 4 y j +3z k )·105 V/m. Si calcoli:
a) il flusso del campo elettrico attraverso la superficie del cubo;
b) la carica Q contenuta nel volume delimitato dal cubo;
c) la densità di carica, supponendo sia costante.
SOLUZIONE. Spezziamo il campo elettrico nelle sue componenti cartesiane
e calcoliamo il flusso attraverso le facce del parallelepipedo ortogonali agli assi:
Per la legge di Gauss:
E, in caso di densità di carica costante,
POTENZIALE ELETTRICO
A.25. Una sfera conduttrice di raggio R1 = 25 cm e carica iniziale q1 = 4 C è posta brevemente in
contatto elettrico con una seconda sfera conduttrice di raggio R2 = 40 cm e carica iniziale
q2 = 2 C posta a d = 3 m di distanza dalla prima sfera. Dopo che il contatto è stato rimosso le due
sfere si respingono con una forza pari a circa
(A) 0 N
(B) 0.95 mN
(C) 8.0 mN
(D) 8.52 mN
(E) 9 mN
9
Fisica generale II, a.a. 2012/2013
ESERCITAZIONE A: ELETTROSTATICA
SOLUZIONE. Durante il contatto elettrico, la carica negativa della seconda sfera neutralizza
parzialmente quella della prima; sul sistema, dopo il contatto, c’è una carica totale
QTOT =q1 + q2 = 2 C che si ridistribuisce sulla superficie dello stesso in modo da renderla
equipotenziale. Indicando con q1’ e q2’ le cariche finali delle due sfere, entrambe positive, e
uguagliando i loro potenziali elettrici V1’ e V2’si ha dunque
(
)
e la forza repulsiva coulombiana tra le sfere è pari a
|
|
A.26. Due sferette conduttrici cariche di raggio pari a R = 1 cm si attraggono inizialmente con una
forza |F1| = 5 N quando sono alla distanza d1 = 1 m. Dopo essere state poste per un attimo in
contatto elettrico mediante un filo conduttore, le due sferette, sempre alla distanza di 1 m, si
respingono con una forza di intensità |F2| = 1 N. Il rapporto tra le cariche iniziali sulle sfere vale in
valore assoluto (si scelga il rapporto >1)
(A) 1.67
(B) 1.86
(C) 2.38
(D) 3.14
(E) 5.83
SOLUZIONE. Poiché F1 è attrattiva, le cariche iniziali sulle due sferette, qA e qB, hanno segno
opposto. Dall’espressione di |F1| si ha:
| | | |
| |
| |
| | | |
Durante il contatto elettrico, una carica totale pari alla somma algebrica QTOT =qA + qB si
distribuisce sulle due sferette in modo da renderle equipotenziali; poiché le sfere hanno lo stesso
raggio, si avrà qA’ = qB’ = QTOT/2, quindi dall’espressione di |F2| si ha:
| |
(
)
√
| |
L’equazione di secondo grado che ha come soluzioni qA e qB con somma e prodotto noto è la
seguente (si assuma la carica totale positiva):
Poiché qA∙qB < 0, il discriminante dell’equazione è sempre positivo e l’equazione ha due soluzioni
reali:
√
√
Scegliendo |qA| > |qB| si trovano i valori numerici |qA| 3.636∙105, |qB| 1.528∙105 e
| |
| |
Si noti che non è possibile stabilire quale sia la carica negativa e quale quella positiva.
10
Fisica generale II, a.a. 2012/2013
ESERCITAZIONE A: ELETTROSTATICA
A.27. Due sferette cariche, ambedue di 0.15 cm di raggio, si attirano inizialmente con una forza di
intensità 90 N quando sono poste alla distanza di 1 m. Dopo essere state poste per un attimo in
contatto elettrico mediante un sottile filo conduttore, le due sferette, sempre alla distanza di 1 m, si
respingono con una forza di 40 N. Tra le seguenti affermazioni sono vere (segnare con V quelle
vere e con F quelle false)
(A) Le due cariche iniziali hanno segno opposto e valori assoluti diversi.
(B) Le due cariche finali hanno lo stesso valore e lo stesso segno.
(C) Con i dati del problema non è possibile determinare i segni delle cariche iniziali e finali.
(D) Il valore assoluto di una delle due cariche iniziali è di 20 C.
(E) Il valore assoluto di una delle due cariche finali è di 66.7 C.
SOLUZIONE. L’affermazione (A) è vera: il segno opposto delle cariche iniziali dipende dal fatto
che la forza coulombiana è inizialmente attrattiva, e la differenza tra i valori assoluti delle cariche
dipende dal fatto che, in caso contrario, dopo il contatto elettrico il sistema sarebbe neutro.
L’affermazione (B) è vera: forza finale repulsiva implica cariche finali concordi, e poiché, dopo il
contatto elettrico, le due sfere sono equipotenziali, essendo esse identiche devono avere la stessa
quantità di carica.
L’affermazione (C) è vera: si veda il problema precedente come esempio.
L’affermazione (E) è vera: il valore delle cariche finali qf (uguali in modulo e segno, vedi punto B)
si trova imponendo:
√
L’affermazione (D) è falsa: se il valore assoluto di una delle due cariche iniziali fosse di 20 C, il
valore dell’altra sarebbe
√
e il valore di qf sarebbe in modulo pari a |22.360.067|/2 11.15 mC in contrasto con quanto
calcolato in (E).
A.28. Una carica elettrica q0 = +1 mC si trova nell’origine di un asse mentre una carica negativa
q1= 4 mC si trova nel punto di ascissa x = –1 m. Sia Q il punto dell’asse dove il campo elettrico si
annulla e P il punto di ascissa positiva dove il potenziale elettrico si annulla. Il rapporto xQ/xP vale
(A) 1/3
(B) 1/2
(C) 1
(D) 2
(E) 3
E0
SOLUZIONE. La situazione è schematizzata nella figura.
E1
q1
Trattiamo dapprima il problema dell’annullamento del
q0
campo elettrico. A destra di q0 (ascisse positive) i due campi
1
0 xP
xQ
E0 ed E1 hanno verso opposto e la loro somma si può
E1
annullare. Tra le due cariche, i due campi hanno lo stesso
E0
verso e non si possono annullare. A sinistra di q1, |E1| è
sempre maggiore di |E0|. Il punto Q in cui il campo elettrico si annulla dovrà quindi avere ascissa
xQ > 0 Uguagliando i moduli dei due campi:
q0
q1
xQ 1 m
E 0 E1 2
xQ2 2 xQ 1 4 xQ2
2
xQ xQ 1
xQ 1/ 3 m
Pertanto xQ = 1 m.
Trattiamo ora il problema dell’annullamento del potenziale elettrico, somma dei potenziali
11
Fisica generale II, a.a. 2012/2013
ESERCITAZIONE A: ELETTROSTATICA
q0
q1
e V1 k e
xP
xP 1
dovuti alle due cariche. Essendo V0 < 0, V1 > 0 e |q1| > |q2|, anche il punto P dovrà avere ascissa
positiva. Per non lavorare con i valori assoluti delle ascisse uguagliamo i quadrati dei potenziali
x 1/ 3 m
q02
q12
xP2 2 xP 1 16 xP2 P
2
2
xP xP 1
xP 1 / 5 m
Pertanto xP = 1/3 m e xQ/xP = +3
V0 k e
A.29. Nei dintorni del punto O (origine degli assi cartesiani) dove si annulla, un campo elettrico è
descritto in ogni punto P dalla relazione vettoriale E(P) A OP con A = 25 kV/m2. Se P1 e P2
sono due punti dell’asse delle x con ascisse x1 = 2 cm e x2 = 3 cm la differenza di potenziale
V(P2) V(P1) vale
(A) 6.25 V
(B) 12.5 V
(C) 0 V
(D) 6.25 V
(E) 12.5 V
SOLUZIONE. Come mostrato in figura, la forza elettrica in O è di tipo elastico (proporzionale al
modulo del vettore spostamento e con verso opposto ad
E
E
E
esso). Applicando la definizione di differenza di
O
P1 P2
Q
potenziale fra i punti P1 e P2 appartenenti all’asse x, si ha:
x
x1
x1
O
O
A
P1P2
V ( P2 ) V ( P1 ) E x dx Ax dx x22 x12 6.25 V
x2
x2
2
La differenza di potenziale è positiva: per portare una carica positiva unitaria da P2 a P1 il campo
elettrico e il vettore spostamento sono paralleli ed equiversi; il lavoro è positivo.
+e
A
19
A.30. Le cariche +e e e (e = 1.6(10 ) C) sono poste nei tre vertici
di un quadrato di lato L = 2(1010) m come in figura. Il potenziale
elettrico nel quarto vertice A vale:
(A) 7.2 V
(B) 9.3 V
(C) 4.65(1010) V
(D) 1.48 (1010) V (E) 1.1(1010) V
0.2 nm
e
+e
SOLUZIONE. Il potenziale in A è la somma dei potenziali dovuti a ciascuna carica. Il contributo
V+ delle due cariche positive vale
mentre quello della carica negativa vale
√
Dunque
(
√
)
(
√
)
A.31. Se nel punto A della figura dell’esercizio precedente si porta una carica +e, l’energia
potenziale del sistema formato dalle quattro cariche vale:
(A) 9.3 eV
(B) 9.3 eV
(C) 0 eV
(D) 7.2 eV
(E) 28.8 eV
12
Fisica generale II, a.a. 2012/2013
+e
+e
B
A
SOLUZIONE. L’energia potenziale elettrica di una carica q posta
in un punto a potenziale elettrico V vale
0.2 nm
C
D
e
+e
ESERCITAZIONE A: ELETTROSTATICA
e l’energia potenziale di un sistema di n cariche vale
∑
In ogni vertice del quadrato, il potenziale elettrico dovuto alle tre
cariche poste negli altri vertici vale:
(
)
√
e l’energia potenziale del sistema di cariche è perciò
∑
[
(
√
)
( )
√
( )
√
(
√
(
)
√
)]
A.32. Due protoni (mp = 1.67 (1027) kg, q = 1.6(1019) C) in un nucleo di nickel sono distanti circa
d = 4(1015) m. La loro energia potenziale vale (in MeV)
(A) 3.92
(B) 0.576
(C) 1.44
(D) 0.36
(E) 0.157
SOLUZIONE. Il potenziale elettrico creato da un protone in un punto a distanza d vale
L’energia potenziale elettrica dei due protoni, pari al lavoro da compiere contro il campo elettrico
per portare il secondo protone a distanza d dal primo, vale
(
)
L’energia potenziale gravitazionale del sistema è trascurabile in quanto inferiore a quella potenziale
elettrica di circa 40 ordini di grandezza.
A.33. Tre elettroni sono collocati ai vertici di un triangolo equilatero di lato L = 0.2 nm. Il
potenziale elettrico nel baricentro del triangolo vale
(A) 21.6 V
(B) 37.4 V
(C) 43.2 V
(D) 24.9 V
(E) 49.9 V
C
SOLUZIONE. Detto M il baricentro del triangolo, i tre elettroni distano da M
√
M
A
H
B
Quindi
A.34. Un lungo cavo coassiale ha come conduttore interno un cilindro di raggio R1 = 0.1 cm e come
conduttore esterno un cilindro cavo di raggio interno R2 = 0.3 cm ed esterno R3 = 0.5 cm. Il
conduttore interno porta una carica di densità lineare 1 = 5(106) C/m mentre quello esterno porta
una carica di densità 2 = 5 (106) C/m. La differenza di potenziale tra un punto a distanza
d = 0.3 cm dall’asse del cavo e un punto sull’asse del cavo vale
(A)98.8 kV
(B)62.4 kV
(C) 0
(D)31.4 kV
(E) ______
13
Fisica generale II, a.a. 2012/2013
ESERCITAZIONE A: ELETTROSTATICA
SOLUZIONE. Il filo conduttore interno e il cilindro esterno dividono lo spazio in
tre regioni: a) tra filo interno e Rint, b) tra Rint e Rext, c) regione esterna al cavo
coassiale. Nella regione a), il filo interno è a potenziale costante e genera a distanza
r un campo elettrico perpendicolare al proprio asse che vale in modulo
x
Rint
Rext
Nella regione b), il campo elettrico è nullo poiché anche il cilindro è un conduttore
a potenziale costante. Nella regione c) il campo è nullo perché 1 = 2
La differenza di potenziale tra un punto a distanza d = 0.3 cm dall’asse del cavo e un punto sull’asse
del cavo è dunque pari al lavoro compiuto dal campo elettrico generato dal cavo per spostare una
carica unitaria positiva da un punto P di ascissa xP = 0.3 cm a un punto Q sulla superficie esterna del
cavo con xQ = 0.1 cm:
∫
(
)
A.35. Una carica q1 = 1.75 (106) C è nell’origine di un sistema di riferimento e una carica
q2 = 8.6 (107) C è nel punto di ascissa x2 = 0.75 m. Nel punto dell’asse x a metà tra le due cariche
il potenziale elettrico vale
(A) 2.14 (104) V (B) 5.46 104V
(C) 3.68 104V
(D) 2.74 103 V
(E) 8.29 103V
SOLUZIONE. Il punto medio M tra le due cariche ha ascissa xM = 0.75/2 = 0.375 m. Il potenziale
in M vale:
A.36. Due cariche puntiformi q1 = 107 C e q = 107 C sono poste alla distanza d = 1 cm. Il modulo
del vettore momento di dipolo vale
(A) 107Cm
(B) 109Cm
(C) 2107Cm
(D) 2105Cm
(E) 106Cm
SOLUZIONE. Il momento di dipolo è un vettore orientato dalla carica positiva alla carica negativa
e il suo modulo è
| | | |
A.37. Il dipolo del problema precedente è posto in un campo elettrico uniforme di modulo
E = 2(105) V/m diretto verso la direzione positiva dell’asse y ed è mantenuto nella direzione che
forma un angolo di 30° con l’asse x. L’energia potenziale del dipolo vale
(A) 1.73(104)J (B) 104J
(C) 1.73(104)J
4
(D) 10 J
(E)_____
y
SOLUZIONE. L’angolo tra il momento di dipolo d e il campo elettrico
E è di 60°, e l’energia potenziale del dipolo vale
Q
E
30°
x
Q+
14
Fisica generale II, a.a. 2012/2013
ESERCITAZIONE A: ELETTROSTATICA
A.38. Un dipolo elettrico, inizialmente orientato lungo
l’asse x, è costituito da uno ione monovalente positivo,
e = 1.6(1019) C, e uno negativo (e) alla distanza
d = 3(1010) m. Il dipolo viene posto in un campo elettrico
uniforme diretto verso la direzione positiva dell’asse y di
modulo E = 2(105) V/m. Se il dipolo può orientarsi nel
campo elettrico la sua energia potenziale diminuisce di
(A) 2eEd
(B) eEd
(C) eEd/2
(D) eEd/3
(E) eEd/4
E
y
d/2
x
e
ed
ed
e
SOLUZIONE. L’energia potenziale di un dipolo d in un campo elettrico E è
Inizialmente, dipolo e campo sono perpendicolari e l’energia potenziale è nulla (cos() = 0). Il
dipolo si orienterà in modo da minimizzare la propria energia potenziale (cos() = 1), disponendosi
parallelamente al campo; l’energia potenziale finale del dipolo è quindi
e la diminuzione di energia potenziale è pertanto e∙d∙E.
A.39. Un dipolo elettrico è costituito da uno ione monovalente positivo e = 1.6(1019) C, e da uno
negativo e alla distanza d = 1010 m. Il dipolo viene posto in un campo elettrico uniforme diretto
verso la direzione positiva dell’asse y di modulo E = 2(105) V/m dove si orienta parallelamente al
campo E. Per orientare il dipolo in modo che formi un angolo di 60° con la direzione positiva
dell’asse y il campo in cui E deve compiere un lavoro pari a
(A) 2.77(1024)J (B) 1.6(1024)J (C) 2.77(1024)J (D) 3.2(1024)J
(E)_____
SOLUZIONE. L’aumento di energia potenziale del dipolo è uguale e opposto al lavoro compiuto
dal campo:
(
)
(
)
A.40. In una regione dello spazio il potenziale elettrostatico è espresso dalla funzione
V(x) = (x36x2+3) V. Calcolare a) in quali punti il campo elettrico si annulla; b) in quale punto il
campo elettrico è massimo; c) il valore massimo del campo elettrico.
SOLUZIONE. Calcoliamo il campo elettrico partendo dal potenziale:
Per trovare i punti in cui E = 0 risolviamo l’equazione
Per trovare in quale punto il campo elettrico è massimo, possiamo per esempio osservare che
l’espressione analitica del campo è quella di una parabola rivolta verso il basso con vertice V di
coordinate
(
)
Dunque il campo è massimo per x = 2 m e il suo valore è Ex,max(x = 2) = 12 V/m.
15
Fisica generale II, a.a. 2012/2013
ESERCITAZIONE A: ELETTROSTATICA
A.41. In una regione dello spazio il potenziale elettrostatico è dato da V(x,y,z) = (xz4y+2z2) V.
Calcolare le componenti del campo elettrico nel punto P(1; 2; 1) (coordinate in metri).
SOLUZIONE. Calcoliamo il campo elettrico partendo dal potenziale:
Pertanto in P l’espressione del campo è (in V/m)
A.42. Il potenziale elettrico lungo la retta y = a di un piano xy è descritto dalla funzione
1
1
V
V ( x) 9
2
2
2
2
x 1 a
x 1 a
La componente Ex del campo elettrico nel punto (0, a =0) vale (tutte le coordinate sono espresse in
metri)
(A) 0.257 V/m
(B) 0.569 V/m
(C) 1.61V/m
(D) 6.36 V/m
(E) 18.0 V/m
SOLUZIONE. Calcoliamo la componente Ex del campo elettrico partendo dal potenziale. Per a = 0
l’espressione del potenziale diventa
(
)
(
)
|
| |
|
√
√
Poichè il punto di interesse ha ascissa x = 0 possiamo riscrivere V(x) eliminando i valori assoluti
come
(
)
e per il campo elettrico si ha quindi
(
)
Pertanto nel punto di ascissa 0 il valore del campo è
z
A.43. Nei punti di una data regione il potenziale è dato da V = a(xy+4y2),
con a = 10 V/m2. Calcolare la carica contenuta in un cubo di lato
L = 10 cm, disposto come in figura. (Suggerimento: usare la divergenza
di E)
SOLUZIONE. Calcoliamo il campo elettrico partendo dal potenziale:
y
x
dunque
e la carica contenuta nel cubo è
16
Fisica generale II, a.a. 2012/2013
ESERCITAZIONE A: ELETTROSTATICA
A
A.44. Il potenziale elettrico è nullo nel baricentro di un triangolo equilatero di
lato L =1 cm e nei tre vertici A, B, C della figura vale VA 7 V, VB = 2 V,
VC = 9 V; se il campo elettrico è uniforme, la componente Ex del campo
elettrico è stimata essere
(A) 0 kV/m (B) 1.1 kV/m
(C)1.2 kV/m
(D)1.2 kV/m (E) 1.6 kV/m
y
x
B
C
SOLUZIONE. Calcoliamo la componente Ex del campo elettrico partendo dal potenziale:
A.45. Tre cariche con il segno mostrato in figura e con
y
Q = 106 C sono fisse sull’asse x. La carica centrale è a
una distanza d = 1 m dalle cariche laterali. Un corpo
puntiforme, di carica q e massa m libero di muoversi
y0
q
normalmente all’asse x, si trova inizialmente nel punto
di ordinata y0 = 1 m.
La carica mobile
+Q
+Q
Q
(A) si muove verso la carica centrale fino a
x
raggiungerla.
d
(B) si allontana indefinitamente lungo l’asse y.
(C) sta ferma.
(D) si allontana inizialmente dall’asse delle x ma poi torna nella posizione iniziale compiendo
un moto oscillatorio.
(E) si avvicina inizialmente all’asse delle x ma poi torna nella posizione iniziale compiendo un
moto oscillatorio.
SOLUZIONE. Quando la carica q è o vicina all'asse delle x (y<d) prevale la repulsione della
carica negativa centrale; quando è molto lontana (y>>d), prevale l’attrazione essendo
complessivamente la carica sull’asse x positiva. Poiché il campo elettrico cambia direzione, vi è
certamente un punto di equilibrio lungo l’asse delle y dove il campo si annulla e in tale punto si
potrebbe avere l’equilibrio. Poiché per y=d la
forza è ancora repulsiva, la carica mobile
inizialmente si allontana (risposte B e D). Poiché Ep
per y=d l’energia potenziale è negativa, la carica
d
y
non può raggiungere l’infinito dove il potenziale
si annulla. Perciò la carica si allontana, torna
indietro, si allontana di nuovo compiendo un
moto oscillatorio. Calcoliamo il punto di
equilibrio lungo il semiasse positivo delle y
calcolando il potenziale lungo questo asse,
derivandolo rispetto a y per ottenere la
componente Ey e annullando tale derivata:
1
dV
2
1
2y
,
V ( y ) Q
0 2
2
2 3/ 2
2
2
y
dy
y
y
d
y
d
d
y 2 d 2 3 2 y y 2 d 2 22 / 3 y 2 y
1.305d
22 / 3 1
17
Fisica generale II, a.a. 2012/2013
ESERCITAZIONE A: ELETTROSTATICA
A.46. Una carica Q è al centro di un guscio sferico conduttore il cui raggio interno vale
Ri = 0.055 m e quello esterno Re = 0.075 m . Se il campo elettrico alla distanza d1 = 1 m dalla carica
Q vale in modulo E = 345 N/C (diretto verso l’esterno), il potenziale elettrico a d2 = 0.065 m dalla
carica vale (in V)
(A) 0
(B) 4600
(C) 5300
(D) 9800
(E) 11500
Q
A
B
P P A
A
P P
SOLUZIONE. Calcoliamo prima la carica Q considerando che a
distanza d1 all’esterno del guscio sferico, campo elettrico e potenziale
sono quelli di una carica puntiforme nel centro della sfera
|
|
Il potenziale in B è perciò
Il guscio è equipotenziale e il potenziale in P (a distanza d2 ) vale 4600 V.
18












