- I.1 -
I - FOTOMETRIA E COLORIMETRIA
1. L’intensità della luce
Nello studio dell’ottica geometrica ci si interessa soltanto della direzione dei raggi luminosi.
Nello studio della fotometria ci si occupa in primo luogo della quantità di luce, anche se
ovviamente la direzione è importante quando si deve calcolare l’intensità di illuminazione in
differenti punti.
La fotometria si occupa solo della sensazione visiva prodotta dalla radiazione. In generale il
flusso di radiazione emesso, per esempio, da un metallo incandescente, comprende energia
luminosa ma non solo questa. Ebbene, le forme di energia radiante che non stimolano la retina
dell’occhio non sono prese in considerazione dalla fotometria.
La sensazione visiva prodotta varia con la lunghezza d’onda della radiazione in misura rilevante
per due motivi. Differenti lunghezze d’onda danno luogo alla sensazione di differenti colori.
Inoltre, l’intensità della sensazione prodotta da un’uguale quantità di energia emessa varia
lungo lo spettro visibile. Nello spettro della luce bianca la porzione più brillante è posta tra il
giallo e il verde e la luminosità diminuisce rapidamente verso le due estremità rossa e violetta.
Se consideriamo una sorgente che emetta uguale energia a tutte le lunghezze d’onda e
facciamo un grafico della luminosità, ossia della sensazione visiva, in funzione della lunghezza
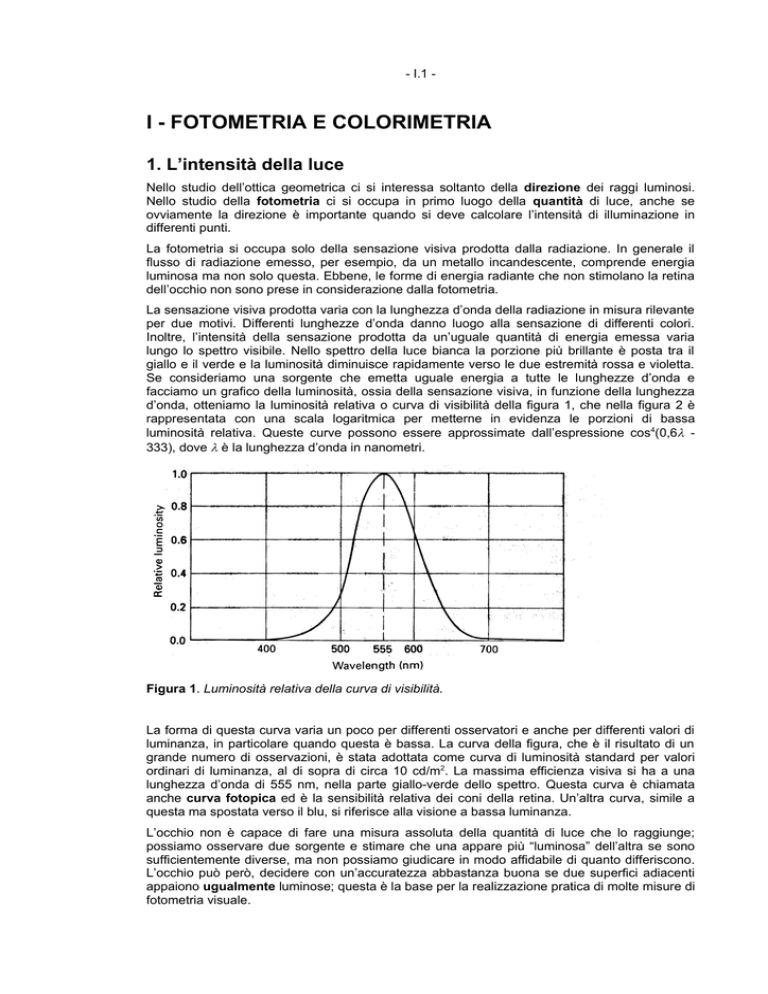
d’onda, otteniamo la luminosità relativa o curva di visibilità della figura 1, che nella figura 2 è
rappresentata con una scala logaritmica per metterne in evidenza le porzioni di bassa
luminosità relativa. Queste curve possono essere approssimate dall’espressione cos4(0,6λ 333), dove λ è la lunghezza d’onda in nanometri.
Figura 1. Luminosità relativa della curva di visibilità.
La forma di questa curva varia un poco per differenti osservatori e anche per differenti valori di
luminanza, in particolare quando questa è bassa. La curva della figura, che è il risultato di un
grande numero di osservazioni, è stata adottata come curva di luminosità standard per valori
ordinari di luminanza, al di sopra di circa 10 cd/m2. La massima efficienza visiva si ha a una
lunghezza d’onda di 555 nm, nella parte giallo-verde dello spettro. Questa curva è chiamata
anche curva fotopica ed è la sensibilità relativa dei coni della retina. Un’altra curva, simile a
questa ma spostata verso il blu, si riferisce alla visione a bassa luminanza.
L’occhio non è capace di fare una misura assoluta della quantità di luce che lo raggiunge;
possiamo osservare due sorgente e stimare che una appare più “luminosa” dell’altra se sono
sufficientemente diverse, ma non possiamo giudicare in modo affidabile di quanto differiscono.
L’occhio può però, decidere con un’accuratezza abbastanza buona se due superfici adiacenti
appaiono ugualmente luminose; questa è la base per la realizzazione pratica di molte misure di
fotometria visuale.
- I.2 -
Figura 2. Come la figura 1, con scala delle ordinate logaritmica.
Secondo la legge di Weber (1834) la minima differenza di luminosità apparente percepibile è
una frazione costante della luminosità. Questa frazione, nota come frazione di Fechner (1858)
è, in un grande intervallo di luminosità, pari a circa l’1%, e l’occhio può quindi distinguere tra
due superfici adiacenti che differiscono in luminosità per questa quantità.
In fotometria dobbiamo distinguere tra le seguenti quantità:
1. La quantità di luce emessa da una sorgente puntiforme, ossia il flusso luminoso e
l’intensità luminosa.
2. La quantità di luce ricevuta per unità di area su una superficie posta in una data posizione,
ossia l’illuminamento della superficie.
3. La quantità di luce emessa o riemessa per unità di area di una superficie, ossia la
luminanza della superficie.
Nel discutere queste misure si deve ricordare che nella fotometria pratica è raro che sia
necessario superare un’accuratezza dell’1%, pari alla frazione di Fechner. Gli esposimetri delle
macchine fotografiche, per esempio, hanno un’accuratezza intorno al 10%. L’intervallo di misura
può però estendersi su molti ordini di grandezza.
La fotometria prende in considerazione solo l’energia radiante che stimola la retina dell’occhio
umano in relazione alla sua risposta visiva. E’ quindi una parte della radiometria, una scienza
più ampia che considera la misura dell’energia radiante nelle bande del ultravioletto, del visibile
e dell’infrarosso attraverso tutte le lunghezze d’onda rilevabili. Al flusso luminoso come è
definito in fotometria, che come vedremo si misura in lumen, corrisponde in radiometria il flusso
di radiazione che si misura in watt. La relazione tra flusso luminoso misurato in lumen e flusso
di radiazione misurato in watt dipende dalla lunghezza d’onda: alla lunghezza d’onda di 555 nm
a cui si ha la massima sensibilità dell’occhio umano 1 W di flusso di radiazione corrisponde a
- I.3 685 lm di flusso luminoso, mentre nell’infrarosso o nell’ultravioletto a 1 W di flusso di radiazione
corrispondono 0 lm di flusso luminoso.
2. Flusso luminoso e intensità luminosa
Le sorgenti luminose più comuni sono sorgenti incandescenti, che emettono energia in
un’ampia gamma di lunghezze d’onda, soprattutto nella parte infrarossa dello spettro. Si tratta di
energia “sprecata” ai fini dell’illuminazione. Nel considerare la quantità di luce prodotta da una
sorgente, l’energia emessa deve essere valutata o “pesata” secondo la sua capacità di
stimolare la sensazione visiva in accordo con la curva di luminosità della figura 1. La misura del
flusso di luce da una sorgente è il flusso luminoso Φ della sorgente, la cui unità di misura è il
lumen (lm), che verrà definito più avanti.
Nessuna sorgente luminosa reale emette una distribuzione di luce uniforme in tutte le direzioni;
è quindi necessario definire la quantità di luce irradiata rispetto a una data direzione. Inoltre
nessuna sorgente luminosa reale emette luce in modo uniforme da ciascuna sua porzione; è
quindi necessario definire la quantità di luce irradiata rispetto rispetto a un punto della sorgente
o assumere che tutta la sorgente sia ridotta a un solo punto. Queste due esigenze possono
essere soddisfatte considerando il flusso emesso da una sorgente puntiforme entro un cono
corrispondente a un angolo solido di piccola ampiezza centrato intorno a una data direzione. La
concentrazione o densità di flusso luminoso per unità di angolo solido è detta intensità
luminosa I della sorgente in quella direzione. L’unità di misura dell’intensità luminosa è la
candela (cd). Se Φ è il flusso luminoso in lumen emesso entro un cono di angolo solido ω
steradianti, che deve essere al limite infinitamente piccolo, allora l’intensità luminosa in quella
direzione in candele è I = Φ/ω.
Ricordiamo che l’unità di misura dell’angolo solido, ossia lo steradiante (sr), è l’angolo solido
corrispondente a un cono che, con il vertice nel centro di una sfera, taglia sulla superficie della
sfera un’area pari al quadrato del suo raggio (figura 3). Il valore di un angolo solido qualsiasi in
steradianti è uguale all’area della superficie sferica compresa nell’angolo solido divisa per il
quadrato del raggio della sfera. Poiché l’area della superficie di una sfera di raggio r è 4πr2,
l’angolo solido per la sfera completa è pari a 4π sr.
Figura 3. L'unità di angolo solido: lo steradiante.
Si può dimostrare che per un cono avente un angolo di semiapertura θ piccolo l’angolo solido ω
è dato da
ω = 2π (1 – cos θ) = π sen2 θ
quando θ è piccolo
(1)
- I.4 Anche se nessuna sorgente luminosa è un punto geometrico, come richiesto dalla definizione di
intensità luminosa, in molti casi le dimensioni della sorgente sono trascurabili alla distanza a cui
si trova.
Esempio
La potenza emessa da un laser ad argon a 514 nm è 20 mW. Determinare il flusso luminoso di
questa sorgente. Ripetere il calcolo per un laser a elio-neon della stessa potenza che emette a
633 nm. Calcolare anche le loro intensità luminose considerando che emettano un fascio di luce
con una divergenza di 0,025°.
Dalla figura 1 ricaviamo che l’efficienza luminosa alla lunghezza d’onda del laser ad argon è
circa il 50% rispetto a quella alla lunghezza d’onda di massima efficienza di 555 nm per la quale
si ha un fattore di conversione di 685 lm/W. Il laser ad argon ha quindi un flusso luminoso di
0,50 × 685 × 0,020 = 6,85 lm
(Argon)
Per la lunghezza d’onda del laser a elio-neon l’efficienza luminosa è circa il 20%. Questo laser
ha quindi un flusso luminoso di
0,20 × 685 × 0,020 = 2,74 lm
(HeNe)
Nessuno di questi valori è particolarmente elevato.
Se entrambi i laser emettono un fascio con una divergenza di 0,025°, l’angolo di semiapertura
del cono di luce è 0,0125°, che per l’equazione (1) dà un angolo solido ω = 6 × 10-10 sr.
L’intensità luminosa è quindi 6,85 / (6 × 10-10) cd ≈ 1010 cd per il laser ad argon e 4 × 109 cd per
il laser a elio-neon. Questi valori sono molto elevati.
3. Illuminamento
Una superficie che riceve luce è detta illuminata, e l’illuminamento E in ogni suo punto è
definito come la densità di flusso luminoso in quel punto, ossia il flusso luminoso diviso per
l’area della superficie, quando questa è illuminata in modo uniforme. L’unità di misura
dell’illuminamento è il lux (lx) o lumen per metro quadrato (lm/m 2), ed è l’illuminamento di una
superficie perpendicolare alla direzione dei raggi luminosi posta a un metro distanza da una
sorgente che ha un’intensità luminosa di una candela.
Se Φ è il flusso da una sorgente luminosa al centro di una sfera di raggio d, l’illuminamento E
sulla superficie della sfera risulta, per definizione,
E=
=
Area della sfera 4 d 2
Poiché Φ/4π è l’intensità luminosa I, si ha
E=
I
d2
(2)
Si tratta della legge dell’inverso del quadrato della distanza. Deve essere chiaro che la formula
(2) si applica solo all’illuminamento ricevuto da una superficie normale alla direzione della luce
proveniente da una sorgente puntiforme, e che I è l’intensità luminosa della sorgente in quella
determinata direzione.
Si dimostra che se si applica la legge dell’inverso del quadrato della distanza a ciascuna parte
di una sorgente che non è puntiforme l’errore introdotto assumendo la sorgente puntiforme è
meno dell’1% se la distanza d è maggiore di 10 volte la dimensione massima della sorgente.
La figura 4 rappresenta la sezione di un fascio di luce proveniente da una sorgente puntiforme
B di intensità luminosa I che cade su una superficie LM perpendicolare al fascio di luce. Se Φ è
il flusso nel fascio di angolo solido ω, allora l’illuminamento della superficie alla distanza d dalla
sorgente è dato da
E=
I
=
= 2
2
Area di LM d d
- I.5 -
Figura 4. La legge del coseno dell'illuminamento.
Se la superficie è ruotata intorno al punto G nella nuova posizione L’M’, lo stesso flusso è
distribuito su un’area più grande, e l’illuminamento della superficie è ora
E'=
Area di L ' M '
Poiché l’illuminamento si riferisce a ogni punto della superficie, possiamo considerare un’area
L’M’ molto piccola rispetto alla sua distanza dalla sorgente, e quindi
Area di L ' M ' =
Area di LM Area di LM
=
cos LGL'
cos i
dove i è l’angolo di incidenza. Quindi
E'=
cos i
I
= cosi
Area di LM d 2
(3)
Perciò l’illuminamento di una superficie varia con il coseno dell’angolo di incidenza; la
legge dell’inverso del quadrato della distanza e la legge del coseno sono le due leggi
fondamentali della fotometria.
Nelle applicazioni pratiche della fotometria spesso si richiede di trovare l’illuminamento in diversi
punti di una superficie piana, come per esempio la superficie di una strada, un cartellone
illuminato, ecc. La figura 5 rappresenta una sorgente B di intensità luminosa I posta sopra una
superficie piana LM; l’illuminamento in ogni punto G’ della superficie sarà
E=
I i cos i
d i2
dove i è l’angolo di incidenza e Ii l’intensità luminoso della sorgente in quella direzione. Si ha
quindi
Figura 5. L'illuminazione di una superficie.
- I.6 -
E=
=
I i cos 3 i
d2
(4)
Ii d
(5)
d 3i
dove d è la distanza perpendicolare della sorgente dalla superficie.
Esempio
Una stanza di 5 m per 4 m è illuminata da una lampada da 100 candele sospesa al centro del
soffitto a un’altezza di 2,4 m dal pavimento. Trovare l’illuminamento del pavimento (s)
direttamente sotto la lampada e (b) in un angolo della stanza, assumendo che l’intensità
luminosa sia 100 cd in entrambe le direzioni e ignorando la luce riflessa dalle pareti.
(a) I = 100 cd
E=
d = 2,4 m
I 100
=
lx=17,4 lx
d 2 2,4
(b) La distanza GG’ (figura 5) dal punto del pavimento direttamente sotto la lampada all’angolo
della stanza è
G G '= x= 2,522 2 m= 10,25 m
La distanza della lampada dall’angolo della stanza è
d i = d x = 5,7610,25 m =4,00 m
2
2
Quindi, per l’equazione (5), si ha
E=
100×2,4
lx=3,75 lx
4,003
Esempio
La luce proveniente da una sorgente da 50 cd, che irradia in modo uniforme in tutte le direzioni,
cade su una lente sferica da +1 D con apertura di 50 mm posta a 500 mm dalla sorgente. Che
frazione del flusso totale della sorgente incide sulla lente? Quale sarà l’illuminamento su uno
schermo posto a 1 m dietro la lente, dalla parte opposta rispetto alla sorgente, perpendicolare
all’asse ottico della lente?
A 500 mm dalla sorgente il flusso totale è distribuito su una sfera di 500 mm di raggio, la cui
area è 4π × 5002 mm2. L’area dell’apertura della lente è π × 252 mm2. Quindi la frazione del
flusso totale ricevuta dalla lente è
×252
1
=
2
1600
4 ×500
Poiché la sorgente è a 500 mm da una lente da +1 D, si forma un’immagine virtuale della
sorgente 1 m davanti alla lente. Quindi il diametro della macchia di luce sullo schermo sarà due
volte il diametro della lente e la sua area quattro volte l’area della lente.
Il flusso totale emesso dalla sorgente è 4πI = 200π lm. Il flusso ricevuto dalla lente è 1/1600 del
flusso totale, ossia 8/π lm. L’area della macchia di luce sullo schermo è π × 502 mm2. Quindi,
trascurando l’assorbimento della luce attraverso la lente,
Illuminamento=
2
2
8××50
lm/mm =
1
2
2
lm/ mm =50 lm/ m =50 lx
20.000
- I.7 -
4. Luminanza
L’illuminamento si riferisce solo alla quantità di luce ricevuta da una superficie, a prescindere
dalla natura della superficie, ma in molti casi siamo più interessati alla quantità di luce emessa
in una data direzione da una superficie. La luce emessa per unità di area da una superficie è la
luminanza B della superficie. Essa dipende, nel caso di un corpo che non emette luce propria,
sia dall’illuminamento sia dalla frazione di luce incidente diffusa dalla superficie. Quest’ultima è
nota come coefficiente di diffusione-riflessione o albedo della superficie. La luminanza si può
riferire anche a una sostanza che trasmette luce diffusa, come il bulbo smerigliato di una
lampadina, o a una sorgente di luce estesa, come una fiamma o una lampada fluorescente.
Nella sua percezione della luminanza l’occhio interpreta il flusso come se provenisse da un’area
proiettata ad angolo retto rispetto alla direzione della visione (il sole o una lampada circondata
da un bulbo diffondente sferico appaiono all’occhio come un disco piatto), e la luminanza di una
superficie è definita come segue: la luminanza in una data direzione di una superficie che
emette luce è l’intensità luminosa misurata in quella direzione divisa per l’area di questa
superficie proiettata perpendicolarmente rispetto alla direzione considerata.
La luminanza è espressa in candele per metro quadrato. Questa unità di misura un tempo era
chiamata nit (nt).
Alcuni valori tipici di luminanza sono dati nella tabella 1.
Tabella 1. Luminanza di alcune sorgenti comuni.
Luminanza (cd/m2)
Cielo sereno
104
Cielo coperto
103
Cielo molto coperto
4 × 102
Candela
2 × 106
Filamento di lampadina da 2 × 106 a 3 × 107
Lampada ad arco
3 × 108
Sole
1,6 × 109
Luna
2,6 × 103
Lampada fluorescente 104
Il valore di 1,6 × 109 cd/m2 per la luminanza del Sole può sembrare strano. Poiché il Sole si
trova a 150 milioni di chilometri di distanza l’idea di considerare un metro quadrato della sua
superficie può sembrare piuttosto teorica. Se, però, un’apertura circolare di 1 m 2 fosse posta
abbastanza lontana da un osservatore perché il Sole apparisse riempirla esattamente,
l’intensità luminosa di questa superficie sarebbe di 1,6 × 109 cd, ossia di 1,6 × 109 lm/sr. Questa
intensità luminosa non sarebbe disponibile in tutto l’angolo solido di uno steradiante perché se
l’osservatore si muovesse non vedrebbe più il Sole riempire esattamente l’apertura circolare.
Se, però, l’apertura circolare fosse allontanata dall’osservatore, la sua luminanza rimarrebbe
invariata anche la dimensione dell’immagine sulla retina si ridurrebbe. Ciò non significa che
l’intensità di questa immagine retinica aumenti, perché l’intensità luminosa è misurata in lumen
per steradiante e allontanando l’apertura si riduce la frazione di angolo solido sottesa dalla
pupilla dell’occhio dell’osservatore. L’intensità (per unità di area) dell’immagine retinica rimane
quindi la stessa. (Questa intensità luminosa, con il valore della luminanza del Sole indicato nella
tabella, è naturalmente dannosa e può produrre facilmente una bruciatura della retina).
Tabella 2. Albedo di alcuni materiali comuni.
Materiale
Frazione di luce incidente riflessa
(misurata a 30° rispetto alla normale)
Ossido di magnesio
0,96
Celluloide bianca opaca 0,80 – 0,85
Carta bianca
0,80 – 0,85
Vetro opalizzato
0,76
Tessuto nero
0,12
Superficie lunare
0,07
Vernice nera
0,02 – 0,04
- I.8 Riferendosi ancora alla tabella 1, si vede che è indicata anche la luminanza della Luna. Non si
tratta di un corpo che emette luce propria e la sua luminanza apparente dipende dal suo albedo.
L’albedo della Luna e di altre superfici più a portata di mano è dato nella tabella 2.
A differenza della riflessione speculare, la riflessione diffusa (come indica il suo stesso nome)
significa che la luce è riflessa in un ampio intervallo di angoli. Un altro metodo per esprimere la
luminanza assume che la superficie sia un diffusore perfetto, ossia che appare ugualmente
brillante da qualsiasi direzione è osservato. Ciò significa che l’intensità luminosa per unità di
area apparente o proiettata è costante per tutti gli angoli. Poiché la superficie piana dell’area
proiettata è proporzionale al coseno dell’angolo tra la direzione di osservazione e la normale
alla superficie, l’intensità luminosa della superficie deve variare nella stessa proporzione. Ciò è
espresso dalla legge del coseno dell’emissione di Lambert (1727-1777) come segue: per
una superficie perfettamente diffondente l’intensità luminosa per unità di area della
superficie varia con il coseno dell’angolo tra la direzione di osservazione e la normale
alla superficie, in modo che la superficie appare ugualmente brillante da qualsiasi
direzione è osservata. Nessuna superficie soddisfa completamente a questo requisito, ma
alcuni materiali, come i rivestimenti di ossido di magnesio e i vetri opalizzati, hanno diffusioni
che si avvicinano all’ideale. Molte superfici si avvicinano a un diffusore perfetto quando l’angolo
di incidenza è piccolo e la direzione di osservazione è quasi normale. Queste superfici si dicono
“opache”.
Considerando la superficie come un diffusore perfetto, la luminanza è espressa in termini del
flusso luminoso totale in lumen emessi per unità di area (reale, non proiettata) della superficie.
Una superficie che emette o riflette 1 lm/cm2 ha una luminanza di un lambert, ma la luminanza
di un millesimo di questo valore, ossia il millilambert (mL) è un'unità di misura generalmente
più utilizzata. La corrispondente unità di misura metrica è l'apostilb (asb), ossia il lumen per
metro quadrato. Si può dimostrare che per una superficie perfettamente diffondente la
luminanza in lumen per unità di superficie è π volte la luminosità in candele per unità di
superficie: una superficie che ha una luminanza di 1 cd/cm2 ha una luminanza di π lambert.
Poiché l'illuminamento E di una superficie è il flusso in lumen ricevuto da un'unità di area della
superficie e di questo flusso una frazione r, che è il fattore di riflessione, è riflessa, la luminanza
di una superficie perfettamente diffondente illuminata è data da rE lumen per unità di area o rE/
π candele per unità di area.
Un altro modo di misurare della luminanza, che considera che la fotometria è basata su
parametri visuali, tiene conto della variazione del diametro della pupilla dell'occhio. Si introduce
il concetto di luminanza retinica da una sorgente estesa assumendo che la retina sia una
superficie regolare. Il valore è dato dalla formula
E=
Bt cos
k
(6)
dove B è la luminanza nella direzione di osservazione (in cd/m2), t è la trasmittanza dell'occhio,
α l'area della pupilla (in mm2), θ l'angolo di incidenza del raggio principale attraverso l'occhio, e
k una costante uguale all'area dell'immagine retinica (in m2) divisa per l'angolo solido del campo
visivo (in sr).
Normalmente cos θ è pari a uno e t e k sono costanti con valori tali che risulta che la luminanza
retinica può essere trovata moltiplicando la luminanza della scena in candele per metro
quadrato per l'area della pupilla in millimetri quadrati:
E(Td) = B(cd/m2) × α(mm2)
(7)
L'unità di misura della luminanza retinica così espressa si chiama troland (Td).
5. Sorgenti di luce standard
Poiché le misure di quantità fotometriche sono in larga misura confronti tra sorgenti è
necessario definire una sorgente standard allo stesso modo che per le altre unità di misura
fondamentali. Lo standard originale per l'intensità luminosa era la candela internazionale.
Nonostante la sua definizione accurata essa non era per nulla costante in intensità, e il suo
colore era notevolmente differente da quello delle sorgenti moderne. La candela come era
- I.9 definita originariamente ha solo interesse storico, anche se ne resta il nome. La candela venne
sostituita da varie lampade a fiamma, la principale delle quali fu la lampada Vernon Harcourt
che bruciava vapore di pentano con una stretta fiamma cilindrica e aveva un'intensità di 10
candele. Poi lo standard fu sostituito da una serie lampadine a filamento di carbone di
particolare costruzione, conservate nei laboratori di metrologia dei vari paesi.
Nel 1948 fu adottato un campione completamente nuovo. Esso è costituito da un piccolo
cilindro contenente platino fuso. La superficie del platino alla temperatura del "punto di
congelamento" del platino ha una luminanza costante. Un sessantesimo dell'intensità luminosa
da 1 cm2 di questa superficie è la candela, come ora è definita questa unità di misura
fondamentale del SI.
Come campioni di uso corrente vengono ora generalmente usate lampade elettriche a filamento
nelle quali il filamento è disposto in un piano perpendicolare al banco di misura fotometrico. Il
bulbo di vetro è notevolmente più grande di quelli usati ordinariamente per minimizzare
l'annerimento causato dal deposito di particelle metalliche sul vetro, e il filamento è
"invecchiato" con almeno 100 ore di funzionamento prima di poterlo utilizzare come campione.
La lampada è utilizzata con corrente costante e una tensione leggermente inferiore a quella
utilizzata per l'invecchiamento.
6. Il colore delle sorgenti luminose
Quando un materiale emette luce perché è caldo si dice che è incandescente. Un materiale
può essere reso incandescente indirizzando una fiamma su uno strato sottile di materiale non
combustibile o mediante il passaggio della corrente elettrica in un filo sottile di materiale
metallico.
Nelle normali lampadine e incandescenza la sorgente di luce è un filamento di tungsteno in cui
passa corrente elettrica. La resistività del materiale permette il riscaldamento del filamento fino
a una temperatura massima di 3500 K. A questa temperatura il tungsteno si ossiderebbe
rapidamente. Per evitarlo il filamento è racchiuso in un involucro di vetro vuoto o riempito con
un gas inerte. Anche con queste precauzioni il tungsteno tende lentamente a evaporare dal
filamento e a depositarsi sulla parete interna dell'involucro di vetro, riducendo la sua
trasmissività. quando il filamento si assottiglia al punto da spezzarsi si conclude la vita della
lampada, normalmente dopo alcune centinaia di ore di funzionamento. La vita della lampada
può essere allungata riducendo la tensione di funzionamento (sottovoltaggio), ma ciò abbassa
la temperatura di colore (si veda più avanti) e riduce anche l'efficienza della conversione della
potenza elettrica in luce. Funzionando alla tensione per cui è progettata una lampadina a
incandescenza ha normalmente un'efficienza tra 15 e 25 lumen per watt. Ciò rappresenta
un'efficienza di conversione di energia elettrica in energia luminosa compresa tra 8 e 13%.
L'efficienza aumenta aumentando la temperatura del filamento, ma la maggiore evaporazione
del filamento alle temperature più elevate ha costituito un ostacolo finché non si è inventata la
lampada al "quarzo-iodio" (più nota come lampada alogena). In questa lampada il gas inerte
contiene un alogeno, iodio o bromo, che ha la proprietà di ridepositare sul filamento il tungsteno
evaporato. Perché ciò avvenga è necessaria una temperatura molto elevata del bulbo della
lampada, che è perciò realizzato in quarzo anziché in vetro, e di dimensioni molto piccole in
modo che possa scaldarsi maggiormente; il quarzo comunque non gioca un ruolo attivo nel
funzionamento della lampada.
Sappiamo che, quando la luce è dispersa per formare uno spettro, ogni porzione dello spettro
consiste di luce una particolare lunghezza d'onda e quindi di una particolare frequenza. Vi è
perciò, nel caso dello spettro continuo della luce bianca, una gamma continua di lunghezza
d'onda che si estende, nella porzione visibile all'occhio umano, da circa 390 nm all'estremità
violetta a circa 760 nm all'estremità rossa dello spettro. Possiamo quindi specificare ogni colore
spettrale determinato dalla sua posizione nello spettro continuo della luce bianca in termini
della lunghezza d'onda corrispondente.
Lo spettro continuo della luce bianca si ottiene normalmente da un solido o un liquido
incandescenti. All'aumentare della temperatura aumenta la quantità di luce emessa, e allo
stesso tempo la sorgente cambia di colore passando dal rosso al bianco fino all'azzurro. Se si
fa un grafico dell'intensità a ciascuna lunghezza d'onda per una sorgente perfetta (corpo nero)
si ottengono curve che variano con la temperatura come nella figura 6.
- I.10 -
Figura 6. Radiazione di corpo nero.
E' quindi possibile specificare i colori dal rosso all'azzurro caratteristici di una sorgente
incandescente in termini di temperatura e si parla allora di temperatura di colore, normalmente
espressa in kelvin. Non è detto che si tratti di una temperatura reale; si si pone un filtro azzurro
davanti a una lampadina a incandescenza la parte rossa dello spettro sarà assorbita più di
quella blu e attraverso il filtro la temperatura di colore apparirà maggiore anche se la
temperatura della lampada resta la stessa. A causa dell'assorbimento dell'atmosfera la
temperatura di colore della luce solare può essere inferiore rispetto alla temperatura di 6000 K
della superficie del Sole. La temperatura di colore della maggior parte delle lampade è
compresa tra 2000 e 4600 K. Si fabbricano lampade campione a specificate temperature di
colore.
Alcuni valori tipici di temperature di colore sono dati nella tabella 3.
Tabella 3. Valori tipici di temperature di colore.
Temperatura (K)
Cielo azzurro chiaro
12.000 - 25.000
Cielo coperto
6.500
Cielo molto coperto
6.000
Candela
2.000
Lampadina a incandescenza 2.600
Lampada ad arco
4.000
Sole
5.000 - 6.000
Luna
3.000 - 4.000
Lampade fluorescenti
varie
Ogni temperatura di colore può essere espressa in termini del valore nella scala "mired"
(MIcroREciprocal Degree) che è dato da 106 diviso per la temperatura di colore in kelvin. L'uso
di questa scala è comodo perché è possibile assegnare ai filtri colorati usati per esempio in
fotografia un valore di "spostamento mired", che può essere positivo o negativo. La luce
emessa da lampade di differente temperatura di colore può essere convertita a una stessa
temperatura di colore utilizzando filtri con il corretto valore in mired. (Ciò si applica in modo
esatto nel caso di luce emessa da lampade a incandescenza, che emettono praticamente come
corpi neri, e in modo meno accurato nel caso di lampade fluorescenti, che hanno uno spettro
differente).
La luce del Sole filtrata dall'atmosfera terrestre, per esempio, ha una temperatura di colore
media di 5000 K, e quindi un valore mired di circa 200. Se il Sole è osservato attraverso un filtro
giallo che abbia uno spostamento mired pari a +120, si ottiene luce con un valore mired di 320,
- I.11 che è equivalente a una temperatura di colore di 3125 K. Quindi filtri mired con valori positivi
riducono la temperatura di colore (assorbono la componente blu dello spettro), mentre filtri
mired con valori negativi aumentano la temperatura di colore (assorbono la componente rossa
dello spettro). L'effetto di uno stesso filtro è più o meno significativo a seconda della
temperatura di colore della luce con cui è utilizzato: per esempio, un filtro con uno spostamento
mired pari a -60, se applicato alla luce solare con una temperatura di colore di 5000 K, produce
luce con una temperatura di colore di 7143 K (10 6/5000 - 60 = 200 - 60 = 140 = 10 6/7143), ma
se è applicato a luce con una temperatura di colore di soli 1000 K ne innalza la temperatura di
colore solo a 1063 K (106/1000 - 60 = 1000 - 60 = 940 = 106/1063).
E' conveniente riferirsi alla luce di ciascuna particolare frequenza o lunghezza d'onda in termini
della sensazione di colore a cui dà luogo quando è ricevuta da un occhio normale, ricordando
comunque che il colore è pura sensazione visiva. La luce che noi diciamo bianca è costituita da
una banda continua di lunghezza d'onda che dà luogo alla sensazione di bianco quando è
ricevuta dall'occhio. La predominanza di una o più porzioni di questa banda di lunghezza d'onda
dà luogo a sensazioni di colori distinti dal bianco. La luce di lunghezza d'onda da 760 nm a 620
nm dà la sensazione del rosso, da circa 580 nm a circa 510 nm la sensazione del verde, e così
via.
Che il tipo di sensazione non è specificamente determinato dalla lunghezza d'onda della
radiazione può essere verificato in diversi modi. Per esempio, la sensazione del giallo prodotta
da una radiazione alla lunghezza d'onda di 589 nm può essere provocata anche presentando
all'occhio una miscela di rosso puro e di verde puro, e quindi luce che non contiene vera
radiazione gialla. Anche la sensazione del bianco può derivare dalla miscela in opportune
proporzioni di determinate coppie di colori puri noti come colori complementari. Riprendere
questa discussione più avanti.
Ogni colore può essere specificato in termini di tre variabili, la tonalità (inglese "hue"), la
saturazione o purezza, e la luminosità. La tonalità è la proprietà che dipende dalla lunghezza
d'onda della luce. La saturazione dipende dalla quantità di bianco presente in aggiunta alla luce
che dà una certa tonalità; meno bianca è la luce è più saturo è detto il colore. Per esempio, per
una stessa tonalità possiamo avere il giallo saturo dello spettro, un giallo più pallido quando il
giallo saturo è miscelato con il bianco, e i diversi marroni quando viene ridotta la luminosità.
Nello spettro ci sono cinque diverse tonalità: rosso, giallo, verde, blu e viola. E' una tonalità
anche il porpora, che non si trova nello spettro, ma è formato dalla miscela di rosso e blu. Una
divisione dello spettro con le corrispondenti lunghezza d'onda è stata data da Abney (18441920) ed è riportata nella tabella 4.
Tabella 4. Divisione di Abney dello spettro.
Lunghezza d'onda (nm)
Viola
< 446
Oltremare
464 - 446
Blu
500 - 464
Verde-azzurro 513 - 500
Verde
578 - 513
Giallo
592 - 578
Arancione
620 - 592
Rosso
> 620
Più recentemente H.B. Tilton ha suggerito l'adozione di bande di tonalità di uguale ampiezza
contenenti ciascuna dieci lunghezze d'onda percepibili come differenti da un occhio normale
tranne che per il viola (otto lunghezza d'onda) e per il rosso (quindici lunghezze d'onda). I nomi
dati a queste tonalità e i loro limiti in lunghezza d'onda sono dati nella tabella 5.
- I.12 Tabella 5. Divisione di Tilton dello spettro.
Viola
Indaco
Blu
Ciano
Turchese
Verde
Smeraldo
Verde pallido
Giallo
Ambra
Ocra
Arancione
Mandarino
Scarlatto
Rosso
Lunghezza d'onda (nm)
388 - 429
429 - 458
458 - 481
481 - 499
499 - 513
513 - 528
528 - 546
546 - 561
561 - 575
575 - 586
589 - 599
599 - 610
610 - 622
622 - 636
636 - 782
Ci sono quindi 143 diverse tonalità che posso essere percepite nello spetto, che potrebbero
essere mostrate lungo il bordo della regione colorata della figura x se la qualità della stampa a
colori lo permettesse.
Il riscaldamento di una sorgente incandescente non è l'unico modo di ottenere emissione di
luce. Le sostanze fluorescenti hanno la proprietà di assorbire energia da elettroni, campi
elettrici, reazioni chimiche e anche dalla luce, in particolare dalla radiazione ultravioletta.
Riemettono poi questa energia sotto forma di luce. Le sostanze fluorescenti più comuni sono
solfati o ossidi o silicati o fosfati di metalli come zinco, calcio, magnesio, cadmio, tungsteno e
zirconio. Sono usate nelle lampade fluorescenti e negli schermi televisivi e in apparecchiature
più complesse come macchine per raggi X e microscopi elettronici.
Le sostanze fluorescenti sono usate nei tubi fluorescenti per ottenere una gamma di colori più
ampia di quelli che si possono ottenere con le lampade a incandescenza. Le lampade a
fluorescenti sono anche più efficienti di quelle a incandescenza, con efficienze luminose fino a
90 lm/W e minore produzione di calore. La luce è prodotta in un processo a due stadi nel quale
una scarica elettrica attraverso vapori di mercurio produce luce verde e ultravioletta; questa luce
ultravioletta è assorbita dal rivestimento fluorescente della parete interna del tubo di vetro che
contiene il gas ed è riemessa come luce bianca.
Negli schermi televisivi le sostanze fluorescenti sono scelte non solo in base al loro colore e alla
loro efficienza, ma anche in base alla rapidità di risposta. L'emissione di luce è stimolata da
elettroni di alta energia che colpiscono il rivestimento fluorescente all'interno dello schermo.
Poiché l'immagine cambia rapidamente è importante che la sostanza fosforescente inizi e
smetta di emettere luce molto rapidamente seguendo le variazioni di flusso degli elettroni.
Esistono lampade che restano sempre accese e non richiedono sorgenti esterne di energia.
Usano sostanze fluorescenti applicate all'interno di contenitori di vetro riempiti con trizio. Questo
è un isotopo radioattivo dell'idrogeno ed emette particelle beta di bassa energia (elettroni), che
sono assorbite dalla sostanza fluorescente e riemesse come luce.
7. Colorimetria
La composizione dei colori
Quando una miscela di luci di due o più colori raggiunge l'occhio, sono prodotte nuove
sensazioni di colore, e l'occhio non è capace di riconoscere i colori originari presenti nella
miscela. Luci di diversi colori si possono miscelare in diversi modi. Due o più proiettori con filtri
colorati possono essere disposti in modo da proiettare fasci di luce che si sovrappongono su
- I.13 uno schermo bianco. Un disco può essere colorato con settori dei colori da miscelare, e
ruotando velocemente il disco i colori si fondono e producono la sensazione corrispondente alla
loro miscela. Una versione perfezionata di questo metodo è il disco di Maxwell. Tre dischi
colorati di rosso, verde e blu-viola, ciascuno con una fessura radiale come nella figura 7,
possono essere riuniti per formare un unico disco, con tre settori, i cui angoli possono essere
variati ruotando uno dei dischi rispetto agli altri due.
Figura 7. Dischi di Maxwell.
Il risultato dell'addizione di colori può essere espresso in un modo generale come segue:
1. Rosso + verde + blu-viola = bianco
2. Rosso + verde = giallo
3. Verde + blu-viola = verde-azzurro
4. Rosso + blu-viola = porpora
Quindi
5. Giallo + blu-viola = bianco
6. Verde + porpora = bianco
Alterando la proporzione dei colori l'uno rispetto agli altri si producono tutte le tonalità; quindi,
partendo dal rosso e aggiungendo progressivamente quantità di verde, la tonalità cambia da
rosso a arancione, giallo, verde-giallo fino a verde. Aggiungendo quantità di blu-viola al verde la
tonalità cambia da verde attraverso varie tonalità di verde-azzurro e blu fino al blu-viola. Allo
stesso modo aggiungendo blu-viola al rosso si ha magenta, le varie porpore e viola.
Ogni coppia di colori che sommati insieme danno la sensazione del colore bianco costituisce
una coppia di colori complementari; quindi, come si è visto sopra, giallo e blu-violetto sono
complementari, e lo sono anche verde e porpora. In molti casi coppie di tonalità spettrali pure,
costituite da luce monocromatica, con opportune intensità relative, sono complementari. Alcune
di queste coppie complementari di lunghezze d'onda con le loro intensità relative come sono
state determinate da Sinden (1923) sono riportate nella tabella 6.
Tabella 6. Lunghezze d'onda e intensità relative di colori complementari.
Complementari
λ1
650
λ2
496 493,5 487,5 480,5 472 466,5
443
L1
42,1
53,4
73,8
85,5 92,2
94,2
97,5
L2
57,9
47,6
26,2
14,5
5,8
2,5
609
586 578,5 574
573 570,5
Luminosità relativa
8,0
Il colore della maggior parte degli oggetti è dovuto ad assorbimento selettivo. Quando la luce
bianca cade su una sostanza colorata opaca, parte di essa passa nella sostanza, mentre
- I.14 alcune frequenze sono riflesse per diffusione dalla superficie. Un oggetto rosso, per esempio,
illuminato con luce bianca, riflette parte della luce bianca dalla superficie, e per un piccolo
spessore all'interno della superficie diffonde il rosso e possibilmente anche l'arancio e il giallo,
mentre verde, blu e violetto sono assorbiti. Lo stesso oggetto illuminato con luce verde o blu
appare quasi nero, tranne che per la piccola quantità di luce di questi colori riflessa dalla
superficie. Le sostanze trasparenti colorate, come i vetri colorati, devono il loro colore a un
motivo simile, dato che per esempio un vetro rosso trasmette solo luce rossa e assorbe luce
degli altri colori.
Il colore di un oggetto dipende ovviamente dal colore della luce che lo illumina, e parlando del
colore di un oggetto ci riferiamo al colore che ha quando è illuminato con luce bianca.
I colori ottenuti per riflessione e trasmissione sono normalmente lontani dall'essere puri, ed
esaminati con uno spettroscopio appaiono contenere bande di frequenze a entrambi i lati della
tonalità prevalente. C'è normalmente anche una considerevole quantità di luce bianca riflessa
dalla superficie, e se questa è diffusa e si mischia con la luce colorata diffusa da sotto la
superficie il colore sarà meno saturo di quando la superficie è lucidata e la luce bianca viene
riflessa solo in una determinata direzione. Questo effetto si può notare osservando la differenza
di colore tra lo stesso legno o lo stesso marmo grezzo o lucidato.
Gli effetti che si hanno mescolando sostanze colorate, come i pigmenti, o combinando filtri
colorati, sono differenti da quelli che si ottengono miscelando luci colorate. E' noto, per
esempio, che la miscela di colori ad acquarello blu e giallo dà verde, mentre abbiamo visto che
l'addizione di luci blu e gialle dà la sensazione del bianco. La spiegazione è semplice: nel caso
dei pigmenti, le particelle blu, se illuminate con luce bianca, assorbono le lunghezze d'onda più
lunghe e riflettono il viola, il blu e il verde; le particelle di pigmento giallo assorbono il viola e il
blu e riflettono il verde, il giallo e il rosso. Una miscela dei due pigmenti quindi assorbirà o
sottrarrà dalla luce bianca tutto tranne il verde che viene riflesso. Se invece poniamo un filtro
rosso su una lampada e un filtro verde su un'altra lampada e proiettiamo le due luci su uno
stesso schermo bianco, la composizione additiva della luce produce la sensazione di giallo, ma
se i due filtri sono posti sulla stessa lampada non passa luce, perché la luce trasmessa da un
filtro è assorbita dall'altro.
Una grande quantità di colori può essere ottenuta dalla miscela di pigmenti di tre colori scelti
opportunamente, che sono noti come colori primari sottrattivi, distinti dai colori primari
additivi che abbiamo considerato sopra. I colori primari sottrattivi sono il magenta, il giallo e il
ciano. Della luce bianca il magenta riflette tutto tranne il verde, il giallo riflette tutto tranne il blu e
il viola, il ciano riflette tutto tranne il rosso e il giallo. Il risultato della sintesi additiva e sottrattiva
è mostrato schematicamente nella figura 8.
Figura 8. Sintesi additiva e sottrattiva.
I colori primari sottrattivi sono i colori usati nella stampa tricromatica. E' come si si fossero
riprese di un oggetto tre fotografie, una attraverso un filtro rosso, una attraverso un filtro verde e
una attraverso un filtro blu. Le stampe sono fatte dai tre negativi nei colori complementari a
quelli dei filtri, e le tre stampe sono poi sovrapposte. Poiché il filtro rosso trasmette solo luce
rossa, la parte scura di una stampa dal negativo preso attraverso il filtro rosso rappresenta
l'assenza di rosso, e una stampa da questo negativo è fatta quindi con "rosso negativo", ossia
ciano. Allo stesso modo la stampa dal negativo preso attraverso il filtro verde deve essere fatta
- I.15 in magenta, e la stampa dal negativo preso attraverso il filtro blu deve essere fatta in giallo. Se i
colori dei filtri e gli inchiostri sono scelti accuratamente si ha un'eccellente riproduzione dei
colori dell'oggetto originale. Sia il sistema della sintesi sottrattiva che della sintesi additiva sono
stati usati in fotografia, ma la sintesi sottrattiva è il sistema di gran lunga più utilizzato.
I diagrammi cromatici CIE 1931 e CIELAB (1976)
Il fatto che la maggior parte delle sensazioni di colore possa essere prodotta dalla miscela di tre
colori primari scelti opportunamente ha portato alla teoria tricromatrica della visione dei colori.
Questa teoria, avanzata prima da Young nel 1802 e poi elaborata da Maxwell e Helmholtz,
presuppone l'esistenza nella retina di tre tipi di ricettori, che quando sono stimolati danno
rispettivamente le sensazioni di rosso (ricettori di tipo L - "Long wavelengths"), verde (ricettori di
tipo M - "Medium wavelengths") e blu (ricettori di tipo S - "Short wavelengths"). Scegliendo un
metodo per associare tre numeri (valori di stimolo) a ciascun colore si definisce uno spazio di
colore. Ogni colore C può quindi essere espresso mediante un'equazione come (che esprime
la legge di Grassmann):
C = r(R) + g(G) + b(B)
dove r, g e b rappresentano la quantità di rosso, verde e blu richieste per ottenere quel colore.
Uno dei primi spazi di colore definiti matematicamente è stato lo spazio colore CIE XYZ, noto
anche come spazio di colore CIE 1931, creato dalla Commissione Internazionale per
l'Illuminazione (CIE) nel 1931. La sua definizione si basa su una serie di esperimenti compiuti
intorno al 1920 da W. David Wright e da John Guild e, come ora vedremo, è piuttosto
complessa.
I risultati sperimentali di Wrighr e Guild portarono alla specificazione di uno spazio di colore CIE
RGB, da cui viene derivato lo spazio di colore CIE XYZ. Nello spazio di colore CIE XYZ i valori
di stimolo non sono gli stimoli S, M e L dell'occhio umano, ma un insieme di valori X, Y e Z che
corrispondono ancora approssimativamente a rosso, verde e blu rispettivamente. Il fatto è che
due luci possono essere composte da differenti miscele di vari colori e apparire comunque dello
stesso colore (si tratta del fenomeno del metamerismo). Se due luci appaiono dello stesso
colore, significa che producono lo stesso insieme di stimoli S, M, e L, indipendentemente dalla
miscela di colori usata per produrle.
Poiché l'occhio umano ha tre tipi di ricettori che rispondono a differenti intervalli di lunghezze
d'onda, una rappresentazione grafica di tutti i colori visibili sarebbe una figura tridimensionale. Il
concetto di colore può però essere diviso in due parti: la luminosità e la cromaticità, che
comprende la tonalità e la saturazione. Il bianco, per esempio, è un colore luminoso, mentre il
grigio si può considerare come una versione meno luminosa dello stesso bianco: in altre parole,
la cromaticità del bianco e del grigio è la stessa, mentre è differente la loro luminosità.
Lo spazio di colore CIE XYZ è stato volutamente definito in modo che il parametro Y fosse una
misura della luminosità o luminanza di un colore. La cromaticità di un colore è quindi
specificata da due parametri x e y che sono funzioni dei tre valori di stimolo X, Y e Z:
x=
X
X Y Z
(8a)
y=
Y
X Y Z
(8b)
Lo spazio di colore specificato dai valori di x, y e è noto come spazio di colore CIE xyY ed è
molto usato in pratica per definire i colori. La figura 9 ne mostra il diagramma di cromaticità.
Il diagramma di cromaticità illustra diverse proprietà interessanti dello spazio di colore CIE
1931:
- Il diagramma rappresenta tutte le cromaticità visibili per un occhio medio. La regione che le
comprende è detta "gamut" (gamma) della visione umana. Il gamut di tutte le cromaticità visibili
nel diagramma CIE è una figura a forma di lingua il cui bordo curvo è il luogo spettrale, ossia il
luogo dei colori spettrali e corrisponde a luce monocromatica, con indicate le corrispondenti
lunghezze d'onda in nanometri. Il bordo retto della parte inferiore del gamut è detto linea delle
porpore. Questi colori non hanno una corrispondenza con luce monocromatica. I colori meno
saturati appaiono all'interno della figura con il bianco al centro.
- I.16 -
Figura 9. Il diagramma di cromaticità dello spazio di colore CIE 1931. Il bordo curvo esterno è il
luogo dei colori spettrali (o monocromatici), con le loro lunghezze d'onda indicate in nanometri.
- Tutte le cromaticità corrispondono a valori positivi di x e y (e quindi a valori positivi di X, Y e Z).
- Se si scelgono due punti sul diagramma di cromaticità, tutti i colori che si possono formare
miscelando questi due colori si trovano tra questi due punti su una linea retta che li congiunge.
Ne segue che il gamut dei colori deve avere una forma convessa. Tutti i colori che si possono
formare miscelando tra sorgenti si trovano all'interno di un triangolo che ha per vertici i punti
corrispondenti a queste tre sorgenti (e lo stesso per la miscela di più di tre sorgenti). Data quindi
tre sorgenti reali, la loro combinazione non può coprire tutto il gamut dell'occhio umano, perché
non ci sono tre punti all'interno del gamut che definiscono un triangolo che lo contenga tutto.
- Una miscela in parti uguali di due colori ugualmente luminosi non si trova generalmente nel
punto medio del segmento che li congiunge. Quindi la distanza sul diagramma di cromaticità xy
non corrisponde al grado di differenza tra due colori. Sono stati definiti altri spazi di colore (in
particolare CIELab) che soddisfano invece a questo requisito.
- La luce con uno spettro piatto corrisponde al punto (x, y) = (1/3, 1/3).
Vediamo allora come sono definite queste coordinate. Wright e Guild condussero
indipendentemente una serie di esperimenti con diversi osservatori, usando un diaframma
circolare del diametro di 2°, corrispondente all'ampiezza angolare della fovea dell'occhio
umano. Da una parte del campo era proiettato un colore di riferimento e dall'altra parte un
colore che poteva essere modificato dall'osservatore, consistente in una miscela di tre colori
primari ciascuno con cromaticità fissa, ma di luminosità regolabile.
All'osservatore era chiesto di modificare la luminosità di ciascuno dei tre colori primari fino a
ottenere la corrispondenza con il colore di riferimento. Non si poté con questa tecnica ottenere
la corrispondenza con tutti i colori di riferimento. Quando si verificava ciò, si aggiungeva una
quantità variabile di uno dei tre colori primari al colore di riferimento, cercando poi la
corrispondenza variando gli altri due colori primari. La quantità di colore primario aggiunta al
colore di riferimento era allora considerata un valore negativo. Si poté in questo modo coprire
tutta la gamma di percezione dell'occhio umano. Per i casi in cui il colore di riferimento è
monocromatico si può tracciare un grafico della quantità di colore primario usato in funzione
della lunghezza d'onda del colore di riferimento. Queste tre funzioni sono dette curve di
specificazione per quel particolare esperimento.
- I.17 Anche se gli esperimenti di Wright e Guild furono fatti con differenti colori primari a varie
intensità, e con un certo numero di osservatori differenti, tutti i loro risultati possono essere
riassunti dalle curve di corrispondenza CIE RGB
b ottenute usando
r , g
e
tre colori primari monocromatici alle lunghezze d'onda di 700 nm (rosso), 546,1 nm (verde) e
435,8 nm (blu), la cui posizione è mostrata nella figura 10.
Figura 10. Posizione dei colori primari utilizzati per ottenere lo spazio di colore CIE 1931.
Le curve di specificazione indicano la quantità di ciascun primario necessaria per ottenere i vari
colori monocromatici. Queste funzioni sono mostrate nei grafici della figura 11 (CIE 1931); si
noti che
r e g
b sono zero a 546,1 nm, e
sono zero a 435,8 nm, r e
e
sono
zero
a
700
nm,
perché
in
questi
casi
il colore di riferimento è uno dei
g
b
colori primari. Le lunghezza d'onda dei colori primari a 546,1 nm e 435,8 nm furono scelte
perché sono facilmente producibili con una lampada a vapori di mercurio. La lunghezza d'onda
di 700 nm, che nel 1931 era difficile da produrre con fascio di luce monocromatica, fu scelta
perché la percezione dei colori da parte dell'occhio cambia poco a quelle lunghezze d'onda, e
quindi piccoli errori nella lunghezza d'onda di questo colore primario avrebbero avuto un effetto
minimo sui risultati.
Figura 11. Le curve di specificazione RGB CIE 1931.
- I.18 Queste curve di specificazione definiscono quello che è detto "osservatore standard CIE 1931".
Si noti che anziché specificare la luminosità di ciascun colore primario, le curve sono
normalizzate in modo da avere la stessa area al di sotto di ciascuna di esse. Questa area è
fissata specificando che
∞
∞
∞
∫0 r d =∫0 g d =∫0 b d
Le curve di specificazione normalizzate sono quindi scalate nei rapporti 1:4,5907:0,0601
rispetto alle curve di specificazione reali relative alla luminanza della sorgente.
Lo spazio di colore che si ottiene con questa procedura è rappresentato nella figura 12.
Figura 12. Il diagramma di cromaticità dello spazio di colore CIE rg. Il triangolo rosso specifica
la trasformazione allo spazio di colore CIE XYZ con i vertici C b-Cg-Cr posizioni (0,0), (0,1), (1,0)
del nuovo spazio.
Figura 13. Le curve di specificazione standard XYZ CIE 1931.
Come si vede dalla figura 12, le coordinate cromatiche dei colori verde-blu assumono valori
negativi in questo spazio di colore. I membri della commissione incaricata della questione
ritennero che fosse più conveniente disporre di uno spazio di colore in cui i valori delle
coordinate cromatiche fossero sempre positivi e compresi tra 0 e 1, mantenendo sempre però il
punto corrispondente al bianco nella posizione (1/3, 1/3). Definirono perciò il nuovo spazio di
- I.19 colore CIE XYZ (quello rappresentato nelle figure 9 e 10), che si ottiene dallo spazio di colore
CIE RGB mediante una trasformazione geometrica tale che gli assi x e y del nuovo spazio
corrispondono rispettivamente ai segmenti Cb-Cr e Cb-Cg indicati in rosso nella figura 12. A
questi punti corrispondono nel nuovo spazio le coordinate (0,0), (0,1), (1,0). Le curve di
specificazione per lo spazio di colore CIE XYZ sono mostrate nella figura 13.
Un problema che è presente nello spazio di colore CIE 1931 è che non dà un modo immediato
per stimare differenze tra colori. Sarebbe desiderabile che la distanza tra due punti sul
diagramma di cromaticità corrispondesse al grado di differenza tra due colori. L'idea di misurare
le differenze tra colori fu sviluppata da D.L. MacAdam e portarono allo sviluppo di nuovi spazi di
colore, derivati dallo spazio di colore CIE 1931 XYZ, nei quale a uguali distanze corrispondono
uguali differenze di colore.
Uno spazio di colore che risponde a questa esigenza è lo spazio di colore CIELUV (il nome
esatto è CIE 1976 L*u*v*). I parametri che contraddistinguono un colore in questo sistema sono
la luminosità L* e i valori di u* e v* che hanno una corrispondenza con i valori di x e y del
sistema CIE 1931 ma si riferiscono a un punto di bianco relativo alla sorgente di luce utilizzata.
Una rappresentazione di questo spazio di colore è data nella figura 14.
Figura 14. Il diagramma di cromaticità dello spazio di colore CIELUV (1976).
Un secondo spazio di colore, che è attualmente considerato il modello più completo per la
descrizione della percezione cromatica dell'occhio umano, è denominato CIELAB (il nome
esatto è CIE 1976 L*a*b*). I tre parametri che contraddistinguono un colore in questo sistema
sono la luminosità L*, che ha un valore 0 per il nero e 100 per il bianco; la posizione tra
magenta e verde a*, con valori negativi per il verde e valori positivi per il magenta; la posizione
tra il giallo e il blu b*, con valori negativi per il blu e valori positivi per il giallo. Poiché CIELAB è
un modello tridimensionale, può essere rappresentato adeguatamente solo in uno spazio
tridimensionale. La figura 15 mostra tre sezioni dello spazio, rispettivamente per luminosità pari
a L* = 25, L* = 50 e L* = 75.
- I.20 -
Figura 15. Sezioni dello spazio CIELAB per luminosità pari a L* = 25, L* = 50 e L* = 75.
8. L'azione dei filtri
A meno che la luce non viaggi nel vuoto, c'è una continua riduzione della sua intensità dovuta al
mezzo attraverso cui passa. In pratica materiali trasparenti come il vetro e l'acqua possono
essere facilmente distinti da materiali opachi come il legno o i metalli, ma in realtà tutti i materiali
trasparenti assorbono anche la luce e ciò risulta evidente quando si ha a che fare con grossi
spessori. Non c'è luce sul fondo degli oceani e la trasmissione della luce attraverso uno
spessore di un metro di vetro ordinario è meno del 50%. Solo con tecniche di fabbricazione
molto particolari si ottengono fibre ottiche con una trasmissione del 50% su distanze dell'ordine
di 10 km. D'altra parte tutti i materiali opachi trasmettono la luce se sono sufficientemente sottili.
La maggior parte dei vetri assorbe poco la luce (tra 450 e 1000 nm), anche se alcuni tipi di vetro
con elevato indice di rifrazione tendono ad assorbire la luce blu. Quando si forniscono tabelle
della trasmissione ottica di un vetro è importante indicare lo spessore a cui i dati si riferiscono e
anche se ci sono o no perdite dovute alla riflessione sulle sue superfici. La figura 16 si riferisce
a campioni di vetro spessi 25 mm e non sono comprese le perdite per riflessione. I materiali
plastici trasparenti sono generalmente peggiori del vetro da questo punto di vista, perché non
solo assorbono di più ma anche perché tendono a diffondere la luce incidente.
Figura 16. Trasmissione di vetri ottici, riferita a spessori di 25 mm.
La trasmittanza T di un campione di materiale è definita come il rapporto tra l'intensità I della
luce trasmessa e l'intensità I0 della luce incidente:
T=
I
I0
(9)
- I.21 La dipendenza dell'assorbimento della luce dallo spessore del materiale non è lineare, ma
segue comunque una legge abbastanza semplice: se, per esempio, metà della luce è assorbita
nel primo millimetro di un materiale, metà della luce rimanente sarà assorbita nel secondo
millimetro, e così via. Quindi la trasmittanza di un materiale dipende dallo spessore nel modo
indicato dalla tabella 7.
Tabella 7
spessore (mm)
Trasmittanza
1
2
3
4
0,5
0,25
0,125
0,0625
5
6
0,03125 0,015625
L'equazione che descrive questa legge è
I = I0 e-αt
(10)
dove e = 2,718... è la base dei logaritmi naturali, t è lo spessore del materiale e α è il
coefficiente di assorbimento, che viene espresso in unità dell'inverso di una distanza, per
esempio in mm-1.
L'espressione (10) è una conseguenza della legge di Lambert, secondo la quale uguali
spessori di uno stesso mezzo assorbente omogeneo assorbono uguali frazioni della luce che le
attraversa. Quindi la luce che entra in una piccola sezione di un mezzo di spessore dt avrà la
sua intensità ridotta da I a I - dI in modo tale che
dI
=− dt
I
(11)
dove α è una costante. Se calcoliamo l'integrale di questa espressione, ossia
∫
dI
= − dt
I ∫
otteniamo
ln I = -αt + C
(12)
dove C è la costante di integrazione. Quando t è zero, l'intensità della luce trasmessa è uguale
all'intensità I0 della luce indicente, perciò deve essere C = ln I0. Facendo l'esponenziale
dell'equazione (12) si ottiene
I = I0 e-αt
(10)
che è l'espressione che si voleva dimostrare.
Nei materiali colorati il valore del coefficiente di assorbimento α dipende dalla lunghezza
d'onda. Si parla in questo caso di assorbimento selettivo. Materiali che assorbono fortemente
una parte dello spettro sono usati come pigmenti per fabbricare vernici ecc. Se piccole
percentuali di questi materiali sono inserite in materiali plastici di per sé trasparenti si ottengono
filtri di assorbimento. In ottica si usano spesso filtri di questo tipo per selezionare determinate
lunghezze d'onda combinandoli in modo da permettere il passaggio della luce tra due zone di
assorbimento adiacenti. La figura 17 mostra il risultato della sovrapposizione di due filtri di
assorbimento di materiali diversi, uno dei quali permette il passaggio della luce al di sopra di
una certa lunghezza d'onda mentre l'altro permette il passaggio della luce al di sotto di quella
lunghezza d'onda. Se lo spessore è aumentato, per esempio di un fattore 2 come mostra la
figura, la banda di trasmissione si restringe ma anche la trasmittanza massima diminuisce.
Si realizzano anche filtri nei quali la trasmittanza praticamente è la stessa per tutte le lunghezza
d'onda. Questi filtri sono detti filtri neutri. Se due di questi filtri hanno valori di trasmittanza per
esempio di 0,4 e 0,6, quando sono sovrapposti la trasmittanza risultante si trova moltiplicando
questi valori, e risulta quindi 0,24. Questo fatto ha portato al concetto di estinzione o densità
ottica, che è l'inverso del logaritmo decimale della trasmittanza. Perciò una trasmittanza del
50%, che significa che viene trasmessa metà della luce incidente, corrisponde a un'estinzione
pari a log10(1/0,5) ossia 0,3. L'uso dei valori di estinzione risulta comodo quando i valori di
trasmittanza sono molto piccoli, come risulta dalla tabella 8. Per ottenere l'effetto della
sovrapposizione di due filtri è necessario moltiplicare le loro trasmittanze, ma se si utilizzano le
estinzioni si devono invece sommare le loro estinzioni.
- I.22 -
Figura 17. Filtro passabanda: ....... assorbimento dei filtri componenti; ______ effetto risultante;
- - - - - effetto per uno spessore doppio.
Figura 18. Filtri ad assorbimento selettivo: A e B filtri passabanda; C e D filtri di conversione del
colore; E filtro ad assorbimento di calore.
La figura 18 rappresenta i valori di trasmittanza al variare della lunghezza d'onda per diversi tipi
di filtri. Le curve C e D rappresentano filtri di conversione della temperatura di colore. Si è già
accennato nel paragrafo 6 all'uso della temperatura per indicare la "bianchezza" di una
sorgente luminosa. Si era detto che filtrando parte della luce rossa la temperatura di colore
effettiva viene aumentata, mentre filtrando parte della luce blu la temperatura di colore viene
diminuita, e che la temperatura di colore viene espressa in mired, che è il reciproco della
temperatura di colore espressa in kelvin e divisa per 106: se per esempio il sole ha una
temperatura di colore di 5000 K, questo valore corrisponde a 200 mired. Il filtro C della figura 18
ha uno spostamento mired di +120, e quindi se il sole è osservato attraverso questo filtro la sua
temperatura di colore risulta pari a 200 + 120 = 320 mired, che corrisponde a 3125 K (ossia
circa la temperatura di colore di una lampadina a incandescenza). Il filtro D ha invece uno
spostamento mired di -60 e quindi aumenta la temperatura di colore.
Il filtro E è un filtro ad assorbimento di calore. Filtri di questo tipo vengono usati nei proiettori
nei quali il contenuto di radiazione infrarossa della radiazione emessa dalla lampada potrebbe
danneggiare la pellicola della diapositiva. Un filtro ad assorbimento di calore trattiene questa
energia scaldandosi, e deve quindi essere raffreddato mediante una ventola.
- I.23 -
Esercizi
1. L’illuminamento della Terra da parte della Luna piena è di 0,2 lm/m 2 e la distanza della Luna
è di 384.000 km. Calcolare la sua intensità luminosa.
2. Come varia l’illuminazione di un punto su uno schermo (a) con la distanza del punto dalla
sorgente; (b) con l’angolo di incidenza della luce? Una piccola sorgente di 100 cd è
sospesa 1,5 m sopra un tavolo orizzontale. Disegnare un grafico che mostri come
l’illuminazione sul tavolo prodotta dalla luce diretta della lampada varia lungo una linea retta
che passa direttamente sotto la sorgente.
3. Distinguere l’intensità della sorgente e l’intensità di illuminazione. Come può essere
misurata la seconda e con che unità di misura? Una superficie riceve luce normalmente da
una sorgente a una distanza di 2,82 m. Se la sorgente è avvicinata a una distanza di solo
2,0 m, di che angolo deve essere ruotata la superficie per ridurre l’illuminamento al valore
originario?
4. Una sorgente puntiforme di luce di 20 cd è posta a 50 cm da uno specchio piano e lungo la
normale al suo centro. Se lo specchio riflette il 90% della luce incidente, calcolare
l’illuminamento su uno schermo a 3 m dallo specchio e parallelo ad esso.
5. Una piccola sorgente di 30 cd è posta a 10 cm da una lente da +5 D che ha un diametro di
10 cm. Trovare l’illuminamento su uno schermo posto a 1 m dalla lente, trascurando le
perdite per riflessione o assorbimento nella lente. Che variazione di illuminamento si
produce riducendo l’apertura della lente a un diametro di 5 cm?
6. La luce proveniente da una lente che ha un diametro di 40 mm converge in un punto a 75
cm dalla lente. Trovare il diametro del fascio a 15, 30 e 80 cm dalla lente. Confrontare
l’illuminamento di uno schermo in queste tre posizioni.
7. Enunciare la legge di Lambert sulla variazione dell’emissione di luce con la direzione. Una
superficie incandescente A perfettamente diffondente di area 1 mm2 e luminanza 20 cd/mm2
è posta parallelamente a 50 cm da uno schermo, con il segmento AB normale allo schermo.
Trovare: (a) l’intensità luminosa della superficie A in candele lungo una direzione AC
inclinata di 30° rispetto alla normale AB, (b) l’illuminamento in lumen per metro quadrato
sullo schermo (i) in B, e (ii) in C (il punto in cui il segmento AC incontra lo schermo).
8. Due lampade, una delle quali di 10 cd, sono poste alle estremità opposte di un banco ottico
lungo 2 m e uno schermo posto tra di esse risulta essere illuminato allo stesso modo dai
due lati quando si trova a 80 cm dalla lampada da 10 cd. Trovare l’intensità luminosa
dell’altra lampada.
9. Una piccola sorgente di luce con un’area di 2 mm 2 è posta a 20 mm da un obiettivo di
condensatore da +60 D del diametro di 40 mm. Il flusso luminoso che cade sul
condensatore dalla sorgente è di 40 lm. Trovare la luminanza della sorgente in candele per
millimetro quadrato e, assumendo che non ci siano perdite, l’illuminamento dell’immagine
della sorgente in lumen per metro quadrato.
10. Due lampade rispettivamente da 30 e 20 cd sono poste a 2 m l’una dall’altra. Trovare la
posizione, su una linea che le congiunge, dove uno schermo sarebbe ugualmente illuminato
dalle due lampade.
11. Spiegare che cosa si intende per superficie perfettamente diffondente. La luminanza di una
superficie piana perfettamente diffondente di area 2 mm2 è di 25 cd/mm2. Qual è l’intensità
luminosa lungo (a) la direzione normale, (b) una direzione inclinata di 60° rispetto alla
normale? Se la luce che lascia la superficie normalmente incide s uno schermo circolare del
diametro di 1 cm a 50 cm dalla sorgente, quale flusso luminoso, in lumen, riceve lo
schermo?
12. Un diffusore uniforme è una superficie che ha la stessa luminanza in tutte le direzioni.
Mostrare che, per una tale sorgente di luce, l’intensità luminosa varia con il coseno
dell’angolo tra quella direzione e la normale alla superficie. Una tale sorgente, di piccola
area, è sospesa parallelamente sopra un tavolo orizzontale a 2 m da esso. L’illuminamento
sul tavolo in un punto A verticalmente sotto la sorgente è 5 lm/mm2. Trovare l’illuminamento
sul tavolo in un punto B a 1 m da A.
- I.24 13. La luce proveniente da una sorgente da 50 cd entra in un occhio con un diametro effettivo
della pupilla di 3 mm; la sorgente è a 50 cm dall’occhio. Quale flusso luminoso, in lumen,
entra nell’occhio?
14. Calcolare l’illuminamento sul pavimento a metà strada tra due lampioni distanti 100 m e alti
5 m, ciascuno con un’intensità luminosa di 450 cd nella direzione considerata. Esprimere il
risultato in lumen per metro quadrato.
15. Due pezzi di vetro, uno blu e l’altro giallo, sono sovrapposti. Che colore si vede? Se i due
pezzi di vetro sono posti uno a fianco dell’altro, non sovrapposti, davanti a una lampada,
che colore si proietta su uno schermo? Spiegare i due casi.
16. Spiegare perché è possibile con due colori spettrali opportunamente scelti (per esempio
rosso e verde) ottenere lo stesso effetto che si ha con la luce solare che contiene tutti i
colori dello spettro.
17. Le lettere di un cartellone stampate con inchiostro rosso scompaiono completamente se
osservate attraverso un vetro rosso. Lo stesso avviene con le lettere stampate su un
cartellone con inchiostro giallo se illuminate con la luce gialla di una lampada al sodio.
Spiegare questi fatti.
18. Spiegare quanto segue: (a) vernice blu e gialla mescolate insieme producono vernice gialla,
ma luci blu e gialle proiettate insieme su uno schermo producono luce bianca; (b) il fumo
emesso dall’estremità di una sigaretta accesa appare blu mentre il fumo che esce dalla
bocca del fumatore appare grigio; (c) materiali con colori saturi e brillanti possono essere
ottenuti nelle tonalità rosso-arancio-giallo, ma nelle tonalità verde-blu si possono ottenere
colori saturi ma non brillanti.