CIRCUITO PURAMENTE RESISTIVO
Un circuito si dice puramente resistivo quando è dotato di resistenza puramente
ohmica ed ha induttanza e capacità nulle o trascurabili.
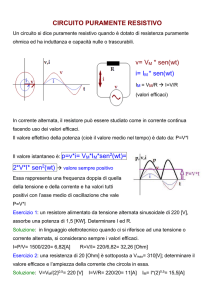
v= VM * sen(wt)
i= IM * sen(wt)
IM = VM/R I=V/R
(valori efficaci)
In corrente alternata, il resistore può essere studiato come in corrente continua
facendo uso dei valori efficaci.
Il valore effettivo della potenza (cioè il valore medio nel tempo) è dato da: P=V*I
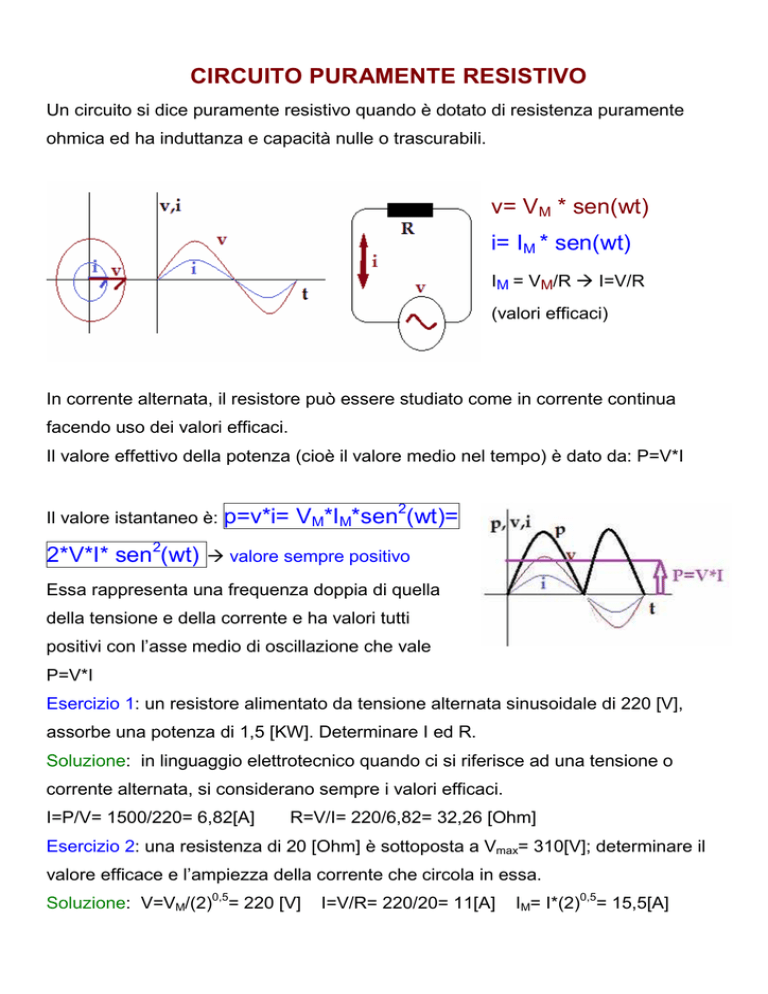
Il valore istantaneo è:
2*V*I* sen2(wt)
p=v*i= VM*IM*sen2(wt)=
valore sempre positivo
Essa rappresenta una frequenza doppia di quella
della tensione e della corrente e ha valori tutti
positivi con l’asse medio di oscillazione che vale
P=V*I
Esercizio 1: un resistore alimentato da tensione alternata sinusoidale di 220 [V],
assorbe una potenza di 1,5 [KW]. Determinare I ed R.
Soluzione: in linguaggio elettrotecnico quando ci si riferisce ad una tensione o
corrente alternata, si considerano sempre i valori efficaci.
I=P/V= 1500/220= 6,82[A]
R=V/I= 220/6,82= 32,26 [Ohm]
Esercizio 2: una resistenza di 20 [Ohm] è sottoposta a Vmax= 310[V]; determinare il
valore efficace e l’ampiezza della corrente che circola in essa.
Soluzione: V=VM/(2)0,5= 220 [V]
I=V/R= 220/20= 11[A]
IM= I*(2)0,5= 15,5[A]
CIRCUITO PURAMENTE INDUTTIVO
Un circuito si dice puramente induttivo quando presenta un certo valore di induttanza
ed ha resistenza e capacità nulle. Si tratta di un circuito ideale dal momento che in
pratica non è realizzabile.
La presenza dell’induttanza produce una tensione autoindotta avente per effetto la
limitazione della corrente che, altrimenti, a causa della resistenza nulla, tenderebbe
ad aumentare all’infinito.
Reattanza induttiva XL= w*L= 2*¶*f*L [Ohm]
Dimostrazione U.M.: w=[rad/sec]=[1/s] ~ E=-∆ c/∆t ∆ c= E*∆t= [V*s]
~ L= ∆ c/ ∆IL=[V*s/A]
I=V/XL
XL=w*L= [1/s*V*s/A] = [V/A]=[Ohm]
v = XL* I = XL*IM*sen(wt+¶/2)
La potenza attiva media è nulla P=0 in quanto
p=v*i= VM*IM*senwt*coswt= V*I*2*senwt*coswt=
V*I*sen(2wt). E’ una sinusoidale con valore medio
nullo, ma andamento alternativo a frequenza doppia di
quella della tensione e della corrente.
Si definisce potenza reattiva e si indica con il simbolo Q:
Q= V*I*senΘ
[voltamperreattivi= VAr]
Essa rappresenta la potenza che si scambia tra generatore e circuito in conseguenza
della circolazione della componente di corrente in quadratura con la tensione.
Questa provoca solo un<<palleggio>> di energia tra il generatore e l’utilizzatore, ma
deve essere comunque considerata dal momento che comporta perdite per effetto
Joule.
Esercizio: un induttore di induttanza L=0,5[H] è alimentato alla tensione alternata
sinusoidale di 100[V] a frequenza f=50[Hz]. Determinare I,Q
Soluzione: XL= 2*¶*f*L = 2*3,14*50*0,5 = 157[Ohm] I=V/XL=100/157=0,637[A]
Q=V*I*senΘ= 100*0,637*1=63,7[VAr]
in quanto sen(90°)=1
CIRCUITO PURAMENTE CAPACITIVO
Un circuito si dice puramente capacitivo quando presenta un certo valore di capacità
ed ha resistenza e induttanza nulle. Si tratta di un circuito ideale.
La tensione alternata produce nel circuito una corrente in anticipo di fase rispetto ad
essa di ¶/2. Tale passaggio di corrente è dovuto alla successione di cariche e
scariche che subisce il condensatore.
Reattanza capacitiva Xc=1/(w*C) =1/(1/s*(A*s/V))=V/A=[Ohm]
Sapendo che C=Q/V=[A*s/V]
~ ( I=Q/s Q=I*s=[A*s] )
V=Xc*I
esprime la legge di Ohm per un circuito capacitivo
La potenza attiva media è nulla P=0
V= VM*sen(wt) i=IM*cos(wt) p= v*I = VM*IM*sen(wt)cos(wt) = V*I*sen(2wt)
Tale espressione è identica a quella ricavata per l’induttore.
Al condensatore si attribuisce una potenza reattiva Q=V*I*senΘ [VAr].
Tale potenza è di segno opposto a quella induttiva perché la corrente qui è in anticipo
sulla tensione anziché essere in ritardo.
Esercizio: un condensatore di capacità C=10[µF] è alimentato a tensione alternata
sinusoidale di 220[V] a frequenza f=50[Hz]. Determinare I, Q.
Soluzione: Xc = 1/(2*¶*f*C) = 1/(2*3,14*50*10*10-6) = 318 [Ohm]
I=V/Xc=220/318= 0,692[A] ~ Q=V*I*senΘ= 220*0,692*1= 152 [VAr]
~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~
Esercizio 1: un forno a resistenza è collegato ad una rete a 220[V] e sviluppa una
potenza termica di 550 [Cal/h]. Determinare P, I, R
Soluzione: P = 550 [Cal/h] =550*4186/3600 = 639 [W]
P=V*I I=P/V= 639/220= 2,9[A] V=R*I R=V/I= 220/2,9= 76 [Ohm]
~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~
Esercizio 2: un induttore di 1,5[H] è alimentato da una tensione V=220[V] ed assorbe
una corrente di 1[A]. Determinare XL, f
Soluzione: V=XL*I XL= V/I= 220/1 = 220 [Ohm] { reattanza induttiva }
XL= w*L= 2*¶*f*L [Ohm] f=XL/(2*¶*L)= 220/(2*3,14*1,5)= 23,3 [Hz]
~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~
Esercizio 3: un induttore è alimentato da una tensione V=125 [V] a frequenza
f=50[Hz] ed assorbe una corrente di 0,5[A]. Determinare XL, L
Soluzione: V=XL*I XL= V/I= 125/0,5 = 250 [Ohm] { reattanza induttiva }
XL= w*L= 2*¶*f*L= 2*3,14* 50*L= 250 [Ohm] L = 250/(2*3,14*50) = 0,796[H]
~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~
Esercizio 4: un condensatore è alimentato da una tensione V=160 [V] a frequenza
f=50[Hz] ed assorbe una corrente di 0,2 [A]. Determinare XC, C
Soluzione: VC=XC*I XC= VC/I= 160/0,2 = 800 [Ohm] { reattanza capacitiva}
XC= 1/(w*C) C = 1/(2*¶*f*XC) = 1/(2*3,14*50*800*10-6)= 4 [µF]