Esame di Probabilità ed Inferenza Statistica
12 Giugno 2003
docente: Prof.ssa J. Mortera
Cognome __________________
Nome
__________________
Matricola __________________
I quesiti in corsivo hanno carattere teorico. La prova si ritiene superata se si raggiunge la
sufficienza sia sugli esercizi sia sulla parte teorica.
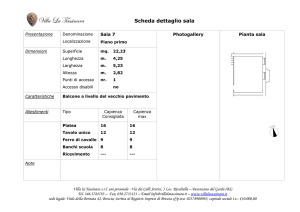
1. [6] Nel 1976 venne condotto un esperimento negli Stati Uniti per valutare se aiutare
gli ex carcerati durante i primi mesi dopo la scarcerazione poteva evitare la recidività.
a) 592 ex carcerati (gruppo di trattamento) vennero aiutati con diversi contributi
economici e il 48,3% di questi venne nuovamente arrestato dopo un anno dal
rilascio. 154 ex carcerati (gruppo di controllo) non vennero supportati in alcun
modo e il 49,4% di questi venne nuovamente arrestato dopo un anno dal
rilascio. Il supporto economico ai detenuti rilasciati riduce la recidività?
Trovare il livello di significatività osservato.
b) Nel primo anno dopo la scarcerazione i soggetti assegnati al gruppo di
trattamento lavorano in media per 16,8 settimane (con una standard deviation
di 15,9 settimane), contro le 24,3 settimane del gruppo di controllo (con una
standard deviation di 17,3 settimane). Un ex carcerato che viene sostenuto
economicamente (gruppo di trattamento) tenderà a lavorare di meno? Usare un
livello di significatività del 1%.
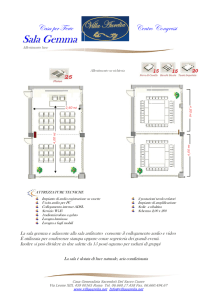
2. [6] Nel cinema multisala “Chenoia” ci sono due sale. Paola ha deciso di andare a
vedere il film che viene proiettato nella sala B, ma è in ritardo. Sa che la probabilità di
trovare ancora un posto nella sala A è pari a 0.3, la probabilità di trovarlo in almeno una
delle due sale è 0.7 e la probabilità che vi sia ancora un posto nella sala B sapendo che c’è
ancora un posto nella sala A è 0.6.
a. Calcolare la probabilità che sia posto sia nella sala A che nella sala B.
b. Qual è la probabilità che Paola riesca a vedere il film che proiettano nella sala B?
c. Come cambia tale probabilità se sappiamo che la sala A è già completa?
2. [6] Il numero di clienti che si presentano ad uno sportello bancario in un giorno è descritto
da una variabile casuale X con distribuzione di Poisson di parametro , cioè
x
, x0 e 0
f ( x; ) e
x!
Al fine di stimare , è stato rilevato per cinque giorni il numero di clienti che si sono
presentati a questo sportello e si è osservato: 12, 10, 4, 10, 18.
a) Determinate lo stimatore di massima verosimiglianza di .
b) Calcolarne la stima in corrispondenza del campione osservato.
c) Definire la proprietà di consistenza di uno stimatore. Lo stimatore trovato è anche
consistente?
3. [4] Illustrare le principali proprietà della distribuzione normale e motivare la rilevanza
della distribuzione normale nell’inferenza statistica.
4. [4] Sia X1, X2, . . ., Xn un campione casuale di ampiezza n, calcolare (non ommetendo i
passaggi) E( X ) e var( X ).
1
3. [6] Sia ( X 1 , X 2 , X 3 ) un campione casuale estratto da una popolazione X con
distribuzione di Poisson di parametro . Dati i due stimatori di :
T1
2X1 X 2 2X 3
X X3
e T2 1
5
2
a) Stabilire se sono non distorti.
b) Ricavare l’errore quadratico medio di T1 e T2 .
c) Quale tra i due stimatori è preferibile? Perché?
4. [3] Presa una variabile casuale X di media e varianza 2, dimostrare che la variabile
standardizzata Z ha media pari a zero e varianza pari uno.
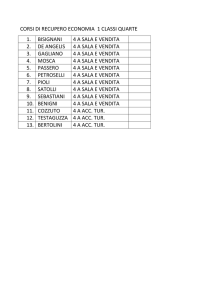
5. [5] Nella contea di Alameda, California, viene condotta un'indagine per valutare se i
soggetti che appartengono alle liste dei possibili giurati sono rappresentative della
popolazione con riferimento alle caratteristiche socio-demografiche. Per quanto
riguarda l'età si ha la tabella seguente:
Età
21-40
51-60
51-60
61+
Percentuale nella popolazione
42
23
16
19
100
Numero di giurati
5
9
19
33
66
Verificare se il campione di giurati è conforme alla composizione della
popolazione . Usare un livello di significatività dello 0,1%.
2