Transistori a effetto di campo.
Sommario
Introduzione ......................................................................................................................................... 2
Transistor Metal Oxide Semiconductor (MOS) .................................................................................... 2
Capacità dell’ossido per unità di superficie COX............................................................................ 3
Introduzione del concetto di tensione di banda piatta V FB .......................................................... 3
Regione di accumulazione ............................................................................................................ 5
Regione di svuotamento ............................................................................................................... 6
Regione di inversione ................................................................................................................... 6
MOSFET nMOS e pMOS ....................................................................................................................... 8
Condizione di banda piatta ................................................................................................................ 10
Regioni di funzionamento di un transistor nMOS ............................................................................. 11
Interdizione (OFF): VGS < VTn ........................................................................................................... 11
Transistor attivo (ON): VGS > VTn ..................................................................................................... 12
Regione lineare (LIN, ON): VGS > VTn, VGD > VTn, 0 < VDS < VDSAT, VSB = 0 ...................................... 12
Staurazione (SAT, pinch-off): VGS > VTn, VGD < VTn, VDS > VGS - VTn, VSB = 0 .................................. 13
Modello regionale nMOS ................................................................................................................... 14
Modello regionale pMOS ................................................................................................................... 16
Effetto Body, modulazione della lunghezza di canale e MOSFET in commutazione ................. 17
Caratteristiche statiche ingresso-uscita ............................................................................................. 20
Amplificatore a source comune (SC) .............................................................................................. 20
Confronto Mosfet vs. BJT............................................................................................................ 22
Configurazione a carico saturo ....................................................................................................... 23
Complementary MOS (CMOS)............................................................................................................ 24
Introduzione
In questa sezione sono discusse le caratteristiche dei Field Effect Transistor (FET), cioè, dei
cosiddetti transistori ad effetto di campo. Il dispositivo a stato solido maggiormente utilizzato nei
circuiti ad alto livello di integrazione (VLSI) come microprocessori e memorie è il Metal Oxide
Semicondutor FET (MOSFET).
Transistor Metal Oxide Semiconductor (MOS)
La struttura di un condensatore MOS è mostrata in Figura 1. È presente un gate metallico (spesso
in alluminio) o in silicio policristallino molto drogato (Metal), un layer di ossido (Oxide),
solitamente biossido di silicio SiO21, e un substrato di silicio detto bulk o body o back contact
(Semicondutor): si tratta di una struttura simile a quella di un condensatore.
Figura 1. Struttura del condensatore MOS con substrato di tipo p.
Tale particolare struttura consente di realizzare una capacità non lineare, funzione della tensione
applicata all’elettrodo di gate VG:
Essendo il substrato a massa, VG è proprio la differenza di potenziale tra gate e bulk, cioè:
L’analisi del comportamento qualitativo del MOS è propedeutico alla comprensione del MOSFET.
Variando VG si ottiene una variazione della carica associata alla regione di semiconduttore
(substrato di tipo p). Questo comportamento si modella introducendo la capacità non lineare
1
Il biossido di silicio è un ottimo isolante che si può realizzare facilmente per ossidazione termica del substrato di
silicio. Questa capacità da parte del silicio di variare da conduttore a isolante, oltre alla sua abbondante presenza sulla
superficie terrestre, lo rende il componente maggiormente utilizzato nell’elettronica integrata.
funzione di VG di cui all’Equazione (1). Al variare di VG si hanno le tre possibili situazioni descritte in
Figura 3.
Capacità dell’ossido per unità di superficie COX
Sfruttando la formula del condensatore a facce piane e parallele, si può ricavare l’espressione della
capacità dell’ossido per unità di superficie associata al condensatore MOS:
Dove εox è la costante dielettrica dell’ossido che separa il gate dal substrato, mentre tox è lo
spessore dell’ossido.
Introduzione del concetto di tensione di banda piatta VFB
Trascuriamo il sottile strato di isolante. Per capire cos’è la tensione di banda piatta, occorre
approfondire la giunzione metallo-semiconduttore, sfruttata, come visto, per realizzare un diodo
Schottky2. Sappiamo che nei metalli il livello di Fermi EF cade all’interno di uno strato continuo di
stati energetici permessi, mentre nei semiconduttori cade tra banda di valenza e conduzione, nella
regione dove non vi sono strati energetici permessi. A causa dei diversi potenziali di estrazione3
degli elettroni nel metallo e nel semiconduttore, nel momento in cui si forma una giunzione
metallo-semiconduttore, ci sarà un trasferimento di elettroni tra metallo e semiconduttore finché i
livelli di Fermi nei due materiali non si saranno allineati (equilibrio), come mostra Figura 2.
Figura 2. Diagramma a bande del metallo, del semiconduttore e della giunzione metallo-semiconduttore.
2
Il diodo Schottky è una giunzione rettificante, in cui cioè la relazione tra la tensione e la corrente sulla giunzione è
non lineare. All’opposto, si parla di contatto ohmico se la caratteristica corrente-tensione è lineare e simmetrica
rispetto alla tensione applicata.
3
L’energia di estrazione di un elettrone da un solido è definita come l’energia necessaria a un elettrone avente
energia pari ad EF per raggiungere il livello energetico dell’elettrone libero (cosiddetto livello di vuoto E 0). Si noti che, a
differenza del metallo, in un semiconduttore è praticamente impossibile trovare un elettrone con energia pari a E F,
tuttavia la definizione di energia di estrazione si riferisce al livello di Fermi. Il potenziale di estrazione è semplicemente
l’energia di estrazione divisa la carica dell’elettrone q. Si noti che, alla giunzione, il diagramma a bande all'equilibrio si
costruisce imponendo che EF sia costante e E0 sia continuo.
Alla transizione c’è una brusca discontinuità degli strati energetici permessi agli elettroni E MS e
dipende dalla scelta della coppia metallo-semiconduttore (nell’esempio in Figura 2, in cui si è
supposto un semiconduttore di tipo n, sul lato semiconduttore gli elettroni possono occupare
livelli ad energia superiore rispetto al lato metallo). Come noto, il salto energetico tra banda di
conduzione e livello di Fermi nel semiconduttore dipende dal drogaggio di quest’ultimo. Il
maggiore scostamento tra EC e EF nel semiconduttore in prossimità della giunzione implica una
ridotta concentrazione di elettroni liberi e quindi una densità totale di carica non nulla e pari a
quella degli ioni fissi delle impurità droganti. Questo si può esprimere dicendo che, una volta
realizzata la giunzione metallo-semiconduttore, in equilibrio, la carica presente sull’elettrodo
metallico dovrà essere bilanciata dalla carica nella regione di semiconduttore. Allo scopo, dovrà
essere avvenuto un trasferimento di elettroni tra metallo e semiconduttore, che determina una
densità totale di carica nel semiconduttore non nulla e quindi la nascita di un campo elettrico. In
generale, la neutralità di carica è garantita dal fatto che la carica presente sul gate è bilanciata
dalla carica nel semiconduttore.
Pertanto, a causa del contatto tra materiali diversi con diversi potenziali di estrazione, tra
metallo e silicio si sarà creata una differenza di potenziale (negativa se il substrato di silicio è di
tipo p, positiva se è di tipo n).
La tensione VFB di banda piatta (Flat Band) è definita come la tensione gate-substrato che rende
costanti le concentrazioni nel substrato p = NA e n = ni2/NA, ovvero, rende costante il potenziale φ
nel semiconduttore4 e, pertanto, rende nullo il campo elettrico lungo l’asse verticale:
Pertanto, il campo elettrico internamente al condensatore MOS (tra l’armatura del gate e
l’armatura del semiconduttore) è nullo se VG = VFB, ovvero, una tensione di gate VG = VFB bilancia
l’effetto del diverso potenziale di estrazione tra metallo e semiconduttore.
Si noti che VFB < 0 se il substrato è di tipo p (VFB > 0 se è di tipo n) e che, oltre al diverso potenziale
di estrazione φMS tra metallo e semiconduttore, ad essa contribuiscono anche le cariche,
tipicamente positive, presenti nell’ossido. Infatti, sull’interfaccia ossido-metallo si può avere
legame non completo, Si0++ sul lato dell’ossido e O-- sul metallo, che contribuisce a VFB.
4
Si può dire che VG = VFB è quella tensione che non solo rende costante il potenziale nel semiconduttore, ma lo rende
nullo, in quanto il semiconduttore è posto a massa.
A seconda del valore della tensione di gate VGB = VG in relazione a VFB, si distinguono tre regioni di
funzionamento per un MOS, come descritto in Figura 3.
Figura 3. Regioni di funzionamento per il condensatore MOS.
Regione di accumulazione
Questa situazione si verifica se al gate è applicata VG < VFB. In tal caso, la carica negativa presente
sul gate è bilanciata da una carica positiva nella regione superficiale del semiconduttore, costituita
da lacune (strato di accumulazione). Nelle regioni interne del substrato, la concentrazione di
lacune sarà inferiore rispetto a quella nello strato di accumulazione. Lo strato di accumulazione è
talmente sottile da poter essere assimilato ad una distribuzione superficiale di cariche.
Supponendo che il substrato è a massa, per cui il potenziale è nullo nel substrato, la tensione V G
non è sufficiente a bilanciare all’interfaccia l’effetti del diverso potenziale di estrazione tra metallo
e semiconduttore. Ne segue che il potenziale lungo l’asse y varia come mostrato in Figura 4.
Figura 4. Potenziale lungo l’asse verticale del MOS, quando è applicata V G < VFB.
Analiticamente, all’interfaccia substrato-ossido si accumulano lacune con concentrazione:
in cui φ0 è il potenziale nel substrato, che è stato supposto collegato a massa, per cui φ0 = 0. La
corrispondente concentrazione di lacune nel substrato è p0. Il potenziale sulla superficie tra ossido
e semiconduttore è φS. Per definizione di tensione di banda piatta, se fosse V G = VFB, il potenziale
nel substrato sarebbe costante. In regione di accumulazione, invece, risulta V G < VFB, per cui la
tensione di gate flette il potenziale verso il basso. Ne segue, che la concentrazione di lacune
all’interfaccia tra ossido e semiconduttore psuperficiale è maggiore della concentrazione di lacune nel
substrato p0 (per questo si parla di “accumulazione” di maggioritari).
Regione di svuotamento
Si applichi una tensione di gate positiva. All’aumentare di VG, le lacune sono progressivamente
respinte verso il substrato, finché la concentrazione di lacune all’interfaccia ossido-semiconduttore
diventa inferiore della concentrazione di lacune nel substrato di tipo p. Questa condizione è detta
di svuotamento, in quanto la regione di semiconduttore sotto il gate risulta svuotata da cariche
libere. Figura 5 mostra come la carica positiva sull’elettrodo di gate è bilanciata dalla carica
negativa degli atomi accettori ionizzati sotto al gate. In accordo all’Equazione (5), siamo nel caso in
cui φS - φ0 > 0, per cui psuperficiale è minore della concentrazione di lacune nel substrato p0.
Figura 5. Potenziale lungo l’asse verticale del MOS, quando è applicata V FB < VG < VT.
Regione di inversione
Se si continua ad aumentare VG, si favoriscono i processi di generazione elettrone-lacuna nella
regione di svuotamento e gli elettroni sono attratti in superficie. A partire da un certo valore di
VG > VT, la concentrazione di elettroni all’interfaccia ossido-semiconduttore diventa maggiore della
concentrazione delle lacune maggioritarie. Si forma così uno strato di inversione superficiale di
elettroni. Lo strato di inversione è talmente sottile da poter essere assimilato a una distribuzione
superficiale di cariche negative all’interfaccia ossido-silicio. La carica positiva sull’elettrodo di gate
è ora bilanciata da una carica negativa nel semiconduttore, data dagli elettroni relativi allo strato
di inversione (cariche negative mobili) e agli ioni accettori relativi alla regione di svuotamento
(cariche negative fisse). La tensione di gate in corrispondenza della quale si genera lo strato di
inversione è detta tensione di soglia VT. Si parla di “inversione” perché il pMOS, avente substrato
di tipo n, si comporta come se fosse un nMOS in regione di accumulazione5. Convenzionalmente,
la tensione di soglia è indicata con VTn per un pMOS, con VTp per un nMOS. Figura 6 mostra cosa
accade in forte inversione: all’aumentare di VG, si ha un aumento della generazione
elettrone/lacuna per effetto del campo elettrico conseguente a V G (contributo G(ε) in
Equazione (6)).
Figura 6. Fenomeno della generazione elettrone/lacuna in regime di forte inversione e formazione di un canale di
elettroni all’interfaccia tra ossido e semiconduttore.
Ai fini del calcolo della differenza di potenziale φS - φ0 in forte inversione, si consideri Figura 7.
All’interfaccia tra ossido e semiconduttore si applica Equazione (7).
dove n0 = ni2/NA e, come visto, φ0 = 0 senza restrizione di generalità. Tenendo conto che per la
neutralità nel substrato dovrà essere nsuperficiale = psubstrato, ne segue:
da cui si ricava la (9).
5
Nota: in forte inversione, nsuperficie ≥ p0. Alcuni testi distinguono una regione di debole inversione, che si ha appena
iniziano ad accumularsi elettroni all’interfaccia tra ossido e semiconduttore, e si ha si caratterizza per avere
p0 ≥ nsuperficie ≥ ni.
Ponendo a massa il substrato, ne segue:
Nell’Equazione (10), il termine φF rappresenta il potenziale di Fermi.
Figura 7. Potenziale lungo l’asse verticale del MOS, quando è applicata VG > VT.
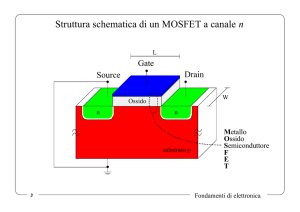
MOSFET nMOS e pMOS
Figura 8 mostra sezione trasversale e simbolo di un MOSFET a canale n (NMOS) e p (PMOS)
Figura 8. Strutture e simboli dei MOSFET a canale n (NMOS) e a canale p (PMOS).
Il bulk e il source sono sempre equipotenziali (VBS = 0 e VSB = 0 nel nMOS e nel pMOS
rispettivamente)6. Le tensioni di soglia sono indicate con VTn > 0 nel caso nMOS e VTp < 0 nel caso
pMOS. Le tensioni gate-source sono:
6
-
VGS ≥ 0 per il MOSFET a canale n;
-
VSG ≤ 0 per il MOSFET a canale p.
Si parla di configurazione a source comune, in quanto tutti i potenziali sono riferiti al source che, cortocircuitato con
il bulk, è al potenziale più basso.
Tale differenza di potenziale gate-source causa la comparsa di un campo elettrico che può essere
sfruttato per aumentare o ridurre la densità di carica mobile nel canale sotto il gate (che si crea
per effetto di una differenza di potenziale gate-bulk). Proprio per questa proprietà, si parla di
dispositivo ad effetto di campo. Inoltre, agendo sul terminale di drain, si può variare la tensione
source-drain per variare la corrente tra questi due terminali.
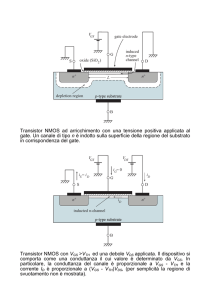
Consideriamo il transistor nMOS in 3D, come mostrato in Figura 9. Nelle zone del substrato
adiacenti al gate sono state realizzate due diffusioni n +, dette regioni di source e drain. Le tensioni
e le correnti per convenzione sono quelle indicate in Figura 10.
Figura 9. Struttura del transistor nMOS.
Figura 10. Versi convenzionali di tensioni e correnti in un nMOS.
Si osservi che le regioni di source e drain formano delle giunzioni pn con il substrato. Queste
giunzioni sono sempre mantenute in condizioni di polarizzazione inversa (substrato di tipo p e
regioni di source e drain di tipo n+), in modo da evitare iniezioni di portatori nel substrato. La
regione di semiconduttore sotto il gate e compresa tra source e drain è detta regione di canale, la
cui lunghezza è L (“length”). La corrente di un nMOS scorrerà tra source e drain nella regione di
canale. La larghezza di canale, invece, è indicata con la lettera W (“width”). L e W sono parametri
progettuali fondamentali nel progetto di circuiti integrati analogici e digitali. Il rapporto W/L è
detto fattore di forma del transistor.
Si noti che, a differenza di un BJT in cui emettitore e collettore non potevano essere scambiati, il
MOSFET è una struttura simmetrica rispetto al gate, ovvero, non è stabilito a priori chi è il
terminale di source e chi è il terminale di drain: il drain sarà il terminale a potenziale maggiore.
Per ricavare la polarizzazione di un transistor nMOS, da quanto detto, è necessario ricavare le tre
correnti IG, ID, IS e le tre tensioni VDS, VGS, VGD. Come nel BJT, due equazioni sono date da:
Ulteriori due relazioni si ricavano chiudendo il BJT su un bipolo sorgente e un bipolo di carico che,
con riferimento a Figura 11, introducono:
Figura 11. Collegamento del MOSFET con una sorgente e un carico.
Resterebbero due equazioni: una (quella relativa alla caratteristica di ingresso) però si ottiene
osservando che IG = 0. Resta dunque un’ulteriore equazione iU = f(vI, vU), ovvero iD = f(vGS, vDS), che
in realtà è iD = f(vDS) parametrica rispetto a vGS.
Condizione di banda piatta
Con riferimento a Figura 12, si consideri VGS = VFB e VDS = VSB = 0 (condizione di banda piatta). Sulle
giunzioni pn, dal lato del substrato (lato p) si forma una carica fissa negativa. Osservando il
potenziale lungo l’asse orizzontale, fissato y = 0, si notano due variazioni in corrispondenza delle
giunzioni pn tra source/drain e substrato, di ampiezza pari al potenziale di built-in delle giunzioni
stesse. Fissando, quindi, un valore di x compreso tra drain e source, si osserva che non ci sono
variazioni del potenziale lungo l’asse y, per cui tra gate e bulk non può scorrere corrente.
Figura 12. Distribuzione di carica spaziale in condizione di banda piatta.
Regioni di funzionamento di un transistor nMOS
Interdizione (OFF): VGS < VTn
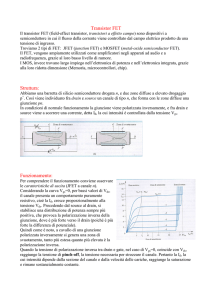
Il transistor nMOS è interdetto quando VGS < VTn, con VDS > 0 e VSB = 0. In tal caso il MOS non
conduce perché non si è formato un canale di elettroni sotto il gate che permetta una corrente tra
source e drain, nonostante VDS > 0, come mostrato in Figura 13. Finché VGS < VTn, si ha un accumulo
di ioni negativi nel substrato, all’interfaccia con l’ossido. Andando a graficare il potenziale φ(x) per
y = 0, si vede che il suo valore in corrispondenza delle giunzioni pn tra source/drain e substrato è
ancora pari al potenziale built-in della giunzione ψBO, mentre nella zona centrale occorre
considerare la differenza di potenziale tra gate e cariche fisse negative. Tale potenziale decrescerà
fino ad annullarsi lungo l’asse y, dove il bulk è a massa. Si noti che l’ipotesi VGS < VTn, essendo
VGD = VGS – VDS < VTn – VDS, con VDS ≥ 0, comporta VGD < VTn. Pertanto, lo strato di svuotamento
sotto il gate congiunge le regioni svuotate source-bulk e drain-bulk.
Figura 13. Transistor nMOS in interdizione.
Transistor attivo (ON): VGS > VTn
Consideriamo preliminarmente VDS = 0, in modo che non possa fluire corrente tra source e drain.
Ne segue anche che VGD = VGS. Pertanto, se VGS > VTn, anche VGD > VTn. In tal caso, tra lo strato di
ioni negativi e l’ossido, nel substrato si crea il canale di elettroni, come in Figura 14.
Figura 14. Transistor nMOS con canale formato.
Regione lineare (LIN, ON): VGS > VTn, VGD > VTn, 0 < VDS < VDSAT, VSB = 0
Se, con canale formato, si aggiunge l’ipotesi 0 < VDS < VDSAT, si crea un moto ordinato di cariche tra
source e drain: gli elettroni nel canale si muovono verso il drain, creando una corrente da drain a
source. La corrente che scorre nel canale causa una caduta di potenziale: modellando la regione
sotto il gate come una resistenza (ipotesi di regione lineare), si ha che il potenziale varia
linearmente da source e drain, come in Figura 15. Il dispositivo si comporta, pertanto, come una
resistenza controllata da VGS: se VDS è sufficientemente piccola, R non dipende dalla corrente che
attraversa il transistor nMOS.
Si noti che il flusso di elettroni nell’attraversare la resistenza del canale si va riducendo passando
da source a drain. Se VDS aumenta, la resistenza del canale aumenta e la corrente tra drain e
source non è più proporzionale a VDS: il canale, cioè, si restringe finché VGD = VGS – VDS = VTn. In
altre parole, se VDS aumenta troppo, si ha che VGD diminuisce fino alla soglia VTn, che causa lo
strozzamento del canale verso il drain (la giunzione pn gate-drain va in interdizione). In
corrispondenza di VGD = VTn, VDS = VGS – VTn e affinché il transistor lavori in regione lineare, VDS deve
essere più piccolo di detto limite.
Figura 15. Transistor nMOS in regione lineare.
Staurazione (SAT, pinch-off): VGS > VTn, VGD < VTn, VDS > VGS - VTn, VSB = 0
Se VGD = VTn, lo strato di inversione tra gate e drain non può essere più mantenuto e il canale si
strozza (entra in pinch-off). Se VGS > VTn e VGD < VTn, si ha che VDS > VGS - VTn (si veda Regione lineare
(LIN, ON): VGS > VTn, VGD > VTn, 0 < VDS < VDSAT, VSB = 0). Pertanto, vi sarà un punto P nel canale sotto
il gate in cui VGP = VTn, limite fino a cui esiste lo strato di inversione, mentre la regione svuotata si
insinua tra canale e drain, fino al punto P, come mostrato in Figura 16.
Figura 16. Transistor nMOS in pinch-off.
Figura 17 mostra un utile grafico per ricavare le relazioni tra le varie tensioni, considerando anche
le differenze di potenziale rispetto al punto P.
Figura 17. Relazioni tra le tensioni nei vari punti del transistor nMOS in pinch-off.
La tensione tra Drain e il punto P sarà VDP = VGP - VGD = VTn – VGD > 0 è la tensione ai capi del
segmento svuotato, a cui è associato un campo elettrico che causa comunque un’iniezione di
portatori nel drain (caso analogo a quello della giunzione base-collettore nel BJT in regione
normale). Essendo VPS = VGS – VGP = VGS – VTn ed essendo VGS > VTn, si ha VPS > 0. Fissando VGS
costante la tensione VPS ai capi del canale non varia con altre grandezze (resta costante al variare
di VDS > VGS - VTn): se VDS > VGS - VTn continua ad aumentare, il punto P si avvicina ulteriormente al
source ma così lentamente da poter assumere la lunghezza del canale di elettroni in saturazione
poco sensibile a variazioni di VDS. La conseguenza è che la corrente tra drain e source è circa
costante al variare di VDS in saturazione.
Modello regionale nMOS
Il simbolo circuitale del transistor nMOS introdotto in Figura 10, è riproposto in Figura 18.
Figura 18. Versi convenzionali di tensioni e correnti in un nMOS.
Relazioni sempre valide:
Interdizione (OFF)
Regione lineare
Se VDS « VGS – VTn:
Equazione (16) dice che la relazione tra la corrente ID e VDS è circa lineare. In essa, kn è:
dove W/L è il fattore di forma del transistor, kn’ è detto fattore di conducibilità intrinseco e ha le
dimensioni di A/V2. Un valore tipico del fattore di conducibilità è kn’ = 170 μA/V2.
Saturazione o Pinch-off
La corrente tra drain e source in saturazione si ottiene dalla (15), sostituendo VDS = VGS – VTn.
In saturazione, pertanto, il transistor nMOS si comporta come un generatore di corrente
indipendente da VDS e variabile al variare di VGS.
Caratteristica statica di uscita (nMOS)7
Le curve in Figura 19. Caratteristica statica di uscita di un transistor nMOS. sono ricavate con
Matlab, supponendo kn’ = 170 μA/V2, W/L = 2, VTn = 0.7 V.
Figura 19. Caratteristica statica di uscita di un transistor nMOS.
La caratteristica di uscita del nMOS è stata analizzata in PSpice (si vedano Figura 20 e Figura 21).
VDS
VDS
M1
VGS
1Vdc
VGS
2N7000/FAI
1Vdc
I
0
Figura 20. Schematico del transistor nMOS polarizzato.
7
La caratteristica statica di ingresso, come già detto (si veda MOSFET nMOS e pMOS), è semplicemente IG = 0.
Figura 21. Caratteristiche statica di uscita del transistor nMOS.
La curva discriminante tra regione lineare e regione di saturazione è una parabola e si ottiene
sostituendo VDS = VGS – VTn nell’espressione di ID in Equazione (18), ottenendo così:
Nota: per VGS < VTn e VGS > VTn si ha un pinch-off inverso in quanto, data la simmetria del nMOS,
questa situazione equivale a invertire drain e source (il drain è quello a potenziale maggiore). In
generale, si ricava il grafico di Figura 22. Regioni di funzionamento di un transistor nMOS..
Figura 22. Regioni di funzionamento di un transistor nMOS.
Modello regionale pMOS
Si faccia riferimento al simbolo circuitale in Figura 23.
Figura 23. Versi convenzionali di tensioni e correnti in un pMOS.
Relazioni sempre valide:
Interdizione (OFF)
Regione lineare
Se VSD « VSG – |VTp|:
Equazione (23) dice che la relazione tra la corrente ID e VSD è circa lineare. In essa, kp è:
dove W/L è il fattore di forma del transistor, kp’ è il fattore di conducibilità intrinseco.
Saturazione o Pinch-off
La corrente tra drain e source in saturazione si ottiene dalla (22), sostituendo VSD = VSG – VTp.
In saturazione, pertanto, il transistor pMOS si comporta come un generatore di corrente
indipendente da VSD e variabile al variare di VSG.
Osservazioni
Tecnologicamente, i pMOS sono più semplici da realizzare degli nMOS, per cui sono stati usati per
primi nei circuiti logici. Oggi si preferiscono gli nMOS, in quanto a parità di dimensioni fisiche sono
più veloci dei pMOS, dal momento che la mobilità degli elettroni (che compare in kn) è circa tre
volte quella delle lacune (fattore presente nell’espressione di kp).
Effetto Body, modulazione della lunghezza di canale e MOSFET in commutazione
Effetto indesiderato, dovuto alla dipendenza di VT da VSB e dalla concentrazione di drogante
nel substrati. Nel caso generale in cui VSB ≠ 0, la tensione di soglia aumenta in modulo:
Nella precedente espressione, φF è il potenziale di Fermi. Lo spostamento del livello di Fermi
causato dal drogaggio del substrato è ΔEF = -q ∙ φF. Il livello di Fermi è dato da:
Per substrato di tipo p (nMOS):
Per substrato di tipo n (pMOS):
Ne segue che variando la concentrazione di drogrante nel substrato, varia φF e con esso
l’espressione di VT. La dipendenza da φF si ha attraverso la funzione γ, che è data da:
In (29), Nsubstrato è la concentrazione di substrato, il segno ‘+’ (o ‘-’) si usa per substrato di tipo p (o
n). Ne segue che, in un nMOS, essendo il substrato di tipo p, al crescere della concentrazione di
accettori nel substrato aumenta VTn.
Si consideri un nMOS in pinch-off. Al crescere di VDS, il punto di strozzamento si sposta
molto lentamente verso il source, causando una riduzione della lunghezza del canale. Tenendo
conto di tale effetto, finora trascurato, si ha che la corrente tra drain e source in saturazione è
data da:
dove λ [V-1] è il parametro di modulazione della lunghezza del canale ed è positivo. Il suo effetto è
pertanto analogo a quello dell’effetto Early nei BJT: la tensione di un nMOS in saturazione non è
esattamente costante, ma varierà linearmente con VDS. Si noti, da Equazione (30), che tutte le
caratteristiche passano per VDS = -1/λ. Solitamente λ assume valori tra 0.001 e 0.1 [V-1]. L’effetto
può essere riprodotto in Matlab, come mostrato in Figura 24. Caratteristica statica di uscita di un
transistor nMOS in presenza di modulazione della lunghezza del canale.
Figura 24. Caratteristica statica di uscita di un transistor nMOS in presenza di modulazione della lunghezza del
canale.
Lo stesso effetto si può verificare in PSpice, usando un’opportuna libreria di componenti (si veda
Figura 25Figura 23. Versi convenzionali di tensioni e correnti in un pMOS.).
Figura 25. Caratteristiche statica di uscita di un transistor nMOS nel cui modello è considerato l’effetto della
modulazione della lunghezza del canale.
Dal grafico della caratteristica statica di uscita complete, si può vedere come il MOSFET si
comporta come una resistenza controllata in tensione. Si supponga VGS > VTn. Posto che la derivata
in un determinato punto della caratteristica è pari alla conduttanza in quel punto (inverso della
resistenza), si può capire che se VDS è piccola, cioè, in regione lineare, la resistenza associata al
transistor è bassa. Se, invece, VDS cresce, il canale si strozza e la resistenza aumenta.
Essendo la struttura del MOSFET basata su un condensatore MOS e su giunzioni S-B e D-B
in inversa, il circuito equivalente del MOSFET in funzionamento dinamico contiene vari contributi
capacitivi. In particolare, con riferimento alla Figura 26, i contributi CSB e CDB si calcolano come
visto per le capacità della giunzione pn (in particolare, occorre considerare la capacità do
giunzione, che prevale per giunzioni pn in inversa).
Figura 26. Contributi capacitivi parassiti in un transistor.
Caratteristiche statiche ingresso-uscita
Amplificatore a source comune (SC)
Consideriamo il circuito in Figura 27. La retta di carico è data da:
Figura 27. Schematico dell’amplificatore a source comune.
a) nMOS OFF:
VGS < VTn, VGD < VTn, ID = 0, VU = VDD.
VGS < VTn VI < VTn.
(32)
(32)
b) nMOS in SAT:
VGS > VTn, VDS < VGS - VTn VGD < VTn
In tal caso:
VGS > VTn VI > VTn.
c) nMOS in RL:
da cui si può ricavare l’espressione di VI rispetto a VU in RL:
Pertanto a VI contribuiscono un termine costante, un termine iperbolico e un termine
lineare in VU. Quello che si vuole fare è ricavare l’andamento di VI in funzione di VU, da cui
ottenere VU in funzione di VI scambiando gli assi. Qualitativamente, l’andamento di VI è
quello in Figura 28. La parte di curva di interessa è quella al di sopra della retta di colore
blu. Pertanto, VU decresce all’aumentare di VI.
Figura 28. Tensione di ingresso VI rispetto a VU in regione lineare.
Considerando il comportamento complessivo, si ha l’andamento mostrato in Figura 29.
Figura 29. Caratteristica statica d’uscita del transistor nMOS a source comune.
Il guadagno di tensione in saturazione è pari a:
Ma in saturazione risulta:
Da cui:
Dalla precedente relazione segue che per avere un guadagno AV in modulo maggiore di 1 occorre
aumentare R.
Figura 30 mostra l’esito della simulazione dello stadio amplificatore a source comune in PSpice.
Figura 30. Simulazione della caratteristica statica dell’amplificatore a source comune in PSpice.
Confronto Mosfet vs. BJT
Per identici valori di resistenza di carico (sul collettore del BCT a emettitore comune e sul drain del
nMOS a source comune RC = RD = R) e di corrente di uscita IC0 = ID0 = I e per tipici valori dei
parametri (F = 100, kn = 10-4 A/V2, VTn = 1 V):
-
Il guadagno di tensione in regione normale del BJT è
-
Il guadagno di tensione in saturazione del MOSFET è
Andando a fare il rapporto dei due guadagni, si ha l’espressione riportata in Equazione (40).
Ne deriva un rapporto sempre favorevole al BJT. Tuttavia, aumentando il fattore di forma W/L del
MOSFET, si causa un aumento di kn, con conseguente riduzione del rapporto.
Inoltre, nel MOSFET la corrente scorre orizzontalmente nel canale nel substrato, sotto il gate, in un
volume molto ridotto. Nel BJT, invece, la corrente scorre verticalmente: la sezione utile per il
passaggio di corrente è tutta l’area della regione di emettitore. Per tali ragioni, il BJT si preferisce
al MOSFET in applicazioni che richiedono corrente elevata in uscita.
NOTA: è errato affermare che il guadagno di corrente del BJT è maggiore di quello del MOSFET in
quanto, essendo IG = 0 la corrente in ingresso al MOSFET, il guadagno di corrente di quest’ultimo
tende a infinito.
Configurazione a carico saturo
Il circuito è quello rappresentato in Figura 31. Si tratta di una configurazione derivabile da quella a
source comune, sostituendo il carico resistivo con un nMOS con VG2 = VDD e VGD2 = 0 (il pull-up dato
dal transistor è assimilabile a una resistenza non lineare V DS = RDS ID). Per il carico, inoltre, sussiste
la relazione VGS2 = VDS2 = VDD – VU. Ne segue, inoltre, che se il canale nel transistor di carico si forma
(cioè, se VGS2 > VTn), allora l’unico stato in cui può lavorare M2 è la saturazione.
Figura 31. Schematico della configurazione a carico saturo per il transistor nMOS.
Se VI = 0, le correnti di drain ID1 e ID2 sono circa nulle (i transistor M1 ed M2 sono OFF). Ponendo la
corrente di pinch-off in M2 nulla, segue:
Pertanto, quando M1 e M2 sono spenti, la tensione in uscita sarà pari alla tensione di
alimentazione diminuita di una soglia VT2. Si tratta del massimo valore che assume l’uscita e,
poiché tale circuito è utilizzato come inverter logico, tale riduzione va a limitare lo swing logico.
Supponendo il driver M1 in pinch-off, si ha: VDS1 > VGS1 – VT1 > 0 VU > VI – VT1. In tal caso,
dovendo risultare ID1 = ID2, si ha:
Supponendo il driver M1 OFF, VI < VT1 VU = VDD – VT2.
Supponendo il driver M1 in RL, VI > VT1, 0 < VU < VI – VT1.
Per ricavare VU, si procede per via grafica, come fatto nel caso dello stadio amplificatore a source
comune.
Complessivamente, si ha la caratteristica proposta in Figura 32. Caratteristica statica d’uscita del
transistor nMOS a carico saturo..
Figura 32. Caratteristica statica d’uscita del transistor nMOS a carico saturo.
La verifica è avvenuta in ADS e Figura 33. Esito della simulazione del transistor nMOS a carico
saturo in ADS. mostra l’andamento dell’uscita.
Figura 33. Esito della simulazione del transistor nMOS a carico saturo in ADS.
Complementary MOS (CMOS)
Lo schema prevede un nMOS di pull down e un pMOS di pull up aventi i gate in comune, come in
Figura 34. Schema circuitale inverter CMOS.. Questa configurazione ha la proprietà di non risentire
dell’effetto Body, in quanto entrambi i transistor hanno il source collegato al relativo substrato (di
tipo n per M2 e di tipo p per M1). Ne segue VSB = 0 perché non c’è caduta di tensione tra source e
substrato8. Diversamente, osservando lo schematico di Figura 31, si vede che il source e il bulk del
8
In pratica, il source del pMOS è a VDD come il relativo bulk, il source del nMOS e il relativo bulk sono a massa.
pull down M1 sono a ground, mentre nel caso di M2, il bulk, essendo lo stesso di M1 resta a
ground, mentre il source è il terminale di uscita, per cui per M2 si può avere V SB ≠ 0. Figura 35
mostra alcune caratteristiche della sezione trasversale dello schema con nMOS a carico saturo a
del CMOS. Pur non essendo aderente a quanto realizzano effettivamente i processi tecnologici,
tale figura aiuta a capire la ragione per cui la tensione source-bulk è nulla nel CMOS e non nulla nel
caso di configurazione a carico saturo.
Figura 34. Schema circuitale inverter CMOS.
Figura 35. Modello approssimato della sezione trasversale dello schematico (a) di Figura 31 e (b) di Figura 34.
Si analizza ora il funzionamento dell’inverter CMOS.
1) M1 OFF: VGS1 = VI < VTn
2) M2 OFF: VSG2 = VDD - VI < |VTp| VI > VDD - |VTp|
Dalle condizioni precedenti segue che se un transistor è OFF, l’altro deve essere ON (o in regione
lineare o in saturazione).
Inoltre:
a) VDS1 = VU > VGS1 – VTn = VI – VTn VU > VI - VTn M1 in saturazione; al contrario, se
VU < VI – VTn M1 in regione lineare.
b) VSD2 = VDD - VU > VSG2 – |VTp| = VDD – VI – |VTp| VU < VI + |VTp| M2 in saturazione; al
contrario, se VU > VI + |VTp| M2 in regione lineare.
Da quanto detto, si ottengono le regioni di funzionamento mostrate in Figura 36.
Figura 36. Regioni di funzionamento dei transistor nell’inverter CMOS.
Se M2 è OFF, allora VDD - |VTp| < VI < VDD (in quanto il massimo valore che può assumere la
tensione di ingresso è limitato a VDD) ID2 = 0 ID1 = 0. Se M1 fosse in P.O., dovrebbe essere
VGS1 = VI = VTn, ma è assurdo in quanto VDD - |VTp| < VI < VDD. Diversamente, se M2 è OFF, M1 in
regione lineare implicherebbe VU(VI – VTn – VU/2) = 0, cioè, due possibilità: VI - VTn = VU/2, che è un
assurdo in quanto in regione lineare deve essere VI – VTn > VU, oppure VU = 0.
Analogamente, se M1 è OFF 0 < VI < VTn ID1 = 0 ID2 = 0. Se M2 fosse in P.O., dovrebbe
essere VSG2 = VDD - VI = |VTp| ma è assurdo in quanto 0 < VI < VTn. Diversamente, se M1 è OFF, M2
in regione lineare implicherebbe (VDD - VU)(VDD – VI – |VTp| – (VDD - VU)/2) = 0, cioè, due possibilità:
(VDD – VI – |VTp| – (VDD - VU)/2) = 0, da cui VI + |VTp| = (VDD + VU)/2, che è un assurdo in quanto in
regione lineare deve essere VI + |VTp| < VU, oppure VU = VDD.
Si suppongano M1 ed M2 in P.O. kn(VI - VTn)2 = kp(VDD – VI - |VTp|)2, da cui:
Dalla (44) si nota che VI = VDD/2 quando kn = kp e VTn = VTp. Questa situazione si ha nella regione
centrale della caratteristica di uscita: sembrerebbe che l’inverter ha un guadagno di tensione
infinito, ma in realtà, causa della modulazione della lunghezza del canale, è finito.
Il comportamento nelle restanti regioni si ha raccordando la caratteristica, come mostrato in
figura 36.
Figura 37. Caratteristica dell’Inverter CMOS.
Anche in tal caso, la verifica è avvenuta in ADS e Figura 38 mostra l’andamento dell’uscita.
Figura 38. Esito della simulazione dell’inverter CMOS.