Dottorato in Fisica XIV ciclo n.s. – 21 gennaio 2013
Prova scritta n.1
Compito
Il candidato svolga a sua scelta uno dei seguenti temi:
1. I processi oscillatori in fisica
2. Conseguenze della corrente di spostamento nelle equazioni di Maxwell.
Esercizi
Il candidato svolga a sua scelta due dei seguenti esercizi:
Esercizio n. 1
Un cilindro di raggio R può ruotare attorno al proprio asse disposto parallelamente alla direzione della
forza-peso. Dato un punto materiale di massa m e detto d il coefficiente di attrito statico tra il punto e la
parete interna del cilindro si calcoli il minimo valore delle velocità angolare del cilindro min affinché il
punto resti in quiete rispetto alla parete del cilindro. Si assuma: m = kg, R = 5 m, d = 0.5, g [acc. di gravità]
= 9.81 m/s2.
Esercizio n. 2
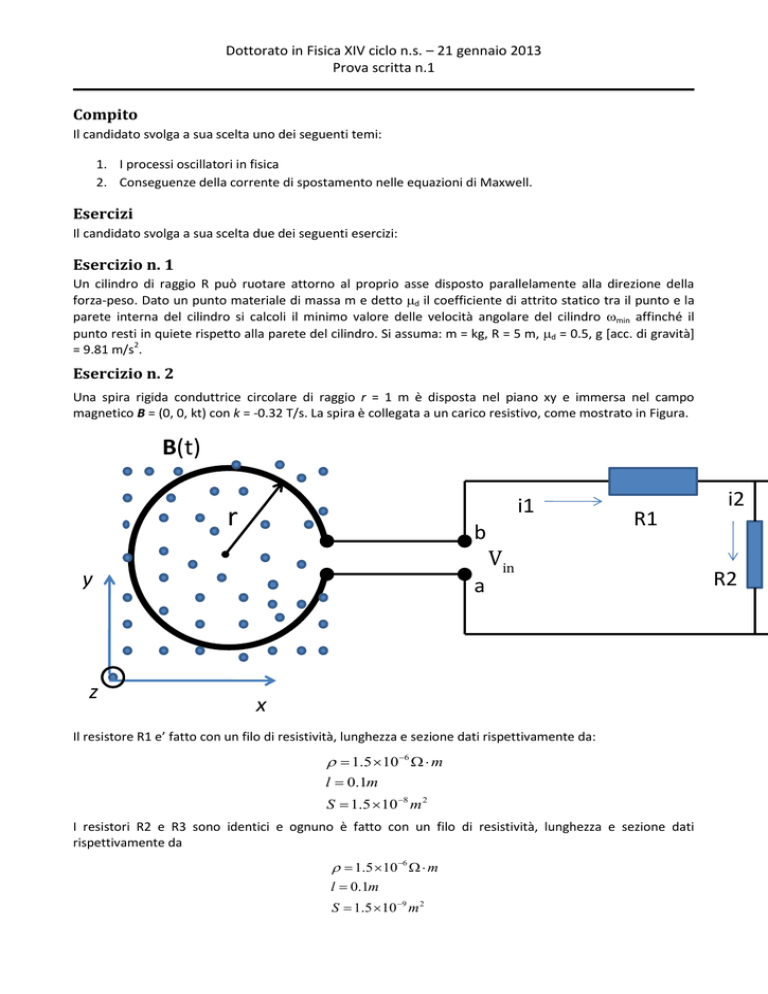
Una spira rigida conduttrice circolare di raggio r = 1 m è disposta nel piano xy e immersa nel campo
magnetico B = (0, 0, kt) con k = -0.32 T/s. La spira è collegata a un carico resistivo, come mostrato in Figura.
B(t)
i1
r
b
Vin
y
z
R1
a
x
Il resistore R1 e’ fatto con un filo di resistività, lunghezza e sezione dati rispettivamente da:
1.5 10 6 m
l 0.1m
S 1.5 10 8 m 2
I resistori R2 e R3 sono identici e ognuno è fatto con un filo di resistività, lunghezza e sezione dati
rispettivamente da
1.5 10 6 m
l 0.1m
S 1.5 10 9 m 2
i2
R2
Dottorato in Fisica XIV ciclo n.s. – 21 gennaio 2013
Prova scritta n.1
Si determini:
1.
2.
3.
4.
5.
6.
La fem indotta tra i terminali a e b, in modulo, Vin =||.
La corrente che circola in R1, R2, R3
La densità di corrente J e il campo elettrico E in R1
La il rapporto tra la tensione Vout tra i terminali c e d e Vin
La potenza dissipata in calore da R1
Il segno della forza radiale cui e’ sottoposta la spira. (Ovvero: la forza e’centripeta o centrifuga?)
Esercizio n. 3
Un sistema quantistico è costituito da una particella di massa m in una buca unidimensionale di altezza
infinita definita da:
se 0 x L
0
V ( x)
altrimenti
Si trovino le autofunzioni dell’hamiltoniana e, per lo stesso sistema nello stato fondamentale, si calcoli:
p (valore di aspettazione dell’operatore impulso nella rappresentazione delle coordinate)
p2 (valore di aspettazione del quadrato dell’operatore impulso nella rappresentazione delle
coordinate)
p
p2 p
2
Per questo esercizio non è richiesto lo svolgimento numerico.
Ai fini dello svolgimento può essere utile ricordare i seguenti integrali:
x sin 2 x
C
2
4
cos 2 x
sin
x
cos
x
dx
C
2
sin
2
x dx
Nelle formule precedenti le quantità C indicano le costanti di integrazione.
Dottorato in Fisica XIV ciclo n.s. – 21 gennaio 2013
Prova scritta n. 2
Compito
Il candidato svolga a sua scelta uno dei seguenti temi:
1. Leggi di conservazione in meccanica classica
2. Il principio d’indeterminazione di Heisenberg e sue conseguenze.
Esercizi
Il candidato svolga a sua scelta due dei seguenti esercizi:
Esercizio n. 1
Una molla elastica ideale ha un estremo libero e l’altro estremo fissato ad un blocco di massa m 2 = 10 kg
inizialmente fermo. Un secondo punto materiale di massa m1 = 2 kg, che si muove con velocità costante
v0 = 2 km/h urta frontalmente l’estremo libero della molla e vi resta attaccato (vedi Figura. 1). Sapendo che
il sistema formato dai due punti è meccanicamente isolato, detta k = 4x104 N/m la costante elastica della
molla determinare la compressione massima che essa subisce in seguito all’urto.
Figura 1
Esercizio n. 2
Una carica positiva puntiforme +Q1 è disposta sull’asse x nella posizione x = -a.
1. Si calcoli il lavoro necessario per portare una carica positiva puntiforme Q2 = Q1 sull’asse x
dall’infinito nella posizione x = +a
2. Con le due cariche Q1 e Q2 in x =- a e x = + a, rispettivamente, calcolare il lavoro necessario per
portare una terza carica puntiforme Q3 = -Q1 dall'infinito nell’origine.
3. Calcolare il lavoro necessario per spostare la carica Q3 dall’origine nel punto x = 2a.
Si assuma Q1 = 100 C, a = 0.05 cm, 1/40 = 8.99×109 Nm2/C2
Esercizio n. 3
Per la barriera di potenziale descritta nella figura seguente
si calcoli il coefficiente di trasmissione T(E,V0,l,m,h) per particelle di massa m incidenti da sinistra con
energia E<V0 .
Dottorato in Fisica XIV ciclo n.s. – 21 gennaio 2013
Prova scritta n. 3
Compito
Il candidato svolga a sua scelta uno dei seguenti temi:
1. La legge di induzione di Faraday e una sua applicazione pratica a scelta del candidato.
2. Evidenze sperimentali del dualismo onda-corpuscolo in meccanica quantistica.
Esercizi
Il candidato svolga a sua scelta due dei seguenti esercizi:
Esercizio n. 1
Un corpo di massa M = 0.5 Kg è appeso ad un filo inestensibile di lunghezza L = 1 m. Un proiettile di massa
m = 0.1 Kg, con una velocità v0 =10 m/sec colpisce orizzontalmente un corpo di massa M rimanendovi
incastrato (figura 1). Calcolare l'angolo formato dal filo del pendolo dopo la collisione e il corrispondente
dislivello h. (Si assuma g [acc. di gravità] = 9,81 m/s2 e si considerino i due corpi come punti materiali).
Figura 2
Esercizio n. 2
Un filo indefinito F1 rigido percorso da una corrente stazionaria I1 = 8 mA diretta nel verso indicato dalla
freccia F1 è disposto nel piano xy parallelamente all’asse x a distanza d1 = 0.300 m da questo. Un secondo
filo indefinito F2 rigido percorso da una corrente stazionaria I2 = 5 mA diretta nel verso indicato dalla
freccia F2 è disposto nel piano xy parallelamente all’asse y a distanza d2 = 0.400 m da questo (vedi figura 2).
Assumendo 0 (permeabilità magnetica del vuoto) = 4 10-7 Tm/A, si determini:
1. Modulo, direzione e verso del campo magnetico totale prodotto nell’origine dalle due correnti.
2. Modulo, direzione e verso della forza magnetica per unità di lunghezza che la corrente I1 esercita
sul filo F2.
N.B. I due fili non sono a contatto nel punto A.
Dottorato in Fisica XIV ciclo n.s. – 21 gennaio 2013
Prova scritta n. 3
Figura 3
Esercizio n. 3
Un sistema quantistico è costituito da una particella di massa m in una buca unidimensionale di altezza
infinita definita da:
se 0 x L
0
V ( x)
altrimenti
Si trovino le autofunzioni dell’hamiltoniana e, per lo stesso sistema nello stato fondamentale, si calcoli:
x (valore di aspettazione dell’operatore posizione)
x2 (valore di aspettazione del quadrato dell’operatore posizione)
x
x2 x
2
Per questo esercizio non è richiesto lo svolgimento numerico.
Ai fini dello svolgimento può essere utile ricordare i seguenti integrali:
x2 x
1
sin 2 x cos 2 x C
4 4
8
3
x x
1 2 1
2
2
x sin x dx 6 4 cos 2 x 4 x 2 sin 2 x C
2
x sin x dx
Nelle formule precedenti le quantità C indicano le costanti di integrazione.