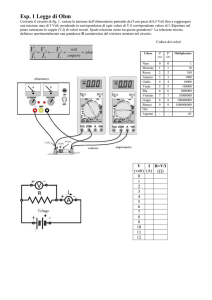
RILIEVO PER PUNTI DELLA CARATTERISTICA INVERSA DI UN DIODO ZENER.
VERIFICA DELLA VARIAZIONE DELLA RETTA DI CARICO AL VARIARE
DELL’ALIMENTAZIONE E AL VARIARE DEL CARICO.
DETERMINAZIONE SPERIMENTALE DEL CIRCUITO EQUIVALENTE DEL DIODO
ZENER E VERIFICA DELLA SUA VALIDITÀ.
VERIFICA DEL FUNZIONAMENTO DI UNO STABILIZZATORE DI TENSIONE
UTILIZZANTE IL DIODO ZENER DI CUI SI È DETERMINATA LA CURVA
CARATTERISTICA E IL CIRCUITO EQUIVALENTE.
CIRCUITO EQUIVALENTE DEL DIODO ZENER
Il diodo zener si comporta da normale diodo in polarizzazione diretta, mentre in polarizzazione
inversa presenta una tensione VZ alla quale entra in conduzione inversa e la corrente può variare
quasi indipendentemente dalla tensione VZ.
VZA
VZ VZB VZK
A
B
0
IZA
IZB
IZ
Dalla caratteristica inversa si ottiene il suo circuito
equivalente. Il tratto più lineare della curva caratteristica
può essere approssimato da una retta. Si scelgono due
opportuni punti A(VZA ; IZA) e B(VZB ; IZB) e si
approssima la caratteristica reale con tale retta;
ovviamente tale approssimazione è valida solo nel tratto
compreso tra i punti A e B.
Pertanto il punto di lavoro del diodo zener si farà variare
(nel tratto AB) non più sulla caratteristica ma su tale retta,
ossia si è linearizzato il comportamento del diodo zener e
lo si schematizzerà mediante elementi lineari.
L’equazione della retta AB è del tipo IZ = mVZ + q.
Le quantità m e q si ricavano imponendo che tale retta
passi per i punti A e B:
⎧I ZB = mVZB + q
⎨
⎩I ZA = mVZA + q
Sottraendo membro a membro, si ottiene m:
⎧I ZB = mVZB + q
⎨I = mV + q
ZA
⎩ ZA
I ZB − I ZA = m(VZB − VZA ) ⇒ m =
I ZB − I ZA
1
=
VZB − VZA R Z
m ha le dimensioni dell’inverso di una resistenza.
1
in una delle due equazioni del sistema, si ottiene q: q = I ZA − mVZA .
Sostituendo m =
RZ
1
L’equazione della retta è:
⎛
V
1
VZ + ⎜⎜ I ZA − ZA
RZ
RZ
⎝
IZ =
Per IZ = 0 si ha l’intercetta con l’asse VZ:
costante viene indicata con VZK.
⎞
⎟⎟ .
⎠
VZ = VZA − R Z I ZA = VZK ,
che, essendo una quantità
− RZ, valore costante, è la resistenza differenziale del diodo zener in polarizzazione inversa e
giustifica l’aumento di tensione ai capi del diodo zener all’aumentare della corrente.
− VZK, valore costante, fissa il valore di tensione al quale il diodo zener inizia a condurre
inversamente.
L’equazione della retta, infine, è:
IZ =
V
1
VZ − ZK
RZ
RZ
⇒
VZ = R Z I Z + VZK
− Il primo termine RZIZ, tramite RZ, tiene conto degli aumenti di differenza di potenziale di VZ
all’aumentare della corrente.
− Il secondo termine VZK viene schematizzato da un generatore di tensione che impone la minima
tensione che si dovrà applicare tra catodo e anodo perché il diodo entri in conduzione inversa.
Il circuito a sinistra nella figura è il circuito equivalente del diodo zener funzionante tra i punti A e
B della curva caratteristica.
POLARIZZAZIONE DEL DIODO ZENER E RETTA DI CARICO
Consideriamo il circuito di polarizzazione del diodo zener.
R è la resistenza di polarizzazione del diodo zener, ed è detta resistenza di carico del diodo.
Applicando il secondo principio di Kirchhoff, si ha:
E = RI Z + VZ
⇒
IZ = −
1
E
VZ +
R
R
Tale equazione viene detta retta di carico del diodo zener. Tale retta nel piano VZ-IZ, in cui viene
riportata anche la curva caratteristica, e una retta i cui punti rappresentano tutti i possibili punti di
lavoro del diodo zener.
2
VZ E
VZQ
Q
0
IZQ
Poiché il punto di lavoro deve stare anche sulla curva
caratteristica, il punto di lavoro del diodo sarà il punto di
intersezione tra la retta di carico e la curva caratteristica,
come mostrato in figura.
La retta di carico viene tracciata calcolando i suoi punti
di intersezione con gli assi
E/R
IZ
VZ
E
1
E
I Z = − VZ +
R
R
0
VZ
IZ
0
E/R
E
0
Al variare della tensione E di alimentazione o al variare
della resistenza di carico, cambia la retta di carico e,
quindi, il punto di lavoro.
E/R
IZ
VZ
E
Se cambia la tensione di alimentazione E mentre la
resistenza di carico rimane costante R rimane costante, il
coefficiente angolare della retta di carico rimane costante
e si ottiene, al variare di E, un fascio di rette parallele,
come mostrato in figura.
0
Se si tiene fissa E e si varia R, cambia il coefficiente
angolare e si ottengono rette di carico che, essendo
costante E, danno origine ad un fascio di rette per il
funto (E ; 0)., come mostrato in figura.
E/R
La verifica della validità del circuito equivalente si
effettua calcolando i punti di lavoro del diodo zener dal
circuito in cui al posto del diodo zener è stato messo il
suo circuito equivalente.
IZ
3
Le formule per il calcolo del punto di lavoro teorico si ottengono applicando il secondo principio di
Kirchhoff:
E = (R + R Z )I Z + VZK ⇒ I Z =
E − VZK
R + RZ
e
VZ = R Z I Z + VZK
I valori di VZ e IZ che si ottengono devono essere quasi coincidenti con quelli che si misurano. Tale
confronto confermerà la validità del circuito equivalente sperimentalmente determinato.
Dimensionamento del circuito. Rilievo della curva caratteristica e circuito equivalente.
Variazione della retta di carico per variazione di R.
Si utilizza un diodo zener PZ = ½W con VZ = 5,6V.
Corrente massima IZM del diodo zener:
I ZM =
PZ 0,5
=
= 89,28mA
VZ 5,6
Si fissa IZMAX = 10mA in corrispondenza di E = EM = 10V e si dimensiona R:
R=
E M − VZ 10 − 5,6
=
= 440Ω ,
I ZMAX
10 ⋅ 10 −3
valore commerciale 390Ω.
La tensione E dell’alimentatore si fa variare da 0V a 10V come riportato nella corrispondente
tabella. In corrispondenza di ogni valore di E, per il quale il diodo zener conduce, si ha una retta di
carico.
Per ottenere il fascio di rette per un punto al variare di R, se ne fa variare il valore in più e in meno
rispetto il valore di 390Ω come riportato nella corrispondente tabella. In corrispondenza di ogni
valore di resistenza R si ha una retta di carico.
In entrambe le misure verrà impiegato un alimentatore variabile e un multimetro 4½ digit.
Circuito di cablaggio e di misura
Procedimento della misura
Rilievo per punti della curva caratteristica
1. Si collegano il generatore e il multimetro utilizzato come voltmetro ai morsetti dell’alimentatore
e si regola l’alimentatore a 2V.
2. Si sposta il voltmetro ai capi della resistenza R e si misura la differenza di potenziale VR ai suoi
capi.
4
3. Si sposta il voltmetro ai capi del diodo zener e si misura la differenza di potenziale VZ ai suoi
capi.
V
E
.
4. Utilizzando i valori misurati si calcolano: la corrente I Z = R e l’intercetta con l’asse IZ
R
R
5. si ripetono i punti 2; 3; 4 con i seguenti valori di E: 4V; 5V; 5,8V; 6V; 6,1V; 6,2V; 6,5V;
7V; 8V; 9V; 10V.
6. Si tabulano i dati. Nella tabella vengono anche riportati il punto alternativo dal quale far passare
la retta di carico nel caso il valore dell’intercetta sia tale da essere fuori grafico e i valori di IZ e
di VZ calcolati dal circuito equivalente mediante foglio Excell (le formule da usare sono quelle
di seguito determinate).
Determinazione sperimentale
caratteristiche al variare di E
del
circuito equivalente e tracciamento delle curve
7. Si riportano i punti (VZ ; IZ) misurati su carta millimetrata su un piano VZ-IZ; si uniscono i punti
con un tratto continuo ad ottenere la curva caratteristica.
8. Si scelgono due punti A e B tra i quali la curva caratteristica è pressappoco rettilinea e si
calcolano gli elementi RZ e VZK del circuito equivalente.
9. Si traccia, su un altro foglio di carta millimetrata, la curva caratteristica e vi si riportano le rette
di carico che si hanno al variare del valore E dell’alimentazione. Nel caso il valore E/R risulti
fuori grafico, si utilizza il punto alternativo.
10. I punti di lavoro trovati sperimentalmente devono risultare ognuno sulla propria retta di carico
(o quasi). Inoltre, i punti di lavoro trovati sperimentalmente devono avere valori molto prossimi
a quelli calcolati con il circuito equivalente determinato sperimentalmente.
Variazione della retta di carico al variare di R e verifica dell’esattezza del circuito equivalente
11. Si fissa il valore del generatore E = 8V.
VR
E
.
e
R
R
13. Si ripete il punto 12 per i seguenti valori di R: 120Ω; 150Ω; 180Ω; 220Ω; 270Ω; 330Ω;
390Ω; 470Ω; 680Ω; 1kΩ; 2,2kΩ.
14. Si tabulano i dati. Nella tabella vengono anche riportati il punto alternativo dal quale far passare
la retta di carico nel caso il valore dell’intercetta sia tale da essere fuori grafico e i valori di IZ e
di VZ calcolati dal circuito equivalente, prima determinato, mediante foglio Excell (le formule
da usare sono quelle di seguito determinate determinate).
15. Si traccia, su un altro foglio di carta millimetrata, la curva caratteristica e vi si riportano le rette
di carico che si hanno al variare del valore R della resistenza di carico. Nel caso il valore E/R
risulti fuori grafico, si utilizza il punto alternativo.
16. I punti di lavoro trovati sperimentalmente devono risultare ognuno sulla propria retta di carico
(o quasi). Inoltre, i punti di lavoro trovati sperimentalmente devono avere valori molto prossimi
a quelli calcolati con il circuito equivalente determinato sperimentalmente.
12. Si inserisce il valore R = 100Ω, si misurano VZ e VR e si calcolano I Z =
Calcolo del punto alternativo
Per le intercette E/R che cadono fuori dal grafico considerato si deve calcolare
il punto alternativo da cui farla passare.
Si fissa il valore della corrente IZ1 , in modo che il punto della retta che si
ottiene cada nel grafico, e si calcola il corrispondente valore VZ1.
5
⎧I Z = I Z1
⎪
⎨
⎪V = E − RI
Z1
⎩ Z1
Curva caratteristica. Variazione della retta di carico al variare dell’alimentazione.
Valori misurati
E
2
4
5
5,8
6
6,1
6,2
6,5
7
8
9
10
Volt
VZ
2
4
5
5,35
5,37
5,38
5,38
5,4
5,42
5,44
5,46
5,47
mA
VR
0
0
0
0,45
0,63
0,72
0,82
1,1
1,58
2,56
3,54
4,53
IZ
0
0
0
1,153
1,615
1,846
2,102
2,820
4,051
6,564
9,076
11,615
E/R
5,128
10,256
12,820
14,871
15,384
15,641
15,897
16,666
17,948
20,512
23,076
25,641
Ω
RZ
10
10
10
10
10
10
10
10
10
10
10
10
Volt
VZK
5,324
5,324
5,324
5,324
5,324
5,324
5,324
5,324
5,324
5,324
5,324
5,324
Valori calcolati
dal circuito
equivalente
Volt
mA
IZ
VZ
0
2
0
4
0
5
1,19
5,335
1,69
5,340
1,94
5,343
2,19
5,345
2,94
5,353
4,19
5,365
6,69
5,390
9,19
5,415
11,69 5,440
Punto
alternativo
Volt
mA
VZ1
IZ1
------------1,9
10
2,1
10
2,2
10
2,3
10
2,6
10
3,1
10
4,1
10
5,1
10
6,1
10
Determinazione del circuito equivalente
Si scelgono i punti A(5,37 ; 1,615⋅10-3) e B(5,47 ; 11,615⋅10-3)
RZ =
1 VZB − VZA
5,47 − 5,37
=
=
= 10Ω
m
I ZB − I ZA
11,615 ⋅ 10 −3 − 1,615 ⋅ 10 −3
VZK = VZA − R Z I ZA = 5,37 − 10 ⋅ 1,615 ⋅ 10 −3 = 5,354V
Variazione della retta di carico al variare di R.
Valori misurati
kΩ
R
0,1
0,12
0,15
0,18
0,22
0,27
0,33
0,39
0,47
0,68
1
2,2
Volt
E
VZ
8 5,49
8 5,51
8
5,5
8 5,47
8 5,45
8 5,45
8 5,44
8 5,44
8 5,43
8 5,41
8 5,39
8 5,35
mA
VR
IZ
2,51
25,1
2,49 20,75
2,5 16,666
2,53 14,055
2,55 11,590
2,55 9,444
2,56 7,757
2,56 6,564
2,57 5,468
2,59 3,808
2,61
2,61
2,65 1,204
Volt
E/R
80
66,666
53,333
44,444
36,363
29,629
24,242
20,512
17,021
11,764
8
3,636
Ω
RZ
10
10
10
10
10
10
10
10
10
10
10
10
6
Volt
VZK
5,324
5,324
5,324
5,324
5,324
5,324
5,324
5,324
5,324
5,324
5,324
5,324
Valori calcolati
dal circuito
equivalente
Volt
mA
IZ
VZ
24,327 5,567
20,584 5,529
16,725 5,491
14,084 5,464
11,634 5,440
9,557 5,419
7,870 5,402
6,69 5,390
5,575 5,379
3,878 5,362
2,649 5,350
1,210 5,336
Punto
alternativo
Volt
mA
IZ1
VZ1
20
6
20
5,6
20
5
20
4,4
20
3,6
20
2,6
-------------------------
Grafici della curva caratteristica e variazione della retta di carico per variazione
dell’alimentazione e della resistenza di carico.
7
8
9
Conclusioni
I valori misurati di VZ e di IZ e quelli calcolati utilizzando il circuito equivalente sperimentale, sono
praticamente coincidenti; ciò evidenzia che il circuito equivalente determinato schematizza, tra i
punti A e B, molto bene il comportamento del diodo zener, ossia ne dimostra la validità.
Le rette di carico determinate sperimentalmente al variare della tensione di alimentazione danno
origine ad un fascio di rette parallele ed ognuna di esse passa per il punto di lavoro del diodo zener
per quel dato valore di E.
Le rette di carico determinate sperimentalmente al variare della resistenza di carico danno origine
ad un fascio di rette per il punto (8 ; 0) ed ognuna di esse passa per il punto di lavoro del diodo
zener per quel dato valore di R.
VERIFICA DEL FUNZIONAMENTO DI UNO STABILIZZATORE DI TENSIONE
UTILIZZANTE IL DIODO ZENER DI CUI SI È DETERMINATA LA CURVA
CARATTERISTICA E IL CIRCUITO EQUIVALENTE
Richiami teorici
R è la resistenza di stabilizzazione; RL è il carico. Il diodo zener, in conduzione inversa, fissa il
valore della differenza di potenziale sul carico alla tensione VZ. Se si hanno variazioni sia di carico,
sia di alimentazione, purché il diodo zener rimanga in zona di conduzione inversa, stabilizza la
tensione VL al valore VZ.
Variazioni del carico RL
E = RI + VZ = RI + VL = RI + R L I L
;
− Se RL aumenta
⇒
poiché VL = RLIL = VZ = costante
poiché E = RI + VZ = cos tan te e I = I Z + I L = cos tan te
compensata da un aumento di IZ ⇒ VL rimane costante.
I = IZ + IL
⇒
⇒
IL deve diminuire
⇒
tale variazione varrà
⇒
IL aumenta
⇒
IZ diminuisce compensando l’aumento di IL
− Se RL diminuisce
dovuta alla variazione del carico ⇒ VL rimane costante.
Variazioni dell’alimentazione E
10
E − VZ
V
⇒ I aumenta ⇒ essendo I = I L + I Z = Z + I Z ,
R
RL
⇒
deve aumentare IZ , compensando la variazione di differenza di
IL non può aumentare
potenziale su R causata dall’aumento di E ⇒ VL rimane costante.
− Se E aumenta, poiché I =
− Se E diminuisce
⇒
I diminuisce
⇒
IZ diminuisce
⇒
VL rimane costante.
Il tutto è valido se le variazioni di IZ non sono tali da portare il diodo zener né in zona di
interdizione (sopra il ginocchio della curva caratteristica) né in una zona prossima a quella di
massima dissipazione della potenza. Pertanto, si dovrà fissare un valore minimo IZMIN e un valore
massimo IZMAX tra cui far variare la corrente IZ del diodo zener.
0
VZ
Per ottenere il massimo campo di variazione bisogna fissare
la corrente IZ al centro di tale intervallo, ossia:
IZMIN
I ZO =
I ZMIN + I ZMAX
2
Il valore IZMIN si sceglie dalla curva caratteristica, appena
sotto il ginocchio.
Il valore IZMAX si scegli in modo che almeno 5 o 10 volte più
P
piccolo di I ZM = Z = corrente massima assoluta del diodo
VZ
zener.
IZO
IZMAX
IZ
Retta di carico e sua variazione. Definizione di RLMIN e di RLMAX.
0
L’equazione della retta di carico si ottiene esplicitando IZ in funzione di VZ dalle seguenti due
equazioni associate al circuito stabilizzatore.
⎧
⎪E = RI + V
Z
⎪⎪
⎨I = I Z + I L
⎪
V
V
⎪I L = L = Z
⎪⎩
RL RL
⇒
IZ = −
⇒
I=
E − VZ
V
= IZ + IL = IZ + Z
R
RL
VZ VZ E
−
+
R RL R
Il coefficiente angolare è:
m=−
⇒
IZ = −
R + RL
E
VZ +
RR L
R
R + RL
1
=−
RR L
R // R L
⇒
E − VZ
V
= IZ + Z
R
RL
retta di carico del diodo zener.
VZ
IZ
0
E
R
R LE
R + RL
e intercetta gli assi nei punti
11
⇒
0
VZ
Variazione del carico RL
R LMIN E
R + R LMIN
R LE
R + RL
0
IZMIN
A(VZMIN; IZMIN)
RL
Se varia il carico RL, il punto (0 ; E/R),
l’intercetta dell’asse IZ, rimane costante, mentre
varia il coefficiente angolare della retta di
carico.
La retta di carico ruoterà attorno al punto (0 ;
E/R).
Poiché
⎛1
R + RL
1
1 ⎞
⎟⎟ ,
=−
= −⎜⎜ +
m=−
RR L
R // R L
⎝ R RL ⎠
RLMIN
Q(VZO;IZO)
IZO
R LMAX E
R + R LMAX
RLMAX
B(VZMAX; IZMAX)
un aumento del carico RL produce una
diminuzione, in valore assoluto, del coefficiente
angolare. Il valore limite per RLMAX si ottiene
imponendo che per tale valore la retta di carico
passi per il punto B della curva caratteristica
corrispondente alla IZMAX fissata.
IZMAX
E
R
IZ
Pertanto:
I ZMAX = −
R + R LMAX
E
VZMAX +
RR LMAX
R
⇒
⇒
⇒
RR LMAX I ZMAX = −RVZMAX − R LMAX VZMAX + R LMAX E
RR LMAX I ZMAX + R LMAX VZMAX − R LMAX E = −RVZMAX
R LMAX (RI ZMAX + VZMAX − E ) = − RVZMAX
⇒
R LMAX =
⇒
⇒
RVZMAX
E − RI ZMAX − VZMAX
I valori VZMIN e VZMAX si determinano dalla curva caratteristica una volta fissati i valori di IZMIN e
IZMAX.
Una diminuzione del carico RL produce un aumento, in valore assoluto, del coefficiente angolare. Il
valore limite per RLMIN si ottiene imponendo che per tale valore la retta di carico passi per il punto
A della curva caratteristica corrispondente alla IZMIN fissata. Pertanto:
I ZMIN = −
R + R LMIN
E
VZMIN +
RR LMIN
R
⇒
R LMIN =
RVZMIN
E − RI ZMIN − VZMIN
Quando varia E, il coefficiente angolare rimane costante, mentre variano le intercette. La retta di
carico si sposterà parallelamente a se stessa.
I valori massimo EMAX e minimo EMIN che l’alimentazione può raggiungere senza che il circuito
perda la sua caratteristica di stabilizzatore si ottengono in corrispondenza delle rette di carico
passanti per i punti A e B.
Per il valore massimo EMAX si ha:
I ZMAX = −
R + RL
E
VZMAX + MAX
RR L
R
⇒
12
E MAX
R + RL
VZMAX
= I ZMAX +
R
RR L
⇒
VZ
R L E MAX
R + RL
R LE
R + RL
R L E MIN
R + RL
0
A(VZMIN; IZMIN)
EMAX
E
⇒ E MAX = RI ZMAX +
IZMIN
R + RL
VZMAX
RL
EMIN
Q(VZO;IZO)
IZO
Per il valore massimo EMIN si ha:
E MIN
R
B(VZMAX; IZMAX)
I ZMIN = −
IZMAX
E
R
⇒
E
R + RL
VZMIN + MIN
RR L
R
E MIN = RI ZMIN +
⇒
R + RL
VZMIN
RL
E MAX
R
IZ
Dimensionamento del circuito
Si fissa: E = 10V ; IZMIN = 1mA ; IZMAX = 19mA ; RL = 1kΩ ; RZ = 10Ω ; VZK = 5,354V.
Si calcolano le coordinate del punto Q: I ZO =
I ZMIN + I ZMAX 1 ⋅ 10 −3 + 19 ⋅ 10 −3
=
= 10mA ;
2
2
in corrispondenza di tale corrente, dalla curva caratteristica, risulta: VZO = 5,46V ;
oppure dal circuito equivalente: VZO = R Z I ZO + VZK = 10 ⋅ 10 ⋅ 10 −3 + 5,354 = 5,454V .
E − VZO 10 − 5,46
=
= 454Ω , valore
I ZO
10 ⋅ 10 −3
commerciale usato 390Ω. La corrente risulterà di poco superiore a 10mA.
Si dimensiona R assumendo il carico di valore infinito:
R=
Calcolo di RLMAX ; RLMIN ; EMAX ; EMIN
Dalla curva caratteristica si ha: VZMIN = 5,35V ; VZMAX = 5,51V,
oppure, dal circuito equivalente, VZMIN = R Z I ZMIN + VZK = 10 ⋅ 1 ⋅ 10 −3 + 5,354 = 5,364V
VZMAX = R Z I ZMAX + VZK = 10 ⋅ 19 ⋅ 10 −3 + 5,354 = 5,44V
R LMAX =
RVZMAX
390 ⋅ 5,51
=
= −736Ω .
E − RI ZMAX − VZMAX 10 − 0,39 ⋅ 10 3 ⋅ 19 ⋅ 10 −3 − 5,51
13
Il valore negativo sta ad indicare che non esiste un limite superiore per RL, ossia IZ risulta minore di
IZMAX per qualunque valore di RL (anche RL = ∞).
R LMIN =
E MAX = RI ZMAX
RVZMIN
390 ⋅ 5,35
=
= 490Ω
E − RI ZMIN − VZMIN 10 − 0,39 ⋅ 10 3 ⋅ 1 ⋅ 10 −3 − 5,35
R + RL
0,39 ⋅ 10 3 + 1 ⋅ 10 3
3
−3
+
VZMAX = 0,39 ⋅ 10 ⋅ 19 ⋅ 10 +
⋅ 5,51 = 15,07V
RL
1 ⋅ 10 3
E MIN = RI ZMIN +
R + RL
0,39 ⋅ 10 3 + 1 ⋅ 10 3
VZMIN = 0,39 ⋅ 10 3 ⋅ 1 ⋅ 10 −3 +
⋅ 5,35 = 7,83V
RL
1 ⋅ 10 3
Scelta dei valori di RL e di E da utilizzare nella verifica
Variazione di RL: poiché 490Ω ≤ RL ≤ ∞ , si scelgono i seguenti valori:
∞ ; 12kΩ ; 4,7kΩ ; 3,3kΩ ; 2,2kΩ ; 1,5kΩ ; 1,2kΩ ; 1kΩ ; 0,82kΩ ; 0,68kΩ ; 0,56kΩ ; 0,47kΩ
Variazione di E: poiché 7,83V ≤ E ≤ 15,07V , si fissa una variazione di ±20% di E, ossia si fa
variare E tra i valori 8V ≤ E ≤ 12V. si scelgono i seguenti valori di E:
8V ; 8,5V ; 9V ; 9,5V ; 10V ; 10,5V ; 11V ; 11,5V ; 12V
Calcolo teorico dei valori da misurare
Si utilizza il circuito equivalente del diodo zener
Utilizzando i principi di Kirchhoff si calcolano I ; IZ ; IL , e, quindi, applicando la legge di Ohm, si
calcolano VR ; VZ ; VL. Si sostituisce la prima nella seconda; dalla terza si esplicita IL e si
sostituisce nella seconda.
⎧
⎪I = I + I
Z
L
⎪
⎪
⎪
⇒
⎨E − VZK = RI + R Z I Z ⇒ RI Z + RI L + R Z I Z = E − VZK ⇒ (R + R Z )I Z + RI L = E − VZK
⎪
⎪
VZK + R Z I Z
⎪
⎪VZK = − R Z I Z + R L I L ⇒ I L =
RL
⎩
14
⇒
(R + R Z )I Z + R VZK + R Z I Z
RL
⎛
RR Z
⎜⎜ R + R Z +
RL
⎝
⇒
⇒
= E − VZK
⎞
R
⎟⎟I Z = E − VZK −
VZK
RL
⎠
(RR L + R Z R L + RR Z )I Z = R L E − R L VZK − RVZK
I = IZ + IL
Nota IZ si calcolano IL e I:
VZ = R Z I Z + VZK
e quindi
;
RR Z
R
VZK +
I Z = E − VZK
RL
RL
(R + R Z )I Z +
⇒
;
⇒
IL =
VL = R L I L
IZ =
⇒
⇒
R L (E − VZK ) − RVZK
RR L + R Z R L + RR Z
VZK + R Z I Z
RL
;
VR = RI
Procedimento della verifica
Variazioni del carico RL
1. Si collega l’alimentatore variabile e lo si regola a 10V.
2. Si lasciano aperti i morsetti del carico
3. Si misurano VL = VZ e VR. quindi, con i valori misurati, si calcolano:
I=
VR
R
;
IL =
VL
RL
;
IZ = I − IL
;
R LE
R + RL
;
E
R
4. Si inseriscono, in successione i valori di RL: 12kΩ ; 4,7kΩ ; 3,3kΩ ; 2,2kΩ ; 1,5kΩ ; 1,2kΩ ;
1kΩ ; 0,82kΩ ; 0,68kΩ ; 0,56kΩ ; 0,47kΩ, e per ognuno di essi si ripete il punto 3.
5. Si tabulano i dati. Nella tabella vengono anche riportati il punto alternativo dal quale far passare
la retta di carico nel caso il valore dell’intercetta sia tale da essere fuori grafico e i valori di IZ e
di VZ calcolati dal circuito equivalente, prima determinato, mediante foglio Excell.
6. Si riportano sul grafico della curva caratteristica le rette di carico che intercettano gli assi nei
⎛ R LE
⎞
⎛ E⎞
punti ⎜⎜
;0 ⎟⎟ e ⎜ 0; ⎟ . Si determinano graficamente le correnti per ogni retta e si
⎝ R⎠
⎝ R + RL ⎠
confrontano con quelli misurai e quelli calcolati.
Variazioni dell’alimentazione
7. Si fissa il valore di RL a 1kΩ e si regola l’alimentatore variabile E a 8V.
8. Si misurano VL = VZ e VR. quindi, con i valori misurati, si calcolano:
I=
VR
R
;
IL =
VL
RL
;
IZ = I − IL
;
R LE
R + RL
;
E
R
9. Si regola, in successione, l’alimentatore E a 8,5V ; 9V ; 9,5V ; 10V ; 10,5V ; 11V ;
11,5V ; 12V e, per ognuno, si ripete il punto 8.
15
10. Si tabulano i dati. Nella tabella vengono anche riportati il punto alternativo dal quale far passare
la retta di carico nel caso il valore dell’intercetta sia tale da essere fuori grafico e i valori di IZ e
di VZ calcolati dal circuito equivalente, prima determinato, mediante foglio Excell.
11. Si riportano sul grafico della curva caratteristica le rette di carico che intercettano gli assi nei
⎛ R LE
⎞
⎛ E⎞
punti ⎜⎜
;0 ⎟⎟ e ⎜ 0; ⎟ . Si determinano graficamente le correnti per ogni retta e si
⎝ R⎠
⎝ R + RL ⎠
confrontano con quelli misurai e quelli calcolati.
Determinazione del punto alternativo
Nel caso che una, o entrambe, delle intersezioni con gli assi cada fuori dal grafico, è necessario
calcolare un altro punto, o due, della retta che cada nel grafico.
Si fissa il valore di IZ = IZ1 e si calcola VZ1:
I Z1 = −
R + RL
E
VZ1 +
RR L
R
⇒
VZ1 =
RL
RR L
RL
(E − RI Z1 )
E−
I Z1 =
R + RL
R + RL
R + RL
Variazione della retta di carico al variare di RL
Valori misurati
kΩ
RL
∞
12
4,7
3,3
2,2
1,5
1,2
1
0,82
0,68
0,56
0,47
E
10
10
10
10
10
10
10
10
10
10
10
10
Volt
VL=VZ
5,48
5,48
5,47
5,47
5,47
5,46
5,46
5,45
5,44
5,43
5,4
5,48
VR
4,52
4,52
4,53
4,53
4,53
4,54
4,54
4,55
4,56
4,57
4,6
4,52
I
11,589
11,589
11,615
11,615
11,615
11,641
11,641
11,666
11,692
11,717
11,794
11,589
Intercette
mA
IL
0
0,4566
1,1638
1,6575
2,4863
3,64
4,55
5,45
6,6341
7,9852
9,6428
11,589
IZ
11,589
11,133
10,451
9,9578
9,129
8,001
7,091
6,216
5,058
3,732
2,152
0
Volt
RLE/(R+RL)
9,996
9,685
9,233
8,943
8,494
7,936
7,547
7,194
6,776
6,355
5,894
5,465
mA
E/R
25,641
25,641
25,641
25,641
25,641
25,641
25,641
25,641
25,641
25,641
25,641
25,641
Valori misurati
kΩ
RL
∞
12
4,7
3,3
2,2
1,5
1,2
1
0,82
0,68
0,56
0,47
E
10
10
10
10
10
10
10
10
10
10
10
10
Volt
VL=VZ
5,440
5,436
5,429
5,424
5,416
5,405
5,397
5,388
5,376
5,36
5,347
5,330
VR
4,559
4,563
4,570
4,575
4,583
4,594
4,602
4,611
4,623
4,636
4,652
4,669
16
I
11,690
11,701
11,718
11,731
11,751
11,780
11,802
11,824
11,853
11,887
11,928
11,973
mA
IL
0
0,453
1,155
1,643
2,462
3,603
4,497
5,388
6,557
7,888
9,549
11,341
IZ
11,684
11,248
10,563
10,087
9,2893
8,1762
7,3048
6,4363
5,2966
3,9989
2,3791
0,632
Punto
alternativo
mA
Volt
IZ1
VZ1
10
6,097
10
5,907
10
5,632
10
5,455
10
5,181
10
4,841
10
4,603
10
4,388
10
4,133
10
3,876
10
3,595
10
3,333
Relativamente all’ultima riga della tabella dei valori misurati, in corrispondenza del carico RL =
470Ω, il diodo risulta non in conduzione, ossia il punto di lavoro risulta al di sopra della zona del
ginocchio della curva caratteristica.
Valori misurati
kΩ
RL
1
1
1
1
1
1
1
1
1
E
8
8,5
9
9,5
10
10,5
11
11,5
12
Volt
VL=VZ
5,36
5,4
5,42
5,44
5,45
5,46
5,47
5,47
5,48
VR
2,64
3,1
3,58
4,06
4,55
5,04
5,53
6,03
6,52
I
6,769
7,948
9,179
10,410
11,666
12,923
14,179
15,461
16,717
E
8
8,5
9
9,5
10
10,5
11
11,5
12
Volt
VL=VZ
5,338
5,351
5,363
5,375
5,388
5,400
5,413
5,425
5,437
Intercette
mA
IL
5,36
5,4
5,42
5,44
5,45
5,46
5,47
5,47
5,48
IZ
1,409
2,548
3,759
4,970
6,216
7,463
8,709
9,991
11,237
Volt
RLE/(R+RL)
5,755
6,115
6,474
6,834
7,194
7,553
7,913
8,273
8,633
mA
E/R
20,512
21,794
23,076
24,358
25,641
26,923
28,205
29,487
30,769
Valori misurati
kΩ
RL
1
1
1
1
1
1
1
1
1
VR
2,661
3,148
3,636
4,124
4,611
5,099
5,586
6,074
6,562
17
I
6,823
8,073
9,324
10,574
11,824
13,075
14,325
15,575
16,825
mA
IL
5,338
5,351
5,363
5,375
5,388
5,400
5,413
5,425
5,437
IZ
1,484
2,722
3,960
5,198
6,436
7,674
8,912
10,150
11,388
Punto
alternativo
mA
Volt
IZ1
VZ1
10
2,949
10
3,309
10
3,669
10
4,028
10
4,388
10
4,748
10
5,107
10
5,467
10
5,827
Grafici della curva caratteristica e variazione della retta di carico per variazione
dell’alimentazione e del carico.
18
19
20
SI RIPETE CON UN DIODO ZENER DI 6,8V ½W
Diodo zener
Dimensionamento del circuito. Rilievo della curva caratteristica e circuito equivalente.
Variazione della retta di carico per variazione di R.
Si utilizza un diodo zener PZ = ½W con VZ = 6,8V.
Corrente massima IZM del diodo zener:
I ZM =
PZ 0,5
=
= 73,53mA
VZ 6,8
Si fissa IZMAX = 8mA in corrispondenza di E = 12V e si dimensiona R:
R=
E M − VZ 12 − 6,8
=
= 650Ω ,
I ZMAX
8 ⋅ 10 −3
valore commerciale 680Ω.
La tensione E dell’alimentatore si fa variare da 0V a 12V come riportato nella corrispondente
tabella. In corrispondenza di ogni valore di E, per il quale il diodo zener conduce, si ha una retta di
carico.
Per ottenere il fascio di rette per un punto al variare di R, se ne fa variare il valore in più e in meno
rispetto il valore di 680Ω come riportato nella corrispondente tabella. In corrispondenza di ogni
valore di resistenza R si ha una retta di carico.
In entrambe le misure verrà impiegato un alimentatore variabile e un multimetro 4½ digit.
Nelle tabelle vengono anche riportati il punto alternativo dal quale far passare la retta di carico nel
caso il valore dell’intercetta sia tale da essere fuori grafico e i valori di IZ e di VZ calcolati dal
circuito equivalente, prima determinato, mediante foglio Excell.
Curva caratteristica. Variazione della retta di carico al variare dell’alimentazione.
Valori misurati
E
0
1
3
5
6
6,5
6,7
6,8
6,9
7
8
9
10
11
12
Volt
VZ
0
1
3
5
6
6,5
6,7
6,782
6,798
6,812
6,827
6,85
6,878
6,907
6,935
mA
VR
0
0
0
0
0
0
0
0,018
0,102
0,188
1,173
2,15
3,122
4,093
5,065
IZ
0
0
0
0
0
0
0
0,026
0,15
0,276
1,725
3,161
4,591
6,019
7,448
E/R
0
1,470
4,411
7,352
8,823
9,558
9,852
10
10,147
10,294
11,764
13,235
14,705
16,176
17,647
Ω
RZ
17
17
17
17
17
17
17
17
17
17
17
17
17
17
17
21
Volt
VZK
6,8
6,8
6,8
6,8
6,8
6,8
6,8
6,8
6,8
6,8
6,8
6,8
6,8
6,8
6,8
Valori calcolati
dal circuito
equivalente
Volt
mA
IZ
VZ
0
0
0
1
0
3
0
5
0
6
0
6,5
0
6,7
0
6,8
0,143
6,802
0,286
6,804
1,721
6,829
3,156
6,853
4,591
6,878
6,025
6,902
7,460
6,926
Punto
alternativo
Volt
mA
VZ1
IZ1
----------------------------------------10
1,2
10
2,2
10
3,2
10
4,2
10
5,2
Determinazione del circuito equivalente
Si scelgono i punti A(6,812 ; 0,274⋅10-3) e B(6,935 ; 7,44⋅10-3)
RZ =
1 VZB − VZA
6,935 − 6,812
=
=
= 17Ω
m
I ZB − I ZA
7,44 ⋅ 10 −3 − 0,274 ⋅ 10 −3
VZK = VZA − R Z I ZA = 6,812 − 17 ⋅ 0,274 ⋅ 10 −3 = 6,8V
Variazione della retta di carico al variare di R.
Valori calcolati dal
circuito equivalente
Valori misurati
kΩ
R
0,56
0,68
1
2,2
3,3
4,7
6,8
8,2
10
12
Volt
E
VZ
12 6,967
12 6,935
12 6,886
12 6,836
12 6,821
12 6,813
12 6,803
12
6,8
12 6,798
12 6,797
mA
VR
5,033
5,065
5,114
5,164
5,179
5,187
5,197
5,2
5,202
5,203
IZ
8,987
7,448
5,114
2,347
1,569
1,103
0,764
0,634
0,520
0,433
Volt
E/R
21,428
17,647
12
5,454
3,636
2,553
1,764
1,463
1,2
1
Ω
RZ
17
17
17
17
17
17
17
17
17
17
22
Volt
VZK
6,8
6,8
6,8
6,8
6,8
6,8
6,8
6,8
6,8
6,8
Volt
IZ
9,012
7,460
5,113
2,345
1,567
1,102
0,762
0,632
0,519
0,432
mA
VZ
6,953
6,926
6,886
6,839
6,826
6,818
6,812
6,810
6,808
6,807
Punto
alternativo
Volt
mA
IZ1
VZ1
10
6,4
10
5,2
10
2
-----------------------------
Grafici della curva caratteristica e variazione della retta di carico per variazione
dell’alimentazione e della resistenza di carico.
23
24
25
Stabilizzatore di tensione
Dimensionamento del circuito
Si fissa: E = 12V ; VZ = 6,8mA ; IZ = 10mA ; RL = 1,8kΩ ; RZ = 17Ω ; VZK = 6,8V.
IL =
VL VZ
6,8
=
=
= 3,77 mA ; I = I Z + I L = 10 ⋅ 10 −3 + 3,77 ⋅ 10 −3 = 13,77mA
R L R L 1,8 ⋅ 10 3
R=
E − VZ
12 − 6,8
=
= 370Ω , valore commerciale usato 390Ω.
I
13,77 ⋅ 10 −3
Calcolo di RLMAX ; RLMIN ; EMAX ; EMIN
Considerando come punti estremi i punti A(6,812 ; 0,274⋅10-3) e C( 7,14 ;20⋅10-3), si ha:
IZMIN = 0,274mA ; IZMAX = 13,33mA ; VZMIN = 6,812V ; VZMAX = 7,03V
Con un carico di valore infinito, morsetti del carico aperti, si ha la massima corrente nel diodo;
quindi, RL non ha un limite superiore. Con RL = ∞ ⇒ IZ = I = 13,33mA.
R LMIN =
E MAX = RI ZMAX +
E MIN = RI ZMIN
RVZMIN
390 ⋅ 6,812
=
= 523Ω
E − RI ZMIN − VZMIN 12 − 0,39 ⋅ 10 3 ⋅ 0,274 ⋅ 10 −3 − 6,812
R + RL
0,39 ⋅ 10 3 + 1,8 ⋅ 10 3
VZMAX = 0,39 ⋅ 10 3 ⋅ 20 ⋅ 10 −3 +
⋅ 7,14 = 16,49V
RL
1,8 ⋅ 10 3
R + RL
0,39 ⋅ 10 3 + 1,8 ⋅ 10 3
3
−3
+
VZMIN = 0,39 ⋅ 10 ⋅ 0,274 ⋅ 10 +
⋅ 6,812 = 8,39V
RL
1,8 ⋅ 10 3
Scelta dei valori di RL e di E da utilizzare nella verifica
Variazione di RL: poiché 523Ω ≤ RL ≤ ∞ , si scelgono i seguenti valori:
∞ ; 12kΩ ; 4,7kΩ ; 3,3kΩ ; 2,2kΩ ; 1,5kΩ ; 1,2kΩ ; 1kΩ ; 0,82kΩ ; 0,68kΩ ; 0,56kΩ ; 0,47kΩ
Variazione di E: poiché 8,39V ≤ E ≤ 16,49V , si fissa una variazione di ±20% di E = 12V, ossia si
fa variare E tra i valori 9,6V ≤ E ≤ 14,4V. si scelgono i seguenti valori di E:
9,5V ; 10V ; 10,5V ; 11V ; 11,5V ; 12V ; 12,5V ; 13V ; 13,5V ; 14V ; 14,5V
Nelle tabelle vengono anche riportati il punto alternativo dal quale far passare la retta di carico nel
caso il valore dell’intercetta sia tale da essere fuori grafico e i valori di IZ e di VZ calcolati dal
circuito equivalente, prima determinato, mediante foglio Excell.
26
Variazione della retta di carico al variare di RL
Valori misurati
kΩ
RL
∞
12
4,7
3,3
2,2
1,5
1,2
1
0,82
0,68
0,56
0,47
E
12
12
12
12
12
12
12
12
12
12
12
12
Volt
VL=VZ
6,95
6,93
6,91
6,9
6,89
6,87
6,84
6,83
6,8
6,8
6,8
6,8
VR
5,05
5,07
5,09
5,1
5,11
5,13
5,16
5,17
5,2
5,2
5,2
5,2
I
7,426
7,455
7,485
7,5
7,514
7,544
7,588
7,602
7,647
7,647
7,647
7,647
Intercette
mA
IL
0,007
0,577
1,470
2,090
3,131
4,58
5,7
6,83
7,647
7,647
7,647
7,647
IZ
7,419
6,878
6,015
5,409
4,382
2,964
1,888
0,772
0
0
0
0
Volt
RLE/(R+RL)
11,991
11,356
10,483
9,949
9,166
8,256
7,659
7,142
6,56
6
5,419
4,904
mA
E/R
17,647
17,647
17,647
17,647
17,647
17,647
17,647
17,647
17,647
17,647
17,647
17,647
Punto
alternativo
mA
Volt
IZ1
VZ1
10
5,196
10
4,921
10
4,542
10
4,311
10
3,972
10
3,577
10
3,319
10
3,095
10
2,842
10
2,6
10
2,348
10
2,125
Valori misurati
kΩ
RL
∞
12
4,7
3,3
2,2
1,5
1,2
1
0,82
0,68
0,56
0,47
E
12
12
12
12
12
12
12
12
12
12
12
12
Volt
VL=VZ
6,926
6,917
6,902
6,892
6,875
6,851
6,832
6,813
6,789
6,761
6,727
6,690
VR
5,073
5,082
5,097
5,107
5,125
5,148
5,167
5,186
5,210
5,238
5,272
5,309
I
7,460
7,474
7,496
7,511
7,536
7,571
7,599
7,626
7,662
7,703
7,753
7,807
mA
IL
0,007
0,576
1,468
2,088
3,125
4,567
5,693
6,813
8,279
9,943
12,013
14,235
IZ
7,453
6,898
6,027
5,422
4,411
3,004
1,905
0,812
-0,617
-2,241
-4,259
-6,427
Relativamente alle ultime 4 righe della tabella dei valori calcolati i valori della corrente IZ sono
negativi; ciò sta ad indicare che il diodo risulta non in conduzione, ossia il punto di lavoro risulta al
di sopra della zona del ginocchio della curva caratteristica.
27
Variazione della retta di carico al variare di E
Valori misurati
kΩ
RL
1
1
1
1
1
1
1
1
1
1
1
E
9,5
10
10,5
11
11,5
12
12,5
13
13,5
14
14,5
Volt
VL=VZ
6,82
6,84
6,86
6,6
6,91
6,93
6,94
6,96
6,9
7,01
7,02
VR
2,68
3,16
3,64
4,4
4,59
5,07
5,56
6,04
6,6
6,99
7,48
I
6,871
8,102
9,333
11,282
11,769
13
14,256
15,487
16,923
17,923
19,179
E
8
8,5
9
9,5
10
10,5
11
11,5
12
11,5
12
Volt
VL=VZ
6,801
6,822
6,843
6,863
6,884
6,904
6,925
6,945
6,966
6,986
7,007
Intercette
mA
IL
6,82
6,84
6,86
6,6
6,91
6,93
6,94
6,96
6,9
7,01
7,02
IZ
0,051
1,262
2,473
4,682
4,859
6,07
7,316
8,527
10,023
10,913
12,159
Volt
RLE/(R+RL)
6,834
7,194
7,553
7,913
8,273
8,633
8,992
9,352
9,712
10,071
10,431
mA
E/R
24,358
25,641
26,923
28,205
29,487
30,769
32,051
33,333
34,615
35,897
37,179
Valori misurati
kΩ
RL
1
1
1
1
1
1
1
1
1
1
1
VR
2,698
3,177
3,656
4,136
4,615
5,095
5,574
6,054
6,533
7,013
7,492
28
I
6,918
8,147
9,376
10,606
11,835
13,064
14,294
15,523
16,752
17,982
19,211
mA
IL
6,801
6,822
6,843
6,863
6,884
6,904
6,925
6,945
6,966
6,986
7,007
IZ
0,116
1,324
2,533
3,742
4,951
6,160
7,368
8,577
9,786
10,995
12,204
Punto
alternativo
mA
Volt
IZ1
VZ1
10
4,028
10
4,388
10
4,748
10
5,107
10
5,467
10
5,827
10
6,187
10
6,546
10
6,906
10
7,266
10
7,625
Variazione della retta di carico al variare di E e di RL
Valori misurati
kΩ
RL
1,8
1,8
1,8
1,5
2,2
1,5
2,2
E
12
9,6
14,4
12
12
14,4
9,6
Volt
VL=VZ
6,878
6,828
6,933
6,879
6,912
6,93
6,859
VR
5,122
2,772
7,467
5,121
5,088
7,47
2,741
I
13,133
7,107
19,146
13,130
13,046
19,153
7,0282
Intercette
mA
IL
3,821
3,793
3,851
4,586
3,141
4,62
3,117
IZ
9,312
3,314
15,294
8,544
9,904
14,533
3,910
Volt
RLE/(R+RL)
9,863
7,890
11,835
9,523
10,193
11,428
8,154
mA
E/R
30,769
24,615
36,923
30,769
30,769
36,923
24,615
Valori misurati
kΩ
RL
1,8
1,8
1,8
1,5
2,2
1,5
2,2
E
12
9,6
14,4
12
12
14,4
9,6
Volt
VL=VZ
6,954
6,854
7,053
6,941
6,965
7,040
6,866
VR
5,045
2,745
7,346
5,058
5,034
7,359
2,733
29
I
12,937
7,038
18,836
12,969
12,908
18,869
7,01
mA
IL
3,863
3,808
3,918
4,627
3,166
4,693
3,120
IZ
9,074
3,230
14,918
8,341
9,742
14,175
3,889
Punto
alternativo
mA
Volt
IZ1
VZ1
10
6,657
10
4,684
10
8,630
10
6,428
10
6,880
10
8,333
10
4,841
Grafici della curva caratteristica e variazione della retta di carico per variazione
dell’alimentazione e del carico.
30
31
32