Modelli Non-lineari di Circuiti CMOS per la

Modelli Non-lineari di Circuiti CMOS per la
Realizzazione VLSI Analogica di Algoritmi Neurali
H. Chible, M. Valle
DIBE-Dipartmento di Ingegneria Biosica ed Elettronica
Universita di Genova-Via Opera Pia 11/A-16145 Genova-ITALIA
ph: +39 10 3532163, fax: +39 10 3532795,e-mail:[email protected]
RIASSUNTO
La realizzazione analogica VLSI rappresenta una via eciente per la realizzazione di reti
neurali: essa infatti permette di ottenere un'area ridotta, una bassa potenza dissipata ed elevate
prestazioni. Tuttavia, il principale inconveniente risulta essere la bassa precisione ed il comportamento non-lineare delle primitive computazionali neurali analogiche. In un precedente
articolo, sono state presentate primitive circuitali analogiche neurali in tecnologia CMOS. In
questa memoria vengono presentati i modelli funzionali delle primitive circuitali che tengono
conto sia delle non-linearita che degli eetti ambientali (variazioni di temperatura, segnali di
riferimento, etc.) che inuenzano il funzionamento dei circuiti. Tali modelli funzionali sono
stati utilizzati nella simulazione di una architettura neurale del tipo Multi-Layer-Perceptron addestrata con l'algoritmo di apprendimento di Back-Propagation in modo da valutare gli eetti
sul comportamento della rete. I risultati ottenuti evidenziano che il numero delle iterazioni
necessarie a completare l'apprendimento aumenta in modo contenuto per cui le prestazioni
della rete non vengono degradate in modo signicativo.
1 Introduzione
Tra le possibilita per l'implementazione hardware di reti neurali ( circuiti dedicati sia
digitali che analogici), alcuni autori, [1], [2], [3], hanno evidenziato i vantaggi (i.e. dimensioni
ridotte, bassa potenza dissipata, etc.) dell'approccio VLSI analogico. In un precedente articolo,
[4], abbiamo presentato una realizzazione analogica di un Multi-Layer-Perceptron (MLP) che
realizza l'algoritmo della Back-Propagation (BP) su chip, [5], e valutato il comportamento
usando un semplice esempio di apprendimento.
In questa memoria, analizziamo le funzionalita dei circuiti analogici che realizzano le primitive computazionali. Di tali circuiti sono presentati i modelli funzionali che tengono conto
delle non-linearita introdotte dal circuito e degli eetti amientali.
Nel paragrafo 2 vengono presentati i circuiti che realizzano le funzionalita del neurone e
della sinapsi. Nel paragrafo 3 viene analizzato il moltiplicatore sinaptico in avanti. Nel paragrafo 4 viene analizzato il moltiplicatore sinaptico per l'aggiornamento dei pesi. La funzione
di attivazione del neurone viene analizzata nel paragrafo 5. I risultati delle simulazioni funzionali che utilizzano i modelli non-lineari ricavati nei paragra precedenti per i moltiplicatori
sinaptici vengono presentati nel paragrafo 6. Le conclusioni sono esposte nel paragrafo 7.
2 Circuiti del Neurone e della Sinapsi
In [4], abbiamo presentato un'architettura VLSI analogica per la realizzazione di un MLP
addestrato con l'algoritmo di BP. Ogni strato del MLP contiene una matrice di sinapsi [Sji]
e un vettore di neuroni [Pj ] (i=1,N) (j=1,M) dove N e il numero degli ingressi e M il numero
delle uscite e N M il numero di sinapsi nel generico strato della rete.
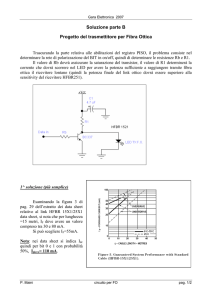
Lo schema funzionale del modulo sinaptico Sji e illustrato in Fig. 1a. Il blocco F esegue
la moltiplicazione in avanti tra la tensione di ingresso alla sinapsi Xi ed il peso sinaptico
(codicato attraverso il valore di una transconduttanza) Wji e genera la corrente di uscita
IFji = Wji Xi ; il blocco B1 esegue la moltiplicazione all'indietro tra la tensione di errore j e
il peso Wji , ottenendo la corrente IB1ji ; il blocco B2 eettua l' aggiornamento del peso dopo
la presentazione di un esemplare in ingresso (fase Q1) ed esegue la moltiplicazione tra Xi e
j , ottenendo la corrente IB2ji ; il blocco somma gli aggiornamenti dei pesi che seguono
alla presentazione di tutti gli esemplari e aggiorna il peso sinaptico (fase Q2); il blocco W
memorizza la tensione di peso VWji.
I Fji
Xi
IFj
A
Oj
F
Q1
Q2
Σ
B2
1- Oj
VWji
W
I B2ji
B1
δj
IDj
D
I B1ji
Tj / IBi
R
δj
(b)
(a)
Figure 1: (a) Schema funzionale del modulo sinaptico Sji; (b) Schema funzionale del modulo
del neurone Pj .
Lo schema funzionale del modulo del neurone Pj e illustrato in Fig. 1b. Il blocco A e il
circuito base del neurone, il suo ingresso e la corrente IFj (che e la somma di tutte le correnti
di uscita di una riga di sinapsi, IFj = Ni=1 IFji): esso applica la funzione di attivazione,
f(.), e genera la tensione di uscita non invertente Oj , e quella invertente (1 ? Oj ); il blocco
D approssima la derivata della funzione di attivazione e genera la corrente IDj ; il blocco
R moltiplica la corrente IDj con la dierenza tra la tensione desiderata Tj e la tensione di
uscita Oj (strato di uscita) oppure con la corrente IBi generata dallo strato successivo (strato
intermedio).
3 Il Moltiplicatore Sinaptico F
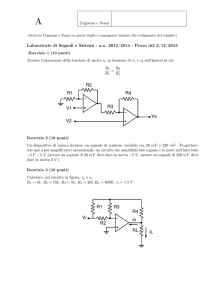
Il circuito del moltiplicatore sinaptico F proposto in [4], e illustrato in Fig. 2a. Esso con∆ Vref
VDD
M3
∆T
M5
M10
∆ Gmji( ∆T, ∆Vref)
M11
IFji
Gmji
M1
VWji
M6
M7
M12 M13
M2
-
Vref
M8
Xi -Vref
M9
M4
+
+
Gmji
M14
Σ
IFji,reale
+
N1( Xi -Vref )
Xi
(a)
(b)
Figure 2: (a) Schema del circuito del moltiplicatore F; (b) Modello funzionale del moltiplicatore
F.
siste di una cella di immagazzinamento della tensione di peso VWji (M1 ; M2 ; M3 ; M4 ) e di due
(OTA)1 complementari (M5 ; M6 ; M7 ; M8 ; M9 ) e (M10 ; M11 ; M12 ; M13 ; M14 ). La cella di immagazzinamento fornisce una azione complementare: essa converte la tensione del peso VWji
1
amplicatore a transconduttanza (Operational Transconductance Amplier)
in due correnti che polarizzano i due OTA, in modo da controllare il valore delle transconduttanze Gm1ji e Gm2ji , (Gmji = Gm1ji + Gm2ji ). Il moltiplicatore F lavora sottosoglia per
cui la transconduttanza e proporzionale alla corrente di canale rispettivamente dei transistori
M5 ,M14 . I pesi sono positivi quando VWji e maggiore del segnale di riferimento (Vref =2.5V)
e negativi quando VWji e minore di Vref .
La corrente di uscita puo essere espressa nella forma seguente[2]:
kVWji ?Vref
kVWji ?Vref
? Io2 e? VT ) tanh k(Xi2?V Vref )
IFji = (Io1 e VT
(1)
T
dove k e un parametro di tipo tecnologico che varia da 0.6 a 0.8, VT = KT=q (K costante di
Boltzmann, q carica dell'elettrone e T temperatura ambiente), Io1 e Io2 sono costanti relative
ai transistori M1 , M2 rispettivamente. Usando l'approssimazione polinomiale di Taylor per la
tangente iperbolica nella Eq.( 1), otteniamo:
IFji = Gmji (Xi ? Vref ) + N1 (Xi ? Vref ) = IFji;ideale + N1 (Xi ? Vref )
(2)
dove la transconduttanza Gmji , che codica il valore del peso Wji, e data dalla relazione
seguente:
Gmji = (Io1 e
kVWji ?Vref
VT
? Io2e?
kVWji ?Vref
VT
)
k
2VT
La funzione non-lineare N1 (Xi ? Vref ) e data da:
N1 (Xi ? Vref ) = (Io1 e
kVWji ?Vref
VT
? Io2e?
kVWji ?Vref
VT
)(? 1 ( k(Xi ? Vref ) )3 + :::)
3
2VT
Le variazioni ambientali (come la temperatura, il segnale di referimento) inuenzano IFji
nella Eq.( 2). In questa analisi, noi non prendiamo in considerazione gli eetti ambientali
sul termine non-lineare N1 (Xi ? Vref ). Come conseguenza, possiamo esprimere la corrente di
uscita IFji;reale come segue:
IFji;reale = IFji;ideale + 4IFji;ideale(4T; 4Vref ) + N1 (Xi ? Vref )
(3)
Possiamo approssimare 4IFji;ideale(4T; 4Vref ) come segue:
@I
4IFji;ideale(4T; 4Vref ) = @IFji;ideale
4
T + Fji;ideale 4Vref
@T
@V
ref
(4)
dove
@IFji @Gmji
= @T (Xi ? Vref )
@T
@IFji @Gmji
=
(X ? V ) ? Gmji
@Vref @Vref i ref
e
kVWji ?Vref
@Gmji
=
?
(
Io1 e VT
@T
? Io2e?
(5)
(6)
kVWji ?Vref k
VT
)
q 1
2 K T2
kVWji ?Vref k
kVWji ?Vref
@Gmji
+
Io2 e? VT )
=
?
(
Io1 e VT
@Vref
2VT
Sostituendo l'Eq.( 5) e l'Eq.( 6) nella Eq.( 4), si ottiene:
mji (X ? V ) ? G )4V
4IFji(4T; 4Vref ) = @G@Tmji (Xi ? Vref )4T + ( @G
i
mji
ref
ref
@V
ref
(7)
Possiamo esprimere l'ultima equazione come segue:
4IFji(4T; 4Vref ) = (Xi ? Vref )4Gmji(4T; 4Vref ) ? Gmji4Vref
(8)
mji
dove 4Gmji(4T; 4Vref ) = @G@Tmji 4T + @G
@Vref 4Vref . La corrente di uscita del moltiplicatore,Eq.( 3), sara:
IFji;reale = fGmji + 4Gmji(4T; 4Vref )g(Xi ? Vref ) ? Gmji 4Vref + N1 (Xi ? Vref ) (9)
Rispetto a queste considerazioni, il modello funzionale del moltiplicatore e illustrato in
Fig. 2b. Una analisi analoga puo essere eseguita per il moltiplicatore B1 perche ha la stessa
realizzazione di F. L'analisi dei blocchi R e e simile perche essi sono basati su circuiti che
utilizzano OTA.
4 Il Moltiplicatore Sinaptico B2
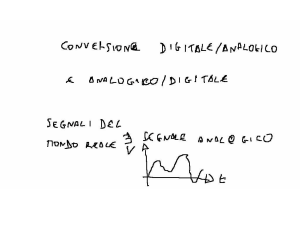
Il circuito del moltiplicatore per l'aggiornamento dei pesi, B2, e illustrato in Fig. 3a. Esso
e basato sul four-quadrant Gilbert multiplier,[2]. La corrente di uscita e data da:
k(j ? Vref )
k(Xi ? Vref )
tanh
(10)
IB2ji = Ib tanh
2VT
2VT
dove Ib e la corrente costante di polarizzazione. Applicando lo stesso procedimento visto in
Vdd
M8
M7
ΙB2ji
∆T
∆Φ(∆T)
δj
M3
M4
M5
M6
+
δj
Vref
X
i
∆ Vref
Φ
Σ
+
M1
M2
Vref
X -Vref
i
Φ
Vb
Ib
Mb
δ j- Vref
(a)
-
+
+
Σ
+
IB2ji,reale
N(X -Vref ,δ j- Vref )
2 i
(b)
Figure 3: (a) Schema del circuito moltiplicatore B2;(b) Modello funzionale del moltiplicatore
sinaptico B2.
precedenza, approssimando con la serie di Taylor la funzione tangente iperbolica, si ottiene
per la corrente di uscita la seguente espressione:
IB2ji = (Xi ? Vref )(j ? Vref ) + N2 (Xi ? Vref ; j ? Vref )
IB2ji = IB2ji;ideale + N2 (Xi ? Vref ; j ? Vref )
(11)
dove = Ib k2 =(4VT2 ) e N2 (Xi ? Vref ; j ? Vref ) e il termine non-lineare. Nell'analisi eettuata
non sono state considerate le variazioni degli eetti ambientali sul termine non lineare. La
variazione della temperatura 4T e della tensione di riferimento di segnale introducono una
variazione nella corrente IB2ji :
IB2ji;reale = IB2ji;ideale + 4IB2ji;ideale (4T; 4Vref ) + N2 (Xi ? Vref ; j ? Vref )
(12)
Possiamo approssimare 4IB2ji;ideale (4T; 4Vref ) come segue:
dove:
e
ji;ideale 4T + @IB2ji;ideale 4V
4IB2ji;ideale(4T; 4Vref ) = @IB2@T
ref
@V
ref
(13)
@IB2ji;ideale @ = @T (Xi ? Vref )(j ? Vref )
@T
@IB2ji;ideale
= ?(Xi + j ? 2Vref )
@Vref
@
k2 q2 1
=
?
Ib
@T
2 K2 T 3
La corrente di uscita del circuito reale puo quindi essere espressa come:
IB2ji;reale = ( + 4)(Xi ? Vref )(j ? Vref ) ? (Xi + j ? 2Vref )4Vref
+N2 (Xi ? Vref ; j ? Vref )
dove
(14)
4 = @@T 4T
L'eq.( 14) puo essere rappresentata attraverso il modello funzionale illustrato in Fig. 3b. La
stessa analisi e stata eettuata per il blocco derivativo D, poiche basato su un four-quadrant
Gilbert multiplier.
5 Circuito della Funzione di Attivazione del Neurone
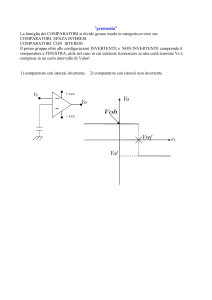
Il circuito A in Fig.1b realizza la funzione di attivazione del neurone f(.). Lo schema
circuitale e illustrato in Fig. 4a: esso e costituito da un amplicatore a singolo ingresso e
uscita dierenziale (guadagno ad anello aperto a) e da un blocco di retroazione (f = 1=RF ).
L'amplicatore e costituito da due stadi: il primo e uno stadio di guadagno realizzato con due
invertitori (M1 ; M2 ; M3 ; M4 ); il circuito RC di reazione sul secondo invertitore garantisce la stabilita nella congurazione ad anello chiuso. Il secondo stadio (M5 ; M6 ; M7 ; M8 ; M9 ; M10 ; M11 ; M12 )
e uno stadio di uscita dierenziale: esso genera le due tensioni di uscita 1 ? Oj e Oj (Vcco Oj Vsso and Vcco 1 ? Oj Vsso ). Lo stadio di uscita dierenziale lavora come un amplicatore in classe AB. Le tensioni S1 = Vcco ? 2:5V e S2 = Vsso ? 2:5V sono i valori di saturazione
della funzione di attivazione f(.). La funzione di attivazione del neurone presenta andamento
di tipo lineare a tratti.L'espressione dalla funzione di attivazione del neurone e la seguente:
8
>< S1
per IFj > S1 =
Oj = f (IFj ) = > IFj per S2 = < IFj < S1 =
(15)
: S2
per IFj < S2 =
dove e la pendenza nella zona lineare ( = a=(1+ af )). Possiamo scrivere l'ultima equazione
nella forma seguente:
S
S
S
S2
)
?
u(IFj ? 1 )g + S1 (IFj ? 1 ) + S2 (1 ? u(IFj ? 2 ))
(16)
dove u(.) e la funzione a gradino. Gli eetti ambientali su Oj sono determinati da T (tramite
la pendenza ); Vsso ; Vcco , per cui la variazione 4Oj determinata dagli eetti ambientali e data
Oj = IFj fu(IFj ?
da:
j 4T + @Oj 4V + @Oj 4V
4Oj = @O
cco @V
sso
@T
@V
cco
sso
(17)
Vdd
M5
Vdd
Vcco
M9
I
Fj
M1
M3
M6
∆T
1- Oj
M2
M7
∆Vsso
∆ Oj( ∆T, ∆Vcco, ∆Vsso, IFj )
M12
M4
∆Vcco
M11 O
j
M10
+
R C
M8
Vsso
RF
IFj
f(I Fj )
+
Σ
Oj,reale
(b)
(a)
Figure 4: (a) Schema circuitale del modulo A del neurone; (b) Modello funzionale del modulo
A del neurone.
Possiamo calcolare la derivata di Oj rispetto alla temperatura nella zona lineare come segue:
da ? a2 df
@Oj @Oj @
dT
=
=
IFji dT
@T
@ @T
(1 + af )2
(18)
La derivata di Oj rispetto a T al di fuori della zona lineare e nulla. Le derivate @V@Occoj e @V@Ossoj non
sono esprimibili in forma esplicita in quanto determinano la variazione dei valori di saturazione
di Oj , rilevabili spermentalmente.
La tensione di uscita reale puo essere espressa come:
Oj;reale = Oj + 4Oj (IFj ; 4T; 4Vcco; 4Vsso )
(19)
L'Eq.( 19) puo essere rappresentata attraverso il modello funzionale illustrato in Fig. 4b.
6 Simulazione Funzionale della Architettura Neurale
I modelli funzionali dei moltiplicatori sinaptici esposti in precedenza sono stati utilizzati
per simulare l'architettura neurale in modo funzionale. La simulazione e relativa all'algoritmo
di BP applicato ad una rete MLP con un unico strato intermedio; nell'algoritmo e stato
realizzata l'accelerazione di Vogl [6]: l'apprendimento avviene by epoch. La rete neurale cosi
denita e stata addestrata per eettuare il riconoscimento di caratteri numerici manoscritti.
Gli esemplari sono caratteri numerici manoscritti (da 0 a 9): ogni esemplare e codicato tramite
una matrice di pixel binari di dimensioni 2816, alla quale e applicata una semplice fase di
pre-elaborazione per la compressione dell'informazione, in modo da ridurre gli ingressi a 28.
Nella fase di apprendimento si usa l'algoritmo di BP per far apprendere alla rete gli esemplari
del training set (100 esemplari, 10 per ogni classe). Nella fase di classicazione la rete deve
classicare esemplari appartenenti al test set (100 esemplari, 10 per ogni classe).
Nella Tabella 1 sono riportati i risultati ottenuti nella simulazione della fase di apprendimento e di test della rete considerando le non linearita dei moltiplicatori F, B1, B2, (Eq.( 1),( 10)).Le
simulazioni sono state eseguite ponendo il momento = 0 ed il learning rate iniziale = 0:1
e utilizzando nello strato nascosto 12 neuroni. Nella Tabella e riportato il numero di epoch
(iterazioni) necessarie per raggiungere il riconoscimento di tutti gli esemplari del training set
e la percentuale di riconoscimento sul test set (capacita di generalizzazione).
Tabella 1
Acc.
Moltiplicazioni Non-linearita Non-linearita
Vogl
ideali
F, B1
F, B1,B2
Si N o di Epoch
119
130
137
Test set [%]
65
64
57
No N o di Epoch
2939
3071
3855
Test set [%]
63
61
59
Dai risultati ottenuti si nota che, a causa dell'introduzione del modello della non linearita
dei circuiti sinaptici, si ottiene un aumento del numero di iterazioni necessarie per eettuare
l'apprendimento della rete, e si abbassa (anche se in modo poco rilevante) la precisione di
classicazione del test set. Tuttavia, le prestazioni della rete non sono degradate in modo
signicativo.
7 Conclusioni
Come evidenziato in [7], i moltiplicatori analogici in passato sono stati progettati avendo in
mente applicazioni convenzionali. Mentre l'elevata linearita rappresenta il principale obiettivo
in tali applicazioni, i sistemi neurali richiedono che le loro primitive circuitali (principalmente
basate su moltiplicatori) siano di dimensioni ridotte e modulari e che presentino una bassa
dissipazione di potenza. Modelli accurati per la descrizione a livello funzionale del comportamento delle primitive neurali analogiche permetteranno di analizzare e validare la realizzazione
di algoritmi neurali tramite sistemi VLSI analogici. Sara quindi possibile ottenere una solida
base per specicare e validare le caratteristiche di questo tipo di realizzazioni. I risultati
presentati in questa memoria si pongono in questo campo di attivita di ricerca.
8 BIBLIOGRAFIA
References
[1] Y. Tsividis, "Analog MOS Integrated Circuits - Certain New Ideas, Trends and Obstacles",
IEEE Journal of Solid State Circuits, Vol. SC-22, No. 3, June 1987, pp. 317 - 312.
[2] C.A. Mead, Analog VLSI and Neural Systems, Addison-Wesley, Reading, 1989.
[3] E.A. Vittoz, "Analog VLSI Implementation of Neural Networks", in Proc. of ISCAS'90,
1990, pp. 2524 - 2527.
[4] M. Valle, D.D. Caviglia, e G.M. Bisio, "An Experimental Analog VLSI Neural Network
with On-Chip Back-Propagation Learning", in Analog Integrated Circuits for Signal Processing,1996 (accepted for pubblication).
[5] D.E. Rumelhart e J.L. McClelland, Parallel Distribuited Processing, MIT Press, Cambridge,
Mass., 1986.
[6] T. P. Vogl, J. K. Mangis, A. K. Rigler, W.T.Zink, e D.L. Alkon, Accelerating the Convergence of the Back-Propagation Method, Biological Cybernetics, pp. 257-263, 1988.
[7] N. Saxen e J. Clark, "A Four-Quadrant CMOS Analog Multiplier for Analog Neural Networks", IEEE Journal of Solid State Circuits, Vol. SC-29, No. 6, June 1994, pp. 746 749.
[8] H. Chible e M.Valle, "Design and Non-linear Modelling of CMOS Multipliers for Analog
VLSI Implementation of Neural Algorithms", in Proc. of MIPRO'95, 1995.