CORSO DI LAUREA SPECIALISTICA IN MATEMATICA

Facoltà di scienze M F.N.
220
________________________________________________________________________________________________
CORSO DI LAUREA SPECIALISTICA IN MATEMATICA
Sede: Complesso Universitario di Monte Sant’Angelo
www.dma.unina.it
Obiettivi e finalità del Corso di Laurea
Il corso di Laurea specialistica in Matematica ha come obiettivo la formazione di una figura
professionale che, basandosi, in generale, su un’approfondita conoscenza del metodo scientifico e,
più in particolare, su una solida preparazione culturale nell’area della Matematica, sia in grado di
svolgere compiti di alta responsabilità in centri di ricerca, sia pubblici che privati, nei servizi e nella
pubblica amministrazione, anche in ambiti applicativi scientifici, ambientali, sanitari, industriali,
finanziari, nonché nel settore della comunicazione della matematica e della scienza. A tal fine i
laureati devono essere in grado di analizzare problemi complessi, anche in contesti applicativi, e di
fornire soluzioni anche ricorrendo a sofisticate tecniche computazionali, probabilistico-statistiche ed
informatiche. Tale capacità di colloquiare con esperti di altri settori presuppone competenze nel
campo della comunicazione e della esemplificazione ed esposizione dei problemi e dei metodi
propri della disciplina. Devono essere inoltre in grado di utilizzare fluentemente, in forma scritta ed
orale, almeno una lingua dell’Unione Europea, oltre l’Italiano, con particolare riferimento al lessico
disciplinare. Devono infine avere capacità decisionali ed essere capaci di lavorare con ampia
autonomia.
REQUISITI DI AMMISSIONE
Per essere ammessi al corso di Laurea specialistica in Matematica occorre essere in possesso della laurea o di altro
titolo di studio conseguito all'estero, riconosciuto idoneo, e possedere i requisiti richiesti dal regolamento didattico
dell'Università degli Studi di Napoli Federico II. Studenti in possesso di altre lauree di primo livello o di un coerente e
congruo numero di CFU potranno essere ammessi con un eventuale debito formativo determinato attraverso la verifica
dei requisiti curriculari e dell’adeguatezza della personale preparazione secondo modalità definite dal Regolamento
dell’ordinamento didattico. Le modalità di ingresso al corso di laurea specialistica, compresa un’eventuale prova di
ammissione, sono definite nel Regolamento didattico.
I 180 crediti formativi universitari acquisiti dai laureati del corso di Laurea in Matematica istituito presso la Facoltà di
Scienze MM FF NN dell’Università degli Studi di Napoli Federico II saranno interamente riconosciuti per l’accesso al
corso di studio per il conseguimento della laurea specialistica in Matematica.
Facoltà di scienze M F.N.
221
________________________________________________________________________________________________
Corso di Laurea Specialistica in Matematica
Il percorso didattico
I anno:
8 esami da 7 crediti + attività formative varie per 4 crediti
II anno:
5 esami da 7 crediti + attività formative varie (2 crediti) + 1 seminario prelaurea (2 crediti) + prova finale (21 crediti)
Curriculum
Algebrico - Geometrico
Laurea Specialistica
Curriculum
Analitico - Modellistico
Facoltà di scienze M F.N.
222
________________________________________________________________________________________________
Corso di laurea Specialistica in Matematica
Curriculum Algebrico - Geometrico
Periodo di attività
I anno - 1° semestre
Insegnamento
Fondamenti di Teoria dei Campi e Algebra Universale
Fondamenti di Geometria Algebrica e Differenziale
Fondamenti di Algebra Omologica
I anno - 2° semestre
Fondamenti di Topologia Algebrica e Differenziale
2 corsi a scelta dello studente (uno nel s.s.d. MAT05 e
I anno - 1° o 2° semestre a scelta l’altro nel s.s.d MAT07) tra gli insegnamenti
dell’elenco A1. Di questi 2 corsi, 1 almeno deve essere
dello studente
scelto tra i primi quattro.
corsi a scelta dello studente di cui uno da scegliere
nell’elenco B1 e gli altri nell’elenco B1 o tra gli affini
Attività formative varie
Crediti
7
7
7
7
Periodo di attività
II anno – attivato a partire dal
2005/ 2006
Crediti
Attività finali
Insegnamento
14
14
4
1 corso a scelta nell’elenco B1
7
corsi a scelta di tipo affine
corsi a scelta nell’elenco B1 o di tipo affine a seconda
della scelta effettuata il I anno (almeno 14 crediti tra
gli affini)
corsi a scelta autonoma
Attività formative varie
Seminario pre-laurea
Prova finale
7
7
14
2
2
21
Facoltà di scienze M F.N.
223
________________________________________________________________________________________________
Elenco A1
Insegnamenti a scelta dello studente.
INSEGNAMENTO
Fondamenti di Analisi Superiore 1
Fondamenti di Analisi Superiore 2
Fondamenti di Fisica Matematica Superiore 1
Fondamenti di Fisica Matematica Superiore 2
Calcolo delle Variazioni
Teorie Relativistiche
Moduli
Modulo Unico
Modulo Unico
Modulo Unico
Modulo Unico
Modulo Unico
Modulo Unico
CFU
7
7
7
7
7
7
s.s.d.
MAT05
MAT05
MAT07
MAT07
MAT06
MAT07
Elenco B1
Insegnamenti a scelta dello studente.
INSEGNAMENTO
Logica Matematica
Teoria degli insiemi
Metodi Algebrici in crittografia
Teoria dei gruppi
Teoria Combinatoria dei gruppi
Teoria dei Moduli
Geometria Algebrica
Geometria Differenziale
Strutture Geometriche Combinatorie
Topologia Algebrica
Fondamenti di Analisi Superiore 1
Fondamenti di Analisi Superiore 2
Analisi Reale
Analisi Funzionale
Calcolo delle Variazioni
Equazioni Differenziali alle Derivate parziali
Processi Stocastici con applicazioni in statistica
Teoria ed Applicazioni delle File di Attesa
Fondamenti di Fisica Matematica Superiore 1
Fondamenti di Fisica Matematica Superiore 2
Modelli Matematici per la Biologia e per l’Ambiente
Stabilità e Controlli
Teorie Relativistiche
Equazioni Integro-Differenziali nella Fisica Matematica
Analisi Numerica
Calcolo Numerico e Programmazione
Moduli
Modulo Unico
Modulo Unico
Modulo Unico
Modulo Unico
Modulo Unico
Modulo Unico
Modulo Unico
Modulo Unico
Modulo Unico
Modulo Unico
Modulo Unico
Modulo Unico
Modulo Unico
Modulo Unico
Modulo Unico
Modulo Unico
Modulo Unico
Modulo Unico
Modulo Unico
Modulo Unico
Modulo Unico
Modulo Unico
Modulo Unico
Modulo Unico
Modulo Unico
Modulo Unico
CFU
7
7
7
7
7
7
7
7
7
7
7
7
7
7
7
7
7
7
7
7
7
7
7
7
7
7
s.s.d.
MAT01
MAT01
MAT02
MAT02
MAT02
MAT02
MAT03
MAT03
MAT03
MAT03
MAT05
MAT05
MAT05
MAT05
MAT05
MAT05
MAT06
MAT06
MAT07
MAT07
MAT07
MAT07
MAT07
MAT07
MAT08
MAT08
Per quanto riguarda la scelta degli insegnamenti affini si ricorda che lo studente potrà scegliere tra i seguenti
insegnamenti:
Fisica Moderna
Complementi di Fisica
Modulo Unico
Modulo Unico
7
7
FIS01-FIS08
FIS01-FIS08
oppure tra tutti gli insegnamenti attivati presso l’Ateneo nei settori disciplinari: da FIS01 a FIS 08, INF 01, SECS-S06.
Facoltà di scienze M F.N.
224
________________________________________________________________________________________________
Curriculum Analitico - Modellistico
Periodo di attività
I anno - 1° semestre
Insegnamento
Fondamenti di Analisi Superiore 1
Fondamenti di Fisica Matematica 1
Fondamenti di Analisi Superiore 2
Fondamenti di Fisica Matematica 2
Processi Stocastici con Applicazioni in Statistica
2 corsi a scelta dello studente tra gli insegnamenti
dell’elenco A2. Di questi 2 corsi, 1 almeno deve essere
scelto tra i primi quattro.
corsi a scelta dello studente di cui uno da scegliere
nell’elenco B2 e gli altri nell’elenco B2 o tra gli affini
Attività formative varie
Crediti
7
7
7
7
7
Periodo di attività
Insegnamento
II anno – attivato a partire dal
1 corso a scelta nell’elenco B2
2005/ 2006
corsi a scelta di tipo affine
corsi a scelta nell’elenco B2 o di tipo affine a seconda
della scelta effettuata il I anno (almeno 14 crediti tra
gli affini)
corsi a scelta autonoma
Attività formative varie
Seminario pre-laurea
Attività finali
Prova finale
Crediti
I anno - 2° semestre
I anno - 1° o 2° semestre a
scelta dello studente
14
14
4
7
7
7
14
2
2
21
Facoltà di scienze M F.N.
225
________________________________________________________________________________________________
Elenco A2
Insegnamenti a scelta dello studente.
INSEGNAMENTO
Fondamenti di Teoria dei Campi e di Algebra Universale
Fondamenti di Algebra Omologica
Fondamenti di Geometria Algebrica e Differenziale
Fondamenti di Topologia Algebrica e di Geometria
Combinatoria
Metodi Algebrici in crittografia
Teoria dei gruppi
Teoria Combinatoria dei gruppi
Teoria dei Moduli
Geometria Algebrica
Geometria Differenziale
Strutture Geometriche Combinatorie
Topologia Algebrica
Moduli
Modulo Unico
Modulo Unico
Modulo Unico
Modulo Unico
CFU
7
7
7
7
s.s.d.
MAT02
MAT02
MAT03
MAT03
Modulo Unico
Modulo Unico
Modulo Unico
Modulo Unico
Modulo Unico
Modulo Unico
Modulo Unico
Modulo Unico
7
7
7
7
7
7
7
7
MAT02
MAT02
MAT02
MAT02
MAT03
MAT03
MAT03
MAT03
Elenco B2
Insegnamenti a scelta dello studente.
INSEGNAMENTO
Logica Matematica
Teoria degli insiemi
Fondamenti di Teoria dei Campi e di Algebra Universale
Fondamenti di Algebra Omologica
Metodi Algebrici in crittografia
Teoria dei gruppi
Teoria Combinatoria dei gruppi
Teoria dei Moduli
Fondamenti di Geometria Algebrica e Differenziale
Fondamenti di Topologia Algebrica e di Geometria
Combinatoria
Geometria Algebrica
Geometria Differenziale
Strutture Geometriche Combinatorie
Topologia Algebrica
Analisi Reale
Analisi Funzionale
Calcolo delle Variazioni
Equazioni Differenziali alle Derivate parziali
Teoria ed Applicazioni delle File di Attesa
Modelli Matematici per la Biologia e per l’Ambiente
Stabilità e Controlli
Teorie Relativistiche
Equazioni Integro-Differenziali nella Fisica Matematica
Analisi Numerica
Calcolo Numerico e Programmazione
Moduli
Modulo Unico
Modulo Unico
Modulo Unico
Modulo Unico
Modulo Unico
Modulo Unico
Modulo Unico
Modulo Unico
Modulo Unico
Modulo Unico
CFU
7
7
7
7
7
7
7
7
7
7
s.s.d.
MAT01
MAT01
MAT02
MAT02
MAT02
MAT02
MAT02
MAT02
MAT03
MAT03
Modulo Unico
Modulo Unico
Modulo Unico
Modulo Unico
Modulo Unico
Modulo Unico
Modulo Unico
Modulo Unico
Modulo Unico
Modulo Unico
Modulo Unico
Modulo Unico
Modulo Unico
Modulo Unico
Modulo Unico
7
7
7
7
7
7
7
7
7
7
7
7
7
7
7
MAT03
MAT03
MAT03
MAT03
MAT05
MAT05
MAT05
MAT05
MAT06
MAT07
MAT07
MAT07
MAT07
MAT08
MAT08
Per quanto riguarda la scelta degli insegnamenti affini si ricorda che lo studente potrà scegliere tra i seguenti
insegnamenti:
Fisica Moderna
Modulo Unico
7
FIS01-FIS08
Complementi di Fisica
Modulo Unico
7
FIS01-FIS08
oppure tra tutti gli insegnamenti attivati presso l’Ateneo nei settori disciplinari: da FIS01 a FIS 08, INF 01, SECS-S06.
Facoltà di scienze M F.N.
226
________________________________________________________________________________________________
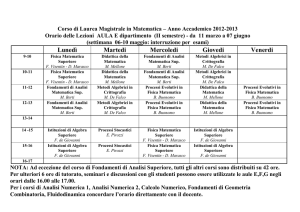
I corsi attivati
I anno
Per l'indicazione dell'aula e dei laboratori dove si svolgono lezioni ed esercitazioni e per il relativo orario informarsi
presso Il Dipartimento di Matematica e Applicazioni “R. Caccioppoli”, MSA.
INSEGNAMENTO
Fond. di Teoria dei Campi e di Algebra Univ.
DIP
Mat. e Appl.
Fond. di Analisi Superiore 1
Fond. di Fisica Matematica Superiore 1
Fond. di Geometria Algebrica e Differenziale
Fond. di Algebra Omologica
Fond. di Analisi Superiore 2
Fond. di Fisica Matematica Superiore 2
Fond. di Top. Alg. e di Geom. Combinatoria
Processi Stocastici con Appl. in Statistica
Calcolo delle Variazioni
Eq. Differenziali alle Derivate Parziali
Geometria Differenziale
Modelli Mat. per la Biologia e per l’AAmbiente
Teoria Combinatoria dei Gruppi
Teorie Relativistiche
Complementi di Fisica
Mat. e Appl.
Mat e Appl.
Mat e Appl.
Mat e Appl.
Mat. e Appl.
Mat. e Appl.
Mat. e Appl.
Mat. e Appl.
Mat. e Appl.
Mat. e Appl.
Mat. e Appl.
Mat. e Appl.
Mat. e Appl.
Mat. e Appl
Sc. Fis.
DOCENTE
S. Franciosi
C. Metelli
N. Fusco
F. Visentin
supplenza
F. de Giovanni
N. Fusco
A. Romano
supplenza
supplenza
V. Coti Zelati
A. Alvino
supplenza
F. Capone
C. De Vivo
G. Grassini
supplenza
Facoltà di scienze M F.N.
227
________________________________________________________________________________________________
Obiettivi formativi degli insegnamenti attivati
Corso
Obiettivi/contenuti
Conoscenza critica dei contenuti e dei metodi dell’algebra moderna: campi
Fondamenti di
Teoria dei Campi e di finiti, campi ordinati, algebra universale e reticoli.
Algebra Universale
Conoscenza critica dei contenuti e dei metodi dell’algebra moderna:
Fondamenti di
argomenti e metodi di algebra commutativa, prodotti tensoriali, elementi di
Algebra Omologica
algebra omologica ed applicazioni
Obiettivo del corso è introdurre la teoria astratta della misura e integrazione
Fondamenti di
con particolare attenzione ai teoremi di passaggio al limite sotto il segno di
Analisi Superiore 1
integrale ed al teorema di Radon – Nikodym
Principali risultati negli spazi di Hilbert e di Banach. Cenni di teoria spettrale
Fondamenti di
Analisi Superiore 2 degli operatori compatti. Alcune applicazioni.
Fondamenti di Fisica Meccanica Analitica lagrangiana ed hamiltoniana. Modelli del Continuo ed
equazioni alle derivate parziali
Matematica 1
Fondamenti di Fisica Meccanica del Continuo, Termodinamica e Fluidodinamica
Matematica 2
Studio di curve e superfici algebriche e delle loro singolarità. Studio di
Fondamenti di
Geometri Algebrica e varietà differenziabili e di fibrati tensoriali ad esse collegati
Differenziale
Fornire un primo esempio di invariante algebrico di uno spazio topologico: il
Fondamenti di
Topologia Algebrica gruppo fondamentale. Fornire esempi di proprietà grafiche e combinatorie e
di teoremi configurazionali in un ambiente proiettivo
e Geometria
Combinatoria
Si forniscono le basi della teoria dei processi stocastici con particolare
riferimento al caso markoviano e alle serie temporali. Il corso mira a fornire
Processi Stocastici allo studente la capacità di costruzione e di analisi di modelli stocastici atti a
con Applicazioni in descrivere talune classi di fenomeni fisici, biologici ed economici. Argomenti
specifici, con livelli di approfondimento dipendenti da particolari esigenze
Statistica
degli studenti, includono: processi di Markov continui, processi di diffusione,
moto browniano, equazioni differenziali stocastiche, serie temporali
Obiettivo del corso è l’introduzione ai classici problemi del Calcolo delle
Calcolo delle
Variazioni unidimensionale e multidimensionale con applicazioni.
Variazioni
Obiettivo del corso è fornire una panoramica dei risultati classici nell’ambito
Equazioni
delle Equazioni a Derivate Parziali con approfondimenti.
Differenziali alle
Derivate Parziali
Sviluppare lo studio delle proprietà metriche e della curvatura delle varietà
Geometria
riemanniane e delle loro sottovarietà
Differenziale
Modelli Matematici Dinamica delle popolazioni e modelli epidemiologici. Sistemi dinamici per
l’ambiente e la meteorologia. Diffusione nei mezzi porosi e nel sottosuolo.
per la Biologia e
Trasporto di inquinanti
l’Ambiente
Conoscenza critica dei contenuti e dei metodi dell’algebra moderna: gruppi
Teoria Combinatoria
liberi, presentazioni di gruppi, varietà
dei Gruppi
di gruppi
Modello geometrico di Minkowski per la Relatività Ristretta. Varietà di
Teorie Relativistiche
Riemann e Relatività Generale. Metrica e Gravitazione.
Acquisizione di conoscenze in ambito di teorie fisiche, con particolare
Complementi di
riguardo agli aspetti di modellizzazione
Fisica
Legenda tipo di attività: LF : Lezione frontale LAB: Laboratorio
Legenda prova finale:
PO :
PSEO:
C:
LO:
TA:
Prova orale PSO:
Prova scritta e orale
Prova scritta e/o orale
Colloquio
Prova di laboratorio e orale
Test di autovalutazione
Tipo
attività
Prova
finale
LF
PO
LF
PO
LF
PO
LF
PO
LF
PSEO
LF
PSEO
LF
PO
LF
PO
LF
PO
LF
PO
LF
PO
LF
PO
LF
PO
LF
PO
LF
PO
LF
PO
Facoltà di scienze M F.N.
228
________________________________________________________________________________________________
PROPEDEUTICITA’
Propedeuticità relative agli insegnamenti attivati
I ANNO
INSEGNAMENTO
Fondamenti di Teoria dei Campi e Algebra
Universale
Fondamenti di Algebra Omologica
Fondamenti di Analisi Superiore 1
Fondamenti di Analisi Superiore 2
Fondamenti di Fisica Matematica Superiore 1
Moduli
Modulo 1
Insegnamenti propedeutici
Algebra 2 (LM triennale)
Modulo 1
Modulo 1
Modulo 1
Modulo 1
Fondamenti di Fisica Matematica Superiore 2
Modulo 1
Fondamenti di Geometria Algebrica e
Differenziale
Fondamenti di Topologia Algebrica e di
Geometria Combinatoria
Processi Stocastici con Applicazioni in
Statistica
Calcolo delle Variazioni
Equazioni Differenziali alle Derivate Parziali
Geometria Differenziale
Inglese
Algebra 2
Analisi Matematica 2 (LM triennale)
Analisi Matematica 2 (LM triennale)
Analisi Matematica 2 e Fisica
Matematica (LM triennale)
Analisi Matematica 2 e Fisica
Matematica (LM triennale)
Geometria 1 e Geometria 2
(LM triennale)
Geometria 1 e Geometria 2
(LM triennale)
Analisi Matematica 2, Probabilità e
Statistica (LM triennale)
Analisi Matematica 2 (LM triennale)
Analisi Matematica 2 (LM triennale)
Fondamenti di Geometria Algebrica e
Differenziale
Fondamenti di Fisica Matematica
Superiore 1
Algebra 2 (LM triennale)
Fisica Matematica (LM triennale)
Fisica 2 (LM triennale)
Modelli Matematici per la Biologia e per
l’Ambiente
Teoria Combinatoria dei Gruppi
Teorie Relativistiche
Complementi di Fisica
Esame di diploma di Laurea
La laurea specialistica in Matematica si consegue dopo aver superato una prova finale, consistente nella discussione di
una tesi specialistica su un argomento specifico preventivamente concordato con almeno un relatore che supervisionerà
l’attività nelle sue diverse fasi. La discussione della tesi avviene alla presenza di una commissione nominata dalle
strutture didattiche e dà luogo all’acquisizione di 21 CFU. L’attività svolta nell’ambito della tesi può essere effettuata
sia nell’interno delle strutture universitarie, sia presso centri di ricerca, aziende o enti esterni, secondo modalità stabilite
dalla strutture didattiche. Prima della dicussione della tesi lo studente terrà un seminario sul lavoro svolto, alla presenza
del relatore e di un altro docente designato, tale seminario comporta il conseguimento di 2 CFU.
Piani di studio
Il corso di laurea prevede la suddivisione in due curricula. Gli studenti, all’atto della domanda di iscrizione dovranno
optare per uno dei due curricula. In seguito, potranno presentare alla Segreteria studenti entro i tempi fissati dal Senato
Accademico, piani di studio individuali che saranno vagliati, sulla base della congruità con gli obiettivi formativi
specificati nell’Ordinamento didattico, dal Consiglio di Corso di Laurea.