VOLTA CELESTE
Tutti i corpi celesti ci
appaiono proiettati su una
superficie sferica, come se
vi fossero incollati: questa
sfera è detta VOLTA
CELESTE
VOLTA CELESTE
In realtà gli astri
non si trovano su
un‟unica sfera e
non si muovono
tutti solidalmente.
Moti, dimensioni e
natura degli astri
furono oggetto di
indagine fin
dall‟antichità, ma
solo gli astronomi
greci cominciarono
a dare delle
risposte
scientifiche
VOLTA CELESTE
La linea dell‟orizzonte
divide esattamente in
due parti uguali la volta
celeste, il che prova che
la Terra è
incredibilmente piccola
rispetto ad essa: quanto
piccola, comincerà ad
essere chiarito solo a
partire dal XVIII° secolo
orizzonte
Volta celeste
SFERICITA’ DELLA TERRA
La sfericità della Terra fu
affermata per motivi
filosofici dai pitagorici e
dimostrata dagli
astronomi greci del
periodo ellenistico.
Eratostene calcolò in
modo esatto la misura
dell‟equatore
DISTANZA TERRA-LUNA
Gli astronomi greci
calcolarono in modo
molto preciso la distanza
Terra-Luna (pari a circa
60 volte il raggio della
Terra) e le sue
dimensioni. Il fatto che la
luna sia un satellite della
Terra non verrà più
messo in dubbio da allora
DISTANZA TERRA-SOLE
Non altrettanto accurato
fu il calcolo della distanza
Terra-sole: tale misura fu
parecchio sottostimata,
rendendo le dimensioni
dell‟universo allora
conosciuto molto più
piccole del vero
ECLISSI
Le eclissi sono dovute al
passaggio periodico della
Terra nel cono d‟ombra
della luna o viceversa.
Questa spiegazione era
già nota ai greci.
Le eclissi sono un
fenomeno periodico e
questo rese possibile la
loro previsione anche
all‟astronomia pre-greca
MOTO DIURNO DEL SOLE
Il sole sorge ad est e
tramonta a ovest,
descrivendo un arco di
cerchio sulla volta
celeste: il tempo che
impiega a tornare ogni
volta sul punto che
indica il sud (meridiano
locale) è fisso ed è detto
GIORNO SOLARE
STELLE FISSE
Le stelle fisse furono così
dette perché le loro
posizioni reciproche
sembravano non cambiare
mai, tanto è vero che
poterono essere
raggruppate in costellazioni,
utilizzate come punti di
riferimento per la
navigazione
MOTO DELLE STELLE FISSE
Anche le stelle fisse
compiono un giro
completo della volta
celeste ogni giorno, salvo
che questo GIORNO
SIDEREO dura circa
quattro minuti in meno di
quello solare.
Questo fa sì che il sole,
ogni giorno, resti indietro
di circa un grado rispetto
alle stelle fisse
ANNO SOLARE
Questo “restare
indietro” del sole è
detto MOTO ANNUO
del sole: esso
riporta il sole nella
stessa posizione
rispetto alle stelle
fisse in circa 365,25
giorni.
Questo periodo è
detto ANNO
SIDEREO
ANNO SOLARE
Il moto annuo non è
uniforme, ma è più veloce
in inverno e più lento in
estate: infatti i mesi estivi
hanno alcuni giorni in più
dei mesi invernali
ECLITTICA E ZODIACO
La circonferenza tracciata
sulla volta celeste dal sole
nel suo moto annuo si
chiama ECLITTICA.
L‟insieme delle dodici
costellazioni attraversate
dal sole nel suo percorso
annuo si chiama ZODIACO
ESTATE E INVERNO
L‟eclittica è inclinata di
circa 23,5° rispetto
all‟equatore, e questo fa sì
che il sole non abbia
sempre la stessa altezza:
d‟estate il sole è sopra
l‟equatore, i giorni sono
più lunghi e caldi.
D‟inverno, al contrario, il
sole è sotto l‟equatore, i
giorni sono più corti e
freddi
SISTEMA SESSAGESIMALE
Nei dati astronomici
compaiono spesso multipli e
sottomultipli di 60: il cerchio è
diviso in 360 gradi, dodici
costellazioni dello zodiaco,
dodici mesi di circa 30 giorni.
Questo è dovuto al fatto che i
babilonesi, i primi a praticare
un‟astronomia matematica,
usavano il sistema
sessagesimale per comodità di
calcolo
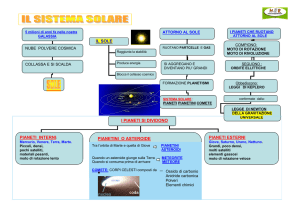
I PIANETI
I moti del sole, della
luna e delle stelle fisse
sono abbastanza facili
da spiegare: esistono
però cinque corpi celesti
il cui moto mise a dura
prova le capacità dei
migliori matematici
greci.
Per descrivere tali moti
furono elaborati
complessi sistemi
matematici: questi corpi
sono i PIANETI
I PIANETI
I pianeti visibili a occhio
nudo sono Mercurio,
Venere, Marte, Giove,
Saturno.
Le loro posizioni rispetto
alle stelle fisse cambiano
continuamente durante
l‟anno e in modo molto
irregolare, salvo
rimanere sempre nella
fascia dello zodiaco.
“Pianeta” significa
appunto “errante”
I PIANETI
A volte un pianeta procede
secondo l‟ordine delle
costellazioni, come il sole,
ma altre volte si ferma e
torna indietro per poi
riprendere il suo corso,
disegnando nel cielo una
specie di laccio detto
“ippopeda”.
Inoltre, la velocità non è
costante: a volte il pianeta
rallenta, a volte accelera
I PIANETI
Anche la luminosità dei
pianeti è variabile, il che
sembra suggerire che essi
non si trovano sempre alla
stessa distanza dalla Terra
VENERE E MERCURIO
Due pianeti, Venere e Mercurio, hanno una notevole
particolarità nel loro moto: non si osservano mai in
opposizione al sole, anzi la loro distanza dal sole,
misurata in gradi, non supera i 46° per Venere, e i 20°
per Mercurio.
Questi due pianeti possono quindi essere osservati solo
al mattino prima dell‟alba o alla sera poco dopo il
tramonto.
L‟osservazione di Mercurio, data la sua estrema vicinanza
al sole, è particolarmente difficile
SISTEMA GEOCENTRICO
Gli astronomi greci cercarono di spiegare tutta questa
varietà di movimenti con complessi sistemi matematici, il
cui scopo era quello di prevedere la posizione dei corpi
celesti.
Questi sistemi erano essenzialmente basati su tre
principi:
• Il cielo è qualitativamente diverso dalla Terra: la
materia celeste è eterna e incorruttibile
• La Terra è immobile al centro dell‟universo, quindi tutti i
moti osservati negli astri sono veri e non apparenti
• I moti dei corpi celesti derivano da una composizione di
moti circolari uniformi
SISTEMA GEOCENTRICO
Tutti i sistemi che prevedono
la Terra immobile si dicono
GEOCENTRICI.
Il più famoso di essi fu il
sistema TOLEMAICO, dal
nome dell‟astronomo greco
Claudio Tolomeo
SISTEMA GEOCENTRICO
Nei sistemi geocentrici le
stelle fisse venivano pensate
come fissate a un‟unica
sfera, mentre agli altri corpi
celesti erano attribuite
diverse sfere, il cui moto,
componendosi, dava origine
al moto complessivo
dell‟astro
SISTEMA GEOCENTRICO
L‟ordine degli astri nel
sistema tolemaico è:
• Luna
• Mercurio
• Venere
• Sole
• Marte
• Giove
• Saturno
• Stelle fisse
SISTEMA GEOCENTRICO
Le eclissi dimostrano che l‟orbita della luna si trova tra la
Terra e il sole.
Per quanto riguarda gli altri astri, il loro ordine nel
sistema geocentrico è del tutto arbitrario: non esiste
infatti nessun punto di riferimento rispetto al quale
calcolarne la distanza dalla Terra.
Il loro ordine nel sistema tolemaico fu deciso
essenzialmente per la loro luminosità più o meno
decrescente e per la loro velocità rispetto alle stelle fisse,
decrescente da Mercurio a Saturno
SISTEMA GEOCENTRICO
La struttura del paradiso
dantesco è fortemente
ispirata al sistema tolemaico
SISTEMA DI EUDOSSO
Nei sistemi geocentrici il
moto fondamentale è
quello diurno della sfera
delle stelle fisse, compiuto
in un giorno sidereo.
Infatti, tutti gli altri moti
sono variazioni di questo
moto fondamentale, come
quello annuo del sole che
resta indietro di un grado
al giorno rispetto alle
stelle fisse.
SISTEMA DI EUDOSSO
Per questo motivo Eudosso di
Cnido, creatore del primo sistema
geocentrico, pensò di spiegare i
moti del sole e dei pianeti
ipotizzando che questi si
trovassero su sfere imperniate
tutte sulla sfera delle stelle fisse:
il moto della sfera delle stelle
fisse spiegava il moto diurno,
mentre quello della sfera propria
di ogni astro il moto annuale
SISTEMA DI EUDOSSO
Ad esempio, il sole si
trova su una sfera il cui
asse è inclinato di 23,5°
rispetto alla sfera delle
stelle fisse, e compie una
rotazione completa in
365,25 giorni in senso
opposto (ecco perché il
sole ritarda rispetto alle
stelle fisse) al moto della
sfera delle stelle fisse
EPICICLO
Questo sistema però non è
sufficiente a spiegare tutti i
fenomeni perché, come è
stato detto, il moto annuo del
sole non è uniforme.
La soluzione fu trovata da
IPPARCO.
Sulla sfera principale
(DEFERENTE), è imperniata
una sfera più piccola
(EPICICLO), sulla quale si
muove il sole
EPICICLO
Quando la velocità dell‟epicilo
si somma a quella del
deferente il sole procede più
velocemente nel suo moto
annuo
EPICICLO
Quando la velocità dell‟epicilo
si sottrae a quella del
deferente il sole procede più
lentamente.
Questo rendeva conto della
differenza di velocità del sole
durante l‟anno, anche se non
in modo del tutto esatto
EPICICLO
Lo stesso sistema poteva
essere applicato alla luna e ai
pianeti. Con un‟opportuna
regolazione delle velocità e
delle dimensioni degli epicicli
e dei deferenti si potevano
ottenere gli strani moti in
avanti e indietro e le fermate
dei pianeti, anche se non in
modo molto preciso
EQUANTE
Per migliorare la
precisione Tolomeo
introdusse il PUNTO
EQUANTE.
Nel sistema tolemaico il
moto del deferente non è
uniforme rispetto al
centro della sfera, ma
rispetto a un punto vicino
al centro detto equante
EQUANTE
Il sistema di Tolomeo era molto più preciso di tutti gli altri,
ma era anche molto artificioso e innaturale.
Il testo di Tolomeo, la “Sintassi matematica” (detto dagli
arabi “Almagesto”) era estremamente complesso.
Nonostante ciò fu considerato il testo di riferimento da tutti
gli astronomi per i successivi tredici secoli.
Dopo i greci furono gli arabi a perfezionare il sistema
geocentrico, tanto è vero che la maggior parte delle stelle
hanno nomi arabi (mentre le costellazioni hanno in genere
nomi della tradizione babilonese o greca)
DIFETTI DEL SISTEMA TOLEMAICO
Il sistema di Tolomeo, oltre alla sua complicazione, aveva
anche alcuni e ben marcati difetti tecnici
• Le posizioni previste dei pianeti non corrispondono mai del
tutto a quelle osservate
• Le variazioni di luminosità di Marte non sono spiegabili con le
piccole variazioni di distanza dalla Terra dovute al moto
sull‟epiciclo
• La luna all‟apogeo dovrebbe essere due volte più lontana, e
quindi più piccola che al perigeo, cosa che non si osservava
• I moti di Venere e Mercurio, possono essere sì ottenuti con
combinazioni “ad hoc” di epicicli, ma non vi è nessuna
spiegazione del perché solo questi due pianeti debbano
seguire il sole
COPERNICO
Nella prima metà del „500
un astronomo polacco,
NICOLA COPERNICO,
propose di eliminare i
difetti del sistema
tolemaico adottando
un‟ipotesi radicalmente
nuova: che la grande
varietà di moti osservata
negli atri fosse in gran
parte dovuta al fatto che
la Terra stessa si muove
SISTEMA COPERNICANO
Nel sistema copernicano il
sole e le stelle fisse sono
immobili, mentre la Terra e
gli altri pianeti ruotano
intorno al sole.
L‟unico punto in comune col
sistema tolemaico è la luna,
che continua ad essere
considerata un satellite della
Terra
PRINCIPI DEL SISTEMA COPERNICANO
• Il sole e la sfera delle stelle fisse sono immobili
• La Terra compie una rotazione completa intorno al suo
asse do ovest a est in 24 ore, e questo spiega il moto diurno
del sole e di tutti gli altri astri
• La Terra compie una rivoluzione completa intorno al sole
rispetto alle stelle fisse in 365,25 giorni, e questo spiega il
moto annuo del sole
• I pianeti compiono una rivoluzione completa intorno al
sole, ciascuno secondo la propria orbita e il proprio periodo,
e questo spiega il loro moto apparente sulla volta celeste
MOTI APPARENTI E REALI
Nel sistema copernicano, dunque:
• I moti del sole e delle stelle fisse sono apparenti e sono
dovuti esclusivamente al moto della Terra
• I moti dei pianeti sono una combinazione del moto della
Terra e dei pianeti stessi, quindi sono in parte reali e in parte
apparenti
DIFFUSIONE
Il testo di Copernico, che
doveva essere intitolato
solo “De Revolutionibus” fu
pubblicato nel 1543, pochi
giorni prima della morte
dell‟autore.
Esso fu ben accolto dagli
astronomi e per
cinquannt‟anni la sua
diffusione non fu
ostacolata dalla Chiesa
SISTEMA SOLARE
Nel sistema eliocentrico i
pianeti sono disposti secondo
quest‟ordine:
• Mercurio
• Venere
• Terra + luna
• Marte
• Giove
• Saturno
SISTEMA SOLARE
Tanto l‟ordine dei pianeti
quanto la loro distanza dal
sole non sono arbitrari, ma
sono precisamente
determinati dalle osservazioni
astronomiche.
Per la prima volta era possibile
determinare le esatte
proporzioni del sistema solare
(non le dimensioni, perché
restava indeterminata la
distanza Terra-sole, base di
tutte le misurazioni)
PIANETI INTERNI
Venere
Mercurio
Nel sistema copernicano le
orbite di Venere e Mercurio
sono interne rispetto a quella
della Terra. Questo spiega
perché tali pianeti non
possono allontanarsi dal sole:
infatti le loro orbite, viste dalla
Terra sono sottese da un
angolo che per Venere è di
92°, per Mercurio di 40°.
MOTO RETROGRADO
Il moto retrogrado dei pianeti
esterni si spiega col fatto che
la Terra, muovendosi più
veloce di essi, ogni tanto li
“sorpassa”, e quando questo
avviene il pianeta sembra
“restare indietro”, per poi
riprendere dopo un po‟ il corso
normale.
Una analoga spiegazione vale
per i pianeti interni, dai quali
siamo invece “sorpassati”
DISTANZE VARIABILI
congiunzione
opposizione
Nel sistema copernicano le
distanze tra la Terra e i pianeti
sono molto variabili, a
seconda che si trovino in
congiunzione o opposizione
rispetto al sole: questo spiega
la loro notevole variazione di
luminosità
EPICICLI
Copernico era ancora convinto
che i moti celesti dovessero
essere circolari uniformi: ma
poiché il moto di rivoluzione
della Terra non lo è fu
anch‟egli costretto ad adottare
gli epicicli, in modo da
ottenere moti non uniformi
componendo moti uniformi
DIFETTI DEL SISTEMA COPERNICANO
• Una volta introdotti tutti i necessari epicicli per
descrivere i moto dei pianeti, il sistema copernicano non
era molto meno complicato di quello tolemaico
• Le posizioni dei pianeti non potevano essere previste
con precisione superiore rispetto al sistema tolemaico
• L‟ipotesi del moto della Terra contrastava la fisica
aristotelica, allora in auge, e col senso comune
ASSENZA DI PARALLASSE
Se la Terra si muovesse, le stelle dovrebbero subire delle
piccole variazioni nella loro posizione sulla volta celeste
nel corso dell‟anno (angolo di parallasse), dovute al
cambiamento del punto di vista.
Le osservazioni non mostravano alcuna variazione, cosa
che fu interpretata da Copernico come dovuta all‟estrema
lontananza delle stelle da noi.
Copernico aveva ragione: la prima parallasse stellare fu
effettivamente osservata solo alla fine del „700 e risultò
essere inferiore al secondo d‟arco
POTERE ESPLICATIVO
Nonostante ciò il sistema copernicano, aveva, rispetto a
quello tolemaico, un potere esplicativo enormemente
maggiore, ovvero riusciva a spiegare molti più fenomeni
ricorrendo a un numero molto minore di ipotesi arbitrarie.
Per questo motivo i migliori pensatori dell‟epoca accolsero
con entusiasmo l‟ipotesi copernicana, pur criticando
l‟eccessivo tecnicismo matematico del testo
GALILEO
Galileo Galilei fu uno
dei maggiori
sostenitori della teoria
copernicana. Grazie
all‟uso del telescopio,
o per meglio dire
cannocchiale, riuscì a
trovare molte prove
decisive a favore del
modello geocentrico
LE MONTAGNE DELLA LUNA
Galileo dimostrò che la luna
non è una perfetta sfera
cristallina, ma vi si trovano
pianure e montagne.
L‟esistenza delle montagne
fu provata osservando dei
punti luminosi vicino alla
linea di divisione giornonotte, che egli interpretò
come le cime dei monti
illuminate dall‟alba
SATELLITI DI GIOVE
Una delle maggiori scoperte di Galileo fu che Giove ha
quattro piccoli satelliti, detti ASTRI MEDICEI. Questo
dimostrava che non tutti i corpi celesti ruotano intorno alla
Terra
FASI DI VENERE
La principale prova che
Galileo portò al
modello eliocentrico fu
la scoperta delle fasi di
Venere
FASI DI VENERE
Se Venere si trovasse sempre tra
la Terra e il sole, come nel
modello tolemaico, dovrebbe
mostrarci sempre solo una piccola
parte della faccia illuminata.
In realtà il pianeta mostra tutte le
sue fasi, dimostrando che, rispetto
alla Terra, esso può trovarsi sia
sotto che sopra il sole, come nel
modello eliocentrico
FASI DI VENERE
GEOCENTRICO
ELIOCENTRICO
IL DIALOGO
Galileo sintetizzò le sue
tesi a favore
dell‟eliocentrismo in un
libro, il “Dialogo sopra i
due massimi sistemi”
Dopo pochi mesi dalla
pubblicazione Galileo fu
messo sotto processo dal
tribunale dell‟inquisizione,
perché la Chiesa aveva
condannato la teoria
copernicana come
contraria alle sacre
scritture
IL PROCESSO
Minacciato di tortura,
Galileo fu costretto a
pronunciare un‟abiura delle
sue teorie di fronte al
tribunale.
Grazie a questo riuscì ad
evitare la condanna per
l‟accusa più grave, quella di
eresia.
Comunque, per essersi
reso sospetto di eresia, fu
condannato al carcere a
tempo indeterminato, poi
scontato in una villa presso
Firenze
KEPLERO
Il sistema copernicano
presentava ancora diversi
difetti che avevano già afflitto
quello tolemaico. Fu un
astronomo tedesco,
GIOVANNI KEPLERO, a capire
che tutti i problemi avrebbero
potuto essere eliminati
rinunciando al dogma dei
moti circolari uniformi
KEPLERO
In gioventù Keplero aveva fatto una
scoperta straordinaria: interponendo
delle sfere tra i cinque solidi regolari
(cubo, tetraedro, dodecaedro,
icosaedro, ottaedro) in modo che
essi fossero inscritti uno dentro
l‟altro, come bambole russe, le sei
sfere così ottenute avevano i raggi
nella stessa proporzione dei raggi
delle orbite dei sei pianeti
KEPLERO
Anche se questo è in realtà
una pura coincidenza, e
comunque la corrispondenza
non è esatta, la fama che
gliene derivò lo portò alla
corte dell‟imperatore Rodolfo
II, a Praga, dove presto
successe a Tycho Brahe
come astronomo imperiale
KEPLERO
Utilizzando le osservazioni di
Tycho Keplero giunse alla
conclusione che l‟orbita di
Marte non poteva essere in
nessun modo riprodotta con
dei moti circolari uniformi.
In un tentativo disperato di
capire come fosse l‟orbita
Keplero provò a disegnarla e
si accorse che assomigliava
molto a una curva già nota ai
greci, l‟ellisse
ELLISSE
L‟ellisse è il luogo dei punti
tali che la somma delle
distanze da due punti fissi
detti fuochi è costante.
Se F1 ed F2 sono i fuochi, X è
un punto dell‟ellisse se
soddisfa la relazione
XF1 XF2 2a
A è detto semiasse maggiore
ed è la metà del massimo
diametro dell‟ellisse, AB nella
figura
PRIMA LEGGE DI KEPLERO
Keplero generalizzò a tutti i pianeti il risultato ottenuto per
Marte, formulando quella che oggi è nota come PRIMA
LEGGE DI KEPLERO
LE ORBITE DEI PIANETI
SONO ELLITTICHE CON IL
SOLE IN UNO DEI FUOCHI
SECONDA LEGGE DI KEPLERO
Keplero osservò poi che la velocità di percorrenza
dell‟orbita non è costante, ma è massima quando il
pianeta si trova al perielio, diminuisce fino a raggiungere
il valore minimo all‟afelio, per poi aumentare di nuovo.
SECONDA LEGGE DI KEPLERO
In un moto circolare uniforme l‟angolo percorso dal raggio
vettore è proporzionale al tempo. Keplero si accorse che
nel moto dei pianeti non è l‟angolo a essere proporzionale
al tempo, ma l‟area descritta dal raggio vettore. Ad
esempio, se le due aree in grigio sono uguali, allora anche
i tempi impiegati a descriverle saranno uguali
SECONDA LEGGE DI KEPLERO
Poiché, per evidenti motivi geometrici, l‟arco percorso dal
pianeta al perielio è maggiore di quello percorso all‟afelio
(possiamo immaginare i due settori come triangoli di
uguale area: maggiore è l‟altezza, minore la base), e i due
archi sono percorsi nello stesso tempo, ne consegue che
la velocità deve essere maggiore al perielio (spazio
maggiore percorso nello stesso tempo) che all‟afelio
SECONDA LEGGE DI KEPLERO
Anche i questo caso Keplero generalizzò a tutti i pianeti il
risultato, formulando quella che oggi è nota come
SECONDA LEGGE DI KEPLERO
L’AREA DESCRITTA DAL RAGGIO
VETTORE CHE UNISCE IL SOLE A
UN PIANETA E’ PROPORZIONALE
AL TEMPO IMPIEGATO A
DESCRIVERLA
SECONDA LEGGE DI KEPLERO
In questa figura i
settori colorati hanno
tutti la stessa area,
quindi sono percorsi
dal pianeta tutti nello
stesso tempo.
Ancora una volta si
nota che l‟arco
descritto a parità di
tempo, ovvero la
velocità, aumenta
man mano che il
pianeta si avvicina al
perielio
SECONDA LEGGE DI KEPLERO
La maggior durata dell‟estate rispetto all‟inverno è dunque
spiegata dal fatto che l‟afelio, per la Terra, cade nel periodo
estivo, quindi il moto è più lento, mentre il perielio, dove in
base alla seconda legge di Keplero il moto è più veloce,
cade nel periodo invernale
TERZA LEGGE DI KEPLERO
Per molti anni Keplero cercò
una relazione tra i parametri
orbitali di tutti i pianeti.
Era già stato osservato da
Copernico che il periodo di
rivoluzione dei pianeti aumenta
all‟aumentare della distanza dal
sole, anche se non in modo
proporzionale.
Questo, secondo Keplero,
dimostrava che il sole era
l‟origine della forza che teneva
uniti i pianeti del sistema
solare
TERZA LEGGE DI KEPLERO
Dopo anni di tentativi egli riuscì nel suo intento,
formulando quella che oggi è nota come TERZA LEGGE DI
KEPLERO
IL QUADRATO DEL PERIODO DI
RIVOLUZIONE DI UN PIANETA E’
PROPORZIONALE AL CUBO DEL
SEMIASSE MAGGIORE
DELL’ORBITA
TERZA LEGGE DI KEPLERO
In formule:
T
2
a
3
costante
La terza legge non si applica solo ai pianeti del sistema
solare, ma a tutti i sistemi in cui un grosso corpo centrale è
circondato da satelliti, come ad esempio Giove, oppure la
Terra, che ormai conta, oltre alla luna, centinaia di satelliti
artificiali.
In tutti i casi i periodi di rivoluzione sono in proporzione ai
cubi dei semiassi maggiori dell‟orbita, anche se con una
costante di proporzionalità diversa: questa, infatti, dipende
dalla massa del corpo attrattore
TERZA LEGGE DI KEPLERO
Ad esempio, l‟orbita geostazionaria (quella su cui si trovano
i satelliti meteorologici e per telecomunicazioni) ha un
raggio circa dieci volte minore dell‟orbita lunare e quindi un
periodo circa trenta volte minore, ovvero di un giorno (per
questo il satellite è sempre sospeso sullo stesso punto)
Infatti il cubo di 10 è 1000, e la radice quadrata di 1000 è
circa 30.
NEWTON
Keplero rivelò, dopo oltre
duemila anni di ricerche,
il vero moto dei pianeti.
Ma per quale motivo i
corpi celesti seguono
queste regole?
Sarà Isaac Newton a
rispondere alla
domanda, con la sua
teoria della gravitazione
universale
NEWTON
?
10 m/s2
Newton sapeva che una
mela, sulla superficie
terrestre, cade con una
accelerazione di circa
10m/s2
Ma, si chiese, con quale
accelerazione sarebbe
caduta la stessa mela
posta a una distanza
pari al raggio dell‟orbita
lunare?
NEWTON
La domanda non era destinata a rimanere senza
risposta, perché tale accelerazione poteva essere
calcolata semplicemente calcolando l‟accelerazione
centripeta della luna, cosa fattibile in quanto raggio e
periodo dell‟orbita lunare erano perfettamente noti
a r
2
NEWTON
L‟accelerazione della mela risultò essere in tal caso pari a
1/360 m/s2, ovvero 3600 volte più piccola rispetto
all‟accelerazione sulla superficie terrestre.
Ora, poiché il raggio dell‟orbita lunare è pari a 60 raggi
terrestri, l‟accelerazione risultava inversamente proporzionale
al quadrato della distanza dal centro della Terra (infatti la
mela sulla superficie terrestre dista un raggio terrestre dal
centro, e il quadrato di 60 è appunto 3600)
2
1 / 360 : 10 1 : 60
2
GRAVITAZIONE UNIVERSALE
Newton sapeva che forza e accelerazione sono direttamente
proporzionali.
Ipotizzò quindi che la caduta della mela fosse governata da
una semplice legge di carattere universale
GRAVITAZIONE UNIVERSALE
Due qualsiasi corpi si attraggono con una forza:
• diretta secondo la linea congiungente i centri dei
due corpi
• direttamente proporzionale alle masse dei due corpi
• inversamente proporzionale al quadrato della
distanza tra i loro centri
LEGGE DI GRAVITAZIONE UNIVERSALE
In formule, indicate con ma e mb le masse di due corpi e
con rab la loro distanza:
F Go
ma mb
2
rab
COSTANTE DI GRAVITAZIONE
UNIVERSALE
La costante Go, detta
costante di gravitazione
universale, può essere
definita come la forza con
cui si attraggono due masse
puntiformi di un
chilogrammo poste alla
distanza di un metro.
Newton ne ignorava il
valore, che venne misurato
solo alla fine del „700 da
Henry Cavendish
COSTANTE DI GRAVITAZIONE
UNIVERSALE
Il valore della costante Go è, nel S.I.
Go 6,67 10
11 3
m / kg s
2
COSTANTE DI GRAVITAZIONE
UNIVERSALE
La misura di Go consentì di calcolare per la prima volta
la massa della Terra. Infatti, se si considera un corpo di
massa m sulla superficie terrestre, cioè a una distanza
R dal centro della Terra, confrontando la legge di
gravitazione con la formula della forza peso
F Go
Si ottiene:
mM
R
2
F m g
g R2
M
Go
PROPORZIONALITA’ PESO-MASSA
Che la forza di gravità sia direttamente proporzionale
alle masse dei corpi è dimostrato dagli esperimenti sulla
caduta dei gravi e sui pendoli, eseguiti originariamente
da Galileo e in modo molto più accurato da Newton.
Il fatto che tutti i corpi, in assenza d‟aria, cadano con la
stessa accelerazione, e quello che il periodo di
oscillazione del pendolo sia indipendente dalla massa,
sono infatti conseguenze della proporzionalità massapeso.
Tale proporzionalità è stata verificata con esperimenti
molto precisi anche in epoca moderna
FORZA CENTRALE
Che la forza di gravità sia una forza centrale, ovvero
che sia diretta verso i centri dei corpi che interagiscono,
ha come conseguenza che il momento angolare orbitale
di un pianeta rispetto al sole si conserva.
(La cosa non è banale: un pianeta non è un sistema
isolato e quindi non è scontato che il suo momento
angolare si conservi)
FORZA CENTRALE
P
F
Infatti, preso come fulcro appunto
il sole, S, si nota che la forza che
agisce sul pianeta, essendo diretta
verso S, non ha braccio, e quindi
non ha momento.
Ma poiché:
E:
S
Ne segue:
M L
M 0
L costante
DIMOSTRAZIONE DELLA SECONDA
LEGGE DI KEPLERO
P
Q
r
La conservazione del momento
angolare orbitale del pianeta ha a
sua volta come conseguenza la
seconda legge di Keplero.
Infatti, il triangolo SPQ descritto dal
raggio vettore del pianeta mentre
questo compie il percorso PQ è
A 1 r PQ
2
S
(In realtà non è un triangolo, ma
consideriamo uno spostamento così
piccolo che la differenza sia
trascurabile)
DIMOSTRAZIONE DELLA SECONDA
LEGGE DI KEPLERO
Dividendo per il tempo impiegato a compiere l‟arco:
A 1 PQ
r
t 2
t
Ma PQ/t è la velocità, e quindi:
A 1
r v
t 2
Ricordando poi la formula del momento angolare:
L m r v
Si ottiene:
A L
t 2m
DIMOSTRAZIONE DELLA SECONDA
LEGGE DI KEPLERO
Ma sia la massa del pianeta sia, per quanto
precedentemente dimostrato, il suo momento angolare,
sono delle costanti: ne segue quindi che il rapporto A/t è
costante
A L
costante
t 2m
Ovvero, l‟area e il tempo sono direttamente proporzionali,
che è appunto la seconda legge di Keplero.
PROPORZIONALITA’ INVERSA AL
QUADRATO DELLA DISTANZA
La terza legge di Keplero è una conseguenza del fatto che
la forza di gravità è inversamente proporzionale al quadrato
della distanza.
Per dimostrarlo consideriamo per semplicità orbite circolari.
Le formule occorrenti sono:
1) la legge della gravitazione
2) la seconda legge di Newton
F Go
m M
r
F m a
3) la formula dell‟accelerazione centripeta
a
2
4
2
T2
r
DIMOSTRAZIONE DELLA TERZA LEGGE DI
KEPLERO
Sostituendo la 3 nella 2
F m
4
T
2
2
r
E uguagliando membro a membro la modificata 2 e la 1
Go
m M
r
2
m
4
T
2
2
r
DIMOSTRAZIONE DELLA TERZA LEGGE DI
KEPLERO
Eliminando la massa del pianeta m, fattore comune, e
portando i fattori r (raggio dell‟orbita del pianeta) e T il suo
periodo orbitale) a sinistra, e le costanti a destra, si ottiene:
4
3
M Go
r
T
2
2
E poiché il membro di destra è fatto solo di termini costanti,
lo è anche quello di sinistra, ovvero il quadrato del periodo
di rivoluzione è proporzionale al cubo del raggio dell‟orbita
(l‟orbita è stata presa circolare, quindi il semiasse coincide
col raggio)
MASSA DEL SOLE
E‟ da notare che, poiché i parametri orbitali dei pianeti sono
noti, con questa formula è possibile calcolare, una volta
trovato il valore di Go, l‟unico fattore che resta incognito,
ovvero la massa del sole M.
M
4 r
2
3
T 2 Go
MASSA DEI CORPI CELESTI
La terza legge di Keplero può essere applicata non solo al
sistema solare, ma a tutti i sistemi in cui piccoli corpi
ruotano intorno a un centro di attrazione, come Giove coi
suoi satelliti. Misurando periodo e raggio orbitali dei satelliti
di Giove si è potuto misurare la massa di Giove, e così per
tutti gli altri corpi celesti
PERTURBAZIONI
I pianeti del sistema solare non sono solo attratti dal sole,
ma si attraggono reciprocamente.
Questo fa sì che le orbite kepleriane vengano leggermente
perturbate e che, ad esempio, il semiasse dell‟orbita non
abbia né direzione né lunghezza fissa.
Si è ipotizzato che le ere glaciali siano dovute alla variazione
della distanza Terra-Sole.
Le anomale perturbazioni nelle orbite dei pianeti conosciuti
consentì la scoperta di due nuovi pianeti, Nettuno e Plutone
(Urano era stato scoperto tramite osservazioni al telescopio)
PERTURBAZIONI
L‟attrazione sole-pianeti (così come quella Terra-Luna) è
reciproca: questo fa sì che anche il corpo centrale, per
quanto di massa maggiore degli altri del sistema, subisca
delle piccole oscillazioni.
E‟ attraverso queste perturbazioni che, ad esempio, è stato
possibile misurare la massa dei corpi che non hanno
satelliti, come la nostra luna.
ESOPIANETI
La ricerca degli esopianeti, ovvero dei pianeti orbitanti
intorno ad altre stelle, è basata in parte sulla misurazione
delle piccole oscillazioni che questi pianeti inducono nella
loro stella-madre.
Oggi conosciamo migliaia di esopianeti e sappiamo che i
sistemi planetari sono tutt‟altro che rari nell‟Universo
ENERGIA POTENZIALE
La formula dell‟energia potenziale della forza peso
U m g h
È solo un‟approssimazione valida sulla superficie terrestre.
La formula completa è:
mM
U Go
r
PALLINA IN UNA BUCA
h
Perché una pallina possa uscire
da una buca di profondità h
deve acquisire un‟energia
cinetica pari all‟energia
potenziale corrispondente alla
profondità della buca (infatti,
salendo l‟energia cinetica è
trasformata in potenziale e,
una volta che tutta è stata
convertita la pallina non può
più salire)
PALLINA IN UNA BUCA
Uguagliando energia cinetica e
potenziale:
U m g h
h
2
1
Ec mv
2
1 mv 2 mgh
2
Si ottiene la velocità necessaria
alla pallina
v 2 gh
VELOCITA’ DI FUGA
mM
U Go
r
2
1
Ec mv
2
Lo stesso calcolo si può
applicare a un veicolo
spaziale che vuole lasciare
definitivamente la Terra,
applicando però la formula
non approssimata
Uguagliando membro a
membro si ottiene
1 mv 2
2
mM
Go
r
VELOCITA’ DI FUGA
Da questa possiamo ricavare la velocità necessaria al
missile per lasciare la Terra, ovvero la velocità di fuga
1 mv 2
2
mM
Go
r
2Go M
v
r
BUCHI NERI
Poiché nulla viaggia più veloce della luce, se la velocità di
fuga da un corpo celeste è maggiore o uguale a c nulla,
nemmeno la luce, potrà sfuggirvi.
Utilizzando la formula della velocità di fuga si ottiene il
raggio di un simile corpo in funzione della massa (detto
raggio di Schwarzschild.
2Go M
c
r
r
2Go M
c2
BUCHI NERI
Il raggio di Schwarzschild
non è da intendersi come
quello di una superficie
solida, ma solo il limite oltre
al quale nemmeno un raggio
di luce può più sfuggire alla
forza di gravità dell‟astro,
detto orizzonte degli eventi.
Simili corpi celesti sono detti
buchi neri e oggi la loro
esistenza è praticamente
certa
CONCLUSIONE
La teoria della gravitazione di Newton riesce a spiegare con
un‟unica semplice legge la quasi totalità dei fenomeni
celesti e permette di scoprirne di nuovi.
Essa può essere considerata come uno dei più alti vertici del
pensiero umano e, sicuramente, contribuì alla rapida
diffusione del pensiero newtoniano.
La meccanica newtoniana soppiantò rapidamente tutte le
altre teorie alternative e per almeno due secoli rimase
l‟indiscusso fondamento di ogni indagine sulla natura.
CONCLUSIONE
In realtà la nostra immagine dell‟universo è oggi molto
diversa da quella che ci restituisce la meccanica
settecentesca.
Nei primi anni del „900 la formulazione di una teoria della
gravitazione rivoluzionaria da parte di Albert Einstein e la
scoperta sperimentale della recessione delle galassie da
parte di Edwin Hubble portarono a una profonda revisione
della nostra concezione dell‟universo, revisione che è ancor
oggi in atto