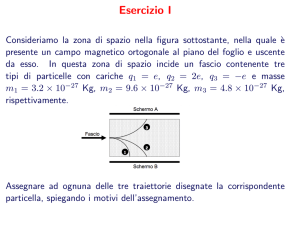
La forza di Lorentz
La forza di Lorentz
Ci proponiamo di trovare la forza che agisce su una carica elettrica in movimento in un campo
magnetico. Ricordiamo che in un tratto di filo lungo l e percorso dalla corrente i quando viene
immerso in un campo magnetico uniforme B rispetto al quale forma un angolo α è soggetto a una
forza la cui intensità è: F i l B sen . Supponiamo allora che la corrente nel filo sia data da una
singola carica q che si muove in esso.
q
Se Δt è il tempo che la carica q impiega ad attraversare il filo lungo l, la corrente è data da: i
.
t
q
l
La forza che agisce sul filo, quindi, si può scrivere come: F l B sen . Il rapporto
dà il
t
t
valore della velocità v con cui la carica q attraversa una sezione del filo. L’angolo α è quello
formato dalla velocità v e dal campo magnetico B . Otteniamo quindi F q v B sen . Tale forza
è detta forza di Lorentz.
La direzione della forza di Lorentz, analogamente alla forza che agisce sul filo percorso da corrente,
è perpendicolare sia alla velocità che al campo magnetico e il suo verso è dato dalla regola della
mano destra: ponendo le dita della mano nel verso del campo B e il pollice nel senso di q v , il
vettore F esce perpendicolarmente dal palmo della mano.
Il moto di una particella carica in un campo magnetico
Una particella carica che entra con velocità v in un campo magnetico B uniforme,
perpendicolarmente alle linee di campo, è soggetta alla forza di Lorentz perpendicolare alla
velocità. Ricordiamo che una forza perpendicolare alla velocità non compie lavoro; quindi, per il
teorema delle forze vive, l’energia cinetica si conserva. Tale forza è pertanto centripeta e modifica
solamente direzione e verso della velocità della particella, lasciandone invariato il modulo. Quindi
la particella si muove su un piano perpendicolare al campo magnetico secondo un moto circolare
uniforme della cui traiettoria determiniamo il raggio. Uguagliamo l’espressione della forza
centripeta a quella della forza di Lorentz: forza centripeta = forza di Lorentz. Ossia:
v2
mv
.
m q v B . Da cui: r
r
qB
2 r
2 r
Ricaviamo il periodo T dalla formula della velocità: v
, Da cui: T
e sostituendo al
T
v
2 m
posto del raggio r la formula precedentemente trovata, abbiamo: T
. Osserviamo che il
qB
periodo non dipende né dalla velocità della particella, né dal raggio di curvatura della traiettoria.
Esempio 1 – Calcolo del raggio della traiettoria e del periodo del moto di una particella carica
in un campo magnetico
Consideriamo un protone di massa m = 1,67 ∙ 10−27 kg e carica q = 1,60 ∙ 10−19 C. Esso entra con
m
velocità v = 1,8 ∙ 107
in un campo magnetico uniforme B = 0,24 T, perpendicolarmente alle linee
s
di campo. Vogliamo calcolare quanto vale la forza di Lorentz che agisce sul protone, qual è il
raggio della traiettoria e il periodo del moto circolare della particella.
Vogliamo inoltre determinare la forza di Lorentz nel caso in cui la particella sia un elettrone anziché
un protone.
Scriviamo i dati del problema
Massa del protone
m = 1,67 ∙ 10−27 kg
carica del protone
q = 1,60 ∙ 10−19 C
m
velocità del protone
v = 1,82 ∙ 107
s
intensità del campo magnetico
B = 0,24 T
massa dell’elettrone
me = 9,11 ∙ 10−31 kg
carica dell’elettrone
e− = − 1,60 ∙ 10−19 C
Incognite
Forza di Lorentz F che agisce sul protone
raggio r della traiettoria percorsa dal protone
periodo T del moto del protone
Forza di Lorentz che agisce sull’elettrone
Analisi e soluzione
Calcoliamo l’intensità della forza di Lorentz sul protone:
m
F = q ∙ v ∙ B = 1,60 ∙ 10−19 C ∙ 1,82 ∙ 107
= 6,99 ∙ 10−13 N
s
Il raggio della traiettoria è dato dalla formula: r
m v
qB
1,67 10 27 kg 1,82 107
1,60 1019 C 0,24T
m
s 0,79 m .
2m 2 1,67 1027 kg
2,73 10 7 s .
m
qB
1,82 107
s
Nel caso in cui la particella sia un elettrone anziché un protone, la forza di Lorentz ha la stessa
intensità di quella sul protone perché la quantità di carica è la stessa, la sua direzione è la stessa, ma
il verso è opposto perché la carica dell’elettrone è negativa, mentre quella del protone è positiva.
Calcoliamo ora il periodo del moto circolare uniforme: T
Applicazioni della forza di Lorentz
Il selettore di velocità
Prendiamo ora in considerazione una particella carica che si muove con velocità v in un campo
magnetico perpendicolarmente alle sue linee di forza. Se oltre al campo magnetico è presente anche
un campo elettrico, sulla particella agisce la risultante vettoriale della forza elettrica e della forza di
Lorentz. Nel caso in cui i due campi siano disposti perpendicolarmente tra loro, per una particolare
velocità v la risultante delle forze è nulla (campi incrociati) e la particella prosegue con moto
rettilineo uniforme. Una carica positiva q che attraversa la regione con una velocità perpendicolare
ad entrambi i campi, subisce la forza di Lorentz diretta verso il basso e la forza elettrica diretta
verso l’alto. La particella prosegue in linea retta se le due forze si equilibrano, cioè se forza elettrica
E
= forza di Lorentz, ossia q ∙ E = q ∙ v ∙ B. Semplificando, v . Se la velocità della particella è
B
maggiore di questo valore, prevale la forza di Lorentz verso il basso, se è minore prevale la forza
del campo elettrico e la particella è spinta verso l’alto. Consideriamo ora un insieme di particelle
che si muovono in varie direzioni e con diverse velocità. Per mezzo di due campi incrociati, uno
E
elettrico e l’altro magnetico, possiamo selezionare le particelle che hanno una velocità pari a
.
B
L’apparecchiatura che produce i due campi incrociati, elettrico e magnetico così regolati, si chiama
selettore di velocità.
Lo spettrometro di massa
Lo spettrometro di massa è uno strumento che permette di misurare la massa atomica o di separare
isotopi, cioè atomi dello stesso elemento, ma di massa diversa.
Il principio di funzionamento è dato dal fatto che il raggio di curvatura della traiettoria di una
particella carica che attraversa in modo perpendicolare un campo magnetico uniforme, dipende
dalla massa della particella.
Riscaldando la sostanza di cui si vuol misurare la massa atomica, vengono prodotti ioni aventi
velocità differenti sia in direzione che in intensità. In un ambiente chiuso e sotto vuoto li si accelera
in una certa direzione e, tramite un selettore di velocità, si selezionano quelli che hanno una
determinata velocità. Gli ioni così ottenuti entrano in un campo magnetico perpendicolare alla loro
velocità e vengono deflessi seguendo una semicirconferenza. Terminano la loro corsa su una lastra
fotografica su cui si imprime il punto di impatto: così si misura il raggio r della loro traiettoria. Con
la misura del raggio della traiettoria, con la velocità degli ioni ottenuta dal selettore e l’intensità del
qB
campo magnetico B , si calcola infine la massa degli ioni mediante la formula: m
r .
v
In particolare, due isotopi della stessa sostanza che attraversano il campo B , avendo la stessa
carica, ma massa diversa, percorrono due traiettorie di raggi diversi separandosi.
Il ciclotrone
Il ciclotrone è un’apparecchiatura che viene utilizzata per accelerare particelle cariche in uno spazio
ridotto.
Esso è costituito da due semicilindri di rame uguali nelle dimensioni, posti uno di fronte all’altro
come in figura e collegati ai morsetti di un generatore che crea tra di loro una differenza di
potenziale. Il generatore inoltre scambia periodicamente le polarità dei
semicilindri. Inizialmente una particella carica positivamente si trova al
centro dei due semicilindri, viene accelerata dalla differenza di
potenziale ed entra con una certa velocità in un semicilindro. Tutta la
regione è immersa in un campo magnetico perpendicolare alle basi dei
due semicilindri a causa del quale la particella percorre una
semicirconferenza fino ad affacciarsi all’altro semicilindro. Il
generatore cambia la polarità dei due semicilindri invertendola
esattamente nello stesso tempo in cui la particella percorre mezza
circonferenza, tempo che è indipendente sia dal raggio della traiettoria
che dalla velocità. In questo modo ogni volta che la particella si affaccia nello spazio tra i due
semicilindri subisce una accelerazione. Le varie semicirconferenze sono quindi percorse con
velocità via via maggiore e aumentano corrispondentemente il loro raggio (che è proporzionale alla
velocità). Questo processo continua finché il raggio della traiettoria è uguale a quello del ciclotrone;
allora la particella esce dall’apparecchio lungo una direzione tangente ai semicilindri.
Esempio 2- Calcolo della forza di Lorentz di una particella con velocità non perpendicolare al campo
magnetico
Una particella α, costituita da due protoni e da due neutroni (m = 6,68∙10−27 kg, q = 3,20∙10−19 C), entra con
m
velocità di 3,40∙107 s in un campo magnetico uniforme di intensità pari a 0,80 T, con la velocità che forma
un angolo di 30° rispetto al vettore B . Vogliamo calcolare la forza di Lorentz che agisce sulla particella α
nel campo magnetico e il raggio di curvatura della traiettoria della particella.
Scriviamo i dati del problema
Massa della particella alfa
m = 6,64∙10−27 kg
carica della particella
q = 3,20∙10−19 C
velocità della particella
m
v = 3,40∙10 s
7
Intensità del campo magnetico uniforme
B = 0,80 T
angolo tra la velocità della particella e il campo magnetico α = 30°
Incognite
Intensità della forza di Lorentz
raggio della traiettoria circolare
Analisi e soluzione
Calcoliamo l’intensità della componente della velocità della particella perpendicolare al campo magnetico:
m
m
v 3,40∙10 s ∙ sen 30° = 1,70∙107 s . Questo valore serve per calcolare il raggio della traiettoria.
m
Determiniamo l’intensità della forza di Lorentz: F = q v B 3,20∙10−19 C ∙ 1,70∙107 s ∙ 0,80 T =
7
4,35∙10−12 N.
mv
Il raggio di curvatura della traiettoria è dato da: r
qB
6,64 10 27 kg 1,70 107
3,20 1019 C 0,80 T
m
s 0,44 m
Verifiche di comprensione
1. Come si calcola l’intensità della forza di Lorentz che agisce su una particella di carica q che si muove
con velocità v in un campo magnetico uniforme B ?
2. Come sono direzione e verso della forza di Lorentz rispetto alla velocità v della carica e al vettore B
del campo magnetico?
3. Che tipo di moto fa una particella carica che entra in una regione in cui è presente un campo magnetico
uniforme con una velocità perpendicolare al campo?
4. Come si calcola il raggio della traiettoria circolare percorsa da una particella carica che si muove in un
campo magnetico uniforme con velocità perpendicolare al campo?
5. Come si calcola il periodo di rotazione di una particella carica in un campo magnetico uniforme?
6. In che cosa consiste il selettore di velocità e che effetto produce sulla velocità di una particella carica?
7. Quale è la relazione tra velocità, campo elettrico e campo magnetico nel selettore di velocità?
8. A che cosa serve lo spettrometro di massa?
9. Che cosa sono gli isotopi di un atomo?
10. Su quale principio si basa il funzionamento dello spettrometro di massa?
11. Come è costituito lo spettrometro di massa e come si determina la massa degli ioni?
12. A che cosa serve il ciclotrone?
13. Da che cosa è costituito il ciclotrone?
14. Come avviene l’accelerazione delle particelle cariche in un ciclotrone?
15. Come risulta il moto di una particella carica che entra in un campo magnetico uniforme con una velocità
non perpendicolare alle linee del campo magnetico?
Verifiche di conoscenza
1. La forza di Lorentz su una particella carica che si muove in un campo magnetico uniforme
perpendicolarmente alle linee di campo, risulta:
a. perpendicolare alle linee del campo e parallela alla velocità della particella
b. parallela alle linee del campo magnetico e perpendicolare alla velocità della particella
c. perpendicolare sia alle linee del campo che alla velocità della particella
2. La forza di Lorentz su una particella carica che entra in un campo magnetico con una certa velocità è
massima:
a. se la velocità è parallela alle linee del campo magnetico
b. se la velocità è perpendicolare alle linee del campo magnetico
c. comunque sia la velocità perché la forza non dipende dall’angolo tra la velocità e le linee di campo
3. Quale delle seguenti particelle non risente della forza di Lorentz?
a. elettrone
b. protone
c. neutrone
d. ioni positivi
e. ioni negativi
f. particella alfa
4. Il raggio di curvatura della traiettoria di una particella carica che entra in un campo magnetico uniforme
è proporzionale:
a. direttamente alla carica e al campo magnetico e inversamente alla quantità di moto della particella
b. direttamente alla quantità di moto della particella e inversamente alla carica e al campo magnetico
c. direttamente alla carica e alla velocità e inversamente alla massa e al campo magnetico
5. Una particella carica entra in una regione in cui è presente un campo magnetico perpendicolarmente alle
linee di campo e percorre una traiettoria circolare. Quali delle seguenti figure, nelle quali il campo
magnetico esce dal piano del foglio, sono corrette?
a.
b.
c.
6. Una particella entra in un campo magnetico perpendicolarmente alle linee di campo. Queste risultano
uscenti dal piano del foglio e la traiettoria della particella è una circonferenza percorsa in senso orario.
La particella è:
a. carica positivamente
b. carica negativamente
c. neutra
7. Una particella carica positivamente attraversa senza essere deviata una regione in cui sono presenti un
campo magnetico e un campo elettrico. Come sono i due campi?
a. il campo elettrico E e il campo magnetico B sono l’uno opposto all’altro in modo da farsi equilibrio,
e perpendicolari alla velocità della particella
b. il campo elettrico E è parallelo alla velocità della particella e perpendicolare al campo magnetico
B
c. il campo elettrico E e il campo magnetico B sono perpendicolari tra loro e perpendicolari alla
velocità della particella
8. Quale delle seguenti affermazioni è corretta?
a. In un ciclotrone una particella carica viene accelerata dal campo elettrico generato dalla differenza di
potenziale tra i due semicilindri
b. In un ciclotrone una particella carica viene accelerata dal campo magnetico che agisce come una
fionda sulla particella stessa
c. In un ciclotrone una particella carica è accelerata sia dal campo magnetico che dal campo elettrico
Problema svolto 1 - calcolo del raggio della traiettoria circolare in presenza di campo magnetico;
calcolo dell’intensità del campo elettrico ad esso incrociato per non deviare la particella
Un protone di massa m = 1,67 ∙ 10−27 kg e carica q = 1,60 ∙ 10−19 C partendo da fermo viene accelerato da una
differenza di potenziale di 2,00∙104 V e poi immesso in un campo magnetico uniforme di intensità B = 0,840
T. Vogliamo calcolare la velocità acquisita dal protone dopo essere stato accelerato e il raggio di curvatura
della traiettoria nel campo magnetico. Vogliamo inoltre determinare l’intensità del campo elettrico E da
porre perpendicolarmente al campo magnetico in modo che il protone prosegua in linea retta.
Scriviamo i dati del problema
Massa del protone
m = 1,67 ∙ 10−27 kg; carica del protone
q = 1,60 ∙ 10−19 C
velocità iniziale del protone
nulla
differenza di potenziale che accelera il protone ΔV = 2,00∙104 V;
Intensità del campo magnetico B = 0,840 T
Incognite
Velocità finale del protone
Vf ; raggio r di curvatura della traiettoria del protone
intensità del campo elettrico E incrociato con il campo magnetico B
Analisi e soluzione
Per calcolare la velocità che il protone acquista uguagliamo la sua energia cinetica finale al lavoro compiuto
1
m v 2f V q . Da questa formula ricaviamo:
2
2
m
2 V q 2 2,00 10 4 V 1,60 10-19 C
12 m
, da cui otteniamo: v f 1,96 106 .
v 2f
3
,
83
10
-27
2
m
1,67 10 kg
s
s
m
1,67 10 27 kg 1,96 106
mv
s 0,0244 m .
Il raggio della traiettoria è dato da: r
19
qB
1,60 10 C 0,84 T
E
Dalla formula v
che dà la velocità della particella non deviata dai campi incrociati, determiniamo
B
m
N
l’intensità del campo elettrico: E 1,96 106 0,840 T 1,65 106 .
s
C
dal campo elettrico E:
Problema svolto 2 – Calcolo del semiperiodo nel ciclotrone
Consideriamo un ciclotrone che accelera protoni. Il campo magnetico vale B = 0,78 T. Vogliamo calcolare il
tempo impiegato dalle particelle a compiere mezzo giro.
Scriviamo i dati del problema
Carica del protone
q = 1,60∙10−19 C; massa del protone
m = 1,67∙10−27 kg
Intensità del campo magnetico B = 0,78 T
Incognite
Tempo per compiere mezzo giro
T
2
Analisi e soluzione
Il tempo impiegato dalla particella a compiere mezzo giro è pari alla metà del periodo:
T 1 2 m
2 1,67 1027 kg
4,2 108 s .
2 2 q B 2 1,60 1019 C 0,78 T
Problemi
1. Un protone si muove con una velocità di 2,40∙107
m
in un campo magnetico uniforme di 0,940 T.
s
Calcola il raggio della traiettoria circolare e il periodo del moto del protone.
2. Un elettrone con velocità di 1,82∙107
m
percorre una circonferenza di raggio 0,360 m. Calcola l’intensità
s
del campo magnetico uniforme in cui è immerso l’elettrone.
3. Uno ione positivo di massa m = 6,62∙10-27 kg e di carica q = 3,20∙10-19 C entra in un campo magnetico
uniforme di intensità B = 0,82 T e percorre una circonferenza di raggio 0,24 m. Calcola la velocità dello
ione.
4. Un protone entra in un campo magnetico di 1,20 T con una velocità di 3,2∙107
m
che forma con il
s
vettore campo magnetico un angolo di 40°. Calcola l’intensità della forza di Lorentz e il raggio della
traiettoria del protone.
5. Una particella di carica q = 3,20∙10−19 C si muove con una velocità di 0,84∙107
m
in un campo
s
magnetico uniforme B = 0,76 T percorrendo una circonferenza di raggio r = 0,23 m. Determina la massa
della particella e il periodo del moto circolare uniforme della particella.
6. Una particella α (m = 6,64∙10−27 kg, q = 3,20∙10−19 C) viene accelerata con una differenza di potenziale di
5,00∙103 V. Essa, dopo essere stata accelerata, entra in un campo magnetico uniforme di 0,85 T. Calcola
la velocità con cui la particella entra nel campo magnetico e il raggio della sua traiettoria.
7. Un elettrone si muove in un campo magnetico uniforme di 6,2∙10−4 T percorrendo una circonferenza di
raggio r = 0,12 m. Calcola la velocità dell’elettrone e la differenza di potenziale che ha determinato la
velocità dell’elettrone partendo da fermo.
8. Calcola la velocità di un protone che attraversa due campi elettrico e magnetico incrociati, di intensità
rispettivamente E = 8,43 103
V
e B = 0,124 T, in modo che prosegua diritto.
m
9. Un protone viene accelerato in un ciclotrone nel quale il campo magnetico vale 1,38 T. Quanto vale il
tempo impiegato dal protone a percorrere un semicilindro e quanto deve essere la frequenza con cui si
invertono le polarità dei due semicilindri?
10. In un campo magnetico uniforme di 0.88 T una particella di carica q = 4,8∙10−19 C si muove lungo una
circonferenza di raggio 0,26 m con un periodo T = 3,6∙10−8 s. Calcola la massa della particella e la sua
velocità.