Il teorema di Pitagora al centro della didattica della geometria nella scuola secondaria di primo grado
di Luciano Porta
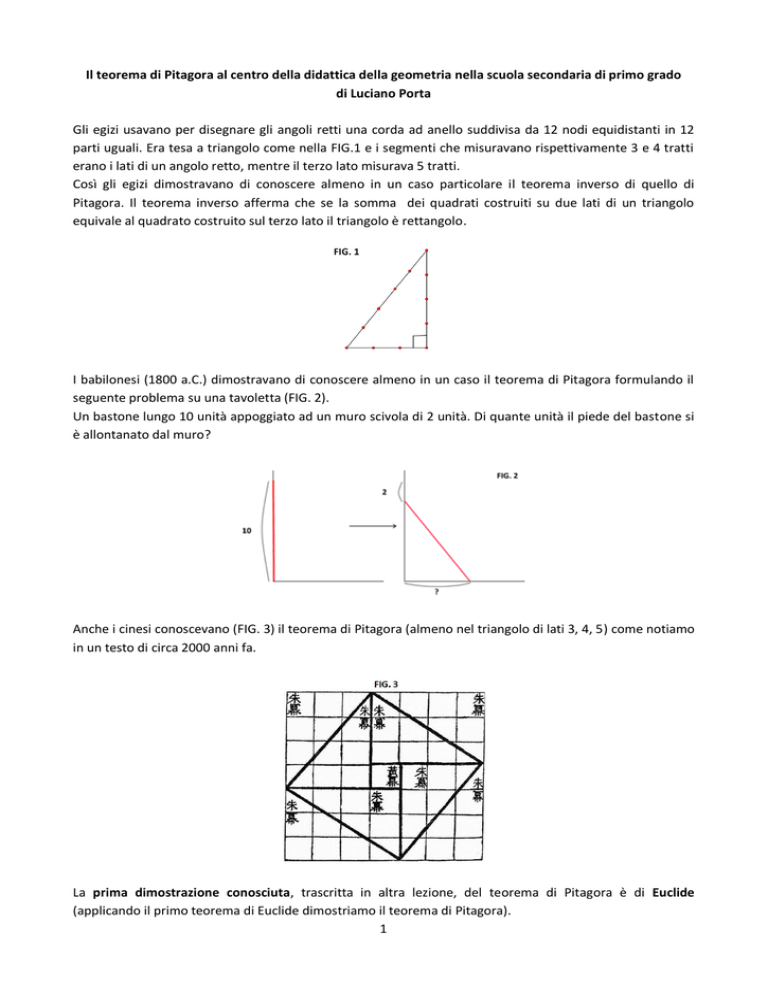
Gli egizi usavano per disegnare gli angoli retti una corda ad anello suddivisa da 12 nodi equidistanti in 12
parti uguali. Era tesa a triangolo come nella FIG.1 e i segmenti che misuravano rispettivamente 3 e 4 tratti
erano i lati di un angolo retto, mentre il terzo lato misurava 5 tratti.
Così gli egizi dimostravano di conoscere almeno in un caso particolare il teorema inverso di quello di
Pitagora. Il teorema inverso afferma che se la somma dei quadrati costruiti su due lati di un triangolo
equivale al quadrato costruito sul terzo lato il triangolo è rettangolo.
I babilonesi (1800 a.C.) dimostravano di conoscere almeno in un caso il teorema di Pitagora formulando il
seguente problema su una tavoletta (FIG. 2).
Un bastone lungo 10 unità appoggiato ad un muro scivola di 2 unità. Di quante unità il piede del bastone si
è allontanato dal muro?
Anche i cinesi conoscevano (FIG. 3) il teorema di Pitagora (almeno nel triangolo di lati 3, 4, 5) come notiamo
in un testo di circa 2000 anni fa.
La prima dimostrazione conosciuta, trascritta in altra lezione, del teorema di Pitagora è di Euclide
(applicando il primo teorema di Euclide dimostriamo il teorema di Pitagora).
1
Ritengo molto efficace dal punto di vista didattico un’ antica dimostrazione grafica indiana che può essere
condotta in modo rigoroso, ma chiaro.
Iniziamo col rappresentare il teorema di Pitagora:
Ora esponiamo l’antica dimostrazione indiana:
Abbiamo costruito due quadrati DEFG e NOPQ , uguali, il cui lato è la somma dei cateti del triangolo dato.
In entrambi sono contenuti quattro triangoli rettangoli uguali al triangolo dato per il primo criterio di
uguaglianza .
Se li sottraiamo sia al primo, sia al secondo otteniamo, rispettivamente, dal quadrato DEFG un
quadrilatero i cui lati sono uguali (per il momento affermiamo che è un rombo) e dal quadrato NOPQ i due
quadrati costruiti sui cateti . Se dimostriamo che il rombo HILM è un quadrato, esso è quello costruito
sull’ipotenusa ed abbiamo dimostrato il teorema di Pitagora.
Considerando ad esempio i due triangoli rettangoli uguali DHM e HIE, osserviamo che gli angoli DHM e EHI
sono complementari e sommati all’angolo MHI generano un angolo piatto: pertanto l’angolo MHI è retto
come retti sono tutti gli angoli del quadrilatero HILM che pertanto è un quadrato, il quadrato costruito
sull’ipotenusa.
2
Esistono decine di altre dimostrazioni (es. FIG. 6) : antiche (come quella di Bhaskara) e moderne (come
quella bellissima di Airy).
Anche l’autore di questa lezione, Luciano Porta , ha ideato una nuova dimostrazione ( 18 aprile 2003 ).
FIG. 6
Il teorema di Pitagora può essere esteso sostituendo i quadrati con poligoni simili. Particolarmente
suggestiva è la costruzione sui lati del triangolo rettangolo dei poligoni regolari (FIG. 7).
La dimostrazione si basa sulla proporzionalità.
FIG. 7
Ritorniamo ora alla didattica e, considerando le aree dei tre quadrati, otteniamo:
1) c2 = a2 + b2
1) c = a2 + b2
2) a2 = c2 – b2
2) a = c2 – b2
3) b2 = c2 – a2 da cui le formule applicative:
3) b = c2 – a2
3
Affinché gli studenti usino consapevolmente le formule applicative è opportuno che esse siano ricavate col
ragionamento e non con il calcolo algebrico.
Ad esempio per determinare la lunghezza dell’ipotenusa dobbiamo conoscere l’area del quadrato Q ;
pertanto calcoliamo le aree di Q1 e Q2 e le sommiamo applicando il teorema. Infine estraiamo la radice
quadrata dell’area di Q e otteniamo la misura dell’ipotenusa.
Invece per determinare la lunghezza di un cateto dobbiamo conoscere l’area del quadrato di cui esso è il
lato; pertanto calcoliamo l’area del quadrato Q e ad essa sottraiamo l’area del quadrato costruito sul
cateto conosciuto, applicando il teorema di Pitagora. Infine estraiamo la radice quadrata dell’area del
quadrato di cui dobbiamo determinare il lato.
Gli studenti devono poi riconoscere i lati di qualsiasi triangolo rettangolo, in qualsiasi posizione (FIG. 8)
anche quando i triangoli sono parte di altre figure geometriche. Nel caso del triangolo la cui ipotenusa è il
diametro di una semicirconferenza e il cui vertice è sulla semicirconferenza, è bene utilizzare un software di
geometria dinamica affinché gli studenti riconoscano l’angolo retto che permane trascinando il vertice.
FIG. 8
Questo itinerario didattico incentrato sul teorema di Pitagora può essere concluso con la descrizione dei
due metodi per generare le terne pitagoriche primitive: quello di Euclide che le genera tutte e quello,
attribuito a Pitagora, che genera infinite terne, ma non la totalità di esse.
Metodo di Euclide (FIG. 9):
X e Y numeri interi tali che:
X>Y>0
X e Y primi tra loro
X pari e Y dispari o X dispari e Y pari (pertanto in ogni caso X + Y = numero dispari)
cateto minore (a) = X2 – Y2
cateto maggiore (b) = 2XY
ipotenusa (c) = X2 + Y2
es. X = 2; Y = 1 a = 3 b = 4 c = 5
4
Ora dimostriamo la regola. Dobbiamo verificare che a2 + b2 = c2 .
Calcoliamo a2 + b2 = (X2 – Y2 )2 + (2XY)2 = X4 – 2X2 Y2 +Y4 +4X2Y2 = X4 + 2X2 Y2 +Y4 = (X2 + Y2)2 = c2
Metodo di Pitagora (FIG. 10):
d = numero dispari
cateto minore (a) = d
cateto maggiore (b) = (d2 – 1)/2
ipotenusa (c) = (d2 + 1)/2
es. d = 3
a=3
b=4
c=5
Data una terna pitagorica primitiva otteniamo una terna derivata moltiplicando i tre numeri per un numero
intero k a scelta; es. se k = 5 si ottiene dalla terna primitiva precedente 15, 20, 25 .
I triangoli che si ottengono da una terna primitiva e dalle terne da essa derivate sono simili tra loro.
Per terminare propongo un problema (Fig. 11) molto interessante che gli studenti devono risolvere
applicando solamente il teorema di Pitagora:
“Unire gli estremi A e B del diametro (25 cm) di una semicirconferenza con un punto C della
semicirconferenza stessa. Determinare il perimetro del triangolo ABC sapendo che l’altezza del triangolo
relativa al diametro misura 12 cm”.
“ Gli sforzi degli studiosi di geometria più avanzati hanno per oggetto l’eleganza “ Évariste Galois
www.webalice.it/lucianoporta i Pitagorici DIDATTICA E DIVULGAZIONE DELLA MATEMATICA E DELLE SCIENZE LEZIONI TRE
5












