Scuola di Fisica nucleare “R. Anni”
Anni” - Otranto
Terzo corso (2007)
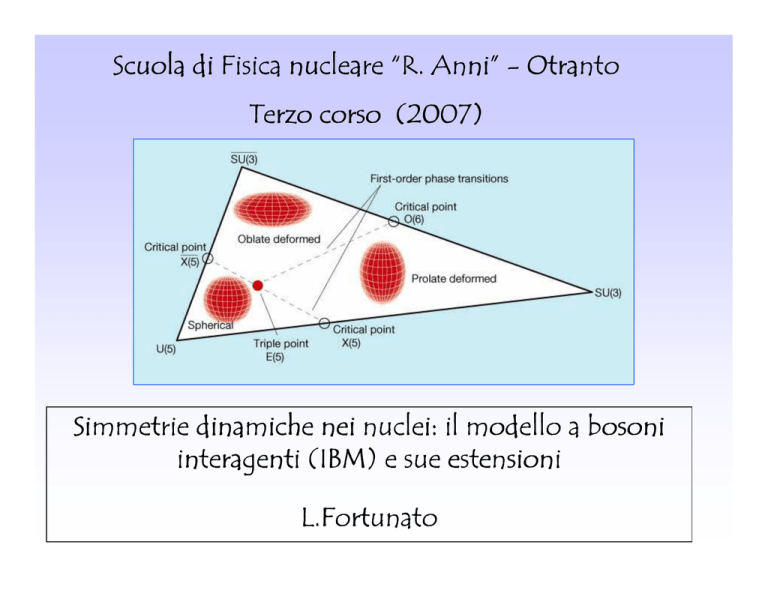
Simmetrie dinamiche nei nuclei: il modello a bosoni
interagenti (IBM) e sue estensioni
L.Fortunato
1 - Introduzione matematica alle algebre di Lie
• Algebre di Lie, subalgebre e
classificazione di Cartan
• Commutatore e costanti di struttura
• Rango, ordine, operatori di Casimir
• Simmetrie dinamiche
Sophus Lie
matematico
norvegese
• Algebre Spectrum Generating
• Rotore, momento angolare ed SO(3)
L. Fortunato
Algebra di Lie
G={g1 , g2 , … , gn} :
spazio vettoriale di dimensione n, i cui elementi siano
operatori (infinitesimi), dotato di una operazione, detta
prodotto di Lie o commutatore [.. , ..] tale che:
• [gi , gj] = Σ ckij gk
∀ gk ∈ G
→ Chiusura [gi ,gj]
• [a , b] = - [b , a]
∀ a,b ∈ G
→ Antisimmetrica
• [α a+β b , c] = α [a,c]+β [b , c]
• [a,[b,c]]+[b,[c,a]]+[c,[a,b]]=0
→ Bilineare
→ id. Jacobi
ckij sono le costanti di struttura
ë
Specificano completamente
un’algebra
L. Fortunato
Algebre Abeliane,
Abeliane, Subalgebre Invarianti
Un’algebra è detta Abeliana, o commutativa, se
[a , b]=0
∀ a,b ∈ G
⇔ cost. strutt. nulle ckij =0
Una Subalgebra G’ di un’algebra di Lie G è un
sottoinsieme G ⊃ G’ degli elementi di G che sia esso
stesso un’algebra:
• è detta propria, se almeno un elem. di G non sta in G’
• e detta invariante, se [a,b] ∈ G’ ∀ a ∈ G’
G (Subalgebra invariante = Ideale)
e ∀ b∈
L. Fortunato
Semplice, Semisemplice,
Semisemplice, etc.
etc.
Un’algebra è detta semplice se non è abeliana e non ha
subalgebre invarianti proprie.
Un’algebra è detta semisemplice se non ha subalgebre
invarianti abeliane
Coroll.: semplice ⇒ semisemplice
Criterio di Cartan: Un’algebra G è semisemplice se e
solo se la sua forma di Killing (il tensore metrico) è
non-degenere, det(g)≠ 0
gµν= cσµρ cρµσ
L. Fortunato
Classificazione di Cartan
Tutte le algebre semisemplici sono note e
classificate:
Elie Joseph Cartan
mat. francese
L. Fortunato
Operatori di Casimir e Rango
Per ogni algebra si può
costruire un set di operatori,
detti operatori di Casimir o
invarianti, C, tali che
[C, Xi]=0 , ∀ Xi ∈ G
Hendrik Casimir (1909-2000) fisico olandese
Il numero di invarianti indipendenti è detto rango della
algebra.
L’ordine è il numero di operatori che formano
un’algebra.
L. Fortunato
Esempio: Momento Angolare → so(3)
L =r × p
→
Lx , Ly , Lz
[Lx , Ly ] = iLz
sono i generatori di so(3)
+ permutazioni cicliche sugli indici
C[so(3)] = L2= Lx2 + Ly2 + Lz2
è l’operatore quadratico di Casimir (rango 1)
[C , Li ] = 0 , ∀ Li ∈ SO(3)
so(3) ⊃ so(2)
↓
↓
L
M
|
Ú
Branching problem
Branching rules:
-L ≤ M ≤ L
L. Fortunato
… continua ...
Occorre specificare l’azione dei generatori su una base
ortonormale |LMÒ
L±|LMÒ = [(L¡M)(L±M+1)]½|LM±1Ò
L± = Lx ± iLy
Lz|LMÒ = M|LMÒ
L2|LMÒ = L(L+1)|LMÒ
Applicazione nel rotore rigido:
H=k L²
→ E=k L(L+1)
con k=(h²/2I)
L. Fortunato
… rotori quantistici
H2
HCl
EJ= B J(J+1)
∆EJ= 2B(J+1)
L. Fortunato
Spectrum Generating Algebra (SGA)
Quando, in generale, possiamo scrivere
H= E0 + Σ ckXk + Σ cklXk Xl +…
con
Xk ∈ G
come un polinomio negli elementi di un’algebra
allora G è detta spectrum generating algebra (SGA)
per H, perché è sempre possibile diagonalizzare
(numericamente) H nella base ONC labellata da tutti i
numeri quantici di un Complete Set of Commuting
Operators (CSCO) di una qualunque catena di
sottoalgebre di G ⊃ G’ ⊃ G’’ ⊃ …
Data l’azione dei vari Xk su |α
αÒ si possono sempre
calcolare gli elementi di matrice di un operatore
come ·α
α|H|α
α’Ò
L. Fortunato
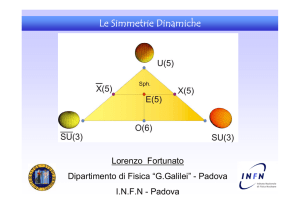
Simmetria dinamica
In casi particolari in
H= E0 + Σ ckXk + Σ cklXk Xl +…
con
Xk ∈ G
abbiamo solo alcuni termini che corrispondono ad
operatori invarianti di una catena di sottoalgebre:
G ⊃ G’ ⊃ G’’ ⊃ …
↓
↓
↓
C C’ C’’
catena di sottoalgebre
H= E0 + aC + a’C’ +a’’C’’ +…
in questi casi si parla di simmetria dinamica e si ha
E= E0 + a‚CÚ + a’ ‚C’Ú +a’’ ‚C’’Ú +…
L. Fortunato
Conseguenze della simmetria dinamicadinamica-1
1) tutti gli stati sono risolubili ed esistono espressioni
analitiche per l’energia e le altre osservabili
E= E0 + a‚CÚ + a’ ‚C’Ú +a’’ ‚C’’Ú +…
2) tutti gli stati sono caratterizzati da numeri quantici
che “etichettano” le rappresentazioni irriducibili
(IRREPS) della catena di sottoalgebre
α1α2...α
αn⟩
|α
3) la struttura delle funzioni d’onda è dettata dalla
simmetria ed è indipendente dai parametri
dell’hamiltoniana
L. Fortunato
Conseguenze della simmetria dinamicadinamica-2
Assumiamo che H commuti con un set di operatori
che formano una certa algebra di Lie:
Se |γγ Ò è autostato di H, allora
anche gi|γγ Ò è autostato di H e si ha degenerazione.
All’origine della degenerazione c’è una quantità che
viene conservata, cioè esiste un invariante, che è
l’operatore di Casimir di qualche gruppo.
L. Fortunato
Multipletti,
Multipletti, degenerazione, splitting.
splitting.
= { | λµν Ò }
base di stati ONC
λ
µ
ν
La simmetria dinamica splitta, ma non mischia gli
stati di una base!
L. Fortunato
Degenerazione “magnetica”
magnetica”
M= +Jz
J2
M= -Jz
J1
O(3)
⊃
O(2)
Gli stati con definito momento angolare totale
comprendono un multipletto di sottostati con diversa
terza componente: sono detti sottostati magnetici
perché si separano quando il sistema è sottoposto ad
un campo magnetico (effetto Zeeman)
Ovvero l’interazione magnetica -µB rompe la
simmetria dell’hamiltoniana.
L. Fortunato
Esempio: Atomo di idrogeno → so(4)
Stati della hamiltoniana dell’atomo di H sono
manifestamente invarianti per SO(3)
L. Fortunato
Ulteriore degenerazione
Nello spettro si osserva un’ulteriore degenerazione in .
Da dove viene?
Degenerazione ⇒ Quantità conservata
vettore di Runge-Lenz:
[H,A]=0
⇒ c’è un gruppo di simm.
più grande che contiene
sia L che A
so(4) ≈ so(3)⊕ so(3)
L. Fortunato
Altre simmetrie dinamiche importanti
From R.Bijker
L. Fortunato
SU(3) di “sapore”
sapore”
Gell-mann e Ne’eman hanno suggerito che i gradi di
libertà interni degli adroni possono essere descritti in
termini di una simmetria dinamica SU(3) di “flavour”
Si ha la formula di massa
di Gellmann-Okubo
(Massa rimpiazza Energia nel
formalismo relativistico)
I=Isospin Y=ipercarica=2(C-Iz)
From R.Bijker
L. Fortunato
2- IBM, u(6) e Simmetrie Dinamiche nei nuclei
• Introduzione al nucleo come sistema a molticorpi
• Interacting Boson Model (IBM) ↔ u(6)
• Simmetrie dinamiche nell’IBM: u(5) su(3) so(6)
• Triangolo di Casten
• Esempi di spettri energetici e transizioni
elettromagnetiche nei tre limiti
R
I
j
ω
Mod. a Shell
IBM
Mod. Collettivo
L. Fortunato
Modello a Bosoni Interagenti (IBM o IBA)
u(6) → SGA per il nucleo atomico
con tre simmetrie dinamiche
Akito Arima
e Francesco Iachello
Nucleo: sistema a molti corpi composto da fermioni
(1~250) dotati di spin 1/2 e di due specie, protoni e
neutroni.
I fermioni hanno la tendenza ad accoppiarsi in bosoni
compositi (analoghi alle coppie di Cooper nei
semiconduttori) di momento angolare totale 0 o 2,
detti bosoni s e d rispettivamente.
L. Fortunato
From R.Bijker
L. Fortunato
Motivazioni
I nucleoni di
valenza hanno la
tendenza a formare
coppie con L=0,2.
Infatti lo stato
fondamentale dei
nuclei pari-pari è
sempre 0+, mentre
il primo stato
eccitato è quasi
sempre un 2+
L. Fortunato
MotivazioniMotivazioni-2
Gli stati collettivi di un nucleo con 2N nucleoni di
valenza sono approssimati con uno stato ad N bosoni:
N = n s + nd
dove ns ed nd non sono necessariamente conservati,
ma il numero totale di bosoni N è conservato.
Se la shell è riempita fino a metà si considerano
coppie di particelle, se è riempita più della metà si
considerano coppie di buchi.
L. Fortunato
MotivazioniMotivazioni-3
C’è l’esigenza di trovare uno schema concettuale che
permetta di “mettere ordine” nella complessità della
spettroscopia nucleare → simmetrie!
?
L. Fortunato
Accoppiamento dei fermioni
I fermioni (s=1/2) in una shell di valenza (j=+s) si
accoppiano, di preferenza, in modo che Jtot =0,2
From T.Otsuka
L. Fortunato
Definizioni:
Bosoni “elementari” con cui si costruisce l’IBM:
bα , bα†
con α=1,…,6
b1 = s
b2,…,6= dµ
Si costruisce l’algebra u(6) prendendo operatori
bilineari:
Tali da chiudersi in u(6):
[Gr , Gs] = Σ ct Gt
L. Fortunato
Limite vibrazionale u(6) ⊃ u(5)
Elementi :
[s†× d](2)µ → 5
Dimensione:
Algebra:
36
u(6)
[d†× s](2)µ → 5
[s†× s](0)0 → 1
[d†× d](0)0 → 1
25
u(5)
[d†× d](3)µ → 7
10
so(5)
[d†× d](1)µ → 3
3
so(3)
[d†× d](2)µ → 5
[d†× d](4)µ → 9
L. Fortunato
Limite rotazionale u(6) ⊃ su(3)
Elementi :
Dimensione:
Algebra:
36
u(6)
[s†× d](2)µ → 5
[d†× s](2)µ → 5
[s†× s](0)0 → 1
[d†× d](0)0 → 1
[d†× d](3)µ → 7
[d†× d](4)µ → 9
[s†× d](2)µ+[d†× s](2)µ
-√(7/2)[d†× d](2)µ → 5
[d†× d](1)µ → 3
8
su(3)
3
so(3)
L. Fortunato
Limite γ-instabile u(6) ⊃ so(6)
Elementi :
Dimensione:
[s†× d](2)µ → 5
36
Algebra:
u(6)
[s†× s](0)0 → 1
[d†× d](0)0 → 1
[d†× d](2)µ → 5
[d†× d](4)µ → 9
[s†× d](2)µ+[d†× s](2)µ → 5
15
so(6)
[d†× d](3)µ → 7
10
so(5)
[d†× d](1)µ → 3
3
so(3)
L. Fortunato
Catene di sottoalgebre:
sottoalgebre:
Con gli operatori definiti nel modello si possono
costruire quindi solo 3 catene di sottoalgebre, che
vengono detti limiti. Esse corrispondono a simmetrie
dinamiche per le quali è possibile scrivere un
operatore hamiltoniano che è analiticamente risolubile.
In realtà c’è una quarta catena, detta su(3), che è
isomorfa ad su(3).
L. Fortunato
Catena I: u(6) ⊃ u(5) ⊃ so(5) ⊃ so(3)
nd
|
nd(nd+4)
v(v+3)
u(6) ⊃ u(5) ⊃ so(5) ⊃ so(3)
N
nd
v
L
L(L+1)
Ú
La base di stati è “labellata” dai numeri quantici della
catena di op. di Casimir (missing label problem)
L. Fortunato
Catena II: u(6) ⊃ su(3) ⊃ so(3)
(λ,µ)
|
u(6) ⊃ su(3) ⊃ so(3)
N
(λ,µ)
L
L(L+1)
Ú
L. Fortunato
Catena III: u(6) ⊃ so(6) ⊃ so(5) ⊃ so(3)
σ(σ +4)
|
v(v+3)
L(L+1)
u(6) ⊃ so(6) ⊃ so(5) ⊃ so(3)
N
σ
v
L
Ú
L. Fortunato
Triangolo di Casten
I parametri si
riferiscono ad
una particolare
hamiltoniana,
detta “Q dot Q”
E’ come una
mappa che
mostra tutta la
fenomenologia
nucleare legata
alle deformazioni
di quadrupolo
L. Fortunato
Triangolo di Casten
Rick Casten,
YALE
Possiede una ricca fenomenologia!
L. Fortunato
Triangolo di Casten esteso
Ha in aggiunta la catena IV che corrisponde ad
avere un rotore assiale oblato invece che prolato
Ci sono fasi diverse e transizioni di fase → Ruben
L. Fortunato
Sferico, Oblato e Prolato
Sferico
Arancia
Calcio
Oblato
Mandarino
Lancio del disco
Prolato
A
g
r
u
m
i
Limone
Rugby
S
p
o
r
t
L. Fortunato
U(5)
R4/2= 2.0
+
+
B( E 2;2 → 0 ) = e N
Slide by D.Warner
2
B
B( E 2;4 + → 2 + )
B( E 2;2 + → 0 + )
= eB2 2( N − 1)
L. Fortunato
SU(3)
R4/2= 3.33
+
+
B( E 2;2 → 0 ) = e
Slide by D.Warner
2
B
N (2 N + 3)
5
10 ( 2 N − 2)(2 N + 5)
=
+
+
B( E 2;2 → 0 ) 7 2 N (2 N + 3)
B( E 2;4 + → 2 + )
L. Fortunato
O(6)
R4/2=
2.5
+
+
B ( E 2;2 → 0 ) = e
Slide by D.Warner
2
B
N ( N + 4)
5
10 ( N − 1)( N + 5)
=
+
+
B ( E 2;2 → 0 ) 7 N ( N + 4)
B ( E 2;4 + → 2 + )
L. Fortunato
Osservabili crucialicruciali-1
Alcune osservabili aiutano a classificare uno spettro:
• ratio R4/2= E(4+)/E(2+)
Figure taken from P.van Isacker
L. Fortunato
Osservabili crucialicruciali-2
• Energia di separazione di due neutroni E(N+1)-E(N)
• Posizione delle bande eccitate, altre ratios R0+/2+
• Isomere shift
• Intensità delle reazioni di trasferimento
• Transizioni elettromagnetiche
• Ratios di B(E2)
Le transizioni e.m. soddisfano a certe regole di
selezione che sono imposte dalla simmetria del
problema e la caratterizzano!
L. Fortunato
L. Fortunato
Transizioni elettromagnetiche e Regole di selezione
Anche l’operatore di transizione elettromagnetica può
essere espresso in termini di elementi dell’algebra e
si possono calcolare analiticamente gli el. di matrice.
Per esempio nel caso del quadrupolo elettrico E2:
Q(χχ)m =[s†×d + d†×s + χd†×d ](2)m
Il calcolo della probabilità di transizione ridotta:
B(E2; L → L’) = (2L’+1)/(2L+1) |‚ L’ 7 T(E2) 7 L Ú|2
implica delle regole di selezione. Per esempio nel caso
di U(5) si ha:
B(E2;
[N],nd+1, v=nd+1, L=2nd+2 → [N],nd, v’=nd, L’=2nd
)=
k(2N-L’)(L’+2)
Ci sono un certo numero di transizioni proibite.
L. Fortunato
3- Estensioni ed IBFM
• Nucleo come sistema a due tipi di particelle
• Interacting Boson Model 2 (IBM2) ↔ u(6)⊕u(6)
• Simmetrie dinamiche nell’IBM2 ed F-spin
• Altre estensioni (breve carrellata)
• Esempi di spettri energetici, scissor mode
• Interacting Boson-Fermion Model (IBFM)
• Superalgebra, supersimmetria dinamica,
supermultipletti
L. Fortunato
IBMIBM-2: protoni e neutroni
Nell’IBM-2 si considerano protoni e
neutroni come specie diverse, ovvero si
definiscono operatori di creazione e
distruzione specifici:
sπ sν dπ dν
sπ† sν† dπ† dν†
I 72 generatori di Uπ(6) ⊗ Uν(6) possono essere
raggruppati in 2 insiemi:
[b†πλm × bπλ’m’ ](λλ)µ → 36 operatori di tipo protonico
[b†νλm × bνλ’m’ ](λλ)µ → 36 operatori di tipo neutronico
L. Fortunato
Catene di algebre
Le algebre in gioco sono tutte bosoniche. Oltre
alle catene triviali che coinvolgono separatamente
ciascuna delle due algebre Uπ(6) e Uν(6), si ha
Uπ(6) ⊗ Uν(6) ⊃ Uπν (6) ⊃ 3 catene ⊃ SOπν (3)
I generatori di Uπν (6) sono ottenuti sommando i
generatori corrispondenti di Uπ(6) e Uν(6).
Esempio:
Lπ,i generano SOπ(3)
Lν,i generano SOν(3)
Lπ,i+Lν,i generano SOπν(3)
L. Fortunato
F-Spin
In analogia col formalismo dell’isospin possiamo
interpretare i bosoni protonici e quelli neutronici
come due diversi “stati di carica” dello stesso bosone
con F=½ e (per convenzione)
MF =
–½ neutroni
+½ protoni
Figure taken from P.van Isacker
L. Fortunato
Cosa aggiunge alla fenomenologia?
Predice gli stati a “forbice” Lπ=1+
(scissors mode): si interpretano,
nel limite classico, come
oscillazioni collettive dell’angolo
tra gli assi di simmetria dei
protoni e dei neutroni. Sono modi
detti isovettoriali.
Si rilevano andando a
misurare le transizioni
magnetiche M1
Lπ → (L+1)π
L. Fortunato
Lπ,i-Lν,i : è l’op. che induce transizioni M1
Sugli stati Lπ=1+ sono costruite delle bande con
Lπ=1+, 3+, 5+, ...
Stati a simmetria mista
Sono detti stati a simmetria mista perché
corrispondono a IRREPS che non sono totalmente
simmetriche né totalmente antisimmetriche nello
scambio di protoni e neutroni:
[Nπ] ⊗ [Nν ] ⊃ [Nπ+Nν ,0,0,...]⊕[Nπ+Nν -1,1,0,...]⊕
⊕[Nπ+Nν -2,2,0,...]⊕ …
L. Fortunato
Hamiltoniana IBM2 e interazione protoneprotone-neutrone
La forma generica di una hamiltoniana bosonica
nell’IBM2 è:
H=E0 + επnπ + ενnν + κQ(2)πQ(2)ν + Vππ + Vπν + Vνν + Mπν
^^^^^^^^^
επ , εν : sono legati all’energia dei bosoni protonici e
neutronici. Gli altri termini descrivono l’interazione tra
le due componenti, tra cui domina l’interazione di
quadrupolo tra protoni e neutroni.
In particolare poi, l’operatore di Majorana Mπν effettua
il collegamento (shift) tra stati a simmetria differente
L. Fortunato
Altre estensioni: IBMA -n con n=1,2,3,4
IBM
Esistono altre estensioni e generalizzazioni, ma
l’algebra si complica e non ce ne occuperemo.
Taken from P.van Isacker
L. Fortunato
IBFM: Interacting Boson Fermion Model
L’IBM e tutte le sue estensioni trattano le
eccitazioni collettive di sistemi con un
numero di particelle pari (even nuclei) in
termini di un set di bosoni interagenti.
F. Iachello
E’ interessante estendere (Iachello &
Scholten,1979) il modello ai nuclei dispari:
- tutte le particelle, eccetto una, sono
accoppiate in bosoni s e d
- la particella rimanente viene trattata
esplicitamente come un fermione che si
muove in un certo orbitale
Olaf Scholten
L. Fortunato
IBFM: Interacting
IBM Boson
ed IBFM
Fermion Model
Nei sistemi dispari, oltre all’accoppiamento dei
fermioni in coppie con L=0,2 c’è sempre anche un
fermione spaiato che interagisce col resto dei bosoni
di valenza: VBB
VBF
L. Fortunato
IBFM, Superalgebra e Supersimmetria
Set di operatori bosonici e fermionici che soddisfino a
certe regole → Superalgebra o algebra di Lie gradata
Set:
X → elementi bosonici
Y → elementi fermionici
1) Relazioni di commutazione/anticommutazione:
(c,d,f sono le costanti di struttura “gradate”)
L. Fortunato
2) Super-identità di Jacobi:
U(n/m) può essere realizzata con le prodotti
bilineari di op. di creazione e distruzione
L. Fortunato
Classificazione delle superalgebre
La loro classificazione è nota (1975-77)
Victor Kac,
matematico
russo
L. Fortunato
Estensione
Alle superalgebre si possono estendere
tutti i concetti già visti:
• esistono delle super-rappresentazioni
• esistono dei super-operatori di Casimir
che commutano con tutti gli operatori
della superalgebra
• esistono le spectrum generating
superalgebras
• esistono le supersimmetrie dinamiche
L. Fortunato
Operatori nell’
nell’IBFM
Ω è la dimensione dello spazio fermionico
L. Fortunato
IBM + fermione con j=3/2
=3/2
Consideriamo il caso dell’IBM + un fermione in
un’orbita con j=3/2:
la superalgebra di Lie è U(6/4)
L. Fortunato
Esempi di “Lattice”
Lattice” o reticolo di superalgebre
L. Fortunato
Esempi di “Lattice”
Lattice” o reticolo di superalgebresuperalgebre-2
UB(6) ⊃ … ⊃ SOB(3)
UF(4) ⊃ … ⊃ SUF(3)
Le due catene vanno combinate in una catena unica
UB(6) ⊗ UF(4) ⊃ SOB(6) ⊗ SUF(4) ⊃
Spin(6) ⊃ Spin(5) ⊃ Spin(3)
L. Fortunato
Classificazione degli stati
Le catene forniscono un modo di classificare gli stati
Sono i n.q. necessari
L. Fortunato
Esempio di Hamiltoniana e di spettro analitico
L. Fortunato
Supermultipletti di U(6/12)
Ad una certa REP del supergruppo si associa un set di
REP dei sottogruppi che corrispondono a nuclei diversi!
L. Fortunato
Confronto tra teoria ed esperimento
Qualitativamente eccellente,
quantitativamente buono
L. Fortunato
Altro
Un altro esempio di applicazione dell’IBFM: 196-Au
L. Fortunato
Ad nauseam
L. Fortunato
Supersimmetrie dinamiche protoneprotone-neutrone
pari-pari
dispari-pari
Nν +1, Nπ +1
194Pt
Nν , Nπ +1, jν
ï
ê
195Au
194Pt
ê
ï
Nν +1, Nπ , jπ
pari-dispari
196Au
Nν ,Nπ , jν , jπ
dispari-dispari
U(6/12)ν ⊗ U(6/4)π
L. Fortunato
Reazioni di trasferimento di un nucleone
Le reazioni di trasferimento di un singolo nucleone
(neutrone o protone) forniscono un test cruciale per
la supersimmetria. L’operatore di trasferimento è:
σ[sπ
T1 = -σ
×
a†π, 3/2](3/2)m + θ[dπ
×
a†π, 3/2](3/2)m
θ[sπ
×
a†π, 3/2](3/2)m + σ[dπ
×
a†π, 3/2](3/2)m
T2 =
gs
gs, exc
è un tensore sotto trasformazioni indotte da Spin(6),
quindi dà luogo a regole di selezione ed espressioni
analitiche per le intensità di transizione.
Esempio :
194Pt
→
195Au
Le intensità teoriche e sperimentali sono
Rexc=0
Exp=0.019
Rgs= 1.12
Exp=1.175
L. Fortunato
Messaggio da portare a casa e conservare
• Alcuni modelli semplici possono essere scritti
“naturalmente” in termini di operatori di creazione e
distruzione.
• Ad essi si associa un’algebra che sottende ad una
simmetria dinamica.
• Sapendo trattare matematicamente l’algebra si
ottengono soluzioni analitiche che possono essere
usate come modelli e confrontate con i dati
sperimentali (non solo: si ottengono anche nuove
soluzioni inaspettate!)
• L’algebra inquadra concettualmente un sistema
complesso e fornisce anche nuova fisica!!
L. Fortunato