Le Simmetrie Dinamiche
Lorenzo Fortunato
Dipartimento di Fisica “G.Galilei” - Padova
I.N.F.N - Padova
Le Simmetrie Dinamiche
Teoria dei Gruppi
Algebre di Lie
Classificazione
Predizioni
Differenze tra gruppo
e algebra.
Transizioni di fase
Varietà Differenziabili
Supersimmetrie
Proprietà Sp. Vett.
… e molto altro!
Atomo di H
Operatori (Hamilt.)
Eq. Schrödinger e
funzioni d’onda
Spettri energetici e
transizioni EM
Meccanica
Quantistica
Spin
Rotovibrazioni
molecolari
Modello a goccia dei
nuclei atomici
Modello standard
Modelli
fenomenologici
L. Fortunato
συμμετρος = commensurato con
• popoli primitivi: decorazioni e simboli dotati di simmetria (=
bellezza estetica), astratti dall’osservazione del mondo
minerale,vegetale e animale.
L. Fortunato
• Civiltà antiche: utilizzano la simmetria nelle arti, pittura,
scultura, architettura, musica, poesia
Fregi
Decorazioni
Decorazioni
egizi e moreschi
celtiche
greche
Canone del granchio (J.S.Bach)
è un duetto tra due violini le cui
partiture sono una l’inverso
temporale dell’altra.
L. Fortunato
• Villa “La rotonda” di
Palladio (a Vicenza)
• Un raffinato esempio di
gourmet ( uh-lah-lah ! )
• Gioco di parole palindromo in tedesco: NURDUGUDRUN
Nur Du Gudrun (solo tu Gudrun, nome femminile)
L. Fortunato
• Keplero credeva così
fortemente nella simmetria
dell’universo (Harmonice
mundi) da proporre
addirittura un sistema nel
Mysterium Cosmographicum
(1581) che unificava il
sistema solare e la musica!
L. Fortunato
Escher e le tassellazioni del piano…
…e anche di altre geometrie per esempio quella iperbolica
(Notate che le tessere sono congruenti anche qui!)
L. Fortunato
συμμετρος = commensurato con
• Oxford Dictionary of Current English :
• un equivalenza tra oggetti, anche astratti
• un equivalenza di un oggetto se visto da due
punti di vista diversi
• l’ invarianza di un sistema in seguito ad una
certa trasformazione o ad una serie di
trasformazioni (collegato al teorema di Noether)
L. Fortunato
Due tipi generali di simmetria
L. Fortunato
Le molteplici forme di simmetria in fisica…
• Simmetrie dello spazio-tempo (geometriche): traslazione,
rotazione, traslazione temporale, trasf. Poincaré. Sono tutte
continue.
• Discrete: permutazione, classificazione dei cristalli, inversione
temporale, spaziale (asse o punto), wallpaper symmetries
(rot.+trasl.) , C (int.deboli!), P, T (2° Princ. Term.), CP, CPT
• Simm. di gauge : una certa lagrangiana rimane invariante
rispetto ad una trasformazione locale (coordinate interne).
Modello standard è una teoria di gauge il cui gruppo di simmetria
è U(1)xSU(2)xSU(3)
• Simmetrie dinamiche: sono simmetrie “nascoste” nell’op.
hamiltoniano (proprietà matematica) e si manifestano fornendo
precise leggi sugli autovalori (stati energetici), sulle transizioni
EM e regole di selezione.
L. Fortunato
La teoria dei gruppi
La teoria dei gruppi è il formalismo matematico che permette
di studiare a fondo le simmetrie.
Cos’è un gruppo? E’ un set di elementi dotato di una
operazione di “composizione”, tale che se si prendono due
elementi e li si “compone” si ottiene ancora un elemento del
set iniziale. Ad esempio il gruppo di simmetria del triangolo
equilatero
…per esempio
L. Fortunato
Più precisamente…
Un gruppo è un set, G, dotato di una operazione bilineare, *,
tale che, dati gli elementi a,b e c di G, si abbiano le proprietà di:
-Chiusura a*b ∈ G
-Associatività (a*b)*c=a*(b*c)
-Esistenza (ed unicità) dell’identità: a*e=e*a=a
-Esistenza (ed unicità) dell’inverso: a*x=x*a=e
Se il set è anche una varietà
differenziabile, tale che il “prodotto”
sia compatibile con le esigenze di
continuità allora il gruppo è detto di
Lie.
L. Fortunato
Algebra di Lie
G={g1 , g2 , … , gn} :
spazio vettoriale di dimensione n, i cui elementi siano
operatori (infinitesimi), dotato di una operazione, detta
prodotto di Lie o commutatore [.. , ..] tale che:
• [gi , gj] = Σ ckij gk
∀ gk ∈ G
→ Chiusura [gi ,gj]
• [a , b] = - [b , a]
∀ a,b ∈ G
→ Antisimmetrica
• [α a+β b, c] = α [a,c]+β [b , c]
→ Bilineare
• [a,[b,c]]+[b,[c,a]]+[c,[a,b]]=0
→ id. Jacobi
ckij sono le costanti di struttura
r
Specificano completamente
un’algebra
L. Fortunato
Classificazione
Elie Joseph Cartan
Matematico
francese
Vibrazioni
Rotazioni
L. Fortunato
Operatori di Casimir
Data un’algebra di Lie, G, qualunque con elementi Xk ∈ G, è
sempre possibile individuare un certo numero di operatori,
detti di Casimir, C, che commutano con tutti gli elementi
dell’algebra:
[C, Xk] = 0 , ∀ Xk ∈ G
Ogni operatore di Casimir è collegato ad un invariante (una
quantità conservata, ovvero un “integrale del moto”).
L. Fortunato
Realizzazione
L’algebra deve essere “realizzata” cioè si devono trovare
oggetti (i vari g) che soddisfano agli assiomi che la
definiscono:
- Matrici n×n che agiscono su vettori. L’operazione è il
prodotto matriciale
- Operatori differenziali che agiscono su funzioni differenziabili
f(x,…), ovvero xa e ∂/∂xb e loro combinazioni. L’operazione è il
commutatore: [∂/∂xb , xa]=δab
- Operatori di creazione e distruzione nel formalismo di
soconda quantizzazione, l’operazione è sempre il
commutatore: [b,b†]=δ
L. Fortunato
Spectrum Generating Algebra
When, in general, one can write a hamiltonian
H= E0 + Σ ckXk + Σ cklXk Xl +…
with
Xk ∈ G
as a polynomial in the elements of an algebra
then G is called spectrum generating algebra (SGA)
for H, because it is always possible to diagonalize
(numerically) H in the ONC basis labelled by all the
quantum numbers of a Complete Set of Commuting
Operators (CSCO) of any of the possible chains of
subalgebras of G ⊃ G’ ⊃ G’’ ⊃ …
L. Fortunato
Simmetria Dinamica
In some cases
H= E0 + Σ ckXk + Σ cklXk Xl +…
with
Xk ∈ G
we have only some terms that correspond to
invariant operators of the algebras in the chain:
G ⊃ G’ ⊃ G’’ ⊃ …
↓
↓
↓
C C’ C’’
chain of subalgebras
(one or more for each subalgebra)
H= E0 + aC + a’C’ +a’’C’’ +…
in these cases we speak of a dynamical symmetry
and we have
E= E0 + aÇC× + a’ ÇC’× +a’’ ÇC’’× +…
L. Fortunato
Processo non facile da digerire…
Do their commutators close?
[Xi,Xj]= ΣX k
Xi i=1,...,n
operators
Can you solve
the branching
problem?
Chain of
nested Lie
algebras
If yes
Lie Algebra
of some rank
(generators)
so(3) must be
contained as a
subalgebra
all classified
known properties:
- invariant op.
- matrix elements
Can H can be expressed
as a lin.comb. of Casimir
operators of the chain ?
Can H can be expressed
in terms of the generators?
If yes
The matrix elements of
the hamiltonain can be
calculated and then H
can be diagonalized
Spectrum generating algebra
If yes
⊃
H is already diagonal in
the O.N. basis defined
by the chain. Spectrum
can be read off directly
Dynamical Symmetry
L. Fortunato
Realizzazioni con operatori differenziali (esempio)
L =r × p
→
[Lx , Ly ] = iLz
Lx , Ly , Lz
sono i generatori di so(3)
+ permutazioni cicliche
C[so(3)] = L2= Lx2 + Ly2 + Lz2
È l’operatore quadratico di casimir (rank 1)
[C , Li ] = 0 , ∀ Li ∈ SO(3)
so(3) ⊃ so(2)
↓
↓
L
M
|
Branching problem
Branching rules:
-L ≤ M ≤ L
L. Fortunato
Rotore Rigido
One must specify the action of the generators on a
given orthonormal basis |LM×
L±|LM× = [(L{M)(L±M+1)]½|LM±1×
iLy
L± = Lx ±
Lz|LM× = M|LM×
L2|LM× = L(L+1)|LM×
Application in the rigid rotor:
H=k L²
→
E=k L(L+1)
with k=(h²/2I)
L. Fortunato
Esempi di rotore rigido quantistico
H2
HCl
EJ= B J(J+1)
ΔEJ= 2B(J+1)
L. Fortunato
Intensità /unità arbitrarie
Spettro a Microonde (Lontano IR )
CO
0
20
40
60
80
100
Numeri d’onda cm-1
EJ= B J(J+1)
ΔEJ= 2B(J+1) ∝ ν
L. Fortunato
Degenerazione Magnetica
M= +Jz
J2
M= -Jz
J1
O(3)
⊃
O(2)
States with a definite total angular momentum contain
a multiplet of substates with different third component:
these are called magnetic substates because can be
separated with a magnetic field (Zeeman effect)
Said another way, the magnetic interaction -μB
breaks the symmetry of the hamiltonian
L. Fortunato
Atomo di idrogeno
The states of the hamiltonian of the H atom are
clearly invariant with respect to SO(3), but…
L. Fortunato
Degenerazione addizionale
The spectrum shows a further degeneration in U.
Where does it come from ?
Degeneration ⇒ Conserved Quantity
Runge-Lenz vector:
[H,A]=0
⇒ there’s a larger symm.
group that contains both
L and A
so(4) ≈ so(3)⊕ so(3)
L. Fortunato
La simmetria unifica lo studio di una collezione di oggetti
L. Fortunato
Fisica Molecolare:
acetilene C2H2
L. Fortunato
Fisica delle Particelle:
Simm. di Sapore
Gell-mann and Ne’eman have suggested that the
internal degrees of freedom of hadrons can be
described by an SU(3) dynamical symmetry (flavour)
We have the GellmannOkubo mass formula
(Mass replaces energy in the
relativistic formalism)
I=Isospin
Y=Hypercharge=2(C-Iz)
From R.Bijker
L. Fortunato
Algebraic models…. give a scheme!
SU(3)…. explains observation!
Other important dynamical Symmetries
From R.Bijker
L. Fortunato
Il nucleo atomico: una fucina di simmetrie dinamiche !
Nel modello a goccia di liquido, le proprietà
del nucleo sono interpretate come se i
costituenti formassero una sfera di liquido
che può vibrare o ruotare collettivamente. Il
grado di libertà più importante è il
quadrupolo (L=2) che è collegato alle
deformazioni di tipo ellissoidale. E’ descritto
dall’hamiltoniana di Bohr. L’energia delle
vibrazioni e delle rotazioni è collegata agli
autostati di questa hamiltoniana.
L. Fortunato
Quadrupolo
Sferico
Arancia
Calcio
Oblato
Mandarino
Lancio del disco
Prolato
A
g
r
u
m
i
Limone
Rugby
S
p
o
r
t
L. Fortunato
Variabili di deformazione
β
γ
L. Fortunato
Il modello di Bohr-Mottelson ↔ U(6)
L. Fortunato
Simmetrie ↔ Fasi
L. Fortunato
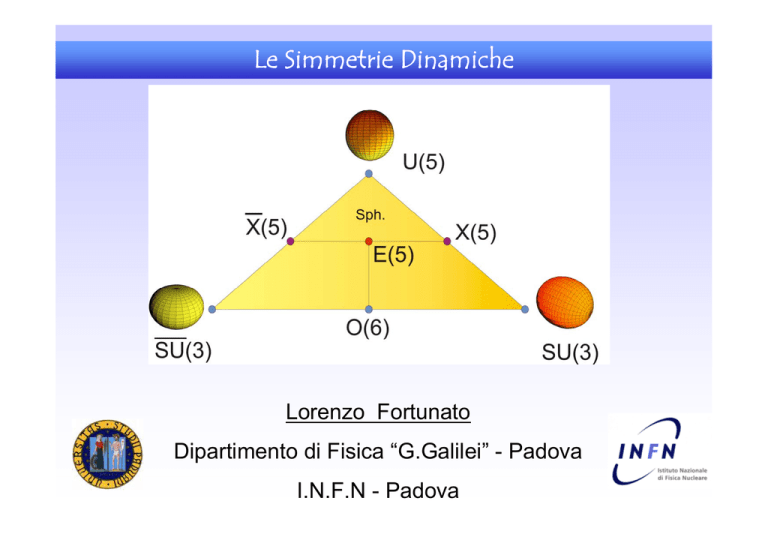
Transizioni di fase di forma – punti critici
In corrispondenza dei vertici del diagramma di fase e dei
punti critici si riscontrano delle simmetrie dinamiche che
portano a soluzioni esatte.
L. Fortunato
Le simmetrie dinamiche forniscono paradigmi…
…e permettono di fare predizioni su quantità misurabili.
L. Fortunato
Alcuni nostri risultati…
8
N=10
6
0
E(β)
4
2
-1
0
0
-2
-4
-2
-1
0
β
1
2
0.25
0.5
0.75
1
L. Fortunato
Per approfondire …
E’ necessario possedere elementi di base in meccanica quantistica e in
teoria dei gruppi, prima di affrontare i seguenti testi:
*** B.G. Wybourne, Classical Groups for Physics, Wiley, New York, 1974.
**** R. Gilmore, Lie Groups, Lie Algebras and some Their Applications,
Wiley, New York, 1974.
*** O.A.Barut and R.Raczka, Theory of Group Representations
* F. Iachello and R.D. Levine, Algebraic Theory of Molecules, Oxford
University Press, 1995.
** F. Iachello and A.Arima, The Interacting Boson Model , Cambridge
University Press, 1987.
* A.Frank and P.van Isacker, Symmetry Methods in Molecules and Nuclei.
* = difficoltà
L. Fortunato