tutti gli appelli

Prova scritta di Meccanica Analitica
Appello del 2 settembre 2016
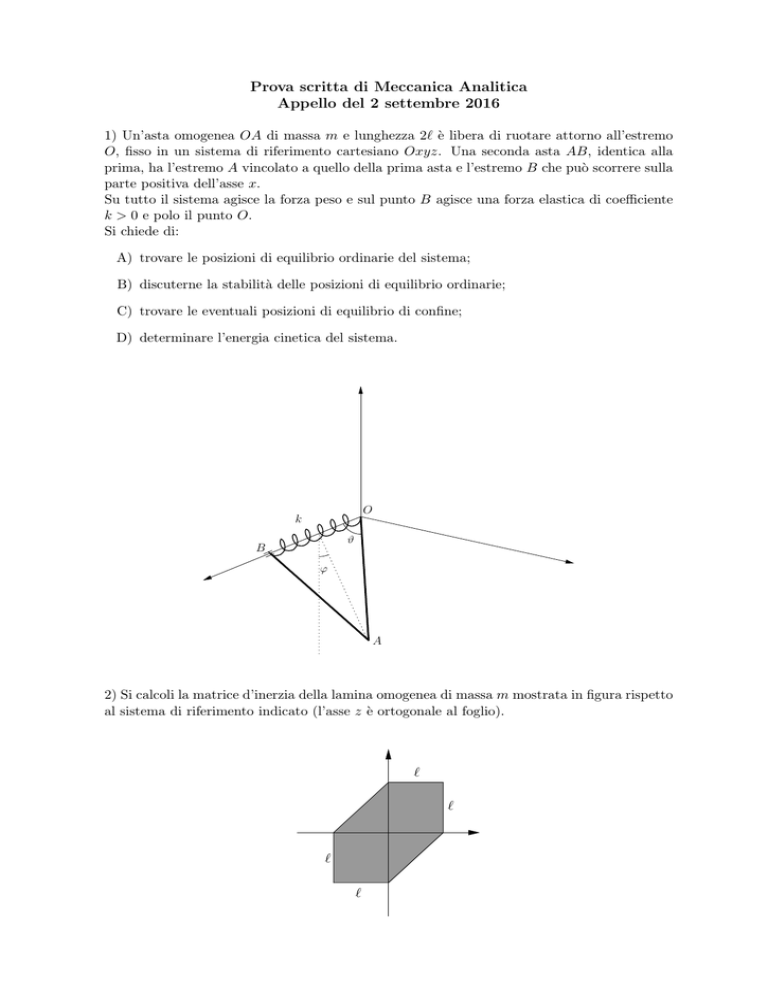
1) Un’asta omogenea OA di massa m e lunghezza 2` è libera di ruotare attorno all’estremo
O, fisso in un sistema di riferimento cartesiano Oxyz. Una seconda asta AB, identica alla
prima, ha l’estremo A vincolato a quello della prima asta e l’estremo B che può scorrere sulla
parte positiva dell’asse x.
Su tutto il sistema agisce la forza peso e sul punto B agisce una forza elastica di coefficiente
k > 0 e polo il punto O.
Si chiede di:
A) trovare le posizioni di equilibrio ordinarie del sistema;
B) discuterne la stabilità delle posizioni di equilibrio ordinarie;
C) trovare le eventuali posizioni di equilibrio di confine;
D) determinare l’energia cinetica del sistema.
O
k
ϑ
B
ϕ
A
2) Si calcoli la matrice d’inerzia della lamina omogenea di massa m mostrata in figura rispetto
al sistema di riferimento indicato (l’asse z è ortogonale al foglio).
ℓ
ℓ
ℓ
ℓ
Prova scritta di Meccanica Analitica
Appello del 15 luglio 2016
1) Una lamina quadrata omogenea ABCD di massa m e lato ` si muove in modo che il lato
AB scorra sull’asse x di un sistema di riferimento Oxyz. Sull’estremo D della lamina agisce
una forza elastica di coefficiente k > 0 e polo il punto E di coordinate (0, 0, `).
Il sistema è soggetto alla forza peso e tutti i vincoli sono lisci. Si chiede di:
1. trovare le posizioni di equilibrio del sistema;
2. discuterne la stabilità;
3. determinare la lagrangiana del sistema;
4. trovare le equazioni differenziali del moto linearizzate attorno a una posizione di equilibrio stabile.
z
E
O
A
k
B
x
y
ϑ
D
C
2) Si trovi la posizione del baricentro della lamina omogenea indicata in figura, formata da
due rettangoli di lati 2`, ` e una corona semicircolare di raggi 2`, `, nel sistema di riferimento
indicato.
2ℓ
ℓ
2ℓ
ℓ
3) Si trovi la matrice d’inerzia della lamina dell’esercizio 2) nel sistema di riferimento indicato.
Prova scritta di Meccanica Analitica
Appello del 24 giugno 2016
1) Un’asta omogenea AB di massa m e lunghezza 2` si muove in modo che l’estremo A
scorra sull’asse orizzontale e l’estremo B sull’asse verticale di un sistema di riferimento piano
verticale Oxy. Sull’asta AB scorre un punto materiale P di massa m.
Sul punto P agisce una forza elastica sempre verticale di coefficiente k > 0 e polo sull’asse
delle ascisse.
Il sistema è soggetto alla forza peso e tutti i vincoli sono lisci. Si chiede di:
1. trovare le posizioni di equilibrio del sistema e discuterne la stabilità;
2. trovare le posizioni di equilibrio di confine;
3. determinare la lagrangiana del sistema;
4. trovare le pulsazioni delle piccole oscillazioni attorno a una posizione di equilibrio stabile.
C
O
A
ϑ
k
ξ
P, m
B
2) Si calcoli la matrice d’inerzia del corpo rigido formato da un’asta omogenea di massa m
e lunghezza 2` e un punto materiale di massa m nel suo baricentro, rispetto al sistema di
riferimento indicato in figura.
y
x
m, 2ℓ
m
π/4
Prova scritta di Meccanica Analitica
Appello del 10 giugno 2016
1) Un corpo rigido è formato da un’asta omogenee OA di massa m e lunghezza 2` a cui è
saldata una lamina quadrata ABCD di massa m e lato `, come si vede in figura. Il corpo si
muove in modo che l’asta OA stia nel piano orizzontale xy di un sistema di riferimento Oxyz
e il punto O sia fisso nell’origine. La lamina quadrata si muove in modo da ruotare attorno
all’asta OA.
Sull’estremo D della lamina agisce una forza elastica di coefficiente k > 0 e polo il punto E
di coordinate (`, 0, 0).
Il sistema è soggetto alla forza peso e tutti i vincoli sono lisci. Si chiede di:
1. trovare le posizioni di equilibrio del sistema e discuterne la stabilità;
2. trovare la matrice d’inerzia del corpo rigido nel sistema indicato in figura;
3. determinare l’energia cinetica del sistema;
4. trovare le pulsazioni delle piccole oscillazioni attorno a una posizione di equilibrio stabile;
5. scrivere la quantità di moto del sistema in funzione dei parametri lagrangiani.
z
z
C
C
O
E
ϑ
k
B
D
ϕ
O
y
x
B
A
2) Determinare per quali valori di k 6= 0 la trasformazione
(
p
− kq
Q(q, p) = q 2 e
p
P (q, p) = e kq
è canonica e trovarne una funzione generatrice del tipo F (q, P ).
D
A
y′
Prova scritta di Meccanica Analitica
Appello del 12 febbraio 2016
1) Un corpo rigido è formato da due aste omogenee AB e BC di massa m e lunghezza `
saldate ad angolo retto nell’estremo comune B. Tale corpo è libero di ruotare attorno al
punto B, che si muove sull’asse verticale di un sistema di riferimento piano Oxy.
Su tutto il sistema agisce la forza peso e sui punti A e C agiscono due forze elastiche sempre
verticali di coefficiente k > 0 e poli sull’asse delle x.
Si chiede di:
A) trovare le posizioni di equilibrio del sistema;
B) discuterne la stabilità delle posizioni di equilibrio;
C) determinare le equazioni differenziali del moto;
D) scrivere le equazioni del moto linearizzate attorno a una posizione di equilibrio stabile.
y
x
O
k
B
m, ℓ
k
C
A m, ℓ
2) Si calcoli la matrice d’inerzia di un corpo rigido formato da due aste omogenee AO e OB di
massa m e lunghezza ` saldate ad angolo retto nel punto O, disposte a 45◦ rispetto al sistema
di riferimento indicato in figura (l’asse z è ortogonale al foglio).
y
B
A
m, ℓ
m, ℓ
x
O
Prova scritta di Meccanica Analitica
Appello del 26 gennaio 2016
1) Un corpo rigido è formato da due
√ aste AD e BC di massa m e lunghezza ` e due aste AB
e CD di massa m e lunghezza ` 2, disposte in un poligono intrecciato come in figura. Si
calcoli la matrice d’inerzia del corpo rigido rispetto al sistema di riferimento indicato (l’asse
z è ortogonale al foglio).
y
D
A
x
C
B
2) Il corpo rigido dell’esercizio precedente è vincolato a mantenere il punto medio dell’asta
AD nell’origine di un sistema di riferimento piano Oxy ed è libero di ruotare attorno ad esso.
Sull’asta BC scorre senza attrito un punto materiale P di massa m.
Il sistema giace in un piano orizzontale e sul punto P agisce una forza elastica di coefficiente
k > 0 e polo sull’asse x, che si mantiene sempre parallela all’asse y.
Si chiede di:
A) trovare le posizioni di equilibrio ordinarie del sistema;
B) trovare le posizioni di confine;
C) discutere la stabilità delle posizioni di equilibrio ordinarie;
D) determinare la lagrangiana del sistema.
y
A
O
x
D
k
C
P, m
B
[Nota: non c’è bisogno di dirvi che “piano orizzontale” significa assenza di forza peso]
Prova scritta di Meccanica Analitica
Appello del 29 settembre 2015
1) Un disco omogeneo di massa m e raggio R rotola senza strisciare sull’asse orizzontale di un
sistema di riferimento piano Oxy. Sul bordo del disco scorre senza attrito un punto materiale
P di massa m.
Su tutto il sistema agisce la forza peso e sul punto P agisce una forza elastica di coefficiente
k > 0 e polo il punto O.
Si chiede di:
1. trovare le posizioni di equilibrio del sistema;
2. discuterne la stabilità delle posizioni di equilibrio;
3. determinare le equazioni differenziali del moto;
4. scrivere le equazioni del moto linearizzate attorno a una posizione di equilibrio stabile.
y
m, R
P, m
k
x
O
2) Data la trasformazione

 Q(q, p) = k e2q
p

P (q, p) = p2 e−2q
determinare per quali k > 0 è canonica e trovarne una funzione generatrice del tipo F (q, P ).
Prova scritta di Meccanica Analitica
Appello dell’11 settembre 2015
1) Un’asta omogenea OA di massa m e lunghezza 2` è libera di ruotare attorno all’origine di un
sistema di riferimento piano Oxy. Un disco omogeneo di massa m e raggio R rotola senza strisciare
sull’asta, in modo che il punto di contatto B non esca dall’asta.
Si denoti con ξ la distanza del punto B dall’origine e con θ l’angolo tra la parte positiva dell’asse
delle ascisse e l’asta.
Su tutto il sistema agisce la forza peso e sul centro C del disco agisce una forza elastica di
coefficiente k > 0 e polo il punto O. Inoltre, sull’estremo A dell’asta agisce una forza F A di
potenziale UA = mgR cos θ.
Supposti i vincoli lisci, si chiede di:
1. trovare le posizioni di equilibrio ordinarie del sistema e discuterne la stabilità in funzione di
k`
λ = mg
;
2. trovare le eventuali posizioni di equilibrio di confine;
3. determinare l’energia cinetica del sistema;
4. nel caso λ = 1 trovare le pulsazioni delle piccole oscillazioni attorno alla posizione di equilibrio
stabile.
y
m, R
C
m, 2ℓ
B
A
FA
x
O
2) Si calcoli la matrice d’inerzia del corpo rigido piano in figura, formato da un’asta omogenea
di massa m e lunghezza 4` e un disco di massa m e raggio `, in cui un punto del bordo del disco è
saldato al baricentro dell’asta, rispetto al sistema di riferimento indicato.
y
m, ℓ
x
m, 4ℓ
Prova scritta di Meccanica Analitica
Appello del 10 luglio 2015
1) Un corpo rigido è formato da due aste omogenee AB e BC, entrambe di massa m e lunghezza
2`, saldate ad angolo retto nell’estremo B. Tale corpo si muove in un piano ruotando attorno al suo
estremo A, che può scorrere sull’asse orizzontale di un riferimento cartesiano ortogonale Oxy.
Su tutto il sistema agisce la forza peso e su A agisce una forza elastica di coefficiente k > 0 e
polo l’origine O. Supposti i vincoli lisci, si chiede di:
1. trovare le posizioni di equilibrio del sistema e discuterne la stabilità;
2. determinare l’energia cinetica del sistema;
3. scrivere le pulsazioni delle piccole oscillazioni attorno a una posizione di equilibrio stabile.
y
A
O
x
k
m, 2ℓ
C
m, 2ℓ
B
2) Si calcoli la matrice d’inerzia dela lamina piana omogenea di massa m rappresentata in figura
rispetto a un opportuno sistema di riferimento centrato in A, sapendo che AB = AF = 2` e
BC = CD = DE = EF = `.
Si calcoli poi il momento d’inerzia della lamina rispetto all’asse r tratteggiato in figura.
r
F
E
D
C
A
B
Prova scritta di Meccanica Analitica
Appello del 26 giugno 2015
1) Un corpo rigido è formato da due aste omogenee OA e AB, entrambe di massa m e
lunghezza 2`, saldate ad angolo retto nell’estremo A. Il corpo si muove in modo che l’asta
OA stia nel piano orizzontale xy di un sistema di riferimento Oxyz e il punto O sia fisso
nell’origine.
Sull’estremo A dell’asta agisce una forza elastica di coefficiente k > 0 e polo il punto C di
coordinate (2`, 0, 0).
Il sistema è soggetto alla forza peso e tutti i vincoli sono lisci. Si chiede di:
1. trovare le posizioni di equilibrio del sistema e discuterne la stabilità;
2. determinare l’energia cinetica del sistema;
3. trovare le equazioni del moto linearizzate attorno a una posizione di equilibrio stabile.
B
O
ϑ
ϕ
C
k
A
2) Determinare per quali valori di a, b ∈ R la trasformazione

 Q(q, p) = aeq + bp2 e−q
p
 P (q, p) = arctan
eq
è canonica e trovarne una funzione generatrice del tipo F (q, P ).
Prova scritta di Meccanica Analitica
Appello del 5 giugno 2015
1) In un sistema piano, un’asta omogenea OA di massa m e lunghezza 2` è libera di ruotare
attorno al suo estremo fisso O, centrato in un riferimento cartesiano ortogonale Oxy. Sull’asta OA
scorre il centro G di una seconda asta BC uguale alla prima e che resta sempre ortogonale a OA,
come in figura.
Su tutto il sistema agisce la forza peso e su G agisce una forza elastica di coefficiente k > 0 e
polo l’origine. Supposti i vincoli lisci, si chiede di:
1. trovare le posizioni di equilibrio ordinarie del sistema e discuterne la stabilità in funzione di
λ = mg/k`;
2. trovare le eventuali posizioni di equilibrio di confine;
3. determinare l’energia cinetica del sistema;
4. nel caso λ = 1, trovare le pulsazioni delle piccole oscillazioni attorno alla posizione di equilibrio
stabile.
y
O
x
k
m, 2ℓ
C
m, 2ℓ
B
A
2) Si calcoli la matrice d’inerzia del corpo rigido formato da due aste omogenee di massa m e
lunghezza ` saldate ad angolo retto in un loro estremo, rispetto al sistema di riferimento indicato in
figura.
A
O
B
Prova scritta di Meccanica Analitica
Appello del 13 febbraio 2015
1) Un’asta omogenea OA di massa m e lunghezza 2` è libera di ruotare attorno al suo estremo
fisso O, centrato in un riferimento cartesiano ortogonale Oxy. All’estremo A dell’asta è agganciato il
vertice di una lamina quadrata omogenea di massa m e lato 2`, che può ruotare liberamente attorno
a A. Su tutto il sistema agisce la forza peso e sul vertice C della lamina agisce una forza elastica
sempre verticale di coefficiente k > 0 e polo sull’asse x. Supposti i vincoli lisci, si chiede di:
1. trovare le posizioni di equilibrio ordinarie del sistema;
2. discuterne la stabilità;
3. determinare l’energia cinetica del sistema;
4. nel caso mg = 10k`, scrivere la lagrangiana approssimata attorno ad una posizione di equilibrio
stabile.
y
O
x
ϕ
m, 2ℓ
k
A
ϑ
B
m, 2ℓ
D
C
2) Una lamina piana è formata da due semicerchi omogenei di raggio R e massa m tangenti in
O e da un triangolo isoscele omogeneo di altezza 3R e massa 2m disposto come in figura. Si calcoli
la matrice d’inerzia della lamina rispetto a un opportuno sistema di riferimento centrato in O.
O
Prova scritta di Meccanica Analitica
Appello del 23 gennaio 2015
1) Una lamina quadrata omogenea di massa m e lato ` è libera di ruotare attorno al suo vertice
fisso O, in modo da non occupare mai il semipiano y > 0 di un riferimento cartesiano ortogonale
Oxy. Al vertice B della lamina opposto ad O è agganciato l’estremo di un’asta omogenea BD di
massa m e lunghezza `, che può ruotare liberamente attorno a B.
Su tutto il sistema agisce la forza peso e sul vertice B agisce una forza elastica sempre verticale
di coefficiente k > 0 e polo sull’asse x. Supposti i vincoli lisci, si chiede di:
1. trovare le posizioni di equilibrio ordinarie del sistema;
2. discuterne la stabilità;
3. trovare le eventuali posizioni di confine;
111111111111111
000000000000000
000000000000000
111111111111111
000000000000000
111111111111111
000000000000000
111111111111111
000000000000000
111111111111111
000000000000000
111111111111111
4. determinare l’energia cinetica del sistema.
O
x
k
ϑ
A
m, ℓ
C
B
m, ℓ
ϕ
D
2) In una lamina quadrata omogenea di lato ` è praticato un foro quadrato concentrico, di lato
`/2, ruotato di 45◦ rispetto alla lamina. Sapendo che la massa della parte rimanente vale m, se ne
calcoli la matrice d’inerzia rispetto al sistema di riferimento indicato.
Prova scritta di Meccanica Analitica
Appello del 25 settembre 2014
1) Sia dato un sistema di riferimento cartesiano ortogonale Oxy in un piano verticale. Una
lamina quadrata omogenea di massa m e lato ` è libera di ruotare attorno al suo vertice A, che
scorre sull’asse verticale.
Sulla lamina agisce la forza peso e sul vertice C opposto ad A agisce una forza elastica sempre
verticale di coefficiente k > 0 e polo sull’asse x.
Supposti i vincoli lisci, si chiede di:
1. trovare le posizioni di equilibrio del sistema;
2. discuterne la stabilità;
3. determinare l’energia cinetica del sistema;
4. trovare le pulsazioni delle piccole oscillazioni attorno a una posizione di equilibrio stabile.
y
E
x
k
m, ℓ
B
A
C
D
2) Una lamina piana omogenea di massa m è formata da due quadrati di lato `/2 opposti al
vertice. Se ne calcoli la matrice d’inerzia nel sistema di riferimento indicato in figura.
y
x
z
Prova scritta di Meccanica Analitica
Appello del 9 settembre 2014
1) Sia dato un sistema di riferimento cartesiano ortogonale Oxy in un piano verticale. Una
lamina omogenea è formata da due dischi di massa m e raggio R saldati in un loro punto sul bordo.
La lamina è libera di ruotare attorno al centro A del primo disco, che scorre sull’asse verticale.
Sulla lamina agisce la forza peso e sul centro B del secondo disco una forza elastica di coefficiente
k > 0 e polo il punto C(2R; 0).
Supposti i vincoli lisci, si chiede di:
1. trovare le posizioni di equilibrio del sistema;
2. discuterne la stabilità;
3. determinare l’energia cinetica del sistema;
4. scrivere la lagrangiana approssimata attorno alla posizione di equilibrio stabile.
y
C
x
k
A
m, R
B
m, R
2) Una lamina piana omogenea di massa m è formata da due quarti di un disco di raggio R
opposti al vertice. Se ne calcoli la matrice d’inerzia nel sistema di riferimento indicato in figura.
y
x
z
Prova scritta di Meccanica Analitica
Appello del 18 luglio 2014
1) Sia dato un sistema di riferimento cartesiano ortogonale Oxy in un piano verticale. Nel
semipiano {x ≥ 0}, una lamina quadrata omogenea ABCD di massa m e lato ` è libera di ruotare
attorno al suo vertice D. Tale vertice può scorrere sull’asse verticale x = 0.
Sulla lamina agisce la forza peso. Inoltre, sul vertice A della lamina agisce una forza elastica di
coefficiente k > 0 e polo l’origine.
Supposti i vincoli lisci, si chiede di:
1. trovare le posizioni di equilibrio del sistema e discuterne la stabilità;
2. discutere l’esistenza di posizioni di equilibrio di confine;
3. determinare la lagrangiana del sistema;
4. scrivere la lagrangiana approssimata attorno alla posizione di equilibrio stabile.
11111
00000
00000
11111
00000
11111
00000
11111
00000
11111
00000
11111
00000
11111
00000
11111
00000
11111
00000
11111
00000
11111
00000
11111
00000
11111
00000
11111
00000
11111
00000
11111
00000
11111
00000
11111
00000
11111
00000
11111
00000
11111
00000
11111
00000
11111
00000
11111
00000
11111
00000
11111
D
00000
11111
00000
11111
00000
11111
00000
11111
00000
11111
00000
11111
00000
11111
00000
11111
00000
11111
00000
11111
k
A
B
m, ℓ
C
2) Data una lamina omogenea a forma di triangolo rettangolo ABC di cateti AB = c, AC = b e
massa m, se ne trovi il momento d’inerzia rispetto all’asse perpendicolare alla lamina passante per
C.
Si applichi tale risultato per trovare il momento d’inerzia di una lamina omogenea a forma di
triangolo equilatero di lato ` e massa m, rispetto ad un asse perpendicolare alla lamina passante per
un suo vertice.
Prova scritta di Meccanica Analitica
Appello del 26 giugno 2014
1) Un corpo rigido è formato da una
√ circonferenza materiale di massa m e raggio R a cui è saldata
un’asta AB di massa m e lunghezza 3R, in modo che gli estremi A e B stiano sulla circonferenza.
Tale corpo rigido si muove in modo che l’asta AB scorra sull’asse y di un sistema di riferimento
cartesiano ortogonale Oxyz, e il corpo sia libero di ruotare attorno a tale asse. Inoltre sull’estremo
A dell’asta agisce una forza elastica di coefficiente k > 0 e polo l’origine.
Tutto il sistema è soggetto alla forza di gravità. Supposti i vincoli lisci, si chiede di:
1. trovare le posizioni di equilibrio ordinarie del sistema e discuterne la stabilità;
2. determinare la lagrangiana del sistema;
3. scrivere la lagrangiana approssimata e trovare le pulsazioni delle piccole oscillazioni attorno
alla posizione di equilibrio stabile.
z
m,
O
k
√
3R
A
B
y
θ
x
m, R
2) La lamina omogenea di massa m in figura è formata da un semidisco di raggio R cui è stato
tolto un semidisco di raggio R/2 e aggiunto un altro semidisco di raggio R/2. Se ne calcoli la matrice
d’inerzia rispetto al sistema di riferimento indicato.
y
x
R
z
Prova scritta di Meccanica Analitica
Appello del 6 giugno 2014
1) Un lamina quadrata omogenea ABCD di lato ` e massa m è libera di ruotare attorno al suo
lato AB, che è fissato sull’asse y di un sistema di riferimento cartesiano ortogonale Oxyz in modo
che A disti ` dall’origine.
Sul lato AD della lamina scorre un punto P di massa m, su cui agisce una forza elastica di
coefficiente k > 0 e polo l’origine.
Tutto il sistema è soggetto alla forza di gravità. Supposti i vincoli lisci, si chiede di:
1. trovare le posizioni di equilibrio ordinarie del sistema e discuterne la stabilità;
2. discutere l’esistenza di posizioni di equilibrio di confine;
3. determinare la lagrangiana del sistema;
4. scrivere le pulsazioni delle piccole oscillazioni attorno alla posizione di equilibrio stabile.
z
O
ℓ
A
B
k
x
y
P, m
m, ℓ
D
C
2) Ricordando che il momento d’inerzia di una lamina a forma di triangolo rettangolo omogenea
di cateti a, b e massa m rispetto a un asse passante per il cateto a vale 61 mb2 , si calcoli il momento
d’inerzia della lamina omogenea di massa m in figura rispetto all’asse indicato.
a
b
Prova scritta di Meccanica Analitica
Appello del 7 febbraio 2014
1) Un corpo rigido piano è formato da un disco omogeneo di massa m e raggio R a cui è sovrapposta
una circonferenza materiale omogenea concentrica di massa m e raggio R. Tale corpo si muove in
modo che il punto A della circonferenza scorra sull’asse y di un sistema di riferimento cartesiano
ortogonale Oxyz. Inoltre il corpo può ruotare attorno all’asse y.
Tutto il sistema è soggetto alla forza di gravità e sul punto B del diametro AB agisce una forza
elastica di polo l’origine e coefficiente k > 0. Supposti i vincoli lisci, si chiede di:
1. trovare le posizioni di equilibrio del sistema e discuterne la stabilità;
2. determinare la lagrangiana del sistema;
3. scrivere le pulsazioni delle piccole oscillazioni attorno alla posizione di equilibrio stabile.
O
A
k
B
2) Data la trasformazione

pp
Q =
1 − kq 2
q
p

P = k 1 − kq 2
si trovino i valori di k ∈ R per cui essa è canonica. Nei casi affermativi si trovi poi una funzione
generatrice del tipo F (q, Q).
Prova scritta di Meccanica Analitica
Appello del 24 gennaio 2014
1) Un corpo rigido è formato da tre aste omogenee OA, AB, BC, ognuna di lunghezza 4` e massa
m, saldate a i tre lati di un quadrato. Il corpo è libero di ruotare in un piano verticale e il punto
O è fisso nell’origine di un sistema di riferimento cartesiano ortogonale. Sull’asta AB scorre poi un
punto P , anch’esso di di massa m.
Tutto il sistema è soggetto alla forza di gravità e sul punto P agisce una forza elastica verticale
con polo sull’asse orizzontale e coefficiente k > 0. Considerando tutti i vincoli lisci, si chiede di:
1. trovare le posizioni di equilibrio ordinarie del sistema e discuterne la stabilità;
2. trovare le eventuali posizioni di equilibrio di confine del sistema;
3. scrivere la lagrangiana del sistema.
O
A
k
C
P, m
B
2) Con riferimento al corpo rigido dell’esercizio precedente (senza il punto P ), se ne trovi la matrice
d’inerzia in un sistema di riferimento baricentrale opportuno.
Prova scritta di Meccanica Analitica
Appello del 19 settembre 2013
1) Una semicirconferenza materiale ACB di diametro AB = 2R e massa m si muove in modo
che il diametro AB scorra sull’asse y di un sistema di riferimento cartesiano ortogonale Oxyz e la
semicirconferenza possa anche ruotare attorno a tale asse.
Tutto il sistema è soggetto alla forza di gravità; inoltre, sul punto C della semicirconferenza più
lontano dall’asse y agisce una forza elastica di polo l’origine e coefficiente k > 0. Supposti i vincoli
lisci, si chiede di:
1. trovare le posizioni di equilibrio del sistema e discuterne la stabilità;
2. determinare la lagrangiana del sistema;
3. scrivere le pulsazioni delle piccole oscillazioni attorno alla posizione di equilibrio stabile.
[Si ricorda che il baricentro di una semicirconferenza di raggio R giace a distanza
O
2R
dal diametro.]
π
A
k
B
C
2) Si calcoli la matrice d’inerzia della figura precedente in un sistema di riferimento opportuno
centrato nel punto A.
Prova scritta di Meccanica Analitica
Appello del 5 settembre 2013
1) In un sistema di riferimento cartesiano ortogonale Oxyz si muovono due aste, OA e AB, entrambe
di massa m e lunghezza 2`. L’estremo O della prima asta è vincolato a stare nell’origine, e le due
aste sono vincolate ad avere l’estremo A in comune. Infine, l’estremo B della seconda asta è libero
di scorrere in modo liscio sulla parte positiva dell’asse y.
Tutto il sistema è soggetto alla forza di gravità; inoltre, sul punto A agisce una forza elastica di
coefficiente k > 0 che ha polo sull’asse y e resta sempre perpendicolare a tale asse.
Si chiede di:
1. trovare le posizioni di equilibrio ordinarie del sistema in funzione del parametro λ =
mg
k` ;
2. trovare le eventuali posizioni di equilibrio di confine;
3. discutere la stabilità delle posizioni di equilibrio ordinarie in funzione di λ;
4. determinare la lagrangiana del sistema.
z
O
B
ϑ
y
ϕ
x
A
2) Si calcoli la matrice d’inerzia del corpo rigido OABC, formato da tre aste OA, OB, BC, tutte di
massa m e lunghezza 2`, rispetto al sistema di riferimento indicato in figura.
[Si faccia attenzione alla possibile presenza di prodotti d’inerzia!]
B
O
C
A
Prova scritta di Meccanica Analitica
Appello del 18 luglio 2013
1) Un corpo rigido è formato da tre aste omogenee AB, BC, CD, ognuna di lunghezza 2` e massa
m, saldate a i tre lati di un quadrato.
Il corpo è libero di ruotare in un piano verticale e il punto A scorre sull’asse x di un sistema di
riferimento cartesiano ortogonale. Inoltre il corpo deve sempre stare nel semipiano delle ordinate
negative.
Tutto il sistema è soggetto alla forza di gravità e sul punto A agisce una forza elastica di polo
l’origine e coefficiente k > 0. Considerando tutti i vincoli lisci, si chiede di:
1. trovare le posizioni di equilibrio ordinarie del sistema e discuterne la stabilità;
2. trovare le eventuali posizioni di equilibrio di confine del sistema;
3. scrivere la lagrangiana del sistema;
4. scrivere le equazioni differenziali del moto linearizzate attorno alla posizione di equilibrio
stabile.
y
O
k
A
θ
x
B
D
C
2) Con riferimento al corpo rigido dell’esercizio precedente, se ne trovi la matrice d’inerzia in un
sistema di riferimento solidale opportuno centrato in A.
Prova scritta di Meccanica Analitica
Appello del 27 giugno 2013
1) Un corpo rigido è formato da quattro aste omogenee AB, BC, CD, DA, ognuna di lunghezza ` e massa m, saldate a formare il perimetro di un quadrato. Al vertice C è saldato un
punto materiale P di massa m.
Il corpo si muove in un piano verticale in modo che il punto A possa scorrere sull’asse
x di un sistema di riferimento cartesiano ortogonale. Inoltre il corpo deve sempre stare nel
semipiano delle ordinate negative.
Tutto il sistema è soggetto alla forza di gravità e sul punto P agisce una forza elastica di
polo l’origine e coefficiente k > 0. Si chiede di:
1. trovare le posizioni di equilibrio ordinarie del sistema in funzione del parametro λ =
mg
k` ;
2. discutere la stabilità delle posizioni di equilibrio ordinarie al variare di λ;
3. trovare le eventuali posizioni di equilibrio di confine;
4. scrivere la lagrangiana del sistema.
y
ξ
O
A
x
θ
B
D
C≡P
2) Con riferimento al corpo rigido dell’esercizio precedente, se ne trovi la matrice d’inerzia in
un sistema di riferimento solidale opportuno centrato in A.
Prova scritta di Meccanica Analitica
Appello del 14 giugno 2013
1) Un corpo rigido è formato da un’asta AB di lunghezza 2` e massa m a cui è saldato un semidisco
di massa m e raggio `, in modo che gli estremi del diametro del semidisco coincidano col punto medio
e con l’estremo B dell’asta.
Tale corpo rigido si muove in un piano verticale e l’estremo A è vincolato a scorrere sull’asse
orizzontale di un sistema di riferimento Oxy. Inoltre il punto B deve sempre stare nel semipiano
delle ordinate negative: denotando con ϑ l’angolo antiorario formato dalla parte negativa dell’asse
verticale con l’asta AB, si deve quindi avere ϑ ∈ [− π2 , π2 ].
Sul punto A agisce una forza elastica di coefficiente k > 0 e polo l’origine. Inoltre sul corpo
rigido agisce un momento M = k`2 sin ϑ e3 .
Sapendo che tutto il sistema è soggetto alla forza di gravità e che i vincoli sono lisci, si chiede di:
1. trovare le posizioni di equilibrio ordinarie e di confine del sistema in funzione del parametro
k`
λ = mg
;
2. discutere la stabilità delle posizioni di equilibrio ordinarie al variare di λ;
3. scrivere la lagrangiana del sistema;
4. nel caso λ =
1
2
scrivere la lagrangiana approssimata attorno alla posizione di equilibrio stabile.
O
k
A
M = kℓ2 sin ϑ e3
ϑ
m, 2ℓ
M
m, ℓ
B
2) Con riferimento al corpo rigido dell’esercizio precedente, se ne trovi la matrice d’inerzia in un
sistema di riferimento solidale opportuno centrato in A.
Prova scritta di Meccanica Analitica
Appello dell’8 febbraio 2013
1) In un piano verticale un’asta omogenea AB di massa m e lunghezza 2` ha l’estremo A vincolato
a scorrere attorno a una guida circolare di centro l’origine e raggio `, e può ruotare liberamente
attorno a tale estremo. All’estremo B dell’asta è saldato un punto materiale di massa m, su cui
agisce una forza elastica di coefficiente k ≥ 0 e polo il punto E della guida circolare di coordinate
(0, `).
Sapendo che tutto il sistema è soggetto alla forza di gravità e che i vincoli sono lisci, si chiede di:
1. trovare il potenziale del sistema;
2. determinare la lagrangiana del sistema;
3. trovare le posizioni di equilibrio del sistema nel caso k = 0;
4. sempre nel caso k = 0, scrivere le equazioni differenziali del moto linearizzate attorno alla
posizione di equilibrio stabile.
E
O
A
k
m, 2ℓ
B, m
2) Data la lagrangiana
L(q, q̇) = log(1 + q 2 )q̇ 2 − q 2 q̇
determinarne l’hamiltoniana associata e le equazioni differenziali di Hamilton.
Prova scritta di Meccanica Analitica
Appello del 25 gennaio 2013
1) In un sistema piano, un’asta omogenea AC di massa m e lunghezza 2` può ruotare attorno al
suo baricentro collocato al centro di un sistema di riferimento Oxy. All’estremo C è vincolato il
centro di un disco di massa m e raggio `/2 e tale disco può ruotare attorno al suo centro. Sul bordo
del disco è saldato un punto materiale P di massa m, su cui agisce una forza elastica di coefficiente
k > 0 e polo il punto B(`, 0). Sapendo che tutto il sistema è soggetto alla forza di gravità e che tutti
i vincoli sono lisci, si chiede di:
1. trovare il potenziale e la lagrangiana del sistema;
2. scrivere le equazioni differenziali del moto linearizzate attorno a una generica posizione di
equilibrio;
3. se il disco viene saldato all’asta, in modo che il punto P si trovi sul prolungamento dell’asta
oltre C, si trovino le posizioni di equilibrio del corpo rigido e se ne discuta la stabilità.
A
m, 2ℓ
B
O
k
C
P
m, ℓ/2
2) Si trovi la matrice d’inerzia dell’asta omogenea di massa m e lunghezza ` nel sistema di riferimento
indicato nella prima figura.
Si usi poi tale risultato per calcolare la matrice d’inerzia di un corpo rigido formato da tre aste,
ognuna di massa m e lunghezza `, disposte a triangolo equilatero secondo il sistema di riferimento
indicato nella seconda figura.
α
Prova scritta di Meccanica Analitica
Appello del 7 settembre 2012
1) In un piano verticale, un corpo rigido è formato da un’asta EC
√ di massa m e lunghezza 2` cui è
vincolata la diagonale di una lamina quadrata ABCD, di lato `/ 2 e massa m, come in figura.
Il corpo rigido ha l’estremo E che può scorrere sull’asse x e ruota attorno a tale punto.
Su C agisce una forza elastica di coefficiente k > 0 e polo l’origine O di un sistema di riferimento
cartesiano ortogonale Oxy.
Sapendo che il sistema è soggetto alla forza peso e che i vincoli sono lisci, si chiede di determinare:
1. le posizioni di equilibrio;
2. la stabilità di tali posizioni;
3. la lagrangiana del sistema;
4. la lagrangiana approssimata attorno a una posizione di equilibrio stabile.
E
O
m, 2ℓ
k
A
D
ℓ
m, √
2
B
C
2) Determinare per quali valori di k ∈ R la seguente trasformazione è canonica:

p

Q = 2 − kq
kq

P = −q 3 .
Nei casi affermativi, trovarne una funzione generatrice del tipo F (q, Q).
Trovare infine come si trasforma l’hamiltoniana H(q, p) = p2 + q 2 .
Prova scritta di Meccanica Analitica
Appello del 13 luglio 2012
1) Un corpo rigido piano è formato da due aste AB e BC di massa m e lunghezza ` saldate perpendicolarmente nel punto B. Il corpo rigido si può muovere in un piano dotato di un sistema di
riferimento Oxy, in modo che l’estremo A sia vincolato in modo liscio all’asse orizzontale.
Si denoti con ξ l’ascissa di A e con θ l’angolo formato dalla verticale discendente con l’asta AB.
Le forze agenti sul corpo rigido sono:
• la forza peso;
• una forza elastica di polo l’origine e coefficiente k > 0 agente sul punto A;
• un momento M = k`2 cos θez (ricordiamo che il potenziale di un momento M = f (θ)ez è una
primitiva di f ).
Si chiede di:
1. trovare le posizioni di equilibrio del sistema;
2. discuterne la stabilità al variare del parametro λ =
k`
mg ;
3. determinare la lagrangiana del sistema;
4. scrivere le equazioni del moto linearizzate attorno a una posizione di equilibrio stabile.
k
M
A
ξ
m, ℓ
m, ℓ
ϑ
C
B
2) Data la lagrangiana
L(q1 , q2 , q̇1 , q̇2 ) =
q̇12
q̇ 2
+ 2 − q̇1 − q̇2
2q2 2q1
se ne trovi l’hamiltoniana associata. Si scrivano poi le equazioni di Hamilton relative all’hamiltoniana
trovata.
Prova scritta di Meccanica Analitica
Appello del 22 giugno 2012
1) Un corpo rigido piano è formato da una semicirconferenza materiale ABC di diametro AC = 2R
e massa m a cui è saldata, a partire dal centro D e perpendicolarmente al diametro, un’asta DB di
massa m e lunghezza R (si veda la figura). Il corpo rigido si muove in modo che il punto B scorra
sull’asse y di un sistema di riferimento cartesiano ortogonale Oxyz e l’asta resti sempre ortogonale
all’asse y (il corpo può anche ruotare attorno a tale asse).
Tutto il sistema è soggetto alla forza di gravità; inoltre, sul punto A agisce una forza elastica di polo
l’origine e coefficiente k > 0. Supposti i vincoli lisci, si chiede di:
1. trovare le posizioni di equilibrio del sistema e discuterne la stabilità;
2. determinare la lagrangiana del sistema;
3. scrivere le pulsazioni delle piccole oscillazioni attorno a una posizione di equilibrio stabile;
4. determinare eventuali integrali primi del sistema.
O
B
k
A
D
2) Data la trasformazione

 Q = − arctan p
q

2
2
P = k(q + p )
se ne trovino i valori di k ∈ R per cui è canonica.
Nei casi affermativi si trovi poi una funzione generatrice del tipo F (q, Q).
C
Prova scritta di Meccanica Analitica
Appello del 13 aprile 2012
1) In un sistema di riferimento cartesiano ortogonale Oxyz, una lamina quadrata omogenea OABC
di lato ℓ e massa m si muove in modo che il suo vertice O sia fisso nell’origine e il lato OA resti
sempre nel piano orizzontale xy.
Tutto il sistema è soggetto alla forza di gravità; inoltre, sul vertice A agisce una forza elastica di
polo il punto E(ℓ, 0, 0) e coefficiente k > 0. Si chiede di:
1. trovare le posizioni di equilibrio del sistema e discuterne la stabilità;
2. determinare la lagrangiana del sistema;
3. scrivere le pulsazioni delle piccole oscillazioni attorno alla posizione di equilibrio stabile;
4. determinare eventuali integrali primi del sistema.
C
#
B
O
'
E
k
A
2) Si calcoli la matrice d’inerzia di un’asta omogenea di massa m e lunghezza 2ℓ nei due sistemi di
riferimento baricentrali indicati in figura (l’asse z è ortogonale al foglio). Le due matrici d’inerzia
sono uguali?
y
y
x
x
Prova scritta di Meccanica Analitica
Appello del 30 marzo 2012
1) Un corpo rigido è formato da tre aste omogenee e mutuamente perpendicolari AB, M N , CD,
tutte di lunghezza 2ℓ e massa m, in modo che M sia saldato nel punto medio di AB e N nel punto
medio di CD.
Tale corpo rigido è vincolato ad avere l’asta AB che scorre su una guida verticale e può liberamente
ruotare attorno a tale asta.
Tutto il sistema è soggetto alla forza di gravità; inoltre, sul punto N agisce una forza elastica di polo
il punto E(0, 2ℓ, 0) e coefficiente k > 0. Si chiede di:
1. calcolare la matrice d’inerzia baricentrale del corpo rigido in un sistema di riferimento opportuno;
2. trovare le posizioni di equilibrio del sistema e discuterne la stabilità;
3. determinare la lagrangiana del sistema;
4. scrivere la lagrangiana approssimata attorno a una posizione di equilibrio stabile e le relative
equazioni del moto linearizzate.
B
M
A
C
N
O
D
k
E
2) Data la trasformazione
{
Q = qp − qeq
P = log(p + keq )
se ne trovino i valori di k ∈ R per cui è canonica.
Nei casi affermativi si trovi poi una funzione generatrice del tipo F (q, P ).
Prova scritta di Meccanica Analitica
Appello dell’11 gennaio 2012
1) In un piano verticale, un’asta OA di lunghezza 2ℓ e massa trascurabile è libera di ruotare attorno
al suo estremo fisso O. Una seconda asta BC, di lunghezza 2ℓ e massa m, si muove nel piano
restando perpendicolare alla prima asta e in modo da avere l’estremo B sulla prima asta.
Tutto il sistema è soggetto alla forza di gravità; inoltre, sul punto B agisce una forza elastica di polo
kℓ
l’origine e coefficiente k > 0. Introducendo il parametro λ = mg
, si chiede di:
1. trovare le posizioni di equilibrio ordinarie del sistema e discuterne la stabilità in funzione di λ;
2. trovare le posizioni di equilibrio di confine;
3. determinare la lagrangiana del sistema;
4. scrivere la lagrangiana approssimata attorno a una posizione di equilibrio stabile (si fissi un
valore di λ opportuno).
O
ϑ
ξ
B
k
A
C
2) Data la trasformazione


 Q = √ kp
p−q

 P = (√p − q)2
se ne trovino i valori di k ∈ R per cui è canonica.
Nei casi affermativi si trovi poi una funzione generatrice del tipo F (q, P ).
Prova scritta di Meccanica Analitica
Appello del 9 dicembre 2011
1) Un corpo rigido è formato da una lamina quadrata ABCD omogenea di massa m e lato ℓ al
cui estremo C è saldato un punto materiale, anch’esso di massa m. Il corpo si muove in un piano
verticale in modo che il punto A possa scorrere sull’asse x di un sistema di riferimento cartesiano
ortogonale.
Tutto il sistema è soggetto alla forza di gravità; inoltre, sul punto C agisce una forza elastica di polo
l’origine e coefficiente k > 0. Si chiede di:
1. trovare le posizioni di equilibrio della sistema;
2. discutere la stabilità delle posizioni di equilibrio in funzione del parametro λ =
mg
kℓ ;
3. determinare la lagrangiana del sistema;
4. scrivere la lagrangiana approssimata attorno a una posizione di equilibrio stabile (si fissi un
valore di λ opportuno).
y
x
A
O
B
D
C
2) Data la lagrangiana
L(q1 , q2 , q̇1 , q̇2 ) = (2 + cos q2 )q̇12 + (2 + sin q2 )q̇22 + q22
se ne determini l’hamiltoniana associata e le equazioni di Hamilton.
Si trovino poi due integrali primi del moto.
Prova scritta di Meccanica Analitica
Appello del 27 settembre 2011
1) Un corpo rigido è formato da un’asta AC di massa trascurabile e lunghezza R/2, saldata
perpendicolarmente nel centro C di un disco di raggio R e massa m.
Il punto A è libero di scorrere sull’asse verticale z di un sistema di riferimento Oxyz, in modo che
l’asta resti sempre nel piano yz e perpendicolare a tale asse.
Su un punto P situato sul bordo del disco agisce una forza elastica di coefficiente k > 0 e polo il
punto B di coordinate (0, R/2, 0).
Il corpo è soggetto alla forza peso e tutti i vincoli sono lisci. Si chiede di:
1. trovare le posizioni di equilibrio del sistema;
2. discuterne la stabilità;
3. determinare la lagrangiana del sistema;
4. scrivere la lagrangiana approssimata del sistema attorno a una posizione di equilibrio stabile.
z
A
C
P
B
y
2) Dati a > b > c > 0, si dica quando è possibile costruire un corpo rigido che ammetta i tre
parametri come momenti principali d’inerzia.
Nei casi in cui è possibile, si dia poi un esempio di tale corpo rigido.
Prova scritta di Meccanica Analitica
Appello del 6 settembre 2011
1) Un corpo rigido è formato da un’asta OA di massa 2m e lunghezza 2ℓ, un’asta AB di massa m
e lunghezza ℓ saldata ad angolo retto alla prima nell’estremo comune A, e da un punto materiale P
di massa m saldato all’estremo B della seconda asta.
Tale corpo rigido si può muovere in modo che l’asta OA stia nel piano verticale yz di un sistema di
riferimento Oxyz e il punto O sia fisso nell’origine.
Sul punto A agisce una forza elastica di coefficiente k > 0 e polo il punto C di coordinate (2ℓ, 0, 0).
Il sistema è soggetto alla forza peso e tutti i vincoli sono lisci. Si chiede di:
1. trovare le posizioni di equilibrio ordinarie del sistema e discuterne la stabilità;
2. determinare la lagrangiana del sistema;
3. trovare la lagrangiana approssimata attorno a una posizione di equilibrio stabile.
z
A
O
C
P ≡B
x
2) Data la trasformazione
(
)

1+p
3
2


+1
 Q = kq cos
q2
(
)

1+p

 P = tan
q2
se ne trovino i valori di k ∈ R per cui è canonica.
Nei casi positivi si trovi poi una funzione generatrice del tipo F (q, P ).
y
Prova scritta di Meccanica Analitica
Appello del 12 luglio 2011
1) Un corpo rigido è formato da due aste, AB e CD, entrambe di massa m e lunghezza 2`, in modo
che l’estremo B della prima asta sia saldato perpendicolarmente alla seconda asta nel punto medio.
L’estremo A del corpo rigido si muove sull’asse z di un sistema di riferimento cartesiano ortogonale,
mentre l’asta CD è vincolata a giacere sempre nel piano xy.
Oltre alla forza peso, sul corpo rigido agiscono due forze elastiche di coefficiente k > 0: la prima ha
polo nell’origine e agisce sull’estremo A, la seconda ha polo nel punto E(2`, 0, 0) e agisce sul punto
B.
k`
Si ponga λ =
. Sapendo che il corpo rigido è soggetto anche alla forza peso e che i vincoli sono
mg
lisci, si chiede di determinare:
1. le posizioni di equilibrio;
2. la stabilità di tali posizioni;
3. la lagrangiana del sistema;
4. le pulsazioni delle piccole oscillazioni attorno a una posizione di equilibrio stabile (scegliendo
un opportuno valore di λ).
A
k
ϑ
O
ϕ
E
k
C
B
D
2) Si determinino i valori di k ∈ R per cui la trasformazione

Q = k √p sin q
P = √p cos q
è canonica. Si trovi poi una funzione generatrice del tipo F (q, P ).
Infine, data l’hamiltoniana H(q, p) = −p sin(2q), si risolvano le equazioni di Hamilton associate alle
nuove variabili (Q, P ).
Prova scritta di Meccanica Analitica
Appello del 28 giugno 2011
1) In un piano verticale, un’asta AB di massa m e lunghezza ` ha l’estremo A che scorre sull’asse
x e si muove nel semipiano y ≤ 0 restando sempre ortogonale a tale asse. All’estremo B dell’asta è
vincolato il vertice di una lamina quadrata BCDE, di lato ` e massa m, che può ruotare liberamente
attorno a B. Inoltre sul vertice C della lamina è saldato un punto materiale P di massa M .
Su B agisce una forza elastica di coefficiente k > 0 e polo l’origine O di un sistema di riferimento
cartesiano ortogonale Oxy.
Sapendo che il sistema è soggetto alla forza peso e che i vincoli sono lisci, si chiede di determinare:
1. le posizioni di equilibrio;
2. la stabilità di tali posizioni;
3. la lagrangiana del sistema;
4. la lagrangiana approssimata attorno a una posizione di equilibrio stabile.
A
O
m, ℓ
k
B
E
P, M
m, ℓ
C
D
2) Determinare per quali valori di k ∈ R la seguente trasformazione è canonica:

Q = log(kq 2 p)
P = kqp.
Nei casi in cui la trasformazione sia canonica, trovarne la funzione generatrice del tipo F (q, Q).
Trovare infine come si trasforma l’hamiltoniana H(q, p) = q 3 p2 e dedurne le nuove equazioni di
Hamilton in funzione di (Q, P ).
Prova scritta di Meccanica Analitica
Appello del 5 aprile 2011
1) Un corpo rigido è formato da due aste omogenee AB e BC, entrambe di massa m e lunghezza `,
saldate ad angolo retto nell’estremo comune B.
Tale corpo rigido si può muovere in un piano verticale in modo che il punto A si mantenga sempre
sull’asse x di un sistema di riferimento Oxy.
Sull’estremo A agisce una forza elastica di coefficiente k > 0 e polo l’origine O.
Il sistema è soggetto alla forza peso e tutti i vincoli sono lisci. Si chiede di:
1. trovare le posizioni di equilibrio ordinarie del sistema e discuterne la stabilità;
2. determinare la lagrangiana del sistema;
3. trovare le equazioni del moto linearizzate attorno a una posizione di equilibrio stabile.
A
O
C
B
2) Data la trasformazione
(
Q = pekq
P = −ehq
si trovino i valori di h, k ∈ R per cui è canonica.
Nei casi positivi si trovi poi una funzione generatrice del tipo F (q, Q).
Prova scritta di Meccanica Analitica
Appello del 25 marzo 2011
1) Un corpo rigido è formato da un disco omogeneo di massa m e raggio R e da un’asta omogenea
OA di massa m e lunghezza 2R. L’estremo A dell’asta è saldato ad un punto del bordo del disco in
modo che l’asta sia perpendicolare al piano del disco.
Tale corpo rigido si può muovere in modo che l’asta OA stia nel piano orizzontale xy di un sistema
di riferimento Oxyz e il punto O sia fisso nell’origine.
Sull’estremo A dell’asta agisce una forza elastica di coefficiente k > 0 e polo il punto B di coordinate
(2R, 0, 0).
Il sistema è soggetto alla forza peso e tutti i vincoli sono lisci. Si chiede di:
1. trovare le posizioni di equilibrio ordinarie del sistema e discuterne la stabilità;
2. determinare la lagrangiana del sistema;
3. trovare le equazioni del moto linearizzate attorno a una posizione di equilibrio stabile.
O
B
k
A
2) Data la trasformazione
(
Q = 2kp
P = q + arccos p
se ne trovino i valori di k ∈ R per cui è canonica.
Nei casi positivi si trovi poi una funzione generatrice del tipo F (q, P ).
Prova scritta di Meccanica Analitica
Appello dell’11 gennaio 2011
1) Un corpo rigido piano è formato da un disco di massa M e raggio R a cui è saldato sul
bordo un punto materiale P di massa m.
Il corpo rigido si muove in un piano verticale, in modo che il centro C del disco possa scorrere
in modo liscio sull’asse orizzontale di un sistema di riferimento Oxy.
Una forza elastica di coefficiente k > 0 e polo l’origine O agisce sul punto P , e tutto il sistema
è sottoposto alla forza peso.
Si chiede di:
(a) trovare le posizioni di equilibrio del corpo rigido, e in particolare discuterne l’esistenza
;
al variare del parametro λ = mg
k`
(b) studiare la stabilità delle posizioni di equilibrio al variare di λ;
(c) determinare la lagrangiana del moto;
(d) trovare le equazioni del moto linearizzate attorno a una posizione di equilibrio stabile.
R, M
O
C
k
P, m
2) Si trovino i valori di k ∈ R per cui la trasformazione

q
Q =
1 − k tan2 p

P = tan p
è canonica. Si trovi poi una funzione generatrice del tipo F (q, P ).
Prova scritta di Meccanica Analitica
Appello del 14 dicembre 2010
1) Un corpo rigido piano è formato da un’asta omogenea AB, di massa m e lunghezza 2`,
con l’estremo B saldato ortogonalmente al centro di un lato di una lamina quadrata CDEF ,
anch’essa omogenea di massa m e lato 2`.
Il corpo si muove in un piano verticale in modo che l’estremo A scorra sull’asse y di un sistema
di riferimento Oxy e il corpo sia libero di ruotare attorno ad A.
Sul centro della lamina quadrata agisce una forza elastica di coefficiente k > 0 e polo l’origine
O; inoltre il corpo è soggetto alla forza peso.
Si chiede di:
1. trovare le posizioni di equilibrio del corpo rigido, e in particolare discuterne l’esistenza
;
al variare del parametro λ = mg
k`
2. studiare la stabilità delle posizioni di equilibrio al variare di λ;
3. determinare la lagrangiana del moto;
4. fissato λ = 9, trovare le equazioni del moto linearizzate attorno a una posizione di
equilibrio stabile.
A
C
B
F
D
E
O
2) Data la lagrangiana
q̇12 q̇22 9 2 1 2 3
1
+
+ q1 + q2 + q1 q̇1 + q2 q̇2
4
8
4
8
2
4
se ne trovi l’hamiltoniana associata e si risolvano le equazioni di Hamilton.
L(q1 , q2 , q̇1 , q̇2 ) =
Prova scritta di Meccanica Analitica
Appello del 28 settembre 2010
1) Un corpo rigido piano è ricavato da una lamina rettangolare di lati AB = 2a e AD = 4a
(a > 0) in cui è praticato un foro semicircolare di raggio a e centro il punto medio del lato
AD. La massa della lamina è m. Tale corpo rigido è incernierato all’asse y di un sistema di
riferimento cartesiano Oxyz in modo che il lato AD sia fermo e il corpo sia libero di ruotare
senza attrito attorno a tale lato. Poniamo per semplicità il punto medio di AD nell’origine.
Inoltre sul profilo semicircolare scorre in modo liscio un punto materiale P di massa m.
Tutto il sistema è soggetto alla forza peso. Si chiede di:
1. trovare il momento d’inerzia della lamina rispetto al lato AD;
2. trovare le posizioni di equilibrio ordinarie del sistema e discuterne la stabilità;
3. analizzare le posizioni di equilibrio di confine;
4. denotando con I il momento d’inerzia al punto 1, determinare la lagrangiana del moto.
z
D
O
A
C
P
B
x
2) Si trovino i valori di k ∈ R per cui la trasformazione

Q = p
2q

P = −(k log p + log(2q) + q 2 )
è canonica. Si trovi poi una funzione generatrice del tipo F (q, P ).
y
Prova scritta di Meccanica Analitica
Appello del 14 settembre 2010
1) Un corpo rigido è formato da un disco omogeneo di massa m e raggio R sul cui bordo
è saldato un punto materiale P , anch’esso di massa m. Il centro C del disco è vincolato a
scorrere con vincolo liscio sull’asse x di un sistema di riferimento cartesiano ortogonale Oxyz,
in modo tale che il corpo rigido resti sempre in un piano parallelo al piano yz. Sul punto C
agisce una forza elastica di coefficiente k > 0 e polo l’origine O; inoltre il corpo è soggetto
alla forza peso.
Si chiede di:
1. trovare le posizioni di equilibrio del corpo rigido e discuterne la stabilità;
2. determinare la lagrangiana del moto;
3. trovare le equazioni del moto linearizzate attorno alla posizione di equilibrio stabile.
z
m, R
O
x
C
m, P
y
2) Si trovino le equazioni di Hamilton associate a
H(q, p) = kq 2 + pq + 2kp2 .
Avendo verificato che il sistema ottenuto è lineare, se ne classifichino le orbite al variare di
k ∈ R.
Prova scritta di Meccanica Analitica
Appello del 20 luglio 2010
1) Un’asta omogenea AB di lunghezza 2` e massa m ha l’estremo B vincolato a passare per
un punto della retta x = ` in un riferimento contenuto in un piano verticale ed è inoltre
vincolata a passare per l’origine. I vincoli sono lisci. Sull’asta agisce un momento di forze
M = b cos ϑ ez , dove ϑ è l’angolo delle coordinate polari nel piano e b > 0 una costante.
Inoltre l’asta è soggetta alla forza peso. Si chiede di:
(a) determinare le posizioni di equilibrio ordinarie dell’asta e la loro stabilità;
(b) determinare l’equazione del moto dell’asta;
(c) studiare l’equilibrio delle posizioni di confine;
(d) scrivere l’equazione cartesiana della curva che contiene la traiettoria descritta dal baricentro dell’asta durante il suo movimento.
[Ricordiamo che il potenziale di un momento M = f (ϑ) ez è una primitiva di f (ϑ).]
B
M
ϑ
O
ℓ
H
A
2) Trovare per quali valori del parametro α ∈ R la trasformazione

p

 Q = α log
2q

 P = − qp
2
è canonica.
Per tali valori si trovi poi una funzione generatrice della forma F (q, Q).
Data infine l’hamiltoniana H(q, p) = qp, scrivere le equazioni di Hamilton nelle nuove variabili
Q, P .
Prova scritta di Meccanica Analitica
Appello del 25 giugno 2010
1) Un corpo rigido è formato da due aste OA e BC, entrambe di massa m e lunghezza 2`,
saldate perpendicolarmente nel loro baricentro. Inoltre un punto materiale P di massa m è
fissato nell’estremo B della seconda asta.
Fissiamo un sistema di riferimento cartesiano ortogonale Oxyz in modo che la forza peso sia
diretta in senso opposto all’asse y. Il corpo rigido si può muovere in modo che l’estremo
O sia fisso nell’origine e l’asta OA ruoti attorno ad O mantenendosi nel piano verticale fisso
Oxy.
Il sistema è soggetto alla forza peso e tutti i vincoli sono lisci. Si chiede di:
1. trovare le posizioni di equilibrio ordinarie del sistema;
2. studiare la stabilità delle posizioni di equilibrio;
3. determinare la Lagrangiana del moto del sistema.
y
O
x
C
ϑ
z
ϕ
P ≡B
A
2) Sia dato un sistema hamiltoniano a vincoli mobili tale che la sua hamiltoniana verifichi la
relazione
∂H
= −H.
∂t
Dimostrare che la funzione H2 è positiva e non crescente lungo i moti del sistema.
Prova scritta di Meccanica Analitica
Appello del 13 aprile 2010
1) Una lamina omogenea di massa m ha la forma di un disco di raggio R in cui è stato
praticato un foro circolare di raggio R/2 tangente internamente al disco. Denotiamo con AB
il diametro del disco grande passante per i due centri, come indicato in figura. La lamina
si muove in un piano verticale in modo che il punto A scorre sull’asse x di un sistema di
riferimento cartesiano ortogonale.
Tutto il sistema è soggetto alla forza di gravità; inoltre, sul punto B agisce una forza elastica
di polo l’origine e coefficiente k > 0. Si chiede di:
1. trovare le posizioni di equilibrio della lamina;
2. discutere la stabilità delle posizioni di equilibrio in funzione del parametro λ =
mg
;
kR
3. determinare la lagrangiana del sistema;
4. scrivere la lagrangiana approssimata attorno a una posizione di equilibrio stabile (si fissi
un valore di λ opportuno).
y
O
x
A
G
C
D
B
2) Si dica per quali valori del parametro h ∈ R l’energia cinetica
K(q̇1 , q̇2 ) = hq̇12 + 4q̇1 q̇2 + hq̇22
è definita positiva.
Nel caso h = 3 si trovi poi l’hamiltoniana associata alla lagrangiana
1
L(q1 , q2 , q̇1 , q̇2 ) = K(q̇1 , q̇2 ) + q13 .
3
Prova scritta di Meccanica Analitica
Appello del 30 marzo 2010
1) Un corpo rigido è formato da un semidisco omogeneo di massa m e raggio R e da un’asta
omogenea di massa m e lunghezza incognita. L’asta è saldata al centro del diametro del semidisco,
ortogonalmente al diametro stesso e dalla parte opposta rispetto al semidisco.
Tale corpo rigido si può muovere in modo che gli estremi A e B del diametro del semidisco si muovano
rispettivamente sull’asse x e sull’asse y di un sistema cartesiano ortogonale.
Inoltre un punto materiale P di massa M può scorrere sulla parte circolare del bordo del semidisco.
Sull’estremo A del diametro agisce una forza elastica di coefficiente k > 0 e polo il punto O.
Il sistema è soggetto alla forza peso e tutti i vincoli sono lisci. Si chiede di:
1. determinare la lunghezza dell’asta in modo che il baricentro del corpo rigido si trovi esattamente
nel centro C del semidisco;
2. trovare le posizioni di equilibrio ordinarie e di confine del sistema;
3. studiare la stabilità delle posizioni di equilibrio ordinarie;
4. determinare le equazioni di Lagrange del moto del sistema.
Nota: si è cosi sicuri che tutti ne sono ampiamente a conoscenza, che non viene neanche in mente
di scrivere che il baricentro del semidisco omogeneo si trova a distanza 4R
3π dal diametro.
y
P
B
ϑ
ϕ
C
O
k
D
2) Data la trasformazione

r

 Q = 1 − p − kq
p

 P = −p + hq
se ne trovino i valori di h, k ∈ R per cui è canonica.
Si trovi poi una funzione generatrice del tipo F (q, Q).
A
x
Prova scritta di Meccanica Analitica
Appello del 12 gennaio 2010
1) Data la lagrangiana
i
1h 2
q̇ − 2kq q̇ + (k 2 − 4)q 2
4
se ne determini l’hamiltoniana associata e il relativo sistema hamiltoniano.
Dopo aver notato che tale sistema è lineare, se ne classifichino le traiettorie al variare di k.
L (q, q̇) =
2) Un corpo rigido è formato da un’asta OA omogenea di lunghezza 2R e massa m, al cui
baricentro è saldato il centro di una lamina circolare omogenea di raggio R e massa m, giacente
nel piano perpendicolare all’asta. Inoltre a un punto del bordo della lamina è saldato un punto
materiale P di massa m.
L’estremo O è fissato nell’origine di un sistema di riferimento cartesiano ortogonale, e il corpo
rigido può muoversi in modo che l’asta stia sempre nel piano verticale xy e il corpo possa
ruotare attorno all’asta.
Sull’estremo A dell’asta agisce una forza elastica di coefficiente k > 0 e polo il punto C di
coordinate (2R, 0).
Il sistema è soggetto alla forza peso e tutti i vincoli sono lisci. Si chiede di:
1. trovare le posizioni di equilibrio del sistema al variare del parametro λ =
kR
;
mg
2. studiare la stabilità delle posizioni di equilibrio nel caso λ = 1;
3. trovare la matrice d’inerzia del corpo rigido rispetto a O in un sistema di riferimento
solidale.
y
A
k
P
O
C
x
Prova scritta di Meccanica Analitica
Appello del 15 dicembre 2009
1) Una lamina omogenea quadrata ABCD di lato ` e massa m ha il lato AD vincolato a
scorrere sull’asse y di un sistema di riferimento cartesiano ortogonale, ed è libera di ruotare
attorno a tale lato. Sul punto A della lamina agisce una forza elastica di coefficiente k > 0 e
polo l’origine O, mentre sul punto B della lamina agisce un’altra forza elastica di coefficiente
k e polo il punto P di coordinate (0, −`, 0).
Il sistema è soggetto alla forza peso e tutti i vincoli sono lisci. Si chiede di:
1. trovare le posizioni di equilibrio del sistema e studiarne la stabilità;
2. determinare le equazioni del moto del sistema;
3. trovare la lagrangiana approssimata nell’intorno della posizione di equilibrio stabile.
z
P
O
k
A
k
D
y
B
x
C
2) Trovare per quali valori del parametro k ∈ R la trasformazione
(
5 2
Q = kq 3 p 3
2
1
P = 3q − 3 p 3
è canonica. Per tali valori si trovi poi una funzione generatrice della forma F (q, P ).
Infine, si esprima nelle nuove variabili la hamiltoniana
H (q, p) = q 3 p3 .
Prova scritta di Meccanica Analitica
Appello del 22 settembre 2009
1) Una lamina omogenea semicircolare di massa m e raggio R rotola senza strisciare su una
retta orizzontale, in modo che il suo diametro AB non superi mai la verticale.
Un’asta rigida omogenea BQ, anch’essa di massa m e lunghezza 2R, è vincolata al punto B
della semicirconferenza e può ruotare senza attrito attorno ad esso.
Il sistema è soggetto alla forza peso. Si chiede di:
1. trovare le posizioni di equilibrio ordinarie e di confine del sistema;
2. studiare la stabilità delle posizioni di equilibrio ordinarie;
3. determinare la lagrangiana del sistema.
A
m, R
B
m, 2R
Q
2) Trovare per quali valori del parametro k ∈ R la trasformazione
(
√
Q = k peq
p
P = pe−q
è canonica. Per tali valori si trovi poi una funzione generatrice della forma F (q, P ).
Prova scritta di Meccanica Analitica
Appello del 4 settembre 2009
1) Una lamina omogenea semicircolare di massa m e raggio R rotola senza strisciare su una
retta orizzontale, in modo che il suo diametro AB non superi mai la verticale.
Un’asta rigida omogenea P Q di massa m e lunghezza 2` scorre senza attrito su una guida
rettilinea infinita sostenuta dal diametro AB.
Tra il baricentro G dell’asta e il punto medio C del diametro AB intercorre una forza elastica
di coefficiente k > 0.
Il sistema è soggetto alla forza peso. Si chiede di:
1. trovare le posizioni di equilibrio ordinarie e di confine del sistema;
2. studiare la stabilità delle posizioni di equilibrio ordinarie;
3. determinare la lagrangiana del sistema.
A
C
m, R
B
P
G
m, 2ℓ
2) Data l’hamiltoniana
Q
q2
+ 4kqp + 4p2
2
dipendente dal parametro k ∈ R, si chiede di scrivere il sistema hamiltoniano associato. Dopo
aver notato che tale sistema è lineare, si studi la classificazione delle sue traiettorie al variare
del parametro k.
H(q, p) =
Prova scritta di Meccanica Analitica
Appello del 17 luglio 2009
1) Un’asta rigida omogenea di massa m e lunghezza ` ha gli estremi A e B vincolati a scorrere
rispettivamente sull’asse z e sull’asse y di un sistema di riferimento cartesiano ortogonale
Oxyz. Una seconda asta, identica alla prima, ha un estremo agganciato ad A e l’altro estremo
C che scorre sull’asse x.
Il sistema è soggetto alla forza peso; inoltre, tra gli estremi B e C intercorre una forza elastica
di coefficiente k > 0.
Supponendo tutti i vincoli lisci, si chiede di:
1. trovare tutte le posizioni di equilibrio del sistema;
2. studiare la stabilità di tali posizioni al variare del parametro λ =
mg
;
2k`
3. determinare l’equazione del moto del sistema;
4. nel caso λ = 15 , risolvere l’equazione linearizzata del moto attorno a una posizione di
equilibrio stabile.
2) Data la lagrangiana
L(q, q̇) = hq̇ 2 + q q̇ − q 2 ,
h 6= 0
si chiede di determinarne l’hamiltoniana associata, il sistema di equazioni di Hamilton e,
dopo aver notato che tale sistema è lineare, la classificazione delle sue traiettorie al variare
del parametro h.
Prova scritta di Meccanica Analitica
Appello del 16 giugno 2009
1) Due guide rettilinee saldate ortogonalmente sono libere di ruotare in un piano verticale
attorno al loro punto comune O, origine di un sistema di assi cartesiani ortogonali Oxy.
Un’asta omogenea AB di massa m e lunghezza ` ha l’estremo A vincolato a scorrere su una
guida rettilinea e l’estremo B vincolato a scorrere sull’altra guida. Sul punto C della prima
guida a distanza 2` da O agisce poi una forza elastica di coefficiente k > 0 e polo il punto H
dell’asse x che sta sulla verticale per C.
Si usino come parametri lagrangiani gli angoli θ e φ in figura.
Tutti i vincoli sono lisci e l’asta è soggetta alla forza peso. Si chiede di:
1. trovare tutte le posizioni di equilibrio per cui 0 ≤ θ, φ ≤
π
2
;
2. studiare la stabilità di tali posizioni;
3. determinare la lagrangiana del sistema;
4. determinare le pulsazioni delle piccole oscillazioni attorno alla posizione di equilibrio
θ = 0, φ = π2 .
H
O
θ
ϕ
A
B
C
2) Dato il cambio di variabili

p
Q = k 3 q 5 p2
3
P = k p
p/q 2
si determini per quali k > 0 la trasformazione è canonica e se ne dia una funzione generatrice
del tipo F (q, P ).
Prova scritta di Meccanica Analitica
Appello dell’1 aprile 2009
1) Un’asta AB di massa m e lunghezza l si muove in un piano verticale xy mantenendo l’estremo
A sull’asse orizzontale x e l’estremo B sull’asse verticale y. All’estremo B è saldato il baricentro di
una seconda asta CD, uguale alla prima, che si mantiene sempre perpendicolare al piano xy.
Inoltre, sull’asta CD scorre un punto materiale P di massa M , che è soggetto a una forza elastica
di coefficiente k > 0 e polo il punto B.
Tutto il sistema è soggetto alla forza di gravità e i vincoli sono lisci. Si chiede di:
1. trovare le posizioni di equilibrio ordinarie e di confine del sistema e discutere la stabilità di
quelle ordinarie;
2. determinare le equazioni del moto del sistema;
3. scrivere le equazioni del moto linearizzate attorno a una posizione di equilibrio stabile.
m,l
B
P,M
D
C
m,l
O
A
2) Si trovi il momento d’inerzia rispetto all’asse x della lamina piana omogenea delimitata dalla
retta x = 3 e dalle curve y = f (x) e y = −f (x), dove
(x − 2) √
3
x + 1,
x ∈ [−1, 3]
f (x) =
3
è la curva rappresentata in figura.
-1
2
3
Prova scritta di Meccanica Analitica
Appello del 17 marzo 2009
1) Una lamina omogenea ha la forma di un disco di raggio R in cui è stato praticato un foro
circolare di raggio R/2 tangente internamente al disco. Tale lamina, di massa M , si muove
in un piano verticale e rotola senza strisciare lungo una retta orizzontale. Inoltre, sul bordo
del foro circolare scorre senza attrito un punto materiale di massa m.
Tutto il sistema è soggetto alla forza di gravità. Si chiede di:
1. determinare la distanza d del baricentro della lamina dal centro del disco grande e il
momento d’inerzia baricentrale della lamina rispetto all’asse perpendicolare al piano del
moto;
2. trovare le posizioni di equilibrio del sistema e discuterne la stabilità in funzione del
m
;
parametro λ = M
3. determinare la lagrangiana del sistema.
G
C
ϑ
P
A
ϕ
2) Si dica per quali valori del parametro k ∈ R la trasformazione

kp



Q = tan


q
q2


P
=
−



1 + tan2 kp
q
è canonica. Si esprima poi nelle nuove variabili (Q, P ) l’hamiltoniana
H(q, p) =
p2
+ q2 .
4q 2
Prova scritta di Meccanica Analitica
Appello del 8 gennaio 2009
1) Un’asta AB di massa M e lunghezza 6R, R > 0, si muove in un piano verticale con
l’estremo A vincolato a stare sull’asse y. All’estremo B è saldato il centro di un disco di
massa M e raggio R, che giace in un piano ortogonale all’asta.
Su A agisce una forza elastica di coefficiente k e polo l’origine O di un sistema di riferimento
cartesiano ortogonale Oxy.
Tutto il sistema è soggetto alla forza di gravità.
Dopo aver individuato tre parametri lagrangiani che descrivano la posizione del sistema, si
chiede di determinare:
1. le posizioni di equilibrio del sistema;
2. la velocità del baricentro del sistema;
3. la lagrangiana del moto.
y
x
O
A
M, 6R
B
2) Dato il sistema hamiltoniano
(
M, R
q̇ = 2pe−q + q 3
ṗ = p2 e−q − 3pq 2
si trovi l’hamiltoniana del sistema e la lagrangiana ad essa associata. Si scriva poi l’equazione
del moto in forma lagrangiana.
Prova scritta di Meccanica Analitica
Appello del 18 dicembre 2008
1) Una disco di massa M e raggio R rotola senza strisciare su una retta orizzontale. Un’asta
AB di massa m e lunghezza 2` è libera di ruotare attorno al suo estremo A che è vincolato a
un punto del bordo del disco.
Inizialmente il sistema è posto in modo che l’estremo A si trovi nell’origine O di un sistema
di riferimento cartesiano ortogonale.
Il sistema è soggetto alla forza di gravità. Si chiede di:
1. determinare le posizioni di equilibrio del sistema e la loro stabilità;
2. determinare le equazioni differenziali del moto.
M, R
A
O
m, 2ℓ
B
2) Stabilire per quali k ∈ R la trasformazione

Q = − k
q2p

P = kq 3 p2
è canonica e trovarne una funzione generatrice della forma F (q, Q).
3) Classificare le posizioni di equilibrio del sistema differenziale lineare
(
ẋ = x + 18hy
ẏ = hy
al variare di h ∈ R.
Prova scritta di Meccanica Analitica
Appello del 30 settembre 2008
1) Una disco di massa M e raggio R rotola senza strisciare su una retta orizzontale. Un’asta
AB di massa M e lunghezza 6R è libera di ruotare attorno al suo punto C distante R da A,
e il punto C è vincolato al centro del disco.
Su C agisce una forza elastica di coefficiente k e polo un punto fisso O dell’asse orizzontale.
Tutto il sistema è soggetto alla forza di gravità. Si chiede di:
1. trovare il potenziale del sistema e determinare le posizioni di equilibrio;
2. determinare la lagrangiana del moto;
3. linearizzare la lagrangiana attorno alla posizione di equilibrio stabile.
A
M, R
C
O
M, 6R
B
2) Dato il sistema hamiltoniano

 q̇ = qp
2
 ṗ = cos q − p
2
si trovi l’hamiltoniana del sistema e la lagrangiana ad essa associata. Si scriva poi l’equazione
del moto in forma lagrangiana.
Prova scritta di Meccanica Analitica
Appello del 4 settembre 2008
1) Un’asta rigida omogenea AB di√massa M e lunghezza 2l è vincolata ad avere un
estremo in un punto fisso A distante l 2 da un piano orizzontale, sul quale scorre senza
attrito l’estremo B. Sull’asta scorre, sempre senza attrito, un punto materiale P di massa m.
Sul sistema agiscono la forza peso, una forza elastica di costante k che attira P nel baricentro
dell’asta e una forza costante applicata in B e contenuta nel piano orizzontale, di modulo F .
Si chiede:
a) Calcolare le posizioni di equilibrio del sistema e discuterne la stabilità, assumendo che
non vi siano posizioni di confine (si immagini che il punto possa appartenere alla retta
contenente l’asta);
b) Scrivere le equazioni differenziali del moto del sistema;
c) Supponendo che l’asta ruoti uniformemente con pulsazione ω attorno al suo asse di
rotazione, determinare le posizioni di equilibrio relativo del punto P .
2) Si trovi per quali valori di h, k ∈ R la trasformazione
 Q = − cos q

k
 P = 2hp
sin q
è canonica.
Data poi la lagrangiana
L = cos q + q̇ 2 ,
se ne determini la hamiltoniana associata e si scriva tale hamiltoniana nelle nuove variabili
Q, P della precedente trasformazione canonica.
Prova scritta di Meccanica Analitica
Appello del 15 luglio 2008
1) Una lamina quadrata di massa m e lato AB = ` è vincolata a muoversi tenendo il vertice A
sull’asse y e il vertice B sull’asse x di un sistema di riferimento cartesiano ortogonale Oxyz,
dove l’asse y è rivolto verso l’alto. La lamina può ruotare attorno all’asse passante per il lato
AB.
Sul punto B agisce una forza elastica di coefficiente k > 0 e polo l’origine O.
Tutto il sistema è soggetto alla forza di gravità e i vincoli sono lisci. Si chiede di:
1. determinare le posizioni di equilibrio;
2. discutere la stabilità di tali posizioni;
3. determinare la lagrangiana del moto.
y
ϕ
A
D
O
B
x
C
2) Si mostri che la trasformazione

√
3p


Q =
3q
p


P = − 2 q 2 3p
3
è canonica e se ne trovi una funzione generatrice della forma F (q, Q).
Prova scritta di Meccanica Analitica
Appello del 25 giugno 2008
1) Un semidisco omogeneo di massa m e diametro AB = 2R è vincolato a scorrere sull’asse z
di un sistema di riferimento cartesiano ortogonale Oxyz. Il semidisco può ruotare attorno a
tale asse e sul punto C distante R dall’asse z agisce una forza elastica di coefficiente k > 0 e
polo l’origine O.
Tutto il sistema è soggetto alla forza di gravità e i vincoli sono lisci. Si chiede di:
1. determinare il momento d’inerzia del semidisco rispetto all’asse z;
2. trovare le posizioni di equilibrio del semidisco;
3. determinare la lagrangiana e le equazioni differenziali del moto.
z
O
ξ
B
x
y
k
C
A
m, R
ϑ
[Nota: si ricorda che il baricentro di un semidisco omogeneo di raggio R si trova alla distanza
dal diametro.]
di 4R
3π
2) Data la lagrangiana
L(q1 , q2 , q̇1 , q̇2 ) = (q12 + 1)q̇12 + 2q̇1 q̇2 +
q12
2
q̇ 2 + q13
+1 2
se ne determini l’hamiltoniana associata e le equazioni di Hamilton.
Si trovino poi due integrali primi del moto.
Prova scritta di Meccanica Analitica
Appello del 10 aprile 2008
1) Una lamina quadrata omogeneo ABCD di massa m e lato ` è vincolato a muoversi in
modo che il vertice B scorra sull’asse y di un sistema di riferimento Oxyz e la diagonale BD
resti sempre verticale. Sul vertice A agisce una forza elastica di coefficiente k > 0 e polo il
punto Q sull’asse z alla stessa altezza del baricentro della lamina. Inoltre, sulla lamina agisce
un momento costante M = λk`2 ez , dove λ ∈ R.
Tutto il sistema è soggetto alla forza di gravità. Si chiede di:
1. trovare le posizioni di equilibrio del quadrato;
2. determinare le equazioni differenziali del moto;
3. nel caso λ = 0, discutere la stabilità delle posizioni di equilibrio.
z
M
D
Q
k
C
A
ϑ
B
y
x
2) Si calcoli il momento d’inerzia rispetto all’asse y del solido omogeneo di massa M delimitato
dalla rivoluzione attorno a y della curva
x2 =
y4 2
(R − y 2 ) ,
R4
y ≥ 0.
y
x
z
Prova scritta di Meccanica Analitica
Appello del 27 marzo 2008
1) Un disco omogeneo di massa m e raggio R è vincolato a rotolare senza strisciare sull’asse
x di un sistema di riferimento Oxyz. Inoltre, il piano del disco può ruotare attorno all’asse x.
Sul centro G del disco agisce una forza elastica di polo il punto Q = (0, 0, 2R) e coefficiente
k > 0.
Tutto il sistema è soggetto alla forza di gravità. Si chiede di:
1. trovare le posizioni di equilibrio del disco;
2. discutere la stabilità di tali posizioni;
3. determinare le equazioni differenziali del moto.
Q(0, 0, 2R)
ϑ
C
R
ξ
2) Si verifichi che la trasformazione
(
Q = 2q 2 + p
P = 4q 4 + p2 + 4q 2 p − q
è canonica e se ne determini la funzione generatrice della forma F (q, Q). Data poi la
hamiltoniana
2
H(q, p) = k(2q 2 + p) 2q 2 + p + (2q 2 + p)2 − q + (2q 2 + p)2 − q
dipendente dal parametro k ∈ R, si scriva il sistema hamiltoniano nelle nuove variabili Q, P .
Osservato infine che tale sistema è lineare, se ne classifichino le orbite al variare del parametro.
Prova scritta di Meccanica Analitica
Appello del 10 gennaio 2008
1) In un piano verticale due dischi, entrambi di massa m e raggio R, sono vincolati a rotolare
senza strisciare l’uno contro l’altro, ed entrambi sono vincolati a scorrere con vincolo liscio
sull’asse x di un sistema di riferimento cartesiano ortogonale Oxy. Sul bordo del primo disco
inoltre è saldato un punto materiale P , anch’esso di massa m.
Sul punto P agisce una forza elastica di centro l’origine O e coefficiente k > 0.
Tutto il sistema è soggetto alla forza di gravità. Si chiede di:
(a) trovare le posizioni di equilibrio del sistema;
(b) discuterne la stabilità;
(c) determinare le equazioni differenziali del moto;
(d) studiare le piccole oscillazioni attorno a una posizione di equilibrio stabile.
y
R, m
k
R, m
P, m
O
x
2) Trovare per quali valori del parametro k ∈ R la trasformazione
(
Q = k ep
P = −kq e−p
definisce una trasformazione canonica, e in corrispondenza di tali valori trovarne una funzione
generatrice della forma F1 (q, Q).
Determinare poi l’espressione dell’hamiltoniana H(q, p) = q + e−p in funzione delle nuove
variabili Q, P .
Prova scritta di Meccanica Analitica
Appello del 18 dicembre 2007
1) Una guida circolare di massa m2 e raggio R è complanare all’asse x di un sistema di
riferimento cartesiano ortogonale e ha un punto fisso O sull’asse x. Il piano in cui giace tale
guida è libero di muoversi attorno all’asse x.
Sulla guida scorre un punto materiale P di massa m1 . Inoltre sul piano della guida agisce un
momento costante Me1 , dove e1 è il versore dell’asse x.
Tutto il sistema è soggetto alla forza di gravità e i vincoli sono lisci. Si chiede di:
(a) trovare le condizioni su M affinché il sistema ammetta almeno una posizione di equilibrio;
(b) sotto le condizioni del punto precedente, trovare le posizioni di equilibrio del sistema e
discuterne la stabilità;
(c) determinare le equazioni differenziali del moto;
(d) studiare le piccole oscillazioni attorno a una posizione di equilibrio stabile nel caso
M = 0.
x
O
M
m2 , R
P, m
ϕ
ϑ
2) Si classifichino le orbite del sistema lineare

u̇ = 2u + kv
v̇ = ku + 2v
al variare di k ∈ R.
Prova scritta di Meccanica Analitica
Appello del 25 settembre 2007
1) Un corpo rigido è formato da un’asta omogenea OA di massa m e lunghezza 2ℓ al cui
estremo A è saldata perpendicolarmente una seconda asta BC, identica alla precedente, nel
suo punto medio.
Tale corpo rigido può ruotare in un piano verticale tenendo fisso il punto O.
Inoltre, un punto materiale Q di massa m è saldato all’estremo C, mentre un altro punto
materiale P di massa m è libero di scorrere nell’asta BC.
Sul punto P agisce una forza elastica di coefficiente k > 0 e polo l’estremo B dell’asta. Tutto
kℓ
. Si chiede di:
il sistema è soggetto alla forza di gravità e i vincoli sono lisci. Si ponga λ = mg
(a) trovare le posizioni di equilibrio ordinarie del sistema;
(b) studiare l’equilibrio delle posizioni di confine;
(c) discutere la stabilità delle posizioni di equilibrio ordinarie;
(d) determinare la lagrangiana del sistema.
O
m, 2ℓ
Q, m
P, m
C
m, 2ℓ
A
k
B
2) Trovare il semigruppo S(t) generato dall’equazione differenziale (unidimensionale)
ẋ = ex
e verificarne le due proprietà caratterizzanti.
Prova scritta di Meccanica Analitica
Appello del 6 settembre 2007
1) Un’asta omogenea AB di massa M e lunghezza 2ℓ è vincolata a mantenere i propri estremi
su una guida circolare di raggio ℓ e centro O, fissa in un piano verticale.
Nell’asta scorre un punto materiale P di massa m su cui agisce una forza elastica di coefficiente
k > 0 e polo il centro O della guida.
Tutto il sistema è soggetto alla forza di gravità e i vincoli sono lisci. Si chiede di:
(a) trovare le posizioni di equilibrio ordinarie e di confine del sistema;
(b) discutere la stabilità delle posizioni di equilibrio ordinarie;
(c) determinare le equazioni differenziali del moto;
(d) determinare le posizioni di equilibrio relativo del punto P corrispondenti a rotazioni
dell’asta di velocità angolare costante ω;
(e) nel caso in cui il punto P non sia presente, fissata una posizione di equilibrio dell’asta,
se ne confrontino le reazioni vincolari con quelle di un’asta uguale ma vincolata nel suo
punto medio nella stessa posizione di equilibrio.
A
M, 2ℓ
O
k
P, m
B
2) Dimostrare la seguente identità:
h h i
i
F, G, [F, G] = − G, [F, G], F .
Prova scritta di Meccanica Analitica
Appello del 10 luglio 2007
1) Un’asta omogenea AB di massa m e lunghezza ` è vincolata a mantenere il proprio
baricentro G su una guida circolare di raggio R che giace in un piano verticale.
Sul’estremo B dell’asta agisce una forza elastica di coefficiente k > 0 e polo il centro O della
guida.
Tutto il sistema è soggetto alla forza di gravità e i vincoli sono lisci. Si chiede di:
1. trovare le posizioni di equilibrio dell’asta e discuterne la stabilità;
2. determinare la lagrangiana del sistema;
3. determinare le pulsazioni delle piccole oscillazioni attorno a una posizione di equilibrio
stabile.
R
O
A
m, ℓ
G
k
B
2) Dato il potenziale generalizzato
U (q1 , q2 , q̇1 , q̇2 ) = −q̇1 sin q2 + q̇2 cos q1
trovare l’espressione del campo di forze Q associato e la matrice U tale che Q = Uq̇.
Prova scritta di Meccanica Analitica
Appello del 19 giugno 2007
1) Un disco omogeneo di massa m e raggio R è vincolato a mantenere un suo punto fisso
A a distanza d dal centro (0 < d < R) sull’asse y di un sistema di riferimento cartesiano
ortogonale Oxyz. Il disco resta sempre in un piano parallelo al piano xz e sul punto A agisce
una forza elastica di coefficiente k > 0 e polo l’origine O.
Tutto il sistema è soggetto alla forza di gravità e i vincoli sono lisci. Si chiede di:
1. trovare le posizioni di equilibrio del disco e discuterne la stabilità;
2. determinare la lagrangiana e le equazioni differenziali del moto;
3. determinare l’hamiltoniana;
4. risolvere le equazioni di Hamilton nell’approssimazione di linearizzazione attorno alla
posizione di equilibrio stabile.
z
m, R
O
A
y
x
2) Verificare che la trasformazione

p

Q
=
−
arccos


sin q

s

p2


P
=
1
−
cos q

sin2 q
è canonica e calcolare la trasformata dell’hamiltoniana H(q, p) = qp.
Prova scritta di Meccanica Analitica
Appello del 12 aprile 2007
1) In un piano verticale si muove un sistema meccanico piano è formato da due aste uguali OA
e AB di massa m e lunghezza `, incernierate nell’estremo A. La prima asta ha l’estremo O
fisso. Su tale sistema agiscono, oltre alla forza peso, due forze costanti F A = −F i e F B = F i,
F > 0, sui punti A e B, rispettivamente.
2F
Posto λ = mg
, si chiede di:
1. trovare le posizioni di equilibrio del sistema;
2. discutere la stabilità di tali posizioni al variare di λ;
3. determinare le equazioni differenziali del moto;
4. scrivere l’energia cinetica linearizzata attorno a una posizione di equilibrio stabile.
j
O
i
FA
A
FB
B
2) Si dimostri che una hamiltoniana della forma H(q, p) = f (αq + βp), con α, β ∈ R, ammette
sempre due integrali primi, e si determinino tali integrali.
3) Si classifichino le orbite del sistema lineare

ẋ = 2x + ky
ẏ = x + y
al variare di k ∈ R.
Prova scritta di Meccanica Analitica
Appello del 27 marzo 2007
1) Un disco omogeneo di massa m e raggio R è vincolato a rotolare senza strisciare su una
guida rettilinea r passante per l’origine di un sistema di riferimento Oxyz. Inoltre, la guida si
muove nel piano xy ruotando attorno ad O, e il disco giace sempre in un piano verticale. Sul
centro G del disco agiscono due forze elastiche di poli i punti A = (2R, 0, 0) e B = (0, 0, R) e
coefficienti kA e kB rispettivamente.
Tutto il sistema è soggetto alla forza di gravità. Si chiede di:
1. trovare le posizioni di equilibrio del disco;
2. discutere la stabilità di tali posizioni;
3. determinare le equazioni differenziali del moto.
B
A
2) Dopo aver verificato che la trasformazione

2 3

Q = q p
1

P = − 2
qp
è canonica, se ne determini la funzione generatrice della forma F (q, Q). Data poi la hamiltoniana
kq 4 p6
1
H(q, p) = −qp + 2 4 −
2q p
2
dipendente dal parametro k ∈ R, si scriva il sistema hamiltoniano nelle nuove variabili Q, P .
Osservato infine che tale sistema è lineare, se ne classifichino le orbite al variare del parametro
k.
Prova scritta di Meccanica Analitica
Appello del 12 gennaio 2007
1) In un piano verticale un’asta OA di massa m e lunghezza ` può ruotare attorno al suo
estremo O, fisso nell’origine di un sistema di riferimento cartesiano ortogonale Oxy. All’estremo A è incernierata una seconda asta AB, uguale alla prima e libera di ruotare attorno
ad A.
Sulle due aste agisce la forza peso. Inoltre, sui punti A e B agiscono due forze elastiche di
coefficiente k > 0 e poli i punti dell’asse x sulla verticale di A e B, rispettivamente.
Si denoti con θ l’angolo formato dalla parte negativa dell’asse y con l’asta OA, e con φ l’angolo
tra la parte negativa dell’asse y e l’asta AB. Si supponga inoltre −π/2 < θ, φ < π/2.
Considerati tutti i vincoli lisci e posto, λ = mg
, si chiede di determinare:
k`
(a) le posizioni di equilibrio del sistema in funzione di λ;
(b) la stabilità delle posizioni di equilibrio nel caso λ < 1;
(c) le equazioni differenziali del moto;
(d) l’equazione delle pulsazioni delle piccole oscillazioni attorno a una posizione di equilibrio
stabile nel caso λ < 1.
O
θ
k
m, ℓ
A
k
φ
m, ℓ
B
2) Determinare per quali valori di k > 0 la seguente trasformazione è canonica:

p

Q = log

2kq
p


P = − (1 + q 2 ) .
2q
Nei casi in cui la trasformazione sia canonica, trovarne la funzione generatrice del tipo F (q, Q) .