DINAMICA DEL PUNTO MATERIALE
E
CONCETTO DI FORZA
Dinamica:
studio delle forze che causano il moto dei corpi
1
Forza
Si definisce forza una qualunque causa esterna che produce
una variazione dello stato di moto o di quiete di un corpo
Alcuni fatti sperimentali dall’esperienza quotidiana:
• Con una forza muscolare si riesce a spostare un corpo “leggero” ma non un
corpo troppo “pesante”;
• Per rallentare un corpo in moto bisogna trattenerlo a forza o farlo muovere
su una superficie ruvida;
• Una superficie riesce a sostenere un corpo “pesante” se è molto solida e se
il peso è ben distribuito su di essa;
• Se un corpo viene tirato o spinto da parti opposte può deformarsi, rompersi
o muoversi in una delle due direzioni a seconda del materiale di cui è
composto e della forza trainante.
2
Forze a contatto
Forze a distanza
3
Leggi di Newton
Sir Isaac Newton (1643 – 1727) è stato un matematico, fisico e alchimista
inglese, è considerato una delle più grandi menti di tutti i tempi.
Formulò le leggi della meccanica, scoprì la legge della gravitazione
universale.
A seguito delle sue teorie fu in grado di spiegare il moto dei pianeti, le maree,
il moto della luna e della Terra.
I suoi contributi alle teorie fisiche furono dominanti fino all’avvento della
Meccanica Quantistica e rimangono importanti ancora oggi.
4
Principio d’inerzia o 1° legge di Newton
In assenza di forze esterne, un corpo in quiete rimarrà in
quiete, ed un corpo in moto persevererà nello stato di moto
con velocità costante (vale a dire, di moto rettilineo a velocità
costante).
• Il principio di inerzia ci dice che cosa
accade in assenza di forze.
• Sistema di Riferimento Inerziale:
sistema di riferimento in cui è valida la
1° legge di Newton.
5
Legge fondamentale della dinamica o
2° legge di Newton
L’accelerazione di un corpo è direttamente proporzionale alla
forza risultante agente su di esso ed inversamente
proporzionale alla sua massa.
𝐹 = 𝑚𝑎
Unità di misura della forza: NEWTON
1𝑁 =
1𝑘𝑔∙1𝑚
1𝑠 2
6
Esercizio 1 (sul 2° principio della meccanica)
Su un corpo di massa 𝑚 = 200𝑔 vengono applicate due forze in
direzione orizzontale: 𝐹1 = 4𝑁 ed forza 𝐹2 = −2𝑁 . Che accelerazione
subisce il corpo?
F1 (4,0)
F2 (2,0)
R F1 F2 ma
R ( Rx , R y )
𝑭𝟐
m
𝑭𝟏
ghiaccio
Ry 0
Rx F1 F2 4 2 2 N
a (a x , a y )
ay
Ry
ax
Rx
2N
m
10 2
m
0.2kg
s
m
𝑚 = 200𝑔
𝐹1 = 4𝑁
𝐹2 = −2𝑁
𝑎 =?
7
Esercizio 2 (sul 2° principio della meccanica)
Un bambino tira una slitta con una corda che forma un angolo 𝜃 = 40°
con una forza 𝐹 = 60𝑁. Determinare la forza 𝐹𝑥 che effettivamente
contribuisce al moto e la componente 𝐹𝑦 che controbilancia la forza
peso 𝑃.
8
9
Principio di azione e reazione
o 3° legge di Newton
Se un corpo 1 esercita una forza su un corpo 2, a sua volta 2
esercita su 1 una forza uguale e contraria.
o anche:
Ad ogni azione corrisponde una reazione uguale e opposta.
𝐹12 = −𝐹21
Esempi quotidiani:
• spinta all’indietro
• sostegno oggetto/tavolo
• propulsione nel nuoto
10
Spinta all’indietro
11
Sostegno oggetto/tavolo
12
Propulsione nel nuoto
Propulsione: spostamento di un fluido (liquido o aeriforme)
• Il fluido viene spinto all’indietro dalle braccia
• Il fluido reagisce con una forza in avanti che fa avanzare il corpo
• Grazie alla propulsione gli aerei volano, le navi navigano, i razzi
vanno in orbita
• In questi casi, i motori effettuano la spinta dell’acqua all’indietro
13
Esercizio 3 (sul 3° principio della meccanica)
Due ragazzi di massa rispettivamente 50 kg e 60 kg, si spingono reciprocamente sui
pattini. Se il primo applica una forza di 50 N al secondo, (a) quale sarà la forza che il
secondo applica al primo? (b) Con quale accelerazioni si muoveranno i due ragazzi
supponendo trascurabili gli attriti?
𝑚1 = 50 𝑘𝑔
𝑚2 = 60 𝑘𝑔
𝐹12 = 50 𝑁
𝐹21 = ?
𝑎1 =?
𝑎2 =?
(a) 𝐹12 = 𝐹21 = 50 𝑁
𝑭𝟐𝟏
m1
𝑭𝟏𝟐
m2
ghiaccio
(b) Sul corpo 1 agisce la forza 𝐹21 , e quindi: 𝐹21 = 𝑚1 𝑎1 , da cui:
𝐹21
50𝑁
𝑎1 =
=
= 1𝑚 2
𝑠
𝑚1 50𝑘𝑔
Analogamente, sul corpo 2 agisce la forza 𝐹12 , e quindi: 𝐹12 = 𝑚2 𝑎2 , da cui:
𝐹12 −50𝑁
𝑎2 =
=
= −0.83 𝑚 2
𝑠
𝑚2
60𝑘𝑔
14
15
Forza gravitazionale
𝐺𝑚1 𝑚2
𝐹=−
𝑟
2
𝑟
Tra due corpi di massa 𝑚1 e 𝑚2 , posti a distanza r, si esercita sempre una
forza di attrazione:
• diretta lungo la congiungente tra i due corpi,
• proporzionale alle due masse ,
• inversamente proporzionale al quadrato della loro distanza ,
• 𝐺 = 6.67 ×
2
−11 𝑁 𝑚
10
𝑘𝑔2
• negativa perché attrattiva
•... troppo piccola per essere osservata tra corpi “normali” ...
Forza gravitazionale
𝑚1
𝑚2
𝐺𝑚1 𝑚2
𝐹=−
𝑟
2
𝑟
Se 𝑚 aumenta,
la forza di gravità aumenta
Se 𝑟 aumenta,
la forza di gravità diminuisce
17
Forza gravitazionale sulla terra
𝐺 𝑚 𝑇𝐸𝑅𝑅𝐴 𝑚
𝐹=−
𝑟 = 𝑚𝑔
2
𝑟𝑇𝐸𝑅𝑅𝐴
• 𝑔 è un’accelerazione
• 𝑔 dipende dalla quota
• nelle vicinanze della superficie della terra: 𝑔 = 9.8
𝑚
𝑠2
Forza peso
L’atmosfera terrestre costituisce una regione di spazio vicina alla superficie
della Terra che è sede di un campo di forza gravitazionale: ogni corpo di
massa 𝑚 che si trova in quella regione risente di una forza peso diretta
verticalmente verso il basso.
𝑷 = 𝒎𝒈
Massa, peso, densità
Massa (𝒎)
• Grandezza scalare fondamentale
• Proprietà intrinseca dei corpi (quantità di materia contenuta in corpo)
• Unità di misura: kg
Peso (𝐏 = 𝒎𝒈 ):
• Forza con cui ogni corpo dotato di massa viene attirato dalla terra
𝑘𝑔∙𝑚
• Unità di misura: N = 2 𝑚
𝑠
Densità (d = massa/volume)
• Relazione tra massa e dimensione dei corpi
𝑘𝑔
• Unità di misura: 3
𝑚
Esercizio 4 (sulla forza gravitazionale e forza peso)
Quanto vale la forza gravitazionale tra la terra e un corpo di massa
𝑚 = 1 𝑘𝑔 posto sulla superficie della Terra?
𝒎
𝑚 = 1 𝑘𝑔
𝑀𝑇𝐸𝑅𝑅𝐴 = 5.98 × 1024 𝑘𝑔
𝑅𝑇𝐸𝑅𝑅𝐴 = 6.38 × 106 𝑚
𝐹 =?
𝑭
mM
F G
2
r
2
11 N m
6.67 10
2
kg
9.799 N
1 kg 5.98 10 24 kg
2
6.38 106 m
21
22
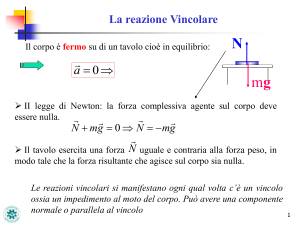
FORZE DI REAZIONE VINCOLARE
• Sono le forze esercitate dai vincoli cui è soggetto il corpo.
• L’azione del vincolo è rappresentata da una forza detta reazione
vincolare.
Il corpo è in equilibrio sotto l’azione della forza peso 𝑷 e della
reazione vincolare 𝑵 (normale alla superficie di contatto).
𝑵 = −𝑷
𝑷 = 𝒎𝒈
𝑵
𝑷
23
Esercizio 5 (sul 2° principio della meccanica)
Una macchina ferma dal peso P è su una salita che forma un angolo 𝜃
con il piano orizzontale. Quale forza devono esercitare i freni per non
farla cadere?
24
Tensione dei fili
Un modo comune di esercitare una forza è tirarlo con una fune.
Un filo inestensibile in tensione sviluppa forze uguali ed opposte ai
suoi capi. La forza 𝑻 si chiama tensione del filo.
Corda fissata ad un estremo
𝑻 𝑭
Corda tirata da ambi gli estremi
• Se la corda venisse tagliata in un punto qualsiasi, la forza
necessaria per mantenere insieme i due pezzi sarebbe proprio
uguale a 𝑻.
• La tensione del filo è sempre parallela al filo.
25
Tensione dei fili
Massa appesa ad una fune
Considerando trascurabile il peso della fune, si ha che la tensione è
uguale lungo tutta la lunghezza della fune.
Questo principio, è alla base dell’utilizzo di carrucole per modificare
la direzione di una forza
−𝑻
𝑷
𝑻
𝑭
26
Esercizio 6 (trazione di una gamba rotta)
Un meccanismo di trazione, che impiega tre pulegge, è applicato ad
una gamba rotta, come mostrato in figura. La puleggia di mezzo è
attaccata alla base del piede ed una massa m fornisce la tensione della
fune. Determinare il valore della massa m se la forza esercitata sulla
base della puleggia di mezzo è 165 N.
𝑵
𝑻𝟏
𝑻𝟏
𝑭
40°
𝑻𝟐
𝑻𝟐
𝑷
27
𝑻𝟏
𝜃 = 40°
𝑭
40°
𝑻𝟐
𝑚 = 11 𝑘𝑔
P = T1 = T2 = mg
𝐹 =?
𝐹 = 𝑇1 𝑐𝑜𝑠𝜃 + 𝑇2 𝑐𝑜𝑠𝜃 =
= 2𝑇 𝑐𝑜𝑠𝜃 =
= 2 𝑚𝑔 𝑐𝑜𝑠𝜃 =
= 2 11𝑘𝑔 9.8 𝑚
𝑠2 0.77 =
= 166 𝑁
28
Forze attrito
Le forze di attrito si sviluppano fra superfici ruvide ed hanno le
seguenti caratteristiche:
• dipendono dallo stato di rugosità delle superfici a contatto
(coefficiente di attrito m);
• hanno la conseguenza di impedire (attrito statico) o
(attrito dinamico) il movimento relativo di tali superfici.
attrito statico
attrito dinamico
decelerare
29