1.
Che cos’è la Fisica?
La Fisica studia i fenomeni naturali e cerca di comprenderli trovando leggi, cioè relazioni, espresse in
forma matematica, tra le grandezze fisiche.
Una qualsiasi affermazione riguardante i fenomeni naturali ha validità scientifica se soddisfa due requisiti
fondamentali:
Deve essere oggettiva cioè interpretabile da chiunque allo stesso modo.
Deve essere verificabile, da chiunque e in qualsiasi momento.
Per questa ragione, le osservazioni relative a un dato fenomeno devono basarsi su caratteristiche dei corpi
che possono essere misurate, alle quali cioè sia possibile associare dei valori numerici. Tali caratteristiche
vengono definite grandezze fisiche.
2.
L’importanza della misura in Fisica
“Ogni qualvolta vi è possibile misurare ed esprimere per mezzo di numeri l’argomento di cui
state parlando, voi conoscete l’argomento di cui state parlando, voi conoscete effettivamente
qualcosa; quando però ciò non vi è possibile o non ne siete capaci, scarsa e insoddisfacente è, da
un punto di vista scientifico, la vostra conoscenza”.
Questa massima di William Thomson (1824 – 1907), eminente fisico inglese (poi Lord Kelvin),
ben evidenzia che il metodo operativo, cioè l’operazione di misura, è il fondamento dello studio
scientifico.
In generale, si può affermare che il processo della conoscenza scientifica passa sempre attraverso
la misurazione di grandezze fisiche, infatti, i dati relativi alle misure effettuate consentono sia la
formulazione di leggi di tipo sperimentale su cui fondare poi dei modelli teorici, sia, viceversa, la
verifica di determinati modelli teorici attraverso la ricerca sperimentale delle misure previste dal
modello stesso. Anche le applicazioni pratiche, legate alle discipline tecnologiche, prevedono la
misurazione di grandezze per giungere alla creazione di tutti gli oggetti di uso quotidiano o a
macchinari che servono per produrre tali oggetti.
3.
Grandezze fisiche e unità di misura
Per misurare qualcosa non possiamo usare i nostri sensi, sia perché a volte ci ingannano (basti pensare
alle illusioni ottiche, che sono veri e propri errori di interpretazione delle sensazioni visive in cui cade il
nostro cervello nel tentativo di valutare dimensioni e forme, o alla sensazione dello scorrere del tempo,
che in taluni casi ci sembra non passare mai e in altri casi ci sembra che sia volato), sia perché comunque
non ci forniscono una valutazione oggettiva ma soggettiva, cioè diversa da persona a persona. Se
vogliamo studiare scientificamente la realtà, non possiamo allora limitarci alle informazioni che danno i
nostri sensi, ma dobbiamo usare strumenti che ci permettano acquisire dati controllabili e il più possibile
svincolati dall’esperienza soggettiva, che ci forniscano quindi una valutazione non soggettiva ma
oggettiva, indipendente dall’osservatore: gli strumenti di misura.
Osserviamo però che non tutto si può misurare, perché non di tutto si può avere una valutazione oggettiva
(es. bellezza, simpatia, etc. sono caratteristiche soggettive). La Fisica si occupa solo di ciò che può essere
misurato.
Chiamiamo grandezza fisica una qualsiasi caratteristica di un corpo o di un fenomeno che può essere
misurata, cioè espressa con un numero. Osserviamo che per misurare una certa grandezza non occorre
fare ragionamenti mentali astratti ma bisogna operare concretamente con strumenti reali; quindi per ogni
grandezza fisica viene elaborato un determinato procedimento di misura. Si dice pertanto che le
grandezze fisiche vengono definite operativamente nel senso che si definisce la grandezza attraverso la
descrizione degli strumenti e della procedura non ambigua (detta protocollo) che servono per misurarla.
Per chiarire meglio questo concetto pensiamo alla seguente definizione che alcuni testi danno
della massa di un oggetto: “la massa è la quantità di materia presente in un corpo”. Pensiamoci
bene: ma che vuol dire questa frase? Utilizzando quello che dice tale frase siamo capaci di
misurare la massa di un certo oggetto? Certamente no.
È invece tutt’altra cosa se si dice che “la massa è quella grandezza fisica che si misura
con una bilancia a bracci uguali”, dando magari istruzioni pratiche precise su come
costruire tale bilancia affinché funzioni nel miglior modo possibile, ed anche istruzioni
su come usarla: mettere in un piatto della bilancia il corpo di cui si vuole conoscere la
massa e sull’altro tante masse campione uguali finché l’asta della bilancia non è in
equilibrio orizzontale; per esempio se l’asta è in equilibrio con tre masse campione da 1 kg, si può dire
che il corpo ha una massa di 3 kg (per verificare che le masse campione sono tutte uguali, basterà
metterne una su un piatto e le altre una alla volta sull’altro piatto e verificare che l’asta è sempre in
equilibrio).
Quest’ultima definizione della massa è una definizione molto diversa dalla prima, che risulta una
definizione puramente astratta senza nessuna applicazione pratica, perché non dice come operare se
vogliamo misurare questa “quantità di materia” e se vogliamo sapere se un corpo ha più o meno “quantità
di materia” di un altro.
Oltre alle caratteristiche, diciamo “astratte” che non si possono misurare (come per esempio la bellezza o
la simpatia citate precedentemente), ci sono altre proprietà dei corpi molto più concrete ma che
nonostante ciò non possono essere considerate grandezze fisiche come per esempio, il sapore, perché non
è stato possibile ancora elaborare per esse un procedimento di misura. La scienza è riuscita a stabilire un
lungo elenco di grandezze misurabili, ed è presumibile che la loro classificazione non sia conclusa. Ciò
che non può essere misurato non può dirsi grandezza fisica, ma ciò non significa che sia qualcosa di
scarsa importanza, significa soltanto che non può essere studiato con i metodi della fisica.
Una precisazione importante: non bisogna confondere la grandezza fisica di un corpo con il corpo stesso!
Di uno stesso corpo si possono misurare più grandezze fisiche. Per esempio, nonostante nella vita
quotidiana spesso si dica, in fisica non ha senso la frase: “misuro un tavolo”; di un tavolo si possono
misurare diverse grandezze fisiche quali la massa, la larghezza, l’altezza, etc. Osserviamo che le
grandezze fisiche non sono oggetti che si possono toccare con mano nel mondo reale, sono concetti
astratti della nostra mente: in natura i fenomeni avvengono, e volendo descriverli scientificamente gli
uomini hanno trovato utile quantificare le loro osservazioni definendo alcune caratteristiche misurabili a
cui hanno dato il nome di grandezze fisiche le quali quindi sono entità astratte che però sono in stretta
relazione con i sistemi materiali che vogliamo studiare.
Esempi di grandezze fisiche sono: la lunghezza, l’area, il volume, il tempo, la massa e molte altre.
4.
Che cosa significa misurare
Come primo esempio semplice ma intuitivo di misura, supponiamo di essere dentro una
stanza i cui lati li chiameremo lato 1 e lato 2 (il terzo sarebbe il lato verticale che però a
noi non interessa) e di voler sapere quante volte il lato 1 è maggiore del lato 2. Senza
nessuno strumento a disposizione pensiamo allora di contare quanti palmi di mano sono
contenuti nel lato 1 e nel lato 2, camminando lungo il bordo e riportando volta per volta il
palmo lungo il bordo stesso. Se per esempio troviamo che il lato 1 contiene 50 palmi
mentre il lato 2 ne contiene 20, concludiamo che il lato 1 è lungo 2 volte e mezzo il lato 2. In questo
processo ci sono appunto le tre fasi tipiche del processo di misura: prima si sceglie la caratteristica dei lati
della stanza da misurare, cioè la loro lunghezza (per vedere quante volte un lato è maggiore dell’altro non
servono altre caratteristiche, come per esempio lo spessore di vernice che c’è su di essi o la loro direzione
rispetto al nord geografico), poi si sceglie l’unità campione (la lunghezza del palmo) e poi si confronta la
lunghezza di ogni lato con l’unità campione, riportando cioè più volte il palmo lungo il bordo di ogni lato
della stanza.
È bene precisare che le ultime due fasi non sempre vengono effettuate direttamente da una persona (come
nell’esempio precedente); molto spesso, quando si sa uno strumento per misurare una certa grandezza,
l’unità di misura è determinata dallo strumento stesso (se uso una bilancia tarata in chilogrammi l’unità
campione non la posso scegliere, sarà per forza il chilogrammo, se uso un righello l’unità di misura sarà
per forza il millimetro) e anche l’operazione di confronto tra l’unità di misura e la grandezza molto spesso
la esegue lo strumento, lasciando a noi solamente la lettura del risultato di tale confronto.
Al termine di ogni processo di misura, a una caratteristica di un corpo (grandezza fisica) viene associato
un ben preciso numero (risultato della misura), che sta a indicare quante volte l’unità di misura scelta è
contenuta nella grandezza misurata. Per esempio, se la lunghezza di una sbarra è 3 m, significa che è pari
a 3 volte quella dell’unità di misura “metro”; se la massa di un oggetto è 4,5 g, significa che è 4 volte e
mezzo quella dell’unità di misura “grammo”.
Riassumendo, quando si vuole misurare una determinata grandezza fisica, si compiono le seguenti
operazioni:
1. Si sceglie quale caratteristica del corpo si vuole misurare (scelta della grandezza fisica)
2. Si sceglie una unità di misura adeguata (detta anche campione di misura o unità campione o
semplicemente campione)
3. Si confronta l’unità di misura con la grandezza, ossia si conta quante volte l’unità campione è
contenuta nella grandezza da misurare (cioè in qualche modo l’unità di misura viene “riportata”
sulla grandezza da misurare).
4. Si determina l’incertezza associata al valore della misura.
Da quanto detto sopra capiamo che una grandezza fisica, per essere tale, deve poter permettere un
confronto. Per esempio, perché la lunghezza è una grandezza fisica? Perché noi possiamo confrontare la
lunghezza di due oggetti e stabilire quante volte uno dei due è più lungo dell’altro. Perché la bellezza non
è una grandezza fisica? Perché non esiste nessun metodo per stabilire quante volte un oggetto è più bello
di un altro.
5. Grandezze fisiche omogenee ed eterogenee
Due grandezze si dicono omogenee quando possono essere confrontate con la stessa unità di misura
(esempio l’area di un tavolo e l’area del pavimento di una stanza). Due grandezze fisiche che non possono
essere confrontate con la stessa unità di misura si dicono eterogenee o non omogenee o eterogenee o
disomogenee (per esempio l’altezza di una persona e la massa di un’automobile).
6. Grandezze fisiche estensive e intensive
Le grandezze fisiche possono essere ulteriormente suddivise in estensive ed intensive.
Si dicono estensive quelle grandezze il cui valore dipende dalla dimensione del campione (estensiva,
ovvero, dipende dall’estensione); sono estensive grandezze quali la massa, il volume, l’energia. Misurare
la grandezza nell’interezza del campione o in una sua piccola parte modifica il risultato.
Si dicono intensive quelle grandezze il cui valore non dipende dalla dimensione del campione; sono
intensive grandezze quali la temperatura, la densità, il calore specifico. Misurare la grandezza
nell’interezza del campione o in una sua piccola parte non modifica il risultato.
campione
porzione del campione
Misurare la massa del campione o della sua porzione dà risultati diversi → la massa è una grandezza
estensiva; misurare la temperatura del campione o della sua porzione dà lo stesso risultato → la
temperatura è una grandezza intensiva.
Dalle grandezze intensive posso ottenere informazioni sulla natura del campione di cui sto misurando la
grandezza; ad esempio, posso avere informazioni sul tipo di sostanza misurandone la densità, il calore
specifico etc.; non posso capire che sostanza sto esaminando misurandone massa, peso, lunghezza… che
sono grandezze estensive.
7.
Unificazione delle unità di misura
Supponiamo di aver misurato il bordo di un tavolo con un pezzo di spago e di aver visto che è lungo 3
volte il pezzo di spago. Se comunichiamo questo risultato a un nostro amico, egli non riuscirà a capire
quanto è lungo il tavolo, a meno che non abbia, o non riesca a procurarsi, un pezzo di spago uguale al
nostro. La comunicazione però resterebbe confinata tra noi e il nostro amico. Se vogliamo comunicare la
lunghezza del nostro tavolo a chiunque, dobbiamo confrontarla con un’altra lunghezza che tutti possano
procurarsi. Se ci mettiamo tutti d’accordo, e ci procuriamo tutti la stessa lunghezza con cui misurare,
ciascuno di noi può comunicare a chiunque altro la lunghezza di qualunque oggetto.
Se non fosse così, sorgerebbero veramente dei problemi: immaginiamo per esempio di ordinare una porta
in legno larga 725 mm; se quello che chiamiamo “millimetro” non fosse uguale al millimetro del
rivenditore, saremmo davvero nei pasticci!
In passato ogni piccola comunità definiva e quindi riconosceva solo le “sue” proprie unità di misura.
Infatti la scelta dell’unità di misura è arbitraria, cioè siamo liberi di definire un’unità in qualunque modo
ci faccia comodo. Si poteva anche avere il caso di uno stesso nome dato a una certa unità di misura da
parte di due civiltà differenti che non aveva lo stesso identico valore: un esempio è lo stadio che per la
Grecia antica era equivalente ai nostri 177 m mentre per l’antico Egitto ai nostri 185 m; oppure: prima
dell'unità d'Italia (1861), sia Firenze che a Bologna le lunghezze erano misurate in braccia, ma il braccio
fiorentino era di 58 cm, mentre il braccio bolognese era di 64 cm.
Dalla seconda metà dell’800 molte esigenze hanno fatto sorgere l’esigenza di una unificazione delle unità
di misura, rispetto alla confusione allora imperante; ad esempio: lo sviluppo delle società industriali,
l’espandersi degli scambi commerciali fra terre sempre più lontane, la necessità da parte della comunità
scientifica di poter confrontare i risultati di esperimenti fatti in luoghi e tempi diversi, etc.
Si è creato quindi un organismo internazionale, che si occupa proprio di definire le unità di misura delle
varie grandezze fisiche a livello mondiale; tale organismo è il BIPM, Bureau International des Poids et
Mesures (ufficio internazionale dei pesi e delle misure) fondato nel 1875 a Sèvres, vicino a Parigi (sito
web www.bipm.org).
In Italia, sono esistiti due organismi che si sono occupati dei problemi legati alle unità di misura: l’Istituto
Elettrotecnico Nazionale “Galileo Ferraris”, istituito nel 1935, con sede a Torino e l’Istituto di metrologia
“Gustavo Colonnetti”, istituito nel 1968, anch’esso istituito a Torino. Dal 2006 il Ferraris e il Colonnetti
si sono fusi nell’Istituto Nazionale di Ricerca Metrologica o INRiM (sito web www.inrim.it), con sede
sempre a Torino, che è un ente pubblico nazionale con il compito di svolgere e promuovere attività di
ricerca scientifica nei campi della metrologia.
8. Sistema di unità di misura
L’insieme delle unità di misura fondamentali, mediante le quali può essere espressa ogni altra grandezza
fisica, costituisce un sistema di unità di misura. Vediamo cosa sono le unità di misura fondamentali. Le
unità di misura si possono suddividere in due gruppi: fondamentali e derivate.
Unità di misura fondamentali: sono quelle unità che vengono definite operativamente. Definire
operativamente un campione significa che nella definizione devono essere indicate le istruzioni pratiche
per costruirlo concretamente. Ricordiamo che le grandezze fisiche sono caratteristiche misurabili dei
corpi che abbiamo nella realtà concreta e pertanto dovranno essere misurate con unità di misura
altrettanto concrete. Per capire meglio cosa significhi che una unità di misura deve essere definita
operativamente, immaginiamo di aver stabilito un contatto radio con una civiltà extraterrestre che abita un
pianeta lontano. Supponiamo che tale civiltà abbia raggiunto lo stesso livello di conoscenze fisiche di noi.
Ovviamente è impossibile che essa usi le nostra stesse unità di misura. Pertanto, se gli dicessimo: “noi
umani siamo alti in media 1,75 m” agli extraterrestri è come se non gli avessimo detto nulla, per loro la
parola “metro” sarebbe semplicemente un nome. Ma se noi riuscissimo a fornirgli tutte le istruzioni
necessarie affinché essi possano costruirsi concretamente nel loro pianeta un campione di lunghezza 1 m,
allora capirebbero cosa significa 1,75 m. Quelle grandezze fisiche che hanno come unità di misura
un’unità di misura fondamentale si chiamano grandezze fisiche fondamentali.
Unità di misura derivate: Le grandezze fisiche non sempre sono indipendenti l’una dall’altra, ma esse
sono legate da opportune relazioni matematiche, soprattutto moltiplicazioni e divisioni. Per esempio, la
grandezza fisica “velocità” si calcola dividendo una lunghezza per un tempo. Pertanto, non è necessario
definire operativamente un campione per ciascuna grandezza fisica (anche perché servirebbero centinaia
di campioni fondamentali!) ma è sufficiente scegliere convenzionalmente un piccolo numero di grandezze
fisiche fondamentali e ricavare da queste tutte le unità delle altre grandezze. Quindi per una grandezza
derivata non esiste nessun campione definito in modo operativo in quanto la sua unità di misura viene
definita utilizzando le unità di misura di quelle grandezze fondamentali che sono legate a essa.
Ritornando alla velocità, non è necessario inventare per essa una nuova unità di misura; poiché infatti la
velocità è il rapporto fra la distanza percorsa e il tempo impiegato per percorrerla, la sua unità di misura
sarà il rapporto tra l’unità di misura della distanza (metro) e l’unità di misura del tempo (secondo), quindi
il m/s. Quelle grandezze fisiche che hanno come unità di misura un’unità di misura una unità derivata si
chiamano grandezze fisiche derivate.
Un buon sistema di unità di misura, per essere tale, deve avere le seguenti caratteristiche:
– I suoi campioni fondamentali devono essere il più possibile invarianti, cioè devono conservare
inalterate le loro caratteristiche nel tempo. Questo ovviamente per far sì che la stessa misurazione dia
sempre il medesimo risultato, se ripetuta. Per chiarire questo concetto facciamo un’analogia presa
dalla vita quotidiana. Supponiamo che un muratore che sta costruendo una casa disponga di un metro
molto sensibile alla temperatura, cioè che si allunga considerevolmente quando la temperatura esterna
è più alta e diventa più corto quando la temperatura si abbassa. È ovvio che le misure delle stanze che
costruirà non coincideranno con quelle stabilite dal progetto e si troverà in una bella confusione
quando si accorgerà che misurando uno stesso lato di una stanza più volte ottiene valori diversi a
seconda del giorno dell’orario nel quale esegue la misura. All’esigenza di rendere invarianti i
campioni di misura di un sistema di unità, si può far fronte in due modi: si può realizzare il campione
in un esemplare unico, conservandolo in condizioni ambientali opportune e accuratamente controllate
(come si fa per il campione di chilogrammo) oppure si può dare al campione una definizione costituita
da regole operative precise, non ambigue, che ne permettano la facile ed esatta riproduzione da parte
di chiunque voglia disporne (come si fa per il campione di lunghezza); in questo secondo caso ci si
riferisce a esemplari “naturali”, come verrà meglio specificato in seguito.
– I suoi campioni fondamentali devono essere facilmente riproducibili. Cioè deve essere relativamente
facile eseguire copie standard del campione, in modo da creare i campioni secondari che si usano
nell’industria, dai quali poi derivano gli strumenti che usiamo nella vita comune. Se il campione è
definito da regole operative abbiamo detto sopra che tutti, attenendosi a tale regole, possono
riprodurre il campione. Se il campione invece esiste in un esemplare unico, è indispensabile che se ne
possano fare con facilità delle copie, il più possibile uguali, che possano servire da campioni
secondari per l’uso corrente. Per esempio il campione di massa, il chilogrammo,
riconosciuto a livello internazionale è un cilindro di platino-iridio (d=39 mm,
h=39mm, Pt 90%, Ir 10%) conservato presso il BIPM. Campioni secondari, ottenuti
mediante il confronto con una bilancia a bracci uguali, sono stati inviati a laboratori
specializzati in altri paesi e le masse di altri oggetti possono essere determinate
pesandole su bilance a bracci uguali insieme ai campioni secondari. I campioni
secondari in possesso dei vari paesi vengono rimossi non più di una volta all’anno
per tarare i campioni terziari che sono usati altrove. Molto raramente i campioni
secondari vengono portati in Francia per riconfrontarli con il campione principale (o
primario). Per l’Italia, la copia numero 62 del chilogrammo campione (campione secondario) è stata
costruita nel 1973 dal BPIM ed è conservata a Torino, presso l’INRiM.
– Le sue unità di misura fondamentali devono essere convenienti cioè devono essere pratiche e
possibilmente comode da usare sia nella vita di tutti i giorni sia nella pratica scientifica. Ossia
conviene, per quanto possibile, che l’unità venga scelta in modo tale che gli esemplari della grandezza
fisica con cui si ha di solito a che fare risultino caratterizzati da numeri né tropo grandi né troppo
piccoli, possibilmente dell’ordine dell’unità (quando ciò non è possibile, o interferisce con altre
richieste più importanti, si rimedia facendo uso in pratica di multipli o sottomultipli convenienti del
campione prescelto). Per esempio, il metro è un’unità a misura d’uomo. Infatti la nostra altezza e
–
–
–
molti oggetti che incontriamo nella vita quotidiana sono dell’ordine del metro. Se fossimo piccoli
come le formiche o grandi come i dinosauri, con ogni probabilità avremmo scelto una diversa unità
per misurare le lunghezze. Una cosa da chiarire è questa: sono le unità di misura a dover essere
convenienti (infatti l’unità “metro”, l’unità “secondo” e l’unità “chilogrammo” sono usate
comunemente da tutti), ma non certo i campioni fondamentali, che vengono infatti realizzati con
procedimenti molto sofisticati (basti pensare all’orologio atomico per realizzare il campione di
secondo). Questo non perché gli scienziati vogliano tenere solo per loro i campioni, ma perché quello
che interessa prima è la loro invariabilità, e poi si fa un grande sforzo per rendere facilmente
accessibili a tutti coloro che ne hanno bisogno dei duplicati il più fedeli possibile ai campioni
fondamentali.
Le sue grandezze fondamentali devono essere indipendenti fra loro e il loro numero deve essere il più
piccolo possibile, ma nello stesso tempo il sistema deve risultare completo, cioè l’insieme delle
grandezze fondamentali deve essere sufficiente a descrivere tutti i fenomeni fisici finora conosciuti.
Deve essere coerente, cioè le grandezze derivate devono ottenersi da quelle fondamentali tramite
prodotti, quozienti e potenze senza alcun coefficiente numerico
Deve avere i multipli e i sottomultipli decimali
9. Il Sistema Internazionale
Il Sistema Internazionale delle unità di misura (abbreviato S.I, pronuncia “ esseì ”) è il più diffuso sistema
di unità di misura ed è usato da tutta la comunità scientifica a partire dal 1961, anno della sua nascita. Al
Sistema Internazionale hanno formalmente aderito la quasi totalità dei paesi di tutto il mondo; in Italia e
in Europa è l’unico sistema di unità di misura ammesso. Ancora oggi esistono alcuni Paesi, come
l’Inghilterra e gli Stati Uniti, che non si sono ancora uniformati totalmente all’S.I. ed utilizzano unità di
misura proprie e non universali, come: pollice, piede, miglio, libbra, oncia, pinta, gallone, grado
Fahrenheit, etc. (sistema britannico). In alcuni settori commerciali, inoltre, continuano ad essere usate
ancora delle unità di misura anomale, come per esempio il carato (200 mg) per le pietre preziose o il
barile per il petrolio. Il sistema britannico permane inoltre in alcuni settori tecnologici (idraulica…):
diametri di tubature (inch, pollici), filettature, etc. Occorre solo ricordare che il sistema britannico è di
natura non decimale (1 foot = 12 inch…). Ritornando al S.I., i suoi campioni sono definiti solo per sette
grandezze fondamentali. Tutte le altre grandezze fisiche sono derivate, cioè le loro unità di misura si
ottengono da quelle delle grandezze fondamentali attraverso le relazioni matematiche che le definiscono.
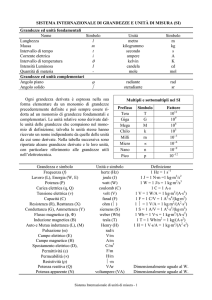
Le unità fondamentali del S.I. sono riportate nella tabella che segue. In essa sono scritte anche le
definizioni delle unità di misura, per quanto possano sembrare quasi tutte pressoché incomprensibili, un
po’ per completezza di documentazione, e un po’ per dare un’idea, seppur vaga, della complessità che
comporta la definizione di un’unità di misura. Accanto alle definizioni sono anche riportate le date in cui
sono state adottate.
Grandezza
fisica
lunghezza
massa
tempo
intensità
1
2
Grandezze fisiche e unità di misura fondamentali del S.I.
Nome
Simbolo
Definizione
dell’unità di
dell’unità
misura
di misura
metro
m
il metro è lunghezza del tragitto percorso nel vuoto
dalla luce in un intervallo di tempo pari alla frazione
1/299.792.458 di un secondo (1983)
chilogrammo
kg
il chilogrammo è la massa del prototipo
internazionale realizzato in platino iridio nel 1889 e
conservato a Sèvres dal BIPM1 (1901)
secondo
s
il secondo è la durata di 9 192 631 770 periodi della
radiazione corrispondente alla transizione tra due
livelli iperfini [...]2 dello stato fondamentale
dell’atomo di cesio-133 (1967)
ampere
A
L’ampere è l’intensità di corrente elettrica che,
Questa è, attualmente, l’unica unità fondamentale basata su un campione materiale.
da (F=4, MF=0) a (F=3, MF=0).
di corrente
elettrica
temperatura
kelvin
K
intensità
luminosa
candela
cd
quantità di
sostanza
mole
mol
mantenuta costante in due conduttori rettilinei,
paralleli, di lunghezza infinita, di sezione trasversale
trascurabile e posti alla distanza di un metro l’uno
dall’altro, nel vuoto, produce la forza di 2 · 10 7 N su
ogni metro di lunghezza di ogni filo (1948)
Il kelvin è la frazione 1/273,16 della temperatura
termodinamica del punto triplo dell’acqua (1967)
la candela è l’intensità luminosa emessa, in una data
direzione, da una sorgente monocromatica di
frequenza 540 · 1012 Hz, e di intensità pari a 1/683
W/sr (1979)
la mole è la quantità di sostanza di un sistema che
contiene tante entità elementari quanti sono gli atomi
contenuti in 0,012 kg di Carbonio 12. (1971)
Le entità elementari devono essere specificate e
possono essere atomi, ioni, elettroni, etc., ovvero
gruppi specificati di tali particelle.
Nella tabella seguente sono elencate alcune delle grandezze fisiche derivate più importanti nell’S.I.:
Principali grandezze fisiche derivate nel S.I.
Grandezza fisica
Simbolo
Simbolo
Nome dell’unità
della
dell’unità
di misura
grandezza
misura
di
Equivalenza in termini di
unità fondamentali S.I.
area
A
metro quadro
m2
volume
V
metro cubo
m3
velocità
v
metro al secondo m/s, m · s-1
accelerazione
a
metro al secondo
m/s2, m · s-2
quadro
densità
ρ, d
chilogrammo
metro cubo
potenza
P
watt
W
forza
F
newton
N
kg · m · s-2
momento della forza
M
newton metro
N·m
(kg · m · s-2) · m
pressione
p
pascal
Pa
N · m-2 kg · m-1 · s-2
energia, lavoro
E
joule
J
N·m
carica elettrica
q
coulomb
C
A·s
differenza di potenziale
V, E
elettrica, tensione elettrica
volt
V
J · C-1 m2 · kg · s-3 · A-1
resistenza elettrica
R
ohm
Ω
V · A-1 m2 · kg · s-3 · A-2
frequenza
f
hertz
Hz
s-1
al
kg/m3, kg · m-3
J · s-1
kg · m2 · s-3
kg · m2 · s-2
Nella tabella seguente sono infine riportate alcune unità di uso corrente che però non fanno parte del S.I.
Unità di misura di uso corrente non facenti parte del S.I.
temperatura
T
celsius
°C
tempo
t
minuto
min
tempo
t
ora
h
tempo
t
giorno
d
volume
V
litro
L, l
pressione
p
atmosfera
atm
pressione
p
bar
bar
massa
m
quintale
q
massa
m
tonnellata
t
energia
E
caloria
cal
angolo
α
grado
°
E’ da notare che, nel corso della storia, le definizioni dei campioni non sono sempre state queste, perché
si sono continuamente evolute. E’ cioè successo che, per una certa grandezza fisica fondamentale, una
nuova definizione di campione ha soppiantato la vecchia, anche se la nuova definizione è sempre stata
scelta in modo da essere il più possibile in accordo con quella vecchia.
Inoltre, la scelta di quali grandezze fisiche debbano essere fondamentali è spesso dettata da motivazioni di
carattere tecnico-pratico. Per esempio, in passato la carica elettrica era considerata una grandezza
fondamentale e l’intensità di corrente elettrica una grandezza derivata; ora i ruoli sono invertiti perché è
tecnicamente più semplice misurare una corrente elettrica che misurare una carica elettrica: è cioè più
semplice costruire sperimentalmente il campione di corrente elettrica che il campione di carica elettrica.
Come si vede dalla prima tabella sopra, tranne che per la massa, per le grandezze fondamentali si usano i
campioni naturali, ossia si sfruttano fenomeni naturali (per il metro si sfrutta la luce, per il secondo si
sfrutta il comportamento degli atomi di cesio, etc). I campioni naturali, a differenza dei campioni
materiali che sono quelli realizzati dall’uomo, non deteriorano nel tempo e sono accessibili a tutti, anche
se tramite strumentazioni sofisticate. Ricordiamo a questo proposito che la precedente definizione di
metro come la lunghezza di quella sbarra di platino-iridio conservata presso il BIPM era legata ad un
campione materiale, e quindi più facilmente variabile nel tempo.
10. Regole di scrittura dei simboli delle unità di misura
I simboli delle unità di misura devono essere scritti nel seguente modo:
– il simbolo è unico! (si scrive 12 s e non 12 sec e neanche 12 secs)
– vanno scritti sempre dopo il valore numerico, mai prima (8 kg e non kg 8)
– non devono essere mai seguiti da un punto (12 m e non 12 m.)
– dopo il valore numerico si usa sempre il simbolo, mai il nome per esteso (4 s e non 4 secondi)
– vanno scritti con la iniziale minuscola. Fanno eccezione i simboli di quelle unità che derivano da nomi
propri. (esempio il volt: V; l’ampere: A; etc.)
– davanti a una unità di misura non si può usare più di un prefisso per i multipli o i sottomultipli (3 nA e
non 3 mA)
– per il separatore decimale è ammesso sia il puntino che la virgola (va bene 3.25 mV e anche 3,25 mV)
11. Multipli e sottomultipli
Spesso, quando le misure delle grandezza rispetto a una prefissata unità di misura sono molto grandi o
molto piccole, si usano particolari prefissi (tabella seguente) per indicare multipli e sottomultipli di base
10 dell’unità di misura prescelta. Si noti che il sistema dei multipli e dei sottomultipli è di tipo decimale:
ciò significa che i multipli e i sottomultipli dell’unità campione si ottengono gli uni dagli altri
moltiplicando o dividendo per 10, 100, 1000 etc. Per esempio, il chilometro (simbolo km) è il multiplo di
fattore 1000 del metro, cioè è 1000 metri; il nanosecondo (simbolo ns) è il sottomultiplo di fattore
1000000000 del secondo, cioè un miliardesimo di secondo.
Qui sotto viene riportata una tabella con i principali prefissi da apporre alle u.d.m. per formarne i multipli
o sottomultipli (in grassetto sono evidenziati i principali):
MULTIPLI
Nome
prefisso
deca
etto
chilo
mega
giga
tera
peta
exa
zeta
yota
SOTTOMULTIPLI
Valore Simbolo Nome prefisso Valore
Simbolo
101
102
103
106
109
1012
1015
1018
1021
1024
d
c
m
μ
n
p
f
a
z
y
da
h
k
M
G
T
P
E
Z
Y
deci
centi
milli
micro
nano
pico
femto
atto
zepto
yocto
10–1
10–2
10 –3
10–6
10–9
10–12
10–15
10–18
10–21
10–24
Ad esempio potremo descrivere la misura l =3,5·10 –9 m come l = 3,5 nm (leggi 3,5 nanometri); allo
stesso modo potremmo scrivere m =3,5·10 –9 g come m = 3,5 ng (leggi 3,5 nanogrammi) oppure
V=3,5·10 -11 L come 35 pL (leggi 35 picolitri).
Esercizini
1. Le dimensioni dei tre lati di una scatola da scarpe sono 21,0 cm, 11,2 cm e 10,5 cm. Esprimi le misure
dei lati in millimetri, in metri, in micrometri, in chilometri; scegli una faccia della scatola e calcola la sua
area esprimendola in cm2, poi in m2, poi in mm2; calcola il volume della scatola in cm3, dm3 e m3.
2. Una bottiglia di acqua minerale ha un volume di 1,5 L. Quante bottiglie servono per riempire una
piccola piscina da 3m3?
3. Eseguire le seguenti equivalenze:
1 cm3 = …
m3
10-4 cm3 =
L
4,5 · 104 dm3 =
km3
-2
3
3
3
–4
3
10 m =
cm
1L=
m
3 · 10 hm =
mm3
7 · 10-3 cm3 =
mm 3
10 L =
dm3
0,8 · 108 m3 =
dm3
3
3
3
10
3
10 L =
mm
45 m =
mm
10 mm =
m³
3
3
-2
3
12.34 mL =
cm
1 km =
L
2.2· 10 mm =
cm3
4. Esprimere 3 g/cm3 in kg/dm3 e in kg/m3.
5. Un agricoltore vuole comprare un terreno in una certa zona. Sapendo che in quella determinata zona un
appezzamento di terreno di 42000 m2 ha un costo di 2100€:
a)
che unità di misura hanno i numeri 42000/2100 e 2100/42000 e quale significato hanno?
b)
Quale sarà il costo di un appezzamento di 200 m2? Spiegare brevemente il ragionamento.
c)
Quale estensione avrà un appezzamento il cui costo è 700 euro? Spiegare brevemente il
ragionamento.
12. Approfondimenti
Come abbiamo già detto in precedenza, nel corso della storia le definizioni dei campioni non sono sempre
state le stesse, perché si sono continuamente evolute. Si è avuto cioè che, per una certa grandezza fisica,
una nuova definizione di campione ha soppiantato la vecchia, anche se la nuova definizione fu scelta in
modo da essere il più possibile in accordo con quella vecchia. Studieremo ora in dettaglio la natura delle
grandezze fisiche lunghezza, tempo e massa e presenteremo la storia delle loro unità e degli strumenti di
misura adottate per esse.
Lunghezza
Nel 1792 la neonata repubblica di Francia stabilì come unità di misura della lunghezza il metro, definito
come la decimilionesima parte della distanza fra il Polo Nord e l’Equatore lungo il meridiano passante per
Parigi. Per ottenere la lunghezza del metro così definito, due astronomi francesi compirono un’impresa
durata sette anni, durante la quale misurarono la lunghezza dell’arco compreso tra Dunkerque (costa
settentrionale francese) e Barcellona (Spagna). Al termine della difficile missione, persino Napoleone
Bonaparte, entusiasta, sentenziò che “il metro durerà per sempre”. Alla fine, per ragioni pratiche, questa
unità di misura riferita alle dimensioni della Terra fu abbandonata e si giunse nel 1889 a definire il metro
come la distanza tra due linee sottili incise vicino alle estremità di una barra di platino-iridio custodita alla
temperatura di 0 °C presso il BIPM. La barra è stata sagomata con una sezione a forma di X per resistere
anche a possibili flessioni. Copie di grande precisione della barra furono mandate a laboratori di
campionatura in tutto il mondo. Questi campioni secondari furono usati per tarare altri campioni, sempre
più accessibili, così che alla fine qualunque dispositivo per la misura di lunghezze derivava la sua autorità
dalla barra del metro campione attraverso una complicata catena di confronti. Venne però il momento in
cui la scienza e le tecnologie moderne pretesero un’unità di misura campione più precisa, e nel 1960 il
metro venne così ridefinito come 1650763,73 lunghezze d’onda di una particolare luce color rosso
arancio emessa dalla scarica in un tubo a gas rarefatto di cripton-86. Questo ostico numero di lunghezze
d’onda fu scelto in modo che la nuova unità di misura fosse il più possibile in accordo con il vecchio
campione del metro – barra. Gli atomi di cripton-86 del campione atomico di unità di misura della
lunghezza si trovano dappertutto, sono identici fra loro ed emettono luce esattamente della stesa
lunghezza d’onda. Il campione che veniva quindi definito era pertanto molto più invariante e accessibile
del precedente; infatti, occorre considerare il fatto che, per quanto i tratti sulla sbarra di platino-iridio
possano essere sottili, rimane sempre una piccola imprecisione nella misura della loro distanza ed inoltre
è inevitabile che le copie presentino piccolissime differenza di costruzione. Verso il 1983 l’esigenza di
maggior precisione era arrivata a tal punto che perfino il campione a cripton-86 non era più adeguato e fu
adottata la definizione riportata sopra in tabella, che viene usata tutt’ora.
Tempo
Ognuno di noi ha un’idea intuitiva del tempo che trascorre tra un evento e un altro, ma se ci chiedessero:
“che cos’è il tempo?” difficilmente sapremmo rispondere “a bruciapelo”. Definire cosa sia il tempo è
difficile, bisogna ammetterlo. Il filosofo Agostino, già 16 secoli fa’, si chiede che cosa sia il tempo e
fornisce una risposta singolare. Trattando del tempo, egli dice: "Se nessuno me lo chiede, lo so; se cerco
di spiegarlo a chi me lo chiede, non lo so."3.
Un tentativo bislacco di definire il tempo si trova in un noto vocabolario della lingua
italiana: "il tempo è lo spazio indefinito nel quale si verifica l’inarrestabile fluire degli
eventi". Dopo aver letto 3 volte questa frase (e non averci capito nulla), uno si
scoraggia! Almeno il buon Agostino è più apprezzabile, in quanto è stato onesto,
confessando candidamente di non sapere cosa sia il tempo.
Queste (e molte altre) frasi che tentano di definire il tempo sono inaccettabili,
semplicemente perché non sono operative, cioè non dicono come si deve fare a misurare. Come si è detto
più sopra, il tempo è una grandezza fisica fondamentale e, come tale, è definita operativamente, ovvero:
definisco la grandezza fisica “tempo” definendo il modo con cui la misuro.
La fisica quindi risponde alla domanda “che cos’è il tempo?” avendo cura di descrivere il metodo di
misura e lo strumento adoperati: la definizione di tempo, semplicemente, è la descrizione di come si fa a
misurarlo; più precisamente, la fisica s’interessa alla misura della durata di un fenomeno, confrontandola
con quella di un altro fenomeno, assunta come unità di misura.
Per la scelta dell’unità di misura del tempo è naturale riferirsi a fenomeni periodici, cioè quei fenomeni
che, mentre si svolgono, hanno la caratteristica di ricominciare da capo, ripetendosi sempre nello stesso
modo. Questi fenomeni possono essere la rotazione della Terra (nelle meridiane solari), la caduta della
sabbia o dell’acqua (nelle clessidre), l’oscillazione di un pendolo (negli orologi a pendolo), l’oscillazione
di una piccola rotella metallica collegata a una molla (il bilanciere, negli orologi meccanici da polso), le
3
Questa frase si trova nel libro XI delle Confessioni, opera in 13 libri scritta attorno al 400 d.C. da Agostino
d’Ippona (354 d.C. - 430 d.C.), meglio noto come sant'Agostino.
vibrazioni di un cristallo di quarzo (in un orologio al quarzo) o le oscillazioni elettromagnetiche prodotte
da alcuni atomi di cesio (negli orologi atomici).
Quindi, se si vuole misurare la durata di un certo fenomeno, si confronta tale durata con la durata di un
fenomeno periodico (cioè che si ripete uguale a se stesso), quest’ultimo assunto come unità di misura,
contando quante volte si ripete quest’ultimo durante la durata del primo.
Per esempio, si può misurare il tempo che impiega a sciogliersi un blocco di ghiaccio mediante una
clessidra. Se osserviamo che il ghiaccio si scioglie mentre la clessidra si svuota venti volte, abbiamo
confrontato la durata di un fenomeno (fusione del ghiaccio) con la durata di un fenomeno periodico (lo
svuotamento e capovolgimento della clessidra) che assumiamo come unità di misura; si dirà quindi che il
ghiaccio si è sciolto in un tempo di 20 clessidre.
Usare una clessidra è quindi un modo semplice per misurare il tempo, ma questo metodo può essere
scomodo, ad esempio perché si deve stare continuamente a guardare la clessidra, in modo da essere subito
pronti a capovolgerla!
Molto più facile è usare un fenomeno periodico che “riparte da solo”: ad esempio il battito del polso è un
fenomeno periodico che sembra ripetersi sempre uguale a se stesso. Potremmo quindi usarlo come unità
di misura del tempo. Ma, a ben vedere, è un fenomeno non troppo regolare: è facile infatti rendersi conto
che il ritmo dei battiti cambia nell’arco della giornata e soprattutto se abbiamo eseguito una certa attività
fisica. Misurare il tempo non è quindi semplice, in quanto non è semplice trovare dei fenomeni che siano
effettivamente periodici.
Durante la sua storia, l’uomo ha sempre cercato dei fenomeni periodici con cui misurare il tempo: il Sole
e la Luna, le stagioni sono stati i primi “orologi” con i quali i popoli primitivi hanno cominciato a
misurare il tempo: infatti l’alternarsi delle stagioni, il percorso del Sole nel cielo o il moto della Luna,
sono fenomeni che sembrano ripetersi con un ritmo regolare, sempre uguali a se stessi, cioè periodici. Le
fonti e le ricostruzioni storiche attestano che, sfruttando questi moti periodici, sin dal tempo dei Sumeri
(Mesopotamia, 4000 a.C., attuale Iraq, Iran e Siria), vennero costruiti orologi solari (meridiane) ed anche
la suddivisione del tempo venne legata al moto apparente del Sole: grazie alla meridiana solare, i Sumeri
avevano diviso la giornata di luce in 12 parti4.
Successivamente, i Babilonesi (Mesopotamia, 3000 a.C.) ereditarono dai Sumeri la divisione in 12 parti,
affiancando ad essa un innovativo modo di suddividere gli interi: i Babilonesi infatti contavano in base
60, per cui suddividevano un intero in 60 parti, ciascuna parte in altre 60 parti e così via5.
Parallelamente alla civiltà dei Babilonesi, per avere misure più precise e indipendenti dalla presenza del
Sole, venne inventata la clessidra, probabilmente dagli Egizi (Egitto, 3000 a.C.); gli Egizi poterono così
estendere la suddivisione in 12 parti, appresa dai Babilonesi, anche alla notte, per un totale di 24 parti per
ogni giorno.
La suddivisione della giornata di luce in 12 parti, le ore, adottata dai Babilonesi si diffuse anche
nell’antica Grecia, giungendo infine al mondo occidentale tramite la civiltà dei Romani: nella Roma
antica la prima ora iniziava all’alba e la dodicesima ora terminava al tramonto.
Va comunque sottolineato che, all’incirca fino al 1300, non si sentì la necessità di avere una unità di
misura del tempo rigorosamente definita ed universale. Questo perché per svolgere le attività di ogni
giorno una definizione approssimativa del tempo (la giornata di luce suddivisa in 12 ore) era più che
sufficiente. Questo anche perché, almeno fino a quel momento, tramite clessidre e meridiane era
praticamente impossibile misurare le frazioni dell’ora.
Fu solo nel 1300 che, con l’invenzione dell’orologio meccanico, divenne possibile misurare le frazioni
dell’ora: si realizzò così, nella pratica, quell’idea di suddividere un’ora in sessanta parti più piccole, tutte
uguali, che si era tramandata e conservata intatta fin dal tempo dei Babilonesi. Ciascuna parte dell’ora
veniva chiamata in latino pars minuta prima, che significa “prima piccola parte”, poi abbreviata in
«minuto»; e queste, a loro volta, venivano suddivise in altre 60 parti ancora più piccole, ciascuna delle
4
I Sumeri usavano la base 12 (base duodecimale) per contare, che ha il vantaggio di avere molti divisori: 6, 4, 3, 2
e che, a confronto con i due soli divisori della base 10 (base decimale), risulta più versatile in aritmetica, soprattutto
per fare le divisioni.
5
I Babilonesi usavano la base 60 (base sessagesimale, da sessagesimo che vuol dire sessantesimo) per contare, cioè
60 era il numero più grande a cui avevano dato un nome; si reputa che la scelta della base 60 derivasse
probabilmente da motivi pratici, soprattutto legati al commercio, visto che 60 è divisibile per 2, per 3, per 4 e per 5
ed è il più piccolo numero ad avere questa proprietà. Similmente i Sumeri, popolo più antico dei Babilonesi, quindi
meno evoluto, avevano scelto di contare in base 12.
quali era chiamata, sempre in latino, pars minuta secunda (seconda piccola parte), poi abbreviata in
«secondo».
Durante il Rinascimento, con gli anni, la tecnologia meccanica si affinò e permise di
misurare il tempo in modo via via migliore. Un contributo rilevante alla misura del
tempo venne nel 1600 da Galileo Galilei, grazie alle sue scoperte sullo studio del
moto di un pendolo. Egli osservò infatti che le oscillazioni di un pendolo, purché non
siano troppo ampie, sono un fenomeno periodico molto regolare. L’unione del
pendolo ai vecchi orologi meccanici permise a Galileo di creare un orologio capace
di contare i secondi in maniera attendibile.
Nel 1875, si arrivò finalmente alla definizione del secondo accettata dalla comunità
scientifica e si stabilì che “il secondo è la frazione 1/86400 del giorno solare medio”.
Il giorno solare è l’intervallo di tempo fra due successivi passaggi di Sole su uno
stesso meridiano; si usò 86400 perché il giorno solare fu diviso in 24 ore, ogni ora in 60 minuti e ogni
minuto in 60 secondi, per un totale appunto di 86400 secondi. Il giorno solare medio è la media aritmetica
del giorno solare fatta in un anno. Infatti già con i cronometri del 1875 si riusciva ad apprezzare che
l’“orologio” Terra batte il giorno non così regolarmente come si può pensare: esso dipende dalle maree
provocate dalla Luna, dalla posizione della Terra sull’eclittica (che varia durante l’anno) e, in minor parte,
dalle perturbazioni atmosferiche su scala mondiale e anche dai terremoti; si ricorse quindi alla media
aritmetica nell’arco di un anno.
I migliori orologi meccanici a pendolo e a bilanciere 6 oggi disponibili possono perdere/acquistare, in un
anno, fino a 10 secondi circa, il che significa che la loro incertezza di misura è 10/(60*60*24*365)
secondi, cioè dell’ordine di 1 microsecondo. Sebbene nella vita quotidiana questo errore non sia rilevante,
può capitare che sia necessaria una misura del tempo più precisa. Per questo scopo si utilizzano le
proprietà del quarzo, un solido cristallino molto rigido. Quando la superficie superiore e la superficie
inferiore del cristallo vengono avvicinate e poi lasciate libere di muoversi, vibrano come se fossero legate
fra loro da una molla. Grazie alla natura piezoelettrica del quarzo, è possibile realizzare circuiti elettrici
sensibili alle sue rapide oscillazioni.
La nascita dell’elettronica e l’invenzione dell’orologio al quarzo (anni ‘30 del Novecento) hanno
permesso di osservare che anche l’anno solare medio non è un tempo così stabile: la velocità con cui la
Terra ruota intorno al proprio asse sta lentamente calando e quindi il secondo definito tramite il passaggio
del Sole su un meridiano avrà, tra un secolo, una durata maggiore di quella che ha oggi.
Durante il Novecento si è pertanto deciso di svincolare la definizione del secondo dai fenomeni
astronomici e di utilizzare le possibilità offerte dalla nascente branca della fisica: la meccanica
quantistica. La meccanica quantistica ha permesso di creare intervalli di tempo basati su fenomeni
periodici che avvengono negli atomi: in questo caso fanno da “pendolo” le oscillazioni di campo
elettromagnetico generato da transizioni di stato di atomi o molecole, fenomeni estremamente costanti nel
tempo e non influenzabili dall’esterno; gli apparati che permettono questo sono detti orologi atomici. Ci
fidiamo molto degli orologi atomici, perché risulta difficile pensare che il comportamento di un atomo
vari con le stagioni o a causa della presenza della Luna!
In un orologio atomico al cesio, un cristallo di quarzo è fatto oscillare in modo da “accordare” la
frequenza del proprio moto a quella dell’onda elettromagnetica che è emessa o assorbita da atomi di cesio
selezionati in maniera opportuna. In questo modo, ciò che determina la precisione dell’orologio non sono
le proprietà dell’oscillatore al quarzo, ma quelle, molto più stabili e precise, dell’onda elettromagnetica
emessa o assorbita dagli atomi di cesio.
Ci fidiamo in particolare degli orologi atomici al cesio perché si può dimostrare teoricamente che due di
questi orologi dovrebbero funzionare 50 milioni di anni prima che si verifichi uno scarto superiore a 1
secondo fra le loro letture di tempo.
Ebbene, nel 1967 si decise di abbandonare le definizioni di tipo astronomico, e venne formulata la
definizione che ancora oggi utilizziamo, riportata nella tabella più sopra. Questa nuova definizione,
6
E' un orologio basato su un anello che, mentre ruota, tende una piccola molla; la molla tesa richiama l'anello verso
la sua posizione di equilibrio e il processo si ripete. E' stato inventato nel 1675 dallo scienziato olandese Christiaan
Huygens.
apparentemente un po’ complicata, si basa sul fatto che gli atomi emettono radiazioni, alcune visibili
(luce) e altre no: ciascuna è contraddistinta da un suo periodo di oscillazione. La definizione attuale
dell'unità di tempo si basa sul conteggio di un numero prestabilito di tali periodi di oscillazione.
Oggigiorno, ad esempio, ogni satellite GPS ha un orologio atomico a bordo che è a sua volta
sincronizzato con il tempo UTC (tempo coordinato universale). In Italia, presso l’ INRiM, è in funzione
un orologio atomico al cesio; il tempo misurato da tale orologio è accessibile liberamente via Internet
usando il protocollo di comunicazione NTP (Network Time Protocol).
Massa
Nel 1791 l’Accademia delle Scienze di Francia ebbe l’incarico di definire il campione universale di
massa, e fissò questo riferimento uguale alla massa di un decimetro cubo di acqua distillata alla
temperatura di 4 °C alla pressione normale di un’atmosfera. In pochi anni, tuttavia, ci si rese conto che
tale campione naturale risultava poco adatto per le misure, e nel 1799 esso fu sostituito da un campione
metallico. L’attuale cilindro di platino-iridio, realizzato nel 1889, è la riproduzione più recente e precisa
di questo campione iniziale e costituisce ancora oggi l’unità campione universale. Esistono sei copie
ufficiali del prototipo, custodite al BIPM (se il chilogrammo campione primario dovesse rovinarsi, il
BIPM lo ricostruirebbe per confronto con queste sei copie). Oltre a queste, esistono altre copie (più di 80,
dette campioni secondari) che sono state distribuite alle varie nazioni che aderiscono al S.I.
Title: Fisica
Author: prof. ing. Gabriele Baldi
Email: gabriele [_D_O_T_] baldi [#A#T#] tin [D@O@T] it
This stuff was released on 02 oct 2016 under a CC BY-NC licence! ||^_^||