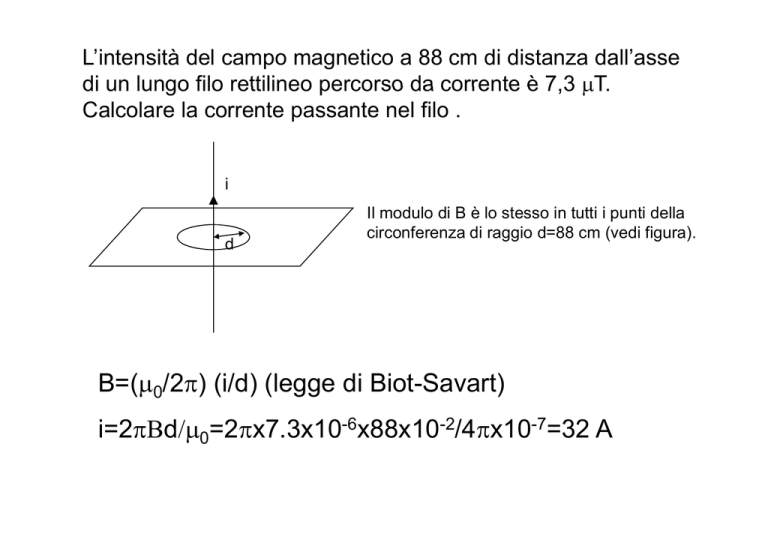
L’intensità del campo magnetico a 88 cm di distanza dall’asse
di un lungo filo rettilineo percorso da corrente è 7
7,3
3 μT.
μT
Calcolare la corrente passante nel filo .
i
d
Il modulo
d l di B è llo stesso
t
iin ttutti
tti i puntiti della
d ll
circonferenza di raggio d=88 cm (vedi figura).
B=(μ
(μ0/2π)) (i/d)
( ) (legge
( gg di Biot-Savart))
i=2πΒd/μ0=2πx7.3x10-6x88x10-2/4πx10-7=32 A
F
v
B
F=qvBsin90°=10
F=qvBsin90
=10-66x104x2=2x10-22 N
F è perpendicolare al piano individuato dal vettore velocità e dal
vettore campo d’induzione magnetica (piano di figura). Il verso è
dato dalla regola della mano destra in modo che vv, B e F formino
una terna cartesiana levogira (F entra nel piano).
B
30°
L
F i L B sin 30°
F=i
30°=10x2x3x0.5=
10x2x3x0 5 30 N
La di
L
direzione
i
d
della
ll fforza è perpendicolare
di l
all ffoglio;
li il verso è
entrante nel foglio (regola della mano destra)
i
B0: campo magnetico uniforme
B0
P2
P1
d
B0
B
B
Il campo di induzione magnetica prodotto dal filo percorso da corrente (B in nero vedi figura), giace in un
piano perpendicolare al filo e,in ogni punto, è tangente alla circonferenza di raggio d (distanza dal filo)
centrata sul filo. La distanza d dal filo si ottiene imponendo che i moduli dei campi B (prodotto dal filo) e B0
(campo stazionario) siano uguali.
B=(μ0/2π)×(i/d)=Β0 da cui: d =(μ0/2π)×(i/ Β0)=(4π ×10-7/2π) ×100/0.005=
=4 ×10-3m
In due punti sulla circonferenza di raggio d (P1 e P2 vedi figura) la direzione della retta tangente avrà la
stessa direzione di B0 Tuttavia solo nel punto P1 il verso di B è opposto a quello di B0, mentre in P2 è
concorde. Solo in P1, quindi, il campo magnetico è nullo.
FE=F
FM
eE=evB;
eE
evB;
da cui:
v=E/B=3.75
E/B 3 75 103 m/s
/
Un elettrone si muove su un’orbita circolare di raggio 1.7 m in un campo
magnetico
g
B di modulo 2.2 x 10-5 T. L’elettrone si muove in direzione
perpendicolare al campo magnetico. Si determini:
a) la velocità dell’elettrone
b) l’energia
l energia cinetica dell’elettrone
dell elettrone in elettronvolt.
(carica dell’elettrone: 1.6x10-19C; massa dell’elettrone: 9.11x10-31kg
a) Per il secondo principio della dinamica:
v2
qvB = m
R
qBR
v=
= 6.7 × 10 6 m / s
m
b) L
L’energia
energia cinetica dell
dell’elettrone
elettrone è data da:
EC =
1 2
mv = 1.9 × 10 −17 J
2
Poiché 1 eV= 1.6 10-19 J segue che:
−17
1 2
1
.
9
×
10
EC = mv = 1.9 × 10 −17 J =
eV = 122 eV
−19
2
1.6 × 10
Un elettrone è accelerato da fermo da una differenza di potenziale di 350
V. Al termine dell’accelerazione esso entra in un campo magnetico
uniforme di intensità pari a 200 μT, perpendicolare alla velocità. Calcolare
la velocità dell’elettrone ed il raggio
gg del suo p
percorso nel campo
p
magnetico. (me=9.11x10-31 kg; e=-1.6x10-19C)
1) eV=1/2 mv2 ; da cui:
v=(2eV/m)0.5= 1
1.1
1 107 m/s
Con “m” si indica la massa dell’elettrone; “V” è la d.d.p; “v” è la
velocità dell’elettrone; (….)0.5 equivale ad estrarre la radice
quadrata.
2) evB= mv2/R ; da cui:
R= mv/eB= 3.1 10-1 m












