Revisione del 28/9/15
ISTITUTO TECNICO INDUSTRIALE “V.E.MARZOTTO” – Valdagno (VI)
Corso di Fisica – prof. Nardon
FUNZIONI – PROPORZIONALITA’ DIRETTA
Richiami di teoria
Due grandezze si definiscono direttamente proporzionali se, al raddoppiare, triplicare, dimezzare …
dell’una corrisponde un raddoppiare, triplicare, dimezzare … della seconda.
Un modo alternativo e migliore di affermare la stessa cosa è il seguente:
Due grandezze Y e X si definiscono direttamente proporzionali se esse si adattano al seguente schema:
Y1 : Y2 = X1 : X2
(formula che la l’aspetto della conosciutissima proporzione)
Una formulazione alternativa (ottenuta scambiando i medi della proporzione precedente) è:
Y1 : X1 = Y2 : X2
Rappresentazione matematica di una proporzione
Y = aX (oppure:
)
Dove il coefficiente a è una costante (positiva o negativa, intera, frazionaria o decimale).
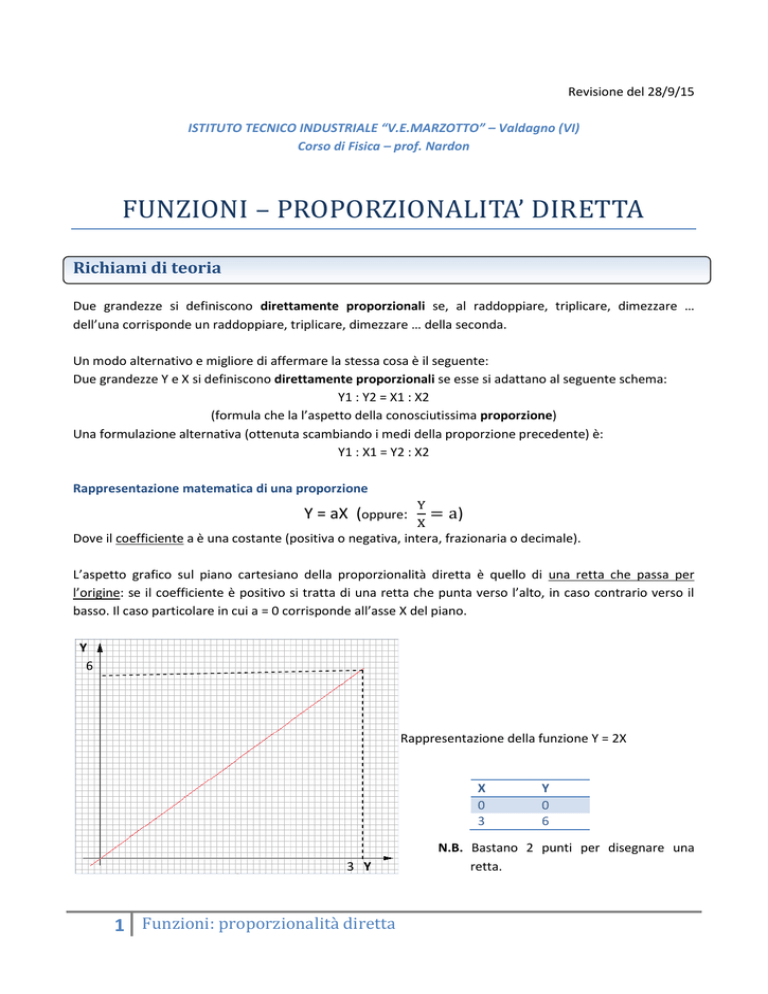
L’aspetto grafico sul piano cartesiano della proporzionalità diretta è quello di una retta che passa per
l’origine: se il coefficiente è positivo si tratta di una retta che punta verso l’alto, in caso contrario verso il
basso. Il caso particolare in cui a = 0 corrisponde all’asse X del piano.
Y
6
Rappresentazione della funzione Y = 2X
X
0
3
3 Y
1 Funzioni: proporzionalità diretta
Y
0
6
N.B. Bastano 2 punti per disegnare una
retta.
Y
15 X
Rappresentazione della funzione Y = -0,2X
X
0
15
Y
0
3
3
Esercizi svolti
Esercizio 1:
Costruire il grafico della funzione: Y = X
Si tratta di una proporzionalità diretta, con coefficiente
. Costruisco perciò una tabella con
alcune coppie X,Y (in realtà, sapendo che dovrà uscire una retta, bastano due soli punti
(coppi X,Y):
X
Y
0
0
1
3
9
2
6
Posso ora disegnare il grafico, usando ad esempio i punti P1 (0,0) e P2 (3,2) (ogni altro punto si
allineerebbe con questi):
Y
2
3
2 Funzioni: proporzionalità diretta
X
Esercizio 2: Trovare la funzione che descrive il seguente grafico:
Y
2
X
-6
Abbiamo 2 punti che appartengono alla retta:
X
0
2
Y
0
-6
Dato che l’equazione di una proporzionalità diretta ( = retta per l’origine) è del tipo:
Y = aX
Ne deriva che
-6 = a* 2
Perciò:
a=
= -3
L’equazione che cerchiamo è perciò:
Y = -3X
Per verificare se è vero, sostituire nell’equazione i valori della tabella che abbiamo costruito e
verificare se l’equazione “funziona”:
0 = -3 * 0
-6 = -3 * 2
Esercizi
[N.B. la difficoltà degli esercizi va da (semplice) a (impegnativo)]
Esercizio 1
Costruire una tabella con almeno 5 righe (a vostra scelta) e disegnare i grafici delle seguenti funzioni:
1.1.
Y = 4X
1.2.
Y=X
1.3.
Y = -X
1.4.
Y= X
1.5.
Y=
(è la stessa cosa di Y = X)
3 Funzioni: proporzionalità diretta
Esercizio 2
Se vi assumono per compiere un lavoro con la paga di 8€ all’ora, scrivete la funzione che esprime il vostro
compenso, costruire la tabella con la paga per le prime 10 ore e il grafico corrispondente.
Esercizio 3
In una passeggiata siete in grado di percorrere 20 Km in 4 ore. Se viaggiate di passo costante, costruite la
formula per calcolare la distanza percorsa, la tabella per le prime 5 ore e il grafico cartesiano.
Esercizio 4
L’automobile della vostra famiglia percorre 15 Km con un litro di carburante. Tracciare un grafico che arrivi
fino a 120 Km di strada percorsa, dopo aver costruito una tabella di appoggio.
Esercizio 5
Vicino a casa vostra viene costruito un palazzo, al ritmo di 3 piano ogni 2 mesi. Scrivere la funzione e
tracciare il grafico, tenendo conto che l’edificio alla fine arriverà fino a 12 piani.
4 Funzioni: proporzionalità diretta
Soluzioni degli esercizi
1.1.
1.2
1.3.
1.4.
1.5.
5 Funzioni: proporzionalità diretta
2.
Y = 8X (Paga = 8€/h*Nh)
X
0
1
2
3
4
5
6
7
8
9
10
Y
0
8
16
24
32
40
48
56
64
72
80
3.
Y = 5X (Distanza = 5Km/h * Nh)
X
0
1
2
3
4
5
Y
0
5
10
15
20
25
4.
Y = 15X (Dist. = 15Km/L * NL)
X
0
1
2
3
4
5
6
7
8
Y
0
15
30
45
60
75
90
105
120
6 Funzioni: proporzionalità diretta
5.
Y = 1,5X
(Nro piani = 1,5Piani/mese * Nm)
X
0
2
4
6
8
Y
0
3
6
9
12
7 Funzioni: proporzionalità diretta