Prof. A. Di Muro
Moto rettilineo uniformemente accelerato ( m.r.u.a. )
Il moto rettilineo uniformemente accelerato è un moto che avviene su una retta con accelerazione
costante.
a = costante
Dalla definizione di accelerazione
v v0 a t
a
v vv0
si ricava la legge oraria della velocità:
t t t 0
con a = costante e con t 0 = 0
Consideriamo la rappresentazione grafica del moto:
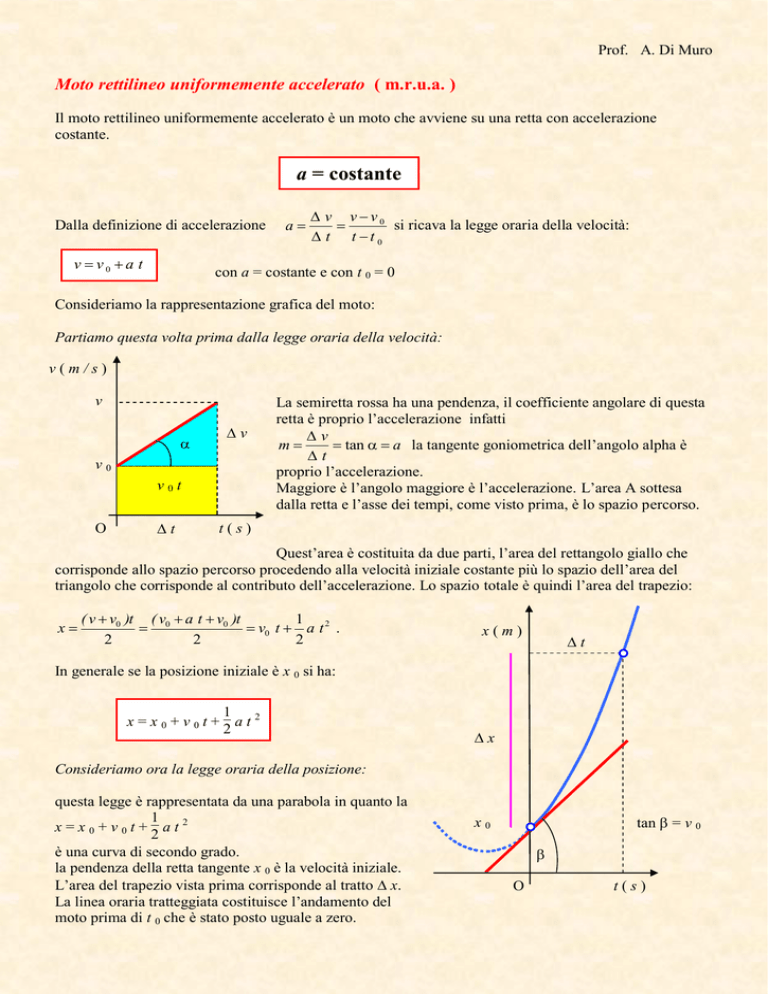
Partiamo questa volta prima dalla legge oraria della velocità:
v(m/s)
v
v
v0
v0t
O
t
La semiretta rossa ha una pendenza, il coefficiente angolare di questa
retta è proprio l’accelerazione infatti
v
m
tan a la tangente goniometrica dell’angolo alpha è
t
proprio l’accelerazione.
Maggiore è l’angolo maggiore è l’accelerazione. L’area A sottesa
dalla retta e l’asse dei tempi, come visto prima, è lo spazio percorso.
t(s)
Quest’area è costituita da due parti, l’area del rettangolo giallo che
corrisponde allo spazio percorso procedendo alla velocità iniziale costante più lo spazio dell’area del
triangolo che corrisponde al contributo dell’accelerazione. Lo spazio totale è quindi l’area del trapezio:
x
( v v0 )t ( v0 a t v0 )t
1
v0 t a t 2 .
2
2
2
x(m)
t
In generale se la posizione iniziale è x 0 si ha:
1
x=x0+v0t+ at2
2
x
Consideriamo ora la legge oraria della posizione:
questa legge è rappresentata da una parabola in quanto la
1
x=x0+v0t+ at2
2
è una curva di secondo grado.
la pendenza della retta tangente x 0 è la velocità iniziale.
L’area del trapezio vista prima corrisponde al tratto x.
La linea oraria tratteggiata costituisce l’andamento del
moto prima di t 0 che è stato posto uguale a zero.
tan = v 0
x0
O
t(s)
Prof. A. Di Muro
Consideriamo infine la legge oraria dell’accelerazione:
essendo l’accelerazione costante la retta ha pendenza nulla ed ha equazione a = tan .
a ( m / s 2)
O
t(s)
Riassumendo le leggi del moto sono:
v v0 a t
1
x=x0+v0t+ at2
2
Se dalla prima ricaviamo t e lo sostituiamo nella seconda si ha:
vv0
vv0
1 vv0 2
e x x0 v0
t
a(
) e dopo semplici passaggi ricaviamo:
a
a
2
a
2 a ( x x 0 ) v 2 v02
questa è una relazione priva del tempo ed è particolarmente importante anche
nella risoluzione degli esercizi.
Moti accelerati e decelerati
Consideriamo un vettore velocità v, se il vettore accelerazione si proietta nello stesso verso di v,
come a 1 , il moto è accelerato perché l’accelerazione favorisce il moto ed aumenta il valore della
velocità.
Se il vettore accelerazione si proietta nel verso opposto di v, come a 2 , il moto è decelerato perché
l’accelerazione ostacola il moto e diminuisce il valore della velocità.
Se infine il vettore accelerazione è perpendicolare a v, come a 3 , il moto non è né accelerato né
decelerato.
Un criterio per stabilire se un moto è accelerato o meno è quello di
fare il prodotto scalare tra i vettori velocità ed accelerazione:
v a > 0 il moto è accelerato
a3
a2
a1
v a < 0 il moto è decelerato
v a = 0 il moto non è né accelerato né decelerato
v
per il moto rettilineo, visto che v ed a hanno la stessa direzione, è sufficiente fare il prodotto tra la
velocità e l’accelerazione.
Prof. A. Di Muro
Esempio:
v(m/s)
2
A
B
2
O
–3
4
6
8
F
E
t(s)
C
D
Nel tratto AB il moto è m.r.u. lo spostamento è xAB vA t 2.0 2.0 4.0 m che corrisponde all’area del
quadrato azzurro. ( consideriamo 2 cifre significative )
Nel tratto BC il moto è decelerato fino ad F perché il corpo con una velocità iniziale di 2.0 m / s si ferma
in F, poi aumenta il modulo della sua velocità fino a C per cui il moto è accelerato, la velocità tuttavia
diventa negativa, ciò significa che il corpo sta tornando indietro percorrendo uno spazio negativo.
v v 0 3.0 2.0
2.5 m / s 2 mentre lo spostamento totale è dato da
t t 0
4.0 2.0
1
1
v0 (t t0 ) a(t t0 )2 2.0(4.0 2.0) ( 2.5)(4.0 2.0)2 1.0 m ;
2
2
L’accelerazione è data da aBC
xBC
per trovare il tempo t F applichiamo la legge del moto al tratto BF:
v v0 a(tF t0 ) cioè 0 2.0 ( 2.5)(tF 2.0) da cui tF 2.8 s
lo spostamento nel tratto BF è
1
1
xBF v0 (t t0 ) a(t t0 )2 2.0(2.8 2.0) ( 2.5)(2.8 2.0) 2 0.80 m che corrisponde all’area del
2
2
triangolo verde;
lo spostamento nel tratto BF è
1
1
xFC v0 (t t0 ) a(t t0 )2 0 ( 2.5)(4.0 2.8)2 1.8 m
2
2
che corrisponde all’area del triangolo arancione;
vediamo che xBC xBF xFC 0.80 1.8 1.0 m .
Prof. A. Di Muro
Nel tratto CD il moto è m.r.u. lo spostamento è xCD vC (t t0 ) 3.0(6.0 4.0) 6.0 m
che corrisponde all’area del quadrato rosa.
Nel tratto DE il moto è decelerato perché alla fine il corpo si ferma, l’accelerazione è
v v 0 0 (3.0)
1.5 m / s 2 ; lo spostamento è
t t 0
8.0 6.0
1
1
v0 (t t0 ) a(t t0 )2 3.0(8.0 6.0) 1.5(8.0 6.0)2 3.0 m
2
2
aDE
xDE
che corrisponde all’area del triangolo giallo.
Lo spazio totale percorso è dato da s xAB xBF xFC xCD xDE 15.6 16 m mentre lo spostamento
totale è dato da x xAB xBC xCD xDE 6.0 m .
vM
La velocità media sull’intero percorso è data da:
x x x 0 6.0 0
0.75 m / s
t t t 0
8.0 0
Segue la legge oraria dell’accelerazione:
a(m/s2)
2
DE
O
AB
2
4
CD
6
8
t(s)
–3
BF
FC
Come si vede nel tratto BF l’accelerazione è negativa mentre la velocità è positiva per cui il prodotto tra
le due è negativo ed il moto è rettilineo uniformemente decelerato, mentre nel tratto FC l’accelerazione e
la velocità sono entrambe negative per cui il prodotto tra le due è positivo ed il moto è rettilineo
uniformemente accelerato.
Nel tratto DE invece l’accelerazione è positiva mentre la velocità è negativa per cui il prodotto tra le due è
negativo ed il moto è rettilineo uniformemente decelerato.
Prof. A. Di Muro
Vediamo ora la legge oraria della posizione sovrapposta a quella della velocità.
x ( m ) 4.8
4
Spazio percorso:
4.0 + 0.80 + 1.8 + 6.0 + 3.0 = 16 m
3
A
B
E
O
3
F
t(s)
C
D
r
Spostamento:
r = – 6.0 m
6
Nel tratto AB il moto è rettilineo uniforme, si ha la retta di equazione:
xAB v(t t0 ) 2.0(t 0) 2.0 t
Nel tratto BC il moto è accelerato e si ha la parabola di equazione:
1
1
xBC x0 v0 (t t0 ) a(t t0 )2 4.0 2.0(t 2.0) 2.5(t 2.0) 2 1.3 t 2 7.0 t 5.0
2
2
Nel tratto CD il moto è rettilineo uniforme, si ha la retta di equazione:
xCD x0 v(t t0 ) 3.0 3.0(t 4.0) 3.0 t 15
Nel tratto DE il moto è accelerato e si ha la parabola di equazione:
1
1
xDE x0 v0 (t t0 ) a(t t0 )2 3.0 3.0(t 6.0) 1.5(t 6.0) 2 0.75 t 2 12 t 42
2
2
ricordando che la pendenza della parabola corrisponde alla velocità, si vede che nel tratto BF la pendenza
è positiva, la pendenza si annulla nel vertice della parabola ( infatti la velocità in quell’istante è nulla ) e
quindi nel tratto FC diventa negativa.
Nel tratto DE la pendenza dell’altra parabola è negativa e si annulla a fine percorso.
Il moto del punto materiale avviene lungo l’asse delle ordinate x con gli spazi percorsi e lo spostamento
totale come in figura.
Prof. A. Di Muro
Il problema dell’inseguimento:
Due punti materiali A e B distanti 800 m si muovono sulla stessa retta e nello stesso verso.
A precede B e si muove con velocità iniziale di 20.0 m / s ed accelerazione costante di 2.00 m / s 2.
B parte da fermo con accelerazione costante di 4.00 m / s 2.
Dopo quanto tempo B raggiunge A?
Quanto spazio hanno percorso i due corpi quando B raggiunge A?
Questi tipi di problemi si possono risolvere agevolmente con il diagramma velocità-tempo.
B
v(m/s)
A
aA tx
aB t x
20
v0 A
O
tx
t(s)
Se t x è l’istante del raggiungimento, lo spazio percorso da A è l’area del trapezio verde mentre lo spazio
percorso da B è l’area del triangolo azzurro.
La differenza delle due aree deve essere evidentemente uguale a 800 m.
800 m
B
A
incontro
1
1
Per cui 800 t x aB t x (2 v0 A aA t x )t x
2
2
da cui t x2 20.0 t x 800 0
e la soluzione positiva dà t x = 40.0 s con x A = 2400 m ed x B = 3200 m.
Da notare che l’intersezione tra le due leggi orarie della velocità ha solo il significato che in quell’istante i
due punti hanno la stessa velocità.
Prof. A. Di Muro
Esercizio :
Risolviamo ora un problema simile senza l’ausilio del diagramma.
Due punti materiali A e B distanti 1200 m si muovono sulla stessa retta, ma in verso opposto.
A si muove con velocità iniziale di 30.0 m / s e sta frenando con decelerazione costante
di 2.00 m / s 2.
B si muove con velocità iniziale di 20.0 m / s con accelerazione costante di 4.00 m / s 2.
Dopo quanto tempo B raggiunge A?
Quanto spazio hanno percorso i due corpi quando B raggiunge A?
1200 m
B
incontro
A
Scelto p. es. un sistema di coordinate con l’asse x positivo nel verso di v 0B, la velocità
v 0A sarà negativa, ma la sua decelerazione positiva.
Occorre innanzitutto chiedersi se B raggiunge A quando questo è fermo o in moto.
Il corpo A si ferma dopo t
e percorre xA
v v0 A 0 (30.0)
15.0 s
aA
2.00
v 2 v02A 0 900
225 m
2a A
4.00
lo spazio è negativo perché contato nel verso negativo delle x.
1
Il corpo B in 15.0 s percorre s v0 B t aB t 2 300 450 750 m
2
Visto che la somma dei moduli degli spazi è minore di 1200, B raggiungerà A quando quest’ultimo è
fermo.
La somma delle due aree deve essere evidentemente uguale a 1200 m.
Il corpo B percorre in definitiva x B = 1200 – 225 = 975 m,
la velocità finale di B, dalla xB
v 2 v02B
sarà:
2aB
v = 90.55 = 90.6 m / s ed il tempo necessario è t
v v0 B 90.55 20.0
17.64 17.6 s
aB
4.00












