Calcolo degli errori e rappresentazioni grafiche
1)Calcola il valore della grandezza G e l’errore assoluto. Scrivi il valore di G
G 2 XY
X 1,2 0,1m, Y 2,3 0,5m.
2)Calcola il valore di G, l’errore assoluto e scrivi il risultato
G
2X
Y
X 1,2 0,1m, Y 2,3 0,5m.
3) Calcola il valore di G, l’errore assoluto e scrivi il risultato
G X Y X 1,2 0,1m, Y 2,3 0,5m.
4) Calcola il valore di G, l’errore assoluto e scrivi il risultato
G 2 XY Z 2 X 1,2 0,1m, Y 2,3 0,5m. Z 3,2 0,5m
5) Calcola il valore di G, l’errore assoluto e scrivi il risultato
G 2 X Z X 1,2 0,1m, Y 2,3 0,5m. Z 3,2 0,5m
6)Rappresenta graficamente le seguenti leggi assegnando alla variabile X valori compresi
tra -5 e 5 con passo 1
a)Y=2X; b) Y=2/X; c) Y=2X2
7)Dalla misura di due grandezze X e Y con X variab. Indip. Si e’ ottenuto:
X
Y
Y/X2
1
0,5
2
2,0
3
4,5
4
7,8
5
12,6
Rappresenta su carta millimetrata i valori e stabilisci se può esservi tra X e Y una
relazione di proporzionalità quadratica Y=kX2. Per trovare la costante K dividi Y per X2
come indicato in tabella. Se non ottieni sempre lo stesso valore prendi per K il valore
medio. Scrivi quindi la legge.
8)Calcola il seguente numero con la calcolatrice e scrivi il risultato in formato scientifico e
indica l’ordine di grandezza.
G
2,3 54,76 81,23 6,76
4,789 34,76 245,87
9)Calcola il valore della seguente espressione e indica l’ordine di grandezza del risultato:
G
2,3 10 2 54,76 10 3 81,23 10 4 6,76
4,789 10 5 34,76 245,87
10)Calcola l’errore assoluto e relativo percentuale della grandezza G:
G 12,345 0,01
Ricerca della legge di proporzionalità diretta
Si cerca di stabilire se tra la lunghezza di una barra di un certo materiale e la sua massa vi
e’ una relazione di proporzionalità diretta. Per ogni valore della lunghezza(variabile
indipendente) si e’ misurata la massa (varabile dipendente). Per ogni valore di lunghezza
si e’ ripetuta la misura della massa 5 volte. La sensibilità della bilancia e’ 0,1g. La
sensibilita’ della lunghezza e’ il millimetro. Si sono ottenuti i seguenti valori:
L(mm)
10
20
30
40
50
60
80
90
100
m1(g)
26
51,1
76,2
101,3
125,9
151
201
226
251
m2(g)
25,5
50,5
76,5
100,5
126,2
152
202,2
226,5
251,2
m3(g)
26,5
52
75,5
102
126,7
151,3
201,5
225,8
251
m4(g)
25
50,8
77,1
101,6
126,6
150,9
201,2
226,1
252
m5(g)
26,4
52,05
76,2
101,4
125,5
150,8
201,3
226,2
251,8
Massa
Media
Errore
Calcolare , per ogni lunghezza, la massa media;
Calcolare per ogni lunghezza l’errore assoluto della massa;
Riportare su carta millimetrata i valori ottenuti e l’errore sulla massa.
Se i punti sono sufficientemente allineati tracciare la retta che li interpola.
Calcolare dal grafico la costante di proporzionalità
Scrivere la legge
Ricorda: Sul grafico la variabile indipendente (la lunghezza) devi rappresentarla sull’asse
orizzontale;
La variabile dipendente(la massa) sull’asse verticale.
Nel tracciare la retta fai in modo che passi dalla maggior parte dei punti(comunque se e’
possibile all’interno dell’intervallo dell’errore) e piu’ vicina ad ognuno di essi.
Per la costante di proporzionalita’ K prendi un punto sull’asse orizzontale (cioe’ la
lunghezza) e traccia un segmento verticale da tale punto fino a toccare la retta. Leggi sulla
scala verticale qual e’ la sua ordinata (la massa). Se la relazione e’ M=KL allora K=M/L.
Trova K e scrivi la legge:
Esercizi di fisica sui vettori
1)In figura trovi i vettori a,b,c. Disegna la somma con la regola del parallelogramma.
2) In figura un vettore e due direzioni assegnate x e y. Disegna le componenti dei vettori
lungo tali direzioni e indica se le componenti sono positive o negative.
3) In figura trovi dei triangoli rettangoli con le misure indicate. Calcola angoli e lati
rimanenti.
4)In figura trovi dei vettori e gli angoli indicati. Calcola le componenti e disegnale con la
massima attenzione
5)In figura trovi tre vettori v,w,z. Disegna le componenti e
valuta l’intensita’. Calcola l’intensità’ e la direzione(cioè
l’angolo che il vettore forma con l’asse delle ascisse) dei
vettori:
a)S=v+w+z;
b)T=v-w-z;
c)H=v+w-z;
d)X=2v-3w+z
6)In figura trovi i vettori v,w,z. v=5; w=5; z=5. Calcola
l’intensità’ e la direzione dei vettori:
S=w+v;
T=w-v;
G=z-w
7)In figura trovi due vettori a e b . Calcola le componenti di
ciascuno . Calcola il modulo del vettore somma e della
differenza d a b . Rappresenta graficamente i vettori
trovati e verifica il risultato con la regola del
parallelogramma.
8)In figura trovi i vettori v e w. Disegna le componenti e
calcolale; calcola la somma v+w, la differenza w-v e la
differenza v-w. V=5 e w=10
9)In figura trovi dei vettori. Disegnali in scala e con la regola
del poligono funicolare costruisci il vettore somma. Disegna
anche i vettori differenza: d a b e f a c
10)In figura trovi dei vettori. Calcola le componenti dei vettori: a=4cm e b=2cm. Gli angoli
sono indicati in figura. Calcola in ogni caso l’intensità’ e la direzione del il vettore somma e
del vettore differenza.
Esercizi di cinematica del moto
1) Un osservatore O e’ posto nell’origine di un sistema di riferimento e inizia a
misurare gli spazi percorsi da un corpo in movimento e i relativi tempi. I valori sono
riportati in tabella.(completa la tabella come mostrato). Calcola lo spazio percorso
dopo 2h (2 ore).
t(sec)
S(m)
0
1
2
3
4
5
6
1
3
5
7
9
11
13
v
S
t
__
V=(3-1)/(1-0)=
V=(5-3)/(2-1)=
Osservi che: la velocita’ e’ costante quindi lo spazio e’ proporzionale al tempo.
Ricaviamo la legge del moto:
Ho dimostrato che la legge del moto uniforme e’ S=vt+s0. Quindi possiamo scrivere:
S=2t+1
(Al tempo zero lo spazio S0 e’ 1, lo leggi dalla tabella).
Dopo 2 ore (cioe’ 2*60*60=7200 sec) si ha:
S=2*7200+1=14401 e v=2m/s (costante)
2)Ripeti l’esercizio con i seguenti dati e calcola lo spazio percorso dopo 2 giorni.
t(sec)
0
2
4
6
8
10
12
S(m)
5
6
7
8
9
10
11
I grafici che descrivono il moto.
(Studia gli appunti e il problema svolto in classe prima di affrontare il quesito)
Rappresenta graficamente lo spazio percorso in funzione del tempo impiegato (S variabile
dipendente, t variabile indipendente) per il quesito 1). Ottieni come grafico una retta. Il
grafico della velocita’ in funzione del tempo, essendo v costante, e’ una retta orizzontale
che passa dal punto (0,2).
Esempio 1) Ricava la legge del moto se i dati sono i seguenti:
(Leggi gli appunti e studia il problema svolto in classe e poi risolvi il quesito)
Un osservatore , posto nell’origine degli spazi e dei tempi osserva un corpo in movimento
e stabilisce quanto segue:
All’istante t=10sec il corpo dista dall’osservatore di un tratto S=5m. All’istante t=20 sec
dista S=15m. Scrivi la legge del moto e calcola dove era 10sec fa e dove sara’ fra 30sec.
Quesiti vari:
1)Vega è la stella più brillante della costellazione della Lira, la quinta più luminosa del cielo
notturno. Vega è una stella piuttosto vicina, posta a soli 25 anni luce di distanza dalla
Terra. Con una astronave che viaggia a 180.000 Km/s in quanti anni terrestri e’ possibile
raggiungerla?
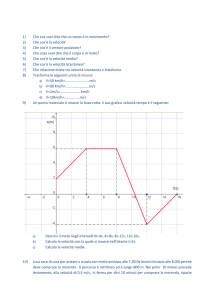
2)Rappresenta graficamente la storia di un corpo A che si e’ mosso, si muove, si
muoverà come di seguito descritto:
Il corpo A si muove con la legge S=2t+3 per 5 secondi; per i successivi 2 secondi si muove
con la legge S=-5t+38; per i successivi 2 secondi si muove con la legge S=3 (cioè sta
fermo); per i successivi 2 secondi si muove con la legge S=-3/2t+33/2.
3)Un corpo all’istante t=5 e’ a +5m dall’osservatore; all’istante t=7 e’ a +10m
dall’osservatore. Calcola la velocità del corpo supponendo il moto uniforme.
4)Un ciclista percorre una strada lunga 200m in 3minuti. In contra una salita lunga 2Km
che percorre in 20min. Di seguito incontra una discesa lunga 800m che percorre in 2 min.
L’ultimo tratto e’ di 500m che percorre in 1 minuto. Quale e’ stata la velocità media?
5)Rispetto ad un osservatore due corpi si muovono come segue: Il corpo A all’istante t=0
si trova a -30m dall’osservatore e si muove con una velocità di 5m/s; il corpo B all’istante
t=0 si trova a +20m dall’osservatore e si muove ad una velocità di -3m/s. Dopo quanto
tempo si incontrano e a quale distanza dall’osservatore?
6)In una corsa campestre un concorrente A parte in anticipo di 2 min rispetto al
concorrente B. A si muove alla velocità di 100m/min. Dopo 2 minuti parte anche B. A quale
velocità deve muoversi perché raggiunga B dopo 1 minuto?
7)Due corpi distano inizialmente di 800 m. Il corpo A si trova nell’origine degli spazi e dei
tempi e si muove ad una velocità di 5Km/h; il corpo B si muove ad una velocità di 0,6 m/s.
Dopo quanto tempo si incontrano e a quale distanza dall’origine?
8)Scrivi la legge del moto del corpo A con i dati seguenti:
a)All’istante t0=0 si trovava a 20m dall’osservatore; si muove di moto uniforme alla velocità
di 5Km/min.
b)All’istante t0=3 secondi e’ a +20m dall’osservatore e si muove alla velocità costante di
30Km/h;
c)All’stante t0=0 si trova nell’origine degli spazi e dei tempi; si allontana dall’origine nel
verso negativo degli spostamenti e alla velocità di 15m/min.
d)Nel problema a) dopo aver scritto la legge calcola dopo quanto tempo giunge dove e’
posto l’osservatore;
e)Nel problema b) calcola dopo quanto tempo sarà a 600m dall’osservatore.
9)Una barca naviga in un fiume che scorre in direzione
EST alla velocità di 10m/s. Il passeggero rema verso la
sponda opposta con un angolo di 30° rispetto alla
direzione orizzontale. La sua velocità e’ di 15m/s.
Calcola il valore della velocità effettiva del passeggero e
l’angolo che la direzione del vettore somma forma con
l’asse orizzontale. L’angolo che la somma forma con l’orizzontale non e’ 30° ma ha un
valore minore. Di quanto diminuisce in percentuale?
10)Devo lanciare da terra una palla ad un ragazzo che e’ su un balcone alto 10m. Quale
velocità devo imprimere alla palla?Quanto tempo impiega a raggiungere il ragazzo?
(t=1,43s e vo=14m/s)
11)Per calcolare lo spazio percorso da un corpo che si muove di moto U.A. si e’ misurato il
tempo per 5 volte ottenendo:
T(sec): 5,56; 5,51; 5,45; 5,70; 5,34.
L’accelerazione e’ a=2,2±1,5 m/s2
Calcolare lo spazio percorso e l’errore assoluto commesso.
12)Un corpo parte da fermo e dal punto A. a)Scrivi
le leggi del moto lungo il tratto AB e calcola quale
velocita’ possiede nel punto B e dopo quanto
tempo vi giunge.
Giunto in B prosegue lungo il tratto BC .dove
subisce una decelerazione costante di 0,5m/s. b) Quale distanza BC percorre prima di
fermarsi? Dopo quanto tempo si ferma?
13)Lascio cadere un corpo da una torre alta 200m . Se trascuro la resistenza dell’aria
quanto tempo impiega a cadere?. Quando giunge a terra produce un suono che si muove
alla velocità costante di 333 m/s. Dopo quanto tempo si ode il tonfo dalla cima della torre?
Quanto tempo complessivamente e’ trascorso dal momento che si e’ lasciato il corpo?
14)Se dalla torre precedente si lascia cadere un corpo ma gli si imprime una velocità
iniziale di 2m/s quanto tempo impiega a cadere?
15)Osservo un corpo e ne misuro la posizione nel tempo. All’istante t=10sec la sua
posizione e’ di 20m dall’osservatore. Dopo ulteriori 20sec la distanza e’ aumentata del
20%. Scrivi la legge con cui si muove il corpo e calcola quanto spazio avrà percorso dopo
100sec dall’istante t=0.
16)Due corpi distano inizialmente 200Km. Il corpo A parte dall’origine degli assi di
riferimento e si muove alla velocità di 150Km/h. Il corpo B parte nello stesso istante e si
muove alla velocità di 120Km/h. Riescono a incontrarsi? Se si incontrano a quale distanza
dall’origine? Dopo quanto tempo?. Rappresenta graficamente le leggi del moto dei due
corpi . Quanto valgono i coefficienti angolari delle due rette? Confrontale con le rispettive
velocità dei due corpi.
17)Un corpo ha una velocità di 140Km/h ed e’ costretto a frenare. Se lo spazio di frenata e
500m quale deve essere la decelerazione? Quanto tempo impiega a fermarsi?
18)Lanciando un corpo da A con velocità
iniziale v0 che si mantiene costante fino al
punto D. Voglio che il corpo giunga nel punto C
con velocità nulla. Quale velocità v0 devo
imprimere al corpo? Quanto tempo partendo da
A giunge in C?
19)Un suono viene emesso da una sorgente che dista 30Km da un ostacolo che riflette il
suono il quale ritorna alla sorgente. Se la velocità del suono e di 334m/s dopo quanto
tempo dal