Modulo 2 Problemi sulle coordinate cartesiane e polari

Modulo 2: Problemi sulle Coordinate Cartesiane e Polari
APPUNTI DI TOPOGRAFIA
MODULO 2
PROBLEMI SULLE COORDINATE CARTESIANE E POLARI
PROF. SPADARO EMANUELE
Modulo 2: Problemi sulle Coordinate Cartesiane e Polari
PREMESSE
Per individuare la posizione di un punto nei piano, e per la successiva rappresentazione
grafica, è necessario dare le sue coordinate rispetto ad un sistema di riferimento.
Le coordinate planimetriche di un punto sono sempre due numeri e possono essere
essenzialmente di due tipi:
 coordinate cartesiane ;
 coordinate polari.
COORDINATE CARTESIANE
Le coordinate cartesiane (più correttamente dette coordinate cartesiane ortogonali perché
gli assi cartesiani di riferimento sono ortogonali fra loro) sono particolarmente utili nella
restituzione (disegno) di un rilievo topografico.
La posizione di ogni punto P è definita dalle due coordinate x p ed yP che ad esso si
associano.
La coordinata x P è la distanza che c'è fra il punto P e l'asse delle Y (asse delle ordinate),
analogamente la y p è la distanza che c'è fra il punto P e l'asse delle X (asse delle ascisse).
Spesso lo studente non riesce ad associare in modo corretto l’asse X o Y al termine
ascisse o ordinate. Si suggerisce la seguente assonanza ascisse = ascix per favorire la
corretta associazione.
Le coordinate cartesiane del punto P possono essere indicate in uno dei seguenti modi:
 esplicito:
x P = ...........;
 implicito:
P(x P; yP);
yP = ..............
P(x P; yP)
nel modo implicito si mette sempre prima la x e poi la y.
http://spadaroemanuele.altervista.org/
2
Modulo 2: Problemi sulle Coordinate Cartesiane e Polari
COORDINATE POLARI
Le coordinate polari sono utili in fase di rilievo. Esse si riferiscono ad un sistema costituito da un
unico asse ON detto asse polare.
Le coordinate polari di un punto P sono:
 la distanza fra l’origine O del sistema (detto polo) e il punto stesso;
 e l’angolo orizzontale (misurato su di un goniometro orizzontale)  OP (detto
azimutale) di cui si deve ruotare, in senso orario, l’asse polare per farlo sovrapporre
alla congiungente l’origine con il punto in questione.
Le coordinate cartesiane del punto P possono essere indicate in uno dei seguenti mo di:
 esplicito:
 OP = ...........;
 implicito:
P( OP ; OP);
OP = ..............
P(OP;  OP )
in questo caso non esiste un ordine di precedenza fra l’angolo e la distanza poiché
l’angolo e la distanza sono grandezze di tipo diverso.
L’angolo azimutale diventa azimut quando l’asse polare ON viene indirizzato verso il
nord oppure è parallelo all’asse Y di un sistema di riferimento cartesiano.
 esplicito: (OP) = ...........;
 implicito: P(OP); OP;
OP = ..............
P(OP); OP
La distanza OP non varia ne come simbolo ne
come valore numerico, mentre l’angolo cambia sia
come simbolo, che come nome, che come valore
numerico.
http://spadaroemanuele.altervista.org/
3
Modulo 2: Problemi sulle Coordinate Cartesiane e Polari
PASSAGGIO DA COORDINATE POLARI A CARTESIANE
Poiché il rilievo viene molto spesso effettuato con coordinate polari (utilizzando tacheometri e
teodoliti che inizieremo a conoscere nel modulo 4), mentre il disegno viene molto spesso effettuato
con coordinate cartesiane (perché è più preciso) è necessario effettuare il passaggio dalle une alle
altre.
Allo scopo si utilizzeranno le formule (1), ricavate applicando il primo e secondo teorema sui
triangoli rettangoli (vedi modulo 1) OP’P in figura
Nella figura si è fatto coincidere l’origine
del sistema cartesiano con l’origine dei
sistema polare e l’asse delle ordinate con
l’asse polare.
xp = OP Sin(OP)
(1)
yp = OP cos(OP)
PASSAGGIO DA COORDINATE CARTESIANE A POLARI
In alcuni problemi didattici e della pratica operativa del Geometra, vengono fornite le coordinate
cartesiane di punti già rappresentati su di un disegno (vertici, ad esempio, di un appezzamento di
terreno), e sì richiede di calcolare le coordinate polari degli stessi rispetto ad un sistema polare con
origine coincidente con quella del sistema cartesiano e asse delle ordinate coincidente con l’asse
polare (allo scopo, ad esempio, dell’effettuazione di calcoli
relativi all’appezzamento in
questione).
Le formule necessarie per raggiungere lo scopo verranno ricavate. come segue, applicando il
primo, secondo e terzo teorema sui triangoli rettangoli (vedi modulo 1) al triangolo rettangolo OP’P
in figura.
Per calcolare la distanza OP possiamo utilizzare
la seguente formula (2) ottenuta applicando il
teorema di Pitagora al triangolo prima detto:
OP  x 2P  y 2P
(2)
oppure una delle seguenti (3) ricavate applicando
il primo e secondo teorema sui triangoli rettangoli
OP = xp / sin(OP)
(3)
OP = yP / cos(OP)
http://spadaroemanuele.altervista.org/
4
Modulo 2: Problemi sulle Coordinate Cartesiane e Polari
Per calcolare l’azimut (OP) applichiamo il terzo teorema sui triangoli rettangoli sempre
al triangolo OP’P:
x p = yP tg(OP)
da cui:
tg(OP) = x p / yP
ed infine:
(OP) = arctg(x p / y P ) + k
(4)
Il k che compare nella (4) è un termine correttivo che consente di eliminare l’errore
che commetterebbe la calcolatrice.
Infatti facendo l’arcotangente di un numero positivo la calcolatrice ci da sempre un
angolo dei primo quadrante (mentre però potrebbe essere anche del terzo) analogamente
tacendo l’arcotangente di un numero negativo la calcolatrice ci da sempre un angolo del
primo quadrante col segno meno (mentre però potrebbe essere un angolo del secondo o del
quarto quadrante).
Stabiliremo il valore da assegnare al k in base al segno di x P e di y p come riassunto
nella tabella che segue:
Segni del
Rapporto
x/y
1°
caso
2°
caso
3°
caso
4°
caso
+/+
+/-/-/+
Quadrante di
Appartenenza dell’angolo
L’azimut è del primo
quadrante
L’azimut è del secondo
quadrante
L’azimut è del terzo
quadrante
L’azimut è del quarto
quadrante
Valore da attribuire al k
sessagesimali centesimali
0°
0g
180°
200 g
180°
200 g
360°
400 g
I valori per k sono stati ricavati in base alle seguenti considerazioni:
Questo è il caso in cui sia la x p che la yP
sono positivi.
Il valore dato dalla calcolatrice facendo
l’arcotangente di x p /y P e quello corretto
perciò al k si attribuisce valore 0°
http://spadaroemanuele.altervista.org/
5
Modulo 2: Problemi sulle Coordinate Cartesiane e Polari
Questo è il caso in cui la x p è positiva
mentre la yP è negetiva.
Il valore dato dalla calcolatrice facendo
l’arcotangente di x p /y P e quello che
corrisponde a (OP)* (che è negativo) per
effettuare la correzione e determinare quindi
l’azimut (OP) cercato bisogna, come si vede
dalla figura, sommare al valore dato dalla
calcolatrice l’angolo piatto (180°).
Perciò a1 k si attribuisce valore 180°.
Questo è il caso in cui sia la x p che la yP è
negativa.
Il valore dato dalla calcolatrice facendo
l’arcotangente di x p /y P e quello che
corrisponde a (OP)* (che è positivo) per
effettuare la correzione e determinare quindi
l’azimut (OP) cercato bisogna, come si vede
dalla figura, sommare al valore dato dalla
calcolatrice l’angolo piatto (180°).
Perciò a1 k si attribuisce valore 180°.
Questo è il caso in cui la x p è negativa
mentre la yP è positiva.
Il valore dato dalla calcolatrice facendo
l’arcotangente di x p /y P e quello che
corrisponde a (OP)* (che è negativo) per
effettuare la correzione e determinare quindi
l’azimut (OP) cercato bisogna, come si vede
dalla figura, sommare al valore dato dalla
calcolatrice l’angolo giro (360°).
Perciò a1 k si attribuisce valore 360°.
http://spadaroemanuele.altervista.org/
6
Modulo 2: Problemi sulle Coordinate Cartesiane e Polari
COORDINATE TOTALI E PARZIALI
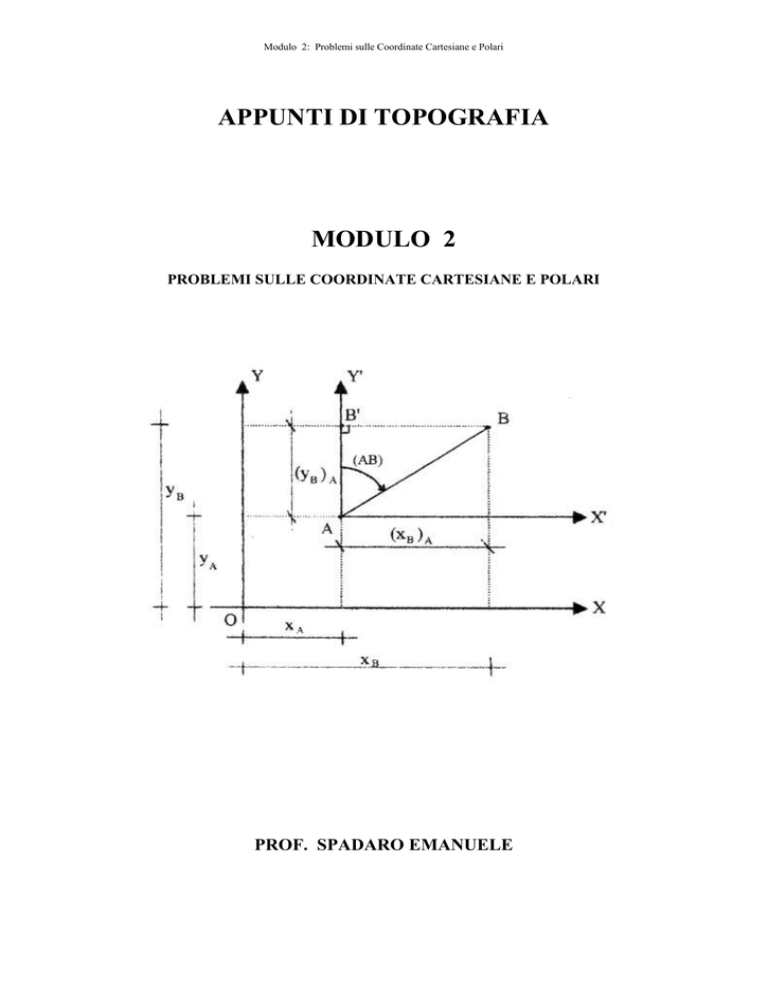
Se in un piano cartesiano vengono date le coordinate cartesiane di due punti A e B si
dice che x A , y A , x B , y B , sono le coordinate totali (che comunque noi chiameremo
semplicemente coordinate) perché si riferiscono all’unico sistema esistente OXY.
Se introduciamo un secondo sistema cartesiano di riferimento con origine in A e con
asse X’ parallelo a X e Y’ parallelo ad Y si avrà che i punti A e B in questione oltre ad
avere le coordinate totali riferite al vecchio sistema (che chiameremo sistema principale)
OXY avranno delle coordinate dette parziali riferite al sistema secondario AX’Y’.
Le coordinate parziali si indicano con
seguenti termini:
(x B ) A e (yB ) A
Il termine:
(x B ) A
si legge x di B rispetto ad A
ed analogamente il termine:
(yB ) A
si legge y di B rispetto ad A
Le coordinate parziali sono legate alle coordinate totali dalle seguenti relazioni ricavate
ragionando sulla precedente figura:
(x B ) A = x B - x A
(5)
(y B ) A = y B - y A
CALCOLO DELLA DISTANZA E DELL’AZIMUT FRA DUE PUNTI DI NOTE
COORDINATE CARTESIANE
Ragionando sul triangolo rettangolo
ABB’ della figura a fianco ed applicando i
teoremi sui triangoli rettangoli, (come
abbiamo fatto nel passaggio da coordinate
cartesiane a polari), per la distanza si
ottiene:
AB  ( x B ) 2A  ( y B ) 2A
Che sostituendo le (5) diventa:
AB  ( x B  x A ) 2  ( y B  y A ) 2
http://spadaroemanuele.altervista.org/
7
(6)
Modulo 2: Problemi sulle Coordinate Cartesiane e Polari
Alla (6), per il calcolo della distanza, si possono affiancare le seguenti:
AB 
(x B ) A
sin( AB)
AB 
(y B ) A
cos( AB)
nelle quali sostituendo le (5) otteniamo:
AB 
xB  xA
sin( AB )
AB 
yB  yA
cos(AB )
(7)
Per calcolare l’azimut (AB) applicando il terzo teorema sui triangoli rettangoli al
triangolo in figura, (come abbiamo fatto nel passaggio da coordinate cartesiane a polar i),
otteniamo:
tg(AB) = (x B ) A / (yB ) A
da cui:
(x )
(AB)  arctg B A  k
(y B ) A
nella quale sostituendo le (5) otteniamo:
( AB )  arctg
xB  xA
k
yB  yA
(8)
il valore da attribuire al k della (8) lo si deduce, in base ai segni che assumono il numeratore
ed il denominatore dopo aver sostituito i numeri, dalla tabella di pag. 5.
AZIMUT E CONTROAZIMUT
Se indichiamo con (AB) l’azimut del segmento che da A va verso B, l’azimut che d a B va
verso A si chiamerà (BA).
I due azimut hanno le stesse lettere ma invertite cioè l’uno è il contrario dell’altro in altri
termini possiamo dire che l’uno è il controazimut dell’altro.
Quindi se diciamo che (AB) è l’azimut (BA) è il suo controazimut. Viceversa se diciamo
che (BA) è l’azimut (AB) è il suo controazimut.
Fra azimut e controazimut la relazione, come sì
vede dalla figura, è la seguente;
(BA) = (A B) ± 180°
dove:
si metterà il segno + se (AB) è minore di 180°
si metterà il segno - se (AB) è maggiore di 180°.
http://spadaroemanuele.altervista.org/
8
Modulo 2: Problemi sulle Coordinate Cartesiane e Polari
RISOLUZIONE DI UN TRIANGOLO DEL QUALE SONO NOTE LE
COORDINATE CARTESIANE DEI VERTICI
Se di un triangolo conosciamo le coordinate cartesiane dei vertici, possiamo
effettuare la risoluzione del triangolo utilizzando:
 le formule per il calcolo della distanza fra due punti di note coordinate
cartesiane per trovare i lati;
 il teorema di Carnot per trovare gli angoli;
 la formula di camminamento per trovare la superficie.
La procedura da seguire per la figura a
fianco é la seguente:
l) si calcolano i lati con le seguenti formule:
AB  ( x B  x A ) 2  ( y B  y A ) 2
AC  ( x C  x A ) 2  ( y C  y A ) 2
BC  ( x C  x B ) 2  ( y C  y B ) 2
2) si calcolano gli angoli con le seguenti
formule:
AB 2  AC 2  BC 2
  arccos
2  AB  AC
2
AB  BC 2  AC 2
  arccos
2  AB  BC
2
AC  BC 2  AB 2
  arccos
2  AC  BC
3) si calcala la superficie con una delle seguenti formule:
S = ½ ACBCsin
S = ½ ABBCsin
S = ½ ABACsin
RISOLUZIONE DI UN POLIGONO DEL QUALE SONO NOTE LE
COORDINATE CARTESIANE DEI VERTICI
Se di un poligono conosciamo le coordinate cartesiane dei vertici, possiamo
effettuare la risoluzione del triangolo utilizzando:
 le formule per il calcolo della distanza fra due punti di note coordinate
cartesiane per trovare i lati;
 la differenza degli azimut per trovare gli angoli (dopo aver trovato gli azimut
con le formule per il loro calcolo):
http://spadaroemanuele.altervista.org/
9
Modulo 2: Problemi sulle Coordinate Cartesiane e Polari
 la formula di camminamento per trovare la superfi cie di un poligono con più di
quattro lati, oppure somma di aree di due triangoli se il poligono è un
quadrilatero oppure le formule di Gauss che dimostreremo nel modulo 9.
La procedura da seguire per la figura a
fianco è la seguente:
1) si calcolano i lati con le seguenti formule:
AB  ( x B  x A ) 2  ( y B  y A ) 2
BC  ( x C  x B ) 2  ( y C  y B ) 2
CD  ( x D  x C ) 2  ( y D  y C ) 2
AD  ( x D  x A ) 2  ( y D  y A ) 2
2) si calcolano gli angoli con le seguenti formule
(AB)  arctg
xB  xA
k
yB  yA
x  xA
(AD)  arctg D
k
yD  yA
(BC )  arctg
xC  xB
k
yC  yB
(BA )  (AB)  180
(CD)  arctg
xD  xC
k
yD  yC
(CB)  (BC )  180

 = (AD) – (AB);

 = (BA) – (BC);

 = (CB) – (CD);
 = 360°- ( +  + )
3) si calcola la superficie con una delle seguenti formule:
 la formula di camminamento per trovare la superficie di un poligono con più di
quattro lati;
 lati somma di aree di due triangoli se il poligono è un quadrilatero;
 le seguenti formule di Gauss che dimostreremo nel modulo 9.
1 n
1 n
x
(
y

y
)
S

;
 i i1 i1
 y i (x i1  x i1 ) (per i vertici che ruotano in senso orario)
2 i 1
2 i 1
1 n
1 n
S   x i ( y i 1  y i 1 ) ; S   y i ( x i 1  x i 1 ) (per i vertici che ruotano in senso antiorario)
2 i 1
2 i 1
S
http://spadaroemanuele.altervista.org/
10
Modulo 2: Problemi sulle Coordinate Cartesiane e Polari
dove per i = 1 si pone 1 - 1 = n, essendo n il vertice antecedente ad i e per i = n si pone
n + 1 = l, essendo 1 il vertice successivo a n.
REGOLA DEL TRASPORTO DEGLI AZIMUT
Alcune volte sono note le coordinate dei vertici dl un po1igono e si richiede la sua
risoluzione (come nel due paragrafi precedenti), altre volte, invece, sono noti tutti gli
elementi di un poligono, le coordinate di un suo vertice ed un azimut e si richiede il calcolo
delle coordinate di tutti gli altri vertici (questo è particolarmente utile nella realizzazione di
un disegno nel modo più preciso possibile)
Se nella figura a fianco
supponiamo di conoscere tutti i
lati (meno eventualmente AF
tutti
gli
angoli
(meno
eventualmente , le coordinate
di A e l’azimut (AB) e
possibile
calcolare
le
coordinate di tutti gli altri
vertici utilizzando invertite le
(7) di pagina 8.
Ad esempio per il punto B
avremo:
x B = x A + AB sin(AB)
yB = yA + AB cos(AB)
Analogamente:
x C = x B + BC sin(BC)
yC = yB + BC cos(BC)
prima però, come si vede dalle formule bisogna calcolare l’azimut (BC). Allo scopo
possiamo applicare la regola del trasporto degli azimut che si enuncia come segue:
l’azimut di un lato è uguale all’azimut del lato precedente più o meno (±) l’angolo al
vertice formato tra i due lati, più a meno (±) l’angolo piatto (180°).
Con riferimento alla figura la regola si può scrivere nel seguente modo:
(BC) = (AB)    180°
Per stabilire i segni nel primo trasporto si ragiona sulla figura:
 si trasporta (AB) sul vertice B;
 si tiene conto che l’azimut (BC) parte dalla direzione verticale passante per B e
raggiunge la direzione BC;
http://spadaroemanuele.altervista.org/
11
Modulo 2: Problemi sulle Coordinate Cartesiane e Polari
 che ruotando in senso orario si effettua somma mentre ruotando in senso antiorar io si
effettua sottrazione;
 ed infine che l’azimut non può essere ne negativo ne maggiore dell’angolo giro
(360 °).
Nel caso della figura si avrà quindi che:
 con + (AB) si e superata la direzione BC quindi si deve tornare indietro (ruotare in
senso antiorario);
 si torna indietro quindi si sottrae 180°, ma si è tornato troppo indietro perciò bisogna
ritornare avanti (ruotare io senso orario);
 si somma quindi .
L’azimut (BC) sarà perciò:
(BC) = (AB) +  - 180°.
Per i trasporti successivi il segno davanti all’angolo del poligono non varia (se gli angoli
sono dalla stessa parte rispetto ad un osservatore che percorre il contorno del poligono, in
caso contrario si ripete il ragionamento fatto sulla figura per il primo trasporto) mentre per il
segno davanti al 180° si avrà che:
 esso sarà positivo se la somma dei primi due termini e minore di 180°;
 viceversa sarà negativo se la somma dei primi due termini é maggiore di 180°.
Infine se sottraendo i 180° (detti sopra) l’azimut rimane maggiore di 360° ad e sso
bisognerà sottrarre ancora 360°.
http://spadaroemanuele.altervista.org/
12
Modulo 2: Problemi sulle Coordinate Cartesiane e Polari
ESERCIZI
1) Del appezzamento triangolare ABC sono note le coordinate cartesiane dei vertici:
A(19,42m, 13,18m);
B(55,26m, 63,98m);
C(80,84m, -18,89m).
Risolvere il triangolo.
(R.: AB = 62,17m; AC = 69,29m; BC = 86,73m;
 = 82°22’07”;  = 52°21’28”;  = 45°16’25”; S = 2134,80m 2 .)
2) Dell’appezzamento quadrilatero ABCD sono note le coordinate cartesiane dei vertici:
A(12,35m, -6,42m);
B(-15,40m, 16,71m);
C(39,41m, 27,82m); D(43,16m, 7,02m).
Effettuare la figura in scala opportuna e risolvere il quadrilatero.
(R.: AB = 36,13m; BC = 55,92m; CD = 21,14m; AD = 33,61m;
 = 116°37’13”;  = 51°16’13”;  = 88°45’41”;  = 103°20’53”; S = 1133,74m 2 .)
3) Di un triangolo ABC sono note le coordinate cartesiane dei suoi vertici:
x A = 12,03m; y A = 9,10m; x B = 65,45m; yB = 89,32m; x C = 142,58m; yC = 63,94m.
Risolvere il triangolo, determinare i1 raggio del cerchio inscritto e le coordinate
dell’incentro. Fare il disegno in scala opportuna.
(R.: AB = 96,38m; BC = 81,20m; AC = 141,60m;  = 33°33’19”;  = 105°26’37”;
 = 41°00’04”; S = 3771,74m 2 ; r = 23,63m; x O = 75,14m; yO = 61,24m.)
4) Della poligonale aperta ABCD sono noti i seguenti elementi:
x A = 13,03m; y A = 20,99m; (AB) = 136°11’
AB = 33,12m; BC = 79,39m; CD = 37,45m; CBA =  = 278°49’; DCB =  = 74°15’.
Determinare le coordinate cartesiane dei vertici della poligonale e le aree dei triangoli AEB
e CDE (essendo E il punto d’incontro fra il lato BC e la congiungente AD). Fare la figura in
scala opportuna.
(R.: x B = 35,96m; yB = -2,91m; x C = 84,14m; yC = 60,19m;
x D = 106,62m; yD = 30,24m; S AEB = …….m 2 ; S CDE = …….m 2 .)
5) Della poligonale aperta ABCDE sono noti i seguenti elementi:
AB = 31,12m;
BC = 8,39m; CD = 23,44m;
ABC =  = 121°10’; BCD =  = 254°15’;
http://spadaroemanuele.altervista.org/
13
DE = 12,12m;
EDC =  = 115°18’.
Modulo 2: Problemi sulle Coordinate Cartesiane e Polari
Determinare le coordinate cartesiane dei vertici della poligonale rispetto ad un sistema di
assi cartesiani con origine in A e semiasse positivo delle ascisse coincidente con il lato AB.
(R.: x A = yA = 0,00m; x B = 31,12m; yB = 0,00m; x C = 35,46m; y C = 7,18m;
x D = 58,06m; yD = 0,95m; x E = 60,14m; yE = -10,99m.)
6) Il triangolo ABC é stato rilevato con un teodolite sessagesimale destrorso
determinando gli elementi riassunti nel seguente specchietto (registro di campagna):
Punto di
stazione
A
B
Punti
collimati
B
C
C
A
Letture al cerchio
orizzontale (azimutali)
31°22’15”
343°44’12”
241°42’05”
196°00’35”
Distanza
topografica
49,042m
----49,044m
Riferendo il triangolo ad un sistema di assi cartesiani con origine in A e semiasse
positivo delle ordinate diretto lungo AB, si determino le coordinate dei vertici e l’area
del triangolo.
(R.: x A = yA = 0,000m; x B = 0,000m; yB = 49,043m;
x C = -25,974m; yC = 23,689m; S = 636,920m 2 .)
7) Il quadrilatero ABCD è stato rilevato con un teodolite sessagesimale destrorso
determinando gli elementi riassunti nel seguente specchietto (regi stro di campagna):
Punto di
stazione
A
Punti
collimati
D
B
C
Letture al cerchio
orizzontale (azimutali)
35°22’45”
335°44’12”
356°12’05”
Distanza
topografica
124,674m
122,383m
179,684m
Riferendo il poligono ad un sistema di assi cartesiani con or igine in A e semiasse
positivo delle ascisse diretto lungo AC.
Determinare le coordinate dei vertici e calcolare gli elementi del quadrilatero.
(R.: A(0,000m, 0,000m); B(114,659m; 42,789m); C(179,684m; 0,000m);
D(96,646m; -78,760m); DC = 114,449m; BC = 77,841m;  = 59°37’50”;
 = 126°11’21”;  = 76°49’53”;  = 97°20’13”; S = 10920,205m 2 .)
8) Di un triangolo A BC , i cui vert i ci ruot ano i n senso ant i orari o, sono note le coordinate
dei punti A e C e i corrispondenti angoli interni:
xA = 12,00m; y A = 36,00 m; xC = 48,00m; yC =156,00 m
 = 92g,0164
 = 65g,9095
Determinare: le coordinate del vertice B; le coordinate del baricentro G e del centro O del cerchio
inscritto al triangolo: l'area del triangolo AGO.
(R .: x B = 185,12m; yB = 6,99m; x O = 67,64m; yO = 70,63m;
xG = 81,70m; yG = 66,33m; SAGO = 363,04 m2.)
http://spadaroemanuele.altervista.org/
14
Modulo 2: Problemi sulle Coordinate Cartesiane e Polari
9) Il quadrilatero ABCD è stato rilevato con un teodolite centesimale destrorso
determinando gli elementi riassunti nel seguente specchietto (registro di campagna):
Punto di
stazione
B
C
Punti
collimati
A
C
B
D
Letture al cerchio
orizzontale (azimutali)
331,345gon
46,125gon
73,347gon
171,893gon
Distanza
topografica
31,99m
35,15m
--46,58m
Sono inoltre noti:
x A = 23,04m; y A = 18,33m; (AB) = 135,389gon
Determinare le coordinale dei vertici e calcolare gli elementi del quadrilatero.
(R.: B(50,21m; 1,35m); C(75,13m; 26,24m); D(39,56m; 56,03m); AD = 41,16m;
 = 109,097gon;  = 114,780gon;  = 77,577gon;  = 77,577gon; S = …….m 2 .)
10)
Di un triangolo ABC, i cui vert i ci ruot ano i n senso ant i orari o, sono note 1e
coordinate dei punti A e B e i lati AC e BC :
x A = 52,00m; yA = 206,00m; xB = 65,00m; yB = 77,00m
AC = 98,50m; BC =112,30m
Determinare: le coordinate del vertice C, le coordinate dei centri Oa, Ob ed Oc dei cerchi ex-inscritti al
triangolo e l'area del triangolo OaObOc.
(R.: xC = ..........m; yC = ...........m; xOa = 151,09m; yOb = -123,75m;
xOb = 227,99m; yOb = 157;39 m; xOc = ...............m; yOc = .................5m; S = 28279,98m2)
11)
In un triangolo ABC sono state misurate le lunghezze dei tre lati:
AB = 57,50m; BC = 74,40m; AC =114,85m
Fissando un, sistema di riferimento cartesiano ortogonale con origine in A e con asse delle ascisse
orientato sulla direttrice AB, determinare: le coordinate del vertice C, le coordinate dell'ortocentro H
del triangolo (ortocentro = punto di intersezione delle altezze di un triangolo), le coordinate del punto
K su BC, intersezione della congiungente tra il punto H e il punto medio M del lato AC e il lato BC,
l'area del triangolo MKC.
(R.: xC = 95,35m; yC = -64,07m; xH = 149,25m; yH = -88,12m;
xK = ............m: yK = ............m; SMKC = ................m2)
12) In un triangolo ABC, i cui vert i ci ruot ano i n senso ant i orari o, sono state misurate le
lunghezze dei tre lati:
AB =152,60m; BC=132,70m; AC =167,56m
Fissando un sistema di riferimento cartesiano ortogonale con origine in A e con asse delle ascisse
orientato sulla direttrice AB, determinare: le coordinate del vertice C, le coordinate del punto K
intersezione tra la bisettrice dell'angolo in A e della mediana relativa al lato AC; le coordinate del
punto O centro del cerchio inscritto a1 triangolo ABK; 1’area del triangolo ABK.
(R.: xC = ..........m; yC = ...........m; xK = 89,79m; yK = 40,63m;
xO = 88,17m; yO =19,02 m; SABK = 3100,17m2)
http://spadaroemanuele.altervista.org/
15
Modulo 2: Problemi sulle Coordinate Cartesiane e Polari
13)
In un quadrilatero ABCD sono note le coordinate dei suoi vertici:
xA = 0,00m; yA = 0,00m; xB = 162,50m; yB = 0,00m
xC = 130,40m; yC = 128,80m; xD = 32,60m; yD = 97,80m
Determinare le coordinate del punto K intersezione delle diagonali, le coordinate del punto H
intersezione tra gli assi dei lati AD e CD, l'area del quadrilatero.
(R.: xK = 70,29m; yK = 69,42m; xH =112,03m; yH = 16,99m; S = 14742,12m2)
14)
In un quadrilatero ABCD sono note le coordinate dei suoi vertici:
xA = 0,00m; yA = 0,00m; xB =162,50m; YB = 0,00m
xC = 130,40m; yC = 128,80m;
xD = 32,60m; yD = 97,80m
Determinare le coordinate del centro O del cerchio inscritto al triangolo ABC, le coordinate del
baricentro G del triangolo che ha come vertici il precedente centro O e i punti medi dei lati AD e CD,
l'area di quest'ultimo triangolo.
(R.: xO = 82,64m; yO = 27,84m; xG = 44,85m; yG = 84,16m; S = 6202,51m2)
15) In un quadrilatero ABCD, i c ui vert i ci ruot ano i n senso ant i ora ri o, sono note le
coordinate dei punti A e C:
xA = 0,00m; yA = 0,00m; xC = 148,00m; yC = 126,00m
Sono poi stati misurati i seguenti elementi:
 = 97g,0709;  = 85g,0171; CD = 137,82m; AD = 135,81m
Determinare: le coordinate dei vertici B e D, le coordinate del punto K intersezione della diagonale
AC con la congiungente i punti medi del lati AD e BC; le coordinate del punto H intersezione della
diagonale BD con la congiungente i punti medi dei lati AD e B C.
(R.: xB = .............m; yB = .............m; xD = .............m; yD = .............m;
xK = 75,58m; yK = 64,35m; xH = 94,61m; yH = 63,44 m)
16)
Di un triangolo ABC, i c ui vert i ci ruot ano i n senso ant i orari o, sono noti:
 = 62g,5200; xA = 0,00m; yA = 0,00m; xC = 106,50m; yC = 70,80m
Non potendo misurare la lunghezza del lato AB si è sviluppata la spezzata AMNB misurando i
seguenti elementi:
BAM = 22g,4500; AMN = 208g,7700; MNB = 117g,5153;
AM = 42,00m; MN = 48,50m;
NB = 51,80m
Determinare: le coordinate del vertice B e le coordinate del baricentro G del triangolo.
(R.: xB =108,98m; yB = - 45,48m; xG = 71,83m; yG = 8,44m; AB = 118,09m)
17)
L'asse di un canale è composto da una sequenza di segmenti di estremi ABCDEF. Si sono
misurati i seguenti elementi:
AB = 85,36m; BC = 110,18m; CD = 101,38m; DE = 92,70m; EF = 74,50m;
ABC =  = 108°,0370; BCD =  = 249°,7407; CDE =  = 132°,0370; DEF =  = 233°,4444
Determinare la distanza tra gli estremi A ed F del canale.
(R.: AF = 383,71m)
http://spadaroemanuele.altervista.org/
16
Modulo 2: Problemi sulle Coordinate Cartesiane e Polari
18)
Si sono collegati gli estremi A ed E di un tratto di strada rettilinea con una spezzata ABCDE, e
sono state effettuate le seguenti misure:
AB = 273,25m; BC = 524,08m; CD = 388,43m; DE = 356,91m;
ABC =  =135g,3210; BCD =  = 144g,0154; CDE =  = 141,2098
Determinare la lunghezza del tratto di strada e gli angoli che essa forma con i lati AB ed ED della
spezzata.
(R.: AE = 930,88m; EAB = 94g,0430; AED = 85g,4104)
19)
Tra i punti A ed E sono presentì ostacoli che impediscono la misura diretta della distanza tra i
punti stessi. Questi sono poi stati collegati con una spezzata ABCDE e sono state effettuate le
seguenti misure:
AB = 165,00m; BC = 72,50m; CD = 90,46m; DE = 122,34m;
ABC =  = 54g,0503; BCD =  = 123g,6391; CDE =  =142g,1165
Determinare: la distanza tra A ed E e le coordinate del punto K intersezione del segmento AE
con Ia bisettrice dell'angolo BCD, rispetto a un sistema di riferimento cartesiano con origine
in A e asse delle ordinate diretto lungo AB.
(R.: AE = ............m; x K = ...........m; yK = ............m)
20)
Tra i punti A ed E sono presenti ostacoli che impediscono la misura diretta della
distanza. Questi sono poi stati collegati con una spezzata ABCDE e sono state effettuate le
seguenti misure:
AB = 65,00m; BC = 92,50m; CD = 110,40m; DE=105,80m
ABC =  = 154g,0503; BCD =  = 163g,6391; CDE =  =142g,1100
Determinare: la distanza tra A ed E e le coordinate del punto K intersezione del segmento AE
con la bisettrice dell'angolo BCD, rispetto a un sistema di riferimento cartesiano con origine
in A e asse delle ascisse diretto lungo AB.
(R.: AE = 272,59m; x K = 47,07m; yK = 116,31m)
21)
Tra í punti A e D è stata sviluppata la spezzata ABCD e sono state effettuate le seguenti
misure:
AB = 75,00m; BC = 112,60m; CD = 83,50m;
ABC =  = 144g,7419; BCD =  = 151g,5315
Determinare: la distanza tra A e D; le coordinate del punto K intersezione tra il
prolungamento de: Iato DC, dalla parte di C. e la perpendicolare, tracciata da A, alla
congiungente AD, rispetto a un sistema di riferimento cartesiano con origine in A e asse delle
ascisse diretto lungo AB, le coordinate del baricentro G del triangolo ADK.
(R.: AD = 221,52m; x K = 160,86m; yK = -135,78m; x G = 101,22 m; yG = 11,18m)
http://spadaroemanuele.altervista.org/
17