s_080704

STATISTICA E MISURAZIONE
venerdì 4 luglio 2008
Prof. Cesare Svelto
Tempo a disposizione 2 ore
terzo appello AA 2007/2008
Aula V.0.8 ore 13.15
Cognome: __________________________
nome: _____________________
Matricola e firma __ __ __ __ __ __
(stampatello)
_____________________ (firma leggibile)
Esercizi svolti (almeno parzialmente): 1 2 3 4 5 (7 + 8 + 7 + 4 + 7=33p)
(crocettare)
N.B. gli esercizi non crocettati non saranno corretti; quelli crocettati ma neanche iniziati comporteranno
una penalità; se possibile, si chiede di crocettare anche i sottopunti svolti.
SOLUZIONI
Esercizio 1 (tempo stimato 25 min)
(svolgere su questo foglio e sul retro)
1) Si intende fare uno studio statistico sul numero di studenti che si iscrivono ad un corso di tutorato. Negli
ultimi 12 anni gli iscritti x sono stati:
x = 35; 24; 28; 26; 29; 30; 32; 29; 38; 27; 28; 34.
3a) Si calcolino media e deviazione standard campionaria.
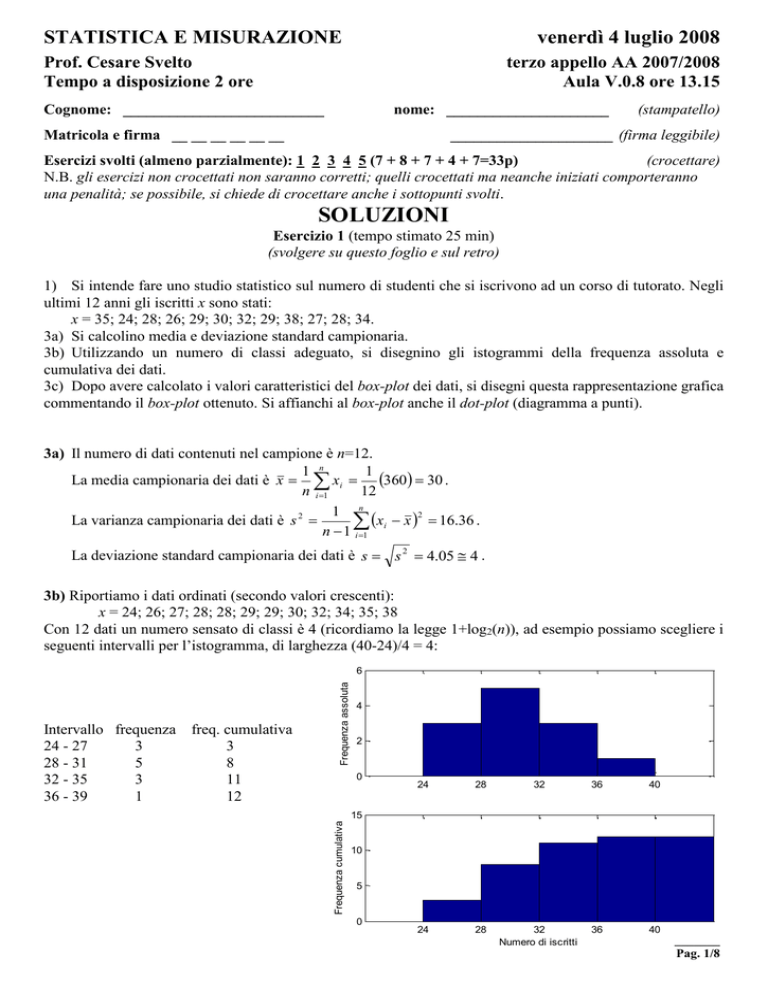
3b) Utilizzando un numero di classi adeguato, si disegnino gli istogrammi della frequenza assoluta e
cumulativa dei dati.
3c) Dopo avere calcolato i valori caratteristici del box-plot dei dati, si disegni questa rappresentazione grafica
commentando il box-plot ottenuto. Si affianchi al box-plot anche il dot-plot (diagramma a punti).
3a) Il numero di dati contenuti nel campione è n=12.
1 n
1
La media campionaria dei dati è x   xi  360  30 .
n i 1
12
1 n
xi  x 2  16.36 .
La varianza campionaria dei dati è s 2 

n  1 i 1
La deviazione standard campionaria dei dati è s  s 2  4.05  4 .
3b) Riportiamo i dati ordinati (secondo valori crescenti):
x = 24; 26; 27; 28; 28; 29; 29; 30; 32; 34; 35; 38
Con 12 dati un numero sensato di classi è 4 (ricordiamo la legge 1+log2(n)), ad esempio possiamo scegliere i
seguenti intervalli per l’istogramma, di larghezza (40-24)/4 = 4:
4
2
0
24
28
32
36
40
24
28
32
Numero di iscritti
36
40
15
Frequenza cumulativa
Intervallo frequenza freq. cumulativa
24 - 27
3
3
28 - 31
5
8
32 - 35
3
11
36 - 39
1
12
Frequenza assoluta
6
10
5
0
_______
Pag. 1/8
3c) Per disegnare il box-plot dei dati dobbiamo innanzitutto calcolare la mediana e il primo e terzo quartile.
La mediana è il 50-esimo percentile, per cui Imediana = (12+1)50 /100 = 6.5, quindi la mediana è la media tra
il sesto ed il settimo dato, che valgono entrambi 29 s.
Mediana=29 s.
Il primo quartile è il 25-esimo percentile, per cui I1Q = (12+1)25 /100 = 3.25, quindi il primo quartile è dato
da:
primo quartile= [ 17 + (18 – 17)  0.25 ] = 27.25 = Q1
Il terzo quartile è il 75-esimo percentile, per cui I3Q = (12+1)75 /100 = 9.75, quindi il terzo quartile è dato
da:
terzo quartile= [ 22 + (24 – 22)  0.75 ] = 33.5 = Q3
La dinamica interquartile vale DIQ= Q3-Q1= 6.25.
I baffi si possono estendere fino a 1.5DIQ = 9.375 al di là del primo e terzo quartile, quindi fino a
27.25-9.375=17.875 e 33.5+9.375=42.875. Ricordiamo comunque che i baffi si fermano all’ultimo dato
contenuto entro questo limite (di 1.5DIQ dalla mediana): in questo caso sino al primo e all’ultimo dato del
campione (non ci sono outliers).
In figura (box-plot) sono riportati anche i punti sperimentali.
1
22
24
26
28
30
32
Numero di iscritti
34
36
38
_______
Pag. 2/8
Esercizio 2 (tempo stimato 30 min)
(svolgere su questo foglio e sul retro)
2a) Si consideri il dado in figura. Quanto vale la probabilità che, su 10 lanci, si abbia almeno per tre volte
testa?
2b) Supponendo che la quantità di consegne richieste a un pony express segua una statistica poissoniana con
valor medio di 60 richieste su 5 ore lavorative, quanto vale la probabilità che in 1 ora il corriere riceva
esattamente 10 richieste?
2c) Supponendo che il telefono del pony express si spenga per 10 minuti, quanto vale la probabilità che in
quel tempo non perda neanche una chiamata?
2d) Una ditta di telefonia mobile produce un modello di cellulare che mediamente emette in prossimità un
campo elettrico di 4.75 V/m, con deviazione standard di 0.5 V/m (dovuta alla variabilità della produzione).
Sapendo che la normativa vigente impone un limite massimo di emissione pari a 6 V/m, che percentuale di
dispositivi verrà scartata in quanto fuori norma?
2a) Dato che ogni prova è un processo di Bernoulli (o esce o non esce testa), le 10 prove sono indipendenti e
la probabilità di successo in ogni prova è costante p =2/6=0.33, la probabilità di x volte testa su n estrazioni
segue la distribuzione binomiale:
n
n
n!
P(n successi su x prove )    p x (1  p) n  x , con   
 x
 x  x!(n  x)!
P(almeno 3 volte testa) = 1 – P(2 volte testa) – P(1 volta testa) – P(mai testa) =
10 
10 
2
1
=1-  0.33 (0.66)102   0.33 (0.66)101  (0.66)10  70 %
2
1
2b) La funzione di probabilità di una variabile poissoniana X vale f ( x) 
Il valor medio di richieste in 1 ora è  = 60 richieste / 5 h = 12 richieste.
La probabilità che arrivino esattamente 10 richieste è pari a
e   10 e 121210
P( x  10) 

 10.5%
10!
10!
e   x
,
x!
x  0,1,2...
2c) Il valor medio in 10 minuti vale  = 12 richieste/h ∙ 1/6 h = 2 richieste.
La probabilità che arrivino esattamente 0 richieste in 10 minuti è pari a
e   0 e 2
P( x  0) 

 0.1353  13.53%
0!
1
2d) Il problema si riduce al calcolo della probabilità di oltrepassare la soglia della normativa (campo elettrico
E > 6 V/m). Per calcolare la probabilità standardizziamo la variabile casuale gaussiana, sapendo che
 = 4.75 V/m e  = 0.5 V/m, ricorriamo quindi alla tabella dei valori della distribuzione cumulativa normale
standard
6
6  4.75 


P( E  6 V/m )  P z 
  P z 
  P( z  2.5)  1  P( z  2.5)  1  0.9938  0.62%
 
0.5 


_______
Pag. 3/8
Esercizio 3 (tempo stimato 25 min)
(svolgere su questo foglio e sul retro)
3) Siamo incaricati di effettuare un controllo statistico su una ditta che produce succhi di frutta. Si vuole
controllare l’esatto livello medio di succo presente in ogni brik, dichiarato 1 litro dalla ditta. Facciamo uno
studio di settore da cui veniamo a conoscenza che la deviazione standard dei sistemi di riempimento dei brik
vale circa lo 0.5 % del contenuto versato. Prendiamo quindi due casse da 6 brik e ne misuriamo il contenuto,
ottenendo un valor medio di 0.996 l.
3a) Effettuare un test statistico allo scopo di valutare se il riempimento delle bottiglie è diverso da quello
dichiarato, con livello di significatività del 5 %.
3b) Calcolare il valore P di questo test.
3c) Se il valore atteso del livello di liquido fosse 0.995 l, quanto varrebbe la potenza del test effettuato?
3a) Dato che la varianza è nota, si può effettuare un test Z. Seguiamo gli 8 passi descritti nel libro di testo.
La deviazione standard vale  = 0.5%× 1 l=5 ml.
1. Il parametro di interesse è la quantità attesa di liquido 
2. H0:  = 1 l
3. H1:   1 l (il test è a due lati, in quanto espressamente richiesto dal testo: si vuole rivelare una
qualsiasi differenza)
4. livello di significatività richiesto  = 0.05
5. La statistica di test è la statistica Z: z0 
X 
X

X 
/ n
6. Rifiutiamo H0 se z0 > Z/2 = 1.96 o z0 < -Z/2 = -1.96 (questi valori si ricavano dalla tabella della
funzione cumulativa in corrispondenza di un valore di probabilità /2=0.025)
7. Calcoliamo quindi z0, z 0 
X 
X

X 
/ n

0.996  1
0.005 / 12
 -2.77
8. Conclusione: dato che z0 = -2.77 < -Z/2 = -1.96 possiamo rifiutare l’ipotesi nulla con livello di
significatività 0.05: c’è abbastanza evidenza che l’ipotesi nulla sia falsa.
3b) Il valore P, che corrisponde al livello di significatività di soglia tra l’accettazione ed il rifiuto di H0, si
può ricavare direttamente dalla tabella dei valori della funzione cumulativa:
ZP/2 = z0 = 2.77, per cui il valore P =20.0028=0.0056.
L’interpretazione di questo valore è che l’ipotesi nulla è dichiarata falsa per qualsiasi livello di significatività
 maggiore dello 0.56 %. In questo caso con  = 5 % abbiamo rifiutato H0.
3c) La potenza di un test statistico è la probabilità di rifiutare l’ipotesi nulla quando questa è falsa. È uguale
a 1- la probabilità  di errore di tipo II:
Potenza = 1 -  = 1 - P(errore di tipo II) = 1 - P(accettare H0 quando H0 è falsa)
 = probabilità che la media campionaria entri nella regione di accettazione, sapendo che il valore atteso della
popolazione è 0.995 l.
La regione di accettazione va calcolata a partire da  (prima l’abbiamo calcolata per la variabile
standardizzata):
X up   0  Z  / 2   x   0  Z  / 2   x / n  1  1.96  0.005 / 12  1.0028 l
_______
Pag. 4/8
X down  0  Z / 2   x  0  Z / 2   x / n  1  1.96  0.005 / 12  0.9972 l
(difatti prima abbiamo rifiutato l’ipotesi nulla, perché 0.996 l è al di fuori della regione di accettazione.
X up   

X

  P z  down






X
X






1.0028  0.995 
0.9972  0.995 
 P z 
  P z 
 
0.005 / 12 
0.005 / 12 


 Pz  5.4  Pz  1.524  1  0.936  6.4 %

  PX down  X  X up con   0.995  P z 
Per cui la potenza del test è
Potenza = 1 -  = 1-0.064=93.6 %
Questo significa che il test effettuato ha il 93.6 % di probabilità di rifiutare l’ipotesi nulla se il valore atteso
della popolazione vale 0.995 l.
_______
Pag. 5/8
Esercizio 4 (tempo stimato 15 min)
(svolgere su questo foglio e sul retro)
4) Si descriva la tecnica di regressione ai minimi quadrati, indicandone l’utilità e la tecnica di calcolo. Si
faccia un esempio (breve e non numerico) di applicazione in cui può convenire impiegare la regressione
lineare ai minimi quadrati.
_______
Pag. 6/8
Esercizio 5 (tempo stimato 25 min)
(svolgere su questo foglio e sul retro)
5) Un aereo da trasporto, con tara 42 000 kg ± 1 % (definita come incertezza standard) trasporta 10 000 kg
di merci la cui massa è nota con incertezza estesa di 300 kg a rappresentare un intervallo di confidenza al
99.7 %. Nel serbatoio sono presenti (20 000 ± 100) l di benzina.
La densità della benzina è ρb=0.68 kg/dm3, nota con incertezza trascurabile.
Il personale dell’aereo è stato pesato prima della partenza, utilizzando una bilancia con risoluzione 10 kg,
ottenendo un valore complessivo di 500 kg, in un’unica pesata.
5a) Si valuti il valore e l’incertezza assoluta delle singole masse descritte (mt, mm, mb, mp), per tara, merci,
benzina, e personale rispettivamente.
5b) Si valuti la massa a pieno carico dell’aereo e la sua incertezza relativa.
5c) Attraverso una serie di misure ripetute si stima la velocità di crociera dell’aereo: 1001; 1005; 998; 997;
1002; 997 (km/h). Si valuti l’energia cinetica dell’aereo durante il volo e la sua incertezza assoluta. Si
esprima la misura dell’energia cinetica anche in notazione di incertezza concisa.
5d) Dalla torre di controllo la velocità di crociera viene stimata in 995 km/h con una incertezza estesa
12 km/h con fattore di copertura k = 2. Si verifichi la compatibilità tra questa misura e quella di velocità
ricavata al punto c).
5a) Le componenti d’incertezza delle singole masse sono:
Massa della tara dell’aereo mt:
mt = 42 000 kg
u(mt) = mt×ur(mt)  420 kg
Massa merci mm:
mm = 10 000 kg
u(mm) = U(mm) / 3 100 kg
Massa benzina mb:
mb = ρb×Vb = 20 000 l × 0.68 kg/dm3 = 13 600 kg
ur(mb) = ur(Vb) = 100/20 000 = 0.005 =0.5%
u(mb)  ur(mb) × mb = 68 kg
Massa personale mp:
mp = 500 kg
mp
u(mp) =
= 2.9 kg
12
5b) La massa a pieno carico dell’aereo maereo,tot è pari alla somma della sua tara mt e del suo carico (mm e mb)
compreso il personale mp:
mtot = mt + mb + mm + mp
Dato che la massa dell’aereo è la somma delle singole masse, la sua incertezza è data dalla somma quadratica
delle singole incertezze (in quanto scorrelate):
mtot = mt + mb + mm + mp= (42 000 kg + 13 600 kg + 10 000 kg + 500 kg)=66 100 kg
u(mtot)= u 2 mt   u 2 mb   u 2 mm   u 2 mp  kg = (420) 2  (68) 2  (100) 2  (2.9) 2 kg  440 kg
La sua incertezza relativa vale infine:
ur(mtot) = u(mtot)/mtot = 440 kg / 66 100 kg = 0.7 %
_______
Pag. 7/8
La misura della massa del furgone è mtot = ( 6610  44 ) × 101 kg = 6610(44) × 101 kg
5c) La velocità v dell’aereo vale: v =
e la sua incertezza: u(v) =
1 N
i = 1000 km/h
N i 1
N
1
i   2 = 1.3 km/h

N ( N  1) i 1
L’energia cinetica dell’aereo vale:
1
Ec= mtotv2 = 0.5 × 66 100 kg × [ 1000 km/h × (1000 m/km) × (1/3600 h/s) ]2  2.550 GJ
2
e la sua incertezza è ur(Ec) =
u r mtot   (2) u r v  =
2
2
2
2
 1.3 km/h 
0.007  4  
  1.4 %
 1000 km/h 
2
u(Ec) = ur(Ec)×Ec = 3.6×107 J = 36 MJ
La misura dell’energia cinetica del furgone è Ec = ( 2.550  0.036 ) GJ =2.550(36) GJ
5d) Per verificare la compatibilità tra le 2 misure di velocità, supposte indipendenti, dobbiamo valutare se
  cos  k u 2    u 2 cos  con un fattore di copertura ragionevole (k=1, 2, o 3). Dove con
u(vcos) = U(vcos) / 2 =6 km/h. Sostituendo i valori, si ottiene verificata la compatibilità già con k=1.
_______
Pag. 8/8