![Propagazione della radiazione elettromagnetica [modifica]](//s1.studylibit.com/store/data/000009909_1-a46af690975338d7754593e4d56e3394-768x994.png)
Radiazione elettromagnetica
Da Wikipedia, l'enciclopedia libera.
(Reindirizzamento da Onde elettromagnetiche)
Vai a: Navigazione, cerca
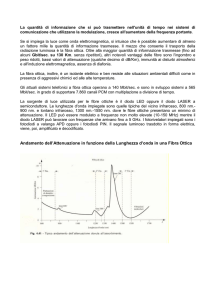
Componenti ortogonali di un'onda elettromagnetica piana polarizzata
In fisica, la radiazione elettromagnetica è la forma di energia associata all'interazione
elettromagnetica, e responsabile della propagazione nello spazio del campo elettromagnetico. Si
tratta di un fenomeno ondulatorio dato della propagazione in fase del campo elettrico e del campo
magnetico, oscillanti in piani tra loro ortogonali e ortogonali alla direzione di propagazione.
Secondo il modello standard, il quanto della radiazione elettromagnetica è il fotone, mediatore
dell'interazione elettromagnetica.
Indice
[nascondi]
1 Storia
2 Equazione delle onde elettromagnetiche
o 2.1 Derivazione dalle equazioni di Maxwell
3 Energia in un'onda elettromagnetica e vettore di Poynting
o 3.1 Intensità dell'onda elettromagnetica
4 Interazione tra radiazione elettomagnetica e materia
o 4.1 Potenza trasferita
o 4.2 Quantità di moto
o 4.3 Momento angolare di un'onda elettromagnetica
5 Polarizzazione
6 Correlazione tra campo elettrico e campo magnetico
7 Propagazione della radiazione elettromagnetica
o 7.1 Velocità di propagazione
o 7.2 Esperimento di Hertz
o 7.3 Esperimento di Michelson e Morley
8 Natura quantistica della radiazione elettromagnetica
9 Applicazioni tecnologiche
10 Effetti biologici delle radiazioni
o 10.1 Radiazioni ionizzanti
o 10.2 Radiazioni non ionizzanti
11 Protezione da Campi Elettromagnetici a radiofrequenze e microonde
o 11.1 Grandezze fisiche coinvolte e loro unità di misura
o 11.2 Definizione del rischio per gli organismi viventi legato all'esposizione a campi
elettromagnetici a RF e MW
12 Note
13 Bibliografia
14 Voci correlate
15 Altri progetti
16 Collegamenti esterni
Storia [modifica]
Le onde elettromagnetiche furono predette teoricamente prima di essere osservate: le equazioni di
Maxwell, che riassumono l'elettromagnetismo classico, ammettono una soluzione ondulatoria
propagantesi nel vuoto alla velocità della luce. Furono poi le esperienze di Hertz a confermare
l'esistenza delle cosiddette "onde hertziane", ed a misurarne la velocità. L'esperienza di Michelson
provò invece l'indipendenza della velocità della luce dalla direzione di propagazione e, grazie ad
altre esperienze che attualmente si considerano sufficienti a falsificare le cosiddette teorie balistiche
della luce, viene oggi considerata l'esperienza cruciale che mise in crisi la meccanica classica
richiedendo la formulazione della relatività ristretta. È sulla base di tale teoria, una delle teorie
meglio controllate empiricamente, che è possibile enunciare le proprietà della radiazione
elettromagnetica nel vuoto.
Equazione delle onde elettromagnetiche [modifica]
Per approfondire, vedi la voce Equazione delle onde.
Si supponga di trovarsi in un dielettrico omogeneo ed isotropo, elettricamente neutro e perfetto e
privo di cariche libere localizzate, sorgenti del campo elettromagnetico. Le equazioni che
descrivono la propagazione del campo sono le equazioni delle onde per il campo elettrico e
magnetico. Si tratta di due equazioni differenziali alle derivate parziali della forma:
.
Si tratta di sei equazioni scalari, e sono ottenute dalle equazioni di Maxwell applicando l'operatore
rotore. Questo comporta che, data una soluzione delle equazioni d'onda, la stessa soluzione
sommata ad un campo irrotazionale è ancora soluzione. Le soluzioni, inoltre, non sono
necessariamente solenoidali: tale condizione aggiuntiva deve essere infatti imposta nella fase
risolutiva.
La soluzione generale dell'equazione delle onde in una dimensione è un'onda della forma:
che si propaga con velocità costante:
Nel vuoto questa velocità diventa la velocità della luce:
.
Si chiama fronte d'onda il luogo dei punti tali che, ad un certo istante, la soluzione delle equazioni
delle onde assume valore costante. A seconda della possibilità di modellizzare l'onda a seconda
della forma del suo fronte d'onda possiamo chiamare onda rettilinea se i suoi fronti d'onda sono
rettilinei, circolare se i suoi fronti d'onda sono circolari e onda piana se i suoi fronti d'onda sono
piani, infine, onda sferica se i suoi fronti d'onda sono superfici sferiche.
La soluzione di queste equazioni, del resto, non è univoca e bisogna imporre la solenoidalità alle
soluzioni con le stesse equazioni di Maxwell, cioè tra tutte le soluzioni bisogna scegliere quelle che
soddisfano tutte le equazioni di Maxwell e non solo le equazioni delle ondem ed a seconda invece
della forma della soluzione, un'onda può essere periodica o non periodica. In generale, la soluzione
delle equazioni delle onde è una funzione
propagazione e del tempo.
funzione della direzione di
Una rappresentazione compatta della equazione dell'onda è ottenuta tramite l'uso dell'operatore di
d'Alembert definito come:
e in questo modo le equazioni delle onde diventano:
Derivazione dalle equazioni di Maxwell [modifica]
Per approfondire, vedi la voce Equazioni di Maxwell.
Si supponga di trovarsi in un dielettrico omogeneo ed isotropo, elettricamente neutro e perfetto e
privo di cariche libere localizzate, in modo che
divengono in questo caso:
e
. Le equazioni di Maxwell
È possibile procedere indifferentemente prendendo la terza o la quarta equazione di Maxwell e
applicando il rotore. Si prenda dunque la terza:
applicando il rotore di ambo i membri:
al secondo membro si sostituisce la quarta equazione in luogo di
:
mentre al primo membro si sfrutta la relazione:
e dal momento che si è supposta l'assenza di cariche libere, sorgenti del campo, si ha che
.
Si ottiene pertanto:
cioè
Analogamente applicando lo stesso procedimento alla quarta equazione otteniamo:
.
che sono entrambe le equazioni delle onde cercate.
Energia in un'onda elettromagnetica e vettore di Poynting
[modifica]
Per approfondire, vedi le voci energia del campo elettromagnetico e vettore di Poynting.
Ogni onda elettromagnetica è in grado di trasferire energia tra due punti dello spazio. Si consideri il
caso di un'onda piana, e si prenda un volume arbitrario τ contenente un campo elettromagnetico. Al
suo interno la densità di energia elettrica vale:
;
la densità di energia magnetica vale:
.
L'energia totale all'interno del volume sarà quindi:
Derivando quest'equazione e sfruttando le relazioni tra gli operatori rotore e divergenza si ottiene:
Il termine:
è il vettore di Poynting, mentre il secondo integrale al secondo membro rappresenta il contributo
dell'energia del campo elettrico per la presenza della carica contenuta nel volume V.
Dal punto di vista fisico la precedente espressione esprime il fatto che la variazione nel tempo
dell'energia contenuta nel volume V delimitato dalla superficie S è pari al flusso del vettore di
Poynting attraverso la superficie, più l'energia dissipata per effetto Joule nella materia contenuta
all'interno.
Intensità dell'onda elettromagnetica [modifica]
Nel caso di un'onda piana, sapendo che i campi elettrico e magnetico sono ortogonali tra loro
e ortogonali alla direzione di propagazione dell'onda, ponendo che non vi siano
effetti dissipativi, si ha che:
dove
è la velocità di propagazione dell'onda. Oppure in termini di campo elettrico:
dove è il versore che identifica la direzione di propagazione dell'onda e
caratteristica del materiale entro cui si propaga l'onda.
è l'impedenza
Il modulo del vettore di Poynting è l'intensità dell'onda, cioè l'energia che attraversa la superficie
ortogonale alla velocità di propagazione nell'unità di tempo:
Se l'onda piana è approssimabile con un'onda monocromatica, essa è caratterizzata da un andamento
sinusoidale del tipo
e lo stesso vale per il campo magnetico. Segue che l'intensità dell'onda è anch'essa una funzione
sinusoidale negli stessi argomenti, e deve essere mediata su un periodo:
dove
è il valore medio dell'intensità d'onda calcolato su un periodo.
Nel caso di un'onda sferica il fronte d'onda è una superficie sferica e la velocità è radiale. Per cui
l'intensità d'onda dipende da r:
dunque essa diminuisce come l'inverso del quadrato della distanza.
Interazione tra radiazione elettomagnetica e materia [modifica]
Potenza trasferita [modifica]
Si consideri un'onda elettromagnetica incidente su un materiale, essa esercita una forza per unità di
volume data da:
dove n è il numero di cariche contenute nell'unità di volume, e q la carica elementare.
La potenza trasferita dall'onda elettromagnetica per unità di volume al materiale è data dalla
precedente espressione moltiplicata scalarmente per la velocità, che essendo ortogonale al vettore
risente del solo contributo del campo elettrico:
dove
. La presenza del solo campo elettrico è inoltre giustificata dal fatto che la forza di
Lorentz non compie lavoro. Poiché per la legge di Ohm generalizzata
e per gli effetti
delle onde elettromagnetiche nei conduttori:
Nel caso considerevole in cui l'onda ha una rappresentazione sinusoidale, anche la densità di
corrente ha una dipendenza sinusoidale, per cui la potenza deve essere mediata su un periodo:
dove abbiamo sviluppato il prodotto scalare e quindi α è l'angolo tra il campo elettrico e il vettore
densità di corrente.
Quantità di moto [modifica]
Oltre all'energia, un'onda trasferisce una certa quantità di moto all'unità di volume del materiale e
per unità di tempo, data dalla media temporale della forza subita dall'unità di volume definita in
precedenza:
diretta lungo la direzione di propagazione dell'onda. Nel vuoto:
dove c è la velocità della luce.
Momento angolare di un'onda elettromagnetica [modifica]
Avendo definito la quantità di moto di un'onda elettromagnetica, è possibile ricavare il relativo
momento angolare:
Inoltre, l'onda possiede anche un momento angolare intrinseco quando essa è polarizzata
circolarmente, dato da:
dove il segno dipende dalla rotazione e la direzione è longitudinale alla direzione di propagazione
dell'onda.
Polarizzazione [modifica]
Per approfondire, vedi la voce Polarizzazione della radiazione elettromagnetica.
Correlazione tra campo elettrico e campo magnetico [modifica]
Nelle misure reali dei campi elettromagnetici, tipicamente ad alta frequenza, può essere necessario
dopo aver misurato il campo elettrico calcolare quello magnetico, oppure viceversa misurare il
campo magnetico con il quale calcolare quello elettrico. In tal caso convenzionalmente si utilizza la
seguente formula:
dove E è il campo elettrico in Volt/metro, mentre H è il campo magnetico in Amper/metro. Questa
formula può essere utilizzata solo in campo lontano (ossia non vicino all'antenna trasmittente), e
viene utilizzata in particolare per la valutazione dell'esposizione umana ai campi elettromagnetici.
L'impedenza d'onda Z si può anche esprimere mediante i parametri dell'onda elettromagnetica e del
mezzo in cui essa si propaga:
dove μ è la permeabilità magnetica, ε la permittività elettrica e σ la conducibilità elettrica del
materiale in cui l'onda si propaga. In questa equazione, j è l'unità immaginaria, e ω la frequenza
angolare dell'onda. Nel caso di un dielettrico (in cui la conducibilità è trascurabile), l'equazione si
riduce nella seguente:
Nel vuoto (e quindi approssimativamente anche in aria) tale rapporto vale circa 377 ohm:
Propagazione della radiazione elettromagnetica [modifica]
Velocità di propagazione [modifica]
Per approfondire, vedi la voce velocità della luce.
La velocità di propagazione è costante ed indipendente dalla velocità della sorgente, dalla direzione
di propagazione, e dalla velocità dell'osservatore; e nel vuoto è pari alla velocità della luce, la quale
è l'esempio più noto di onda elettromagnetica. La velocità della luce nel vuoto si indica in genere
con la lettera c ed il suo valore numerico in unità del sistema internazionale risulta di circa 300 000
km al secondo (c = 299 792,458 km/s). È importante notare che tale valore è stato assunto come
esatto: ciò vuol dire che la velocità della luce è posta per definizione uguale a c, e per questo motivo
essa non è affetta da alcuna incertezza, al contrario di ciò che avviene per i valori che derivano da
un processo di misura. Quest'assunzione ha comportato anche la modifica della definizione del
metro.
Nei mezzi materiali e nelle guide d'onda la propagazione della radiazione elettromagnetica diviene
un fenomeno più complesso. Innanzitutto la sua velocità è diversa rispetto a quella nel vuoto
secondo un fattore che dipende dalle proprietà del mezzo o della guida d'onda. Può dipendere
inoltre dalla frequenza della radiazione, secondo una relazione di dispersione. Restano definite due
velocità, dette velocità di gruppo e velocità di fase.
L'astronomo danese Ole Romer fu il primo a determinare empiricamente la velocità della luce per
mezzo dell'osservazione del satellite di Giove di nome "Io". Annunciò la sua scoperta nel
1675[senza fonte].
Romer misurò il tempo che il satellite impiegava ad attraversare il cono d'ombra provocato da
Giove notando che il tempo impiegato era diverso ad ogni misurazione. Questo perché quando "Io"
entrava nel cono d'ombra di Giove la distanza di questi dalla terra era una, mentre, quando "Io"
usciva dal cono d'ombra, la distanza dalla terra era diversa. Così ogni volta che la misura viene
ripetuta il tempo impiegato appare diverso (a seconda che la terra si stia avvicinando a Giove,
tempo più breve del reale, o che si stia allontanando, tempo più lungo). Attraverso l'osservazione di
questo fenomeno riuscì infine a calcolare la velocità della luce ottenendo un valore (2,2 x 10^8
m\s[senza fonte]) molto simile al valore reale (299 792 458 m/s).
Oggi la velocità della luce viene misurata direttamente, calcolando il tempo che impiega un impulso
luminoso emesso da un laser a percorrere un determinato spazio. Dal momento che questa
procedura è molto precisa e la velocità della luce è costante nel vuoto, si è pensato di definire il
metro in termini di velocità della luce (vedere in proposito metro).
Esperimento di Hertz [modifica]
Questa sezione sull'argomento fisica è solo un abbozzo. Contribuisci a migliorarla secondo le
convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento.
Hertz fece scoccare una scintilla interponendo un dielettrico tra due elettrodi sottoposti ad una
differenza di potenziale elevata. Sottopose poi una spira al campo elettromagnetico prodotto dalla
scintilla, la spira non era chiusa, aveva anch'essa due elettrodi sottoposti ad una differenza di
pontenziale, dovuti al flusso concatenato sulla spira, dal campo elettromagnetico prodotto dalla
scintilla. Questo esperimento contribuì a formulare la sua teoria sull'elettromagnetismo.[1]
Esperimento di Michelson e Morley [modifica]
Per approfondire, vedi la voce Esperimento di Michelson-Morley.
Natura quantistica della radiazione elettromagnetica [modifica]
Gli studi sull'effetto fotoelettrico, tra i quali spicca il contributo del 1905 di Albert Einstein (che gli
valse il premio Nobel) evidenziarono l'esistenza di una frequenza di soglia sotto la quale tale effetto
non ha luogo, indipendentemente dall'intensità (ampiezza) della radiazione incidente. Esperienze
correlate, quali la misura dello spettro di corpo nero, ed i relativi tentativi di giustificazione teorica,
indussero i fisici dell'inizio del secolo scorso a riaprire il secolare dibattito sulla natura della luce, di
cui le equazioni di Maxwell sembravano costituire la soluzione definitiva, introducendo la nozione
di quanto di energia. Il quanto di radiazione elettromagnetica prende il nome di fotone ed è una
particella (nel senso della meccanica quantistica) che segue la statistica di Bose-Einstein, ovvero un
bosone.
Applicazioni tecnologiche [modifica]
La radio e la televisione, i telefoni cellulari, i computer e il radar, il forno a microonde e le
radiografie: gli utilizzi tecnologici della radiazione elettromagnetica sono così diffusi che non vi
facciamo nemmeno più caso. Le applicazioni possono essere divise in due macrofamiglie: nella
prima le onde elettromagnetiche vengono utilizzate per trasportare informazioni ( radio,
televisione), nella seconda per trasportare energia ( forno a microonde ).
Effetti biologici delle radiazioni [modifica]
Gli effetti della radiazione elettromagnetica sugli esseri viventi dipendono principalmente da due
fattori: la frequenza della radiazione e le modalità di esposizione (intensità della radiazione, durata
dell'esposizione, parti del corpo esposte...). Per quanto riguarda la frequenza della radiazione si usa
distinguere tra radiazioni ionizzanti e radiazioni non ionizzanti.
Radiazioni ionizzanti [modifica]
Per approfondire, vedi la voce Radiazioni ionizzanti.
Per approfondire, vedi la voce Malattia da radiazione.
Per radiazioni ionizzanti si intendono le radiazioni elettromagnetiche di frequenza sufficientemente
alta da essere in grado di ionizzare gli atomi della sostanza esposta. Tali radiazioni sono quindi
capaci di modificare la struttura chimica delle sostanze su cui incidono e possono produrre effetti
biologici a lungo termine sui viventi interagendo con il DNA delle cellule.
Radiazioni non ionizzanti [modifica]
Si designano come non ionizzanti quelle radiazioni elettromagnetiche non in grado di produrre
ionizzazione nei materiali ad esse esposti. Un esempio di radiazioni non ionizzanti sono le onde
radio. Si ritiene comunemente (vedere in proposito la voce elettrosmog) che le radiazioni non
ionizzanti possano avere effetti sui viventi solo per i loro effetti termici, non possedendo quindi il
potenziale mutageno e cancerogeno delle radiazioni ionizzanti[2].
Le radiazioni non ionizzanti, dette NIR dall'acronimo inglese Non Ionizing Radiation, comprendono
tutte le radiazioni elettromagnetiche non ionizzanti, dalle ELF fino all'ultravioletto vicino.
Per quanto riguarda gli effetti biologici e sanitari, una certezza è data dal fatto che un'onda e.m.
trasferisce calore e quindi un effetto dell'interazione di un'onda e.m. con un sistema vivente è che
parte dell'energia viene rilasciata, con un aumento della temperatura locale o di tutto il sistema. Per
quanto riguarda gli effetti termici, occorre verificare quanto l'organismo umano è in grado di
sostenere un rialzo termico. Poiché il principale "scambiatore" di calore presente nel corpo umano è
costituito dal sangue, si può pensare che gli organismi meno vascolarizzati costituiscano organi
critici per quanto riguarda l'esposizione alle radiazioni e.m., in quanto, se riscaldati dall'esterno non
hanno più modo di ridistribuire il calore ricevuto tramite un'idonea circolazione sanguigna. Da
questo punto di vista gli organi critici per eccellenza sono il cristallino e le gonadi maschili.
Protezione da Campi Elettromagnetici a radiofrequenze e
microonde [modifica]
Negli ultimi anni sono andati crescendo gli interrogativi sui possibili effetti sulla salute legati
all'esposizione a campi elettromagnetici a radiofrequenze (RF) e microonde (MW). Nuove
tecnologie si vanno diffondendo a tutti i livelli nella società, con una varietà di applicazioni mai
viste prima. In molti laboratori si sta lavorando intorno a interrogativi quali l'effetto della
applicazione di un campo elettromagnetico sulla permeabilità delle membrane cellulari a
determinate specie ioniche e su quali basi biofisiche sia ipotizzabile un'influenza diretta del campo
elettromagnetico sull'integrazione e l'elaborazione dei segnali nervosi.
Grandezze fisiche coinvolte e loro unità di misura [modifica]
Le unità di misura usate per esprimere l'entità dell'esposizione a campi a radiofrequenze e
microonde sono il Volt/metro (V/m), in riferimento all'intensità della componente elettrica E del
campo, l'Ampere/metro (A/m), per l'intensità della componente magnetica H del campo, ed il
Watt/m2 (W/m2), per la densità S di potenza irradiata.
Sono stati definiti anche opportuni parametri per quantificare l'energia assorbita dal corpo umano
esposto a campi elettromagnetici. Di fondamentale importanza è il tasso di assorbimento specifico
di energia, indicato con l'abbreviazione SAR (dall'inglese "Specific Absorption Rate") misurato
solitamente in W/kg che rappresenta la potenza di campo elettromagnetico assorbita per unità di
massa. Bisogna tener presente che questa grandezza dipende fortemente dalla frequenza del campo
e.m. perché presenta fenomeni di risonanza legati alle dimensioni fisiche della persona investita.
Definizione del rischio per gli organismi viventi legato all'esposizione a campi
elettromagnetici a RF e MW [modifica]
Un'onda elettromagnetica che si propaga nello spazio trasporta energia che viene in parte assorbita e
in parte riflessa dagli oggetti che tale onda incontra sul suo percorso. L'assorbimento avviene con
modalità ed in misura diversa a seconda delle caratteristiche del mezzo. L'effetto sugli organismi
viventi di tale assorbimento di energia da un campo elettromagnetico a radiofrequenza e microonde
è da una ventina d'anni oggetto di numerose indagini scientifiche.
A livello microscopico, manca ancora uno schema interpretativo soddisfacente dell'azione di un
campo elettromagnetico sulle cellule degli organismi viventi. Questo dipende innanzitutto
dall'incompleta conoscenza dei fenomeni a livello di membrana cellulare legati allo scambio di
materiali ed informazioni tra cellule a ambiente esterno. In secondo luogo, la complessità strutturale
dei tessuti biologici e la loro disomogeneità, rende assai problematico un calcolo dettagliato della
deposizione locale di energia nei tessuti da parte dell'onda elettromagnetica incidente.
La controversia sulla possibilità di manifestazione di effetti non termici, cioè dovuti ad esposizioni
a livelli di campo elettromagnetico a radiofrequenze e microonde non abbastanza elevati da
produrre riscaldamento dei tessuti, si riflette nella scelta degli standard ammissibili di esposizione
per lavoratori e popolazione civile da parte di Stati ed Organizzazioni internazionali diversi.
Le ricerche compiute nei Paesi occidentali hanno condotto alla conclusione (ANSI, 1982) che
l'esposizione protratta per un periodo inferiore ad 1 ora, e comportante un tasso di assorbimento
specifico medio al corpo intero inferiore a 4 W/kg non è in grado di produrre effetti sulla salute. Per
cautelarsi dai possibili effetti cumulativi dovuti ad esposizioni prolungate (giorni oppure settimane)
si è considerato per l'uomo un valore limite di SAR 10 volte inferiore, pari quindi a 0.4 W/kg.
![Propagazione della radiazione elettromagnetica [modifica]](http://s1.studylibit.com/store/data/000009909_1-a46af690975338d7754593e4d56e3394-768x994.png)