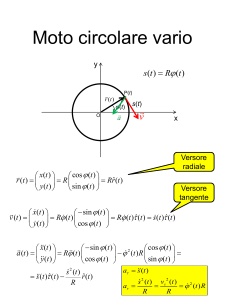
velocità e accelerazione vettoriale
La rapidità di cambiamento della posizione nel tempo è data dalla velocità. La posizione,
individuata mediante il raggio vettore rispetto all'origine di un sistema di assi cartesiani
ortogonali, cambia perchè o cambia la distanza dall'origine, o cambia la direzione (il
raggio vettore ruota) o il verso (una rotazione di 180°).
La velocità viene a dipendere dalla rapidità con cui cambia la distanza e dalla rapidità con
cui cambia l'inclinazione (rispetto all'asse x per esempio) ossia dalla rapidità di rotazione
del raggio vettore.
In un intervallo !t la velocità media è
Δ r v=
Δt
mentre la velocità istantanea è
Δ r d r v = lim v m = lim
=
Δt→ 0
Δt→ 0 Δt
dt
Il vettore r si può scrivere come il prodotto fra il modulo (r) e il versore ( r̂ ), r = r ⋅ r̂ ;
trovare la velocità è calcolare la derivata del prodotto r = r ⋅ r̂ *. Questa operazione è
valida per ogni vettore e verrà illustrata per un generico vettore b̂ . La derivata di b̂ è la
derivata del prodotto b = b ⋅ b̂ , cioè !b = !(b ⋅ b̂) = !(b) ⋅ b̂ + b ⋅ !(b̂) . La difficoltà di
derivare il vettore si sposta quindi a calcolare la derivata del versore.
Derivando rispetto al tempo si ha
db d(b ⋅ b̂) db
db̂
=
=
⋅ b̂ + b ⋅
dt
dt
dt
dt
db̂
Δb̂
Per trovare
si deve valutare
e poi passare al limite; Δb̂ è il vettore che definisce
dt
Δt
la variazione fra il versore b̂ ad un certo istante ( b̂') e il versore b̂ ad un istante
successivo ( b̂" ).
Graficamente
Δb̂
b̂"
∆α
b̂'
con !α l'angolo di rotazione. Il modulo di Δb̂ si può calcolare considerando che il
triangolo di lati b' e b" è un triangolo isoscele ( b̂' e b̂" hanno modulo 1) e che per piccoli
*
Da notare che sia come velocità media, che come velocità istantanea, il vettore velocità ha la stessa
direzione di
Δ r o di d r , cioè parallelo alla traiettoria.
valori di !α il lato !b̂ può essere considerato come un elemento di circonferenza* di
valore !b̂ = !α ⋅ b̂ = !α ⋅1 = !α , con !α misurato in radianti.
Quando si considera l'intervallo temporale !t sempre più piccolo (tende a zero), !α
diventa trascurabile e gli altri due angoli del triangolo isoscele tendono a 90°; il vettore
!b̂ tende a diventare perpendicolare a b̂ .
!b̂ !α ⋅ b̂ ⊥ !α = lim
= lim
b̂ ⊥ = ω b̂ ⊥ con ω la velocità
!t→ 0 !t
!t→ 0
!t→ 0 !t
!t
angolare e b̂ ⊥ il versore perpendicolare a b̂ .
In questa situazione lim
Si ricava la regola generale che la derivata di un versore è un vettore perpendicolare al
versore stesso con modulo pari alla velocità angolare ω, cioè alla rapidità di rotazione del
versore.
Applicando questo risultato al vettore velocità
d r d(r ⋅ r̂) dr dr̂ dr v=
=
=
r̂ + r
=
r̂ + rω r̂⊥
dt
dt
dt
dt
dt
Il risultato è un vettore con due componenti, una nella direzione di r̂ e l'altra nella
direzione di r̂⊥ , perpendicolare a r̂ .
Il moto rettilineo è descritto da una ω nulla e la velocità si riduce a
dr v=
r̂
dt
e il moto circolare è descritto da un raggio r costante e la velocità contiene solo termini
di rotazione
v = rω r̂⊥
Trovata la velocità si può, allo stesso modo, ricavare l'accelerazione; dalla espressione
generale della velocità si può notare che l'accelerazione avrà una componente parallela
(radiale) ed una perpendicolare ad r̂ . Per semplicità valuteremo i casi di moto rettilineo e
moto circolare uniforme, ω costante.
Nel moto rettilineo l'accelerazione ha come modulo la derivata del modulo della velocità e
la direzione del raggio vettore r
dv d2r a=
r̂ =
r̂
dt
dt2
Nel moto circolare uniforme ω è costante e in questo modo varia solo la direzione del
vettore velocità.
dr̂⊥ dv d(r ⋅ ω ⋅ r̂⊥ ) a=
=
= r ⋅ω ⋅
= r ⋅ ω ⋅ ω ⋅ r̂⊥ ⊥ = ω 2 ⋅ r ⋅ r̂⊥ ⊥
dt
dt
dt
misurando l’angolo in frazioni del fattore 2" (misura in radianti) ogni arco di circonferenza può essere
valutato come il prodotto fra il raggio della circonferenza e il valore dell’angolo.
*
Il versore r̂⊥ ⊥ è un versore perpendicolare a r̂⊥ il quale a sua volta è perpendicolare a r̂ .
Risulta quindi ruotato di 180° rispetto a r̂ . E' quindi un versore opposto a r̂ : r̂⊥ ⊥ = -r̂ ;
l'accelerazione diventa
oppure
a = -ω 2 ⋅ r ⋅ r̂ = - ω 2 ⋅ r
a + ω2 ⋅ r = 0
Questa ultima relazione è detta equazione armonica e lega l'accelerazione che subisce un
corpo con la sua posizione.
L'equazione si può scrivere per componenti e lungo una direzione (x ad esempio)
ax + ω2x = 0
o scrivere genericamente
a + ω2x = 0
dove x ed a (o ax ) dipendono dal tempo. Le soluzioni di questa equazione sono quelle
funzioni f(t) tali che la loro derivata seconda renda nullo il primo membro dell'equazione
armonica.
d2f = - ω2 ⋅ f .
2
dt
Se x(t) = xo cos (ωt + ϕ) , questa è soluzione dell'equazione armonica. Qui ω è la velocità
angolare e la ϕ rappresenta il generico valore della x per t = 0, ossia la fase.
Infatti, poiché
d2x dv a=
=
dt
dt2
per calcolare l'accelerazione occorre calcolare la velocità
dx v=
= ω ⋅ x 0sen(ω t + ϕ )
dt
da cui
d2x dv a=
=
= - ω ⋅ x 0 ⋅ ω cos(ω t + ϕ ) = - ω 2 ⋅ x 0cos(ω t + ϕ ) = - ω 2 ⋅ x
2
dt
dt
che sostituita nell'equazione armonica
- ω2 x + ω2 x = 0
la rende nulla, ossia la soddisfa.
Più in generale, ogni funzione in sin o cos è soluzione dell'equazione armonica, ma anche
una qualunque combinazione purchè lineare è ancora soluzione dell'equazione armonica.
L'equazione armonica si suole far derivare dal moto circolare uniforme e da qui ω
mantiene il nome di velocità angolare. Tuttavia ha una sua origine indipendente come nei
moti lineari come l'oscillazione dell'estremo libero di una molla o il moto di un pendolo,
Per questi moti la dizione velocità angolare è priva di senso e la ω è chiamata pulsazione.
Per completare la descrizione del moto circolare introduciamo il periodo T, il tempo
necessario a compiere una rivoluzione completa. Possiamo valutare il periodo
considerando la velocità media necessaria a descrivere una circonferenza di raggio r
2"r 2"r 2"r 2" da cui T =
=
=
T
v
ωr
ω
Un'altra grandezza che si accompagna al periodo è la frequenza f, cioè il numero di
rivoluzioni effettuate nell'unità di tempo
numero di giri f=
tempo
v=
Se nel tempo t l'oggetto ruota di un angolo α il numero di giri compiuti si ricava dividendo
l'angolo α per 2π
α 1 1 α ω f=
=
=
2" t 2" t
2π
e la frequenza risulta l'inverso del periodo
1 f=
T