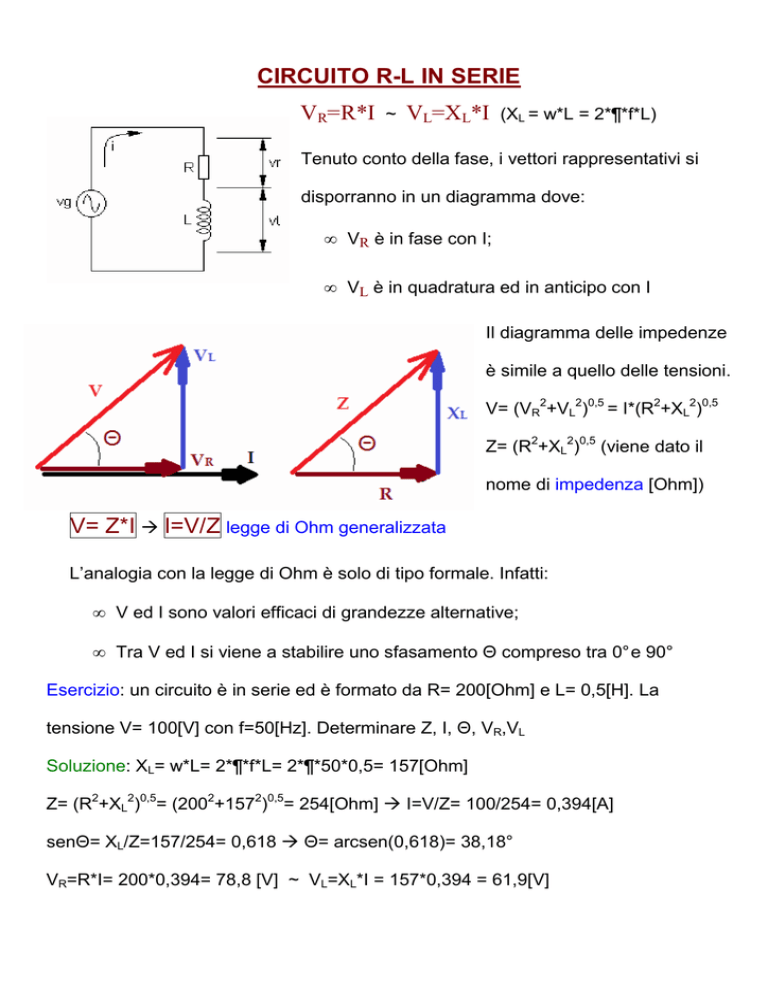
CIRCUITO R-L IN SERIE
VR=R*I
~
VL=XL*I
(XL = w*L = 2*¶*f*L)
Tenuto conto della fase, i vettori rappresentativi si
disporranno in un diagramma dove:
• VR è in fase con I;
• VL è in quadratura ed in anticipo con I
Il diagramma delle impedenze
è simile a quello delle tensioni.
V= (VR2+VL2)0,5 = I*(R2+XL2)0,5
Z= (R2+XL2)0,5 (viene dato il
nome di impedenza [Ohm])
V= Z*I I=V/Z legge di Ohm generalizzata
L’analogia con la legge di Ohm è solo di tipo formale. Infatti:
• V ed I sono valori efficaci di grandezze alternative;
• Tra V ed I si viene a stabilire uno sfasamento Θ compreso tra 0° e 90°
Esercizio: un circuito è in serie ed è formato da R= 200[Ohm] e L= 0,5[H]. La
tensione V= 100[V] con f=50[Hz]. Determinare Z, I, Θ, VR,VL
Soluzione: XL= w*L= 2*¶*f*L= 2*¶*50*0,5= 157[Ohm]
Z= (R2+XL2)0,5= (2002+1572)0,5= 254[Ohm] I=V/Z= 100/254= 0,394[A]
senΘ= XL/Z=157/254= 0,618 Θ= arcsen(0,618)= 38,18°
VR=R*I= 200*0,394= 78,8 [V] ~ VL=XL*I = 157*0,394 = 61,9[V]
CIRCUITO R-C IN SERIE
VR=R*I
~
VC=XC*I
(XC = 1/w*C = 1/( 2*¶*f*C) )
Tenuto conto della fase, i vettori rappresentativi si
disporranno in un diagramma dove:
• VR è in fase con I;
• VC è in quadratura ed in ritardo con I
Il diagramma delle impedenze è
simile a quello delle tensioni.
V= (VR2+VC2)0,5 = I*(R2+XC2)0,5
Z= (R2+XC2)0,5 (viene dato il nome
di impedenza [Ohm])
V= Z*I I=V/Z legge di Ohm generalizzata
Esercizio 1: un circuito è in serie ed è formato da R= 100[Ohm] e C= 40[µF]. La
tensione V= 220[V] con f=50[Hz]. Determinare Z, I, Θ, VR,VC
Soluzione: XC= 1/ w*C= 1/ (2*¶*f*C)= 106/(2*¶*50*40)= 79,6 [Ohm]
Z= (R2+XC2)0,5= (1002+79,62)0,5= 128[Ohm] I=V/Z= 220/128= 1,72[A]
senΘ= XC/Z=79,6/128= 0,622 Θ= arcsen(0,622)= 38,5°
VR=R*I= 100*1,72= 172 [V] ~ VC=XC*I = 79,6*1,72 = 137 [V]
Esercizio 2: un circuito è in serie ed è formato da R= 300[Ohm] e C= 2 [µF]. La
tensione V= 220[V] con f=50[Hz]. Determinare Z, I, Θ, VR,VC
Soluzione: XC= 1/ w*C= 1/ (2*¶*f*C)= 106/(2*¶*50*2)= 1592 [Ohm]
Z= (R2+XC2)0,5= (3002+15922)0,5= 1620 [Ohm] I=V/Z= 220*1000/1620= 136[mA]
Θ= arcsen(XC /Z)= 79,3°
VR=R*I= 300*1,36/1000= 40,8 [V] ~ VC=XC*I = 1592*136/1000 = 216,5 [V]
CIRCUITO R-C-L IN SERIE
VR=R*I
~
VC=XC*I
XL>XC X=XL-XC
X>0 Il circuito si
presenta di tipo RL
VL=XL*I
(XL = w*L = 2*¶*f*L)
(XC = 1/w*C = 1/( 2*¶*f*C) )
XL<XC X=XL-XC X<0
Il circuito si
presenta di tipo RC
XL=XC RISONANZA
X=XL-XC X=0 Il circuito
si presenta puramente
resistivo
Θ= arctang((XL-XC)/R)
La particolare condizione XL=XC prende il nome di risonanza. XL=w*L XC=1/w*C
w*L=1/w*C w2=1/(C*L) quindi pulsazione di risonanza w0= 1/(CL)0,5
e frequenza di risonanza f0= 1/2*¶(CL)0,5 IMPEDENZA = (R2+X2)0,5= (R2+(XL-XC)2)0,5
Esercizio: un circuito è in serie ed è formato da R= 100[Ohm] , C= 10[µF] ed
L=0,5[H]. La tensione V= 220[V] con f=50[Hz]. Determinare Z, I, Θ, VR,VC,VL
Soluzione: XC= 1/ w*C= 1/ (2*¶*f*C)= 106/(2*¶*50*10)= 318 [Ohm]
XL= w*L= 2*¶*f*L= 2*¶*50*0,5= 157[Ohm] X=XC-XL=318-157=161[Ohm]
Z= (R2+X2)0,5= (1002+1612)0,5= 190[Ohm] I=V/Z= 220/190= 1,16[A]
senΘ= X/Z=161/190= 0,847 Θ= arcsen(0,847)= 57,9°
VR=R*I= 100*1,16= 116[V] ~ VC=XC*I =318*1,16= 369[V] ~VL=XL*I =157*1,16=182 [V]