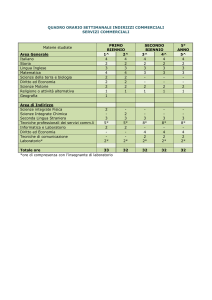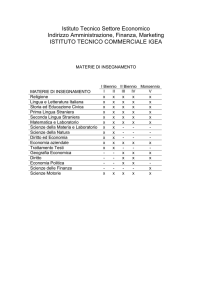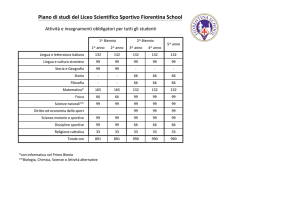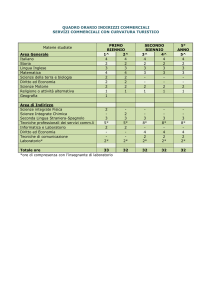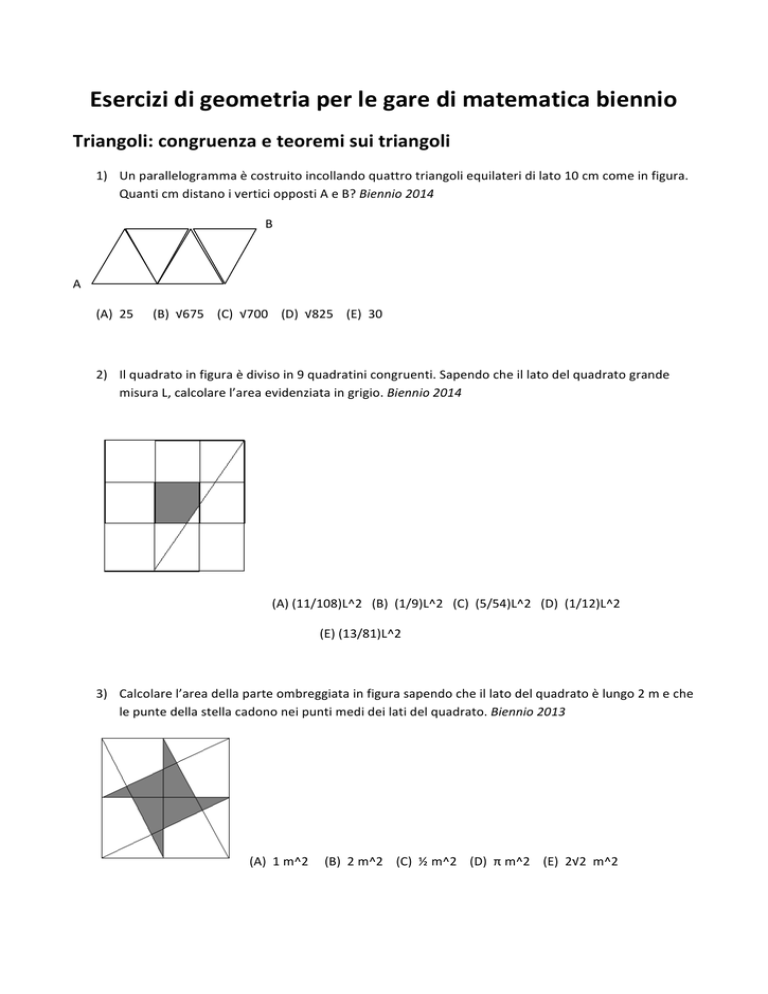
Esercizi di geometria per le gare di matematica biennio Triangoli: congruenza e teoremi sui triangoli 1) Un parallelogramma è costruito incollando quattro triangoli equilateri di lato 10 cm come in figura. Quanti cm distano i vertici opposti A e B? Biennio 2014 B A (A) 25 (B) √675 (C) √700 (D) √825 (E) 30 2) Il quadrato in figura è diviso in 9 quadratini congruenti. Sapendo che il lato del quadrato grande misura L, calcolare l’area evidenziata in grigio. Biennio 2014 (A) (11/108)L^2 (B) (1/9)L^2 (C) (5/54)L^2 (D) (1/12)L^2 (E) (13/81)L^2 3) Calcolare l’area della parte ombreggiata in figura sapendo che il lato del quadrato è lungo 2 m e che le punte della stella cadono nei punti medi dei lati del quadrato. Biennio 2013 (A) 1 m^2 (B) 2 m^2 (C) ½ m^2 (D) π m^2 (E) 2√2 m^2 4) Sia dato un esagono regolare di lato di lunghezza 1 m, i cui vertici, elencati in senso orario, sono A, B, C, D, E, F. Siano X e Y le intersezioni del segmento AC con i segmenti BF e BD rispettivamente. Calcolare la distanza tra X e Y. Biennio 2012 (A) ½ m (B) √3/3 m (C) √3/6 m (D) (2√3)/3 m (E) √3/2 m 5) Il cortile della casa di Luigi ha la forma di un triangolo rettangolo isoscele. Sapendo che l’area del cortile è 16 m^2, quanto misura il lato più lungo del cortile? Biennio 2012 (A) 2 m (B) 4 m (C) 4√2 m (D) 8 m^2 (E) 8√2 m 6) Sia ABC un triangolo acutangolo e sia H sul lato AB il piede dell’altezza dal vertice C. Supponiamo che l’area del triangolo AHC stia a quella del triangolo ABC come AC sta a 2AB. Quale delle seguenti affermazioni è sicuramente vera? Biennio 2012 (A) ABC è rettangolo (B) l’angolo CAB = 60° (C) AB = 2AH (D) AB = AC (E) ABC è equilatero 7) In un triangolo rettangolo ABC i cateti BC e CA misurano 7 cm e 24 cm rispettivamente. Sia H la proiezione di C sull’ipotenusa AB. Quanto vale il perimetro del triangolo HBC? Biennio 2008 (A) 262/25 cm (B) 501/49 cm (D) 801/49 (E) ¾ 8) In un quadrato ABCD di lato 1 cm, sono dati un punto M sul lato BC e un punto N sul lato CD tali che BM = ND. Si sa inoltre che l’area del triangolo AMN è pari a 4/9 cm^2. Quanto vale la lunghezza del segmento ND? Biennio 2008 (A) ¼ cm (B) 1/3 cm (C) ½ cm (D) (√5 – 1)/2 cm (E) √3/2 cm 9) Ciro taglia un triangolo equilatero fatto di carta, di lato 20 cm, in alcuni pezzi che poi dispone sul suo tavolo in modo che non si sovrappongano e che formino un quadrato. Quanto è lungo il lato del quadrato? Biennio 2011 !
!
(A) 20 cm (B) 10 3 cm (C) 15 cm (D) 8 2 cm (E) 10√3 cm 10) Un triangolo rettangolo ha un cateto lungo 40 cm e il raggio del cerchio inscritto misura 10 cm. Quanto misura l’ipotenusa? Biennio 2011 (A) 10√3 cm (B) 40 cm (C) 20√5 cm (D) 50 cm (E) 60 cm Circonferenza, cerchio, corona circolare e triangoli rettangoli particolari 11) Sono date tre circonferenze aventi tutte raggio 1 cm e tangenti due a due come in figura. Calcolare l’area in cm^2 della parte compresa tra le due circonferenze, evidenziata in grigio in figura. Biennio 2014 (A) (√3 – π/2) (B) √3 (C) 3 (D) π/2 (E) π 12) Francesco vuole seminare una zona del giardino della sua casa, che ha la forma riportata in figura (casa in grigio e giardino in bianco tutto intorno). Per far questo, lega una corda di 2 m all’angolo A della casa, la tende e, spostandone l’estremità, disegna il perimetro della zona da seminare. Quanti m^2 seminerà Francesco? Biennio 2013 (A) 2π + √3 (B) (15/4)π -­‐ √3/2 (C) (31/12)π + √3/2 (D) (9/4)π (E) 4π -­‐ √3/2 – 1 13) In una scultura di arte moderna è rappresentato un cerchio nascosto in parte da un triangolo equilatero, come in figura: il cerchio ha il diametro lungo quanto l’altezza del triangolo, la quale misura √6 m. Quanto vale l’area della parte del cerchio non coperta dal triangolo? Biennio 2013 (A) ((3/2)π – 8/√3) m^2 (B) π/2 m^2 (C) (π -­‐ 3√3/4) m^2 (D) ((3/2)π -­‐ 9√3/8) m^2 (E) 3/2 m^2 14) Sia dato un esagono regolare di lato 2 m. Calcolare l’area della corona circolare delimitata dal cerchio inscritto e dal cerchio circoscritto all’esagono. Biennio 2012 (A) π/2 m^2 (B) π m^2 (C) 4π/3 m^2 (D) 2π m^2 (E) π/9 m^2 15) Il raggio della circonferenza a fianco è di 5 cm; inoltre i punti A, B e C dividono la circonferenza in tre archi di uguale lunghezza. Calcolare l’area delimitata dalle corde AC e BC e dall’arco di estremi A e B contenente D. Biennio 2008 (A) 25(π/3 + √3/2) cm^2 (B) 25(π/6 + √3) cm^2 . (C) 15(π/3 + √3/2) (D) (25√3)/2 (E) (25/2)(π/3 + √3/2) cm^2 16) In un parallelogramma di area 1 m^2 le lunghezze di due lati consecutivi sono una il doppio dell’altra. Inoltre uno degli angoli interni misura 60°. Quanto misura la diagonale minore? Biennio 2011 !
!
(A) √3/2 m (B) (2 3)/3 m (C) 1 m (D) (2√3)/3 m (E) 3