Ele t trologia /
c i r c u i t i a c o r r e n t e c o n t i n u a e a lt e r n ata
UE3050211
Resistenza di una bobina
nel circuito a corrente alternata
UE3050211
B A S I GE NE RALI
ANALISI
Qualsiasi variazione della corrente generata da una bobina induce una
forza controelettromotrice che agisce in direzione opposta alla variazione di corrente. Nei circuiti a corrente alternata, la tensione della
bobina precede pertanto la corrente generata dalla bobina. Matematicamente, questa relazione è descrivibile con più semplicità utilizzando
corrente, tensione e impedenza come grandezze complesse e osservandone le parti reali.
Secondo l’equazione (4), la resistenza induttiva XL è proporzionale alla
frequenza f e all’induttanza L. Nei diagrammi corrispondenti, i valori
misurati si trovano pertanto su una retta passante per l’origine nei limiti
della precisione di misurazione.
La corrente generata dalla bobina ritarda la tensione dalla bobina nella
fase di 90°, poiché ogni variazione di corrente induce una forza controelettromotrice.
La relazione corrente - tensione per una bobina è la seguente:
U = L⋅
(1)
dI
dt
I: Corrente, U: Tensione, L: Induttanza
Con una tensione
(2)
U = U0 ⋅exp(i ⋅2π ⋅ f ⋅t )
la corrente è quindi data da
(3)
F UN Z IONI
SCOPO
Determinazione della resistenza induttiva in funzione di induttanza e frequenza
• Determinazione di modulo e fase della
resistenza induttiva in funzione dell’induttanza.
• Determinazione di modulo e fase della
resistenza induttiva in funzione della
frequenza.
120
U0
⋅exp(i ⋅2π ⋅ f ⋅t ) .
i ⋅2π ⋅ f ⋅L
XL =
U
= i ⋅2π ⋅ f ⋅L
I
Qualsiasi variazione della corrente causata da una bobina induce una tensione. In presenza di corrente alternata, la tensione alternata viene indotta con uno spostamento di fase rispetto alla corrente.
Matematicamente, questa relazione è descrivibile con più semplicità utilizzando corrente, tensione e
impedenza come grandezze complesse e osservandone le parti reali. Nell’esperimento, un generatore
di funzione fornisce tensione alternata con frequenze fino a 2 kHz. Un oscilloscopio a due canali registra corrente e tensione, in modo da rilevare ampiezza e fase di entrambe le grandezze. La corrente
generata dalla bobina corrisponde alla caduta di tensione di una resistenza di misura il cui valore è
trascurabile rispetto alla resistenza induttiva.
Appa re c chi ne cess a ri
(6a)
(7a)
80
60
20
0
0
10
30
40
50
Fig. 3: Resistenza induttiva XL come funzione dell’induttanza L
π
= I0 cos ⎛⎜ ωt − ⎞⎟
⎝
2⎠
U0
= 2π ⋅ f ⋅L
I0
XL / Ù
Nell’esperimento, un generatore di funzione fornisce tensione alternata
con frequenze fino a 2 kHz. Un oscilloscopio a due canali registra corrente
e tensione, in modo da rilevare ampiezza e fase di entrambe le grandezze.
La corrente generata dalla bobina corrisponde alla caduta di tensione di
una resistenza di misura il cui valore è trascurabile rispetto alla resistenza
induttiva.
300
200
Cat. no
1
Scheda per componenti
1012902
2
Bobina S con 1200 spire
1001002
1
Resistenza 10 Ω, 2 W, P2W19
1012904
1
Generatore di funzione FG 100 (230 V, 50/60 Hz)
1009957o
Generatore di funzione FG 100 (115 V, 50/60 Hz)
1009956
1
Oscilloscopio USB 2x50 MHz
1017264
2
Cavo ad alta frequenza, connettore 4 mm / BNC
1002748
1
Set di 15 cavi per esperimenti, 75 cm, 1 mm²
1002840
100
0
0
500
1000
1500
2000
f / Hz
Fig. 4: Resistenza induttiva XL come funzione della frequenza f
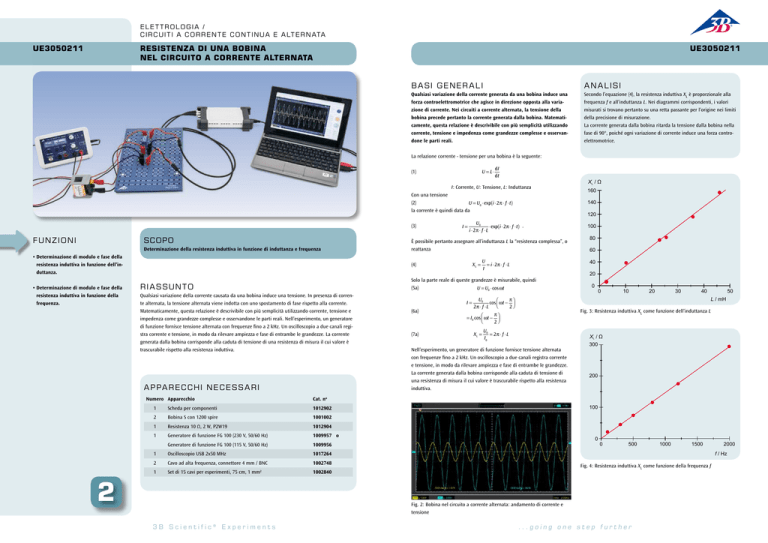
Fig. 2: Bobina nel circuito a corrente alternata: andamento di corrente e
tensione
3B Scientific® Experiments
20
L / mH
U0
π
I=
cos ⎛⎜ ωt − ⎞⎟
2⎠
2π ⋅ f ⋅L ⎝
XL =
100
40
Solo la parte reale di queste grandezze è misurabile, quindi
(5a)
U = U0 ⋅cosωt
RIA S S UNTO
2
140
È possibile pertanto assegnare all’induttanza L la “resistenza complessa”, o
reattanza
(4)
Numero Apparecchio
I=
XL / Ù
160
...going one step further












