COSTRUZIONE DI UN MODELLO DI SISTEMA SOLARE IN SCALA
Questo percorso è stato costruito a partire da un’esperienza, proposta ai bambini del secondo ciclo
delle elementari ed ai ragazzini delle medie, dalla prof. A. Turricchia dell’Aula didattica del
Planetario del comune di Bologna. Adattandolo ad un’utenza di ragazzi più grandi si è potuto
renderlo più complesso dal punto di vista sia matematico che formale, arricchendolo di tutta una
serie di argomenti collaterali che lo rendono funzionale allo svolgimento del programma di fisica
della classe prima di un ITIS, senza perdere la forte impressione finale che danno questi “pianeti”,
spesso più piccoli di uno spillo, spersi in un’immensità di vuoto.
La prima capacità che si chiede di acquisire ai nostri studenti è quella di saper eseguire
correttamente una misura, sia diretta che indiretta, e fornirne il risultato in maniera completa con
il numero corretto di cifre significative, il che, nel caso di misure indirette, comporta l’utilizzo della
propagazione dell’errore. Normalmente la prima misura che viene proposta ai ragazzi in
laboratorio è una misura (diretta) di lunghezza, di solito seguita da alcuni esempi di misure
indirette, di lunghezza, superficie, volume e densità. La misura, diretta ed indiretta, di una
lunghezza nel prato della scuola rientra in pieno in questa logica.
Fra gli altri argomenti iniziali del programma c’è un congruo ripasso sulla lettura e produzione di
grafici; il concetto di fattore di scala dovrebbe essere fra i prerequisiti ed è stato ampiamente
trattato nella scuola media, ma non sempre è il caso di darlo per assodato.
Il concetto di modello, invece, è caratteristico della fisica e viene progressivamente sviluppato nei
due anni del corso; per chiarirlo può essere utile far vedere ai ragazzi come la medesima realtà sia
stata interpretata in maniere diverse nel corso della storia, secondo un percorso che non
necessariamente è di evoluzione lineare verso la “verità”. La storia dell’astronomia, sia pure in
pillole, si presta anche a tutta una serie di divagazioni di carattere locale (la nostra scuola è in via
G.D.Cassini, per esempio) e di connessioni con la storia generale, in modo da poter
contestualizzare la scienza, che forzatamente presentiamo nei nostri programmi come un’entità
avulsa da riferimenti politici, sociali o solo culturali in senso lato.
Nel corso della prima gli studenti devono imparare a comunicare correttamente con un discreto
linguaggio tecnico e cominciano ad elaborare una relazione di ciascuna esperienza, secondo il
classico schema: titolo, scopo, materiali, strumenti, montaggio, dati, elaborazione, conclusioni.
Naturalmente non tutti entrano subito in questa logica, che anzi, per lo più, rimane loro ostica per
un certo periodo; quello che viene qui presentato come risultato del loro lavoro è il collage delle
parti migliori di ogni singola relazione (a parte un caso) e quindi complessivamente migliore di
ciascuna di esse. Questa specie di relazione collettiva è stata distribuita ai ragazzi insieme alle
relazioni corrette (e commentate singolarmente) e discussa analiticamente per mostrare agli
studenti ciò che ci si aspetta da loro e ciò che sono comunque in grado di fare.
La classe scelta, la 1a C, aveva ampiamente trattato la parte di astronomia del programma di
scienze; l’insegnante, prof.F.Rambelli, li ha accompagnati ad una lezione al planetario e, in
occasione di quell’uscita, i ragazzi hanno anche visitato la grande meridiana che Cassini ha
tracciato nel pavimento della chiesa di S.Petronio. Come conclusione del percorso, invece, sono
stati accompagnati all’Osservatorio astronomico di S. Giovanni in Persiceto.
Dunque la prima prova è stata una misura diretta: si trattava di sapere quanto spazio avessimo a
disposizione nel prato, in modo da poter impostare poi la proporzione. Il tempo a disposizione è
stato quello di una normale prova di laboratorio, cioè due ore; a questo punto del programma
ormai era stata svolta quasi tutta la parte di teoria della misura.
1
MISURA DIRETTA DEL PRATO DELLA SCUOLA
Scopo: misurare la lunghezza del giardino della scuola, partendo dall’albero vicino al blocco delle
aule fino alla recinzione dalla parte opposta, dopo il blocco dei laboratori B2 , seguendo una linea
retta.
Strumento: cordella metrica,
portata 20,00 m
sensibilità 0,01 m
incertezza usata 0,02m
Procedimento: Come strumento abbiamo usato la cordella metrica, che riportiamo fino ad ottenere
la misura del prato. Abbiamo usato il cacciavite per tenere il segno.
– allineare lo zero della cordella con il punto d’inizio, su una radice dell’albero,
− stendere la cordella per tutta la sua lunghezza cercando di proseguire in linea retta, tenendo un
albero al di là del recinto come punto di riferimento;
– ripetere l’operazione fino ad arrivare alla recinzione;
– contare il numero di volte e sommare le misure;
– calcolare l’errore.
L’incertezza è di 0,02 m perché la cordella poteva essere più o meno tesa ed il cacciavite ha un
certo spessore, quindi l’errore rispetto alla sensibilità aumenta.
Dati: 13 volte 20,00 m la 14a invece 6,75 m
Calcoli: D = 13 × 20 + 6,75 = 266,75 m
Propagazione dell’errore: ∆D = 0,02 × 14 = 0,28 m
Conclusioni: il giardino misura (266,8 ± 0,3) m.
MISURA INDIRETTA DI LUNGHEZZA NEL PRATO DELLA SCUOLA
La seconda esperienza di laboratorio ha fatto eseguire ai ragazzi un’altra misura, sempre di
lunghezza, ma in modo indiretto, affinché potessero apprezzare la differenza tra i due metodi, la
precisione del secondo e la sua praticità nel fornirci informazioni sulla distanza di oggetti
inaccessibili, non solo di corpi celesti. A questo scopo la classe è stata divisa in due gruppi: il
primo doveva testare il metodo e trovarne la precisione, il secondo applicarlo concretamente ad un
oggetto “irraggiungibile”, non perché particolarmente lontano, ma perché situato al di là della
rete di recinzione.
La prova si è svolta nei tempi normali di un laboratorio, anche se ha richiesto molto tempo la
successiva discussione delle relazioni. Da qui il discorso si è allargato alla potenza dei metodi di
misura indiretti, che ci permettono di conoscere non solo le dimensioni del sistema solare, ma la
distanza delle stelle, la dimensione della nostra galassia, quelle del gruppo locale e così via, in un
concatenarsi di metodi di misura via via più complessi. I ragazzi erano già in possesso di parecchie
di queste nozioni, per esempio il red shift, apprese nel programma di scienze.Non sono stati
discussi due punti abbastanza delicati relativi alla precisione della misura. Il primo è la critica del
goniometro usato, in particolare della centralità del perno, dell0’allineamento del traguardo, della
sensibilità della scala. Il secondo è vedere se, e come, vari la precisione al crescere della distanza
da misurare, poiché non possiamo arrivarci dalla propagazione dell’errore con ragazzi che
ignorano la trigonometria. In tutto sono state dedicate all’argomento quattro ore (due laboratori).
Quello che segue è il collage delle parti migliori delle singole relazioni, che è servito per la
correzione collettiva e la discussione in classe.
2
GRUPPO 1
SCOPO: misurare una distanza tramite la triangolazione e confrontarla con la misura diretta della
stessa distanza, per vedere anche se è precisa come la misura diretta.
La triangolazione consiste nel misurare distanze inaccessibili (a causa di ostacoli naturali), o troppo
grandi, con l’ausilio di triangoli rettangoli immaginari. Per usarla bisogna conoscere almeno due
angoli ed un lato del triangolo. Esempio: mi trovo nel punto B e devo misurare quanto dista il punto
C. Mi sposto da B perpendicolarmente al segmento BC fino al punto A. Lo spostamento da B ad A
deve essere tale per cui il goniometro che misura l’angolo A si muova maggiormente della propria
sensibilità. Dopodichè misuro l’angolo A ed il segmento AB, si riportano i dati in scala sul foglio di
carta millimetrata e, visto che due triangoli si dicono simili se l’ampiezza dei loro angoli è uguale e
i lati sono in proporzione fra loro, se ne ricava la lunghezza del lato desiderato misurandolo e
considerando le scale. La classe si è divisa in due; il gruppo uno ha messo a confronto la misura
diretta e quella indiretta nel prato e ne ha ricavato l’errore percentuale. La percentuale, che
ricaveremo dall’operazione D2 /D1 ×100, servirà poi nella misurazione delle distanze inaccessibili e
verrà usata dal secondo gruppo per dare l’errore alla loro misura.
MATERIALI: biffa, cioè asta non graduata che serve per segnare un punto qualsiasi, “paletto di
riferimento”; un cacciavite con cui segnare la misura ogni volta che la cordella viene stesa
completamente, nel nostro caso ogni 20 metri.
STRUMENTI: cordella metrica, portata 20,00 m, sensibilità 0,01 m, incertezza usata 0,02 m
perché tirando o non posizionando bene la cordella metrica ci si poteva sbagliare;
goniometro, portata 180°, sensibilità 1°, incertezza usata 0,5° perché la distanza tra due tacche è tale
da permettere di apprezzare il mezzo grado come errore.
PROCEDIMENTO:
nel
campo
di
pallacanestro ci sono già due rette a 90°,
quelle che delimitano i bordi: il loro
incrocio è il punto A; mettere il paletto di
riferimento lontano nel prato, nel punto
deciso, cioè alla distanza che si vuole
misurare e che per noi rappresenta il punto
C del triangolo da costruire; mettere il
goniometro nel punto A e posizionare una
lancetta lungo il cateto minore (il lato
piccolo del campo da basket) e l’altra verso
il punto dove abbiamo posizionato la biffa;
misurare l’angolo assicurandosi che sia di
90°; andare all’altra estremità della linea di
fondo del campo nel punto B e misurare
col goniometro l’angolo ABC; misurare la
lunghezza del cateto piccolo, cioè del
segmento AB (lato corto del campo da
basket).
Tre ragazzi del gruppo hanno misurato
direttamente la lunghezza del cateto
maggiore AC.
Riportiamo i dati su un foglio di carta
millimetrata e confrontiamo la distanza
ottenuta e quella reale.
3
4
DATI: angolo α=(90,0 ±0,5)° angolo β=(83,0±0,5)°
segmento AB=(14,10±0,02) m segmento AC=(119,7±0,1) m (propagazione dell’errore)
ELABORAZIONE: dal disegno viene il segmento AB = 3,5 cm in proporzione; la distanza AC =
27,5 cm in proporzione 3,5:14,10 = 27,5:D2 da cui D2 = 111 m
distanza diretta D1 = 119,7 m distanza indiretta D2 = 111 m
D2 /D1 ×100 = 93 Il metodo è preciso al 93%, le misure saranno errate del 7%
CONCLUSIONI: D2 è 111m e l’errore percentuale commesso dal primo gruppo durante la
triangolazione è il 7%.
GRUPPO 2
SCOPO: misureremo in modo indiretto la distanza che va dalla linea del campo da pallacanestro ad
un oggetto al di fuori del giardino della scuola, servendoci della triangolazione. Abbiamo scelto il
comignolo di una casa (punto inaccessibile) in modo tale che l’angolo α sia di 90°, quindi in
direzione del lato AC.
MATERIALI: nessuno
STRUMENTI: gli stessi del gruppo 1
PROCEDIMENTO: analogo a quello
del gruppo uno. Partendo dall’angolo
α all’incrocio delle righe del campo,
cercare un oggetto che gli sia di
fronte, in modo tale che l’ampiezza
dell’angolo sia di 90°. Usando il
goniometro, puntare le due “lancette”
una verso il comignolo e l’altra verso
l’angolo opposto a quello da dove
misuriamo; spostarsi lungo la linea di
fallo laterale del campo (misurandola
con la cordella metrica) che è il lato
che unisce l’angolo α all’angolo β;
arrivati all’intersezione con la linea di
fondo abbiamo misurato l’angolo β
che si forma tra la linea del campo e la
linea immaginaria che lo congiunge al
comignolo; disegnare in scala su un
foglio di carta millimetrata il triangolo
ottenuto, ne misuriamo il lato e così facendo si calcola la distanza tra il campo di pallacanestro e il
comignolo. Infine correggere secondo la tolleranza che ci ha dato il gruppo 1.
DATI: angolo α =(90,0±0,5)° angolo β=(66,5±0,5)° segmento AB=(26,10±0,02) m
ELABORAZIONE: lato AC = 14,7 cm (scala 1:400) dunque AC=14,7 cm ×400 = 58,8 m
CONCLUSIONI: il cateto AC è lungo 58,8 m. Il primo gruppo ha ricavato l’errore percentuale e
quindi noi possiamo scrivere 58,8 m ± 7 % cioè (59±4)m.
5
6
Prima di poter riprodurre il sistema solare in scala, sono state dedicate due ore di teoria alla
discussione schematica della storia dei metodi di misura delle dimensioni del sistema, dagli antichi
greci al settecento. Tutti i metodi sono concettualmente alla portata dei ragazzi, anche se non
sempre sono state loro chiare le connessioni storiche e logiche fra i diversi periodi ed i successivi
scienziati. Cronologicamente questo lavoro si è collocato tra la misura indiretta di lunghezza e la
sua correzione, il che spiega l’inversione fra i metodi di misura su grandi scale, di cui abbiamo
parlato prima, e quelli che seguono.
Come prima, ecco il collage delle parti migliori delle relazioni che hanno prodotto i ragazzi, anche
se in questo caso viene testata quasi esclusivamente la loro abilità nel prendere appunti. Come
sopra, questa rielaborazione degli insegnanti è stata distribuita ai ragazzi insieme ai singoli
elaborati corretti.
QUANTO E’ GRANDE IL SISTEMA SOLARE?
All’inizio dell’anno scolastico abbiamo approfondito l’argomento della misura diretta di lunghezza
e di quella indiretta. Perciò, dopo aver fatto alcuni esempi in merito, si è arrivati alla conclusione
che nella misura diretta si fa il confronto fra l’unità di misura e la grandezza da misurare, quindi
l’unità di misura è omogenea alla grandezza da misurare, mentre in quella indiretta sono diverse.
Le misure dirette di lunghezza sono fattibili fino ai 100 km, dopo di questi si deve ricorrere alla
misura indiretta, che si può utilizzare anche per distanze inaccessibili.
Prima di occuparci della costruzione del sistema solare in scala, studiamo la storia della misura
delle distanze tra i corpi del sistema compiute dai nostri predecessori.
Un famoso matematico, astronomo, geografo greco fu ERATOSTENE (272-192 a.C.) che sostenne
l’ipotesi della sfericità della Terra e calcolò, con notevole approssimazione, la lunghezza del
meridiano terrestre. Nato a Cirene, dopo aver
vissuto a lungo ad Atene, fu chiamato ad
Alessandria d’Egitto, importante centro
culturale dell’epoca e
sede della famosa Biblioteca. Egli sapeva
che a Siene, nell’alto Egitto, il sole veniva
riflesso nei pozzi il 21 giugno, giorno del
solstizio d’Estate, quando si trova sul tropico
del cancro.
Quel giorno un bastone verticale, o gnomone,
non avrebbe fatto alcuna ombra perché il sole
si trovava sullo zenit di Siene.
Quindi misurò l’angolo che faceva l’ombra
con un bastone verticale ad Alessandria,
trovando 1\50 di 360°. Il prolungamento dei
bastoni si incontra in un punto che è il centro
della Terra. Utilizzando la geometria (rette
parallele tagliate da una trasversale)
riconobbe che α=β=1\50 di 360, per cui
bastava moltiplicare la distanza Alessandria – Siene per 50 per ottenere la circonferenza. Ottenne
così 250 000 stadi (lo “stadio” era la misura standard) pari a 39 690 km, preciso entro poche
centinaia di chilometri.
ARISTARCO (intorno al 280 a.C.) misurò il rapporto tra la distanza Terra-Luna e quella TerraSole; decise di sfruttare l’inclinazione dei raggi solari quando sulla Luna arrivano a 90° (cioè alla
7
quadratura, quando è illuminata a metà). Misurò l’angolo delimitato dal segmento che andava dal
circolo di illuminazione della Luna alla Terra e dalla Terra al Sole, trovando 87°, cioè che il Sole
era 20 volte più lontano della Terra. Il metodo è in linea di principio esatto, ma per ottenere dei
risultati veramente corretti occorre eseguire delle misure particolarmente precise poiché l’angolo α
è molto vicino ad un angolo retto. Per tale motivo il valore trovato da Aristarco è assai diverso da
quello odierno. Aristarco scrisse un libro “Sulle dimensioni e la distanza del Sole e della Luna”,
dove descrive i metodi usati, che sono gli stessi adottati da Ipparco.
IPPARCO di Nicea, matematico ed astronomo vissuto intorno al 130 a.C. La distanza Terra-Luna è,
secondo le sue misure, 60 volte il raggio della Terra, quindi il raggio della Luna è 0,273 volte quello
della Terra, un risultato veramente buono. Invece la distanza Terra-Sole non riuscì a calcolarla. I
problemi per misurare questa distanza sono due: il fatto che non si pensasse che potessero esistere
distanze così grandi e che un angolo venisse così vicino all’angolo retto e perciò difficile da
misurare.
L’astronomo alessandrino del II sec. Claudio TOLOMEO trovò i metodi geometrici per calcolare
come si spostano in cielo il Sole, la Luna, i pianeti. Secondo lui i pianeti girano facendo un cerchio
il cui centro gira su un’orbita circolare. Tutto il sistema ha come centro la Terra.La teoria tolemaica
fu accettata fino al XVI sec., quando fu messa in crisi da quella copernicana.
Nel medioevo la scienza fu in calo e non ci
furono nuove misurazioni. Vediamo che
DANTE crede ancora che la Terra sia al centro
dell’universo, che sia piatta, con un “imbuto”
immaginario, che è l’inferno, che scende nel
centro. Pensava che l’universo avesse la forma
di una cipolla; negli strati di cristallo di questa
immaginaria cipolla ruotano delle specie di
biglie, nelle quali sono incastonati, come
diamanti, i pianeti. Tutto attorno ci sono le
stelle. Nulla si crea nelle sfe re, ma solo nel cielo che è compreso fra la Terra ed il primo involucro
di cristallo (quello della Luna). Da qui nacque il problema dell’altezza delle comete. Si cercò
dunque di misurarne l’altezza con la parallasse (XVI sec), osservandola da due punti della
superficie terrestre, ma non funzionò, per cui le comete risultano essere troppo alte e viaggiano
attraverso le bucce di cristallo. Ciò è impossibile, perciò cade il sistema.
8
Nel XVI sec. l’astronomo polacco Niccolò COPERNICO (1473-1543) rivoluzionò l’astronomia
formulando quella che viene definita la teoria eliocentrica o copernicana, ripresa successivamente
da Galileo e da Keplero. Copernico sosteneva, infatti, che il Sole fosse immobile al centro
dell’universo e tutti i pianeti, fra cui la Terra stessa, gli ruotassero attorno su orbite circolari. I
pianeti, inoltre, girando su se stessi, danno origine al giorno ed alla notte. L’ipotesi eliocentrica
segnò l’abbandono della cosmologia tolemaica
Più tardi Giovanni KEPLERO (1571 – 1630) formulò le tre leggi che regolano il moto dei pianeti.
Infatti, studiando il movimento di Marte, scoprì che le orbite dei pianeti non sono circolari, bensì
ellittiche ed il Sole occupa uno dei fuochi (prima legge), mentre i pianeti non si muovono a velocità
costante, ma in prossimità del Sole si spostano più velocemente, come enunciato dalla seconda
legge: il raggio vettore che congiunge un pianeta al Sole spazza aree uguali in tempi uguali.
Dunque la velocità è massima quando il pianeta è al perielio, minima quando è all’afelio. La Terra
si trova al perielio il 3 gennaio, durante il periodo invernale il nostro pianeta si muove più
velocemente lungo la propria orbita, il che spiega la diversa durata delle stagioni. La terza legge
mette in relazione il tempo di rivoluzione di ciascun pianeta con la sua distanza dal Sole: i quadrati
dei tempi di rivoluzione dei pianeti sono proporzionali ai cubi dei semiassi maggiori delle loro
orbite.
Queste leggi aiutarono molto NEWTON (1642-1727) nella scoperta della legge di gravitazione
universale, insieme con le scoperte di GALILEO (1564-1641) che, grazie al perfezionamento del
cannocchiale, scoprì che la Luna non è liscia e rotonda come una sfera di cristallo, bensì con
montagne altissime e crateri immensi, che Giove ha quattro satelliti, che Venere presenta delle fasi
e quindi ruota attorno al Sole; Galileo era, naturalmente, un copernicano convinto.
Newton concepì la cosiddetta legge di gravitazione universale, secondo cui due corpi di massa m1 e
m2 si attraggono con una forza direttamente proporzionale alla moltiplicazione delle masse stesse ed
inversamente proporzionale al quadrato della distanza F = G m1 m2 /d2 . Da questa legge si possono
ricavare le tre di Keplero.
In base a questa legge Newton affermò anche che la forma della Terra è quella di una sfera
schiacciata ai poli e più larga all’equatore (geoide). Alcuni scienziati francesi, non convinti,
dichiararono l’opposto. Giandomenico CASSINI (1625 – 1712), italiano, ma direttore
dell’osservatorio di Parigi, aveva insegnato all’Università di Bologna e costruito la grande
meridiana in S.Petronio; scoprì la rotazione di alcuni pianeti attorno al proprio asse, quattro satelliti
di Saturno e la discontinuità degli anelli che porta il suo nome. Progettò e contribuì alla misura del
meridiano di Parigi sul suolo francese, completata poi dal figlio, che disegnò anche la carta
geografica della Francia; confrontando i dati con altre misure di altri meridiani si dovette poi, per
quanto riguarda la forma della Terra, dare ragione agli inglesi.
Cassini triangolò la distanza Terra – Venere, usando come punti di riferimento sulla superficie
terrestre Parigi e la Cayenna. Questo permise di dare tutte le grandezze del sistema solare fino a
Saturno.
Grazie a questi studiosi ora siamo in grado di misurare qualsiasi distanza nel sistema solare, quindi
di portarla in proporzione e rappresentarla su una cartina. Noi abbiamo cercato di costruire,
naturalmente in proporzione, il sistema solare nel prato della nostra scuola.
9
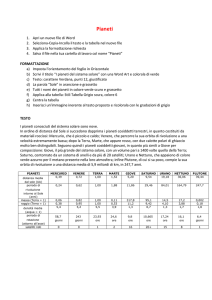
Prima di realizzare il modello abbiamo fatto calcolare ai ragazzi le distanze e i diametri in scala a
partire dai dati reali, costruendo le tre tabelle che seguono. Non ci aspettavamo di impiegarci più
di una mezz'oretta, ma le nostre ottimistiche previsioni si sono scontrate con un’insufficiente
comprensione del concetto di fattore di scala, la difficoltà che alcuni alunni hanno nell’uso delle
potenze del 10, persino l’incapacità di impostare una proporzione. Non pensiamo che le due ore
impiegate per risolvere questa difficoltà siano state tempo perso; dal momento che sono tutti
prerequisiti indispensabili nello svolgimento del “normale” programma, le abbiamo messe in conto
recupero in itinere ed assegnato esercizi a casa sull’argomento.
Per l’effettiva realizzazione del modello basta un’ora, anche se per far vedere ai ragazzi le tre
successive situazioni sarebbe meglio avere un po’ più di tempo. Noi abbiamo cominciato con un
Sole piuttosto grande, di 230 cm di diametro, in modo da sfruttare tutto lo spazio per vedere
l’orbita della Terra. In realtà, dopo aver visto le minuscole biglie che si portano via gli incaricati
di sistemare i “pianeti”, si fa fatica a vedere il ragazzo ne tiene una in mano; nella foto si vede lo
spigolo del “Sole” ed il gruppetto che ha sistemato un birillo nella posizione di Mercurio. La Terra
e la Luna andranno a finire in fondo al prato, sotto l’albero che s’intravede nello sfondo.
La descrizione del lavoro, questa volta, è opera di un singolo autore (ovviamente uno degli alunni
migliori), che, per la cronaca, era responsabile di “Venere”.
Le altre foto mostrano le biglie e palline collezionate per riprodurre i pianeti e la realizzazione del
“Sole”.
SISTEMA
ENTRO
L’ORBITA
DELLA
TERRA
Distanza vera
dal Sole
(× 1012 m)
Sole
0
Raggio vero
(× 106 m)
250 m sono la
distanza tra
Distanza dal
Sole in scala
(m)
Diametro in
scala
(mm)
696
Sole e Terra
0
2320
Mercurio
0,058
2,43
Sole e Terra
97
8
Venere
0,108
6,08
Sole e Terra
180
20
0,150
6,38
Sole e Terra
250
21
Luna (dalla Terra,
× 108 m) 3,84
1,74
Sole e Terra
0,64
(dalla Terra)
6
Terra
10
SISTEMA SOLARE IN SCALA (Fabio)
SCOPO: dopo aver misurato il prato, decidiamo di utilizzare250 m (1/4 di km) per riprodurre il
sistema solare fino alla Terra. Sia le distanze che le dimensioni dei pianeti saranno in proporzione
secondo un rapporto
250 : distanza Terra-Sole = x : y
La distanza Terra –Sole è di 1,496 × 1011 m, x e y cambieranno di volta in volta.
Quando y sarà sostituita col raggio del Sole (696 × 106 m) x corrisponderà al raggio solare in
proporzione. Y sarà sostituita con: distanza Sole-Mercurio (0,0579 × 1012 m), raggio di Mercurio
(2,433 × 106 m), distanza Sole-Venere (0,108 × 1012 m), raggio di Venere (6,08 × 106 m), raggio
della Terra (6,38 × 106 m), raggio della Luna (1,74 × 106 m), distanza Terra-Luna (3,84 × 108 m).
Così facendo otterremo tutte le misure in proporzione del nostro piccolo sistema.
MATERIALI: coni o birilli, biglie, spago, scotch, ventosa, nastro adesivo.
STRUMENTI: cordella metrica, portata 20,00 m sensibilità 0,01 m, incertezza usata 1m
calibro, portata 140,00 mm, sensibilità 0,05 mm, incertezza usata 1mm
PROCEDIMENTO:
1) risolvere le proporzioni per ottenere le varie dimensioni dei pianeti, del Sole e della Luna;
2) scegliere le biglie delle giuste dimensioni pianeta per pianeta; utilizzare il calibro per
l’operazione. Per il raggio del Sole bisogna tagliare lo spago della lunghezza che risulta
dalle proporzioni;
3) disegnare il sole sul camioncino: a- attaccare al centro del furgoncino la ventosa; b- legare
un’estremità dello spago a essa e tenere in tensione; c- in corrispondenza dell’estremità del
filo non attaccata alla ventosa attaccare un pezzo di nastro per carrozzai; d- ripetere
l’operazione fino ad ottenere una sorta di cerchio;
4) andare a posizionare il “Sole” all’estremità del giardino;
5) posizionare le biglie che rappresentano i pianeti alle distanze che risultano dalle proporzioni;
6) i”pianeti”, cioè le biglie, possono essere tenute in mano da un ragazzo o appoggiate sui coni,
fissandole per mezzo di scotch o nastro biadesivo.
11
12
Distanza vera
dal sole
(× 1012 m)
SISTEMA
SOLARE
VISIBILE
Raggio vero
(× 106 m)
250 m sono la
distanza tra
Distanza dal
Sole in scala
(m)
Diametro in
scala
(mm)
696
Sole e Saturno
0
244
Mercurio
0,058
2,43
Sole e Saturno
10,2
0,9
Venere
0,108
6,08
Sole e Saturno
18,9
2,1
0,150
6,38
Sole e Saturno
26,4
2,2
Luna (dalla Terra,
× 108 m) 3,84
1,74
Sole e Saturno
0,07
(dalla Terra)
0,6
0,228
3,39
Sole e Saturno
39,9
1,2
0,778
71,4
Sole e Saturno
136,1
25,0
Saturno
1,429
60,4
Sole e Saturno
250,0
21,1
Sole
0
Terra
Marte
Giove
Il secondo modello comprendeva il sistema solare visibile: il “Sole” si era ridotto a 24 cm di
diametro, come si vede dalla foto, ed ora l’albero segna la posizione di Saturno. Nella seconda foto
si vedono “Mercurio”, “Venere”, “Terra”e “Marte” nelle loro posizioni, mentre si stanno
aspettando “Giove” e “Saturno” che si allontanano sullo sfondo. Nella terza, come prima, i nostri
“pianeti”.
13
14
Distanza vera
dal sole
(× 1012 m)
Raggio vero
(× 106 m)
250 m sono la
distanza tra
Distanza dal
Sole in scala
(m)
Diametro in
scala
(mm)
696
Sole e Plutone
0
60
Mercurio
0,058
2,43
Sole e Plutone
2,5
0,2
Venere
0,108
6,08
Sole e Plutone
4,6
0,5
0,150
6,38
Sole e Plutone
6,3
0,5
Luna (dalla Terra,
× 108 m) 3,84
1,74
Sole e Plutone
0,016
(dalla Terra)
0,1
0,228
3,39
Sole e Plutone
9,6
0,3
0,778
71,4
Sole e Plutone
32,9
6,0
Saturno
1,429
60,4
Sole e Plutone
60,5
5,1
2,875
25,6
Sole e Plutone
121,6
2,2
Nettuno
4,504
22,7
Sole e Plutone
190,5
1,9
1,10
Sole e Plutone
250,0
0,1
Sole
SISTEMA
SOLARE
COMPLETO
0
Terra
Marte
Giove
Urano
Plutone
5,91
15
L’ultimo passaggio è stato quello di
realizzare il sistema completo. Il “Sole” si
era ridotto ad un diametro di 6 cm, in fondo
al prato va a finire “Plutone”. Nella foto si
vede il “Sole”(in mano ad una ragazza che è
di spalle), “Mercurio”, “Venere”, “Terra” e
“Marte”, mentre i ragazzi più lontani stanno
misurando per andare a sistemare “Giove”. I
pianeti interni, in questa scala, sono così
piccoli da essere di diametro inferiore a
quello di uno spillo (infatti “Mercurio” si è
punto…), ed è con questi che sono stati
riprodotti, come si vede nella seconda foto.
Per concludere abbiamo tentato di
visualizzare l’enorme vuoto che ci separa
dalle stelle, sia pure le più vicine: se Proxima
fosse sempre sotto il solito albero, l’intero
sistema si ridurrebbe alle dimensioni del
tappo di un barattolino da pellicola.
a.s.2001-2002
ITIS “O. BELLUZZI” BOLOGNA CLASSE 1aC
prof. E. BAIADA M. BALDAZZI
16