Lezione 2 marzo 2000 – Fondamenti della meccanica quantistica
Radiazione elettromagnetica – elementi essenziali
1.
In questo paragrafo si richiamano le informazioni ed i risultati più importanti ottenuti a partire dalle
equazioni dell’elettromagnetismo classico di Maxwell che, ricordiamo, conducono alla
caratterizzazione rigorosa di onde elettromagnetiche che propagano nel vuoto con velocità c e con
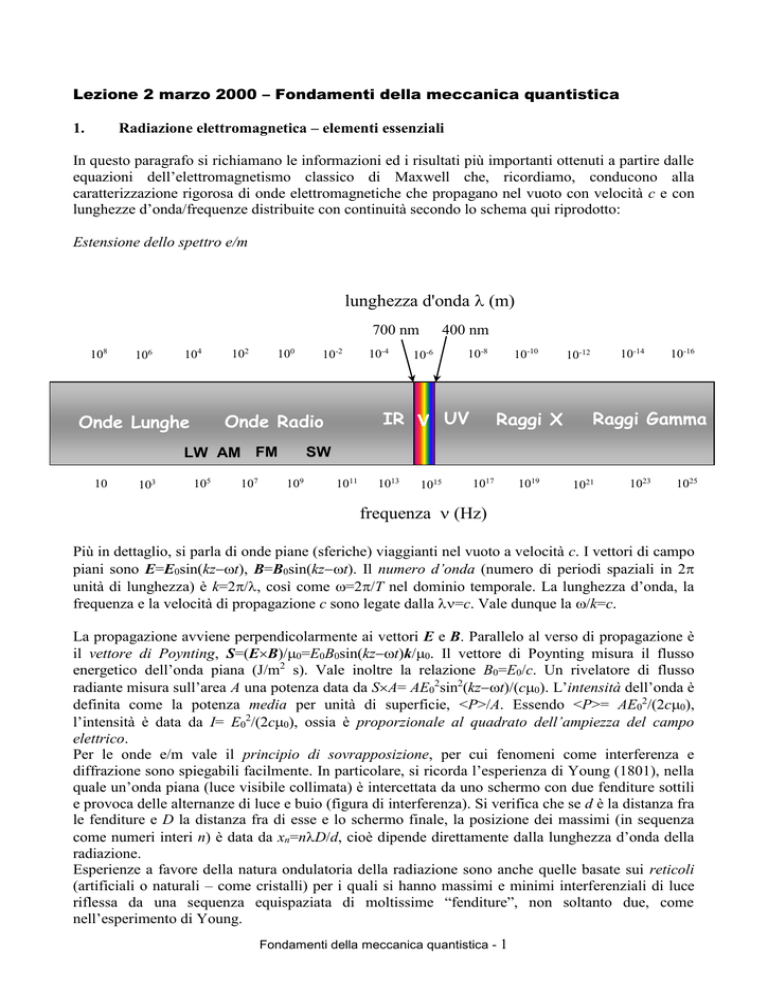
lunghezze d’onda/frequenze distribuite con continuità secondo lo schema qui riprodotto:
Estensione dello spettro e/m
lunghezza d'onda (m)
700 nm
108
106
104
102
100
LW AM FM
103
105
TV
107
10-4
10-6
10-8
IR V UV
Onde Radio
Onde Lunghe
10
10-2
400 nm
10-10
Raggi X
10-14
10-12
10-16
Raggi Gamma
SW
109
1011
1013
1015
1017
1019
1021
1023
1025
frequenza (Hz)
Più in dettaglio, si parla di onde piane (sferiche) viaggianti nel vuoto a velocità c. I vettori di campo
piani sono E=E0sin(kzt), B=B0sin(kzt). Il numero d’onda (numero di periodi spaziali in 2
unità di lunghezza) è k=2/, così come =2/T nel dominio temporale. La lunghezza d’onda, la
frequenza e la velocità di propagazione c sono legate dalla =c. Vale dunque la /k=c.
La propagazione avviene perpendicolarmente ai vettori E e B. Parallelo al verso di propagazione è
il vettore di Poynting, S=(EB)/0=E0B0sin(kzt)k/0. Il vettore di Poynting misura il flusso
energetico dell’onda piana (J/m2 s). Vale inoltre la relazione B0=E0/c. Un rivelatore di flusso
radiante misura sull’area A una potenza data da SA= AE02sin2(kzt)/(c0). L’intensità dell’onda è
definita come la potenza media per unità di superficie, <P>/A. Essendo <P>= AE02/(2c0),
l’intensità è data da I= E02/(2c0), ossia è proporzionale al quadrato dell’ampiezza del campo
elettrico.
Per le onde e/m vale il principio di sovrapposizione, per cui fenomeni come interferenza e
diffrazione sono spiegabili facilmente. In particolare, si ricorda l’esperienza di Young (1801), nella
quale un’onda piana (luce visibile collimata) è intercettata da uno schermo con due fenditure sottili
e provoca delle alternanze di luce e buio (figura di interferenza). Si verifica che se d è la distanza fra
le fenditure e D la distanza fra di esse e lo schermo finale, la posizione dei massimi (in sequenza
come numeri interi n) è data da xn=nD/d, cioè dipende direttamente dalla lunghezza d’onda della
radiazione.
Esperienze a favore della natura ondulatoria della radiazione sono anche quelle basate sui reticoli
(artificiali o naturali – come cristalli) per i quali si hanno massimi e minimi interferenziali di luce
riflessa da una sequenza equispaziata di moltissime “fenditure”, non soltanto due, come
nell’esperimento di Young.
Fondamenti della meccanica quantistica - 1
2.
Effetto fotoelettrico: inadeguatezza della descrizione ondulatoria della luce
Esperimento di Hertz (1887): metalli illuminati da radiazione e/m emettono una corrente di elettroni
(detti fotoelettroni). Nel vuoto un metallo (emettitore) è illuminato ed un elettrodo (collettore) è
posto ad una differenza di potenziale variabile rispetto
l’emettitore. Si misura una corrente in funzione di vari tipi di
illuminamento (intensità e frequenza) ed in funzione della
E
C
differenza di potenziale applicata.
e
La possibile descrizione classica del fenomeno prevede che
(a) gli elettroni possiedono un’energia (cinetica)
i
proporzionale all’intensità della radiazione luminosa
(che viene loro ceduta per interazione con il campo
V
elettrico medio). Questa energia è misurabile
variando la tensione applicata al collettore;
(b) gli elettroni vengono emessi per qualunque frequenza (“colore”) della luce (l’intensità della
radiazione non dipende dalla frequenza);
(c) l’effetto di emissione inizia dopo un tempo abbastanza lungo (dell’ordine del secondo)
perché l’interazione con ciascun elettrone del metallo avviene in un’area molto piccola e
l’energia trasferita è corrispondentemente piccola.
I risultati sperimentali sono invece i seguenti:
(a) l’energia massima posseduta dagli elettroni (misurabile tramite un opportuno potenziale
applicato al collettore di segno negativo) non dipende dall’intensità dalla radiazione
luminosa: quando questa aumenta cresce la corrente fotoelettrica solamente;
(b) l’effetto di fotoemissione avviene solamente sopra ad una frequenza della radiazione (in
funzione del metallo, ed è detta frequenza di taglio);
(c) l’effetto inizia pressoché immediatamente con l’arrivo della radiazione.
In pratica si assiste al fallimento completo della previsione classica, basata sulla natura ondulatoria
della radiazione luminosa. Anche se nel 1900 Planck aveva discusso aspetti simili che affrontiamo
nel paragrafo seguente, ora seguiamo la generalizzazione proposta da Einstein nel 1905 a supporto
di queste evidenze sperimentali: la luce è costituita da “pacchetti di energia”, detti fotoni, con
energia data da
E=h=hc/
dove h è la costante detta di Planck e vale 6.62607551034 J s e è la frequenza della radiazione.
Per i fotoni (vedi sez. precedente) E=pc e dunque il loro momento si può scrivere come
p=h/.
i fotoelettrica
L’effetto fotoelettrico, in questa ipotesi, avviene per cessione
I3
I2
(immediata) di quanti di energia dipendenti solo dalla
I1
frequenza (interazione elettrone-fotone). L’energia massima
int.
luce
acquistata da un fotoelettrone si può scrivere come Tmax=h,
VC
VS
dove è il “potenziale d’estrazione” del metallo (energia per
strappare l’elettrone) e dunque non dipende dall’intensità della
radiazione ma solo dalla sua frequenza. Se il potenziale
VS
+
ritardante al collettore è abbastanza negativo (VS), il
+
fotoelettrone si ferma e h=. Sotto una frequenza di soglia
+ +
non c’è corrente fotoelettrica.
Questi risultati sono in pieno accordo con l’esperimento.
Fondamenti della meccanica quantistica - 2
3.
Radiazione termica: la prima evidenza contro la natura ondulatoria della luce
Si studia con metodi della termodinamica ed elettromagnetismo classici la radianza di un oggetto in
funzione della sua temperatura. Si tratta di analizzare l’intensità di radiazione e/m in uno stretto
intervallo di frequenze o lunghezze d’onda emessa da un corpo ad una data temperatura. La
radianza R() è definita dalla dI= R()d, dove I è l’intensità
totale (energia/tempoarea). Sperimentalmente si osserva
R()
l’andamento riportato ed i fatti che (a) l’intensità totale (radianza
T3
integrata) aumenta con la temperatura secondo la legge di Stefan,
4
8
2 4
I=T (=5.710 W/m K è la costante di Stefan-Boltzmann) e
(b) all’aumentare della temperatura il massimo di radianza si
T2
sposta verso piccole lunghezze d’onda (alta frequenza:
riscaldanto un corpo passa dal rosso al giallo, da 700 nm a 500
T1
nm), secondo la legge dello spostamento di Wien,
maxT=cw=2.9103mK.
Per ottenere una radianza indipendente dal tipo di materiale si effettuano le misure adottando un
sistema di riferimento detto corpo nero: il foro aperto in una cavità dalla quale la radiazione non
viene pressoché riemessa ma solo assorbita.
La descrizione classica del fenomeno è riassunta nei seguenti passi:
(a) la cavità è riempita da onde e/m stazionarie in equilibrio con le pareti;
(b) il numero di onde stazionarie con lunghezze d’onda comprese fra e +d nel volume V è
dato da dN=N()d=8V d/4;
(c) dalla termodinamica classica, ogni onda apporta un contributo energetico kT in virtù dello
scambio all’equilibrio con gli oscillatori atomici delle pareti;
(d) dalle equazioni di Maxwell, si ricava che la radianza è esprimibile tramite la densità di
energia e/m u() tramite la R()=cu()/4;
(e) la densità è data dal numero di onde per volume per l’energia associata ad ogni onda,
dunque u()=8kT/4 e la radianza risulta pari a R()=2ckT/4.
Quest’espressione è la legge di Rayleigh-Jeans e prevede che R() per 0, completamente
contro l’evidenza sperimentale. Si parla di catastrofe ultravioletta.
La risposta è data da Planck nel 1900, che trova il modo di ridurre l’evidente sovrastima della
componente ad alta frequenza: se ci sono troppe onde con bassa ciò è da imputarsi al fatto che
troppi atomi ad alta frequenza (energia) interagiscano con la radiazione. Ipotizza dunque che gli
atomi scambino energia con la radiazione in modo discreto, secondo quanti di energia
proporzionali alla frequenza della radiazione. La loro energia massima è comunque kT, quindi
questo risolve la catastrofe ultravioletta.
Gli oscillatori dunque scambiano quanti di energia multipli di h, E=nh, n=1,2,…, trasportati da
fotoni (che quindi hanno ancora momento p=h/). Il calcolo basato su questa ipotesi conduce alla
nuova formula di Planck per la radianza di corpo nero:
2πc hc / λ
R( λ) 4 hc / λkT
,
λ e
1
in totale accordo con l’esperimento. Questa formula permette di confermare la legge di spostamento
di Wien e, stabilita la massima lunghezza d’onda ad una data temperatura, collegare la costante h
con quella di Stefan-Boltzmann, =(25k4)/(15c2h3). Il risultato per h è in ottimo accordo con
misure di h effettuate con l’effetto fotoelettrico da Millikan.
Si ha dunque un’altra evidenza sperimentale e modellizzazione teorica consistente
dell’inadeguatezza della descrizione ondulatoria della radiazione e/m a favore di una natura
corpuscolare e quantizzata.
Fondamenti della meccanica quantistica - 3
4.
Altri fenomeni a favore della natura corpuscolare della radiazione elettromagnetica
4.1 Effetto Compton
Si considera l’interazione fra luce (fotoni) e materia (elettroni debolmente legati ad atomi). L’esito
sperimentale non è supportato da una trattazione ondulatoria, per cui si considera una descrizione
puramente corpuscolare, di urto fra particelle (fotoni ed elettroni).
Si applicano le regole consuete di conservazione (energia e quantità di moto).
La conservazione dell’energia viene scritta
E+mc2=E’+Ee,
dove E, E’ sono le energie cinetiche del fotone prima e dopo l’urto (E=h=hc/ ed E’=h’=hc/’),
mc2 è l’energia (a riposo) dell’elettrone prima dell’urto ed Ee la
sua energia (relativistica) dopo l’urto. La conservazione della
h’, p’
quantità di moto è data da
h, p
p = p’cos + pecos (lungo x)
0 = p’sin pesin (lungo y),
e
dove p, p’ sono le quantità di moto del fotone prima e dopo
l’urto (p=h/, p’=h/’) e pe è il momento dell’elettrone dopo
l’urto.
La risoluzione di queste tre equazioni, tenendo presente che vale la Ee2=pe2c2+m2c4, conduce al
risultato
’=C(1cos),
dove C=h/(mc)=0.00243 nm è detta lunghezza d’onda Compton. In pratica, in un esperimento di
interazione come quello descritto si osserva radiazione diffusa (deviata) ad un angolo con
lunghezza d’onda ridotta secondo l’espressione sopra riportata. Il valore della lunghezza Compton
permette ancora una stima della costante di Planck, di nuovo in accordo con le misure fotoelettriche
e di corpo nero.
4.2 Radiazione di frenamento e produzione di raggi X
Si investe un materiale con un fascio di elettroni energetici:
l’interazione con il mezzo provoca un frenamento ed una
conseguente emissione di radiazione elettromagnetica
(bremsstrahlung, raggi X) ancora una volta governata dalle
leggi di quantizzazione della radiazione stessa. E’ una
situazione opposta all’effetto fotoelettrico: si hanno urti di
elettroni su atomi che liberano fotoni con energia (massima)
data da h=Ek (energia cinetica degli elettroni) e dunque
h=eV, dove V è il potenziale accelerante degli elettroni.
h
e
V
X
e
A
e
4.3 Produzione/annichilazione di coppie
Si tratta di conversione pura energia/massa nel processo e++efotone secondo la reazione
h2mc2=1.02 MeV. Le particelle create/distrutte sono coppie “materia/antimateria”.
Fondamenti della meccanica quantistica - 4
5. Punti di arrivo e di partenza per una nuova fisica
Secondo la nuova visione iniziata da Planck e formalizzata da Einstein la radiazione
elettromagnetica, negli esperimenti sopra descritti ha le seguenti proprietà:
(a)
(b)
(c)
(d)
(e)
(f)
va intesa come quanti, pacchetti d’energia detti fotoni;
i fotoni viaggiano con velocità c;
sono privi di massa a riposo;
trasportano energia h=hc/ e momento p=h/c=h/ ;
vengono creati/distrutti in processi di interazione radiazione/materia;
si comportano come particelle in collisioni con elettroni o altre particelle materiali.
Le differenze rispetto la trattazione ondulatoria sono assolutamente drastiche. Resta comunque il
fatto che in altre classi di esperimenti la radiazione elettromagnetica presenta unicamente
caratteristiche ondulatorie, come nell’esperienza della doppia fenditura di Young.
A tale proposito, è essenziale sottolineare che in questo esperimento la visione corpuscolare di fatto
prevede che il fotone passi o in una o nell’altra fenditura, mentre la visione ondulatoria richiede
che la radiazione, per condurre ad interferenza, passi attraverso entrambe le fenditure.
E’ possibile stabilire che questa dualità onda-particella non è scindibile a seconda dell’esperimento
effettuato, ma è una caratteristica intrinseca della radiazione: essa non è né onda né particella, ma
di queste due nature presenta le caratteristiche a seconda del tipo di indagine su di essa effettuata
separatamente ed incompatibilmente.
Il termine più adatto per descrivere questa situazione (che sfugge alle possibilità percettive del
senso comune) è complementarietà delle nature ondulatoria e corpuscolare.
E’ anche possibile pensare ai processi di emissione e rilevazione della radiazione in termini
unicamente corpuscolari (interazione fotone/particella) ed al processo di propagazione ed
eventualmente interferenza dalle fenditure in termini unicamente ondulatori. La conclusione è che
l’osservazione delle figure di interferenza conducono alla corrispondenza fra intensità dell’onda
elettromagnetica (proporzionale al modulo quadrato dell’ampiezza di campo elettrico dell’onda)
con la probabilità di osservare fotoni sullo schermo. Questa connessione è alla base del
funzionamento quantistico di tutti i fenomeni fisici, non solo quelli riguardanti la radiazione
elettromagnetica e lega in modo esplicito gli aspetti ondulatori (intensità dell’onda) e corpuscolari
(conteggio medio dei fotoni).
La generalizzazione di questo schema richiede una serie di ipotesi alla base di una una scienza fisica
detta meccanica quantistica o ondulatoria.
6.
Proprietà ondulatorie della materia
L. De Broglie nel 1924 ipotizza che il dualismo onda/particella stabilito per la radiazione
elettromagnetica va esteso ad ogni forma di materia.
Si associa ad ogni particella con momento p un’onda di lunghezza =h/p, e è detta lunghezza
d’onda di De Broglie.
Il salto concettuale è enorme: si tratta di accettare che la materia, in determinate circostanze,
presenta le caratteristiche tipiche delle onde, ovvero può dare luogo ad effetti interferenziali, si
delocalizza nello spazio e nel tempo, vi sono diffrazioni, riflessioni parziali, e così via. Sarà anche
essenziale prepararsi ad affrontare argomentazioni di natura tipicamente statistica, se si vorranno
conciliare in modo consistente i due estremi del dualismo di questa teoria.
La lughezza d’onda di De Broglie non è sperimentalmente accessibile per sistemi macroscopici a
causa della piccolezza di h: una particella di polvere (m=109 g) che viaggia a 1 cm/s conduce a
=71020 m. Un elettrone di energia 1 eV ha =1.2 nm, cioè sperimentalmente accessibile.
Fondamenti della meccanica quantistica - 5
Domanda centrale: cos’è l’onda di De Broglie? Qual è il suo significato fisico?
Una prima riposta può essere: l’onda di De Broglie è quella che si manifesta ogni volta che
effettuiamo su una particella un’esperimento che ne possa rilevare la sua natura ondulatoria. Visti i
valori sopra citati, l’esperimento in questione dovrà riguardare oggetti submicroscopici:
nell’esperienza di Young ci si aspettano massimi di interferenza spaziati come D/d: siccome D/d è
dell’ordine di al più 103-104, non sarà possibile osservare interferenza di De Broglie per
un’automobile o per qualcosa comunque “meno ondulatorio” di un atomo.
Prima evidenza sperimentale dell’ipotesi ondulatoria della materia: misure di interferenza di
elettroni su cristalli (usati come reticoli naturali) ad opera di Davisson e Germer (1926) e Thompson
Jr. (1927). Si ottiene un valore di h in eccellente accordo con i dati relativi all’ipotesi corpuscolare
della radiazione e/m (fotoelettricità, corpo nero …).
L’ipotesi di De Broglie va estesa comunque a tutte le particelle (non solo gli elettroni). Le difficoltà
per la realizzazione sperimentale di misure di interferenza da fenditura doppia sono state superate
solo di recente. Ora si osservano interferenze di neutroni, atomi, ecc. e lo studio della diffrazione di
particelle di varia natura è tecnica assestata di indagine della materia atomica e subatomica.
Vale un principio di complementarietà anche nel dualismo onda/corpuscolo di De Broglie: non è
possibile osservare simultaneamente entrambe le nature della particella, ma entrambe
contribuiscono a definire la “sostanza” del sistema. In un esperimento di Young per elettroni, nel
momento che si cerca di stabilire in quale delle due fenditure passino gli elettroni, si distrugge la
figura interferenziale (stabilire la fenditura di passaggio equivale a rivolgere l’attenzione all’aspetto
corpuscolare dell’elettrone). L’interferenza si osserva solo in condizioni di “assenza di interesse”
per quest’ultimo aspetto (che dunque non può essere specificato oltre una certa misura o
precisione, come vedremo fra poco parlando di principio di indeterminazione).
7.
Relazioni di indeterminazione classiche e di Heinseberg
In un’onda piana la lunghezza d’onda (o il numero d’onda, k) sono perfettamente definiti, e l’onda è
totalmente delocalizzata nello spazio. Non sembra dunque
adatta a “descrivere” una particella nel senso di De Broglie.
A prescindere da questo aspetto, è peraltro chiaro che
sovrapponendo due onde piane di diversa lunghezza d’onda
si assiste ad un fenomeno più o meno marcato di
“battimento”: l’onda risultante tende periodicamente a
“localizzarsi” in corrispondenza delle interferenze
costruttive. Aggiungendo altre lunghezze d’onda la
sovrapposizione tende sempre più a concentrarsi, fino ad
assumere l’aspetto di un “pacchetto” localizzato in una
zona di ampiezza x. La posizione viene determinata
sempre meglio a spese della lunghezza d’onda, in modo che
xk1: se l’onda è poco “sparpagliata”, è difficile
ottenere una stima precisa della sua lunghezza d’onda e
viceversa. Lo stesso discorso è fattibile nel dominio del
tempo: per un’onda viaggiante, la determinazione precisa
della frequenza temporale richiede un tempo lungo di
ripetizioni cicliche ovvero, se l’onda dura poco tempo, la
sua frequenza sarà male determinata. Dunque t1.
E’ ora possibile estendere queste regole di
2
1.5
1
0.5
0
-0.5
-1
-1.5
-2
0
10
20
30
40
50
60
70
80
90
100
0
10
20
30
40
50
60
70
80
90
100
10
8
6
4
2
0
-2
-4
-6
-8
-10
Fondamenti della meccanica quantistica - 6
indeterminazione all’onda di De Broglie con fondamentali conseguenze nella comprensione fisica
del modello ondulatorio della materia.
Si scrive p = h/ = (2h)/( 2) = ħk; dalla kx1 si ottiene p x ħ.
Analogamente, si scrive E=h=(2h)/(2)=ħ; dalla t1 si ottiene E t ħ.
Queste due relazioni costituiscono la forma (rispettivamente spazio-momento ed energia-tempo) del
principio di indeterminazione di Heisenberg. In pratica esso stabilisce l’impossibilità di
determinare simultaneamente con precisione assoluta posizione e velocità (energia e tempo) di una
particella.
Le implicazioni sono profonde: è facile accettare e comprendere l’indeterminazione spaziale di
un’onda del mare (viste le argomentazioni classiche sulle onde piane sopra descritte), ma per una
particella materiale questo è molto più complicato e comunque al di fuori della portata del senso
comune. Di fatto è la natura stessa che impone un limite all’accuratezza con la quale possiamo
effettuare misure.
Considerando ad esempio un elettrone con velocità lungo x pari a 3.6106 m/sec, nota con
precisione dell’1%, la precisione nella posizione lungo x è stimata a partire da:
px=3.31024 Kg m/s, px=3.31026 Kg m/s, x ħ/px=3.2109 m (circa 10 diametri atomici).
Per comprendere più a fondo la procedura associata all’applicazione dell’indeterminazione di
Heisenberg richiamiamo l’idea fondamentale che a partire da un’onda piana (totalmente
delocalizzata spazialmente) è possibile costruire un pacchetto localizzato su un’estensione x che di
fatto stabilisce un’indeterminazione nell’assegnazione del momento, ossia della lunghezza d’onda
tramite la relazione di De Broglie: l’indeterminazione richiede la costruzione di un pacchetto
d’onde con dispersione in lunghezza d’onda. Partendo da due onde viaggianti con numeri d’onda k1,
k2 e pulsazioni 1, 2, la loro sovrapposizione può essere scritta come inviluppo del tipo
y1+y2=cos[(xkt)/2]cos[(k1+k2) x/2(1+2) t/2].
Si osserva che l’inviluppo avanza con velocità di gruppo vg=/k, che nel limite della
sovrapposizione continua di infinite onde diventa vg=d/dk (ogni componente d’onda piana ha
invece velocità di fase data da /k). Nel caso del pacchetto d’onde associato alla rappresentazione
di De Broglie, ricaviamo che
dω dω dE dp 1 dE
dE
vg
.
dk dE dp dk dp
dp
Per una particella non relativistica con solo energia cinetica, E=T=p2/(2m) e dunque vg=v, che
dunque spiega il significato fisico primario della rappresentazione a “pacchetto” della particella.
Quale l’influenza dell’indeterminazione di Heinseberg sulle procedure di misura?
Se si “prepara” un sistema fisico in un certo modo, potremo misurare grandezze rilevanti entro la
loro indeterminazione. Ripetendo la misura si otterranno valori differenti, anche se lo stato iniziale
del sistema è lo stesso. Si evidenziano dunque forti connessioni con la teoria della probabilità e
statistica: è impossibile prevedere il singolo evento, ma con tante misure (o con tanti sistemi eguali)
si giunge ad una distribuzione di probabilità. La meccanica quantistica fornisce l’apparato
matematico per calcolare tali distribuzioni.
C’è una differenza critica fra statistica e meccanica quantistica: nella prima l’indeterminismo è
causato dalla incompleta conoscenza del sistema all’inizio, nella seconda l’indeterminismo è
intrinseco alla natura, insuperabile.
L’ampiezza dell’onda di De Broglie è collegata alla probabilità di trovare la particella: così come
la probabilità di trovare il fotone di Planck è proporzionale al modulo quadro dell’ampiezza del
campo elettrico dell’onda, la probabilità quantistica è proporzionale al modulo quadro
dell’ampiezza d’onda di De Broglie.
Fondamenti della meccanica quantistica - 7
8. ESERCIZI
(a) Calcolare l’energia ed il momento di un fotone “rosso”, con lunghezza d’onda =650 nm e
calcolare la lunghezza d’onda di un fotone con energia pari a 2.0 eV
(b) Sapendo che il potenziale d’estrazione del tungsteno è =4.52 eV, determinare la frequenza
di taglio fotoelettrica per questo metallo, la massima energia cinetica dei fotoelettroni
quando la radiazione ha lughezza d’onda di 200 nm ed il potenziale frenante in questo caso.
(c) Utilizzando la legge di Wien, calcolare la lunghezza d’onda alla quale un oggetto a
temperatura ambiente (T=20°C) emette la massima radiazione termica e stabilire fino a
quale temperatura va riscaldato l’oggetto perché si presenti di colore rosso (=650 nm).
(d) Ricavare esplicitamente la relazione di Compton per la diffusione elastica di fotoni da
elettroni debolmente legati.
(e) Raggi X di lunghezza d’onda 0.24 nm sono diffusi secondo la relazione di Compton e il
fascio diffuso è osservato ad un angolo di 60° rispetto la direzione di incidenza. Calcolare la
lunghezza d’onda dei raggi X diffusi, l’energia dei fotoni X diffusi, l’energia degli elettroni
diffusi e la loro direzione rispetto quella d’incidenza.
(f) Stimare le lunghezze d’onda di De Broglie per (a) un’automobile dal peso di 1000 kg che
viaggia a 100 km/h e (b) un protone con energia di 150 MeV.
(g) Una palla da biliardo di massa m=100 g è “ferma” su un piano entro la lunghezza di 1 m.
Per il principio di indeterminazione possiamo ammettere che in realtà la biglia abbia una
piccola velocità. Calcolarne il valore e commentare il risultato.
Letture consigliate
Trent’anni che sconvolsero la fisica – G. Gamow – Zanichelli
Corso di Fisica Generale – 5. Fisica Atomica – D. V. Sivuchin – Edizioni MIR
La fisica di Feynman – Vol. III – Feynman, Leighton, Sands
Fondamenti della meccanica quantistica - 8












