Fenomeni e strutture dati

Fenomeni e strutture dati
●
●
●
La modellazione del mondo e dei fenomeni che lo popolano può
essere basata su oggetti territoriali o campi
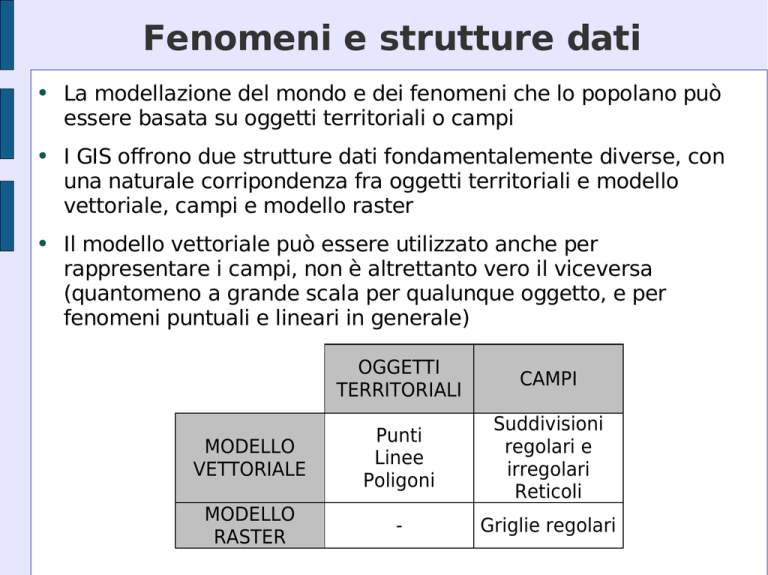
I GIS offrono due strutture dati fondamentalemente diverse, con
una naturale corripondenza fra oggetti territoriali e modello
vettoriale, campi e modello raster
Il modello vettoriale può essere utilizzato anche per
rappresentare i campi, non è altrettanto vero il viceversa
(quantomeno a grande scala per qualunque oggetto, e per
fenomeni puntuali e lineari in generale)
OGGETTI
TERRITORIALI
CAMPI
MODELLO
VETTORIALE
Punti
Linee
Poligoni
Suddivisioni
regolari e
irregolari
Reticoli
MODELLO
RASTER
-
Griglie regolari
Dato geografico e layer
●
●
Un dato geografico è caratterizzato da:
–
Geometria
–
Attributi
–
Relazioni topologiche
–
Tempo di rilievo e tempo di validità
Un layer è un insieme geometricamente e semanticamente
uniforme di dati geografici. E' l'equivalente di una tabella nei
database relazionali, così come il dato geografico è una entità del
modello E/R.
Relazioni topologiche
●
Relazione topologica: è una relazione fra figure geometriche che
rimane immutata sotto una deformazione continua delle figure
geometriche stesse
Punto
Linea
Poligono
Punto
Sovrapposizione
Disgiunzione
Fine di
Disgiunzione
Contenimento
Sul bordo di
Disgiunzione
Linea
Contenimento
Disgiunzione
Intersezione
Confluenza
Disgiunzione
Attraversamento/intersezione
Contorno (linea – lato)
Contatto (nodo - lato, linea – vertice)
Disgiunzione
Poligono
Contenimento
Disgiunzione
Contenimento
Disgiunzione
Sovrapposizione
Contenimento
Adiacenza (lato-lato)
Contatto (vertice-vertici, lato vertice)
Scala nominale
●
●
●
●
●
I dati nel calcolatore sono salvati mediante coordinate espresse in
codifica intera o floating point (spesso la seconda)
La codifica floating point ha una elevata risoluzione (fino a 15
cifre significative), ma le coordinate sono soggette agli errori di
misura sul campo (e di eventuale trattamento informatico)
Il GIS può effettuare qualunque livello di zoom: l'utente può
rendere la visualizzazione non adeguata ad una misura diretta su
video
Scala nominale: massima scala alla quale il dato può essere
rappresentato correttamente, ovvero misura del grado di
accuratezza delle coordinate nel dato informatico.
Scala nominale 1:20.000: errore nelle coordinate massimo di 4
metri (si veda anche la definizione di errore di graficismo)
Raster
●
●
●
Raster: rappresentazione del mondo secondo una discretizzazione
spaziale (tassellazione) regolare
Proprietà desiderabili di una tassellazione:
–
Semplicità geometrica
–
Possibilità di suddivisione ulteriore con lo stesso schema
–
Velocità di calcolo e semplicità
di compressione
Queste caratteristiche sono
tipiche della tassellazione
a celle quadrate o
rettangolari
Raster
●
●
●
Un layer raster è dunque una matrice di celle regolari, ciascuna
delle quali di norma contiene un valore numerico intero o floating
point (o la marca di assenza di valore, detto valore nullo o
semplicemente null).
Elementi per la definizione di un layer raster:
–
Sistema di riferimento geodetico ed eventuale rappresentazione (-> la
griglia può essere metrica o in coordinate geografiche);
–
Tipo di dato contenuto nella cella;
–
Posizione dell'origine, orientamento degli assi, dimensione dell'area
rappresentata
–
Dimensione della cella (risoluzione o numero righe/colonne)
In alcuni casi occorrono griglie
accessorie di georeferenziazione
(immagini satellitari), in cui per
ogni cella sia espressa in modo
esplicito la posizione del centro
Y
X
x=x 0i× x
y=y 0  j× y
La cella e il suo valore
●
●
Modi per decidere il valore
della cella:
–
Centro cella: campionamento
puntuale al centro, veloce, non
sempre rappresentativo
–
Prevalenza: assegna alla cella il
valore che ne occupa la maggior
parte dell'area
–
Importanza: assegna alla cella il
valore più importante in una
scala ordinate, purché ne ricopra
almeno un parte significativa
(soglia percentuale)
–
Media (solo per attributi di tipo
interval/ratio)
In fase di rilievo i sensori da
telerilevamento adottano
naturalmente un calcolo del
totale dell'energia emessa
Attributi in un raster
●
●
●
●
Storicamente vi sono stati vari tentativi di gestione del dato
raster, attualmente c'è convergenza verso una modalità di
gestione che prevede:
–
Un solo attributo mappato per layer
–
Una griglia regolare
In tal modo il raster può essere visto come una matrice di valori
numerici (gli attributi) cui sono associati metadati di
georeferenziazione
Questa struttura si presta bene alla compressione ed è di facile
gestione da parte del calcolatore
I singoli valori numerici possono essere associati a etichette
descrittive, in particolare nel caso di attributi nominali o ordinali,
codificati con numeri interi (1: corso d'acqua, 2: coltivazione a
cereali, 3: urbanizzato, 4: prato, ...)
Valori nulli
●
●
●
Il raster copre uniformemente una data area di interesse
Può accadere che il dato non sia disponibile o stimabile su tutta la
superficie
Occorre quindi un valore convenzionale per rappresentare questa
mancanza di informazione, il valore null (NODATA)
Di norma viene codificato con
l'intero più piccolo (-MAXINT)
o mediante un NaN (Not a
Number) se si fa uso di valori
floating point in standard IEEE
Gli operatori che eseguono analisi
sui dati raster devono trattare in
modo speciale questi valori
Scala nominale e topologia
●
Quale è la scala nominale di un raster? Si può legare alla
risoluzione(Dx, Dy) in un ipotetico raster a celle rettangolari.
E=   x 2 y 2
E   x  y
den. scala= =


2
2
Esempio: raster a celle quadrate da 20m -> scala nominale
1:100.000
●
Topologia raster: esiste soltanto il concetto di adiacenza di cella,
utilizzato da vari algoritmi per decidere come “muoversi” sul
raster (esempio: ricerca di un percorso minimo su una superficie
di costo)
Salvataggio dati raster
●
●
●
Forma matriciale pura: il dato viene salvato così come è in
formato binario, senza adottare tecniche di compressione. Esiste
una intestazione con informazioni di georeferenziazione e quindi
la matrice di valori numerici. (si veda ad esempio il GTOPO30,
http://edcdaac.usgs.gov/gtopo30/gtopo30.html)
Run-length: si osserva che in alcuni raster vi sono sequenze di
valori che si ripetono, vengono codificate come valore e numero
di ripetizioni. Se la riga così codificata occupa più spazio
dell'originale, si salva la forma non compressa.
E' il metodo adottato da GRASS
Block encoding: analogo al RLE,
registra blocchi rettangolari
uniformi piuttosto che di parti
di riga
Salvataggio dati raster
●
●
Chain codes: registrano il bordo di aree
di forma irregolare ma a valore uniforme
Le strutture dati riportate sino ad ora
sono strutture:
–
mono-risoluzione: non è possibile estrarre in
modo efficiente dal dato una versione del
raster a risoluzione più bassa
–
Senza perdita (lossless): il dato raster viene
salvato senza alcuna alterazione. Questo è un
requisito fondamentale per dati raster con
significato fisico (modelli di elevazione digitale,
eccetera), ma è meno importante per
fotografie aeree, soprattutto se la tecnica di
compressione adottata non altera l'immagine
in modo facilmente discernibile dall'occhio
umano
Quadtree
●
●
●
Suddivisione
ricorsiva
dell'immagine in
quattro parti
L'algoritmo si ferma
quando il valore in
un blocco è
uniforme o quando
raggiunge la
risoluzione nativa
E' un formato multirisoluzione lossless
NW NE
SW SE
Wavelet
●
●
Tecnica di compressione lossing basata sulle geometrie frattali
Consente una forte compressione dei dati e permette di accedere
al dato con risoluzioni multiple, molto adatta dunque al
salvataggio e alla visualizzazione di fotografie aeree o satellitari
nel campo del visibile usate come sfondo per la cartografia
Tecnica
Matrice
Run-length
Wavelet
MB
Fatt. comp.
90,5
1
17,7
5,1
2,3
39,3
Formati:
–
MrSid (www.lizardtech.com): proprietario
–
ECW (www.ermapper.com): proprietario, decoder gratuito per molti sistemi
GIS, encoder a pagamento. Solo per Windows.
–
JPEG2000 (http://www.remotesensing.org/jpeg2000): standardizzato e
aperto, ma poco diffuso. Trattato in modo nativo dalle librerie per l'imaging
di Java. Ne esiste una versione per dati geografici detta JP2, e può
funzionare anche in modalità lossless
Dati vettoriali
●
●
Rappresentazione del mondo secondo entità definite dalla propria
forma geometrica e un insieme di attributi
Proprietà della geometria:
–
Basata su primitive geometriche semplici (punti e segmenti retti)
–
In funzione della scala nominale cui il layer fa riferimento:
●
●
Uso della primitiva geometrica più adatta
Scelta del dettaglio geometrico (numero di punti che compongono il bordo della
linea o del poligono)
Proprietà del modello/formato usato per
gestire le geometrie:
Topologico: alcune relazioni
topologiche vengono trattate
esplicitamente
Non topologico: salvataggio delle
sole geometrie, le relazioni
topologiche restano implicite
Definizione
●
●
Elementi per definire un layer vettoriale:
–
Sistema di riferimento geodetico/cartografico in cui sono espresse le
coordinate
–
Primitiva geometrica (punto, linea, ...)
–
Nome e tipo degli attributi associati
–
Relazioni topologiche esplicitate nel modello
Primitive geometriche (esempi)
–
Punto
–
Linea
–
Poligono (con isole interne)
–
Multipunto (insieme di punti)
–
Multilinea (insieme di linee)
–
Multipoligono (insieme di poligoni)
–
Collezione generica (insieme di geometrie elementari)
Primitive geometriche
●
●
●
Linea: sequenza di
segmenti retti.
Può essere:
–
Semplice o non semplice
(auto-intersecante)
–
Chiusa (3, 4) o aperta (1)
Composte di:
–
Nodi: punto terminale di
una linea
–
Vertici: punto intermedi
Multilinea: insieme non
necessariamente
connesso di linee
Poligoni
●
●
Poligoni semplici,
non necessarimente
convessi, con una o
più isole interne
Multipoligoni:
insieme di poligoni
semplici fra loro non
sovrappositi
Modellazione
●
●
●
●
Punto: pozzo, numero civico, cassonetto, albero, segnaletica
stradale, autogrill, aeroporto, ospedale, città, ecc.
Linea: fiume, strada, elettrodotto (reti tecnologiche in genere), ma
anche isolinee per modellare un campo con primitive vettoriali
Poligono: casa, sede stradale, area urbanizzata, lago, stato. Viene
usata anche per campi come le suddivisioni politiche del territorio
(regioni, provincie), l'uso del suolo, la litologia di superficie, e per
rappresentare anche campi a variazione continua mediante
classificazione (aree con quota compresa fra 0-100 metri, fra 100
e 200 metri, eccetera).
Multipoligono: ad esempio, uno stato (vedi il caso dell'Italia, con la
penisola, isole maggiori e isole minori)
Scala nominale
●
●
●
Il dato vettoriale contiene due tipi di approssimazione:
–
Approssimazione nella specifica dei valori delle coordinate (legato
all'accuratezza del rilievo)
–
Numero di coordinate effettivamente utilizzate per rappresentare i contorni
di un oggetto
Il secondo aspetto è di particolare importanza quando si voglia
snellire un dato geografico per renderlo adatto alla
rappresentazione in scale più piccole: si riduce opportunamente il
numero di punti con un procedimento di generalizzazione
cartografica (trattata nel capitolo sull'analisi spaziale)
La misura di accuratezza in
ultima analisi è data dalla
distanza fra i punti che
compongono i bordi reali
e quelli usati per la rappr.
informatica, non dai soli
nodi o vertici
Vettoriali non topologici
●
●
Il formato non topologico
considera il bordo di ogni
linea e poligono in modo
separato, senza
considerare le relazioni
topologiche.
Modello a poligoni:
–
viene salvato il bordo di ogni
poligono come una lista di
punti
–
Eventuali punti in comune
sono salvati due volte e non
c'è nessuna informazione
esplicita su questa
sovrapposizione o
sull'adiacenza fra poligoni
Vettoriali non topologici
●
Nel caso di multipoligoni o isole, occorre considerare più anelli.
Due modi per riconoscere gli anelli interni e quelli esterni:
–
Ogni poligono è salvato separatamente, l'anello esterno è il primo, gli anelli
interni seguono
–
Il multipoligono viene salvato in un'unica struttura dati, le coordinate degli
anelli esterni sono salvati in senso orario, gli interni in senso antiorario
Modello a lista di punti:
I punti vengono salvati separatamente
insieme ad un ID
Il poligono è l'elenco degli ID dei punti
che formano il suo bordo
Evita la ridondanza dei punti, ma il
poligono deve essere ricostruito per
poter essere visualizzato
Multipoligoni e isole sono gestire come
nel caso precedente
Vettoriali topologici
●
●
Strutture dati che memorizzano alcune fra le relazioni topologiche
fra oggetti come elemento costitutivo della struttura dati. Tali
relazioni sono in genere:
–
Confluenza fra archi
–
Adiacenza di poligoni
–
Appartenenza di un arco ad un poligono
–
Relazione di fine linea fra archi e nodi
Eventuali altre relazioni topologiche devono essere modellate in
modo esplicito usando gli attributi (ovvero legando fra di loro gli
identificatori delle entità coinvolte nella relazione come nei
database relazionali).
Planar enforcement
●
●
Di norma i vettoriali topologici sono sottoposti ad una serie di
regole dette di planar enforcement:
–
Le linee sono orientate e non si intersecano, ogni eventuale intersezione
deve essere risolta spezzando le linee e creando un nodo
–
Non esistono sovrapposizioni fra poligoni
–
Ogni punto è all'interno di un poligono o su un bordo
Procedimento partendo da un insieme di linee, cui vengono
aggiunte le quattro linee che formano il perimetro dell'area di
interesse:
–
Ogni insersezione o contatto fra linee, così come la fine di linee isolate,
genera un punto detto nodo. In tale punto le linee vengono spezzate.
–
Ogni sequenza di segmenti fra due nodi è un arco
–
Un poligono è formato da sequenze di archi chiuse che possono contenere
altri archi solo nel caso in cui questi facciano anch'essi parte del bordo del
poligono (isole)
Strutture vettoriali topologiche
●
DIME (Dual Independent Map Encoding)
–
L'informazione di base è il segmento retto senza vertici intermedi
–
Di ogni segmento è noto il nodo di inizio e fine e il poligono destro e sinistro
Ogni segmento e ogni poligono sono
identificati, ed è possibile
associarvi degli attributi (poco
efficiente per reti lineari, segmenti
conseguenti possono avere gli
stessi attributi).
I segmenti non si intersecano fra di
loro
Ogni poligono deve essere ricostruito
per ricerca nella tabella dei
segmenti (sfruttando nodi e
orientamenti per riconnettere gli
anelli e distinguere gli anelli
esterni dalle isole)
Modello “storico”, creato dal
Strutture vettoriali topologiche
●
Modello a catena:
–
Simile al DIME, ma basata sul concetto di arco piuttosto che su quello di
sequenza, ciascuna catena, nodo e poligono possono essere associati ai
propri attributi
–
Più compatta dal punto di vista degli attributi
–
Richiede ancora dei join per ricostruire tanto i poligoni quanto gli archi
Strutture vettoriali topologiche
●
Topologia arco-nodo
–
Evoluzione del modello a catena, in cui le coordinate degli archi sono tenute
in una sequenza
–
Gli archi non devono più essere ricostruiti
–
I poligoni richiedono ancora la ricostruzione
–
È la struttura geometrica di base del sistema ArcGis (ex ARC/INFO)
Tabella dei nodi
ID
...
X
...
Y
....
Strutture vettoriali topologiche
●
●
●
Due ulteriori tabelle
possono essere
utilizzate per codificare
i poligoni
Richiede, come nelle
strutture topologiche
viste in precedenza, la
presenza di un
“poligono universo” o
di un marcatore che
specifichi l'assenza di
poligono destro o
sinistro
Ogni elemento
geometrico può essere
associato ad un record
in una tabella di DBMS
Attributi
Possono essere
presenti anche le
tabelle dei nodi,
delle relazioni
arco nodo, e la
NAT (Node
Attribute Table)
ID
...
A1
...
A2
....
...
...
AAT (Arc Attribute Table)
ID
...
A1
...
A2
....
...
...
PAT (Polygon Attribute Table)
●
Variante alla arco nodo
classica: ogni nodo è
associato con l'elenco di
archi entrati e uscenti
(usando il segno). Utile
per gli algoritmi di routing.
TOPOLOGIA POLYGON-LINE
Strutture vettoriali topologiche
Sovrastrutture: regioni
–
Regioni: struttura costruita su un
vettoriale topologico poligonale con
planar enforcement per rappresentare
multipoligoni, composizioni
gerarchiche, sovrapposizioni (ad
esempio, carta degli incendi, alcune
aree sono state bruciate più volte in
diverse occasioni).
–
Vengono introdotte due ulteriori
tabelle: la tabella che associa ogni
regione ai poligoni che la compongono,
e la tabella degli attributi della regione
COMPOSIZIONE GERARCHICA
SOVRAPPOSIZIONE
MULTIPOLIGONO
Sovrastrutture: route system
●
●
Consente di creare percorsi su una rete lineare senza replicarne
la geometria
Utile, ad esempio, per tracciare i percorsi del trasporto pubblico
su gomma nella rete stradale
Fermata
autobus
Route link 1
Route segment
(30% - 100%)
Route link 2
–
Route segment: porzione di arco
identificata da una coppia di
percentuali (che individuano punto
di inizio e di fine sull'arco orientato)
–
Route link: sequenza di route
segment che forma un percorso sul
layer
–
Route system: l'insieme dei link
–
I route link possono essere associati
ad una propria tabella di attributi, fra
cui si può trovare l'impedenza di
attraversamento (eventualmente
due, una per direzione) usata dagli
algoritmi di calcolo dei percorsi
minimi
Vettoriali topologici/non topologici
NON TOPOLOGICO
Struttura dati semplice
Ottime prestazioni per la
visualizzazione
Ridondante (diversi elementi ripetuti
più volte)
Regole molto limitate, la struttura
consente di generare un numero
elevato di errori di editing
Consente la sovrapposizione fra
poligoni
TOPOLOGICO
Complesso nell'interpretazione e
Le geometrie devono essere
ricostruite mediante dei join
Ridondanze contenute
Planar enforcement, l'editing può
risultare difficoltoso
La sovrapposizione non è consentita,
occorre far uso di sovrastrutture
specifiche
La struttura gerarchica di
La struttura gerarchia può essere
composizione può essere espressa espressa mediante le region senza
solo come associazione
dover duplicare le geometrie di bordo
Varie strutture che insistono su una Tali strutture possono essere espresse
stessa geometria devono essere
mediante le region e i route system.
gestite come dati separati, ci sono
La ricostruzione delle geometrie a
dunque i classici problemi di
scopo di visualizzazione o analisi è
gestione del dato ridondante
però computazionalmente più
Vettoriali/raster
PARAMETRO
Volume di dati
Generalizzazione
VETTORIALE
Struttura dati compatta
Complessa
Topologia
Accuratezza
Complessità di
elaborazione
Modelli di elevazione
Visualizzazione
RASTER
Meno compatta
Semplice per ricampionamento,
spesso insita nelle strutture dati
multirisoluzione
Varie strutture dati possibili,
Topologia semplice, usata
con diversi livelli di gestione
soltanto per pilotare il
esplicita dell'informazione
movimento di alcuni algoritmi sul
Teoricamente è limitata solo
Limiti di accuratezza espliciti
dalla precisione del calcolatore, nella risoluzione del raster. E'
di fatto occorre tenere in
possibile generare un raster con
considerazione gli errori di
la stessa scala nominale di un
rilievo e trattamento
vettoriale
Richiede algoritmi di geometria Gli algoritmi più comuni sono
computazionale
semplici e veloci
Possono essere gestiti con le
Gestione semplice ed efficiente
strutture TIN, che hanno il
ma a risoluzione fissa
pregio della risoluzione
In funzione della struttura di
Richiede elaborazioni non banali,
dati può essere più o meno
ma supportate tanto dai
efficiente
processori quanto dalle schede
grafiche, durante lo zoom del
Raster is faster, but raster is vaster
Triangulated Irregular Network
●
●
●
Le superfici e i modelli di elevazione digitale in genere possono
essere rappresentati mediante le strutture raster
Difetto delle strutture dati raster classiche: sono a passo fisso,
rappresentano con la stessa risoluzione zone ad alta variazione
del valore e zone a bassa variazione
Il TIN è una struttura dati vettoriale basata su triangoli con maglia
irregolare, capace di fornire elevata risoluzione solo dove questa
è necessaria
Triangolazione
●
●
●
I triangoli vengono generati unendo i punti
rilevati in una rete di maglie triangolari che
soddisfano il criterio di Delaunay: un cerchio
disegnato per i tre punti di un triangolo non
deve contenere altri punti
Ogni punto è connesso con i due più vicini per
formare un triangolo
La triangolazione di Delaunay è un algoritmo di
geometria computazionale piana, il TIN
considera però i punti come dotati di quota, e
questo genera la superficie 3D. Si tratta
nuovamente di una struttura 2D + 1, incapace
di rappresentare alcuni fenomeni, come ad
esempio una scarpata (lo stesso difetto viene
condiviso dalle strutture raster)
Topologia nei TIN
●
●
I TIN sono una struttura dati
topologica composta di nodi
e facce (triangoli)
Si possono quindi salvare le
relazioni di definizione del
triangolo a partire dai suoi
nodi, e le adiacenze fra
triangoli