Regressione Regressione

Regressione
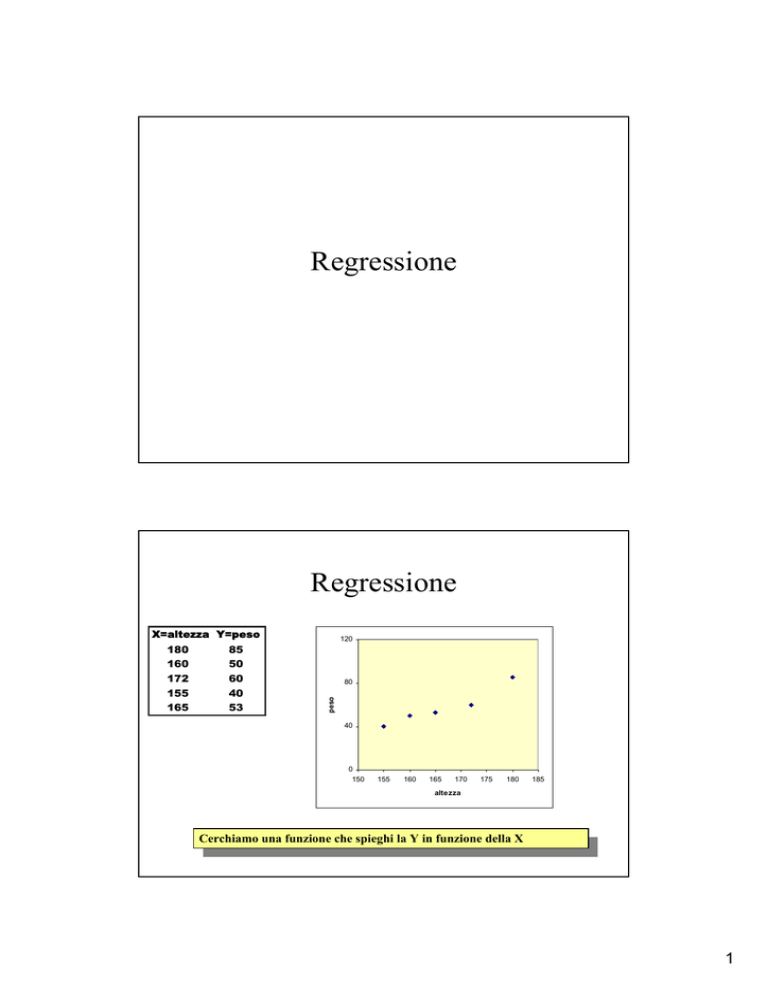
Regressione
X=altezza Y=peso
85
50
60
40
53
120
80
peso
180
160
172
155
165
40
0
150
155
160
165
170
175
180
185
altezza
Cerchiamo una funzione che spieghi la Y in funzione della X
Cerchiamo una funzione che spieghi la Y in funzione della X
1
Regressione
120
peso
80
40
0
150
155
160
165
170
175
180
185
alte zza
La funzione può essere una funzione nota nella’analisi
La funzione può essere una funzione nota nella’analisi
matematica(retta, parabola, esponeziale…)
matematica(retta, parabola, esponeziale…)
Regressione
120
peso
80
40
0
150
155
160
165
170
175
180
185
alte zza
Se scegliamo una funzione lineare di equazione Y=a+bX,
Se scegliamo una funzione lineare di equazione Y=a+bX,
occorre stimare i parametri a e b, cioè trovare tra tutte le
occorre stimare i parametri a e b, cioè trovare tra tutte le
rette possibili quella che interpola meglio la nuvola di punti
rette possibili quella che interpola meglio la nuvola di punti
2
Regressione
120
peso
80
y*i
yi
ei
40
0
150
155
160
165
170
xi
175
180
185
alte zza
Se la retta interpolasse i dati in modo perfetto avremmo che yi=a+bxi per ogni i, in
Se lairetta
i dati
in modo
che yi=a+bxi per ogni i, in
realtà
puntiinterpolasse
non sono tutti
allineati
e siperfetto
ha che yavremmo
i=a+bxi+ei dove ei è una componente
realtà
i
punti
non
sono
tutti
allineati
e
si
ha
che
y
=a+bx
+e
i
i
i dove ei è una componente
di errore.
di errore.
Il punto individuato dalla funzione lineare è
Il punto individuato dalla funzione lineare è
y*i=a+bxi
y*i=a+bxi
Regressione
120
peso
80
y*i
yi
ei
40
0
150
155
160
165
170
xi
175
180
185
alte zza
Noi vorremmo individuare i valori dei parametri a e b tali che i valori ei siano i più
Noi vorremmo
piccoli
possibili. individuare i valori dei parametri a e b tali che i valori ei siano i più
piccoli possibili.
2
Quindi: n
Quindi:
*
∑ ( yi
i =1
− yi
)
= min!
ei=residui
3
Metodo dei minimi
quadrati
2
D =
n
∑ ( yi
i =1
D =
n
∑ ( yi
i =1
− y i*
)
= m in !
− a − b ⋅ xi
)
2
= m in !
Il problema di minimo si risolve derivando D rispetto al paramero a e rispetto al
Il problema
minimo si risolve
derivando
D rispetto
al paramero
a e rispetto
parametro
b e di
uguagliando
a 0 le derivate
parziali.
Il sistema
che si ottiene
è UN al
parametro
b
e
uguagliando
a
0
le
derivate
parziali.
Il
sistema
che
si
ottiene
è UN
SISTEMA LINEARE IN DUE EQUAZIONI IN DUE INCOGNITE, HA
SISTEMA
LINEARE
IN
DUE
EQUAZIONI
IN
DUE
INCOGNITE,
HA
UN’UNICA SOLUZIONE
UN’UNICA SOLUZIONE
 ∂D
 ∂a = 0

 ∂D = 0
 ∂b
b* =
σ xy
σ x2
; a* = y - bx
Regressione
X=altezza Y=peso (x-M(x)) (y-M(y)) x-M(x))*(y-M(y)
180
85
13.6
27.4
372.64
160
50
-6.4
-7.6
48.64
172
60
5.6
2.4
13.44
155
40
-11.4
-17.6
200.64
165
53
-1.4
-4.6
6.44
832
288
641.8
medie
M(x)
M(y)
166.4
57.6
varianze
V(x)
V(y)
77.84
229.04
covarianza
correlazione
b=
a=
128.360
0.961
1.649
-216.798
4
Regressione
120
y = 1.649x - 216.8
peso
80
40
0
150
155
160
165
170
175
180
185
altezza
Regressione
X=Anzianità
10
12
14
14
13
16
Y=Salario
2000
2800
3200
3100
3000
3400
ni
4
5
6
7
2
1
25
xini
40
60
84
98
26
16
324
yini
8000
14000
19200
21700
6000
3400
72300
medie
12.96
2892
xi2ni
400
720
1176
1372
338
256
4262
yi2ni
16000000
39200000
61440000
67270000
18000000
11560000
213470000
xiyini
80000
168000
268800
303800
78000
54400
953000
varianze
covarianza
2.5184
175136
639.68
sqm
correlazione
1.586947 418.49253 0.963191639
b= 254.00254
a= -399.8729
639.68/2.5184
2892-254.00254*12.96
5
Bontà di Adattamento
SCOMPOSIZIONE DELLA VARIANZA DI Y
SCOMPOSIZIONE DELLA VARIANZA DI Y
La varianza di Y può essere scomposta in una parte che il modello di regressione
La varianza
di Y
può
essere
partenon
cheriesce
il modello
di regressione
riesce
a spiegare
e in
una
partescomposta
che inveceinil una
modello
a cogliere,
cioè la
riesce a spiegare e invarianza
una parte
che
invece
il
modello
non
riesce
a
cogliere,
cioè la
dei residui di regressione ei
varianza dei residui di regressione ei
1
n
n
∑ ( yi
i =1
)
− yi
σ y2
2
1
=
n
n
∑(
i =1
= σ
Varianza di Y
y i*
2
y
− yi
)
2
1
+
n
n
∑ ( yi
−
i =1
y i*
)
2
σ e2
+
Varianza dei
Residui
Varianza dovuta
alla Regressione
Bontà di Adattamento
2
2
σ
σ
y
R 2 = ( D 2 ) = 1 − e2 = 2
σy σy
Indice di adattamento: misura quanta parte di variabilità totale di Y il modello
Indice di adattamento:dimisura
quanta
partea di
variabilità totale di Y il modello
regressione
riesce
spiegare
di regressione riesce a spiegare
0 ≤ R2 ≤ 1
Se R2 vale 0 significa che la varianza
spiegata dal modello di regressione è 0. La
varianza dei residui coincide con la
varianza di Y
Se R2 vale 1 significa che la
varianza dei residui è 0. La varianza
spiegata dal modello di regressione
coincide con la varianza di Y
NESSUN ADATTAMENTO
ADATTAMENTO PERFETTO
6
Bontà di Adattamento
Si può verificare che l’indice di adattamento R2 2coincide
Si può verificare che l’indice di adattamento R coincide
esattamente con il coefficiente di correlazione lineare ρ2 2(ciò
esattamente con il coefficiente di correlazione lineare ρ (ciò
semplifica notevolmente i calcoli)
semplifica notevolmente i calcoli)
R2 = ρ 2
Se c’è una dipendenza lineare perfetta sia positiva (ρ=1) che negativa
(ρ=-1) allora ρ2=1, se c’è incorrelazione (ρ=0) allora anche ρ2=0
0 ≤ ρ
2
≤ 1
NOTA: Tale equivalenza vale solo se la funzione interpolante è una retta. Dal
NOTA:
Tale
equivalenza
vale sololineare
se la funzione
interpolante
è una retta.
Dal
momento
che
ρ misura
la dipendenza
di X e Y,
una retta (funzione
lineare)
momento
che
ρ
misura
la
dipendenza
lineare
di
X
e
Y,
una
retta
(funzione
lineare)
spiegherà Y in funzione di X in misura di quanto esse solo linearmente legate
spiegherà Y in funzione di X in misura di quanto esse solo linearmente legate
Bontà di Adattamento
X=Anzianità Y=Salario ni
10
2000
4
12
2800
5
14
3200
6
14
3100
7
13
3000
2
16
3400
1
25
xini
40
60
84
98
26
16
324
yini
8000
14000
19200
21700
6000
3400
72300
medie
13
2892
2
xi ni
400
720
1176
1372
338
256
4262
2
yi ni
1,6E+07
3,9E+07
6,1E+07
6,7E+07
1,8E+07
1,2E+07
2,1E+08
xiyini
80000
168000
268800
303800
78000
54400
953000
varianze
2,52 175136
covarianza
639,68
sqm
correlazione
0,96
1,59
418,49
2
yi*
ei
eini
ei *ni
2140,15 -140,15 -560,61 78570,87
2648,16 151,84 759,21 115280,63
3156,16
43,84 263,02 11530,28
3156,16 -56,16 -393,14 22079,70
2902,16
97,84 195,68 19145,29
3664,17 -264,17 -264,17 69784,59
17666,96 -166,96
0,00 316391,36
QuickTime™ e un
decompressore
sono necessari per visualizzare quest'immagine.
LA MEDIA DEI RESIDUI E' =0!!!
ARIANZA DEI RESID
12655,65
2
R
regressione
b=
a=
254,00
-399,87
0,93
2
ρ
0,93
R2=0.93
indica un buon adattamento, il 93% della varianza del SALARIO
R2=0.93
indica spiegata
un buon da
adattamento,
il 93%
della
varianza del SALARIO
può essere
una funzione
lineare
dell’ANZIANITA’
può essere spiegata da una funzione lineare dell’ANZIANITA’
7
Analisi dei Residui
e i = y i − y i*
I residui del modello lineare ottenuto sostituendo ad a e b i valori di a* e b* hanno
I residui
modellominima
lineare ottenuto
ad a edib qualsiasi
i valori dialtro
a* e modello
b* hanno
media
zerodel
e varianza
(cioè più sostituendo
piccola di quella
media zero e varianza minima (cioèlineare)
più piccola di quella di qualsiasi altro modello
lineare)
1 n
M ( ei ) = ∑ ei = 0
n i =1
Gli scostamenti positivi e
negativi si compensano
2
1 n
1 n
V ( ei ) = ∑ ( ei − M ( ei ) ) = ∑ yi − yi*
n i =1
n i =1
(
)
2
= min!
Il minimo che otteniamo con il metodo dei minimi quadrati coincide con la varianza dei
Il minimo che otteniamo con il metodoresidui
dei minimi quadrati coincide con la varianza dei
residui
Cov(ei ,e j ) = 0 ∀i ≠ j
Inoltre i residui risultano tra loro incorrelati, cioè il residuo j-esimo non dipende dal residuo iInoltre i residui risultano tra loro
incorrelati,
il residuo
esimo
per ogni cioè
i diverso
da j j-esimo non dipende dal residuo iesimo per ogni i diverso da j
Proprietà degli stimatori dei minimi quadrati
Aˆ : al variare del campione produce una stima aˆ di a
Bˆ : al variare del campione produce una stima bˆ di b
Teorema di Gauss
Teorema
di Gauss
Markov
Markov
Stimatori corretti
E ( Aˆ ) = a e E ( Bˆ ) = b
A varian za m in im a
1
x2
σ 2Aˆ = V a r ( Aˆ ) = σ 2  +
2
 n ∑ in= 1 ( x i − x )
σ2
2
ˆ
σ Bˆ = V a r ( B ) =
2
∑ in= 1 ( x i − x )



8
Proprietà degli stimatori dei minimi quadrati
L a varian za d eg li erro ri σ 2
è stim ata in m o d o co rretto d a
1
1
2
2
s e2 =
∑ in= 1 ( y i − yˆ i ) =
∑ in= 1 e i
n−2
n−2
p er cu i
1
x2
s = s  +
2
 n ∑ in= 1 ( x i − x )
s e2
s B2ˆ =
2
∑ in= 1 ( x i − x )
2
Aˆ
2
e



Proprietà degli stimatori dei minimi quadrati
Ipotesi ulteriore sui residui
Ipotesi ulteriore sui residui
2
e ≈ N (0, σ
)
allo ra
Aˆ ≈ N ( a , σ 2Aˆ ) e Bˆ ≈ N ( b , σ 2Bˆ )
Tale risultato ci consente di costruire intervalli di confidenza e statistiche per la verifica
Tale risultato ci consente di costruire
intervalli
d’ipotesi
per adi
e bconfidenza e statistiche per la verifica
d’ipotesi per a e b
Ta
le q u a n tità
Aˆ − a
Bˆ − b
e Tb =
=
S Aˆ
S Bˆ
s i d i s t r i b u i s c o n o c o m e u n a v .c .
t d i S tu d e n t c o n n -2 g r a d i d i lib e r tà
9
Intervalli di confidenza


ˆ + S ⋅t
P  Aˆ − S Aˆ ⋅ t
≤
a
≤
A
α
α  = 1− α
Aˆ
n − 2 ;1−
n − 2;1−

2
2 


ˆ
ˆ
 a − s Aˆ ⋅ t
α ; a + s Aˆ ⋅ t
α
n − 2;1−
n − 2;1−

2
2


ˆ
ˆ
P  B − S Bˆ ⋅ t
α ≤ a ≤ B + S Bˆ ⋅ t
α  = 1− α
n − 2 ;1−
n − 2;1−

2
2 


ˆ
ˆ
b − s Bˆ ⋅ t
α ; b + s Bˆ ⋅ t
α
n − 2;1−
n − 2;1−

2
2
Verifica d’ipotesi
 H 0 : a = a0

 H 1 : a ≠ a0
e
 H 0 : b = b0

 H 1 : b ≠ b0
Normalmente si pongono a0=0 e b0=0, cioè ci si chiede se a e b esistono nel modello.Si
Normalmente
si pongono
a0=0ipotesi
e b0=0,dicioè
ci si chiededei
se acoefficienti.
e b esistono nel modello.Si
chiamano
infatti
significatività
chiamano infatti ipotesi di significatività dei coefficienti.
si calco lan o le q u an tità
aˆ − a 0
bˆ − b 0
aˆ
bˆ
ta =
=
=
e tb =
s Aˆ
s Aˆ
s Bˆ
s Bˆ
si rifiu ta H 0 se
ta ≥ t
n − 2 ;1 −
α
2
e
tb ≥ t
n − 2 ;1 −
α
2
Per il coefficiente b rifiutare l’ipotesi nulla significa affermare che la variabile X
Per il coefficiente b rifiutare l’ipotesi
nulla
affermare che la variabile X
influenza
lasignifica
Y
influenza la Y
10