Andrea Gatto
Maria Elena Pacchioni
PRODUZIONE
METALMECCANICA
IL NUOVO
VOLUME
3
11 COMANDO NUMERICO DELLE MACCHINE UTENSILI
11.0 Introduzione
La cronologia elementare del controllo numerico si può così riassumere:
• fine anni ‘40: J. Parson e F. Stulen (Parson Corporate Michigan), sub contraenti U.S. Air Force usano
dati in coordinate numeriche per muovere la tavola di lavoro di una fresatrice;
• 1949: su incarico dell’U.S. Air Force il MIT sviluppa una macchina utensile prototipo basata sul controllo numerico;
• 1956: l’U.S. Air Force sponsorizza lo sviluppo delle macchine a controllo numerico presso diverse aziende;
• 1958: viene sviluppato il linguaggio programmabile APT (Automatically Programmed Tooling);
• 1958-1960: le MU a CN vengono introdotte in diverse industrie interessate alla produzione aerea;
• 1960: Direct Numerical Control (DNC), vengono eliminate le schede perforate e i programmatori
inviano il file direttamente alle macchine utensili;
• 1968: costruttori di macchine utensili Kearney & Trecker mettono sul mercato il primo centro di lavorazione;
• 1970: compaiono le macchine utensili CNC a controllo numerico distribuito;
• 1980; vengono introdotti i sistemi grafici CAM basati sui sistemi disponibili Unix e PC;
• 1990: sensibile calo dei prezzi della tecnologia CNC;
• 1997: controllo ad architettura modulare aperta basata su PC-Windows/NT; diffusione “popolare” dei
sistemi di controllo.
La successione delle varie generazioni di controlli numerici è caratterizzata da due stadi principali di sviluppo:
•h
ard-wired, le prime generazioni di unità di governo; tutte le funzioni del controllo venivano sviluppate circuitalmente; questo significa che tutte le funzioni quali interpolazione, verifica del formato
dell’informazione, controllo della posizione ecc. erano determinate dai componenti elettronici fisicamente presenti nell’unità di governo. Questo stadio di sviluppo può anche essere definito come CN
“classico” e ha caratterizzato le unità di governo sino agli anni ‘70 del secolo scorso;
• s oft-wired o CNC (Computerized Numerical Control), le unità di governo attuali; tutto ciò che nella
versione precedente era ottenuto con l’hard-wired è ora ottenuto via soft-wired, usando come hardwired uno o più microprocessori. In questo contesto il termine “free-programmable” viene sovente
usato nell’ambito dei CNC della quarta generazione. Ciò significa che il sistema presenta un’enorme
possibilità di svolgere funzioni diverse e quindi di essere personalizzato.
11.1 Sistemi di controllo
Problemi dell’ingegneria dei sistemi di controllo
L’ingegneria dei sistemi di controllo prende in considerazione fondamentalmente due problemi: l’analisi e il progetto della struttura di un sistema di controllo. Il primo problema consiste nel determinare
le proprietà di un sistema esistente, mentre il secondo concerne la scelta e la connessione dei componenti del sistema di controllo affinché esso soddisfi certe prescrizioni.
11. Comando numerico delle macchine utensili
44
Andrea Gatto
Maria Elena Pacchioni
PRODUZIONE
METALMECCANICA
IL NUOVO
VOLUME
3
Esistono due metodi di progetto:
1. progetto per analisi, attuato modificando le caratteristiche di un sistema standard o comunque esistente;
2. progetto per sintesi, realizzato individuando direttamente la struttura del sistema in base alle specifiche di progetto.
11.2.2 Trasduttori di posizione
Tipi di trasduttori di posizione
Varie sono le realizzazioni dei due dispositivi, vediamo qualche esemplare.
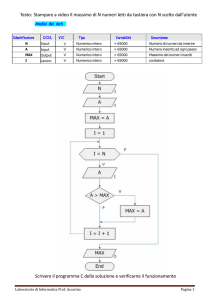
Resolver. È un trasduttore di posizione che fornisce un segnale assoluto ciclico e
rileva spostamenti angolari (figura 1). È uno strumento elettrico costituito da uno
statore e da un rotore, aventi ciascuno due avvolgimenti disposti a 90° tra loro,
percorsi da corrente alternata di uguale frequenza. La fase relativa e le ampiezze
dei segnali degli avvolgimenti del rotore (solidale all’albero di cui si vuole misurare
lo spostamento angolare) variano con la loro rotazione e con il rapporto delle tensioni di entrata negli avvolgimenti dello statore. Montati a una estremità della vite a
ricircolo di sfere le quali muovono ciascun carro controllato della macchina, ciascun
resolver è in grado di indicare la posizione angolare e i giri della vite istante per
Figura 1
istante (figura 2). In tal modo il controllo del computer, con i dati forniti dai resolver,
Resolver,
è in grado di determinare istante per istante la posizione lineare dei carri e quinutilizzato per
di dell’utensile. Il programma di lavoro ha fornito al controllo sia la posizione da
rilevare spostamenti
raggiungere sia l’avanzamento con il quale raggiungerla, cosicché il controllo è in
angolari.
grado di calcolare in ogni istante le coordinate di tutti i punti in cui devono passare
i carri, per arrivare
alla posizione voluta. Istante per istante il
controllo è quindi in grado di confrontare
la posizione reale in cui si trova il carro
con quella teorica fissata dal programma,
di calcolare l’eventuale differenza delle
due posizioni e di inviare i segnali per
l’azionamento del corrispettivo motore a
c.c. per annullare la differenza di posizione (errore d’inseguimento o scarto).
Figura 2
Rappresentazione schematica semplificata
di un asse controllato di una macchina utensile
a CNC con trasduttore rotativo tipo resolver.
11. Comando numerico delle macchine utensili
45
Andrea Gatto
Maria Elena Pacchioni
PRODUZIONE
METALMECCANICA
IL NUOVO
VOLUME
3
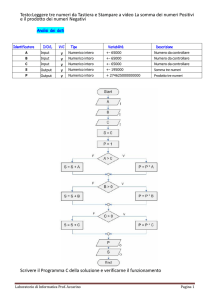
Inductosyn. È un trasduttore di posizione che fornisce un segnale assoluto ciclico e rileva spostamenti
lineari (figura 3) o angolari (figura 4).
L’inductosyn lineare (figura 5) è formato da una riga collegata all’organo fisso composta da un circuito
di rame, stampato a greca, con passo di 2 mm (statore) e da un’altra riga (cursore o slider) costituita da
due circuiti stampati a greca, di rame, con il medesimo passo, ma sfalsati tra loro di 0,5 mm, connessi
all’organo mobile.
Alimentando la parte fissa con una tensione alternata di frequenza dell’ordine di 10 kHz e facendo scorrere la riga mobile di lettura (slider), si generano per induzione due tensioni alternate sfasate tra loro
di 90°, che consentono di prelevare un segnale elettrico che permette di identificare la posizione dello
slider con un’incertezza di ±1 m. Vi sono anche inductosyn rotativi per misure angolari che possono
raggiungere precisioni di 1 secondo di grado. I due dischi, che costituiscono rispettivamente lo statore
e lo slider e che portano serpentine di rame, sono posti vicinissimi tra loro per eliminare le dispersioni
del campo magnetico dovute allo strato di aria.
Figura 3
Inductosyn lineare, utilizzato
per rilevare spostamenti
lineari.
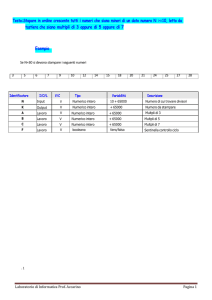
Figura 5
Figura 4
Schema dell’inductosyn lineare.
Inductosyn rotativo, usato per rilevare
spostamenti angolari.
11.2.4 Tipo di controllo per il raggiungimento di una posizione
Per quanto detto prima l’interpolatore più usato è l’interpolatore lineare che opera tra due o più assi
lineari o circolari.
Esistono diverse tecniche per realizzare un interpolatore; di seguito se ne descriverà una, molto semplice, a puro titolo di esempio: la tecnica detta searchstep.
11. Comando numerico delle macchine utensili
46
Andrea Gatto
Maria Elena Pacchioni
PRODUZIONE
METALMECCANICA
IL NUOVO
VOLUME
3
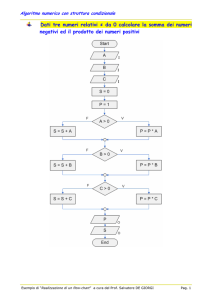
Si tratterà il caso dell’interpolazione lineare nel piano per la sua maggiore evidenza (figura 6).
F (X, Y) > 0
Pe
Ye
Ys
P1
Ps
F (X, Y) < 0
Xs
Xe
Figura 6
Schema dell’interpolazione lineare.
Ogni punto di un contorno piano soddisfa la relazione F(X,Y) = 0, mentre per qualunque altro punto,
esterno al suddetto contorno, varrà ovviamente la relazione F(X,Y)<>0. L’entità del valore assunto dalla
funzione e il suo segno dipendono dalla corrispondente entità dello scostamento e dalla sua direzione.
Ciò è particolarmente evidente nel caso della retta. Si osservi la figura 6; la retta congiungente i due
punti PS e PE deve essere interpolata secondo la direzione positiva dell’asse X; è facile verificare come
tutti i punti che sono situati al disotto della retta rendono negativa la funzione:
F(X,Y) = y − a ⋅ x − b = 0
mentre la rendono positiva tutti i punti situati al disopra della stessa.
Si parta dal punto PS, incrementando di una quantità piccola a piacere una delle sue due coordinate:
nell’esempio si è incrementata di DX la sua ascissa. Si calcoli quindi il segno della funzione; il successivo
incremento si darà in modo da modificare tale segno.
Nel caso in esame, F(X, Y) > 0 produrrà una correzione secondo X mentre F(X,Y) < 0 una correzione
secondo Y.
Nel caso particolare in cui F(X,Y) = 0, essendo il punto esattamente sulla retta, ci si troverà come alla
partenza e quindi sarà indifferente la scelta dell'incremento da attribuire.
11. Comando numerico delle macchine utensili
47