Variabili Gaussiane Variabili Gaussiane

Corso di:
Affidabilità delle costruzioni meccaniche
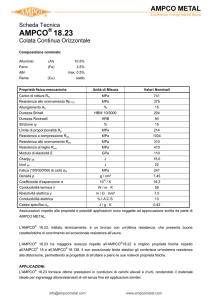
Verifiche sforzo‐resistenza
Variabili Gaussiane
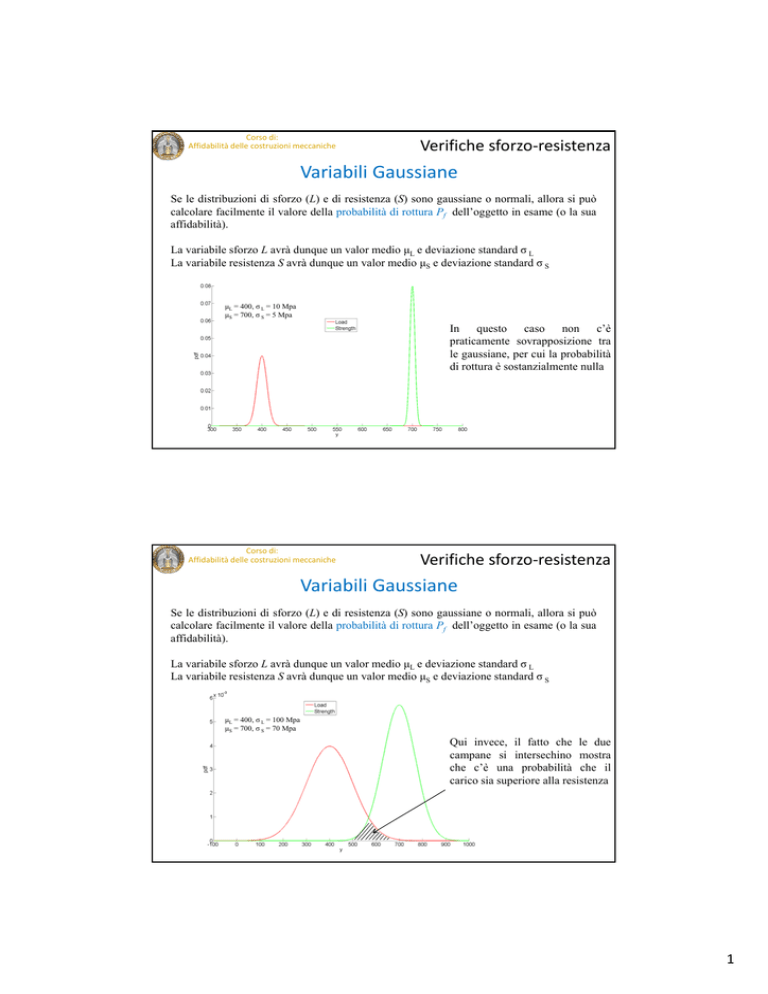
Se le distribuzioni di sforzo (L) e di resistenza (S) sono gaussiane o normali, allora si può
calcolare facilmente il valore della probabilità di rottura Pf dell’oggetto in esame (o la sua
affidabilità).
La variabile sforzo L avrà dunque un valor medio μL e deviazione standard σ L
La variabile resistenza S avrà dunque un valor medio μS e deviazione standard σ S
μL = 400, σ L = 10 Mpa
μS = 700, σ S = 5 Mpa
In questo caso non c’è
praticamente sovrapposizione tra
le gaussiane, per cui la probabilità
di rottura è sostanzialmente nulla
Corso di:
Affidabilità delle costruzioni meccaniche
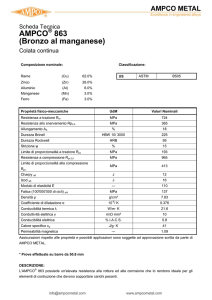
Verifiche sforzo‐resistenza
Variabili Gaussiane
Se le distribuzioni di sforzo (L) e di resistenza (S) sono gaussiane o normali, allora si può
calcolare facilmente il valore della probabilità di rottura Pf dell’oggetto in esame (o la sua
affidabilità).
La variabile sforzo L avrà dunque un valor medio μL e deviazione standard σ L
La variabile resistenza S avrà dunque un valor medio μS e deviazione standard σ S
μL = 400, σ L = 100 Mpa
μS = 700, σ S = 70 Mpa
Qui invece, il fatto che le due
campane si intersechino mostra
che c’è una probabilità che il
carico sia superiore alla resistenza
1
Corso di:
Affidabilità delle costruzioni meccaniche
Verifiche sforzo‐resistenza
Variabili Gaussiane
Nel caso si variabili gaussiane, si può definire il parametro Loading Roughness (LR) come:
LR 
L
 S2   L2
che rappresenta quanto il carico sia
“distribuito”
distribuito rispetto alla resistenza
- LR = 0 significa che la resistenza è molto più “dispersa” rispetto al carico
- LR = 1 significa che il carico è molto più disperso “rispetto” alla resistenza
Nel caso di LR estremi, la probabilità di rottura Pf si può ricavare come area sottesa dalla pdf
Corso di:
Affidabilità delle costruzioni meccaniche
Verifiche sforzo‐resistenza
Variabili Gaussiane
Nei casi più generali conviene invece definire la variabile D = S-L (anch’essa gaussiana)
con parametri:
D  S  L
 D   S2   L2
in accordo con l’algebra delle variabili gaussiane
In questa rappresentazione, la probabilità di rottura è rappresentata graficamente dal’area
sottesa dalla curva per valori di D < 0
2
Corso di:
Affidabilità delle costruzioni meccaniche
Verifiche sforzo‐resistenza
Variabili Gaussiane
Quanto vale allora la probabilità di cedimento?
P f  Prob ( L  S )  Prob ( D  0 )
Essa è calcolabile semplicemente rispondendo alla domanda: qual è la probabilità
che la variabile D sia minore di 0?
Come al solito occorre passare alla variabile standardizzata
z = (y-μD)/σD, ponendo y = 0.
 0  D
P f  F ( 0 )   
 D

 
     D

 D



Il termine tra parentesi prende il nome di Safety Margin.
Esso rappresenta il modo più corretto per calcolare la
probabilità di rottura

S  L
S  L

P f    SM     
SM  D 
2
2

D
 s2   L2
s L

Corso di:
Affidabilità delle costruzioni meccaniche




Verifiche sforzo‐resistenza
Variabili Gaussiane
Andamento della probabilità di rottura Pf in funzione del Safety Margin SM
SM = 0 significa che le gaussiane del carico e della resistenza hanno lo stesso
valore medio -> 50% di probabilità di rottura
3
Corso di:
Affidabilità delle costruzioni meccaniche
Verifiche sforzo‐resistenza
Esercizio
Si consideri una verifica di resistenza sulla base delle seguenti grandezze
caratteristiche:
L = 100 MPa
S = 270 MPa
L = 50 MPa
S = 30 MPa
Variabile D
D = S - L = 70 MPa
D   
2
s
2
L
SM 
 58.30952
S  L
D

 2.915476
D
 s2   L2
P f   (  SM )  0.18%
Calcolando il coefficiente di sicurezza come rapporto tra il percentile 5% della
distribuzione della resistenza e il percentile 95% dello sforzo si ottiene:
 = 1.21
Corso di:
Affidabilità delle costruzioni meccaniche
Verifiche sforzo‐resistenza
Esercizio
Si consideri una verifica di resistenza sulla base delle seguenti grandezze
caratteristiche:
L = 600 MPa
S = 870 MPa
L = 50 MPa
S = 30 MPa
Variabile D
D = S - L = 275 MPa
 D   s2   L2  58.30952
SM 
S  L
D

 4.722834
D
 s2   L2
P f   (  SM )  0.0001%
Calcolando il coefficiente di sicurezza come rapporto tra il percentile 5% della
distribuzione della resistenza e il percentile 95% dello sforzo si ottiene:
 = 1.21
4
Corso di:
Affidabilità delle costruzioni meccaniche
Verifiche sforzo‐resistenza
Esercizio
Si richiede di valutare l’affidabilità di un tirante di una struttura metallica, il cui
materiale ha tensione di snervamento media di 350 N/mm2, con deviazione
standard 20 N/mm2. Si consideri che la tensione di lavoro media è di 280 N/mm2
con deviazione standard di 80 N/mm2
Si chiede inoltre di determinare di quanto occorre aumentare la resistenza media
del materiale (mantenendo inalterata la deviazione standard) per avere una
probabilità di rottura minore dello 0.1%.
Corso di:
Affidabilità delle costruzioni meccaniche
Verifiche sforzo‐resistenza
Esercizio
Calcolare la probabilità di rottura di una barra sottoposta a trazione in base alle
seguenti distribuzioni:
F = N(70000,5000)
N(70000 5000) [N]; d=N(20,0.1)
d=N(20 0 1) [mm]; σu= N(240,12)
N(240 12) [MPa]
5
Corso di:
Affidabilità delle costruzioni meccaniche
Verifiche sforzo‐resistenza
Variabili NON Gaussiane
dR  f L l dl   f S s ds  f L l dl 1  FS l 

l

R
f L l 1  FS l dl

0
-3
3
x 10
load
strength
2.5
2
1.5
dl
1
[1‐FS(l)]
0.5
0
0
l
500
Corso di:
Affidabilità delle costruzioni meccaniche
1000
1500
Verifiche sforzo‐resistenza
Variabili NON Gaussiane
R


0
f L l 1  FS l dl
R  1  Pf 
Pf 


0


0
f L l R S l dl
f L l FS l dl
6
Corso di:
Affidabilità delle costruzioni meccaniche
Verifiche sforzo‐resistenza
Variabili NON Gaussiane
dR  f S s ds   f L l dl  f S s ds  F L s 
s
0
R


0
f S s   F L s ds
-3
3
x 10
load
strength
2.5
2
1.5
1
ds
FL(s)
0.5
0
0
s
500
Corso di:
Affidabilità delle costruzioni meccaniche
1000
1500
Verifiche sforzo‐resistenza
Variabili NON Gaussiane
R


0
f S s   F L s ds
d
R  1  Pf 
Pf 


0


0
f S s F L s ds
f S s R L s ds
7
Corso di:
Affidabilità delle costruzioni meccaniche
Verifiche sforzo‐resistenza
Esercizio
Calcolare la probabilità di rottura di un componente, assegnate le seguenti
distribuzioni per il carico e la resistenza:
σ = W(400,
W(400 1.7)
1 7) [Mpa]
σu= W(1100,8)
W(1100 8) [MPa]
8