i Triangoli - Salesiani Bra

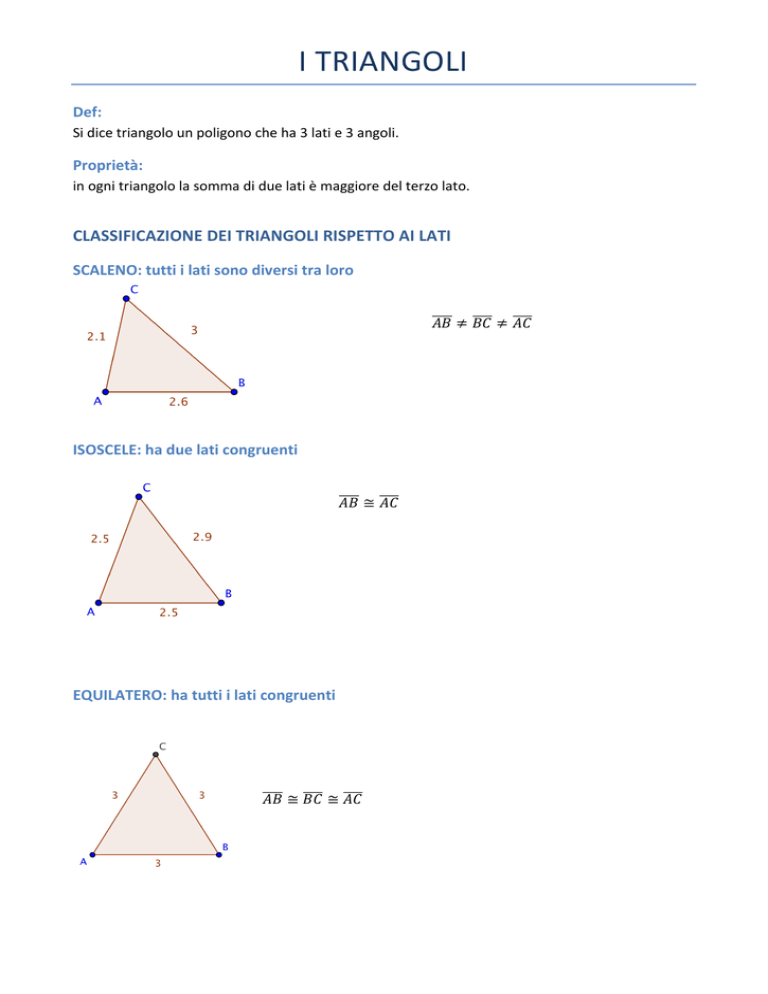
I TRIANGOLI Def: Si dice triangolo un poligono che ha 3 lati e 3 angoli. Proprietà: in ogni triangolo la somma di due lati è maggiore del terzo lato. CLASSIFICAZIONE DEI TRIANGOLI RISPETTO AI LATI SCALENO: tutti i lati sono diversi tra loro 𝐴𝐵 ≠ 𝐵𝐶 ≠ 𝐴𝐶
ISOSCELE: ha due lati congruenti 𝐴𝐵 ≅ 𝐴𝐶 EQUILATERO: ha tutti i lati congruenti 𝐴𝐵 ≅ 𝐵𝐶 ≅ 𝐴𝐶
CLASSIFICAZIONE DEI TRIANGOLI RISPETTO AGLI ANGOLI OTTUSANGOLO: ha un angolo maggiore di 𝟗𝟎° e minore di 𝟏𝟖𝟎° RETTANGOLO: ha un angolo retto, ovvero di 𝟗𝟎° ACUTANGOLO: ha tutti gli angoli acuti, ovvero minori di 𝟗𝟎° TRIANGOLI PARTICOLARI ISOSCELE 𝐴𝐵 𝑏𝑎𝑠𝑒 𝐴𝐶 ≅ 𝐵𝐶 𝑙𝑎𝑡𝑖 𝑜𝑏𝑙𝑖𝑞𝑢𝑖 C 𝑎𝑛𝑔𝑜𝑙𝑜 𝑎𝑙 𝑣𝑒𝑟𝑡𝑖𝑐𝑒 𝐴 ≅ 𝐵 𝑎𝑛𝑔𝑜𝑙𝑖 𝑎𝑙𝑙𝑎 𝑏𝑎𝑠𝑒 Proprietà: un triangolo isoscele ha sempre i LATI OBLIQUI CONGRUENTI e gli ANGOLI alla BASE CONGRUENTI. EQUILATERO 𝐴𝐵 ≅ 𝐴𝐶 ≅ 𝐵𝐶 𝐴 ≅ 𝐵 ≅ 𝐶 Proprietà: un triangolo equilatero ha sempre tutti i LATI CONGRUENTI e tutti gli ANGOLI CONGRUENTI RETTANGOLO 𝐶 = 90° 𝐴𝑁𝐺𝑂𝐿𝑂 𝑅𝐸𝑇𝑇𝑂
Proprietà: un triangolo rettangolo ha sempre un ANGOLO RETTO (90°). I lati che formano l’angolo retto si chiamano CATETI; il lato opposto all’angolo retto si chiama IPOTENUSA. Osservazione: dato che la somma degli angoli interni di un triangolo è 180! 𝐶 = 90!
allora 𝐴 + 𝐵 = 90!
ALTEZZE di un triangolo Def: si dice ALTEZZA di un triangolo RELATIVA ad UN LATO il segmento perpendicolare al lato e passante per il vertice opposto. Il lato si dice allora BASE dell’altezza. TRIANGOLO ACUTANGOLO Le 3 altezze sono: 𝐶𝐻, 𝐴𝐾, 𝐵𝑇 e si incontrano nel punto O, interno al triangolo. TRIANGOLO OTTUSANGOLO Le tre altezze sono 𝐶𝐻, 𝐴𝐾, 𝐵𝑇 e si incontrano nel punto O esterno al triangolo. TRIANGOLO RETTANGOLO Le tre altezze sono: 𝐶𝐻 altezza relativa all’ipotenusa; 𝐴𝐶 𝑒 𝐵𝐶 che sono anche i cateti. Le altezze si incontrano nel punto C, che è il vertice dell’angolo RETTO. Def: il punto O di incontro delle tre altezze di un triangolo si chiama ORTOCENTRO. MEDIANE di un triangolo Def: si dice MEDIANA di un triangolo, relativa ad un lato, il segmento che unisce il vertice con il PUNTO MEDIO del lato opposto. TRIANGOLO ACUTANGOLO Si devono trovare i punti medi di ogni segmento: M, N, P e poi si deve unire ogni vertice con il punto medio opposto: 𝐶𝑀, 𝐴𝑁, 𝐵𝑃 sono le tre MEDIANE. Il loro punto d’incontro è G, interno al triangolo. TRIANGOLO OTTUSANGOLO Le tre mediane sono: 𝐶𝑀, 𝐴𝑁, 𝐵𝑃. Si incontrano nel punto G, interno al triangolo. TRIANGOLO RETTANGOLO Le tre mediane sono 𝐶𝑀, 𝐴𝑁, 𝐵𝑃. Si incontrano nel punto G interno al triangolo. Def: il punto di incontro delle MEDIANE si dice BARICENTRO e si indica con la lettera G. Proprietà: il BARICENTRO divide ogni mediana in due parti, di cui una è il doppio dell’altra; ovvero il segmento che va dal VERTICE al baricentro è il DOPPIO del segmento che va dal baricentro al PUNTO MEDIO. 𝐴𝐺 = 2 𝐺𝑁 𝐶𝐺 = 2 𝐺𝑀 𝐵𝐺 = 2 𝐺𝑃 BISETTRICI di un TRIANGOLO Def: Si dice BISETTRICE di un triangolo relativa ad un angolo il segmento che divide a metà l’angolo e incontra il lato opposto. Le BISETTRICI sono 𝐶𝑅, 𝐵𝑇, 𝐴𝑆. Si incontrano sempre all’interno di qualsiasi triangolo, nel punto I. Def: l’incontro delle BISETTRICI di un triangolo si chiama INCENTRO. Proprietà: in ogni triangolo l’INCENTRO è EQUIDISTANTE dai lati, ovvero la distanza di I dai lati è uguale per ogni lato. 𝐼𝐷 ≅ 𝐼𝐸 ≅ 𝐼𝐹 ASSI di un TRIANGOLO Def: l’ASSE di un segmento è la retta PERPENDICOLARE al segmento passante nel PUNTO MEDIO. TRIANGOLO ACUTANGOLO I tre assi si incontrano nel punto C, interno al triangolo. TRIANGOLO OTTUSANGOLO I tre assi si incontrano nel punto C, esterno al triangolo. TRIANGOLO RETTANGOLO I tre assi si incontrano nel punto C, sull’ipotenusa e coincidente con il punto medio M. Def: i tre assi del triangolo si incontrano nel punto detto CIRCOCENTRO. PUNTI NOTEVOLI DI UN TRIANGOLO ORTOCENTRO Intersezione delle ALTEZZE Acutangolo ! interno Ottusangolo ! esterno Rettangolo ! coincidente con il vertice dell’angolo retto BARICENTRO Intersezione delle MEDIANE Sempre interno INCENTRO Intersezione delle BISETTRICI Sempre interno CIRCOCENTRO Intersezione degli ASSI Acutangolo ! interno Ottusangolo ! esterno Rettangolo ! coincidente con il punto medio dell’IPOTENUSA CRITERI DI CONGRUENZA DEI TRIANGOLI Def: un movimento RIGIDO in geometria è uno spostamento che NON deforma la figura. Def: due triangoli sono CONGRUENTI se è possibile con un MOVIMENTO RIGIDO sovrapporli in modo da farli coincidere. !con uno spostamento rigido coincidono Due triangoli 𝐴𝐵𝐶 e 𝐴′𝐵! 𝐶′ sono CONGRUENTI se hanno gli angoli e i lati congruenti: 𝐴 ≅ 𝐴′ 𝐴𝐵 ≅ 𝐴′𝐵′ 𝐵 ≅ 𝐵!
𝐵𝐶 ≅ 𝐵′𝐶′
𝐶 ≅ 𝐶′
𝐴𝐶 ≅ 𝐴′𝐶′
Primo criterio di congruenza LAL Due triangoli 𝐴𝐵𝐶 e 𝐴’𝐵’𝐶’ sono congruenti se hanno due lati e l’angolo compreso congruenti. 𝐴𝐵 ≅ 𝐴′𝐵′ 𝐴𝐶 ≅ 𝐴! 𝐶 ! ! 𝐴𝐵𝐶 ≅ 𝐴′𝐵′𝐶′ 𝐴 ≅ 𝐴′ Secondo criterio di congruenza ALA Due triangoli 𝐴𝐵𝐶 e 𝐴’𝐵’𝐶’ sono congruenti se hanno due angoli e il lato compreso congruenti. 𝐴𝐵 ≅ 𝐴′𝐵′ 𝐴 ≅ 𝐴′ ! 𝐴𝐵𝐶 ≅ 𝐴′𝐵′𝐶′ 𝐵 ≅ 𝐵′ Terzo criterio di congruenza LLL Due triangoli 𝐴𝐵𝐶 e 𝐴’𝐵’𝐶’ sono congruenti se hanno tre lati congruenti. 𝐴𝐵 ≅ 𝐴′𝐵′ 𝐴𝐶 ≅ 𝐴! 𝐶 ! ! 𝐴𝐵𝐶 ≅ 𝐴′𝐵′𝐶′ 𝐵𝐶 ≅ 𝐵! 𝐶 !