Laboratorio di Algoritmi e Strutture Dati
II Semestre 2005/2006
Templates C++ ed Alberi di Ricerca
Marco Antoniotti
Comunicazioni di servizio
• Laboratorio
– Da settimana prossima di venerdì
• 12, 19 e 26
• 1 giugno e 8 giugno da vedere (avete sovrapposizioni?)
II Semestre 2005/2006
Laboratorio Algoritmi - Marco Antoniotti
1/22
1
Il problema dei tipi di dato
“contenitori”
•
•
Diversi concetti devono essere sviluppati nel modo più indipendente
possibile e devono essere combinati solo quando serve ed in maniera
controllata
L’esempio classico è quello di tipi di dato “contenitore” - liste, vettori,
dizionari ecc. ecc. - che hanno una struttura propria superimposta a
quella dei valori in essi contenuti
–
–
–
–
•
•
Liste di interi
Vettori di numeri in virgola mobile
Vettori di matrici
Dizionari <C.A.P., località>
In C abbiamo risolto questo problema con l’utilizzo consistente di
void * come tipo di un elemento da inserire in un contentitore
In C++ (ed in Java, Ada ecc. ecc.) si usa invece la nozione di template
o generic per risolvere questo problema
– Ovvero, si introducono costrutti che ci permettono di “generare” codice a
seconda del tipo che viene passato come parametro in liste di argomenti
particolari
II Semestre 2005/2006
Laboratorio Algoritmi - Marco Antoniotti
2/22
Templates C++: esempio
•
•
Supponiamo di voler definire una classe Coda di valori arbitrari
In C++ con templates abbiamo la soluzione seguente
template <class ValueType> class Coda {
public:
class NodoCoda {
ValueType value;
NodoCoda * next;
NodoCoda(ValueType v) : value(v), next(0) {}
}
NodoCoda * head, last;
ValueType insert( ValueType v) {
if (isEmpty()) head = last = new NodoCoda(v);
else last = (last->next = new NodoCoda(v));
return v;
}
// costruttori ed altri metodi.
}
II Semestre 2005/2006
Laboratorio Algoritmi - Marco Antoniotti
3/22
2
Templates C++: esempio
•
Per dichiarare e poter usare una coda di stringhe (usando la classe
String) scriviamo il codice seguente
Coda<String> sc;
String s1 = “Nel mezzo del cammin”;
String s2 = “di nostra vita”;
sc.insert(s1);
sc.insert(s2);
•
Per dichiarare e poter usare una coda di interi (usando il tipo base int)
scriviamo il codice seguente
Coda<int> ic;
int qd = 42;
ic.insert(qd);
II Semestre 2005/2006
Laboratorio Algoritmi - Marco Antoniotti
4/22
Templates C++: funzioni
•
•
•
•
Il primo uso naturale dei templates è di definire classi come string,
vector e map
Ma, immediatamente dopo, sorgono altri bisogni
Non è necessario usare il concetto di template solo su classi; infatti lo
si può usare anche per “semplici” funzioni
Ad esempio, vediamo la seguente dichiarazione ed il suo uso
template <class ElemType > void sort(vector<ElemType >&);
void f(vector<int>& vi, vector<string>& vs) {
sort(vi);
sort(vs);
}
// In forma piu` estesa...
void f(vector<int>& vi, vector<string>& vs) {
sort(vi);
sort<string>(vs);
}
II Semestre 2005/2006
Laboratorio Algoritmi - Marco Antoniotti
5/22
3
Templates C++: altre caratteristiche
• I templates C++ hanno altre caratteristiche che si integrano
bene con il resto del linguaggio
• In particolare
– Specializzazione: è possibile definire dei templates che
specializzano altri templates; ad esempio, in ordine di
specializzazione
template <class T> Vector {…}
template <class T> Vector<T*> {…}
template <> Vector<void*> {…}
– Ereditarietà: le regole che controllano l’ereditarietà di classi
influiscono anche sulla manipolazione dei templates
– Conversioni di tipo: i templates possono essere usati per definire
conversioni di tipo controllate a livello di compilazione (compile
time)
II Semestre 2005/2006
Laboratorio Algoritmi - Marco Antoniotti
6/22
Templates C++: compilazione
•
La compilazione di programmi e librerie C++ che contengono templates
è più complicata rispetto al caso “normale”
•
Una unità di compilazione (in genere un file) che istanzia un template
deve avere a disposizione non solo il template della dichiarazione, ma
anche il template della definizione di un componente da compilare
•
I diversi compilatori C++ hanno scelto diverse strategie per risolvere
questo problema
– Istanziazione automatica dei templates
• Salvataggio automatico delle definizioni generate in modo da faciliatere il lavoro
del linker (che deve essere più sofisticato)
• Generazione esplicita delle definizioni delle istanze di templates
– Scelta fatta da GCC
– Ovvero, l’operazione di compilazione separata può risultare difficile
• Specie in GCC dove è necessario includere i templates delle definizioni nello
scope dell’istanziazione
II Semestre 2005/2006
Laboratorio Algoritmi - Marco Antoniotti
7/22
4
Templates C++: riferimento
• Useremo i templates C++ per alcuni algoritmi e strutture dati nel
resto del corso
• Il riferimento principale per i templates è il capitolo 13 di “The
C++ Programming Language” di Bjarne Stroustroup, AddisonWesley
II Semestre 2005/2006
Laboratorio Algoritmi - Marco Antoniotti
8/22
Alberi di Ricerca Binaria
5
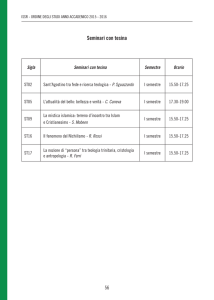
Dizionari ed Alberi di Ricerca Binaria
• Dizionario: tipo di dato astratto che ammette almeno le
operazioni
– Inserimento (insert) di un dato (indicizzato per chiave) con un
valore associato
– Ricerca (search) di un valore associato ad una chiave
– Rimozione (delete) una coppia <chiave, valore>
• Binary Search Trees (BSTs)
Una rappresentazione interna per il tipo di dato astratto
Dizionario
• Altre rappresentazioni
– Hash tables
II Semestre 2005/2006
Laboratorio Algoritmi - Marco Antoniotti
10/22
Dizionari e BSTs: concetti principali
• Nel descrivere il tipo di dato astratto “dizionario” dobbiamo
definire alcuni elementi di base
– Chiavi: elementi di insiemi su cui è definita una relazione d’ordine
totale
– Valori: essenzialmente senza struttura
• Problema 1: come garantire le prestazioni di un dizionario
• Problema 2: come espandere l’insieme di operazioni ammesse
– Selezione
– Concatenazione
– Ordinamento
II Semestre 2005/2006
Laboratorio Algoritmi - Marco Antoniotti
11/22
6
BSTs
• Un BST è un albero binario in ordine
simmetrico
• Un BST è
– o vuoto
– o un “nodo” <chiave, valore>
(<key, value>) con due BST associati
• Ordine simmetrico
– Chiavi nei nodi
– Le chiavi a “sinistra” sono tutte minori
– Le chiavi a “destra” sono tutte maggiori
II Semestre 2005/2006
Laboratorio Algoritmi - Marco Antoniotti
12/22
BSTs: forma dell’allbero
• Forma dell’albero
– Vi sono parecchi alberi che hanno le proprietà descritte
precedentemente e che corrispondono ad un dato insieme di chiavi
– Le prestazioni delle operazioni di dizionario dipendono da queste
forme
II Semestre 2005/2006
Laboratorio Algoritmi - Marco Antoniotti
13/22
7
BSTs in C++
•
Definiamo innanzitutto una classe BinaryTree che contiene una classe
BinaryNode
– La classe BinaryNode ha 4 campi
template <class Key, class Value >
class BinarySearchTree {
protected:
class BinaryNode {
Key key;
Value value;
BinaryNode * left;
BinaryNode * right;
BinaryNode(Key k, Value
BinaryNode(Key k, Value
BinaryNode *
BinaryNode *
}
// … continua …
II Semestre 2005/2006
v);
v,
l,
r);
Laboratorio Algoritmi - Marco Antoniotti
14/22
BSTs in C++
• Continuiamo con la definizione
// La radice dell’albero.
BinaryNode * root;
public:
// Un costruttore minimo.
BinarySearchTree() : root(0) {};
// Le operazioni di dizionario.
Value search(Key k);
Value insert(Key k, Value v);
}
II Semestre 2005/2006
Laboratorio Algoritmi - Marco Antoniotti
15/22
8
BST search
• L’operazione di search è molto semplice ma è meglio utilizzare
una funzione ausiliaria
– Si noti anche tutta la necessaria struttura per la gestione dei templates
template <class Key, class Value>
Value BinarySearchTree<Key, Value>::search(Key k) {
BinaryNode* result = searchNode(getRoot(), k);
if (result)
return result->getValue();
else
throw MissingKey(k);
}
Notate l’eccezione MissingKey
II Semestre 2005/2006
Laboratorio Algoritmi - Marco Antoniotti
16/22
BST search
• L’operazione searchNode diventa
template <class Key , class Value >
typename BinaryTree<Key , Value >::BinaryNode *
BinaryTree<Key , Value >::searchNode(BinaryTree::BinaryNode * n, Key k) {
if (n == 0) return (BinaryNode*) 0;
Key nk = n->getKey();
if (nk == k) return n;
else if (nk < k) return searchNode(n->getRight(), k);
else if (nk > k) return searchNode(n->getLeft(), k);
}
Notate la nuova keyword typename
II Semestre 2005/2006
Laboratorio Algoritmi - Marco Antoniotti
17/22
9
BST insert
• L’operazione di inserimento è (quasi) simmetrica
• Anche in questo caso utilizziamo una funzione ausiliaria
template <class Key, class Value >
Value BinarySearchTree<Key, Value >::insert(Key k, Value v) {
if (isEmpty())
return setRoot(new BinaryNode(k, v))->getValue();
else
return insertNode(getRoot(), k, v)->getValue();
}
II Semestre 2005/2006
Laboratorio Algoritmi - Marco Antoniotti
BST insertNode
•
18/22
Inserimento a destra
L’operazione di insertNode diventa
template <class Key, class Value>
typename BinarySearchTree<Key, Value >::BinaryNode*
BinarySearchTree<Key, Value >::insertNode(BinaryNode * n,
Key k,
Value v) {
Key nk = n->getKey();
BinaryNode* nl = n->getLeft();
BinaryNode* nr = n->getRight();
Caso normale
if (nk == k) {
n->setValue(v);
return n;
}
else if (nk < k) {
if (nr) return insertNode(nr, k, v);
else
return setRight(n, new BinaryNode(k, v));
}
else if (nk > k) {
if (nl) return insertNode(nl, k, v);
else
return setLeft(n, new BinaryNode(k, v));
}
}
Caso destro nullo
II Semestre 2005/2006
Laboratorio Algoritmi - Marco Antoniotti
19/22
10
BST esempio di inserimento
• Supponiamo di voler inserire le seguenti chiavi in un BST
ASERCHINGXMPL
II Semestre 2005/2006
Laboratorio Algoritmi - Marco Antoniotti
20/22
BSTs: analisi
• Costi per search e insert in un BST
– Proporzionali alla profondità di un nodo
– Corrispondenza 1-1 con le partizioni operate da quicksort
• La profondità di un nodo corrisponde alla profondità delle chiamate
ricorsive di quicksort quando un nodo viene “partizionato”
• Teorema: quando le chiavi sono inserite in modo casuale
(random), allora l’altezza di un BST è Θ(lg(N)), eccetto che per
una probabilità esponenzialmente bassa. Quindi, search e
insert richiedono O(lg(N)) tempo
• Problema: il caso peggiore per insert e search è O(N)
II Semestre 2005/2006
Laboratorio Algoritmi - Marco Antoniotti
21/22
11
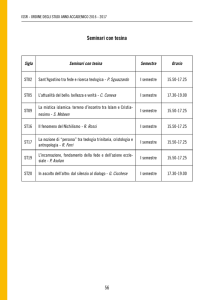
Implementazioni di Dizionari a
confronto
Caso peggiore
Caso medio
Implementazione
Search
Insert
Delete
Search
Insert
Delete
Array ordinato
lg(N)
N
N
lg(N)
N/2
N/2
Lista non ordinata
N
N
N
N/2
N
N
Hash Table
N
1
N
1*
1*
1*
BST
N
N
N
lg(N)
lg(N)
?
Per BST search e insert O(lg(N)) solo se le chiavi da inserire arrivano in ordine casuale
II Semestre 2005/2006
Laboratorio Algoritmi - Marco Antoniotti
22/22
Sommario
• Templates C++ e note sulle loro caratteristiche
– Verbosità iniziale fa rispiarmiare tempo in seguito
• Dizionari
– Chiavi e Valori
– Operazioni base
• Inserimento
• Ricerca
• Alberi di ricerca binaria
– Semplice implementazione con templates C++ delle operazioni
base del tipo di dato astratto Dizionario
– Teorema sulla forma di un BST quando le chiavi da inserire
arrivano in ordine casuale
II Semestre 2005/2006
Laboratorio Algoritmi - Marco Antoniotti
23/22
12