PERCORSO FORMATIVO: TERZA MEDIA SERALE
CTP SCUOLA MEDIA DI PRATA DI PORDENONE
a.s. 2000/2001
AREA SCIENTIFICA: UDM di matematica
Titolo
Le scienze matematiche
Prerequisiti
Conoscere gli aspetti fondamentali della
disciplina matematica
Obiettivi generali
Obiettivi specifici
1) Apprendere gli elementi fondamentali 1.1) Riconoscere i vari insiemi di numeri e le
dell’algebra.
loro differenze.
2) Conoscere l’aritmetica e saper correttamente 1.2) Mettere in relazione l’esistenza dei numeri
operare con i numeri.
ad esigenze concrete dell’uomo.
3) Conoscere gli elementi principali della 1.3) Utilizzare correttamente le operazioni di
geometria piana.
somma,
sottrazione,
moltiplicazione,
divisione ed elevamento a potenza con i
diversi insiemi numerici.
1.4) Acquisire una terminologia matematica
precisa ed un metodo di operare rigoroso.
1.5) Acquisire la capacità di risolvere espressioni
numeriche.
1.6) Conoscere il calcolo letterale.
1.7) Comprendere l’importanza dell’uso delle
lettere, che esprimono casi generali,
nell’enunciazione di proprietà o regole.
1.8) Saper risolvere espressioni implicanti l’uso
di termini letterali.
1.9) Conoscere le equazioni di primo grado e
comprendere il loro possibile utilizzo.
2.1) Conoscere le quattro operazioni e le loro
proprietà.
2.2) Conoscere l’elevamento a potenza in
relazione ad esempi concreti (le superfici e i
volumi) ed imparare ad usare le proprietà di
questa operazione.
2.3) Conoscere l’estrazione di radice.
2.4) Capire il concetto di termine intero e
frazionario.
2.5) Imparare il concetto di multiplo e divisore.
2.6) Saper applicare le operazioni di somma,
sottrazione, moltiplicazione, divisione ed
elevamento a potenza ad espressioni con
termini frazionari.
2.7) Conoscere i numeri decimali e saper operare
con essi.
3.1) Conoscere gli elementi che costituiscono la
base della geometria (punti, rette, segmenti,
Contenuti
L’algebra: i numeri relativi, le potenze con i
numeri relativi, il calcolo letterale e cenni alle
equazioni di primo grado.
L’aritmetica: gli insiemi numerici N, Z, Q e le
quattro operazioni. L’elevamento a potenza e
l’estrazione di radice.
La geometria: gli enti geometrici fondamentali
(il punto, la retta, il segmento, l’angolo). I
poligoni (triangoli, quadrilateri) e il cerchio.
Modalità di valutazione (strumenti e criteri)
Strumenti: risoluzione di esercizi riguardanti le
varie operazioni e le loro proprietà. Risoluzione
di espressioni sia con termini numerici (interi o
frazionari) sia con termini letterali.
Risoluzione di problemi di geometria.
Criteri di valutazione: capacità di risolvere
correttamente espressioni matematiche di vario
tipo. Saper riconoscere ed applicare alcune
proprietà dei numeri. Acquisire padronanza
nell’utilizzo delle regole matematiche. Procedere
nella risoluzione di una espressione con uno
schema ordinato e preciso. Risolvere un
problema di geometria identificando e
rappresentando correttamente i dati di partenza e
applicando in modo opportune le formule.
Capacità di collegare tra di loro i vari argomenti
trattati in un quadro più generale.
angoli, ecc.)
3.2) Saper riconoscere le figure geometriche
piane ed individuarne le caratteristiche.
3.3) Acquisire familiarità nell’uso dei termini
della geometria.
3.4) Saper risolvere problemi rispettando precisi
schemi di lavoro.
Modalità formative
Lezione frontale interattiva e conversazione.
Esercitazioni alla lavagna con successiva
discussione collettiva. Consegna di esercizi da
risolvere a casa. Utilizzo del libro di testo.
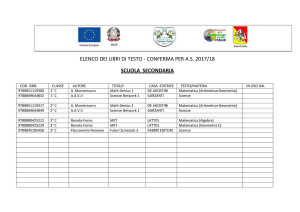
Testi utilizzati: E Bovio, L. Manzone Bertone –
Diagrammi e algebra – teoria – Lattes & C.,
Torino, 1999.
E Bovio, L. Manzone Bertone – Diagrammi e
algebra – Esercizi – Lattes & C., Torino, 1999.
E Bovio, L.Manzone Bertone – Aritmetica –
Lattes & C., Torino, 1999.
E Bovio, L. Manzone Bertone – Geometria
sperimentale – Lattes & C., Torino, 1999.
Durata