6. Il circuito risonante LC
Un semplice circuito (di resistenza trascurabile), che produce una corrente elettrica
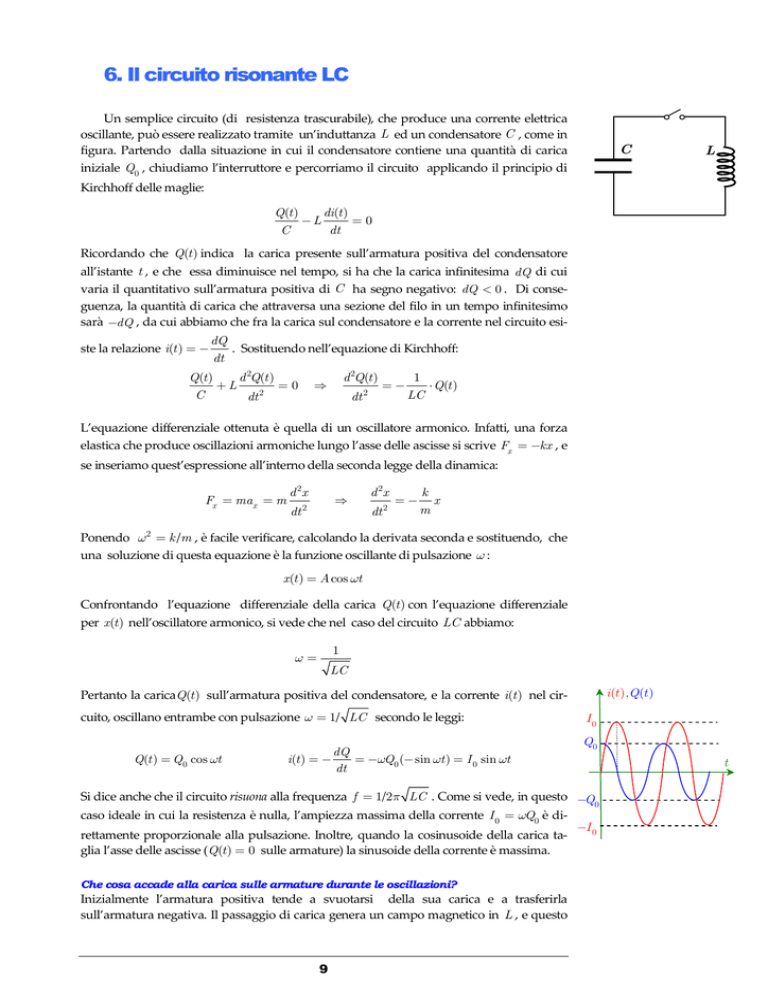
oscillante, può essere realizzato tramite un’induttanza L ed un condensatore C , come in
figura. Partendo dalla situazione in cui il condensatore contiene una quantità di carica
iniziale Q0 , chiudiamo l’interruttore e percorriamo il circuito applicando il principio di
C
L
Kirchhoff delle maglie:
Q(t )
di(t )
L
0
C
dt
Ricordando che Q(t ) indica la carica presente sull’armatura positiva del condensatore
all’istante t , e che essa diminuisce nel tempo, si ha che la carica infinitesima dQ di cui
varia il quantitativo sull’armatura positiva di C ha segno negativo: dQ 0 . Di conseguenza, la quantità di carica che attraversa una sezione del filo in un tempo infinitesimo
sarà dQ , da cui abbiamo che fra la carica sul condensatore e la corrente nel circuito esiste la relazione i(t )
dQ
. Sostituendo nell’equazione di Kirchhoff:
dt
Q(t )
d 2Q(t )
L
0
C
dt 2
d 2Q(t )
dt
2
1
Q(t )
LC
L’equazione differenziale ottenuta è quella di un oscillatore armonico. Infatti, una forza
elastica che produce oscillazioni armoniche lungo l’asse delle ascisse si scrive Fx kx , e
se inseriamo quest’espressione all’interno della seconda legge della dinamica:
Fx max m
d 2x
dt
2
d 2x
dt
2
k
x
m
Ponendo 2 k /m , è facile verificare, calcolando la derivata seconda e sostituendo, che
una soluzione di questa equazione è la funzione oscillante di pulsazione :
x (t ) A cos t
Confrontando l’equazione differenziale della carica Q(t ) con l’equazione differenziale
per x (t ) nell’oscillatore armonico, si vede che nel caso del circuito LC abbiamo:
1
LC
i (t ),Q (t )
Pertanto la caricaQ(t ) sull’armatura positiva del condensatore, e la corrente i(t ) nel circuito, oscillano entrambe con pulsazione 1/ LC secondo le leggi:
Q(t ) Q0 cos t
dQ
i(t )
Q0 ( sin t ) I 0 sin t
dt
I0
Q0
Si dice anche che il circuito risuona alla frequenza f 1/2 LC . Come si vede, in questo Q
0
caso ideale in cui la resistenza è nulla, l’ampiezza massima della corrente I 0 Q0 è diI 0
rettamente proporzionale alla pulsazione. Inoltre, quando la cosinusoide della carica taglia l’asse delle ascisse (Q(t ) 0 sulle armature) la sinusoide della corrente è massima.
Che cosa accade alla carica sulle armature durante le oscillazioni?
Inizialmente l’armatura positiva tende a svuotarsi della sua carica e a trasferirla
sull’armatura negativa. Il passaggio di carica genera un campo magnetico in L , e questo
9
t
produce subito un campo elettrico autoindotto, che si oppone alla variazione della stessa
corrente che l’ha generato. Il processo va avanti, e non si arresta nemmeno quando
l’armatura positiva ha perduto tutta la sua carica ed è divenuta neutra. Infatti, il campo
elettrico indotto si opporrebbe alla variazione di corrente che seguirebbe ad un brusco arresto del passaggio di carica. Così il processo deve proseguire in modo da spegnersi gradualmente. L’armatura inizialmente positiva - ma adesso neutra - perde ancora altre cariche positive, caricandosi negativamente. Nel contempo l’altra armatura diviene positiva. Il processo rallenta progressivamente fino a quando l’altra armatura ha accumulato
una carica uguale a quella iniziale, ma di segno opposto. Infatti , non è possibile che il
condensatore si carichi oltre il valore iniziale Q0 , proprio come un pendolo ideale non
può risalire oltre la quota iniziale dalla parte opposta. In caso contrario, infatti, violeremmo la legge di conservazione dell’energia inizialmente stipata in C , che come sappiamo
ha valore Q02 /2C . A questo punto si è completata metà oscillazione, e la carica riparte a
muoversi in senso inverso. Tutto il processo si ripete, e l’armatura iniziale torna ad essere
positiva.
antenna
Quali applicazioni ha il circuito LC?
C
Il circuito LC è utilizzato per la creazione e la ricezione delle onde radio, soprattutto FM e
TV (30MHz 300MHz) e delle microonde, come quelle dei radar e dei telefoni cellulari
L
variabile
(circa 1.8 GHz ). Come ricettore, collegato ad un’antenna, diviene sede di corrente per
opera delle onde elettromagnetiche che fanno oscillare gli elettroni entro l’antenna stessa.
Di tutte le frequenze ricevute, come abbiamo visto, solo quelle corrispondenti alla pulsazione 1/ LC possono instaurarsi nel circuito LC , che quindi permette di effettuare
una selezione. Se il valore del condensatore viene reso variabile attraverso una manopola,
si può di volta in volta cambiare la frequenza alla quale il circuito risuona. Questo è il sistema utilizzato per la sintonizzazione di un apparecchio radio alla frequenza della stazione emittente desiderata.
v(t)
L
C
i (t )
La corrente nel circuito dipende dalla frequenza della radiazione ricevuta?
R
La presenza dell’antenna produce oscillazioni nel circuito, come se in esso fosse presente
un generatore di tensione alternata v(t ) V0 sin t . Indichiamo con R la resistenza
0
si instaura nella serie RLC ha un’intensità dipendente dalla pulsazione con la quale
oscilla il generatore di tensione, secondo l’equazione:
complessiva di tale circuito, nel caso generale in cui essa non sia trascurabile. Una tale
configurazione è detta serie RLC . Uno studio dettagliato mostra che la corrente i(t ) che
I0
i(t ) I 0 sin(t )
I0
V0
R 2 (L 1/C )2
t
I 0
T 2 LC
Qual è il significato della presenza della fase iniziale nella corrente?
Come si vede, la corrente oscilla con la stessa della tensione, ma ha una diversa fase
iniziale . Questo significa che, nel grafico della sinusoide che esprime l’andamento nel
tempo di i(t ) , i massimi ( e i minimi) di corrente non sono raggiunti simultaneamente ai
massimi di tensione imposti dal generatore alla serie dei tre dispositivi. Essi arriveranno
un po’ prima oppure un po’ dopo a seconda di quanto vale , che a sua volta dipende da
R , L e C . Si può dimostrare che 0 quando il generatore oscilla con 1/ LC .
In questo caso si dice che corrente e tensione ai capi della serie sono in fase.
10
In che modo l’intensità I0 della corrente dipende dalla pulsazione ?
Il denominatore nell’espressione di I 0 diviene minimo se la parte di esso che dipende
dalla pulsazione si annulla, cioè per L 1/C . Questo accade quando si fa oscillare il
V0
I0
R
generatore con 1/ LC . In corrispondenza del minimo denominatore, l’ampiezza
I 0 della corrente assume la massima intensità. L’andamento di I 0 in funzione di è illu-
strato in figura, dove si vedono i due effetti contrastanti per opera di C ed L . Come
sappiamo, il condensatore, collegato a un generatore di tensione continua, si comporta da
circuito aperto. C’è una breve fase in cui si carica, durante la quale tutto va come se passasse corrente, ma rapidamente il processo termina, perché ai capi di C si ricrea, con segno opposto, la stessa differenza di potenziale del generatore. Nel circuito RLC , per bassi valori della pulsazione siamo praticamente in tensione continua e il passaggio di corrente è quindi impedito da C . L’unico modo di far passare corrente attraverso il condensatore è di caricarlo e scaricarlo in continuazione ( alta). Per elevati valori della pulsazione,
però, l’induttore impedisce che passi corrente perché la legge di Faraday-Neumann prevede opposizione ogni volta che tentiamo di variare il flusso del campo magnetico autoindotto. Più rapidamente il generatore tenta di far variare il flusso (grandi valori di ),
più efficace è il contrasto a tale cambiamento per opera di L , con il risultato che la corrente si annulla. I due effetti contrastanti di condensatore (che fa passare le alte frequenze) e
induttore (che fa passare le basse frequenze) trovano un equilibrio al valore di risonanza
1/ LC
1/ LC .
Come funzionano i metal detector?
I metal detector sono circuiti RLC (con due induttanze affacciate) che stanno oscillando
alla frequenza di risonanza. Quando degli oggetti di metallo sono portati nelle loro vicinanze, il campo magnetico generato dal circuito mette in moto i loro elettroni di conduzione, trasformandoli a loro volta in magneti. Se questi magneti si muovono in prossimità
del circuito, esso sperimenta la presenza di un campo magnetico variabile dovuto al loro
avvicinamento/allontanamento. La conseguente variazione del flusso magnetico concatenato al circuito RLC, sposta il circuito dalla condizione di risonanza, e quest’effetto è segnalato da un allarme acustico. Un simile sistema è utilizzato per rivelare la presenza di
oggetti metallici all’aeroporto. Il passeggero avanza nello spazio fra due bobine accordate
fra loro, in un circuito in cui la curva di risonanza è molto stretta e basta un piccolo flusso
magnetico aggiuntivo, come quello prodotto da un mazzo di chiavi, per disturbare
l’equilibrio.
7. Onde elettromagnetiche
Tutte le onde elettromagnetiche si propagano nel vuoto ad una velocità costante
c 3.0 108 m/s , detta velocità della luce, e sono generate dal moto accelerato di particelle cariche, libere (cioè non legate ad un atomo). L’accelerazione può essere un
cambiamento nel modulo della velocità lungo una traiettoria lineare: ad esempio
degli elettroni che vanno avanti ed indietro entro un’antenna radio. Ma il moto è accelerato anche quando le particelle cariche percorrono una traiettoria curvilinea a velocità costante. Ad esempio irraggiano le particelle cariche che seguono una traiettoria elicoidale avvitandosi attorno alle linee di un campo magnetico esterno. Il moto
rettilineo a velocità costante, invece, non produce alcun irraggiamento.
Perché una carica in moto uniforme non può produrre onde elettromagnetiche?
Sappiamo che una particella carica in quiete genera un campo elettrico e nessun
campo magnetico. Ad essa non è associata alcuna radiazione. È semplice convincersi
11
induttanza
che anche una particella carica in moto uniforme trasporta semplicemente con sé i
propri campi E e B senza generare alcuna radiazione intorno. Difatti, il moto a velocità costante, una volta instauratosi, non produce alcun cambiamento nel campo
elettrico, e di conseguenza non si può applicare l’equazione di Ampère-Maxwell per
giustificare una variazione del campo magnetico come risultato di un cambiamento
di E . Inoltre, non vi sarebbe alcuna sorgente da cui trarre energia per immetterla
nell’eventuale radiazione: la particella dovrebbe attingere alla propria energia cinetica, col risultato di rallentare il proprio moto rettilineo uniforme senza che si intervenga dall’esterno su di essa. Il che violerebbe il principio d’inerzia. E se anche una
tale radiazione esistesse, potremmo veder la particella smettere di irraggiare, semplicemente iniziando a correre accanto ad essa alla sua stessa velocità. Nel nostro rife
rimento la carica sarebbe in quiete e avremmo B 0 e quindi di nuovo nessun irraggiamento. Tutto questo è paradossale, dato che la particella non può interrompere
un’eventuale emissione di onde solo perché decidiamo di correre affianco ad essa.
Possiamo classificare le onde elettromagnetiche in base alla loro frequenza?
Le equazioni di Maxwell non contengono la frequenza, quindi le onde elettromagnetiche sono qualitativamente un unico fenomeno ondulatorio, indipendentemente dal
numero di oscillazioni che si producono in un secondo. La frequenza di un’onda
elettromagnetica teoricamente può andare da zero ad infinito, quindi si osservano
valori che differiscono anche di molti ordini di grandezza. L’insieme delle frequenze
possibili viene chiamato lo spettro elettromagnetico. Per comodità, e per motivi più storici che fisici, lo spettro elettromagnetico è suddiviso in sette regioni secondo valori
crescenti della frequenza: onde radio, microonde, infrarosso, luce visibile, ultravioletto,
raggi X, raggi gamma. I confini di queste regioni sono sfumati e in parte anche sovrapposti. Vediamo ora una descrizione di queste regioni, ricordando che per le onde elettromagnetiche, come per le onde meccaniche, vale una relazione che lega insieme frequenza f , velocità c e lunghezza d’onda :
f c
Quali sono le caratteristiche delle onde radio?
Osservate per la prima volta nel 1888, vengono chiamate onde radio tutte quelle radiazioni
elettromagnetiche di frequenza inferiore a 1 GHz (109 Hz) . La corrispondente lunghezza
d’onda va da molte migliaia si chilometri fino a 30 cm .
12












