Corso Statistica Applicata - Iac-Cnr

Test di Ipotesi (su una singola popolazione)
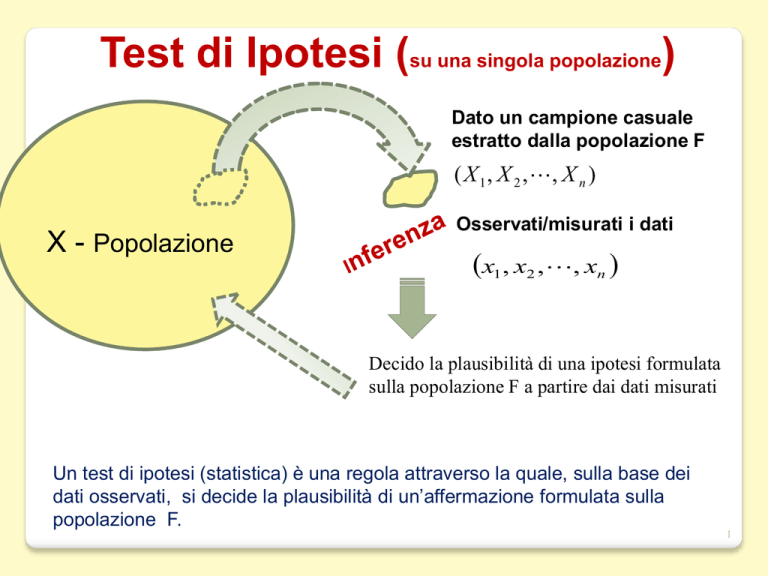
Dato un campione casuale
estratto dalla popolazione F
( X 1 , X 2 ,, X n )
X - Popolazione
Osservati/misurati i dati
x1 , x2 ,, xn 
Decido la plausibilità di una ipotesi formulata
sulla popolazione F a partire dai dati misurati
Un test di ipotesi (statistica) è una regola attraverso la quale, sulla base dei
dati osservati, si decide la plausibilità di un’affermazione formulata sulla
popolazione F.
1
Non si fanno assunzioni circa la forma
analitica della distribuzione stessa, ma si
Test Non Parametrici esprime un’ipotesi su di essa o su alcune sue
caratteristiche
Test Parametrici
si assume nota la forma analitica della
distribuzione stessa e si esprime un’ipotesi
circa uno o più dei suoi parametri.
F x |  
Noi ci occupiamo solo dei test parametrici
2
Esempi
Test Parametrico
La moneta è “truccata”?
Test Non Parametrico
C’è un’associazione tra un dato
SNP ed una patologia?
Test Parametrico
L’altezza (media) della
(popolazione) è 100 cm?
L’altezza (media) della
bambine è uguale all’altezza
media dei bambini?
Test Non Parametrico
Le due popolazioni hanno distribuzioni
uguali?
3
Definizione di
Ipotesi statistica
Un'ipotesi statistica è un'affermazione che specifica parzialmente o
completamente la legge di distribuzione della probabilità di una variabile
casuale X che descrive la popolazione di interesse
Sia
F  N (  ,1)
la popolazione da cui è estratto il campione
Affermazione che specifica completamente la
Ipotesi semplice legge di distribuzione. Esempio:
Ipotesi composta
 1
Affermazione
che
NON
specifica
completamente la legge di distribuzione.
Esempio:
 1
4
L’ipotesi che viene formulata è detta ipotesi nulla H 0. Essa rappresenta lo stato
di fatto o l’ipotesi neutra. L’ipotesi contraria, è detta l’alternativa.
ACCETTO
H0
NON LA RIFIUTO
NON C’E’ EVIDENZA SPERIMENTALE PER RIFIUTARLA
ACCETTO H 1
RIFIUTO
H0
C’E’ EVIDENZA SPERIMENTALE PER RIFIUTARLA
5
Accettare l’ipotesi nulla non significa che questa sia vera, ma “solo” che non
c’è nulla che ci porti a credere il contrario (i.e., manca l’evidenza del contrario).
Viceversa rifiutare l’ipotesi nulla significa che, dati alla mano (sebbene
possibile), appare molto improbabile che l’ipotesi nulla sia vera
Per gli esercizi….:
Se devo smentire/confutare un’ipotesi la uso come ipotesi nulla di un test statistico.
…vedi Esercizio Cap. 8 n.1 in un sistema giudiziario garantista H0: innocenza
Se devo provare/testare (sperimentalmente) un’ipotesi la uso come alternativa
…vedi esempio seguente la moneta è truccata?
6
Esempio: moneta truccata?
H0
: La moneta è onesta
H1
: La moneta è truccata
Matematicamente
X
Variabile Casuale Bernulliana
P(X=0)=q=(1-p).
Lanciamo n volte la moneta e registriamo il
numero di volte che esce ogni faccia
P(X=1)=p
H0 :
p
1
2
H1 :
p
1
2
n=100
Totale 40
pˆ 
Totale 60
2
 0.4
5
Cosa vi sembra?
7
Come costruiremo un test statistico…..
Dato il campione casuale X 1 , X 2 ,, X n estratto dalla popolazione
di interesse


Si sfrutta una Statistica Test X ts  g X 1 , X 2 ,  , X n che ad ogni set di
dati fa corrispondere un valore numerico e di cui conosciamo la distribuzione PH 0  X ts 
supponendo H 0 vera.
PH 0  X ts   PH 0 g  X 1 , X 2 ,, X n 
Si costruisce una regione di rifiuto identificando un insieme di valori che hanno
bassa probabilità di accadere se l’ipotesi nulla H è vera. Quanto bassa lo
0
decide l’utente specificando il LIVELLO DI SIGNIFICATIVITA’ del test.
8
Regola di decisione: Se il valore della statistica osservato sul campione estratto
cade nella regione critica o di rifiuto allora l’ipotesi nulla viene rifiutata, altrimenti
viene accettata (i.e. non rifiutata)
Nell'accettare o rifiutare, sulla base dell'evidenza sperimentale, una
determinata ipotesi nulla, si può agire “correttamente”, e cioè accettare
l’ipotesi nulla quando è vera o rifiutare l’ipotesi nulla quando è falsa,
oppure si possono commettere errori di diversa natura:
a) errore di I specie o di I tiporifiutare l’ipotesi nulla quando essa è vera .
Falso positivo
b) errore di II specie o di II tipoaccettare l’ipotesi nulla quando essa è
falsa. Falso negativo
decisione
Accettare è inteso
come “non rifiutare”
H0 è vera
H0 è falsa
Accetto H0
Decisione Corretta
1-α
Errore Tipo II
β
Rifiuto H0
Errore Tipo I
α
Decisione Corretta
1-β
9
  Prifiutare H 0 | H 0 è vera 

  Paccettare H 0 | H 0 è falsa 

1    Prifiutare H 0 | H 0 è falsa 
1 
Idealmente si vorrebbe
 0
Livello di significatività del test
(coincide con la probabilità di
commettere un errore di tipo I)
probabilità di commettere un
errore di tipo II
Potenza del test (probabilità
di individuare ipotesi false)
1   1    0
la soluzione ideale dovrebbe essere costituita da un test capace di minimizzare
simultaneamente le probabilità di commettere gli errori di I e di II tipo, ma
avendo a disposizione solo un campione della popolazione questo non è
possibile.
10
Distanza tra ipotesi nulla ed
alternativa
PDati | H 0 è vera   PH 0 Dati 
PDati | H 0 è falsa   PH1 Dati 
Varianza statistica
campionaria
α
β
11
Poiché errore di tipo I ed errore di tipo II sono in competizione
La procedura che si esegue è quella di fissare la misura della
probabilità di commettere un errore di primo tipo (si stabilisce cioè il
livello di significatività α) e nell'individuare poi il test che minimizza la
probabilità di commettere un errore di II tipo.
In generale: Fissate le ipotesi ed il livello di significatività del test, per
aumentare la potenza occorre aumentare la taglia del campione.
tra tutti i test statistici che si possono costruire per una prefissata coppia di
ipotesi, si cercherà di trovare (se possibile) quello con la potenza più grande a
parità della taglia del campione.
12
Fasi da eseguire per un test delle ipotesi

H0
Specificare le ipotesi da testare
H1
(le ipotesi devono essere esaustive e mutuamente esclusive )


Fissare il livello di significatività

Definire una statistica X ts  g  X 1 , X 2 ,  , X n  per il test (i.e., una statistica
per cui sia “calcolabile” la distribuzione campionaria quando l’ipotesi nulla è
vera) .

Definire sulla base della statistica scelta la regione di rifiuto per H 0 (i.e., i
valori della statistica di probabilità <  quando H 0 è vera).

Eseguire il campionamento (i.e., l’esperimento) e calcolare il valore della
statistica osservato sul campione casuale, i.e. xts  g  x1 , x2 ,  , xn 

Se xts  g  x1 , x2 ,  , xn  cade nella regione di rifiuto, si decide di rifiutare H 0 ,
altrimenti si decide di non rifiutare H 0
La risposta del test è “rifiuto” o “non rifiuto”
13
P-value
In corrispondenza di una particolare realizzazione
xts  g  x1 , x2 , , xn 
assunta da una qualunque Statistica Test X ts  g  X 1 , X 2 ,  , X n 
si dice P-value la probabilità dei valori che superano, (in valore assoluto) e
nella direzione estrema, il valore osservato.
La probabilità sopramenzionata è calcolata assumendo che H 0 è vera
In pratica, il p-value è una misura di ottenere realizzazioni ancora più estreme
di quella osservata.
Intuitivamente è una misura di plausibilità dell’ipotesi nulla.
Un p-value molto piccolo viene interpretato come una misura a sfavore dell’ipotesi
nulla.
14
PH 0 ( X ts )
15
Approccio alternativo per un test delle ipotesi

H0
Specificare le ipotesi da testare
H1
(le ipotesi devono essere mutuamente esclusive ed indurre una partizione dello
spazio degli eventi)


Fissare il livello di significatività

Definire una statistica X ts  g  X 1 , X 2 ,  , X n  per il test (i.e., una statistica
per cui sia “calcolabile” la distribuzione campionaria quando l’ipotesi nulla è
vera)

Eseguire il campionamento (i.e., l’esperimento) e calcolare il valore della
statistica osservato sul campione casuale. xts  g  x1 , x2 ,  , xn 

Calcolare il p-value associato alla statistica osservata

Se
p̂   si decide di rifiutare H 0 , altrimenti si decide di non rifiutare H 0
La risposta del test è “rifiuto” o “non rifiuto” + p-value
16
Test sulla media di una popolazione
Sia la popolazione del campione una
N ( , 2 )
Obiettivo: testare una delle seguenti
H 0 :   0
H1 :   0
Dove
H 0 :   0
H 0 :   0
H1 :   0
H1 :   0
 0 è un valore noto
Si estrae il campione casuale X 1 , X 2 ,, X n
2

Caso a)
varianza nota
Caso b)  2 varianza incognita
(di taglia n)
Z
X  0
/ n
X  0
T
S/ n
Statistica test
Statistica test
A seconda della tipologia della coppia nulla/alternativa da testare il test sarà
“ad una coda” oppure “a due code”
17
Par. 8.3.1)
caso a)  2 varianza nota
Si sfrutta il fatto che la Statistica Test Z 
X  0
~ N 0,1 sotto l’ipotesi   0
/ n
Distribuzione (estrema) assumendo
che l’ipotesi nulla sia vera. Per
determinate la regione critica
occorre individuare le zone a bassa
probabilità
Il caso “varianza nota” è un caso pressoché “ideale” (con valore principalmente
“didattico”). Nelle applicazioni reali molto raramente si è in grado di conoscere la
varianza della popolazione.
In R c’è z.test
In Matlab c’è ztest
18
Test a due code
1
H 0 :   0
N 0,1
H1 :   0


2
2
 z
2
Regione rifiuto
Regione accettazione
Z   z
Z  z
2
2
0
z
2
 z  Z  z
2
2
19
20
Esempio 1 (Ross Cap8 n.6)
Supponiamo di sapere che negli Stati Uniti la statura media di un maschio adulto
è di 70 pollici, con una deviazione standard di 3 pollici. Per verificare che gli
uomini di una città sono “nella media”, si sceglie un campione di 20 maschi
adulti e se ne misura la statura, ottenendo i risultati seguenti:
72 68.1 69.2 72.8 71.2 72.2 70.8 74 66 70.3 70.4 76 72.5 74 71.8 69.6 75.6 70.6
76.2 77
Cosa concludi? Spiega quali assunzioni stai facendo.
H 0 :   70
H1 :   70
X  72.01   3
n  20  0  70
Ipotizziamo che la v.a. statura di un maschio
adulto sia una normale ed eseguiamo uno z-test
a due code con varianza nota
X  70
 3.004
3 / 20
21
Esempio 1 (continuazione)
Decidiamo un livello di significatività e stabiliamo se rifiutare l’ipotesi nulla che
il campione di uomini sia nella media.
  0.05  | 3.004| 1.96  z0.025
  0.01  | 3.004| 2.576  z0.005
In ambedue i casi
rifiutiamo ipotesi nulla
3.004
pvalue  P ( Z  3.004)  2 P ( Z  3.004)  0.0027
22
Test ad una coda
H 0 :   0
‘left’
H1 :   0
N 0,1
H 0 :   0
‘right’
H1 :   0
N 0,1
1


1
 z
0
Regione rifiuto
Regione accettazione
0
Z   z
Z   z
z
Regione rifiuto
Regione accettazione
Z  z
Z  z
23
24
Esempio 2 (Ross Cap8 n.10)
I salmoni cresciuti ogni anno in un allevamento commerciale hanno dei pesi con
distribuzione normale di deviazione standard 1.2 libbre. La ditta dichiara che il
peso medio dei suoi pesci quest’anno è superiore alle 7.6 libbre. Supponi che un
campione casuale di 16 pesci sia risultato in un peso medio di 7.2 libbre. Si può
dire che questo dato sia abbastanza forte da farci respingere l’affermazione
dell’azienda (a) al 5% di significatività? (b) All’1% di significatività? (c) Quanto
vale il p-dei-dati di questo test?
H 0 :   7.6
H1 :   7.6
Poiché nel testo ci chiedono se possiamo respingere l’ipotesi
basandoci sui dati, scegliamo proprio questa come H0
X  7.2   1.2
n  16  0  7.6
7.2  7.6
 - 1.3333
1.2 / 16
25
Esempio 2 (continuazione)
In base al livello di significatività, stabiliamo se rifiutare l’ipotesi nulla che la
media del peso dei salmoni sia superiore a 7.6 libbre.
  0.05   1.333 1.645  z0.05
  0.01   1.333  2.326  z0.01
In ambedue i casi
non possiamo rifiutare
l’ipotesi nulla e dunque
non possiamo respingere
l’affermazione anche se
questo non significa sia vera
pvalue  P ( Z  1.333)  0.0913
26
27
Par. 8.3.2)
caso b)  2 varianza incognita
Si sfrutta il fatto che la Statistica Test T 
X  0
~ t n  1 sotto l’ipotesi
S/ n
  0
Distribuzione (estrema) assumendo
che l’ipotesi nulla sia vera. Per
determinate la regione critica
occorre individuare le zone a bassa
probabilità
Il t-test è uno dei test statistici più utilizzati (spesso anche male utilizzato). Ne
esistono diverse varianti. In questa fase vediamo il caso del t-test per la media
di una popolazione
In R il presente test (e le sue generalizzazioni) è implementato dalla
funzione t.test
28
Test a due code
T n  1
H 0 :   0
H1 :   0
 t / 2,n 1
Regione rifiuto
T  t 
2
Regione accettazione
 t
2
, n 1
, n 1
T  t
2
 T  t
2
t / 2,n 1
, n 1
, n 1
29
30
Esempio 1
Supponendo che il livello medio di colesterolo in soggetti
adulti sani sia di 180. Si consideri la popolazione di soggetti
adulti affetti da una determinata patologia, si vuole verificare
se tali soggetti associano un livello di colesterolo diverso da
quello dei soggetti sani.
H 0 :   180
Test a due code
H 1 :   180
Caso 1) Supponiamo di estrarre n=10 campioni
Fissato α=0,05
t 0.025,9  2.26
 t 0.025,9  2.26
Supponiamo di aver calcolato che X 10  190
 2,26  2,108  2,26
Quanto vale il p-value?
T
X 10  180 Ha 9 gradi di
S10 / 10 libertà
S10  25 da cui
T  2,108
Decisione: L’ipotesi nulla non
può essere rifiutata
31
Esempio 1 (continuazione)
Caso 2) Supponiamo di estrarre n=15 campioni
Fissato α=0,05
t 0.025,14  2.145
Supponiamo di aver calcolato che X 15  190
T
X 15  180 Ha 14 gradi di
libertà
S15 / 15
 t 0.025,14  2.145
S15  25 da cui
T  2.582
T  2.582  2.145  t0.025,14
Decisione: L’ipotesi
nulla deve essere
rifiutata
Aumentare la taglia del campione
casuale estratto consente di
riconoscere meglio le differenze
(da un punto di vista matematico
aumenta la potenza del test).
“esempio
artificiale”:
nelle
applicazioni reali se si aumenta la
taglia del campione (o se si cambia il
campione) le stime della media
campionaria
e
della
varianza
campionaria risultano diverse
Quanto vale il p-value?
32
Test ad una coda
H 0 :   0
H1 :   0
‘left’
H 0 :   0
H1 :   0
‘right’
T n  1
T n  1
t ,n 1
 t ,n1
Regione rifiuto
Regione accettazione
T  t ,n 1
T  t ,n 1
Regione rifiuto
T  t ,n 1
Regione accettazione
T  t ,n 1
33
34
Esempio 2
Si supponga di aver somministrato ad un gruppo di n=12
cavie un particolare farmaco e di aver riscontrato i
seguenti incrementi di peso: 55, 62,54, 57, 65, 64, 60, 63,
58, 67, 63 e 61 grammi. Sapendo che le cavie del tipo
considerato (di uguale età e condizione), quando non
sono sottoposte a trattamenti, mostrano un incremento
medio di peso pari a 65 grammi.
Ci si domanda se le osservazioni siano tali da poter attribuire al farmaco la
differenza riscontrata nell'incremento medio di peso; in particolare si vuole
sapere cioè se il farmaco possa consentire una riduzione dell’aumento del peso
o oppure se tale differenza possa essere attribuita a fattori aventi carattere
puramente accidentale
H 0 :   65
H 1 :   65
Test ad una
coda (“left”)
35
Esempio 2 (continuazione)
T
dove
X  65
Ha 11 gradi di libertà
S / 12
X  60,75
Fissato α=0,05
S  16,38
 t 0.05,11  1.80
T  3,63
T  3,63  t 0.05,11  1.80
Decisione: L’ipotesi
nulla deve essere
rifiutata
 3.63
-3.63 -1.80
 t0.05,110
pvalue  PH 0 T  3.63  0.004
36
Esempio 3
Si vuole verificare l’efficacia di una data dieta dimagrante
te, pertanto vengono monitorati n=11 individui al tempo
t=0 (inizio della dieta) e t=3 mesi da quando la dieta è
iniziata.
A parte il regime dietetico gli individui selezionati
continueranno a seguire lo stile di vita cui erano abituati.
Si osservano i seguenti risultati
T=0 mesi
T=3 mesi
Individuo 1
64.6
61.5
Individuo 2
63.9
62.2
Individuo 3
68.6
65.0
Individuo 4
59.4
57.5
Individuo 5
55.3
54.8
Individuo 6
53.7
53.4
Individuo 7
62.0
62.4
Individuo 8
59.7
58.2
Individuo 9
53.2
53.6
Individuo 10
61.5
59.5
Individuo 11
66.3
63.0
Possiamo concludere che la dieta è
efficace con una significatività di 0.01?
D  1.5545
H0 : d  0
H1 : d  0
S D  1.4243
Test ad una coda
t0,01;10  2.7638
T  3.6198
Decisione: L’ipotesi nulla
deve essere rifiutata
La dieta è
efficace
37
Par. 8.6 Test sulla proporzione di una popolazione
Bernulli ( p )
Sia la popolazione del campione una
Obiettivo: testare una delle seguenti
Dove
H 0 : p  p0
H 0 : p  p0
H 1 : p  p0
H 1 : p  p0
H 0 : p  p0
H 1 : p  p0
p0 è un valore noto
Si estrae il campione casuale X 1 , X 2 ,, X n
Caso a) np0 (1  p0 )  20
Caso b)
np0 (1  p0 )  20
(di taglia n)
n
X   X i  Bin(n, p )
Statistica test
i 1
Z
X  np0
 N (0,1)
np0 (1  p0 )
Statistica test
A seconda della tipologia della coppia nulla/alternativa da testare il test sarà
“ad una coda” oppure “a due code”
38
Caso a)
np0 (1  p0 )  20
n
X   X i  Bin (n, p)
Si sfrutta la statistica
i 1
Obiettivo: dato
p0
testare l’ipotesi
H 0 : p  p0
H 1 : p  p0
Si estrae il campione casuale X 1 , X 2 ,, X n
(di taglia n)
Si calcola x numero di successi ottenuti nel campione di taglia n
sfruttando la distribuzione di X sotto l’ipotesi nulla


pvalue  2 min Pp0 ( X  x), Pp0 ( X  x)
Eq. (8.6.4) del libro
p 
accetto H0
p 
rifiuto H0
39
Caso a)
np0 (1  p0 )  20
n
X   X i  Bin (n, p)
Si sfrutta la statistica
i 1
Obiettivo: dato
p0
testare l’ipotesi
H 0 : p  p0
H 1 : p  p0
Si estrae il campione casuale X 1 , X 2 ,, X n
(di taglia n)
Si calcola x numero di successi ottenuti nel campione di taglia n
sfruttando la seguente disuguaglianza Pp  p ( X  x)  Pp ( X  x)
0
0
n i
    p0 (1  p0 ) n i
ix  i 
n
pvalue
Eq. (8.6.2) del libro
x
pvalue  
accetto H0
pvalue  
Rifiuto H0
40
Caso a)
np0 (1  p0 )  20
n
X   X i  Bin (n, p)
Si sfrutta la statistica
i 1
Obiettivo: dato
p0
testare l’ipotesi
H 0 : p  p0
H 1 : p  p0
Si estrae il campione casuale X 1 , X 2 ,, X n
(di taglia n)
Si calcola x numero di successi ottenuti nel campione di taglia n
sfruttando la seguente disuguaglianza Pp  p ( X  x)  Pp ( X  x)
0
0
n i
    p0 (1  p0 ) n i
i 0  i 
x
pvalue
x
pvalue  
accetto H0
pvalue  
rifiuto H0
Caso b)
np0 (1  p0 )  20
Si sfrutta la statistica
 z
X  np0
Z
 N (0,1)
np0 (1  p0 )
0
0
Test ad una coda
“left”
z
2
Test ad una coda
“right”
H 0 : p  p0
H 0 : p  p0
H 1 : p  p0
H 1 : p  p0
Regione rifiuto
Regione
accettazione
Z   z
Z   z
 z
Regione rifiuto
Z  z
Regione
accettazione
Z  z
0
z
2
Test a due code
H 0 : p  p0
H 1 : p  p0
Regione
rifiuto
Z   z Z  z
2
2
Regione
 z  Z  z
accettazione 2
2
42
Esempio: moneta truccata? (continua)
H0 :
p
1
2
H1 :
p
1
2
Test a due code
Sono stati effettuati n=100 lanci
Totale 40
le condizioni di applicabilità
11
n  25  20 sono valide, pertanto si può
22
utilizzare la seguente
statistica test
Totale 60
Z
Con i dati osservati si ha
Z
pˆ  0.4
  0.05
z


0.4  0.5
 2
0.51  0.5
100
Pˆ  p0
p0 1  p0 
n
L’ipotesi nulla è rifiutata
 1.96
2
-1.96
01.96
43
Esempio 4
Un’azienda farmaceutica dichiara che il suo farmaco è efficace in più del 90%
dei casi. In un campione di 30 persone che lo hanno utilizzato si è rilevato
efficace in 25 casi. Stabilire se l’affermazione può considerarsi legittima con
livello di significatività del 0.01
H0 :
p  0.90
Test ad una coda
H1 :
p  0.90
E’ stata verificata l’efficacia su n=30 individui
Lo z.test non può essere utilizzato!!
(se lo utilizzassimo i risultati non
sarebbero attendibili)
Test “esatto” per p
di bernulli
np(1-p)=30*0.9*0.1=2.7
La condizione di
applicabilità non è
verificata,
Aumentare la numerosità del
campione fino a soddisfare le ipotesi
(per p=0.9n>223)
44
Esempio 4 (continuazione)
Un’azienda farmaceutica dichiara che il suo farmaco è efficace in più del 90%
dei casi. In un campione di 30 persone che lo hanno utilizzato si è rilevato
efficace in 25 casi. Stabilire se l’affermazione può considerarsi legittima con
livello di significatività di 0.01
H0 :
p  0.90
H1 :
p  0.90
Test ad una coda …. vediamo se c’è evidenza
sperimentale dell’affermazione della ditta p>0.9
Valutiamo il p-dei-dati
 30  i
 PH 0 ( X  25)    0.9 (1  0.9 ) 30i  0.92
i  25  i 
30
pvalue
Essendo il p-dei-dati una misura di plausibilità dell’ipotesi
nulla. Un p-value di 0.92 non ci autorizza a rifiutare
l’ipotesi nulla a nessun livello di significatività plausibile.
I DATI NON LEGITTIMANO L’AFFERMAZIONE DELLA DITTA
45
Esempio 4 (continuazione)
Nello stesso esempio del caso precedente, ma con un campione di 300 persone
(che hanno utilizzato il farmaco) di cui in 250 casi si è rilevato efficace.
H0 :
p  0.90
Test ad una coda
H1 : p  0.90
E’ stata verificata l’efficacia su n=300 individui
n*p*(1-p)=27
le condizioni di applicabilità sono valide
pˆ 
250
 0.8333
300
Z
0.833  0.9
 - 3.8509
0.91  0.1
300
z0, 01  2.326
- 3.8509
2.326
Il valore critico è si su
una coda, ma su
quella “sbagliata”
L’ipotesi nulla è
accettata (i.e, non si
può rifiutare)
46
Conclusioni
Come nel caso della stima dei parametri, anche nel caso dei test di ipotesi, per
trarre conclusioni su un parametro caratterizzante una popolazione ci basiamo
sui risultati ottenuti su un singolo campione.
I singoli risultati che si ottengono dipendono dal campione estratto
pertanto sono variabili casuali. L’interpretazione viene fatta su basi
probabilistiche. Di conseguenza non sempre si giungerà a delle conclusioni
corrette, ad esempio non è garantito che la decisione presa sul se accettare
l’ipotesi nulla o se rifiutarla in favore dell’alternativa sia corretta. Si possono
verificare infatti due tipi di errori (errore di primo tipo,. i.e, rifiutare l’ipotesi
nulla quando questa è vera; ed errore di secondo tipo, i.e. accettare l’ipotesi
nulla quando questa è falsa).
La logica del test di ipotesi considerata controlla solo l’errore di primo tipo.
Il rischio pratico è quello di “scaricare” questa scelta sull’errore di secondo tipo,
cioè non essere in grado di individuare delle differenze presenti dei dati.
In questo senso occorre ricordare che: accettare l’ipotesi nulla non significa
che questa sia vera.
47
Esercizio da fare da soli…..
Una compagnia di assicurazioni vuole valutare l’entità media delle richieste di risarcimento
danni per incidenti automobilistici. Un’indagine svolta su di un campione di 25 richieste
ha dato i seguenti risultati (con X si indica la variabile “richiesta di risarcimento in migliaia
di euro”)
25
 xi  112.12
i 1
25
2
x
 i  629.89
i 1
Ipotizzando che X abbia distribuzione gaussiana:
a) Stimare l’entità media delle richiesta e la varianza delle richieste di risarcimento,
giustificando la scelta degli stimatori usati;
b) calcolare l’intervallo di confidenza al 95% per la richiesta media di risarcimento,
commentando i passaggi;
c)saggiare, ad un livello di significatività   0.05 , l’ipotesi
l’alternativa H1 :   3
, commentando i passaggi. ;
(nota che dalla tavola A.3 ho
H0 :  3
t0.025, 24  2.064 t0.05, 24  1.711
contro
)
48