Cinematica2_7_14_nov13

28
Il moto nel piano: coordinate cartesiane e coordinate polari
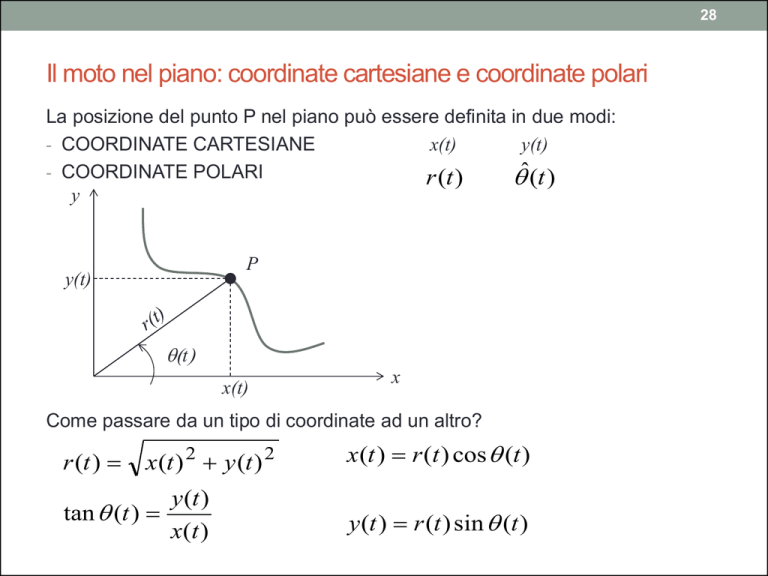
La posizione del punto P nel piano può essere definita in due modi:
- COORDINATE CARTESIANE
x(t)
y(t)
- COORDINATE POLARI
r (t )
ˆ(t )
y
P
y(t)
(t)
x(t)
x
Come passare da un tipo di coordinate ad un altro?
r (t ) 
x(t ) 2  y (t ) 2
tan  (t ) 
y (t )
x(t )
x(t )  r (t ) cos  (t )
y (t )  r (t ) sin  (t )
29
Il moto nel piano: coordinate cartesiane e coordinate polari
La posizione del punto P nel piano può anche essere definita con il raggio
vettore. Mentre nei moti rettilinei abbiamo potuto trascurare la natura vettoriale
di spostamento velocità e accelerazione, nei moti sul piano, dobbiamo
considerare tali grandezze come vettori.

OP  r (t )
y



r (t )  r x (t )  r y (t )


 x(t ) u x  y (t ) u y
P
y(t)
ry
(t)
rx
x(t)
RAGGIO VETTORE
x
30
Il moto nel piano: spostamento e velocità
y
Spostamento:
P(t+Dt)
Dr
P(t)
y
Per Dt  0 dr diventa tangente alla
traiettoria e in modulo diventa pari allo
spostamento infinitesimo ds:


d r  ds uT
 ds 

v  uT  v uT
dt
P(t+Dt)
v
O



Dr d r

Velocità vettoriale: v  lim
dt
Dt 0 Dt
x
O



r (t  Dt )  r (t )  Dr
 

Dr  r (t  Dt )  r (t )
P(t)
x
Il vettore velocità individua con la sua
direzione e il suo verso la direzione e il
verso del moto e con il suo modulo
individua la velocità istantanea con cui è
percorsa la traiettoria
31
Il moto nel piano: componenti della velocità
y
Componenti cartesiane
Poiché
P(t)
vy
O



r  x ux  y u y

 dr dx 


dy 
v

u x  u y  vxu x  v yu y
dt dt
dt
vx
v
x
vx e vy sono le componenti cartesiane della
velocità del punto P.
vx e vy dipendono dalla posizione degli
assi.
v  v x2  v 2y
32
Il moto nel piano: componenti della velocità
v
v
vr

O
Componenti polari
  
dr 
d 
v  vr  v 
ur  r
u
dt
dt
vr e v sono le componenti polari radiale e trasversa. La
componente radiale dipende dalle variazioni del modulo del
raggio vettore; la componente trasversa dipende dalle
variazioni di direzione del raggio vettore.
33
Il moto nel piano: accelerazione
L’accelerazione nel moto piano esprime le variazioni di velocità in modulo e
in direzione: avrà perciò 2 componenti.
Nei moti rettilinei invece abbiamo visto che essa ha un’unica
componente perchè la direzione non cambia.
aT


2
 dr
essendo v 
dt
Si ricava che:
 dv
d r
a

dt
dt 2
aN
 

dv 
v2 
a  aT  a N 
uT 
uN
dt
R
La prima componente è parallela alla velocità e prende il nome di
accelerazione tangenziale, la seconda componente dipende dalla
variazione della direzione della velocità ed è ortogonale a questa; essa
prende il nome di accelerazione normale o centripeta.
a
34
Il moto nel piano: componenti dell’accelerazione nei diversi moti
Vediamo quali sono le componenti
•
•
•
•
Moto rettilineo uniforme
Moto rettilineo uniformemente accelerato
Moto curvilineo
Moto curvilineo uniforme
aN = 0
aN = 0
aN ≠ 0
aN ≠ 0
aT = 0
aT ≠ 0
aT ≠ 0
aT = 0
 

dv 
v2 
a  aT  a N 
uT 
uN
dt
R
aT
aN
a
35
Composizione di due moti rettilinei
Consideriamo una pallina che rotola su un piano con velocità costante. Quando
il piano del tavolo finisce la pallina comincia a cadere a terra.
Vogliamo determinare con quale velocità toccherà terra e a quale distanza
rispetto al limite del tavolo la pallina toccherà terra.
vx
36
Composizione di due moti rettilinei
Consideriamo una pallina che rotola su un piano con velocità costante. Quando
il piano del tavolo finisce la pallina comincia a cadere a terra.
Vogliamo determinare con quale velocità toccherà terra e a quale distanza
rispetto al limite del tavolo la pallina toccherà terra.
y
vx
y0
0
xf
x
37
Composizione di due moti rettilinei: tempo di caduta
Se la pallina, da ferma, cadesse dall’altezza del tavolo, essendo la sua
accelerazione costante e pari a g e il moto avverrebbe lungo un’unica direzione,
quella verticale (asse y) in modo uniformemente accelerato.
y
Il tempo che essa
impiegherebbe per cadere
sarebbe dato da:
2 y0
t
g
vx
y0
0
xf
x
38
Composizione di due moti rettilinei: velocità durante la caduta
Tuttavia la pallina non cade da ferma, bensì ha una componente di velocità
lungo l’asse orizzontale (asse x). Questo fa sì che le due velocità (orizzontale e
verticale) debbano essere composte per poter individuare la velocità finale
(direzione, verso e modulo) .
La velocità con cui si
y
muove la pallina dopo aver
lasciato il tavolo è:
  
v  vx  v y
In modulo:
vx
vy
y0
0
2
v
xf
 Ds 
2
v     (gt ) 2
 Dt 
x
Quindi la velocità varia al variare del tempo.
39
Composizione di due moti rettilinei: spostamento massimo
La distanza dal limite del tavolo in cui la pallina toccherà terrà è la componente
orizzontale dello spostamento che sarà determinata a partire dalla componente
orizzontale della velocità e del tempo impiegato durante la caduta:
y
x f  x0  v x t  x0  v x
vx
y0
0
xf
x
2 y0
g
40
Moto circolare
È un moto la cui traiettoria è rappresentata da una circonferenza. Si dice che il
moto è uniforme se la velocità con cui il punto si sposta lungo la circonferenza è
costante in modulo (ma non in direzione e verso) e l’accelerazione tangenziale è
nulla, per cui avrò solo la componente centripeta.
L’equazione oraria del moto può essere scritta in coordinate curvilinee o in
coordinate polari.
y
P
R

x
41
Moto circolare: velocità
Geometricamente l’arco di circonferenza percorso è: ds  R d
Il vettore velocità è tangente alla traiettoria e il suo modulo è pari alla velocità
istantanea.
Poiché la velocità istantanea è: v = ds/dt
d
Allora v 
R  wR dove w è la velocità angolare; esprime il rapporto tra
dt
l’angolo descritto dal punto in movimento e il tempo impiegato per descriverlo.
y
d ds 1 1 ds v
w



dt
R dt R dt R
v
P
w
v  wR
R
R
s

x
42
Moto circolare: accelerazione
Il vettore accelerazione è composto dai due vettori uno tangente alla traiettoria e
uno normale alla traiettoria.
La componente normale alla traiettoria dipende dalla velocità istantanea con cui
viene percorsa la traiettoria e dalla sua curvatura (R).
 
v2 
v2
a  aN 
uN
in modulo a N 
 w2R
R
R
y
P
R

s
x
x
43
Moto circolare: accelerazione angolare
Se il moto è circolare ma non uniforme:
2
 

dv 
v 
a  aT  a N 
uT 
uN
dt
R
Possiamo definire una grandezza nuova che è l’accelerazione angolare:
dw 1 dv aT


dt
R dt
R
aT   R

v2
aN 
 w2R
R
Da cui l’accelerazione vettoriale può essere scritta come:
 


2 
a  aT  a N  ( R )uT  (w R )u N
44
Moto circolare uniforme: equazione oraria
L’equazione oraria del moto può essere scritta in coordinate curvilinee o in
coordinate polari.
coordinate curvilinee: s (t )  s0  v (t  t 0 )
coordinate polari:
y
P
R

x
 (t )   0  w (t  t 0 )
Il moto circolare è un moto periodico perciò
il punto ripassa nelle stesse posizioni ad
intervalli di tempo fissi.
Si definisce PERIODO l’intervallo di tempo
impiegato dal punto per coprire una
circonferenza; si definisce FREQUENZA il
numero di giri compiuti in un intervallo di
tempo unitario.
P
2R 2

v
w
f 
v
w

2R 2
45
Moto circolare uniforme: coordinate del punto in movimento
La posizione del punto in funzione del tempo può essere determinata se sono note
le coordinate del punto al passare del tempo:
x(t )  R cos  (t )
y (t )  R sen (t )
ma  (t )   0  w (t  t 0 ) quindi
y
P
R
0
x
x(t )  R cos( 0  wt )
y (t )  R sen( 0  wt )
46
Moto parabolico
Analizziamo ora il moto nel vuoto di un punto P lanciato dall’origine O con
velocità iniziale v0 formante un angolo  con l’asse orizzontale, x.
Vogliamo determinare:
1) Traiettoria
2) Posizione G in cui il punto ricade sull’asse x (GITTATA)
3) Massima altezza raggiunta
Nel punto in O:
Accelerazione a = g = -g uy
Posizione: r = 0
Velocità: v = v0
Istante iniziale: t0 = 0 s
v0
O
G
47
Moto parabolico: velocità
Il moto avviene nel piano individuato dai vettori g e v. Entrambi i vettori
possono essere quindi scomposti secondo gli assi cartesiani x e y.
Il moto è soggetto alla componente tangenziale dell’accelerazione
gravitazionale che ne fa decelerare il moto prima che il punto raggiunga la
massima altezza e fa accelerare il moto subito dopo.
La velocità è dunque esprimibile secondo la relazione:
t









v (t )  v0  a (t ) dt  v0  gt u y
v (t )  v0 cos  u x  v0sen u y  gt u y 


0



v
cos

u

(
v
sen


gt
)
u
0
x
0
y
v0  v0 cos  u x  v0sen u y

y
T
v0
O
-guT

-guy
guT
-guy
G
x
48
Moto parabolico: spostamento
Possiamo scrivere le leggi orarie dei moti proiettati:
x(t )  v0 cos  t (1)
y (t )  v0 sen t 
1 2
gt (2)
2
Se per diversi istanti di tempo andiamo a tracciare le posizioni così calcolate
sul diagramma cartesiano, otteniamo la traiettoria del punto e vediamo che
essa è una parabola. Possiamo anche determinarlo matematicamente
ricavando il tempo dall’equazione 1 e sostituendolo nell’equazione 2.
0.6
Si ottiene:
y (t )  x tan  
g
2v02 cos 2 
y
x2
0.4
0.2
0
0
2
4
x
6
8
49
Moto parabolico: gittata
Calcoliamo ora la gittata ossia la distanza da O in cui il punto tocca l’asse delle
x. In questo punto la coordinata y della posizione è nulla. Pertanto dobbiamo
porre y(x) = 0.
y 0.6
y ( x)  x tan  
g
2v02 cos 2 
x2  0
Abbiamo due soluzioni: per x=0 e per :
2v02 cos 2  tan 
xG 
 2 xM
g
0.4
0.2
0
0
2
xM
4
Da cui ricaviamo che l’altezza massima raggiunta è:
yM
v02 sen 2

2g
N.B. Si calcola che l’angolo di lancio per il quale la gittata è massima è un
angolo di 45° (/4)
6
x
8