Esercizio 1
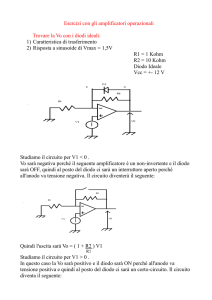
Nel circuito in figura, si consideri
l’Opamp ideale, mentre il diodo D è
descritto dal modello a soglia nulla.
Si determini la caratteristica di
ingresso-uscita Vo=Vo(Vi).
Esercizio 2
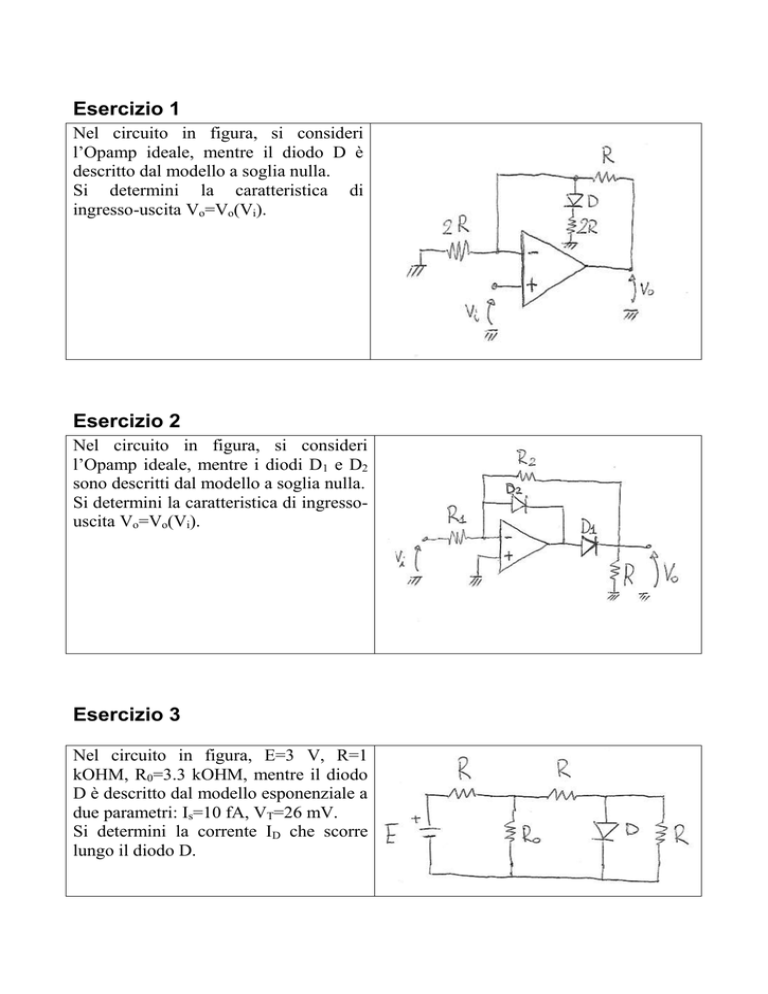
Nel circuito in figura, si consideri
l’Opamp ideale, mentre i diodi D1 e D2
sono descritti dal modello a soglia nulla.
Si determini la caratteristica di ingressouscita Vo=Vo(Vi).
Esercizio 3
Nel circuito in figura, E=3 V, R=1
kOHM, R0=3.3 kOHM, mentre il diodo
D è descritto dal modello esponenziale a
due parametri: Is=10 fA, VT=26 mV.
Si determini la corrente ID che scorre
lungo il diodo D.
Esercizio 4
Nel circuito in figura l’Opamp è NON
ideale. L’unica non idealità è
rappresentata dalla tensione di offset
Voff=3 mV.
Siano RA=100 kOHM, R=100 OHM,
R1=1 kOHM, R2=22 kOHM.
Si determini:
1. la caratteristica di ingresso-uscita
Vo=Vo(Vi) quando VA=0 V.
2. il valore di VA che annulla
l’effetto di Voff sulla tensione di
uscita Vo
3. la caratteristica di ingresso-uscita
Vo=Vo(Vi) quando VA assume il
valore calcolato al punto 2.
Esercizio 5
Con riferimento al circuito in figura,
considerando l’Opamp ideale, si
determini:
1. L’espressione simbolica del
guadagno di tensione Av(j),
nel dominio dei fasori
2. con i valori numerici R=140
kOHM, R0=10 kOHM, c=15 pF,
calcolare la risposta Vo(t)
all’ingresso:
Vi(t)=0.2+0.5cos(105 t)
Esercizio 6
Con riferimento al circuito in figura, si
consideri l’Opamp ideale con VM=5V,
e i seguenti valori numerici R2=10
kOHM, R1=90 kOHM e C1=1 nF.
Se Vi è un ingresso sinusoidale con
ampiezza 1V:
1. Calcolare la minima frequenza
utilizzabile per Vi
affinché
l’Opamp
non
entri
in
saturazione
2. Descrivere il procedimento
usato per rispondere alla
domanda precedente.