Università degli Studi di Salerno
Facoltà dii Scienze Matematiche, Fisiche e Naturali
N
Corso di Laurea in Fisica
TESI DI LAUREA
Diagramma colore-magnitudine
colore magnitudine
dell’ammasso aperto NGC 6633
Relatore
Candidato
Prof. Valerio Bozza
Giuseppina Lotano
Matr. 552//000013
Correlatore
Prof. Giuseppe Grella
Anno Accademico 2011/12
Indice
Indice
Introduzione
1
1.
La classificazione stellare e i diagrammi H-R ....................... 1
1.1 La classificazione stellare e la sequenza di Harvard ............... 3
1.2 Interpretazione fisica degli spettri stellari: la metallicità......... 7
1.3 Il diagramma Hertzsprung-Russell ...................................... 8
1.4 Il sistema M-K.................................................................. 11
1.5 Luminosità e colore come funzione della classe spettrale e
il ruolo degli ammassi ....................................................... 12
2.
Gli ammassi stellari
13
2.1 Formazione e caratteri generali di un ammasso .................... 13
2.2 Diagrammi H-R di un ammasso .......................................... 16
2.2.1 Evoluzione di un ammasso aperto e la gap di
Hertzsprung ............................................................ 16
2.2.2 Il punto di turn-off di un ammasso aperto................... 18
2.2.3 Confronto tra gli ammassi aperti e gli ammassi
Globulari................................................................. 21
2.3 Stima dell’età di un ammasso aperto .................................. 23
2.4 Ammassi aperti o galattici: descrizione e classificazione ........ 24
3.
L’ammasso NGC 6633
26
3.1 L’ammasso aperto NGC 6633 ............................................. 26
3.2 Fotometria: il cielo notturno e gli effetti del seeing ............... 27
3.2.1 Il cielo notturno ....................................................... 28
3.2.2 Effetti del seeing ..................................................... 29
3.3 Fotometria: aspetti pratici ................................................. 30
3.4 Rivelatori CCD .................................................................. 32
3.5 Lo studio sperimentale di NGC 6633 ................................... 33
3.5.1 La strumentazione dell’Osservatorio ........................... 33
3.5.2 Fasi del lavoro sperimentale ...................................... 34
3.5.3 Acquisizione dati...................................................... 34
3.5.4 Analisi dati .............................................................. 38
3.6 L’articolo di Jeffries, Totten, Harmer e Deliyannis ................. 41
3.7 Conclusioni ...................................................................... 44
Appendice
45
A1 La magnitudine ...................................................................... 45
A2 Il colore ................................................................................ 46
Bibliografia
Ringraziamenti
48
49
I
Introduzione
Introduzione
La nostra Galassia contiene numerosi agglomerati di stelle. Tra questi, gli
ammassi aperti giocano un ruolo fondamentale nella comprensione
dell’Universo. La formazione stellare è un processo costante che
caratterizza tali oggetti stellari ed è, di conseguenza, determinante
l’apporto che forniscono alla teoria dell’evoluzione stellare. Inoltre, il loro
studio è essenziale per la determinazione delle luminosità di alcuni tipi
spettrali, poiché in essi si trovano stelle la cui luminosità può essere
calibrata localmente. La distribuzione spaziale degli ammassi fornisce
anche informazioni importanti sulla struttura del disco Galattico.
Determinare le temperature effettive di ogni stella di un ammasso
tramite un’analisi degli spettri stellari è piuttosto complicato. Risulta più
semplice ottenere i loro indici di colore (B-V), tramite i quali si costruisce
un diagramma colore-magnitudine. Tali diagrammi permettono di testare
molti aspetti della teoria dell’evoluzione stellare. Stimando, infatti, le
tracce evolutive di stelle di masse diverse, con la stessa composizione
chimica dell’ammasso, è possibile rappresentare la posizione di ogni
campione sul diagramma H-R quando i modelli raggiungono l’età
dell’ammasso. Si hanno così informazioni importanti sulle scale dei tempi
relative all’evoluzione stellare.
Il lavoro sperimentale che abbiamo effettuato ha preso in esame
l’ammasso aperto NGC 6633. L’acquisizione di immagini in filtro V e in
filtro B delle stelle, effettuata tramite il telescopio del Dipartimento di
Fisica dell’Università di Salerno, e la loro successiva elaborazione, ci ha
permesso di ottenere un diagramma colore-magnitudine dell’ammasso.
La tesi segue un approccio lineare, tipico del metodo scientifico, e
presenta uno schema ben definito.
Si parte, nel capitolo 1, con argomenti prettamente teorici e generali.
L’introduzione della classificazione stellare tramite la ben nota sequenza
spettrale di Harvard e l’interpretazione fisica degli spettri permettono di
avere un quadro chiaro dei parametri essenziali per lo studio delle stelle.
Agli spettri sono direttamente collegati la luminosità e il colore di una
stella, come si vede dai diagrammi Hertzsprung-Russell e dai diagrammi
colore-magnitudine.
1
Introduzione
Il capitolo 2 entra nel merito dell’argomento trattato. Gli ammassi stellari
sono descritti nei loro caratteri generali. Si spiega in modo dettagliato la
classificazione e l’evoluzione nel tempo, sottolineando la straordinaria
importanza nel campo dell’astrofisica di tali oggetti celesti. Fondamentali,
a tale scopo, risulteranno essere il diagramma colore-magnitudine e i
concetti legati alla gap di Hertzsprung, al punto di turn-off e all’isocrona
di un ammasso. Essenziale è anche il confronto con gli ammassi
globulari.
Infine, il capitolo 3 descrive la parte sperimentale del lavoro, ovvero la
fase più importante e dinamica. Gli aspetti peculiari della fotometria e i
problemi annessi sono affrontati nei primi paragrafi e ci portano
direttamente nel vivo dello studio effettuato. Le fasi che ci hanno visti
impegnati sono state molteplici e tipiche del lavoro scientifico.
L’acquisizione e l’analisi dei dati in primis ne sono stati il punto
fondamentale. I metodi e i risultati sono riportati in modo dettagliato.
A seguire il confronto con i risultati di uno studio analogo, riportati in un
articolo di Jeffries et al (“Membership, metallicity and lithium abundances
for solar-type stars in NGC 6633”), ci ha permesso di tirare le somme
dell’intero lavoro, portandoci alle conclusioni.
2
Capitolo 1 La classificazione stellare e i diagrammi H-R
1.1 La classificazione stellare e la sequenza di Harvard
Capitolo 1
La classificazione stellare e i diagrammi H-R
1.1
La classificazione stellare e la sequenza di Harvard
Quando parliamo di una stella, siamo interessati a sapere di quale tipo si
tratti, ovvero se è giovane o vecchia, se è rossa o blu, se emette nella
banda dell’infrarosso o dei raggi X e così via. Per ottenere una risposta a
domande di questo tipo, è necessario confrontare la stella in questione
con altre ben note: si raggruppano le stelle in classi, in base alle
proprietà osservate ed, in tal modo, si ottengono le relazioni richieste. E’
dunque necessario avere schemi di classificazione opportuni.
Le osservazioni stellari necessitano, essenzialmente, di due funzioni: lo
spettro, ovvero l’intensità di radiazione in funzione della lunghezza
d’onda, e la sua curva di luce, ovvero l’intensità di radiazione in funzione
del tempo. In realtà, la maggior parte delle stelle ha curve di luce
piuttosto costanti che non forniscono informazioni rilevanti (eccezioni
sono date da tutte le classi di stelle variabili e dalle pulsars, che
presentano variazioni evidenti di luminosità nel tempo); di conseguenza
gli spettri restano essenziali per le classificazioni stellari.
Ci sono due modi per ottenere informazioni di natura astrofisica dagli
spettri:
•
•
L’analisi spettrale
La classificazione spettrale
Per quanto riguarda l’analisi spettrale, dobbiamo ricordare che, quando
esaminiamo la luce emessa da una stella attraverso uno spettrografo,
osserviamo un continuo brillante di radiazione sul quale si sovrappongono
linee di assorbimento (e, occasionalmente, linee di emissione). La
distribuzione di energia nel continuo e il profilo delle linee sono
determinate dalle condizioni fisiche nell’atmosfera stellare, quali la
temperatura, la densità, l’abbondanza degli elementi chimici, il campo
magnetico e così via. Quindi, da un’opportuna analisi di questi caratteri,
possiamo ricavare un dettagliato quadro fisico della struttura e della
composizione degli strati esterni di una stella. In modo sintetico, i dati
essenziali necessari per un’analisi spettrale sono la descrizione della
variazione di frequenza del continuo (ottenuta tramite gli indici di colore)
e la descrizione del profilo delle linee (ottenuta tramite la determinazione
dello spessore equivalente di ogni linea).
3
Capitolo 1 La classificazione stellare e i diagrammi H-R
1.1 La classificazione stellare e la sequenza di Harvard
Per quanto riguarda la classificazione spettrale, si tratta
sostanzialmente di raggruppare spettri che hanno strutture simili tra loro,
senza considerarne, in prima istanza, il significato fisico. In principio, si
potrebbe utilizzare l’intero spettro, ma in pratica se ne considera solo
quella parte trasmessa attraverso l’atmosfera terrestre.
Si definiscono delle categorie scegliendo le stelle standard con
caratteristiche spettrali ben definite e distinte tra loro. Di conseguenza,
ogni categoria avrà uno spettro caratteristico determinato dalla stella
standard che lo definisce e, dunque, un unico tipo spettrale del sistema in
questione. E’ possibile classificare ogni stella rispetto ai campioni
ottenuti, confrontando il suo spettro con le stelle standard. Riusciamo, in
definitiva, ad ottenere un opportuno schema di classificazione che ci
assicuri la catalogazione richiesta. Una volta che il sistema sia stato ben
definito, si può introdurre una calibrazione in termini di parametri fisici,
quali temperatura, composizione e così via. A quel punto, si può dire che,
se qualche stella è di un certo tipo spettrale, le proprietà relative a quel
determinato tipo possono essere associate ad essa senza ulteriori analisi.
Dunque il tipo spettrale fornisce una descrizione concisa sia dello spettro
sia delle proprietà fisiche di una stella. Nel 1817 Joseph Fraunhofer notò
che stelle diverse avevano spettri differenti tra loro e li classificò in base
ad uno schema. A seguire, nel 1860, Secchi, Huggins e Vogel divisero le
stelle in quattro classi spettrali. Il primo grande passo verso il sistema
attuale avvenne all’Osservatorio di Harvard, nel 1890: sotto la direzione
di Pickering, Williamina Fleming pubblicò un catalogo di 10000 stelle
divise in tipi spettrali, denotati dalle lettere maiuscole dell’alfabeto A, B,
C e così via, in base allo spessore delle linee di assorbimento
dell’idrogeno.
Qualche anno dopo, un’altra assistente di Pickering, Annie Jump Cannon,
perfezionò il sistema inserendo nuove lettere e la suddivisione decimale
dei tipi spettrali. Riuscì, in questo modo, a catalogare 225000 stelle e tali
classificazioni furono pubblicate sotto il nome di Henry Draper Catalog.
Tenendo conto degli stati di ionizzazione degli elementi chimici visibili
tramite lo spessore delle righe e dei dati fotometrici, la sequenza
spettrale
definitiva
di Harvard,
O,B,A,F,G,K,M,
risultò
essere
sostanzialmente una sequenza di temperatura decrescente, dalle stelle
blu molto calde di tipo spettrale O a quelle più fredde di tipo M.
4
Capitolo 1 La classificazione stellare e i diagrammi H-R
1.1 La classificazione stellare e la sequenza di Harvard
In seguito, a tale sequenza, vennero aggiunte le lettere R, N ed S per
tener conto di stelle di differente composizione chimica.
L’ulteriore suddivisione numerica prevista per ogni lettera divide gli
spettri con cifre da 0 a 9 (ad esempio A0…A9), seguendo sempre la
sequenza di temperatura decrescente. Le stelle che cadono all’inizio della
sequenza sono dette di tipo “early”, quelle che cadono alla fine di tipo
“late”.
La classificazione spettrale di Harvard era basata sulla temperatura, ma
non aveva basi fisiche consistenti. Furono l’avvento della meccanica
quantistica e della teoria di ionizzazione di M.Saha nel 1920 a rendere
possibile un’analisi quantitativa; nel 1925 Cecilia Payne nel suo libro
Stellar Atmosphere fornì finalmente un’interpretazione teorica della
sequenza di Harvard e scoprì il ruolo determinante dell’idrogeno
nell’Universo.
Sappiamo che le linee di assorbimento si hanno quando un atomo
assorbe un fotone con l’energia necessaria affinché un elettrone compia
una transizione da un’orbita interna ad una più esterna. Viceversa, le
linee di emissione si hanno nel processo inverso, quando un elettrone
compie una transizione da un’orbita esterna ad una interna e un fotone
trasporta l’energia persa dall’elettrone. Di conseguenza, la lunghezza
d’onda del fotone dipende dall’energia degli orbitali coinvolti nelle
transizioni. Per ottenere una spiegazione fisica, bisogna ricorrere alla
meccanica statistica per sapere in quali orbitali si possano trovare con
maggiore probabilità gli elettroni e quale sia il numero di atomi nei vari
stati di ionizzazione.
In definitiva, la distinzione tra gli spettri di stelle con diverse temperature
è dovuta agli elettroni che occupano i diversi orbitali atomici
nell’atmosfera stellare. Può essere piuttosto complicato interpretare i
dettagli riguardanti la formazione delle righe spettrali, poiché gli elettroni
possono essere in uno qualsiasi degli orbitali e in un qualsiasi stato di
ionizzazione, denotato da un numero romano che segue l’elemento in
questione. Ad esempio, HI e He I indicano, rispettivamente, l’idrogeno e
l’elio neutro; He II indica l’elio ionizzato una sola volta e così via. La
classificazione di Harvard definitiva ottenuta da Cannon è riportata in
Tabella 1, in cui sono descritti i caratteri principali che definiscono i vari
tipi spettrali.
5
Capitolo 1 La classificazione stellare e i diagrammi H-R
1.1 La classificazione stellare e la sequenza di Harvard
Tipo spettro
Descrizione
Temperatura
superficiale
Esempi
O
Stelle molto calde blubianche con poche
linee: forti linee di
assorbimento di He I e
He II
Stelle molto calde da
bianco- blu(B0) a
bianche (B9). Niente
righe di emissione, ma
righe di assorbimento
dominanti
dell’idrogeno e dell’elio
Stelle bianche: spettri
dominanti dalle righe
dell’idrogeno. Le linee
di assorbimento di Ca II
diventano più intense
Stelle giallo-bianche. Le
linee del Ca II si
rafforzano, mentre
quelle di Balmer
diventano più deboli.
Linee di assorbimento
di metalli neutri (Fe I,
Cr I)
Stelle gialle. Spettri di
tipo solare. Le linee di
Ca II diventano più
forti. Le linee di Fe I e
di altri metalli più
neutri diventano più
forti.
Stelle arancioni fredde.
Le linee del Ca II, H e K
diventano più forti a
K0, diventando più
deboli a seguire. Spettri
dominati da linee di
assorbimento
metalliche
Stelle rosse molto
fredde rosso-arancioni.
Spettri dominati da
bande di assorbimento
molecolari, specie
dell’ossido di titanio
(TiO)
Da 40000 °C a 35000
°C
γ Velorum
ξ Puppis
Da 25000 °C per B0 fino
a 12000 °C per B9
Rigel
8000 °C - 10000 °C
Sirio, Vega, Altair
B
A
F
G
K
M
Procione, Polare
6000 °C – 7500 °C
5000 °C - 6000 °C
Capella (gigante)
Sole (nana)
3500 °C – 5000 °C
Arturo, Aldebaran,
Polluce
3000 °C – 3400 °C
Mira Ceti, Betelgeuse,
Antares, Proxima
Centauri
Tabella 1: Classificazione spettrale di Harvard
6
Capitolo 1 La classificazione stellare e i diagrammi H-R
1.2 Interpretazione fisica degli spettri stellari: la metallicità.
1.2
Interpretazione fisica degli spettri stellari: la metallicità.
La struttura di un’atmosfera stellare, e quindi la distribuzione di energia
emessa da una stella, è determinata da tre parametri atmosferici:
1) la temperatura effettiva
≡
(1.1)
dove σ è la costante di Stefan-Boltzmann, L la luminosità totale e R
il raggio della stella. Teff è una misura della temperatura del gas che
forma la maggior parte dell’atmosfera stellare.
2) la gravità di superficie
≡
(1.2)
dove G è la costante gravitazionale e M la massa stellare. La gravità
superficiale fissa il gradiente di pressione nell’atmosfera e determina la
densità delle linee spettrali formate.
3) la composizione chimica dell’atmosfera che determina la variazione
in frequenza dell’opacità del materiale stellare e il relativo spessore delle
linee spettrali delle differenti specie atomiche presenti. In prima
approssimazione, la composizione chimica di una stella vicina al Sole può
essere caratterizzata dall’abbondanza degli elementi pesanti calcolati
rispetto all’idrogeno. L’elemento più importante è il Fe, poiché le stelle
che presentano un’abbondanza di Fe tendono ad essere più ricche di
elementi più pesanti dell’elio. Nel tener conto di questo fenomeno si parla
di metallicità di una stella per indicarne la composizione chimica
completa. Le abbondanze dei vari elementi presenti in una stella sono
riportate generalmente rispetto ai valori solari. Ad esempio, l’abbondanza
di ferro, denotata [Fe/H], è definita come:
/
≡
( )
( ) !" ##$
−
( )
( ) &'#
(1.3)
In modo simile, l’abbondanza di un elemento diverso dal ferro, espresso
come [O/Fe], si definisce come:
(/
≡
())
( ) !" ##$
−
())
) &'#
(1.4)
In generale
-3<[Fe/H]<0. I rapporti del tipo [O/Fe] coprono un
intervallo più ristretto, il che vuol dire che stelle povere di Fe sono
generalmente povere anche di altri metalli. Di conseguenza è utile
definire dei parametri (X,Y,Z), che danno la frazione relativa
all’abbondanza di idrogeno (X), elio (Y) e altri elementi chimici (Z).
7
Capitolo 1 La classificazione stellare e i diagrammi H-R
1.3 Il diagramma Hertzsprung-Russel
1.3
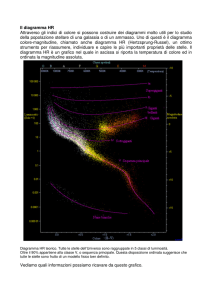
Il diagramma Hertzsprung-Russell
Sebbene le relazioni stellari che legano luminosità, temperatura, massa,
raggio, in pratica quelle relative ai parametri intrinseci di una stella,
forniscano un’idea di insieme dell’intervallo di variabilità delle
caratteristiche stellari, informazioni più significative si possono ottenere
esaminando la correlazione esistente tra tali grandezze. Ciò emerge dalla
costruzione di un diagramma, noto come “diagramma di HertzsprungRussell” o diagramma H-R. La sua origine risale agli studi effettuati nel
1910 da Ejnar Hertzsprung e Henry Norris Russell sulle relazioni tra le
magnitudini assolute e i tipi delle classi spettrali delle stelle osservabili. Il
diagramma H-R fornisce uno dei test più importanti per la teoria
dell’evoluzione stellare e per l’esplorazione della storia dell’intera
Galassia.
Nella sua forma originale, il diagramma H-R era un grafico della
magnitudine visuale assoluta e del tipo spettrale, ma attualmente si
utilizzano varianti in cui il tipo spettrale discreto è sostituito da una
coordinata continua. Dal punto di vista sperimentale, la forma più utile è
il diagramma colore-magnitudine (CM), che è un grafico di un colore
rispetto alla magnitudine assoluta (per stelle di distanza nota) o rispetto
alla magnitudine apparente (per stelle che sono tutte alla stessa
distanza). Dal punto di vista teorico, la forma più conveniente del
diagramma H-R è un grafico di Teff rispetto al log(L/L0), detto
diagramma H-R teorico. Ma quali furono i presupposti che portarono
alla nascita di tali diagrammi?
La sequenza di Harvard aveva portato allo sviluppo di una teoria
dell’evoluzione stellare fondamentalmente errata. Si osservò che le stelle
di tipo O alla fine della sequenza tendono ad essere più luminose e calde
di quelle di tipo M. Inoltre, la relazione massa-luminosità mostrava che le
stelle di tipo O sono più massive di quelle di tipo M. La conclusione fu
quella di pensare che le stelle, invecchiando, si raffreddano: una stella
nasce di tipo O, giovane e brillante e, invecchiando, perde parte della
propria massa a mano a mano che brucia il suo carburante; di
conseguenza si raffredda e diventa meno luminosa, fino a diventare una
stella rossa, vecchia. Ancora oggi una traccia di questa teoria rimane
nella denominazione di stelle di tipo “early” e “late”. In seguito a questa
teoria, Hertzsprung pensò che dovesse esserci una relazione tra la
magnitudine assoluta e la classe spettrale di una stella. Dopo l’analisi di
stelle i cui valori suddetti erano ben noti, confermò tale relazione ma
rimase sorpreso dalla scoperta che stelle di tipo G coprissero un intervallo
ampio di magnitudini nonostante fossero, appunto, della stessa classe
spettrale. Contemporaneamente Russell, in modo del tutto indipendente
8
Capitolo 1 La classificazione stellare e i diagrammi H-R
H
1. Il diagramma Hertzsprung-Russel
1.3
dal suo collega, arrivò alle stesse conclusioni e pubblicò i suoi risultati in
un diagramma, nel quale vi era la magnitudine assoluta sull’asse verticale
e la classe spettrale su quello orizzontale. A partire da questo, ne furono
furo
in seguito pubblicate altre versioni, fino ad arrivare al noto diagramma
H-R (magnitudine e classe spettrale) (figura 1) e alla
la versione in cui si
sostituisce l’indice di colore alla classe spettrale (figura 2).
Figura 1:: diagramma H-R
H R nella sua versione originale
Figura 2:
2 diagramma colore-magnitudine
La maggior parte delle
elle stelle rappresentate cade all’interno di una banda
obliqua che va dalle stelle di tipo O nella parte superiore sinistra fino a
quelle di tipo M nella parte inferiore destra. Questa banda è detta
SEQUENZA PRINCIPALE,
PRINCIPALE, nella quale cade circa l’80% di tutte le stelle.
9
Capitolo 1 La classificazione stellare e i diagrammi H-R
1.3 Il diagramma Hertzsprung-Russel
In alto a destra, fuori dalla sequenza principale, cadono stelle dette
GIGANTI, mentre in basso a sinistra ci sono le NANE BIANCHE.
Il passo più complesso per la costruzione di un diagramma come quello
appena descritto è la determinazione della distanza di ogni stella, al fine
di poter calcolare la magnitudine assoluta a partire da quella apparente.
La conoscenza del diagramma CM può essere migliorata dallo studio degli
AMMASSI STELLARI. La nostra Galassia contiene molti agglomerati di
stelle, che includono una grande varietà di tipi stellari. In generale, non
conosciamo la distanza di un ammasso, quindi non possiamo ottenere un
diagramma CM in cui compaia la magnitudine assoluta. C’è da dire, però,
che molti ammassi sono sufficientemente piccoli rispetto alla distanza che
ci separa da loro da poter ritenere valida l’assunzione che tutte le stelle
dell’ammasso siano alla stessa distanza dall’osservatore. Di conseguenza,
la differenza tra magnitudine assoluta e apparente sarà la stessa per ogni
stella, così, per un ammasso, il diagramma CM si ridurrà ad un grafico di
magnitudine apparente rispetto all’indice di colore. Infatti, come
vedremo, i caratteri di un diagramma CM di un ammasso tendono ad
essere più marcatamente definiti di quelli di un normale gruppo stellare.
L’assenza di errori dovuti alle indeterminazioni nelle distanze delle stelle
riduce la dispersione nelle sequenze stellari di un ammasso rispetto a
quello delle sequenze di stelle vicine. Inoltre, emerge il fatto che
l’omogeneità delle proprietà stellari di un ammasso permette la
rappresentazione in una regione piuttosto ristretta e definita del
diagramma CM.
10
Capitolo 1 La classificazione stellare e i diagrammi H-R
1.4 Il sistema M-K
1.4
Il sistema M-K
Con il lavoro di E. Hertzsprung e H.N. Russell, divenne evidente che stelle
di un dato tipo spettrale potevano avere luminosità molto differenti tra
loro e questo fatto implicava che esse potessero avere raggi e densità
atmosferiche differenti. Dunque è necessario introdurre un secondo
parametro per la descrizione completa di uno spettro. Un sistema a due
dimensioni, il sistema M-K, fu sviluppato da Morgan, Keenan e
Kellerman (1943). In aggiunta alla classe spettrale, assegnarono cinque
classi di luminosità, con numeri romani da I a V. In termini fisici, una
classe di luminosità stellare riflette la misura esterna della stella e la
densità atmosferica e si collega quindi alla sua gravità superficiale. Il
sistema di classificazione MK è quello attualmente usato. I tipi spettrali
del sistema MK sono essenzialmente quelli della sequenza di Harvard. Le
classi di luminosità sono riportate in Tabella 2.
Tipo
Descrizione
Ia–0
Ia
I ab
Ib
II
III
IV
V
Supergiganti estreme
Supergiganti luminose
Supergiganti moderate
Supergiganti meno luminose
Giganti brillanti
Giganti normali
Sub- giganti
Nane
Tabella 2: classi di luminosità
11
Capitolo 1 La classificazione stellare e i diagrammi H-R
1.5 Luminosità e colore come funzione della classe spettrale e il ruolo degli
ammassi
1.5 Luminosità e colore come funzione della classe spettrale e il
ruolo degli ammassi
Come già detto, la classe di luminosità MK è un’indicazione della
luminosità della stella. L’intervallo delle luminosità associate ad una data
classe varia con il tipo spettrale; dunque la classificazione spettrale MK è
necessaria per estrarre informazioni di luminosità dallo spettro di una
stella.
Figura 3: dipendenza combinata della luminosità e della classe spettrale
La figura 3 fornisce un’indicazione della dipendenza combinata della
luminosità dalla classe spettrale e dalla classe di luminosità: ad un dato
tipo spettrale, stelle di ogni classe di luminosità cadranno nell’intervallo
compreso tra una o due magnitudini sulla curva in figura. Dal momento
che il tipo spettrale MK è fortemente correlato con l’indice di colore B-V, e
la classe di luminosità MK è connessa con la luminosità, la classificazione
completa MK di una stella fornisce un’idea corretta della posizione della
stella sul diagramma colore-magnitudine.
Gli ammassi giocano un ruolo importante nella determinazione delle
luminosità di certi tipi spettrali, poiché in essi si trovano stelle la cui
luminosità può essere calibrata localmente (utilizzando la parallasse
trigonometrica) e anche stelle che non possono essere studiate vicino al
Sole. Dal momento che tutte le stelle in un dato ammasso sono alla
stessa distanza, la conoscenza della luminosità di una stella qualsiasi
nell’ammasso fornisce in linea di principio una buona stima della
luminosità delle altre stelle dell’ammasso.
12
Capitolo 2 Gli ammassi stellari
2.1 Formazione e caratteri generali di un ammasso
Capitolo 2
Gli ammassi stellari
2.1 Formazione e caratteri generali di un ammasso
La nostra Galassia contiene numerosi agglomerati di stelle. Lo studio
degli ammassi stellari (o cluster) ha giocato un ruolo determinante
nello sviluppo e nella comprensione dell’Universo. Gli ammassi
presentano numerose variazioni per quanto riguarda la compattezza della
loro struttura, la luminosità e la metallicità. Ne esistono due tipi:
•
•
Ammassi globulari: compatti, luminosi e poveri di metalli
Ammassi aperti: poco compatti, meno luminosi e più ricchi di
metalli
Figura 4: Ammasso globulare M80
Figura 5: Ammasso aperto delle Pleiadi
13
Capitolo 2 Gli ammassi stellari
2.1 Formazione e caratteri generali di un ammasso
Ma da quali tipi di stelle è composto un ammasso?
Le stelle nascono dal mezzo interstellare (polveri e gas); attraverso i
venti stellari gran parte del materiale torna al mezzo interstellare tramite
l’emissione di nebulose planetarie o tramite l’esplosione di supernovae.
La materia espulsa, comunque, si è arricchita di elementi più pesanti
tramite le reazioni nucleari che governano la vita di una stella. Di
conseguenza, quando si forma una nuova generazione di stelle, questa
possiede una concentrazione più alta di elementi pesanti rispetto alle sue
antenate. Questo processo ciclico di formazione stellare, morte e rinascita
è evidente nelle variazioni di composizione stellare.
E’ generalmente accreditata l’ipotesi che l’Universo si sia formato circa
13.5 miliardi di anni fa in seguito al Big Bang e che l’idrogeno e l’elio
siano stati essenzialmente gli unici elementi prodotti dalla nucleosintesi
avvenuta durante l’esplosione primordiale. Di conseguenza, le prime
stelle formate erano estremamente povere di metalli (con il termine
metalli si intendono tutti gli elementi più pesanti dell’elio). A seguire, le
successive generazioni stellari avevano concentrazioni sempre maggiori
di elementi più pesanti, fino ad arrivare a stelle ricche di metalli per le
quali Z ≈0.03. Le stelle povere di metalli sono dette di POPOLAZIONE
II e sono principalmente stelle rosse luminose vecchie in un ambiente
privo di gas e polveri. Le stelle più ricche di metalli sono dette di
POPOLAZIONE I: si tratta di giovani stelle blu luminose accompagnate
da polveri e gas.
Le classificazioni in POPOLAZIONI I E II sono dovute alle loro
identificazioni originarie con gruppi distinti dal punto di vista cinematico
nella nostra Galassia. Le stelle di Popolazione I hanno velocità rispetto al
Sole più basse di quelle di Popolazione II; inoltre le stelle di Popolazione I
si trovano principalmente nel disco della Via Lattea, mentre quelle di
Popolazione II sono sia sopra sia sotto il disco. Solo in seguito gli
astronomi hanno analizzato le differenti composizioni chimiche delle due
popolazioni, ricavandone informazioni preziose sulla formazione e
sull’evoluzione della Via Lattea.
Alcuni degli elementi pesanti trovati nelle stelle sono prodotti solamente
nelle esplosioni di supernova che sono lo stadio finale della vita di molte
stelle. Quindi, la presenza di questi elementi in una stella indica che la
stella debba contenere materiale sintetizzato dalle supernovae in una
generazione stellare precedente. La differenza tra le abbondanze di
metalli nelle due popolazioni stellari si riconduce ancora una volta ad una
differenza di età. Una stella che si è formata tardi nella storia di una
galassia sarà composta da materiale che è stato processato da
generazioni precedenti di stelle, ed avrà quindi generalmente grande
14
Capitolo 2 Gli ammassi stellari
2.1 Formazione e caratteri generali di un ammasso
abbondanza di metalli (stelle di popolazione I). Di contro, una stella che
si è formata molto prima sarà stata prodotta dal materiale le cui
abbondanze chimiche sono molto più vicine alla composizione primordiale
dell’Universo, con una percentuale molto bassa di metalli, e dunque la
stella apparterrà alla popolazione II.
Durante il collasso di una nube molecolare, si ha un processo di
frammentazione a cascata. Questo processo porta alla creazione degli
ammassi stellari, composti da decine o centinaia di stelle. Ogni membro
di un dato ammasso è nato dalla stessa nube, nello stesso istante, e tutti
hanno la stessa composizione. Quindi, il teorema di Vogt-Russell,
enunciato come segue:
“La massa e la composizione di una stella ne determinano in modo
univoco il raggio, la luminosità e la struttura interna, così come la sua
evoluzione successiva”.
suggerisce che le differenze negli stati evolutivi tra le varie stelle
dell’ammasso sono dovute esclusivamente alle loro masse iniziali. Gli
ammassi di Popolazione II estrema si sono formati quando la Galassia era
molto giovane, dunque sono gli oggetti più vecchi della Via Lattea e
contengono molte stelle. Si parla, in questo caso, di AMMASSI
GLOBULARI. Essi forniscono informazioni fondamentali sull’età
dell’Universo, sulla comprensione della struttura Galattica e sul modo in
cui si è formata la Via Lattea.
Gli ammassi di POPOLAZIONE I tendono ad essere più piccoli e più
giovani e sono detti AMMASSI GALATTICI o APERTI.
Come già accennato in precedenza, i diagrammi H-R degli ammassi
possono essere costruiti in maniera auto-consistente senza la conoscenza
dell’esatta distanza. Dal momento che le dimensioni tipiche di un
ammasso sono piccole rispetto alla distanza che lo separa dalla Terra, si
avrà un errore trascurabile se si assume che tutti i membri dell’ammasso
siano alla stessa distanza. Di conseguenza, riportare in un grafico la
magnitudine relativa piuttosto che quella assoluta equivale a introdurre
uno shift sul grafico equivalente alla posizione della singola stella.
Mettendo insieme la sequenza principale osservata e quella calibrata sulla
magnitudine assoluta, si determina la distanza dell’ammasso
dall’osservatore. Questo metodo di determinazione della distanza è detto
fitting di sequenza principale. Piuttosto che determinare le temperature
effettive di ogni membro di un ammasso tramite un’analisi dettagliata
degli spettri stellari, è molto più semplice ottenere i loro indici di colore
(B-V), per la costruzione di un diagramma colore-magnitudine.
15
Capitolo 2 Gli ammassi stellari
2.2 Diagrammi H-R di un ammasso
2.2.1 Evoluzione di un ammasso aperto e la gap di Hertzsprung
2.2
Diagrammi H-R di un ammasso
Gli ammassi e i relativi diagrammi H-R associati permettono di testare
molti aspetti della teoria dell’evoluzione stellare. Stimando, infatti, le
tracce evolutive di stelle di masse diverse, con la stessa composizione
chimica dell’ammasso, è possibile graficare la posizione di ogni campione
sul diagramma H-R quando i modelli raggiungono l’età dell’ammasso. La
curva che congiunge queste posizioni è detta isocrona. Il numero
relativo di stelle in ogni punto dell’isocrona dipende sia dal numero di
stelle nei diversi intervalli di masse che dal tasso differente di evoluzione
durante ogni fase. Dunque, i conteggi stellari in un diagramma coloremagnitudine possono fornire indicazioni sulle scale dei tempi coinvolte
nell’evoluzione stellare.
2.2.1 Evoluzione di un ammasso aperto e la gap di Hertzsprung
Analizziamo l’evoluzione di un ammasso aperto seguendo il diagramma
colore-magnitudine di un ammasso aperto doppio, h e χ Persei, riportato
in figura 6.
Figura 6: diagramma CM dell’ammasso aperto h e χ Persei
Sono evidenti le giganti rosse e le stelle di massa piccola appartenenti
alla pre-sequenza principale. Nel diagramma è evidente anche la
completa assenza di stelle nella zona che va dalle stelle massive che
stanno lasciando la sequenza principale e le poche giganti rosse. È
altamente improbabile che questo diagramma rappresenti una veduta
incompleta, dal momento che le stelle mancanti nell’intervallo suddetto
sono quelle più luminose dell’ammasso. In realtà, tale mancanza è la
16
Capitolo 2 Gli ammassi stellari
2.2.1 Evoluzione di un ammasso aperto e la gap di Hertzsprung
prova dell’evoluzione rapida che avviene dopo che le stelle hanno lasciato
la sequenza principale. Questa struttura, nota come gap di
Hertzsprung, è una caratteristica comune dei diagrammi coloremagnitudine di ammassi giovani, ovvero degli ammassi aperti.
Nel 1942 Schönberg e Chandrasekhar avevano trovato teoricamente che
l’idrogeno brucia tanto più rapidamente quanto più la stella é luminosa e
di massa elevata. Quando una certa percentuale di idrogeno si é
trasformata in elio, la stella lascia la sequenza principale. A quel punto la
stella diventa più luminosa e meno blu e poi, passando rapidamente per
una fase in cui non é in equilibrio, diventa una gigante rossa. Questa
teoria spiega:
· la parte alta, incurvata, della sequenza principale, formata appunto
dalle stelle che se ne stanno staccando;
· il gruppo delle giganti rosse;
· la gap di Hertzsprung
Quando il nucleo della stella che ha esaurito l’idrogeno supera il limite (o
massa) di Schönberg-Chandrasekhar (definito come il limite superiore
che può raggiungere la massa costituita dalla materia degenere capace di
opporsi al collasso gravitazionale. Il suo valore corrisponde a 1.4 M ), si
ha la gap vista in figura 6, tipica degli ammassi aperti.
Si può, così, interpretare sinteticamente il diagramma H-R degli ammassi
aperti. In principio, tutte le stelle si trovano sulla sequenza principale,
tranne quelle di piccola massa, in basso a destra, che ancora non l'hanno
raggiunta. Col passare del tempo, le stelle di massa più elevata si
staccano per diventare giganti rosse. Poiché le stelle più luminose
evolvono più rapidamente, abbiamo poche probabilità di osservare una
stella durante quel breve intervallo della sua vita in cui passa dalla
sequenza principale alla regione delle giganti rosse. Ciò spiega perché
non si trovi quasi nessuna stella nella gap di Hertzsprung. Dato che
l'evoluzione é più lenta a più basse luminosità, la gap si assottiglia con
l’aumentare dell’età dell'ammasso. Negli ammassi più vecchi la gap é
totalmente assente. Dalla posizione da cui le stelle migrano dalla
sequenza principale verso la regione delle giganti rosse, é possibile
dunque calcolare l’età dell'ammasso. Cosa accade dopo che una stella é
passata attraverso lo stadio di gigante? Questo lo possiamo dedurre dai
diagrammi H-R dei più vecchi ammassi conosciuti, come M67 e degli
ammassi globulari. In questi casi appare un nuovo ramo, che non é
presente in nessuno degli ammassi più giovani: il ramo orizzontale
corrispondente alle variabili RR Lyrae(vedi figura 7).
17
Capitolo 2 Gli ammassi stellari
2.2.2 Il punto di turn-off di un ammasso aperto
Figura 7: Ammasso globulare M3
Così, le luminose stelle blu che una volta popolavano la parte superiore
della sequenza principale di un vecchio ammasso sono prima diventate
supergiganti rosse. In seguito, quando l'elio é diventato la loro più
importante sorgente di energia, esse si sono trasferite a sinistra, nella
regione delle RR Lyrae. Infine, dopo una successione di eventi, le stelle
raggiungono lo stadio finale, diventando, a seconda della loro massa,
nane bianche, stelle di neutroni o, forse, buchi neri.
2.2.2 Il punto di turn-off di un ammasso aperto
I diagrammi H-R forniscono informazioni sullo stato evolutivo
dell’ammasso in questione. La profondità di un ammasso aperto è molto
minore della distanza dell’ammasso stesso dalla Terra: ci si aspetta,
dunque, che la sequenza nel diagramma CM sia piuttosto definita. I
diagrammi di questo tipo sono di più facile costruzione rispetto a quelli
degli ammassi globulari, in quanto la natura diffusa di questi sistemi
permette di evitare la confusione che impedisce la fotometria stellare. Di
contro, però, bisogna essere abili a minimizzare gli effetti della
contaminazione stellare dovuta alle stelle di campo presenti sul piano
Galattico. Questo può essere fatto selezionando le stelle appartenenti
all’ammasso in base alla loro cinematica oppure prendendo solo quelle
stelle i cui colori siano consistenti con gli oggetti arrossati dalle polveri
presenti tra noi e l’ammasso stesso. Una volta che si è tenuto conto delle
difficoltà sopra descritte, la sequenza principale di un ammasso aperto
appare simile a quella riportata in figura 8.
18
Capitolo 2 Gli ammassi stellari
2.2.2 Il punto di turn-off di un ammasso aperto
Figura 8: diagramma CM dell’ammasso aperto NGC 4755
Si può notare che la sequenza è molto estesa, fino ad arrivare alle stelle
blu in alto. La presenza di stelle massive e di vita breve indica che alcune
stelle dell’ammasso sono molto giovani. Inoltre, la netta delineazione
della sequenza implica che tutte le stelle sono di età molto simile tra loro,
dal momento che nessuna delle stelle meno massive con tempi di vita più
lunghi sulla sequenza principale ha già iniziato a spingersi verso il ramo
delle giganti. Verso la parte inferiore della sequenza principale, essa
diventa più spessa, con una tendenza delle stelle ad andare verso il
rosso. Lo spessore di tale sequenza non può essere attribuito ad errori di
osservazione, ma è una conseguenza dell’età giovane del sistema. Prima
infatti che le stelle raggiungano la sequenza principale, esse evolvono dal
lato destro del diagramma colore-magnitudine lungo tutta la sequenza,
con stelle di massa minore che impiegano più tempo per fare questa
transizione. E’ da notare che la disposizione diversa di queste stelle nel
diagramma CM implica che esse non si sono formate simultaneamente,
poiché stelle differenti con le stesse masse sono evolute in modo diverso
tra loro.
L’invecchiamento graduale dell’ammasso conduce, in sintesi, al seguente
processo: le stelle più massive e meno abbondanti arriveranno per prime
sulla sequenza principale, evolvendo rapidamente. Prima che le stelle di
massa minore abbiano raggiunto la sequenza principale, quelle più grandi
sono già arrivate nella regione delle giganti rosse, subendo
probabilmente anche un’esplosione di supernova.
19
Capitolo 2 Gli ammassi stellari
2.2.2 Il punto di turn-off di un ammasso aperto
La breve scala di tempi in cui le stelle passano attraverso lo stadio di
giganti indica che le sequenze di evoluzione finale nel diagramma CM
sono scarsamente popolate, con una gap di Hertzsprung molto
pronunciata.
Per confrontare i diagrammi CM di differenti ammassi, dobbiamo metterli
su una stessa scala di magnitudine assoluta. La calibrazione della scala
può essere fatta più facilmente rispetto ad un ammasso globulare, dal
momento che esiste un grande numero di stelle vicine con parallasse
trigonometrica nota, che hanno metallicità molto simili a quelle delle
stelle dell’ammasso. La natura estensiva della sequenza principale degli
ammassi aperti risulta essere sicuramente utile per il fitting, dal
momento che si ha a disposizione un ampio intervallo di colori e
magnitudini.
Figura 9: sequenze di un gruppo di ammassi nel diagramma CM, traslati tutti
sulla stessa scala di magnitudine assoluta
La figura 9 riporta una sequenza per alcuni ammassi scelti. Nonostante la
sequenza possa, ad un primo impatto, sembrare molto simile per tutti gli
ammassi, il carattere più evidente nella figura è il diverso punto di turnoff per ogni ammasso; per alcuni si ha anche una brusca interruzione
della sequenza principale. In realtà, le differenze tra le sequenze possono
essere attribuite a una differenza di età tra gli ammassi aperti.
Dal momento che i tempi di vita del nucleo che brucia idrogeno sono
inversamente proporzionali alla massa, l’evoluzione dell’ammasso fa sì
che il punto di turn-off sulla sequenza principale, definito come il punto
20
Capitolo 2 Gli ammassi stellari
2.2.3 Confronto tra gli ammassi aperti e gli ammassi globulari
dove le stelle dell’ammasso lasciano la sequenza principale, diventa più
arrossato e meno luminoso nel tempo. Di conseguenza, è possibile
stimare l’età di un ammasso dal punto più alto della sua sequenza
principale.
Se si osserva la figura 9, si può notare che l’ammasso globulare M67 non
presenta la gap di Hertzsprung. Questo è una prova che tale gap è
presente solo negli ammassi aperti più giovani. Come già detto, per
masse con valori inferiori a 1.25 M , la rapida fase di contrazione
collegata al limite di Schönberg-Chandrasekhar è molto meno
pronunciata. Di conseguenza, i diagrammi colore-magnitudine di
ammassi globulari vecchi con punti di turn-off vicini a 1 M presentano
distribuzioni continue di stelle che arrivano fino alla regione delle giganti
rosse.
2.2.3 Confronto tra gli ammassi aperti e gli ammassi globulari
La varietà di punti di turn-off degli ammassi aperti è in forte contrasto
con quello che accade per gli ammassi globulari. La struttura tipica di un
ammasso globulare è riportato nella figura 10, mentre in figura 11 è
riportato un diagramma CM di alcuni ammassi.
Figura 10: diagramma CM di un ammasso globulare
21
Capitolo 2 Gli ammassi stellari
2.2.3 Confronto tra gli ammassi aperti e gli ammassi globulari
Figura 11: diagramma CM composito di vari ammassi
Come si evince dalla figura 10, il ramo delle sub giganti di un ammasso
globulare è molto stretto e confina con la sequenza principale in un punto
di turn-off ben definito. Questa struttura indica che tutte le stelle che
sono originariamente sulla sequenza principale proprio sopra il punto di
turn-off si stanno allontanando da tale sequenza, evolvendo. Questo
implica che le stelle dell’ammasso globulare hanno essenzialmente la
stessa età. L’assenza di un numero significativo di stelle che evolvono
dalla sequenza principale sotto il punto di turn-off indica che l’ammasso
non contiene stelle più vecchie di quelle presenti sul punto di turn-off. La
nitidezza delle sequenze osservate pone forti limiti sull’intervallo di tempo
in cui gli ammassi globulari si sono formati. Se le stelle si fossero formate
in un arco di tempo molto lungo, i rami delle sub-giganti e delle giganti
rosse sarebbero composti dalla sovrapposizione di isocrone di età
differenti. Dal momento che la posizione di questi rami, specie di quello
delle sub-giganti, si sposta in modo significativo con l’età, la strettezza di
queste strutture nei diagrammi CM degli ammassi globulari vincola il
periodo di formazione stellare di tali sistemi a non più del 2% dell’età
dell’intero ammasso (Stetson 1993). La posizione dei rami delle subgiganti e delle giganti rosse dipende dalla metallicità dell’ammasso: la
figura 11 mostra come queste sequenze si spostino verso destra nel
diagramma CM e come il ramo delle sub-giganti diventi sempre più piatto
spostandosi da ammassi poveri di metallo ad ammassi ricchi di metallo.
Dunque, in definitiva, mentre i diagrammi degli ammassi aperti possono
mostrare andamenti estremamente diversi, gli ammassi globulari, invece,
22
Capitolo 2 Gli ammassi stellari
2.3 Stima dell’età di un ammasso aperto
sono più o meno tutti simili tra loro: a dimostrare il fatto che, mentre i
primi possono avere le età più diverse (alcuni, come l’ammasso di Orione,
sono ancora in formazione, mentre altri, come M67, hanno età di diversi
miliardi di anni), i globulari, viceversa, hanno tutti un’età estremamente
veneranda, dell’ordine di oltre dieci miliardi di anni.
2.3 Stima dell’età di un ammasso aperto
Dal momento che la posizione del punto di turn-off scende lungo la
sequenza principale, la magnitudine assoluta del punto di turn-off,
MV(TO)
fornisce
la
misura
diretta
dell’età
dell’ammasso.
Quantitativamente, Bergbusch e VandenBerg (1992) hanno trovato che
MV(TO) è collegata all’età dell’ammasso, t, e alla metallicità, [Fe/H],
tramite:
MV(TO)= 2.70 log(t/Gyr)+0.30[Fe/H]+1.41
(2.1)
Per estrarre l’età dell’ammasso da questa equazione, determiniamo la
magnitudine apparente del punto di turn-off; poi troviamo la distanza
dell’ammasso, tramite un fitting della sequenza principale, e la usiamo
per calcolare la magnitudine assoluta del punto di turn-off. Infine
misuriamo la metallicità dell’ammasso dagli spettri. Applicando
l’equazione (2.1) agli ammassi aperti riportati in figura 9, si ottiene una
stima dell’età che va da 1 Myr fino a 10 Myr.
Il vasto intervallo di età in cui sono compresi gli ammassi aperti implica
che essi sono in continua formazione nel disco della Galassia. Mermilliod
(1980) costruì un database degli ammassi compresi fino a 750 pc dal
Sole. Si accorse che la densità degli ammassi più vecchi era più bassa di
quelli giovani. Questo fatto potrebbe essere interpretato come la prova
evidente che l’efficienza con cui si formano nuovi ammassi è aumentata
notevolmente negli ultimi miliardi di anni. Ma è stato visto che gli
ammassi aperti non sono strutture robuste e massicce: essi possono
essere frammentati quando si scontrano con le nubi molecolari presenti
nel disco Galattico (Spitzer 1958). Se si ritiene valida quest’ultima
ipotesi, la minore presenza di ammassi vecchi può essere dovuta proprio
a questi incontri. L’evidenza in favore di questa idea è arrivata
dall’osservazione che gli ammassi vecchi si trovano in linea di massima a
distanze molto grandi dal centro galattico e dal piano galattico, dove
questo tipo di incontri sono meno probabili. Ciò ha consentito a questi
ammassi vecchi di resistere abbastanza da poter essere osservati da noi
[van den Bergh e McClure (1980)].
23
Capitolo 2 Gli ammassi stellari
2.4 AMMASSI APERTI o Galattici: descrizione e classificazione
Ulteriori prove di questa ipotesi sono fornite da studi delle proprietà
morfologiche degli ammassi aperti in funzione dell’età. Janes e Phelps
(1994) hanno trovato che mentre il 49% degli ammassi aperti vecchi nel
database di Lynga (1987) sono, nella classificazione di Trumpler, di
classe r (si tratti di ammassi composti da più di cento stelle. Vedi, a tale
proposito, paragrafo 2.4), solo il 18% degli ammassi più giovani cade
nella medesima classe. Inoltre gli ammassi più vecchi cadono nelle classi
di concentrazione più elevate (I e II), mentre solo il 62% degli ammassi
giovani ha gradi di concentrazione così alti. Di conseguenza lo scenario
sarebbe il seguente: poiché gli ammassi più poveri e meno concentrati al
centro sono meno gravitazionalmente legati, essi non riescono a superare
gli incontri con le nubi molecolari e, dunque, non raggiungono età
avanzate.
Una volta che l’ammasso si è dissolto dopo l’incontro, si avranno membri
appartenenti ad esso che “ricorderanno” ancora la direzione in cui si
stava muovendo nel momento della sua frammentazione, e
continueranno a seguire orbite simili nella Galassia, anche se essi non
sono più legati gravitazionalmente tra loro. Sono stati osservati, infatti,
gruppi di stelle in movimento che hanno velocità e metallicità simili anche
se ricoprono una vasta area del cielo.
2.4 Ammassi aperti o galattici: descrizione e classificazione
Non tutti gli agglomerati di stelle nella Via Lattea presentano una
struttura definita, ma hanno bassa simmetria e perdono la caratteristica
concentrazione centrale degli ammassi globulari. Per questo motivo si
parla di ammassi aperti. Diversamente dagli ammassi globulari, gli
ammassi aperti sono fortemente localizzati verso il piano della Via Lattea
e, per tali motivo, sono anche chiamati ammassi Galattici. Il loro
aspetto piuttosto frammentato ne rende più complessa l’individuazione;
inoltre, essendo vicini al piano Galattico, tendono ad essere facilmente
oscurati dalle polveri e dalla densità stellare. Di conseguenza, il catalogo
di Messier cataloga solo 27 ammassi aperti. Tuttavia, essi sono sistemi
intrinsecamente abbondanti: il database compilato da Lynga nel 1987 è
composto da 1200 ammassi, che coprono solo una parte della Via Lattea.
Gli ammassi aperti cadono in un largo intervallo di luminosità e
morfologia, variando da ammassi di luminosità totale pari a MV ≈ -3 fino
ad arrivare a sistemi di molte centinaia di stelle di MV ≈ -9. Generalmente
ricoprono diametri molti ampi e, poiché osserviamo esemplari vicini, essi
occupano vaste regioni di cielo e, quindi, angoli di diversi gradi. Le
densità di questi sistemi sono più alte delle stelle di campo e arrivano fino
a 103 stelle per pc-3. I sistemi a densità più basse vengono detti
associazioni e si distinguono per la presenza di stelle di tipo inusuale.
24
Capitolo 2 Gli ammassi stellari
2.4 AMMASSI APERTI o Galattici: descrizione e classificazione
Le proprietà di un ammasso aperto possono essere riassunte nella
classificazione di Trumpler (Trumpler, 1930) che specifica:
•
•
•
•
Il grado di concentrazione con un numero romano I…IV, dove i
numeri più piccoli indicano concentrazioni più elevate.
L’intervallo di luminosità delle stelle misurato su una scala da 1 a
3, dove i numeri più piccoli indicano un intervallo di luminosità
minore.
La ricchezza, specificata con p (sistema povero, contenente meno
di 50 stelle), m (sistema moderato, composto di 50/100 stelle) o r
(sistema ricco, composto da più di 100 stelle).
Si aggiunge la lettera n alla classificazione se c’è un’emissione
diffusa intorno alle stelle dell’ammasso.
La presenza di un’emissione diffusa intorno alle stelle negli ammassi
aperti è in aperto contrasto con la nitidezza dell’emissione degli ammassi
globulari. Questa nebulosità proviene dalla luce stellare riflessa dai
granelli di polvere nell’ammasso; la polvere è accompagnata da materiale
gassoso e, di conseguenza, da questo fatto si ha che gli ammassi aperti
contengono un mezzo interstellare piuttosto significativo. Questa
osservazione delinea un’ulteriore differenza tra i due tipi di ammassi: gli
ammassi aperti contengono stelle blu, luminose e questo implica che tali
sistemi si siano formati più recentemente rispetto agli ammassi globulari,
che risultano invece privi di alcuni tipi stellari e, di conseguenza, sono più
vecchi. Il gas presente negli ammassi aperti è in realtà materiale che non
è stato convertito in stelle. La formazione stellare è dunque un processo
dinamico e costante in questi sistemi. Anche lo studio della loro
metallicità fornisce una prova dell’origine relativamente recente; studi
spettrali forniscono valori
-0.75<[Fe/H]<0.25.
Gli ammassi aperti hanno giocato un ruolo chiave nella comprensione
dell’astronomia galattica. La presenza di stelle blu ha permesso l’indagine
di stelle di massa grande. La distribuzione spaziale degli ammassi aperti
fornisce inoltre un test della struttura del disco Galattico e, dal momento
che si crede che molte delle stelle nel disco della Via Lattea siano nate
negli ammassi aperti, le proprietà di questi sistemi forniscono indicazioni
sull’intero disco.
25
Capitolo 3 L’ammasso aperto NGC 6633
3.1 L’ammasso aperto NGC 6633
Capitolo 3
L’ammasso NGC 6633
3.1
L’ammasso aperto NGC 6633
L'ammasso aperto NGC 6633 contiene circa una trentina di stelle blu,
brillanti. E' abbastanza esteso, ma non molto concentrato e, proprio per
questo, l'osservazione migliore deriva da uno strumento a campo largo.
Nelle notti senza Luna può essere visto anche ad occhio nudo, ma il fatto
che intorno a questo ammasso non ci sia niente di particolarmente
brillante lo rende difficilmente scovabile. Le stelle sono di magnitudine 8
e 9, la magnitudine complessiva è di 4.6. La sua forma tende ad
allungarsi da Nord-Est a Sud-Ovest con maggiore concentrazione verso la
fine. E’ stata stimata un’età di 660 milioni di anni.
NGC 6633 fu scoperto dall’astronomo svizzero
Phylippe Loys de
Chéseaux negli anni 1745-46. Fu riscoperto in modo indipendente da
Caroline Herschel il 31 luglio 1783. Suo fratello William lo incluse nel suo
catalogo col nome H VIII.72. Questo oggetto è inserito in molte liste,
come No.11 nella Paul Ahnert's Easy Object List, nella SAC 110 Best
NGC List, ,nella John Caldwell's List,, nella RASC's Finest N.G.C. Objects
Objects list, e nella Astronomical League's Deep Sky Binocular Club List.
Le coordinate astronomiche dell’ammasso sono:
A.R.: 18:27:18
Declinazione: Nord 6:31:0
[epoca J(2000.0)]
Figura 12: Ammasso NGC 6633. [Osservatorio di Palomar]
26
Capitolo 3 L’ammasso aperto NGC 6633
3.2 Fotometria: il cielo notturno e gli effetti del seeing
3.2
Fotometria: il cielo notturno e gli effetti del seeing
Ma come possiamo ottenere informazioni dalle stelle? La fotometria
misura il flusso ricevuto da un oggetto celeste, ovvero la radiazione
elettromagnetica che esso emette. La misura del flusso, messa in
relazione con la distanza dell’oggetto osservato, può fornire informazioni
sulla temperatura, sulle dimensioni e sulle altre proprietà fisiche delle
stelle.
I corpi celesti emettono radiazione elettromagnetica. In teoria, potremmo
misurare la distribuzione spettrale completa di questa radiazione. A
seguire, potremmo determinare l’energia ricevuta in termini del flusso
per intervallo di frequenza o di lunghezza d’onda sull’intero spettro.
In pratica, però, la misura delle distribuzioni assolute di energia risulta
molto complessa, per due motivi. Per prima cosa, bisogna conoscere la
risposta della strumentazione usata per le osservazioni. Inoltre,
frequenze differenti di energia elettromagnetica penetrano l’atmosfera
terrestre a diverse profondità. Di conseguenza, in determinati intervalli di
frequenza, le osservazioni possono essere fatte solo in siti particolari o
nello spazio.
Quindi, per ottenere la distribuzione assoluta di energia di un oggetto
celeste, è necessario combinare i dati ottenuti da vari strumenti ma,
come accade spesso, mancano quelli relativi ad un dato intervallo di
frequenza.
Per molti scopi, fortunatamente, non abbiamo bisogno di trovare la
distribuzione completa di energia di un oggetto; basta avere l’energia
totale ricevuta da un rilevatore in un intervallo definito di frequenze,
ovvero il flusso di radiazione integrato f misurato in unità di W m-2,
contenuto in un intervallo di frequenze ∆ν. In particolare, possiamo usare
i rivelatori come le CCD per misurare la luminosità apparente degli
oggetti in varie bande nella regione dello spettro dell’ottico e
dell’infrarosso. Si parla, in questo caso, di fotometria astronomica.
Esistono delle difficoltà legate alla fotometria. Per prima cosa, il cielo non
è mai completamente scuro. Inoltre l’atmosfera non è del tutto
trasparente. Questi due fattori influenzano notevolmente le osservazioni.
Analizziamo nel dettaglio le problematiche che si presentano.
27
Capitolo 3 L’ammasso aperto NGC 6633
3.2.1 Il cielo notturno
3.2.1 Il cielo notturno
La luminosità del cielo notturno senza luna è data principalmente da
quattro contributi:
•
•
•
•
Il calore prodotto da processi fotochimici nell’alta atmosfera.
Questa componente ha uno spettro molto irregolare, ma è più
evidente a lunghezze d’onda maggiori. La sua intensità varia da
punto a punto nel cielo in modo irregolare, mentre in media
aumenta dalla latitudine di 20° fino a 70° di un fattore 2. La
fluttuazione in magnitudine è di circa il 20% in un intervallo di
tempo di circa dieci minuti. In molti osservatori, questa
componente è aumentata dalle linee di radiazione del mercurio e
del sodio dalle luci stradali presenti nelle città vicine.
La luce zodiacale, che è luce solare dispersa dal materiale
particolato nel sistema solare.
Stelle deboli e non risolte nella nostra Galassia.
Luce extragalattica diffusa, proveniente da galassie distanti,
deboli, non risolte.
Le proporzioni relative delle varie componenti elencate e l’intensità totale
prodotta dalla somma di tutti i fattori dipendono dal sito osservativo e
dalle longitudine e latitudine galattica ed eclittica. In linea generale, la
luce zodiacale è la fonte maggiore di luminosità, seguita dalla
componente termica e dalla luce extragalattica diffusa. Messi insieme,
questi contributi portano sulla superficie della Terra più luce di tutte le
stelle risolte, nebulose e galassie messe insieme.
Il cielo notturno è piuttosto rosso; ha un indice di colore (B-V) =0.9,
simile a quello di una galassia debolmente rossa. Il cielo è più scuro di un
fattore che varia con la lunghezza d’onda e la distanza dall’eclittica. Nella
banda V questo fattore può essere dell’ordine di 1.5 mag, mentre il
fattore aumenta al crescere della lunghezza d’onda. La fotometria
effettuata dallo spazio è relativamente facile da correggere per quanto
riguarda la luminosità del cielo notturno, poiché il riscaldamento dell’aria,
che varia molto rapidamente nel tempo e nello spazio, non contribuisce ai
dati spaziali.
La luce del cielo, a causa della sua natura fotonica, produce rumore che
rende più difficile individuare il segnale stellare. Non è importante la
quantità di segnale che ci perviene dalla stella, ma il rapporto tra questo
ed il rumore presente. Dunque, o si aumenta il segnale (maggiore è il
diametro del telescopio, maggior è l’intensità del segnale raccolto) o si
diminuisce il rumore (più è scuro il cielo, più diminuisce il rumore).
28
Capitolo 3 L’ammasso aperto NGC 6633
3.2.2 Effetti del seeing
I primi passi nella riduzione delle osservazioni fotometriche delle
immagini sono riportati sinteticamente a seguire (in seguito verranno
affrontati in maniera più dettagliata):
•
•
Determinare la sensibilità di ogni pixel del dispositivo che forma
l’immagine
Misurare l’attenuazione delle immagine verso i bordi del campo
visuale del telescopio, cioè la vignettatura del campo. Il processo
di correzione di questi errori è chiamato flat-fielding, e gli errori
associati a questo processo dominano solitamente l’errore finale.
Una volta effettuato il flat-fielding, bisogna sottrarre il contributo del
fondo cielo dal flusso misurato in ogni regione del cielo. Questo
contributo sarà in generale più grande dell’oggetto stesso. Inoltre, la
luminosità del cielo nel punto in cui si trova l’ammasso non può essere
misurata direttamente. Per ottenerla, è necessario estrapolarla dai
dintorni del cielo vuoto. E’ dunque preferibile usare un rivelatore che
copra l’area più ampia possibile di cielo, specialmente se l’oggetto celeste
in questione ha un diametro angolare grande.
3.2.2 Effetti del seeing
Senza l’atmosfera, i raggi di luce proveniente dalle stelle arriverebbero al
telescopio tutti paralleli l’uno all’altro ed il telescopio focalizzerebbe questi
raggi in una piccola zona, detta disco di Airy (non si tratta esattamente di
un punto, a causa degli effetti della diffrazione). Il passaggio dei raggi
luminosi attraverso i pochi chilometri di atmosfera mescola i raggi stessi,
causando la perdita del loro esatto parallelismo. La turbolenza dell’aria
sopra il telescopio causa, quindi, un movimento delle immagini che
provoca fluttuazioni nella fase del fronte d’onda entrante nel telescopio.
Risulta un’immagine stellare più simile ad un globo di luce che non ad
un’immagine netta. Nel 1970 A. Labeyrie si accorse che il pattern di luce
prodotto da una stella nel fuoco di un grande telescopio è composto da
puntini o macchie. Ogni macchia è un’immagine stellare indipendente. In
un’esposizione permanente più lunga di una frazione di un secondo, tutte
queste macchie si sovrappongono per produrre un’unica macchia
luminosa. Si dice, in questo caso, che l’immagine è stata rovinata dal
fenomeno del seeing, e ci si riferisce all’intero spessore della macchia
preso a metà del punto massimo come il seeing. Più precisamente, gli
astronomi distinguono il seeing in base al FWHM angolare, che
rappresenta la dimensione angolare dell’immagine stellare a livello della
metà del picco. La tecnica dell’interferometria a macchie prevede che si
ottengano un gran numero di esposizioni brevi del campo. Un’esposizione
individuale è così breve che il pattern a macchie non si muove in modo
29
Capitolo 3 L’ammasso aperto NGC 6633
3.3 Fotometria: aspetti pratici
apprezzabile e, quindi, contiene informazioni sulla misura angolare della
stella. D’altra parte, anche quando la stella rappresentata è poco
brillante, il numero di fotoni in un’esposizione individuale non è grande e,
di conseguenza, la qualità dell’immagine ottenuta è molto bassa.
Comunque, mettendo insieme informazioni di un gran numero di
esposizioni, si compensa la bassa qualità delle singole immagini.
Uno degli effetti del seeing è quello di influire sulla fotometria di oggetti
stellari. Il seeing è caratterizzato dalla point-spread function (PSF)
P(d) che fornisce la densità di probabilità che un fotone colpisca il
dispositivo che forma l’immagine nel punto che è spostato del vettore d
rispetto al punto che sarebbe colpito in assenza di seeing. Se, in assenza
di seeing, la luminosità superficiale nella posizione R’ nel rivelatore è It
(R’), allora la luminosità misurata nel punto R sarà:
*$++ (,) = / 01 , 2 3(, − , 2 )*" (,′)
(3.1)
In pratica la PSF rappresenta la forma di un’immagine CCD di una
sorgente di luce puntiforme. La PSF ideale dovrebbe avere simmetria
circolare e può essere rappresentata in un diagramma come il flusso
rispetto al raggio di una stella. La forma di una PSF reale trattata dal
seeing è più complessa e può essere approssimata da una zona centrale
di tipo gaussiano e da un grande alone che segue una legge di potenza.
La dimensione angolare è caratterizzata dalla FWHM (Full Width at Half
Maximum) che rappresenta il diametro compreso tra i punti dove il flusso
decade a metà rispetto al suo valore massimo.
3.3 Fotometria: aspetti pratici
La misura del flusso di una stella è dunque influenzata da diversi fattori
che non permettono la cosiddetta fotometria assoluta. Potrebbe
sembrare, in prima istanza, che la fotometria risulti piuttosto semplice: si
utilizza un sensore (nello specifico una CCD) con un supporto di filtri
disposto anteriormente, che seleziona la banda spettrale legata
all’intervallo di lunghezze d’onda della stella di cui vogliamo rilevare il
flusso. Si potrebbe pensare di puntare il telescopio in direzione della
stella, misurare il numero di unità (fotoni) che il sensore registra ogni
secondo, poi trovare l’energia corrispondente alle unità registrate e
ricavare l’energia ricevuta dalla stella. Ma risulta arduo, se non
impossibile, risalire al flusso di una stella direttamente dai conteggi di
unità del sensore.
30
Capitolo 3 L’ammasso aperto NGC 6633
3.3 Fotometria: aspetti pratici
La prima ovvia complicazione è data dal fatto che il sensore non rivela
realmente ogni singolo fotone, di conseguenza è necessario introdurre
una correzione per la misura di fotoni. Se si considera un telescopio
riflettore, bisogna considerare che l’area di raccolta della luce non è data
solo dallo specchio, ma anche lo specchio secondario e la relativa
struttura di sostegno bloccano la luce. Inoltre, dobbiamo ricordare che gli
specchi dei telescopi sono esposti agli agenti atmosferici e che ogni vetro
del sistema ottico assorbe una certa quantità di luce, in relazione alla
lunghezza d’onda. Infine, l’estinzione atmosferica crea ulteriori
complicazioni.
Come possiamo allora con buona affidabilità misurare il flusso di una
stella? L’idea chiave consiste nel misurare il flusso dell’oggetto incognito
unitamente al flusso di un gruppo di stelle (le cosiddette stelle
standard), il cui flusso è già stato accuratamente misurato. Misurando il
nostro oggetto nonché la stella standard, possiamo esprimere il flusso
della nostra stella in funzione del flusso di quest’ultima. Molti dei fattori
citati sopra, dai problemi legati alle ottiche fino all’efficienza quantica del
CCD, non alterano il rapporto tra il flusso incognito della stella e quello
delle stelle standard, dato che intervengono in misura uguale su di essi.
Dal momento che l’atmosfera assorbe parte dei fotoni, e un’altra parte di
essi non viene rivelata dai telescopi, non misuriamo in realtà
direttamente il flusso fν della stella. Misuriamo invece:
9
5 ≡ / 56
6 6 ,7 08
(3.2)
dove Tν è la trasmissione dell’atmosfera, Fν è la trasmissione del filtro
utilizzato per restringersi ad un particolare intervallo di frequenze e Rν è
l’efficienza del telescopio, ovvero Rν = energia rivelata/energia incidente.
1) La trasmissione dell’atmosfera segue la legge 6 ∝ ;$ , dove < è
proporzionale alla densità della colonna d’aria lungo la linea di
osservazione. Ovviamente è minore allo zenith e aumenta all’orizzonte.
Si definisce:
massa d’aria ≡ </<
dove < è il valore di < allo zenith.
31
Capitolo 3 L’ammasso aperto NGC 6633
3.4 Rivelatori CCD
2) Per un’atmosfera parallela al piano, la massa d’aria = sec z, dove z
è la distanza dalla zenith dell’oggetto osservato. In definitiva
l’estinzione atmosferica produce un’attenuazione della luce stellare in
accordo alla legge (3.3).
m(z)=k secz + cost
(3.3)
dove k è una costante e m(z) è la magnitudine stellare osservata alla
distanza dallo zenith z.
3) La trasmissione del filtro Fν si può determinare facilmente,
scegliendola a piacere per misurare l’energia contenuta in un intervallo di
lunghezze d’onda definite. Molti sistemi fotometrici usano differenti filtri,
e bisogna sempre specificare quale banda si sta utilizzando per il filtro
quando si fornisce un valore di magnitudine apparente. Un grafico di Fν e
della lunghezza d’onda sarà caratterizzato da una gobba, ovvero una
, e uno spessore laterale.
lunghezza d’onda effettiva o centrale =
4) L’efficienza strumentale ,6 è composta dall’efficienza del sistema
ottico del telescopio e la sensibilità del ricevitore di fotoni stesso. Data la
difficoltà della determinazione di questi due fattori, è necessario calibrare
il sistema misurando la sua risposta ad una sorgente di luminosità nota.
In generale, si tratta di una stella standard, la cui luminosità è molto
difficile da determinare. Per tale motivo conosciamo la luminosità relativa
delle stelle molto meglio di quella assoluta.
3.4 Rivelatori CCD
Un rivelatore digitale rivela fotoni e restituisce in uscita un numero
linearmente proporzionale al numero di fotoni incidenti sulla superficie
dello stesso. Un CCD (Dispositivo ad accoppiamento di carica) è un
rivelatore che può registrare un’immagine bidimensionale. E’ composto
da un chip di silicio sensibile alla luce, diviso in un gran numero di parti
indipendenti, chiamate pixel. Il CCD rivela quanta luce cade sui pixel e
fornisce un’immagine digitale, che consiste di una matrice di numeri, uno
per pixel. Ciascun numero è legato alla quantità di luce che incide su quel
pixel. Esiste una quantità che tiene conto dell’efficienza del CCD, la
cosiddetta efficienza quantica. Essa indica la frazione di fotoni incidenti,
effettivamente rivelati dal CCD.
32
Capitolo 3 L’ammasso aperto NGC 6633
3.5 Lo studio sperimentale di NGC 6633
3.5.1 La strumentazione dell’Osservatorio
3.5 Lo studio sperimentale di NGC 6633
Il lavoro sperimentale che abbiamo condotto
è consistito
nell’acquisizione di immagini al telescopio delle stelle appartenenti
all’ammasso NGC 6633.
6633 Tramite
ramite fotometria in filtro V e in filtro B, i
diagrammi colore-magnitudine
magnitudine ottenuti hanno permesso l’individuazione
della sequenza principale dell’ammasso e del ramo delle giganti rosse. I
risultati ottenuti sono stati messi a confronto con quelli pubblicati
nell’articolo “Membership, metallicity and lithium abundances” di Jeffries,
Totten, Harmer e Deliyannis.
Deliyannis. L’articolo, pubblicato nel 2002, è uno studio
della metallicità e delle caratteristiche peculiari di NGC 6633.
3.5.1 La strumentazione dell’Osservatorio
dell’
Figura 13: Osservatorio dell’Università degli Studi di Salerno
Le osservazioni astronomiche sono state effettuate presso l’Osservatorio
l
del Dipartimento di Fisica dell’Università degli Studi di Salerno.
Salerno
L’Osservatorio
ha
le
seguenti
coordinate:
(Lat. 40°46'30''N, Lon. 14°47'20''E).
14°47'20''E
La cupola (Sirius University Observatory)
Observatory) ha un diametro di 6.7 m.
Il telescopio è un CELESTRON C-14
C 14 (diametro 0.35 m, f/11).
La montatura permette di avere una precisione di puntamento inferiore
al grado.
La CCD è una SBIG
G ST-2000XM
ST
con 1600x1200 pixel. Il campo visivo è
14’x11’,
x11’, grazie ad un riduttore focale a f/7.9. La CCD è dotata di un
focheggiatore elettronico e di un portafiltri
filtri con un sistema UBVRI
Johnson, dei filtri O--III e H-alpha,
alpha, e di un reticolo di diffrazione per la
spettroscopia.
33
Capitolo 3 L’ammasso aperto NGC 6633
3.5.2 Fasi del lavoro sperimentale
3.5.3 Acquisizione dati
3.5.2 Fasi del lavoro sperimentale
Le fasi fondamentali del nostro lavoro possono essere schematizzate
come segue:
1. Acquisizione dati
•
•
•
2.
Riduzione
Allineamento e media delle immagini
Fotometria
Analisi
•
•
•
•
•
Matching stellare
Grafico CMD (grafico colore-magnitudine) con calibrazione sulla
stella SAO 123493
Isocrona
Individuazione del ramo delle sub-giganti
Stima dell’errore
3.5.3 Acquisizione dati
Analizziamo le varie immagini (o frame) che si acquisiscono al telescopio
e i relativi utilizzi.
Light frame (fotogramma dati)
Si tratta dell’immagine dell’oggetto che riprendiamo. Dopo aver puntato il
telescopio nella direzione di interesse, si apre l’otturatore per consentire
alla luce di cadere sul CCD. Dopo un certo tempo di posa, si effettua la
lettura. Il CCD funziona sul principio dell’integrazione; il segnale si
accumula con il tempo. Il tempo di integrazione (o di posa) è controllato
da un otturatore. L’obiettivo è quello di ottenere un’immagine della
sorgente con il miglior rapporto segnale rumore (S/N) possibile. Poiché il
segnale è composto di fotoni, c’è una quantità di rumore associata al
conteggio stesso dei fotoni, che è impossibile evitare del tutto.
Raccogliendo un numero maggiore di fotoni, possiamo migliorare il
rapporto S/N, sapendo che il segnale varia linearmente con il tempo, il
rumore varia come la radice quadrata del tempo.
34
Capitolo 3 L’ammasso aperto NGC 6633
3.5.3 Acquisizione dati
Dark frame (fotogramma di buio)
Il light frame non è ancora il numero effettivo di fotoni incidenti su
ciascun pixel. Bisogna sottrarre una componente di offset (bias) e una
componente di dark current. Vediamo brevemente di cosa si tratta. Se
eseguiamo un’integrazione del CCD per un certo tempo senza che la luce
lo colpisca, ci sarà un rumore associato a quel segnale causato
dall’eccitazione termica degli elettroni nel CCD. Questo è chiamato il
segnale di buio o semplicemente dark, che va sottratto all’immagine.
Flat frame (fotogramma piatto)
Se il CCD viene illuminato in maniera uniforme, non si genera lo stesso
segnale su ogni pixel. Disuniformità sono causate da una leggera
differenza nelle dimensioni di ogni pixel e da piccole variazioni dello
spessore del silicio lungo il chip. Bisogna tener conto anche di granelli di
polvere e della vignettatura. Per correggere queste variazioni è
necessario esporre il CCD ad una luce uniforme e vedere come si
presenta il segnale (e di conseguenza l’immagine). Il fotogramma,
chiamato flat, viene quindi utilizzato per correggere queste disuniformità.
Bias frame (fotogramma di bias)
Se leggiamo il CCD senza alcuna integrazione, ovvero considerando
un’esposizione con zero secondi di posa, ci sarà un segnale di bias,
dovuto al rumore elettronico del sensore. Anche questo segnale deve
essere misurato e sottratto alle immagini che registriamo.
Figura 14: Andamento dei vari tipi di segnale
35
Capitolo 3 L’ammasso aperto NGC 6633
3.5.3 Acquisizione dati
Le fasi essenziali nel trattare un’immagine ripresa con il CCD sono le
seguenti:
1) Si prende un certo numero di light frame con ciascun filtro.
2) Si prende un certo numero di dark frame (con lo stesso tempo di
integrazione utilizzato per gli oggetti). Facciamo la mediana pixel per
pixel dei dark frame. Otteniamo il master dark frame.
3) Si prendono dei flat con ciascun filtro, puntando il telescopio sul cielo
del crepuscolo. Ma quanto deve essere lungo il tempo d'integrazione per
ottenere un buon flat-field frame? Sicuramente dobbiamo evitare di
saturare il sensore. Facciamo la mediana di un certo numero di flat -field
frame. Otteniamo il master flat-field frame. I dark devono essere sottratti
anche ai flat, se la corrente di buio non è trascurabile nell’intervallo del
tempo di posa. In questo caso, i dark associati ai flat sono detti darkflat e
la loro media è detta masterdark dei flat. A seguire, sottraiamo il
masterdark dei flat al masterflat. Il livello nel segnale dei flat è arbitrario,
dipende da quanto era luminoso il cielo nel momento in cui sono stati
acquisiti. Abbiamo bisogno delle informazioni di differenze di segnale
attraverso il chip. Quindi normalizziamo il segnale in modo tale che il
segnale medio in ciascun pixel sia 1. Ciò si ottiene dividendo per il
segnale medio.
4) Si sottrae il masterdark dalle immagini dell’oggetto osservato. Quindi
si divide per il flat normalizzato.
I fotogrammi acquisiti, nel nostro caso, sono elencati di seguito:
•
•
•
•
•
•
N° 5 fotogrammi raw (light frame) dell’ammasso in filtro V con
tempi di posa di 1 minuto ciascuno
N° 5 fotogrammi raw (light frame) dell’ammasso in filtro B con
tempi di posa di 1 minuto ciascuno
N° 5 fotogrammi di dark con tempi di posa di 1 minuto ciascuno
N° 5 fotogrammi flat in filtro V
N° 5 fotogrammi flat in filtro B
N° 5 fotogrammi di darkflat
1) I fotogrammi di dark sono stati sottratti ai fotogrammi raw.
L’operazione è stata ripetuta sia per il filtro V che per quello B.
,>?@ = ,?@ − A?@
dove ,>?@ è l’immagine finale dell’ammasso ottenuta sottraendo il rumore.
36
Capitolo 3 L’ammasso aperto NGC 6633
3.5.3 Acquisizione dati
2) Ai fotogrammi di flat sono stati sottratti i darkflat. L’operazione è stata
ripetuta sia in filtro V che in filtro B.
>?@ =
?@
−A
?@
dove >?@ è il flat a cui è stato sottratto il rumore.
3) Il passaggio successivo è stato quello di normalizzare il segnale di flat:
⟨
dove ⟨
?@ ⟩
>?@
?@ ⟩
è il segnale medio di flat.
4) L’immagine finale del nostro oggetto sarà dunque l’immagine raw,
ottenuta sottraendo il rumore di dark divisa per il flat normalizzato:
D?@ =
,>?@
⟨> ⟩
>?@ ?@
dove D?@ è l’immagine finale del nostro oggetto.
A questo punto dell’elaborazione, abbiamo ottenuto, in definitiva, N°5
immagini dell’ammasso in filtro V e N°5 immagini in filtro B. Si è fatta
una media delle cinque immagini, dopo averle allineate. La composizione
delle immagini in filtro B e di quelle in filtro V ha fornito un’immagine a
colori dell’ammasso, riportata in figura 15.
Figura 15: Ammasso NGC 6633
37
Capitolo 3 L’ammasso aperto NGC 6633
3.5.4 Analisi dati
La fotometria di apertura è stata fatta col programma CCDSoft. Essa
consiste nel sommare il valore degli ADU dei pixel che si trovano
all’interno di un cerchio di raggio fissato, centrato su ciascuna stella. Il
raggio di apertura è stato scelto uguale alla FWHM delle stelle
dell’immagine, che risultava essere pari a 10 pixel. Questa scelta
consente di massimizzare il rapporto segnale-rumore. Il CCDSoft ha
generato un file di testo .SRC per ciascuna delle due immagini. Ogni file
contiene una tabella, nella quale ogni riga corrisponde ad una stella. Per
ogni stella il file riporta le coordinate (x,y), la magnitudine strumentale e
la FWHM, oltre ad altre informazioni che non utilizziamo.
L’elaborazione successiva è stata fatta utilizzando il programma
Mathematica. I file .SRC ottenuti per il filtro V e per il filtro B sono stati
importati dal programma. Siamo arrivati alla parte vera e propria
dell’analisi dati.
3.5.4 Analisi dati
Per costruire il diagramma colore-magnitudine è stato necessario trovare
la corrispondenza tra le stelle di un file .SRC e quelle dell’altro file .SRC.
Per prima cosa, abbiamo individuato la stella più luminosa, in ciascuno
dei due file, riscontrando una differenza tra le coordinate (x,y). Questo
offset è stato sottratto alle coordinate di tutte le stelle del secondo file
.SRC, al fine di riallineare le due immagini. A questo punto, per ogni
stella del primo file, abbiamo cercato nel secondo file la stella che
distasse di meno da quella del primo, in modo da ottenere la
corrispondenza tra tutte le stelle del primo e del secondo file (matching
stellare). Per ogni stella abbiamo ottenuto, quindi, le magnitudini
strumentali nei filtri B e V. Per calibrare le nostre magnitudini abbiamo
utilizzato la stella di riferimento SAO 123493, le cui magnitudini
apparenti sono mV=8.29 e mB=8.52. Questo ci ha permesso di
rappresentare tutte le stelle nel piano [B-V, V].
Il passo successivo è stato quello di calcolare l’isocrona, per poterla
integrare nel grafico CMD e verificare l’andamento dei dati ottenuti. Il
programma di riferimento utilizzato per il calcolo è: IAC-STAR synthetic
color-magnitudine diagram computation alghoritm.
I parametri utilizzati per il calcolo sono presi dai valori riportati
nell’articolo, riguardanti l’ammasso NGC 6633:
metallicità Z= 0.02, età dell’ammasso = 600 Myr
Il grafico finale CMD completo di isocrona è riportato in figura 16.
38
Capitolo 3 L’ammasso aperto NGC 6633
3.5.4 Analisi dati
Figura 16: Grafico sperimentale CMD completo di isocrona
Figura 17: Grafico CMD completo di isocrona ottenuto da Jeffries, Totten,
Harmer e Deliyannis nel loro studio su NGC 6633. Gli oggetti di cui è stata fatta
la spettroscopia sono rappresentati da quadrati, quelli che sono considerati
appartenere all’ammasso sono rappresentati da quadrati riempiti. La linea
rappresenta un’isocrona arrossata.
39
Capitolo 3 L’ammasso aperto NGC 6633
3.5.4 Analisi dati
Osservando la figura 16, si evince la presenza di una stella del ramo delle
sub-giganti. La stella in questione è SAO 123496, di classe spettrale A2,
di mV =8.21 e mB = 8.95.
Riportiamo in figura 18 un’immagine dell’ammasso che evidenzia le stelle
utilizzate nel diagramma colore-magnitudine ottenuto.
Figura 18: Immagine a colori dell’ammasso NGC 6633 che mette in evidenza le
stelle considerate per la costruzione del diagramma CM ottenuto
sperimentalmente. La freccia in giallo evidenzia la sub-gigante SAO 123496,
quella in rosso la stella SAO 123493, usata per la calibrazione.
In figura 19, è riportato un grafico dell’errore poissoniano associato al
diagramma CM ottenuto: è rappresentato sia l’errore in banda V che
quello in banda B.
40
Capitolo 3 L’ammasso aperto NGC 6633
3.6 L’articolo di Jeffries, Totten, Harmer e Deliyannis
Figura 19: Errore associato al diagramma CM in banda V in banda B
3.6 L’articolo di Jeffries, Totten, Harmer e Deliyannis
Gli autori hanno effettuato osservazioni spettroscopiche e fotometriche di
NGC 6633.
Le osservazioni spettroscopiche riguardano stelle di tipo spettrale F, G
e K dell’ammasso NGC 6633, ovvero stelle di tipo solare che, negli
ammassi aperti, sono importanti per lo studio dell’evoluzione e delle scale
di tempo di molti fenomeni fisici. Ad esempio, gli ammassi delle Pleiadi e
delle Iadi sono stati ampiamente studiati e hanno fornito informazioni
determinanti sull’emissione di raggi X e le abbondanze superficiali di litio.
Gli autori, utilizzando anche i risultati di un precedente articolo di Jeffries
(1997), hanno ritenuto che lo studio di NGC 6633, un ammasso con età
molto vicina alle Pleiadi e alle Iadi, potesse fornire informazioni
importanti, visto che ogni ammasso ha un suo proprio momento
angolare, che ne influenza il comportamento successivo, e differenti
abbondanze di elementi chimici.
Dagli spettri hanno individuato una decina di stelle di tipo solare, incluso
un sistema binario a corto periodo. Sono state considerate anche le circa
30 stelle studiate da Jeffries in precedenza.
Studi di NGC 6633 hanno stimato la metallicità dell’ammasso, risultando
inferiore a quella di altri ammassi di riferimento della stessa età. Schmidt
(1976) ha stimato anche una distanza di 348 pc, Cameron (1985) di 336
pc. Il catalogo Lynga (1987) utilizza come valori di riferimento medie
41
Capitolo 3 L’ammasso aperto NGC 6633
3.6 L’articolo di Jeffries, Totten, Harmer e Deliyannis
pesate di differenti studi, fornendo in definitiva [M/H] = -0.11, un’età di
630 Myr, una distanza di 312 pc e un valore E(B-V)=0.17.
La fotometria dalla quale hanno selezionato le stelle dell’ammasso è
presa dallo studio descritto da Jeffries (1997) e Harmer (2001). Si tratta
di esposizioni brevi (10 s) e lunghe (200 s) nei filtri B, V, I.
Entrando nel merito del lavoro, il diagramma [B-V, V] è stato fatto su
stelle che vanno da V=10.5 (la saturazione nelle esposizioni ha limitato la
fotometria a tale valore) fino a V≈20, utilizzando un algoritmo di Naylor
(1998) che genera diagrammi colore-magnitudine degli ammassi aperti.
Il diagramma riportato in figura 17 utilizza un’isocrona arrossata e la
scelta dei campioni spettroscopici è stata fatta anche in base alla distanza
dalla sequenza principale di riferimento: si è scelto come criterio una
distanza pari a ±0.5 in V. Il criterio non è stato selettivo in maniera
assoluta, specie nelle regioni limite del diagramma, dove molte stelle
sono chiaramente fuori dalla sequenza principale. In realtà, c’è un’unica
stella (J104) che risulta essere più di una magnitudine al di fuori della
sequenza principale.
Gli autori hanno selezionato le stelle di NGC6633 scegliendo quelle che
hanno una velocità radiale simile alla velocità media dell’intero ammasso.
Il criterio di selezione è stato il seguente: la velocità radiale media pesata
di una stella deve rientrare entro un intervallo di 2σ della velocità media
dell’ammasso, dove σ è la somma quadratica dell’errore sulla velocità
radiale e della dispersione prevista di ≈1 km s-1 di un ammasso aperto.
Dunque, in pratica, sono state scelte stelle che rientrassero in un
intervallo di ±5 km s-1 rispetto alla velocità media dell’ammasso,
stimata essere pari a -28 km s-1. Gli autori dichiarano di non aver
certamente osservato tutte le possibili stelle dell’ammasso, almeno per
V>15; sicuramente per V<18 il catalogo fotometrico è completo al 97%.
L’incompletezza non è di per sé un problema, lo è maggiormente il fatto
di includere stelle non appartenenti all’ammasso, poiché la presenza di
taluni oggetti esterni può influenzare la stima della presenza di litio. La
contaminazione purtroppo resta un problema, poiché il moto proprio
molto ridotto dell’ammasso ne rende difficile una valutazione più precisa
che potrebbe essere di aiuto. Una valutazione più accurata delle velocità
radiali permetterebbe, inoltre, una scrematura maggiore dei campioni
spettroscopici, ma, a causa della dispersione intrinseca dell’ammasso, si
otterrebbe, di contro, anche l’eliminazione di stelle appartenenti ad esso.
Gli autori hanno verificato che la metallicità è inferiore a quella di
ammassi di età simile, come le Iadi e il Presepe. Ne è stata fatta sia una
stima spettroscopica che una fotometrica. La prima ha fornito un valore
di [Fe/H]=-0.096±0.081.
42
Capitolo 3 L’ammasso aperto NGC 6633
3.6 L’articolo di Jeffries, Totten, Harmer e Deliyannis
La stima fotometrica della metallicità di NGC 6633 è fortemente
legata all’arrossamento. Il fattore correttivo di arrossamento E(B-V)
è stato stimato essere 0.165 ± 0.011, dove 0.011 è una stima
dell’errore associato al colore intrinseco di ogni stella dell’ammasso.
Utilizzando tale valore, si è ottenuto [Fe/H]=-0.04±0.10. Vale la pena
spiegare brevemente come è stata fatta la correzione sull’arrossamento
delle stelle.
Sono state utilizzate le relazioni trovate in studi precedenti sull’ammasso:
E(B-V) =E0 (B-V) [1-0.08 (B-V0)]
(3.4)
E(F;GH )
E(I;F)
(3.5)
= J 1 + 0.06(P − Q) + 0.014S(P − Q)
dove (B-V)0 è il colore intrinseco, E0 (B-V) è l’eccesso di colore per una
stella con (B-V)0=0 e C0 è il valore relativo ad una stella con (B-V)0=0
I valori utilizzati sono stati i seguenti:
E(V-IC) è calcolato dalla (3.5)
C0 =1.29 ± 0.04
(B-V)0≈0.6
Avendo determinato l’arrossamento dell’ammasso e la sua metallicità, gli
autori hanno infine stimato la distanza tramite un fitting di sequenza
principale. Il modello di sequenza principale di NGC 6633 è stato
generato utilizzando i calcoli teorici di Siess, Dufour & Forestini (2000),
assumendo un età dell’ammasso di 600 Myr. Il modello empirico di
riferimento è quello delle Pleiadi, dunque va sottolineato che la distanza
calcolata è strettamente relativa ad una distanza assunta per le Pleiadi.
Dunque, in definitiva, utilizzando la metallicità fotometrica (-0.04± 0.10),
la distanza di NGC 6633, relativa ad una distanza delle Pleiadi di 118
pc, è di (358 ± 40) pc.
43
Capitolo 3 L’ammasso aperto NGC 6633
3.7 Conclusioni
3.7
Conclusioni
Il lavoro sperimentale risulta essere in buon accordo con i risultati
dell’articolo, come si evince dalle figure 16 e 17. L’intervallo di
magnitudini in cui ricadono le stelle osservate è diverso nei due casi:
8<V<16 nel nostro caso, 10<V<20 nel caso dell’articolo. Gli autori hanno
avuto la possibilità di arrivare a magnitudini più spinte, essendo questo
ovviamente legato all’utilizzo di siti osservativi migliori e di ottiche più
avanzate.
Il diagramma colore-magnitudine ottenuto rispecchia piuttosto bene
l’isocrona. Esiste un problema legato alla contaminazione dell’ammasso.
Purtroppo, la regione di cielo in cui si trova NGC 6633 è molto affollata.
La situazione è evidente in entrambi i grafici, maggiormente nel caso
dell’articolo. La figura 17, infatti, rende evidente la presenza di molte
stelle non appartenenti all’ammasso, specie nella parte inferiore del
grafico. Sicuramente, il guadagno in magnitudini degli autori è stato
contrastato dalla presenza di una maggiore contaminazione di materiale
stellare. Se si osserva la figura 16, si evince che, anche nel nostro caso, a
magnitudini comprese nell’intervallo tra 14 e 16, c’è una presenza
piuttosto forte di stelle non appartenenti all’ammasso.
44
Appendici
A1 La magnitudine
Appendici
A1 La magnitudine
La luminosità apparente delle stelle (flusso di energia o energia ricevuta
nell’unità di tempo e per unità di area) si misura in termini della loro
magnitudine apparente. Gli astronomi greci divisero le stelle in sei
gruppi di magnitudini equidistanti tra loro in luminosità. Le stelle più
luminose erano di prima magnitudine, mentre quelle più difficili da vedere
ad occhio nudo erano di sesta magnitudine. Studi successivi hanno
evidenziato il fatto che differenze uguali di luminosità percepite
dall’occhio corrispondono a uguali rapporti di energia radiante; questo
vuol dire che la risposta dell’occhio allo stimolo della luce è di tipo
logaritmico rispetto all’intensità. Quindi, se m1 e m2 denotano le
magnitudini assegnate alle stelle con flussi di energia f1 e f2, si avrà:
m1 –m2 = -k log10
(1.1 A)
dove il segno meno permette di associare valori numerici più piccoli alle
stelle più luminose.
Studi fotometrici nel diciannovesimo secolo mostrarono che stelle di sesta
magnitudine sono circa cento volte più deboli di quelle di prima
magnitudine. Dunque, seguendo la proposta di N. Pogson, si definì un
sistema di magnitudini in cui una differenza di 5 magnitudini corrisponde
esattamente a un fattore di cento nel rapporto dei flussi di radiazione.
Quindi, poiché f1/f2 = 100, m2-m1=5. Quindi, il valore di k dell’equazione
precedente è pari a 2.5 e si ottiene, in definitiva:
m1 –m2 = -2.5 log10
(1.2 A)
oppure
= 10;
. (T ;T )
(1.3 A)
E’ da notare che m1-m2 = 0.921 loge (f2/f1), così che la scala definita dagli
antichi Greci era essenzialmente basata sul logaritmo naturale. In
particolare, se (f1/f2) = 1+∆f è vicina all’unità (∆f <<1), si avrà:
∆m≡m2 –m1 ≈1.086 ∆f
(1.4 A)
cioè la differenza di magnitudine tra due oggetti (se piccola) è uguale alla
piccola differenza delle loro luminosità relative.
Segue dall’equazione (1.3 A) che la differenza di una magnitudine
corrisponde al rapporto tra i flussi di 100.4 ≈2.512, e 2.5 magnitudini
corrispondono a un rapporto tra i flussi di 10.
45
Appendici
A2 Il colore
Il flusso di energia che riceviamo sulla Terra da un oggetto celeste
dipende sia dalla sua luminosità intrinseca che dalla sua distanza. Se F è
il flusso ricevuto quando l’oggetto è a distanza D, il flusso f che
riceveremmo se l’oggetto fosse a distanza d è dato dalla legge (1.5 A).
5 =
U 1
V
(1.5 A)
Ovviamente, più lontano è un oggetto più ci apparirà poco luminoso e,
per ottenere informazioni sulla sua luminosità intrinseca, dobbiamo tener
conto delle differenti distanze che ci separano dagli oggetti in questione.
Definiamo quindi la magnitudine assoluta M come la magnitudine
apparente che un oggetto dovrebbe avere se fosse localizzato ad una
distanza standard D. Dalle equazioni (1.2 A) e (1.5 A), otteniamo:
W − X = −2.5
= 5
V
U
(1.6 A)
La quantità (m-M) è chiamata modulo di distanza dell’oggetto. Se
conosciamo m e d, riusciamo ad ottenere immediatamente M
dall’equazione (1.6 A). Viceversa, se conosciamo m e M, ricaviamo d.
A2 Il colore
Supponiamo di avere un sistema fotometrico con diverse bande di filtri a
lunghezze d’onda differenti. Prendendo la differenza in magnitudine
misurata in due bande differenti, possiamo formare un colore, o indice
di colore.
Il sistema fotometrico usato oggi è basato sul
(Ultravioletto- Blu-Visibile) di Johnson & Morgan (1953)
sistema
UBV
Le lettere corrispondono a diversi filtri:
U per ultravioletto, B per blu, V per visuale
Le lunghezze d’onda centrali dei filtri sono, pressappoco, le seguenti:
U: 3600 Angstrom
B : 4400 Angstrom
V: 5500 Angstrom
La banda passante è di circa 1000 A per ciascun filtro nel sistema a
banda larga UBV. Ad esempio, il filtro B lascia passare la luce compresa
tra 3900 Angstrom e 4900 Angstrom.
Un altro sistema usato è quello a cinque colori, il sistema UBVRI (dove
R sta per rosso e I sta per infrarosso).
46
Appendici
A2 Il colore
Si definiscono le magnitudini nella banda di ciascun filtro. Ad esempio mV
(o anche solo V) rappresenta la magnitudine con il filtro V. Il colore di un
oggetto è correlato alla variazione del flusso in funzione della lunghezza
d’onda. Usando filtri a banda larga, come gli UBV, si definisce l’indice di
colore come la differenza tra le magnitudini misurate in due diversi colori.
In pratica:
B-V= mB-mV
(2.1 A)
definisce l’indice di colore come B-V.
Quale informazione ci dà B-V circa l’indice di colore di un oggetto? Dalla
definizione (1.1A), si vede che una differenza di magnitudini corrisponde
ad un rapporto di flusso. Il rapporto è rappresentato dal flusso nella
banda B rispetto a quello nella banda V per lo stesso oggetto, invece di
due oggetti distinti:
B-V =mB-mV= -2.5 log10 (fB/fV) +k
(2.2 A)
dove fB è la media del flusso con il filtro B e fV la media del flusso con il
filtro V, mentre k è una costante, che compare nell’equazione per il modo
in cui è stato definito il punto di zero del sistema dei colori.
Si potrebbe pensare che se si ha B-V = 0,00, allora fB = fV, ma non è
questa la definizione data.
Storicamente, gli astronomi hanno selezionato un gruppo di stelle di tipo
A (inclusa Vega), ed hanno definito il colore medio di queste stelle in
modo da avere tutti i colori uguali a 0,00. Per una stella A, fB non è mai
uguale a fV, in tal modo risulta necessario introdurre una costante non
nulla, nella equazione (2.2 A), per far sì che il colore risulti pari a 0,00.
Così il colore B - V di Vega risulta 0,00, praticamente per definizione.
Il colore B-V del Sole, più rosso di Vega, è circa 0,67.
Valori di B-V inferiori a 0,00 indicano semplicemente oggetti più blu di
Vega.
47
Bibliografia
Bibliografia
Bergbusch P.S. & VandenBerg D.A. (1992), ApJS, 81, 163
Binney James and Merrifield Michael (1998), Galactic
Princeton Series in Astrophysics, New Jersey
Astronomy,
Cameron L.M. (1985), A&A, 147, 39
Harmer S., Jeffries R.D., Totten E.J., Pye J.P. (2001), MNRAS, 324, 473
Janes K.A. & Phelps R.L. (1994), AJ, 108, 1773
Jeffries R.D. (1997), MNRAS, 292, 177
Jeffries R.D., Totten E.J., Harmer S. and Deliyannis C.P. (2002),
“Membership, metallicity, and lithium abundances for solar-type in NGC
6633”, Royal Astronomical Society, 336, 1109-1128
Lynga G. (1987), Catalog of Open Clusters, Centre de Données Stellaires,
Strasbourg
Mermilliod J.C. (1980), In Star Clusters, IAU Symp. 85, Hesser
Morgan W.W., Keenan P.C. & Kellerman E. (1943), An Atlas of Stellar
Spectra, Chicago University Press, Chicago
Naylor T. (1998), MNRAS, 296, 339
Ostlie Dale A. and Carroll Bradley W. (1996), An Introduction to Modern
Stellar Astrophysics, Addison-Wesley Publishing Company, USA
Romanishin William (2001), An introduction to Astronomical Photometry
using CCDs, University of Oklahoma
Schmidt E.G. (1976), PASP, 88, 63
Siess L., Dufour E., Forestini M. (2000), A&A, 358, 593
Spitzer L. (1958), ApJ, 127, 17
Stetson P.B. (1993), In The Globular Cluster-Galaxy Connection, ASP
Conf. Ser., Smith & Brodie, San Francisco
Trumpler R.J. (1930), Lick Obs. Bull., 14, 154
Van den Bergh S. & McClure R.D. (1980), A&A, 88, 360
48
Ringraziamenti
Ringraziamenti
“...a volte deve pur succedere che nell’avventura d’un libro riuscito o
nell’esistenza d’uno scrittore fortunato, ci sia stato qualcuno, un poco in
disparte, che non lascia passare la frase inesatta o debole che per
stanchezza vorremmo lasciare; qualcuno capace di rileggere con noi fino
a venti volte, se è necessario, una pagina incerta [...]; qualcuno che ci
sostiene, ci approva, alle volte ci contraddice; che partecipa con lo stesso
fervore alle gioie dell’arte ed a quelle della vita [...]; e non è né la nostra
ombra né il nostro riflesso e nemmeno il nostro complemento, ma se
stesso; e ci lascia una libertà divina ma, al tempo stesso, ci costringe ad
essere pienamente ciò che siamo.” (Marguerite Yourcenar)
Durante questo percorso di studi così affascinante e intenso, ma anche
pieno di difficoltà e qualche amarezza, è stato fondamentale il supporto
che ho ricevuto dalle persone vicine a me.
Potrei dire che la caparbietà e la mia voglia di andare avanti, nonostante
tutto, siano stati essenziali per arrivare alla fine di un percorso non
semplice. Non nego che a volte lo sconforto e la stanchezza siano stati
acerrimi nemici contro i quali ho dovuto combattere. Anzi, a dir la verità,
queste “battaglie mentali” più volte mi hanno vista perdente.
Due forti motivazioni mi hanno permesso di andare avanti. In primis,
l’amore indiscusso per la conoscenza: non potrei farne a meno, sarebbe
come negare una parte di me stessa.
Secondo motivo, ma non meno importante, la voglia di non deludere chi
ha creduto in me sin dall’inizio. Ho sempre pensato che se non ci
sentiamo compresi ed amati, difficilmente possiamo essere quello che
siamo.
E qui potrei iniziare con un lungo elenco. Ma vale la pena fare le cose per
bene.
Grazie al Professor Bozza per la disponibilità immensa che mi ha dato e
per la “divina libertà” di espressione che mi ha lasciato. Ha rispecchiato in
pieno, lungo tutto il cammino di questo lavoro, l’idea che ho del Fisico
ideale. Competenza, creatività e...passione, passione e ancora passione.
Un grazie particolare va ai miei genitori: hanno creduto in me e mi hanno
fatta sentire costantemente una persona migliore, probabilmente anche
molto più di quello che, in realtà, io sia.
49
Ringraziamenti
Grazie a mia sorella, sempre discreta, mi ha fatto sentire la sua presenza
nei momenti più difficili.
Grazie di cuore a Samantha, Amica di infanzia, Amica oggi, Amica
sempre. Questo percorso di studi condiviso con lei è stato per me una
fonte costante di crescita e confronto. Il sostegno, la comprensione, la
presenza...Cose impagabili che solo un’Amicizia come la sua avrebbe
potuto darmi.
Un grazie immenso va a Simona: senza il suo sostegno, la sua fiducia
incondizionata, il suo sentirmi dire sempre, anche nei momenti più bui,
“sono fiera di te”, senza tutto ciò, oggi non sarei quella che sono. Le mie
insicurezze e fragilità sono ancora lì, ma adesso, grazie a lei, ho più forza
per affrontarle.
Grazie alle mie Amiche, sostegno impagabile in molti momenti.
Infine, grazie ai miei nonni, di cui porto la loro parte più bella dentro di
me. Due di loro mi hanno lasciata poco prima di questo evento per loro
così importante. Ed è a loro che dedico questo giorno.
50