lezioni 11-12

Trasp. 84
Campo magnetico
Campo magnetico
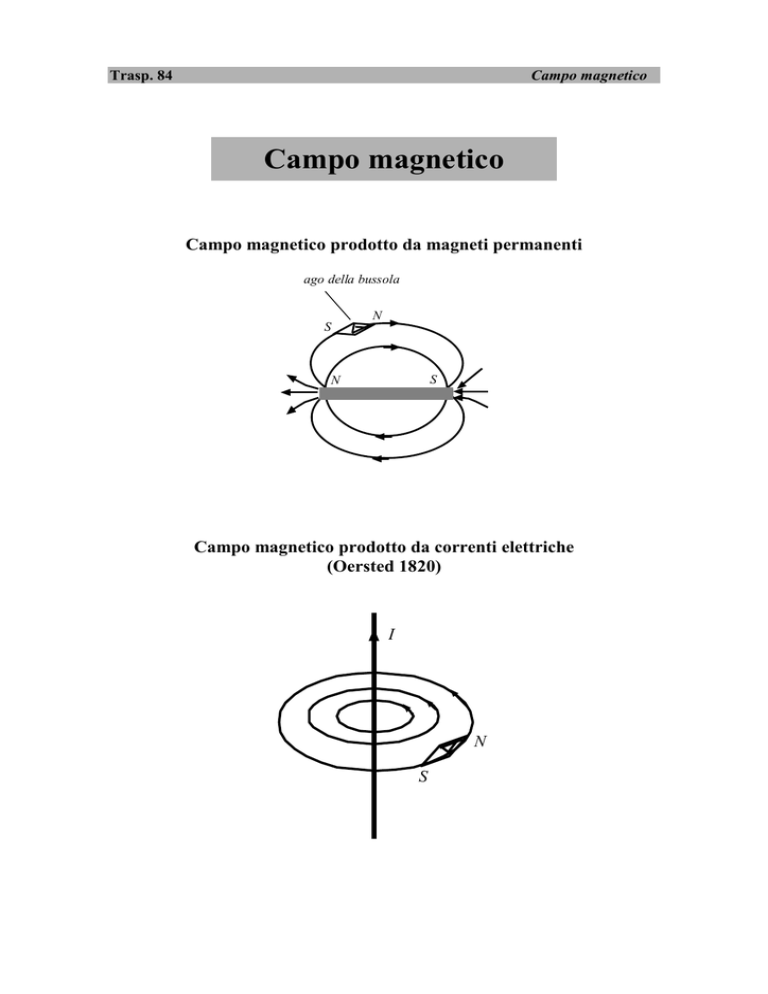
Campo magnetico prodotto da magneti permanenti
ago della bussola
N
S
S
N
Campo magnetico prodotto da correnti elettriche
(Oersted 1820)
I
N
S
Trasp. 85
Campo magnetico
Forze tra correnti elettriche
(Ampère 1821)
I
I
F
-F
Definizione del campo magnetico
Campo vettoriale - simbolo: B
elemento di corrente in un campo magnetico
B
I dl
dl
F
Osservazioni sperimentali:
Trasp. 86
Campo magnetico
1.
all’elemento di corrente è applicata una forza (forza magnetica)
perpendicolare a I dl.
2.
Vi è un’unica direzione per cui all’elemento di corrente non è
applicata alcuna forza: è la direzione di B.
3.
La forza è perpendicolare alla direzione di dl e alla direzione di B.
4.
L’intensità della forza è proporzionale alla lunghezza dell’elemento
di corrente, all’intensità della corrente I e a sin ( = angolo tra il
vettore I dl e il vettore B):
dF  B I dl sin 
B

I dl
F
Definizione di B
dF  I dl B
Unità di misura nel sistema SI: tesla (T = N A-1 m-1)
Forze magnetiche su correnti elettriche
Trasp. 87
Campo magnetico
Spira o tratto di filo percorso da corrente I in un campo B
FI
Esempio:
 dl B
l
filo rettilineo di lunghezza l percorso da corrente I in campo
magnetico B uniforme.
B
I

F
FI lB
F  I l B sin 
Interpretazione atomica della forza magnetica
I   Ne ev A
(v  v d )
Trasp. 88
Campo magnetico
(ved. Trasp. 78)
F  Ne e v A l  B  A l Ne e v  B
Forza sul singolo portatore di carica (elettrone)
F1  e v  B
Forza di Lorentz
Forza a cui è soggetta la carica q in moto
con velocità v in un campo B
F  qv B
B
-F

v
(-q)
q
F
Osservazioni
1.
La forza di Lorentz ha direzione perpendicolare al piano contenente
v e B. Il verso è dato dalla regola del prodotto vettoriale e dal
segno di q.
Trasp. 89
2.
Campo magnetico
Il modulo della forza di Lorentz è
F  q v B sin 
v0
 0


2
2.

F0

F0

Fmax  q v B
Il lavoro compiuto dalla forza di Lorentz durante lo spostamento
della carica a cui è applicata è nullo:
dW  F dr  F vdt  0
(Fv)
Carica in moto in un campo elettrico
e in un campo magnetico
Formula di Lorentz
F  q E  v  B
Spira in un campo magnetico uniforme
Trasp. 90
Campo magnetico
F 2  F 4

effetto nullo
F1  F3
(coppia)

rotazione della spira
Trasp. 91
Campo magnetico
F  F1  I Ba
  Fb sin 
(momento meccanico)
  I B a b sin   I ABsin 
mIA
(momento magnetico della spira)
  m B sin 
= mB
Dipolo magnetico in un campo B
Trasp. 92
Campo magnetico
= mB
Energia di un dipolo magnetico in un campo B
Lavoro W per ruotare il dipolo da 0 a 
W
W

   d
0

 mBsin  d  mBcos
0
0
 cos 
Variazione di energia potenziale
Trasp. 93
Campo magnetico

W  U  U0
U0  0  0   / 2
Energia del dipolo magnetico in B

U  m Bcos
U   m B
Campo magnetico prodotto da correnti
Legge di Biot-Savart
Trasp. 94
Campo magnetico
Campo B prodotto da un elemento di corrente
dB 
 0 Idl sin 
4
r2
Legge di Biot-Savart
dB 
 0 Idl  rˆ
4 r 2
Permeabilità magnetica del vuoto
 0  4  10 7 N A 2
Osservazioni
1.
Altre unità di misura del campo magnetico B:
SI

T = N A-1 m-1 = V s m-2 = Weber m-2
Trasp. 95
Campo magnetico
1 gauss = 10-4 tesla
2.
Altre unità di misura della costante 0:
SI

N A-2 = T A-1 m = Henry m-1
3.
Il vettore dB giace in un piano perpendicolare alla direzione di dl
ed è perpendicolare al piano individuato da dl e r.
4.
Le linee di forza di B (linee di induzione) sono ciconferenze
giacenti su piani perpendicolari alla direzione di dl. Il loro verso è
concorde con quello di rotazione di una vite destrorsa che avanza
nel verso della corrente.
5.
Legame tra la costante dielettrica e la permeabilità magnetica del
vuoto:
 0 0 
1
c2
Campo B prodotto da un circuito (spira)
Trasp. 96
Campo magnetico
B
r
dl
I
l
Legge di Biot-Savart generalizzata
B
0
4

l
Idl  rˆ
r2

L’integrando è un campo vettoriale

integrare sulle tre componenti
Trasp. 97
Applicazioni della legge di Biot-Savart
Applicazioni della legge di Biot-Savart
1.
Campo magnetico sull’asse di una spira circolare
dl
r
dB
R

dB
P
dB x
x
I
dB
dB
dB 
 dB
y
0
 dB
z
dBx  dB cos  
 0 I dl
4  r2
0

By  0
Bz  0
0 R

R
I
dl  0 I
dl
4 r 3
4  R2  x 2 3/2
Bx =
Bx =
0
 dB
l
x
I R2
2 R2  x 2 3/2
Centro della spira
Trasp. 98
Applicazioni della legge di Biot-Savart
x0
Bx 
0 I
2 R
Grande distanza dalla spira
x 
Bx 
B
I
 0 I R2
2
x3
Trasp. 99
2.
Applicazioni della legge di Biot-Savart
Momento di dipolo magnetico di una spira
m
I
A
Modulo del momento di dipolo magnetico m
mIA
Unità di misura nel sistema SI: A m2 (J T-1)
Campo magnetico nel centro della spira
B
0 m
2  R3
A grandi distanze dal dipolo (sull’asse)
Bx 
 0 2m
4 x3
Confronto tra dipolo elettrico e dipolo magnetico
Trasp. 100
Applicazioni della legge di Biot-Savart
linee di campo aperte
linee di campo chiuse


p
m
Dipolo elettrico
Dipolo magnetico
Componenti dei campi a grandi distanze dai dipoli
Dipolo elettrico
Er 
1 2p
cos
4  0 r 3
E 
1
4  0
p
sin 
r3
Dipolo magnetico
Br 
 0 2m
cos 
4  r3
B 
0 m
sin 
4  r3
Trasp. 101
Teorema di gauss per B
Il teorema di Gauss per il campo B
Flusso del campo magnetico
Superficie aperta:
B 
 B dS   B cos dS
B 
 BdS   B cos dS
S
S
Superficie chiusa:
S
S
Unità di misura nel sistema SI: Weber (Wb = T m2)
Teorema di Gauss per il campo B
Trasp. 102
Teorema di gauss per B
Il flusso del campo magnetico attraverso
una superficie chiusa è sempre nullo
B  0

 B  dS  0
S
Osservazioni
1.
B = 0 esprime il fatto che non esistono cariche magnetiche
isolate (monopoli magnetici);
2.
Le linee di campo di B sono sempre linee chiuse: non vi sono punti
sorgenti del campo.
Trasp. 103
Teorema di Ampère
Teorema di Ampère
Circuitazione del campo B
CB 
 B  dl
l
l = linea di integrazione chiusa
B

dl
l
Teorema di Ampère
CB   0 I

 B  dl  
l
0
I
Trasp. 104
Teorema di Ampère
I = somma delle sole correnti concatenate con la curva chiusa
I
I
k
k

l
I1
I2
I3
Osservazioni
1.
Il teorema di Ampère è valido solo per correnti stazionarie e per
campi magnetici che non variano con il tempo (statici).
2.
CB = 0 non significa necessariamente che B = 0 in ogni punto, ma
solo che la corrente totale, attraverso un’area di cui la curva chiusa
è contorno, è nulla.
Azione del campo magnetico su
Trasp. 105
Teorema di Ampère
cariche elettriche in moto
Forza tra fili rettilinei percorsi da corrente
I2
I1
dl 2
r
B1
F 2  I2
 dl
2
 B1
F2
x B1
Trasp. 106
Teorema di Ampère
I2
I1
dl1
B2
F1
r
B2
F1  I1
F2  I2


dl1  B2
 0 I1
 II
dl  0 1 2 l
2 r 2 2 r 2
Forza par unità di lunghezza (N m-1)
f2  f1 
 0 I1 I2
2 r
Trasp. 107
Teorema di Ampère
F 2  F1
f 2  f 1
I2
I1
F1
r
F2
I2
I1
F1
r
Applicazioni del teorema di Ampère
F2
Trasp. 108
1.
Teorema di Ampère
Campo B prodotto da un filo rettilineo indefinito percorso da
corrente I
CB  B
 dl  B 2 r 
l
Teorema di Ampère
Trasp. 109
Teorema di Ampère

B 2 r    0 I

B
2.
0 I
2 r
Campo B all’interno di un cavo coassiale percorso da corrente I.
r
I
I
B
R1
R2
1)
All’interno (tra i due conduttori)  filo rettilineo indefinito.
2)
All’esterno  corrente totale nulla  B = 0.
Trasp. 110
Teorema di Ampère
B
0 I
2 r
B0
3.
R1  r  R2
r  R2
Campo B prodotto da un solenoide percorso da corrente I.
B
I
Solenoide indefinito
Campo B uniforme all’interno del solenoide (linee di campo parallele
all’asse), nullo all’esterno.
Trasp. 111
Teorema di Ampère
l
A
B
a
CB  B a
N 
B a   0  a I
 l 


B  0 n I
l = lunghezza del solenoide.
N = numero di spire del solenoide.
n = N/l = numero di spire per unità di lunghezza.
B
Trasp. 112
Onde elettromagnetiche
Moto di una particella carica in un campo magnetico
1.
Moto circolare in un campo magnetico uniforme
S
q
+
B
v
N
F qvB
F  q v B sin 
Trasp. 113
Onde elettromagnetiche
v
+
q
•
•
•
B
v
•
•
•
•
•
•
+
q
K
K
1
m v 2  costante
2
1
m v 2  costante
2
F v

moto circolare uniforme (a = accelerazione centripeta = v2/r)
Fma

qv B 
m v2
R
Trasp. 114
Onde elettromagnetiche
R
T
mv
qB
2 R 2 m

v
qB
f
qB
2 m
c 
q
B
m
(frequenza di ciclotrone)
La frequenza di ciclotrone è indipendente
dalla velocità della particella
Velocità della particella non perpendicolare a B
Trasp. 115
Onde elettromagnetiche
B

y
v
+
q
x
v x  v sin 
v y  v cos
moto risultante elicoidale
B
R
2.
m v sin 
qB
Moto in un campo elettrico e magnetico uniformi(E  B)
Trasp. 116
Onde elettromagnetiche
E
v
z
+
q
B
y
x
FEz  qE
FBz  q v B
La particella non viene deviata se
q E  qv B
v
E
B
Valori di Campi Magnetici
Trasp. 117
Onde elettromagnetiche
T (Tesla)
- Elettromagnete superconduttore
20
- B creato dall’elettrone al centro
10
dell’atomo di idrogeno
- Sulla superficie del Sole
5
- Elettromagnete di laboratorio
2
10-1
- Calamita
5 10-5
- B terrestre
- B a 1 m da un filo rettilineo
percorso da una corrente di 1 A
2 10-7
Valutazioni numeriche
1.
Definizione di ampère (A) (I = 1 A, r=1 m):
f
2.
 0 I 2 4  10 7
7
1

 2 10 N m
2 r
2
Molecola di ossido nitrico (NO - composto paramagnetico) come
dipolo magnetico in un campo magnetico uniforme B = 1.5 T.
Momento di doplo magnetico (permanente) di una molecola di ossido
nitrico:
Trasp. 118
Onde elettromagnetiche
m  9 10 24 JT 1
Energia potenziale minima della molecola in B:
U min
 0
B

B
m
m
U  mB cos
Umin  mB
Umin  (9 10 24 )  (1.5)   1.4 10 23 J
Energia cinetica media della molecola alla temperatura T=400 K:
kT  (1.38 10 23 JK-1 )(400 K)  6 10 21 J
Frazione di molecole allineate con il campo B:
f
1. 4 10 23
3
 2.3 10
6 10 21