E.1 – LA DIVISIBILITÀ
Curiosità
Pitagora nacque a Samo, isola greca nel 576 a. C. A Crotone, in Calabria, fondò una scuola che accoglieva uomini
e donne. Si occupava di matematica, musica e religione.
Pitagora per mostrare che il numero 48 è un multiplo del 2 e del 24 lo rappresentava così:
Scopriremo, a partire dai divisori e dai multipli, il mondo dei numeri primi e dei numeri composti.
Hai imparato che la divisione non è un’operazione interna nell’insieme dei numeri naturali, per esempio possiamo
avere:
36 : 3 = 12 divisione eseguibile in N
27 : 2 divisione non eseguibile in N
possiamo avere due casi:
! divisioni esatte con resto zero (36: 3)
! divisioni non esatte con resto diverso da
zero (27 : 2 ha come resto uno) (fig.1)
Diamo quindi la seguente definizione:
Figura 1: Divisione esatta e con resto
Dati due numeri a e b, si dice che a è divisibile per b se la divisione è esatta,
cioè con resto zero.
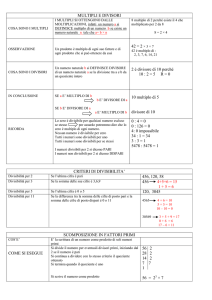
GUARDANDO L’ESEMPIO 36 : 4 POSSIAMO AFFERMARE CHE:
36 E’ DIVISIBILE PER 4
4 E’ UN DIVISORE DI 36
36 E’ UN MULTIPLO DI 4
4 E’ UN SOTTOMULTIPLO DI 36
!
133
E.1.1 – Multipli e divisori
L’omino della memoria ti ha introdotto un nuovo concetto. Abbiamo visto come una divisione esatta possa essere
letta in quattro differenti modi. Per ogni numero naturale è, quindi, possibile determinare un numero infinito di
multipli. Osserva attentamente le immagini proposte.
E.1.2 - Prova TU
Decidi se l’affermazione è corretta:
a. 45 è multiplo di 5
sì!
b.
36 è multiplo di 2 ma non di 12
sì!
c.
f.
!
no!
0 non è multiplo di alcun numero
sì!
e.
no!
Tutti i multipli di 9 sono anche multipli di 3
sì!
d.
no!
no!
I multipli di 4 sono tutti pari
sì!
no!
sì!
no!
36 non è multiplo di 7
134
La ricerca dei divisori
Consideriamo un numero naturale, per esempio 12. Determiniamo i suoi divisori, ricordando che: dati a e b, b è un
divisore di a se la divisione è a : b esatta, ossia il resto è nullo.
Procedendo con le divisioni otterremo che:
E.1.3 - Mettiamo in pratica
1.
Rispondi alle domande:
a.
Se b è un divisore di a, a è multiplo di b?
sì!
b.
0 è un divisore di ogni numero?
sì!
c.
no!
2 è divisor di 27 perche 27 : 2 = 13 con resto 1?
sì!
!
no!
30 è divisibile per 2, per 3 e per 5?
sì!
f.
no!
Un divisor di a è sempre minore o uguale ad a?
sì!
e.
no!
1 è divisore solo di se stesso?
sì!
d.
no!
no!
135
2.
Completa la tabella
Numero
È multiplo di
2
3
5
9
10
11
45
50
3
5
7
9
10
17
49
100
2
10
12
24
36
42
75
100
90
126
168
324
432
630
918
1530
12
24
30
36
55
70
81
90
100
3.
Completa la tabella
Numero
È multiplo di
1
20
35
49
51
72
84
119
200
4.
Completa la tabella
Numero
È divisore di
2
3
4
5
7
10
12
25
50
5.
Completa la tabella
Numero
È divisore di
6
14
18
21
24
30
42
51
87
!
136
6.
Sostituisci ai puntini il termine “multiplo” e “divisore”:
2 è................... di 24;
35 è.................. di 5;
9 è ................. di 72;
28 è................... di 14;
35 è.................. di 140;
72 è ................. di 36;
81 è................. di 9;
3 è...............di 24;
32 è...............di 8;
25 è................. di 75;
100 è...............di 25;
85 è................di 17;
4 è.................. di 16;
42 è................di 6;
7 è................ di 70;
12 è.................. di 36;
11 è...................di 44;
37 è...................di 148;
7.
Scrivi i primi 12 multipli dei seguenti numeri:
a) 4, 7, 8, 9, 11, 15, 25, 30
b) 19, 23, 28, 32, 37, 44, 52, 66
8.
Scrivi tutti divisori dei seguenti numeri:
a) 4, 9, 10, 15, 18, 25, 30, 42
b) 26, 39, 44, 50, 56, 63, 72, 100
9.
Sulla pista di pattinaggio (Kangourou, 2001)
Nikita e Sasha corrono sulla pista dello stadio. Nikita impiega 3 minuti per ogni giro, mentre Sasha impiega 4
minuti per ogni giro. Partono allo stesso momento. Dopo quanti minuti essi passeranno ancora la linea di
partenza insieme?
[12]
E.2 – I CRITERI DI DIVISIBILITÀ
Hai imparato che per stabilire se un numero a è divisibile per un numero b bisogna eseguire la divisione a : b e il
resto deve essere zero. In alcuni casi, per sapere se due numeri sono divisibili o no, non è necessario ricorrere
alla divisione per controllare se è esatta o no.
Esistono infatti delle regole, che prendono il nome di criteri di divisibilità, che permettono di stabilire se un
numero è divisibile per un altro, senza effettuare la divisione.
Vediamo come cercare i divisori di un numero utilizzando i criteri di divisibilita:
!
137
A questo punto è facile capire il criterio di divisibilità per 10, 100, 1000:
E.2.1 - Prova TU
1.
!
Indica con una crocetta le affermazioni V e quelle F.
a.
Se un numero è divisibile per 2 allora è divisibile anche per 10
V
F
b.
Se un numero è divisibile per 9 allora è divisibile anche per 3
V
F
c.
Un numero è divisibile per 5 se termina con 0
V
F
d.
350 è divisibile per 2, 5 e 100
V
F
e.
990 è divisibile per 11
V
F
f.
350 è divisibile per 2, 5 e 100
V
F
g.
207 è divisibile per 7
V
F
138
OSSERVAZIONE
Se due numeri sono divisibili per uno stesso numero, anche la loro
somma, la loro differenza e il loro prodotto sono divisibili per quel
numero.
ESEMPIO:
I numeri 45 e 30 sono entrambi divisibili per 5, allora
30 + 45 = 75 è divisibile per 5
45 - 30 = 15 è divisibile per 5
45 x 30 = 1350 è divisibile per 5
E.2.2 - Mettiamo in pratica
1.
Scrivi cinque numeri di due cifre divisibili per 2.
2.
Scrivi sei numeri di tre cifre divisibili per 3.
3.
Scrivi otto numeri di due cifre divisibili per 10.
4.
Scrivi cinque numeri di due cifre divisibili per 2, per 5 e per 10.
5.
Cerchia in rosso i numeri divisibili per 2.
8, 26, 91, 13, 80, 44, 15, 18, 52, 63, 22, 150, 401, 557, 204, 600, 326, 1 103, 4 345,
32 324, 55 638
6.
Cerchia in rosso i numeri divisibili per 3.
15, 65, 42, 33, 67, 72, 54, 35, 83, 109, 582, 243, 309, 504, 330, 787, 2 003, 6 892,
72 600, 15 584
7.
Cerchia in rosso i numeri divisibili per 5.
10, 52, 45, 75, 13, 29, 90, 64, 27, 110, 225, 302, 456, 545, 625, 102, 8 910, 6 830,
11 230, 10 208
8.
Cerchia in rosso i numeri divisibili per 7.
17, 56, 107, 123, 182, 235, 315, 924, 364, 462, 5021, 10 626, 32 437, 43 785, 28 665
9.
Cerchia in rosso i numeri divisibili per 11.
77, 111, 242, 433, 542, 792, 377, 462, 165, 4 061, 1 914, 6 835, 73 326, 50 237
10.
Completa i seguenti numeri inserendo una cifra che li renda divisibili per 4.
2.., 6.., 42.., 34.., 12.., 7..8, 3..6, 4..4, 8..2, 8 70.., 6 88.., 5 52.., 3 70.., 32 12..
11. Completa i seguenti numeri inserendo una cifra che li renda divisibili per 9:
6.., 11.., 25.., 52.., 38.., 80.., 1 28.., 9 42.., 8 19.., 1 77.., 94 25.., 35 46..
12. Scrivi cinque numeri divisibili contemporaneamente per 2 e per 3.
13. Verifica quali fra i seguenti numeri sono divisibili per 15 (Basta osservare che sono contemporaneamente
divisibili per 3 e per 5):
30, 136, 279, 105, 240, 335, 606, 840, 2 340, 1 250, 3 645, 3 021, 5 520
14. Scrivi otto numeri divisibili per 18. (Basta osservare che sono contemporaneamente divisibili per 2 e per
9)
15. Dati i numeri 136 e 450, divisibili per 9, verifica che anche la loro somma, la loro differenza e il loro
prodotto sono divisibili per 9.
!
139
16. Completa le seguenti addizioni in modo da ottenere somme divisibili per 100.
358+….., 127+….., 1 388+……, 4 570+…..
17. Completa le seguenti tabelle applicando i criteri di divisibilità:
Numero
È divisibile
per
2
3
4
5
7
9
10
11
È divisibile di
2
3
4
5
7
9
10
11
18
33
56
66
75
88
140
210
360
Numero
147
279
328
385
495
737
972
1240
2184
18. Qual è il più piccolo numero, composto di soli 1, divisibile per 3?
[111]
19. Qual è il più piccolo numero che puoi sommare a 271 per rendere il risultato divisibile per 3 e per 5? [14]
20. Luisa dice a Giorgia: “Se togli 1 a un numero ottieni un numero divisibile per 3 e per 4. Se aggiungi 1 al
numero ottieni un numero divisibile per 5. Qual è il numero?
[49]
21. Scrivi un numero di quattro cifre; poi scrivi un altro numero permutando le stesse cifre. Verifica che la
differenza tra i due numeri è divisibile per 9.
22. Qual è il più piccolo numero di tre cifre divisibile:
sia per 2 sia per 3?
sia per 2 sia per 5?
sia per 3 sia per 5?
contemporaneamente per 2, per 3 e per 5?
!
[102]
[100]
[105]
[120]
140
E.3 – NUMERI PRIMI E COMPOSTI
L’enigma dei numeri primi
Sapete dire qual è il più grande problema insoluto che più affascina i matematici? “L’ipotesi di Riemann”.
La successione dei numeri primi ha rappresentato infatti fin dall’antica Grecia uno dei misteri più affascinanti della
scienza.
La teoria dei numeri primi nasce intorno al 300 a.c. ad Alessandria con Euclide che negli Elementi afferma che
esistono infiniti numeri primi e ogni numero primo può scomporsi nel prodotto di più numeri primi e tale
scomposizione è unica.
Qualche anno dopo Eratostene definisce un metodo per trovare la lista di tutti i numeri primi minori di un dato
numero.
Eulero, circa 2000 anni dopo Euclide, diede una nuova dimostrazione dell’infinità dei numeri primi.
Nel 1859, il matematico tedesco Riemann formulò una sua ipotesi, che sembrava rilevare una relazione tra i primi
e gli altri numeri. Da allora, tale ipotesi ossessiona i matematici, e oggi chi riuscisse a dimostrarla conquisterebbe
fama immortale.
Oggi la disponibilità di computer con elevate capacità di calcolo ha permesso di scoprire numeri primi sempre più
grandi, tuttavia sappiamo ancora molto poco sui numeri primi, in particolare:
• Non si conosce una formula che permetta di generare i numeri primi, una regola per stabilire ad esempio
quale sarà il centesimo numero primo.
• Non si conosce se ci sia un ordine prevedibile nella serie dei numeri primi.
E.3.1 – Dai divisori ai numeri primi
Consideriamo i numeri:
2, 3, 8, 30, 34, 11, 18, 43
e scriviamo i rispettivi divisori:
D(2) = {1; 2}
D(3) = {1; 3}
D(8) = {1; 2; 4; 8}
D(30) = {1; 2; 3; 5; 6; 10; 15; 30}
D(34) = {1; 2; 17; 34}
D(11) = {1; 11}
D(18) = {1; 2; 3; 6; 9; 18}
D(43) = {1; 43}
Si può notare che i numeri 2, 3, 11 e 43 hanno come divisori solo il numero 1 e se stessi, i rimanenti ne hanno
anche altri.
I numeri 2, 3, 11, 43 si dicono numeri primi, gli altri si dicono numeri composti.
In generale:
Un numero si dice primo se è divisibile solo per 1 e per se stesso, in caso
contrario si dice composto (ammette altri divisori oltre a 1 e a se stesso).
!
141
OSSERVAZIONI:
• IL NUMERO UNO NON VIENE CONSIDERATO NÉ NUMERO PRIMO, NÉ
NUMERO COMPOSTO (PERCHÉ HA UN SOLO DIVISORE)
• I NUMERI PRIMI SONO INFINITI
• I NUMERI PARI, AD ECCEZIONE DEL 2, SONO SEMPRE NUMERI
COMPOSTI, PERCHÉ AMMETTONO COME DIVISORI, SEMPRE, SE STESSI, IL
NUMERO 1 E IL NUMERO 2
• I NUMERI DISPARI POSSONO ESSERE NUMERI PRIMI O COMPOSTI
Algoritmo per riconoscere un numero primo
Supponiamo, per esempio, di voler stabilire se il numero 383 è primo.
Applicando i criteri di divisibilità, notiamo che non è divisibile né per 2, né per 3, né per 5, né per 7, né per 11.
Continuiamo dividendolo per 13, 17, 19,…
Osserviamo che nessuna divisione, fino a quella per 23, è esatta, ed essendo nell’ultima il quoziente 16 minore del
divisore 23, possiamo concludere che 383 è un numero primo.
In generale,
Per riconoscere se un numero è primo,
lo dividiamo per i successivi numeri primi 2,3,5,7,11,13,..
Se otteniamo un quoziente esatto, il numero è composto;
altrimenti continuiamo le divisioni fino a quando non troviamo
un quoziente minore o uguale al divisore.
In tal caso concludiamo affermando che il numero è primo
E.3.2 – La storia racconta
Il più grande numero primo sin qui noto, è composto da ben 17.425.170 cifre. Il nuovo
numero primo è esprimibile come 257.885.161 −1, e oltre ad essere il più esteso numero primo
mai calcolato rappresenta anche un esponente della elusiva classe di numeri nota come
numeri primi di Mersenne (fig.2), dal monaco francese che per primo li studiò nel 17esimo
secolo.
A scoprire il nuovo numero primo è stato Curtis Cooper, matematico della University of
Central Missouri che partecipa al network GIMPS. Per saperne di più:
http://www.magiadeinumeri.it/Mersenne.html
Figura 2: Marsenne
(1588-1648)
Il crivello di Eratostene
Eratostene, grande matematico e geografo, nato a Cirene, all’inizio del terzo secolo a.C., elaborò un procedimento
per ricercare tutti i numeri primi compresi tra due numeri naturali. Tale sistema prese il nome di CRIVELLO di
ERATOSTENE.
E’ un grosso setaccio che consente di separare i numeri primi dai numeri composti.
Vediamo come:
!
142
supponiamo di voler ricercare i numeri primi fino a 120.
Consideriamo la seguente tabulazione:
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
Eliminiamo dalla tabella i multipli del numero 2 (evidenziati in rosso):
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
Proseguiamo considerando il successivo del numero 2, il 3, e eliminiamo dalla tabella i suoi multipli (evidenziati in
rosso):
2
3
5
7
9
11
13
15
17
19
21
23
25
27
29
31
33
35
37
39
41
43
45
47
49
51
53
55
57
59
61
63
65
67
69
71
73
75
77
79
81
83
85
87
89
91
93
95
97
99
101
103
105
107
109
111
113
115
117
119
Ora consideriamo il successivo del numero 3, il 5, e eliminiamo dalla tabella i suoi multipli (evidenziati in rosso):
2
3
5
7
11
13
17
19
23
25
29
31
35
37
41
43
47
49
53
55
59
61
65
67
71
73
77
79
83
85
89
91
95
97
101
103
107
109
113
115
119
Proseguiamo considerando il successivo del numero 5, il 7, e eliminiamo dalla tabella i suoi multipli (evidenziati in
rosso):
2
3
5
7
11
13
17
19
23
29
31
37
41
43
47
49
53
59
61
67
71
73
77
79
83
89
91
97
101
103
107
109
113
119
I numeri che rimangono sono numeri primi.
2
3
5
7
11
13
17
19
23
29
31
37
41
43
47
53
59
61
67
71
73
79
83
89
97
101
103
107
109
113
Ora gioca tu…trovando i numeri primi compresi tra 100 e 200 utilizzando il crivello di Eratostene
!
143
E.3.3 - Prova TU
Indica con una crocetta le affermazioni V e quelle F.
a.
Tutti i numeri pari maggiori di 2 sono composti
V
F
b.
Tutti i numeri dispari sono primi
V
F
c.
Un numero primo ammette come divisori soltanto il numero 1 e se stesso
V
F
d.
Un numero composto ammette come divisori il numero 1 e se stesso e
almeno un altro divisore
V
F
e.
Il numero 1 è il più piccolo numero primo
V
F
f.
Non esistono numeri dispari composti
V
F
E.3.4 - Mettiamo in pratica
1)
Scrivi cinque numeri primi.
2)
Scrivi i numeri primi <20.
3)
Scrivi i numeri primi maggiori di 50 e minori di 100.
4)
Scrivi il numero 7 come somma di due numeri primi.
5)
Scrivi tutti i numeri pari compresi tra 20 e 60 come somma di due numeri primi.
6)
La coppia di numeri primi 3 e 5 sono tali che la loro differenza è uguale a 2. Scrivi dieci coppie di numeri
primi minori di 70, la cui differenza sia uguale a 2.
7)
Riconosci quali, fra i seguenti, sono numeri primi:
23, 21, 43, 55, 71, 81, 89, 47, 63, 91
103, 251, 123, 290, 121, 193, 307, 133
171, 312, 163, 277, 645, 251, 161, 113
8)
Applicando il metodo del crivello di Eratostene costruisci la tabella dei numeri primi compresi tra 150 e
250.
E.4 – SCOMPOSIZIONE IN FATTORI PRIMI
La fattorizzazione
Abbiamo imparato che i numeri primi ammettono come unici divisori uno e se stessi. Per i numeri composti è utile
!
144
sapere da quali fattori sono costituiti cioè si riscrive il numero composto sotto forma di prodotti.
Per esempio il numero 18 lo si può pensare come:
18 = 18 x 1
18 = 2 x 9
18 = 3 x 6
In questi casi si dice che abbiamo fattorizzato il numero.
Nella sequenza di immagini troverai tutto ciò che ti serve.
In alcune situazioni sarò necessaria una particolare fattorizzazione, quella in cui i fattori sono tutti numeri primi.
Analizziamo questi casi particolari:
Ogni potenza di 10,
scomposta in fattori primi, è
uguale al prodotto dei fattori
primi 2 e 5, elevati a
potenza con esponente
uguale al numero degli zeri
che seguono l’unità.
!
E.4.1 – Criterio generale di divisibilità
Consideriamo due numeri, per esempio 7560 e 252, e calcoliamo la divisione:
7560 : 252 = 30 resto 0
Essi risultano divisibili.
Sarebbe stato possibile stabilirlo senza eseguire la divisione?
!
145
Si, se si utilizzano in modo opportuno le rispettive scomposizioni; vediamo come.
7560
756
378
189
63
21
7
1
2x5
2
2
3
3
3
7
252
126
63
21
7
1
2
2
3
3
7
7560 = 23 x 33 x 5 x 7
252 = 22 x 32 x 7
Esaminando le scomposizioni, ci si accorge che nel primo numero compaiono tutti i fattori del secondo con
esponente maggiore o uguale.
Due numeri sono divisibili se, scomposti in fattori primi,
nel primo numero compaiono almeno tutti i fattori del secondo,
con esponente maggiore o uguale a quello con cui compaiono
nel secondo.
Un applicazione del criterio generale di divisibilit ci consente di calcolare il quoziente fra due numeri dopo che se
n verificata la divisibilit .
Il quoziente di due numeri divisibili, scomposto in fattori primi, dato dal prodotto di tutti i fattori del dividendo
aventi come esponente la differenza degli esponenti con cui compaiono nel dividendo e nel divisore.
ESEMPIO
Supponiamo di voler calcolare 5616 : 108
5616
2808
1404
702
351
117
39
13
1
2
2
2
2
3
3
3
13
108 2
54 2
27 3
9 3
3 3
1
5616 = 24 x 33 x 131
108 = 22 x 33 x 130
I due numeri sono divisibili:
5616 : 108 = 24-2 x 33-3 x 131-0 = 22 x 30 x 131 = 4 x 1 x 13 = 52
E.4.2 – Ricerca di tutti i divisori di un numero
Mediante le scomposizioni è anche possibile trovare tutti i divisori, primi e composti, di un numero.
Vediamolo con un esempio
Supponiamo di voler trovare i divisori di 90.
Scomponiamo il numero:
90 2 x 5
9 3
90 = 2 x 32 x 5
3 3
!
1
Costruiamo una tabella (tab.1) scrivendo:
!
146
"
"
nella prima riga l’unità e tutte le potenze del I fattore fino a quella con cui compare nella scomposizione;
nella seconda riga l’unità e tutte le potenze del II fattore fino alla potenza con cui compare nella
scomposizione e così via per tutti i fattori;
" moltiplichiamo tutti i numeri della prima riga con tutti quelli della seconda e successivamente
moltiplichiamo i prodotti ottenuti per tutti i numeri della terza riga.
90 = 2 x 32 x 5
Tabella&1:&Ricerca&dei&divisori&
I numeri dell’ultima riga sono i divisori di 90: D (90) = { 1; 2; 3; 5; 6; 9; 10; 15; 18; 30; 45; 90 }
E.4.3 - Prova TU
Indica con una crocetta le affermazioni V e quelle F.
a.
Un numero composto è scomposto in fattori primi quando è scritto come prodotto di numeri primi
2
V
F
V
F
b.
La scomposizione di 18 è 2 x 3
c.
Il numero 24 si scompone come prodotto dei fattori 3 x 8
V
F
d.
Il numero 13 non è composto perché 13= 13 x 1
V
F
e.
320 è divisibile per 16
V
F
f.
540 è divisibile per 12
V
F
E.4.4 - Mettiamo in pratica
1.
!
Scomponi in fattori primi i seguenti numeri:
a) 24 36 45 69 81
b) 44 78 42 65 99
c) 39 26 14 25 32
d) 76 54 60 18 22
e) 49 92 34 68 12
f) 44 84 28 50 87
g) 144 360 225 121 200
h) 142 693 308 252 378
i) 675 188 486 525 636
j) 744 627 175 484 528
k) 624 125 336 108 189
l) 256 486 945 285 306
m) 627 889 977 1296 4293
n) 567 909 207 1296 4752
o) 102 333 715 1386 2925
p) 715 519 989 1456 8008
147
2.
Scomponi in fattori primi i seguenti numeri:
(Ricordando che 10=2x5, 100=22 x 52 , 1000=23 x 53 ,…)
a) 70 130 30 540 720
b) 160 330 50 280 460
c) 250 1300 500 360 900
d) 1210 1680 2750 2520 2040
e) 3200 1830 5460 8100 3150
f) 3920 7850 9870 8280 5130
g) 110250 105000 240500 609810 395000
h) 26950 723520 308000 400020 144 900
3.
a)
Completa le seguenti scomposizioni in fattori primi:
84 2
105
3
324 2
42 ….
35 ….
162 ….
21 ….
7 ….
81 …
7 ….
1
27 …
1 ….
9 …
3 …
1
84=…………
b)
528
264
….
….
….
….
…
2
2
….
….
….
….
105= ………………
660 2 x 5
66 …
…. …
…. …
….
324= ……………
462
….
….
….
….
2
…
…
….
528=……………….. 660=…………….. 462=……………….
4.
Applicando il criterio generale di divisibilità stabilisci se il primo numero di ciascuna delle seguenti coppie è
divisibile per il secondo:
a) 81 e 27 64 e 16 99 e 27 60 e 15 88 e 16 75 e 25
b) 128 e 32 208 e 102 225 e 25 400 e 80 64 e 36 144 e 24
c) 69 e 39 80 e 16 147 e 21 108 e 27 198 e 66 150 e 70
d) 480 e 120 115 e 25 216 e 72 810 e 135 525 e 35 124 e 28
e) 360 e 45
488 e 122 324 e 54 243 e 27
312 e 72 540 e 180
f) 1296 e 144 2540 e 110 485 e 125 3276 e 156 9612 e 267 4050 e 675
5.
Mediante la scomposizione in fattori primi, determina tutti i divisori dei seguenti numeri:
a) 20 45 28 56 75 98
b) 72 80 275 432 63 175
c) 84 120 144 280 189 207
d) 504 528 720 1056 1134 2450
e) 414 312 426 518 702 900
6.
Elvira rompe il salvadanaio e trova 12 euro. Decide di spenderli per comperare caramelle. Può comperare
buste di caramelle al latte da 1 euro e alla frutta da 1,50 euro. In quanti modi può spendere i 12 euro?
[3]
7.
Nel periodo dei saldi Claudio vuole comperare shorts da 20 euro e t-shirts da 10 euro. Ha a disposizione
80
euro.
In
quanti
modi
può
spendere
la
somma
che
ha
a
disposizione?
[5]
8.
La mamma dà a Luisa 6 euro per comperare alcune matite. Deve scegliere tra matite da 0,50 euro e altre
da 0,75 euro. In quanti modi può spendere la cifra che ha a disposizione?
[5]
!
148
9.
Determina un numero minore di 52 che è multiplo di 8 e diviso per 7 dà come resto 3.
[64]
10.
Determina un numero che è multiplo di 5, è minore di 64 e diviso per 2 dà come resto 5.
[40]
11.
E.5 – M.C.D. E m.c.m.
Il bilanciamento
Quando hai parlato di materia nelle scienze, avrai parlato di sostanze semplici e sostanze composte, le prime
formate da atomi tutti dello stesso tipo, le seconde no.
L’anno prossimo studierai che un elemento può unirsi ad altri elementi secondo regole ben precise. Questa
“unione” si rappresenta mediante una scrittura chiamata equazione chimica.
Per scrivere correttamente queste formule si calcola il minimo comune multiplo delle valenze (capacità degli
atomi di legarsi ad altri atomi) dei vari elementi.
Come potrai intuire, un bravo chimico deve conoscere molto bene l’argomento che affronterai in questa sezione.
!
149
E.5.1 – Ricerca di MCD
Considerati i numeri 18 e 24, determiniamo tutti i loro divisori utilizzando come hai imparato:
I due numeri hanno dei divisori comuni: 1, 2, 3 e 6; il più grande comune è il 6, diremo allora che 6 è il Massimo
Comune Divisore e scriveremo:
M.C.D. ( 18; 24 ) = 6
Consideriamo ora i numeri 15, 30 e 45 e determiniamo tutti i loro divisori. Scomponendoli in fattori otterremo:
I divisori comuni sono: 1, 3, 5 e 15. quindi il Massimo Comune Divisore è 15. Quindi, scriveremo:
M.C.D. ( 15; 30; 45 ) = 15
In generale, diremo che:
Il Massimo Comune Divisore (M.C.D.) tra due o più numeri è il più
grande tra i loro divisori comuni.
ATTENZIONE A…
Il M.C.D. tra due o più numeri è sempre più piccolo dei numeri dati; al più è uguale al più piccolo
di essi.
Se tra due numeri il M.C.D. è uno, allora i numeri si dicono primi fra loro.
!
150
• Non confondere il concetto di numero primo con numeri primi fra
loro.
• Un numero è primo se ammette come suoi unici divisori l’unità e se
stesso.
• Due numeri sono primi fra loro quando il più grande divisore in
comune è l’unità.
• I numeri primi sono necessariamente primi fra loro, il viceversa non è
sempre vero.
E.5.2 – Calcolo di MCD
Il metodo più rapido per calcolare il M.C.D. è quello che prevede l’uso della scomposizione in fattori primi.
Supponiamo di voler calcolare il M.C.D. tra 120, 150 e 198. Scomponiamo i tre numeri in fattori primi.
Il M.C.D. sarà dato dal prodotto dei fattori primi comuni a tutti e tre i numeri, in questo caso 2 e 3, entrambi
con il minimo esponente con cui figurano nelle scomposizioni. Se considerassimo l’esponente maggiore o
anche i fattori non comuni non otterremmo un divisore comune. Quindi:
M.C.D. ( 120; 150; 198 ) = 2 x 3 = 6
Per calcolare il M.C.D. tra due o più numeri, si scompongono i
numeri in fattori primi e si moltiplicano i fattori comuni una sola
volta con il minimo esponente.
E.5.3 – Ricerca di mcm
Hai imparato il concetto di multiplo di un numero naturale. Ricerchiamo i multipli dei numeri 4 e 18 (non
consideriamo lo zero):
M(4) = {4; 8; 12;16; 20; 24; 28; 32; 36; 40; 44; 48; 52; 56; 60; 64; 68; 72; 76;..}
M(18) = {18; 36; 54; 72; 90; 108; 126; 144; 162; 180; 198;…}
I due numeri hanno dei multipli in comune, tra quelli riportati sopra il 36 e il 72; il più piccolo multiplo che hanno in
comune è 36; diremo che 36 è il minimo comune multiplo dei numeri 4 e 18 e scriveremo:
m.c.m. (4; 18) = 36
!
151
Ripetiamo lo stesso ragionamento precedente e troviamo i multipli dei numeri 4, 12 e 16:
M(4) = {4; 8; 12;16; 20; 24; 28; 32; 36;.…64; 68; 72; 76;….96; …108;}
M(12) = {12; 24; 36; 48; 60; 72; 84; 96; 108; 120; 132; 144; 156; 168;…}
M(16) = {16; 32; 48; 60; 72; 96; 108; 120; 132; 144; 156; 168;…}
I tre numeri hanno dei multipli in comune, tra quelli riportati sopra il 72, il 96 e il 108; il più piccolo multiplo che
hanno in comune è 72; diremo che 72 è il minimo comune multiplo dei numeri 4 e 18 e scriveremo:
m.c.m. ( 4; 12; 18 ) = 72
E.5.4 – Calcolo di mcm
Il metodo più rapido per calcolare il m.c.m.. è quello che prevede l’uso della scomposizione in fattori primi.
Supponiamo di voler calcolare il m.c.m. tra 8, 12 e 30. Scomponiamo i tre numeri in fattori primi.
Il m.c.m. sarà dato dal prodotto dei fattori primi, comuni e non comuni, presi con il maggior esponente con cui
figurano nelle scomposizioni. Se considerassimo gli esponenti minori o solo i fattori comuni non otterremmo un
multiplo di tutti. Quindi nel nostro caso:
m.c.m. ( 8; 12; 30 ) = 23 x 3 x 5 = 120
Per calcolare il m.c.m. tra due o più numeri, si scompongono i
numeri in fattori primi e si moltiplicano i fattori comuni e non
comuni una sola volta con il massimo esponente.
E.5.5 - Prova TU
1. Indica con una crocetta le affermazioni V e quelle F.
a.
I divisori comuni di 12 e 36 sono: 2, 3, 4, 6, 12.
V
F
b.
Il M.C.D fra due o più numeri esiste sempre.
V
F
c.
Se due numeri sono primi fra loro, sono anche numeri primi.
V
F
d.
M.C.D. (6,30)= 6.
V
F
e.
4 e 5 sono numeri primi fra loro.
V
F
f.
Due numeri si dicono primi tra loro se il loro M.C.D. è 1.
V
F
2. Indica con una crocetta le affermazioni V e quelle F.
!
a.
Il m.c.m. fra due o più numeri non esiste sempre.
V
F
b.
Il m.c.m. fra due o più numeri è il più piccolo dei multipli comuni ai numeri dati.
V
F
152
c.
m.c.m. (15,30)= 5
V
F
d.
Se due numeri sono primi tra loro, il loro m.c.m. non esiste.
V
F
e.
Se due numeri sono primi tra loro, il loro m.c.m. è il prodotto dei due numeri.
V
F
f.
m.c.m. (7,12)= 84
V
F
E.5.6 - Mettiamo in pratica
!
1.
Determina i divisori comuni delle seguenti coppie di numeri:
a) 15 e 20 12 e 18
6 e 18 14 e 28
b) 24 e 36 15 e 20 11 e 33 16 e 32
c) 9 e 27
25 e 50 40 e 64 20 e 50
2.
Determina i divisori comuni delle seguenti terne di numeri:
a) 10, 30, 50
18, 27, 45
12, 28, 32 16, 24, 40
b) 15, 20, 35
14, 21, 42
33, 55, 66 12, 24, 36
c) 20, 40, 60
15, 25, 40
13, 42, 65 14, 18, 20
3.
Determina i divisori dei numeri dati e individua, per ogni gruppo di numeri, il M.C.D.:
a) D35, D56, D63
D27, D45, D90
D15, D25, D40
b) D12, D36, D48
D22, D44, D66
D30, D70, D90
c) D18, D54, D72, D90
D13, D39, D78, D104
4.
Determina quali numeri delle seguenti coppie sono primi tra loro:
a) 4 e 9
12 e 20
10 e 27 16 e 15
11 e 13
b) 30 e 40
7e 8
15 e 25 24 e 36
9 e 49
5.
Verifica che i numeri delle seguenti terne sono primi tra loro:
a) 8, 15, 49
23, 41, 53
11, 26, 35
b) 37, 17, 40
16, 43, 59
12, 25, 19
6.
Calcola, mediante il metodo della scomposizione in fattori primi, il M.C.D. dei seguenti gruppi di numeri:
a) 10, 12
24,36
15, 25
21, 49 20, 40 32, 64
b) 35, 60
27, 81 60, 36
75, 80 12, 44 15, 45
c) 42, 72, 81 30, 45, 50 88, 56, 32
64, 42, 24
d) 48, 12, 26 45, 60, 75 21, 14, 98
60, 108, 120
e) 858, 693
910, 858 560, 896
f) 120, 168, 264
270, 90, 126 240, 384, 720
g) 132, 110, 150, 66 84, 120 125,54 102, 85, 51, 153
h) 616, 1176
560, 800 875, 1500
i) 1734, 3042 2800, 3920 2106, 2448
j) 400, 500, 900 3800, 2166, 1750
7.
Luca deve confezionare tanti sacchetti di caramelle in modo che ciascun sacchetto sia formato dallo
stesso numero, il maggiore possibile, di caramelle dello stesso gusto. Ha a disposizione 180 caramelle,
150 alla menta e 120 alla liquirizia. Calcola il numero di caramelle di ciascun sacchetto ed il numero dei
sacchetti. [30,15]
8.
Tre rotoli di nastro, per confezionare pacchi regalo, devono essere tagliati in parti uguali e della maggiore
lunghezza possibile. Calcola la lunghezza di ciascuna parte e il numero delle parti, sapendo che i tre rotoli
sono lunghi rispettivamente 90m, 126m e 270m. [18m, 27 parti]
9.
Un piastrellista deve pavimentare una camera rettangolare le cui dimensioni misurano rispettivamente
336 cm e 280 cm. Può utilizzare piastrelle quadrate di lato 12 cm e piastrelle quadrate di 14 cm. Quali
piastrelle deve utilizzare per non effettuare tagli? [14 cm]
153
10. Un gruppo di turisti di diversa nazionalità, in visita al museo della carta, devono essere suddivisi in gruppi
che comprendano il maggior numero possibile di visitatori. Sapendo che i turisti sono 144 italiani, 120
inglesi e 96 tedeschi, da quanti turisti è formato ogni gruppo e quanti gruppi visiteranno il museo? [24, 15]
11. Un orafo vuole realizzare il maggior numero possibile di bracciali, uguali fra loro, con pietre colorate. Ha a
disposizione 96 pietre turchesi, 72 verdi e 144 bianche. Quanti bracciali può realizzare? Quante pietre di
ogni tipo sono contenute in ciascun bracciale? [24, 4 turchesi, 3 verdi, 6 bianche]
12. Un grossista deve sistemare 72 kg di melanzane, 108 kg di zucchine e 420 kg di peperoni nel minor
numero possibile di cassette in modo che siano di ugual peso e contengano una sola qualità di ortaggi.
Quanto peserà ciascuna cassetta e quante cassette deve preparare? [12 kg, 50 cassette]
13. Un giardiniere deve allestire tre aiuole di un giardino condominiale con piantine di gerani in modo che
siano equidistanti fra loro e alla maggiore distanza possibile. Sapendo che i lati delle aiuole misurano
rispettivamente 4,8 m, 5,6 m e 4,2 m e che ogni piantina costa 0,70 euro, calcola quanto spende per
l’allestimento. [51,10 euro]
14. Un negoziante vuole confezionare scatole contenenti ciascuna dolci di una stessa qualità ed in modo che
il numero sia il maggiore possibile. Quanti dolci si devono mettere in ciascun sacchetto e quanti sacchetti
si possono confezionare se ha a disposizione 480 ovetti, 288 cioccolatini e 366 caramelle? [48, 23]
15. Calcola mentalmente il m.c.m. delle seguenti coppie di numeri:
3, 9
4, 8
5, 10
7, 21
8, 18
3, 16
12, 4
6, 36
9,12
5, 25
8, 16
14, 28
24, 36
20, 30
12, 15
14, 42
15, 45
25, 30
12, 15, 18
4, 9, 12
3, 7, 35
16, 32
12, 18
24, 40
8, 16, 10
5, 8, 16
24, 32, 12
15, 25
14, 20
16, 36
15, 25, 30
10, 40, 50
6, 20, 15
16. Ricerca il m.c.m. tra i seguenti numeri mediante la scomposizione in fattori primi:
15, 20
24, 40
10, 25
12, 48
30, 70
15, 45
32, 42
49, 35
48, 64
50, 75
27, 81
12, 21
11, 13
42, 27
84, 98
54, 90
63, 99
32, 50
36, 60
55, 17
30, 35
64,100, 24
105, 135, 49
132, 110, 66
80, 120, 15
112, 98, 70
84, 120, 125
48, 56
44, 66
18, 40
88, 56, 72
180, 108, 40
144, 147, 112
17. Completa le tabelle:
!
a
b
21
45
60
25
12
32
14
21
18
25
35
32
56
24
18
54
12
36
42
45
25
63
54
45
16
44
30
50
90
20
30
132
144
100
16
36
60
108
120
11
33
64
135
121
a
b
7
M.C.D.
m.c.m.
c
M.C.D.
m.c.m.
154
18. Trova il m.c.m. e il M.C.D. tra i seguenti numeri:
9,27
15, 30
48, 36 16, 24
18, 10 25, 45
11, 33 21, 49
32, 40 23,46
35, 10, 28
51, 85, 30
27, 39, 26
4, 17, 34
121, 33, 55
45, 135, 20
117, 264
912, 760
444, 740
342, 396, 18
780, 650, 120
4200, 3500, 560
3159, 468, 702
1815, 495, 297
4752, 1782, 864
19. Luca e Giovanni hanno giocato insieme a scacchi. Sapendo che Luca va a giocare ogni 3 giorni e
Giovanni ogni 5 giorni, fra quanti giorni si ritroveranno a giocare insieme? [15]
20. Tre semafori, disposti lungo un viale, in questo istante hanno tutti la luce rossa accesa. Sapendo che nel
primo la luce rossa compare ogni 0 secondi, nel secondo ogni 40 secondi e nel terzo ogni 24 secondi, fra
quanti secondi i semafori saranno contemporaneamente rossi? [120s]
21. Lisa, Rossana e Michele sono reperibili di notte come medici di reparto. Lisa è reperibile ogni 9 giorni,
Rossana ogni 12 e Michele ogni 18 giorni. Se stasera sono tutti in servizio insieme, fra quanti giorni si
ritroveranno? [36]
22. Tre autobus partono contemporaneamente dal capolinea. Il primo, per percorrere l’intera tratta impiega 75
minuti, il secondo ne impiega 90 e il terzo 60. Dopo quanto tempo si ritroveranno insieme al capolinea?
[15 minuti]
23. Un corriere consegna la merce al primo negozio ogni 12 giorni, al secondo ogni 10 giorni, al terzo ogni 20
giorni, al quarto ogni 15 giorni e al quinto ogni 30 giorni. Se oggi consegna la merce a tutti insieme, fra
quanti
giorni
consegnerà
di
nuovo
la
merce
a
tutti
insieme?
[60 giorni]
24. In un’insegna luminosa, le luci gialle si accendono ogni 4 secondi, le luci bianche ogni 6 secondi e le luci
verdi ogni 8 secondi. In questo momento l’insegna è completamente illuminata, fra quanti secondi lo sarà
di nuovo? [24 s]
25. Andrea, Leonardo e Francesco oggi si incontrano in piscina dove iniziano i corsi di nuoto per stili diversi:
quello seguito da Andrea si svolgerà ogni 3 giorni, quello di Leonardo ogni 6 giorni e quello di Francesco
ogni 4 giorni. I tre amici decidono che, quando si incontreranno in piscina, andranno insieme in
paninoteca. Sapendo che consumeranno un panino a testa da 1,80 euro e una bibita da 0,80 euro per
ciascuno e che il corso durerà 4 mesi, quante volte si incontreranno i tre amici e quanto spenderanno, in
tutto, in paninoteca insieme? (considera il mese di 30 giorni) [10, 78 euro]
26. In un paese della Puglia, ogni 40 giorni si ferma la bancarella dello zucchero filato, ogni 4 mesi si ferma il
circo e ogni 3 mesi si fermano le giostre per i bambini. Se stasera sono tutti e tre presenti in paese, fra
quanti mesi si ritroveranno tutti insieme nel paese? [12]
27. Si vogliono realizzare dei nastri aventi la stessa lunghezza tale da poter essere esattamente divisi in parti
di uguale lunghezza e cioè di 28 cm, 35 cm e 42 cm. Qual è la minima lunghezza che devono avere i
nastri? [420 cm]
!
155
E.5.7 – Invalsi no problem!
E le PROVE
INVALSI!?!?!
!
Ora non ci
spaventano
più!!!!
1.
2.
Quale dei seguenti insiemi è composto solo da numeri primi?
A.!{0;!1;!2;!3;!4;!5}!
C.!{2;!4;!6;!8;!10;!12}!
B.!{2;!3;!5;!7;!11;!13}!
D.!{3;!5;!7;!9;!11;!13}!
L’insegnante chiede: “Un numero primo maggiore di 2 è sempre dispari?”. Quattro studenti rispondono
così:
Chi ha ragione?
!
Paolo!
Cristina!
Giorgio!
Monica!
156