Alberi - Università di Trento

!
!
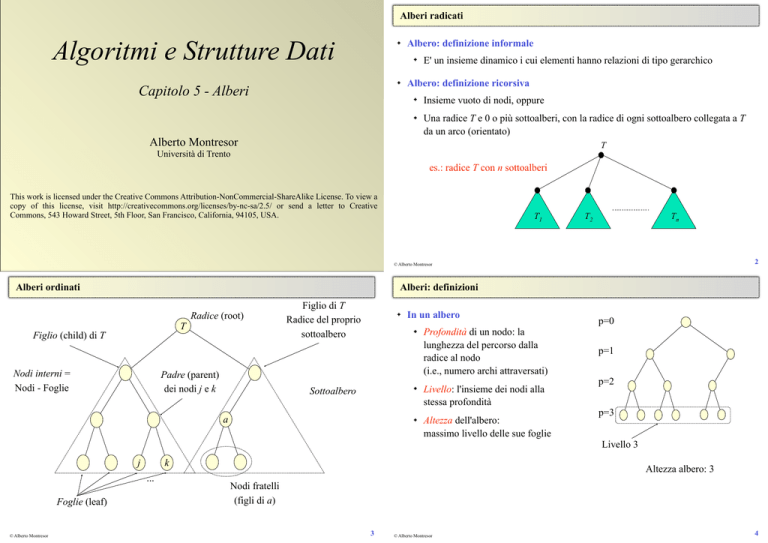
Alberi radicati
Algoritmi e Strutture Dati
✦
Albero: definizione informale
✦
!
✦
Capitolo 5 - Alberi
Albero: definizione ricorsiva
✦
!
!
!
Alberto Montresor
E' un insieme dinamico i cui elementi hanno relazioni di tipo gerarchico
✦
Insieme vuoto di nodi, oppure
Una radice T e 0 o più sottoalberi, con la radice di ogni sottoalbero collegata a T
da un arco (orientato)
T
Università di Trento
!
!
!
es.: radice T con n sottoalberi
This work is licensed under the Creative Commons Attribution-NonCommercial-ShareAlike License. To view a
copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/2.5/ or send a letter to Creative
Commons, 543 Howard Street, 5th Floor, San Francisco, California, 94105, USA.
1
© Alberto Montresor
Alberi ordinati
T
Nodi interni = Nodi - Foglie
Radice (root)
Padre (parent)
dei nodi j e k
Figlio di T
Radice del proprio
sottoalbero
Tn
2
© Alberto Montresor
✦
j
In un albero
✦
Sottoalbero
✦
a
✦
Profondità di un nodo: la lunghezza del percorso dalla radice al nodo (i.e., numero archi attraversati)
Livello: l'insieme dei nodi alla stessa profondità
Altezza dell'albero: massimo livello delle sue foglie
k
...
© Alberto Montresor
T2
Alberi: definizioni
Figlio (child) di T
Foglie (leaf)
T1
p=0
p=1
p=2
p=3
Livello 3
Altezza albero: 3
Nodi fratelli
(figli di a)
3
© Alberto Montresor
4
Coniferali, Gnetali, Angiosperme, Dicotiledoni, Monocotiledoni;
possibile
Postvisita:
Alghe,
cheAlberi:
permettonouna
diCianoficee,
leggere
e scrivereBatteri,
ilspecifica
contenuto
dei nodi.Mixomiceti, Funghi, Tallofite, Briofite, Pteridofite, Archegoniate,
Crittogame,
Cicadali,
Ginkgoali, Coniferali, Gnetali, Gimnosperme, Dicotiledoni,
T REE
% Costruisce un nuovo
albero, costituito daFanerogame,
un solo nodo e contenente
v vegetale;
Monocotiledoni,
Angiosperme,
Regno
Alberi?
Tree(I TEM v)
Invisita
= 1): Cianoficee, Tallofite, Batteri, Alghe, Mixomiceti, Funghi, Crittogame, Briofi% Legge(i
il valore
I
TEM
read
()
te, Archegoniate, Pteridofite, Regno vegetale, Cicadali, Gimnosperme, Ginkgoali, Coniferali,
% ScriveFanerogame,
v nel nodo
Gnetali,
Dicotiledoni, Angiosperme, Monocotiledoni;
write(I TEM v)
DAG
Per% livelli:
vegetale,
Crittogame,
Fanerogame, Taliofite, Archegoniate, Gimnosperme,
RestituisceRegno
il padre; nil
se questo nodo
è radice
T REE parent() Cianoficee, Batteri, Alghe, Mixomiceti, Funghi, Briofite, Pteridofite, Cicadali,
Angiosperme,
% Restituisce il primo figlio; nil se questo nodo è foglia
Ginkgoali,
Coniferali, Gnetali, Dicotiledoni, Monocotiledoni.
T REE leftmostChild()
Radice
%In
Restituisce
il prossimo
fratello
nodo anticipato
a cui è applicato;
nil se assente
pratica,
l’ordine
di del
visita
coincide
con
T REE rightSibling()
Foresta
© Alberto Montresor
5
Algoritmi di visita degli alberi
✦
✦
✦
leftmostChild() restituisce nil, il nodo è foglia (ovviamente, un nodo può essere radice e foglia
contemporaneamente). Se rightSibling() restituisce nil, è stata ispezionata l’intera lista di figli.
visitaProfondità(T REE t)
Visita (o attraversamento) di un albero:
✦
La creazione di nuovi alberi sfrutta la ricorsività della definizione di questa struttura di dati; oltre
al caso base, rappresentato
dalla costruzione di alberi costituiti da singoli nodi isolati
precondition:
t ⇤= nil
(descritta in precedenza), è possibile “aggiungere” un sottoalbero come figlio (operazione insertChild
()) o come
fratello successivo
insertSibling
(1) esame
“anticipato”
del (operazione
nodo radice
di t ()) di un particolare nodo. La
precondizione per applicare questi metodi con successo è che l’albero da aggiungere non sia
già sottoalbero
un altro
albero (parent() =()nil). Infine, sono presenti le operazioni deleteT REE udi ⇥
t.leftmostChild
Child() e deleteSibling() che distruggono il sottoalbero radicato nel primo figlio e nel fratello
while u ⇤= nil do
successivo del nodo su cui si applica l’operazione. Gli effetti delle operazioni insertChild(),
Algoritmo per “visitare” tutti i nodi di un albero
In profondità (depth-first search, a scandaglio): DFS
✦
Vengono visitati i rami, uno dopo l’altro
✦
Tre varianti
visitaProfondità(u)
u ⇥ u.rightSibling()
(2)
In ampiezza (breadth-first search, a ventaglio): BFS
✦
quello del diritto di successione al trono %nell’albero
genealogico
di
una
dinastia
regnante.
Per
illustrare la differenza tra gli ordini
Inserisce il sottoalbero t come primo figlio di questo nodo
di visita
anticipato
e posticipato, c’è un modo pittoresco che non tira in ballo la ricorsione. Si
insertChild
(T REE t)
precondition: t.parent() = nil
immagini
che l’albero sia una sorta di isola fatta a fiordo: i cerchietti rappresentano fari e le
% Inserisce il sottoalbero t come successivo fratello di questo nodo
linee
che collegano coppie di fari rappresentano alte scogliere. Una nave fa la circumnavigainsertSibling(T REE t)
t.parent
() = nil dalla radice e costeggiando sempre le scogliere. Il capitano segna sul
zioneprecondition:
dell’isola,
partendo
%
Distrugge
il
sottoalbero
radicato
nel primo figlio
questo
nodo incontrato nella navigazione, ma solo quando
libro di bordo il nome
di ciascun
farodiche
viene
deleteChild()
lo incontra per la prima volta. È facile verificare che se la circumnavigazione procede in senso
% Distrugge il sottoalbero radicato nel prossimo fratello di questo nodo
antiorario,
allora si ottiene proprio l’ordine di visita anticipato, mentre se procede in senso
deleteSibling()
orario
si
ottiene
l’ordine di visita posticipato inverso (cioè letto da destra verso sinistra, ovvero6
© Alberto Montresor
Sono presenti le operazioni parent(), leftmostChild() e rightSibling(), che restituiscono ridall’ultimo nodo visitato al primo). Il seguente schema di procedura serve per effettuare sia la
spettivamente il padre, il primo figlio e il fratello successivo di un nodo. Le ultime due possono
visita
anticipata
che
essere
utilizzate
per scorrere
laquella
lista deiposticipata.
figli. Se
() restituisce
nil, il nodo(previsita)
è radice; se
Visita
alberi:
in profondità
inparent
ordine
anticipato
T
a
b
c
e
d
f
d
e
g
esame “posticipato” del nodo radice di t
A livelli, partendo dalla radice
Sequenza: a
© Alberto Montresor
7
© Alberto Montresor
b
c
f
g
8
dall’ultimo nodo visitato al primo). Il seguente schema di procedura serve per effettuare sia la
visita
anticipata
quella posticipata.
Visita
alberi: che
in profondità
in ordine posticipato (postvisita)
visitaProfondità(T REE t)
esame “anticipato” del nodo radice di t
c
e
d
f
f
g
g
esame “posticipato” del nodo radice di t
Sequenza: c
87
d
b
e
a
nella riga (1), ignorando la riga (2), si ottiene la
o nella riga (2), ignorando la riga (1), si ottiene
complesso;
quando invisita() viene eseguito sul
© Alberto Montresor
icorsivamente sui primi i figli di t, se presenti;
ndi invisita
viene richiamata
sui restanti figli.
Visita()alberi:
in ampiezza
9
visitaAmpiezza(T REE t)
precondition: t ⇥= nil
Q UEUE Q
Queue()
Q.enqueue(t)
while not Q.isEmpty() do
T REE u
Q.dequeue()
esame “per livelli” del nodo u
u
u.leftmostChild()
while u ⇥= nil do
Q.enqueue(u)
u
u.rightSibling()
T
a
Sequenza: a
o visitaAmpiezza() utilizza un approccio comuna visita ricorsiva (che implicitamente utilizza
una coda. All’inizio, si inserisce la radice nella
inseriti tutti i suoi figli nella coda, in ordine. È
del©livello
i-esimo vengono esaminati prima dei
Alberto Montresor
b
e
d
e
5.3 Realizzazione con puntatori padre/primo-figlio/fratello
g
f
c
La visita per livelli illustrata nell’algoritmo visitaAmpiezza() utilizza un approccio comSequenza
(i=1):
c ricorsiva
b (che
d implicitamente
a
f
eutilizza
g
pletamente diverso. Invece di essere
basata su una
visita
una pila), è una procedura† iterativa basata su una coda. All’inizio, si inserisce la radice nella
coda. Quando un nodo viene estratto, vengono inseriti tutti i suoi figli nella coda, in ordine. È
facile
dimostrare per induzione che tutti i nodi del livello i-esimo vengono esaminati prima dei10
© Alberto Montresor
nodi del livello (i + 1)-esimo.
Nelle tre procedure
di visita
profondità descritte viene effettuata esattamente una chiaRealizzazione
con vettore
deiinfigli
mata ricorsiva per ciascun nodo, per un totale di n chiamate, dove n è il numero di nodi del/
l’albero. Nella visita in ampiezza, ogni nodo è/inserito in coda esattamente una volta. Pertanto,
la complessità delle quattro procedure di visita è (n), purché si fornisca una realizzazione in
cui le operazioni utilizzate nelle procedure di visita richiedano tempo O(1).
/ / /
b
c
T
Q UEUE Q
Queue()
a
Q.enqueue(t)
b
while not Q.isEmpty
() do e
T REE u
Q.dequeue()
d
f nodogu
esamec“per livelli”
del
u
u.leftmostChild()
while u ⇥= nil do
Q.enqueue(u)
u
u.rightSibling()
T REE u
t.leftmostChild()
integer k
0
while u ⇥= nil and k < i do
k
k+1
invisita(u)
u
u.rightSibling()
esame “simmetrico” del nodo t
while u ⇥= nil do
invisita(u)
u
u.rightSibling()
a
b
precondition: t ⇥= nil
precondition: t ⇥= nil
T
T REE u ⇥ t.leftmostChild()
while u ⇤= nil do
visitaProfondità(u)
u ⇥ u.rightSibling()
(2)
visitaAmpiezza(T REE t)
invisita(T REE t)
precondition: t ⇤= nil
(1)
nodo t, la stessa procedura viene richiamata ricorsivamente sui primi i figli di t, se presenti;
viene
effettuata
simmetrica
di t, e simmetrico
quindi invisita(invisita)
() viene richiamata sui restanti figli.
Visita
alberi:lainvisita
profondità
in ordine
d
/ / / /
f
g
11
/ / /
/ / / /
/ /
/ / / /
/ / //
/ / / /
La realizzazione più naturale, detta a puntatori padre/primo-figlio/fratello, segue fedelmente la specifica, memorizzando per ogni nodo il valore, il puntatore al padre, il puntatore
al primo figlio e il puntatore al fratello successivo. La Fig. 5.6 illustra un albero realizzato in
/ / /memorizzati /direttamente
/ / /
/ / /
questo modo. I nodi /sono
in /strutture
di tipo T REE, che vengono
Padre
create come nodi isolati contenenti un singolo valore.
Le operazioni per spostarsi lungo l’albero (parent(), leftmostChild() e rightSibling
Array ()), cosı̀
Rischio di sprecare memoria se
Nodo
Figli realizcome le operazioni di lettura e scrittura del valore del nodo
(read() e write()) di
vengono
molti nodi hanno grado minore
del grado massimo k.
© Alberto Montresor
12
CAPITOLO
5. ALBERI
Realizzazione
con puntatori padre/primo-figlio/fratello
Realizzazione con puntatori padre/primo-figlio/fratello
89
/
T REE
/
N ODE parent
N ODE child
N ODE sibling
I TEM value
/
T REE
N ODE parent
N ODE child
/
N ODE sibling
I TEM value
Tree(I TEM v)
T REE t
t.value
t.parent
return t
/
new T/ REE
/
v
t.child
t.sibling
% Puntatore al padre
% Puntatore
al/primo
/
/ figlio /
% Puntatore al successivo fratello
% Valore del nodo
/
/
child
T REE t
t.value
t.parent
return t
/
nil
Nodo
t.parent
this
t.sibling
child
child
t
Primo
Figlio Fratello
t.parent
this
t.sibling
sibling
% Inserisce t prima dell’attuale fratello
Realizzazione con puntatori padre/primo-figlio/fratello
sibling
t
deleteChild()
N ODE newChild
13
% Inserisce t prima dell’attuale fratello
deleteChild()
14
N ODE newChild
child.rightSibling()
delete(child)
Realizzazione
con vettore dei padri
child
newChild
deleteSibling()
✦
child.rightSibling()
L'albero
rappresentato
da un
vettore()i cui elementi contengono N ODE ènewBrother
sibling.
rightSibling
l'indice
padre
deletedel
(sibling)
sibling
newChild
✦
Esempio:
newBrother
delete(T REE t)
deleteSibling()
0 a
N ODE u
t.leftmostChild
1 b ()
while u ⇥= nil do
1 e
T REE next
u.rightSibling
()
delete(u)
2 c
u
next
2 d
delete t
N ODE newBrother
sibling.rightSibling()
delete(sibling)
sibling
newBrother
delete(T REE t)
N ODE u
t.leftmostChild()
while u ⇥= nil do
T REE next
u.rightSibling()
delete(u)
u
next
delete t
© Alberto Montresor
% Inserisce t prima dell’attuale primo figlio
© Alberto Montresor
delete(child)
child
nil
t.parent
this
t.sibling
sibling
sibling
t
% Inserisce t prima dell’attuale primo figlio
insertSibling(T REE t)
% Crea un nuovo nodo
insertSibling(T REE t)
t
© Alberto Montresor
new T REE
v
t.child
t.sibling
insertChild(T REE t)
/
Padre
insertChild(T REE t)
Soluzione:
usare una lista
t.parent
this
di t.sibling
figli (fratelli).
child
Tree(I TEM v)
% Crea un nuovo nodo
/
% Puntatore al padre
% Puntatore al primo figlio
% Puntatore al successivo fratello
% Valore del nodo
3 f
T
a
b
c
e
d
f
g
3 g
15
© Alberto Montresor
16
di seguito una semplice realizzazione, tralasciando per semplicità di memorizzare i valori dei
Realizzazione con vettore dei padri
nodi.
T REE
integer[ ] p
Alberi binari
Definizione
✦
% Vettore dei padri
% Costruisce una “foresta” con n nodi isolati
Tree(integer n)
p
new integer[1 . . . n]
for i
1 to n do p[i]
0
✦
Un albero binario è un albero ordinato in cui ogni nodo ha al più due figli e
✦
si fa distinzione tra il figlio sinistro ed il figlio destro di un nodo.
Nota:
✦
✦
% Restituisce il padre del nodo i; restituisce 0 se i è radice
integer parent(integer i)
return p[i]
due alberi T e U aventi gli stessi nodi, gli stessi figli per ogni nodo e la stessa
radice, sono
CAPITOLO
5. distinti
ALBERI qualora un nodo u sia designato come figlio sinistro di
91un
nodo v in T e come figlio destro del medesimo nodo in U
livello
% Rende il nodo i un figlio del nodo j
setParent(integer i, integer j)
p[i]
j
2
92
5.5 Alberi binari
17
© Alberto Montresor
Un albero binario è un particolare albero ordinato in cui ogni nodo ha al più due figli e si
faAlberi
distinzione
tra il figlio sinistro ed il figlio destro di un nodo. Questa proprietà è assai sottile,
binari
poiché impone che due alberi T e U aventi gli stessi nodi, gli stessi figli per ogni nodo e la
Figliodidestro
Figlio
sinistro
stessa radice,
siano
distinti qualora un nodo u sia designato come figlio sinistro
un nodo v
Radice
Radice
del
in T e come
figlio
destro
del
medesimo
nodo
in
U
.
Radice del
sottoalbero destro
5
T
1
Algoritmi
e Strutture di Dati
2
5
3
T
2
3
Una possibile specifica per gli alberi binari include le operazioni per leggere e scrivere i18
Figura 5.7: Alberi ordinati e alberi binari.
figli destro e sinistro, che sostituiscono le operazioni per leggere e scrivere il primo figlio e i
Alberisuccessivi.
binari: specifica
fratelli
precondition: t.parent = nil
L’importanza degli alberi binari risiede sia sulla semplicità della loro struttura che sulle
a
innumerevoli applicazioni in cui possono essere impiegati.
si
precondition: t.parent = nil
a<b
no
c
c <nodo
b
% Distrugge il sottoalberob <sinistro
(destro) di questo
si
no
si
no
deleteLeft()
a<c
c,b,a
a<c
deleteRight()
a,b,c
k
si
© Alberto Montresor
4
3
© Alberto Montresor
insertRight(T REE t)
destro
a.left()
4
1
Esempio 5.7 (Albero delle scelte). Le possibili sequenze di confronti (a due alternative) effettuate da un algoritmo per risolvere un problema possono essere visualizzate con un albero
T REEbinario, detto albero delle scelte. In tale albero, i nodi con figli rappresentano confronti tra
% Restituisce
il figlio
sinistro
(destro)i risultati
di questo
restituisce
nilsoluzioni
se assente
dati del problema,
le coppie
padri-figli
deinodo;
confronti,
e le foglie
possibili
T REE
()
del left
problema.
Un percorso radice-foglia rappresenta la sequenza di confronti effettuati per
individuare
T REE
right() una soluzione e il livello massimo di una foglia dà il numero di confronti effettuati
nel caso pessimo. Un albero delle scelte che minimizzi il livello massimo delle foglie fornisce
% Inserisce
il sottoalbero t come figlio sinistro (destro) di questo nodo
con tale valore una limitazione inferiore al numero di decisioni che ogni algoritmo che risolva
insertLeft
(T
REE
il problema devet)effettuare nel caso peggiore.
sottoalbero
sinistro
Esempio
5.6 (Alberi
binari). La Fig. 5.7 mostra tre alberi T1 , . . . , T3 . Visti come alberi ordinati, essi sono tutti identici tra loro. T1 nonj.parent()
è binario, perché non è chiara la convenzione per
distinguere i figli sinistri dai destri. Considerando
i figli disegnati a sinistra (destra) come figli
Padre del
sinistri (destri), allora T2 e T3 sono binari; inoltre essi sono tra loro distinti, poiché non hanno
nodo j (e k)
gli stessi
figli destri e sinistri.
Sottoalbero
Sottoalbero
sinistro
0
2
3
5
T
1
2
4
3
(n log n).
j
1
1
a.right()
a,c,b
19
no
c,a,b
si
b,a,c
no
b,c,a
Una realizzazione ragionevole fa uso di puntatori, come nel caso degli alberi ordinati, i cui
Figura
5.8: Albero
per l’ordinamento
di tre numeri.
campi child e sibling sono
sostituiti
dadelle
leftscelte
e right.
La complessità
di tutte le operazioni è O(1),
con esclusione di quella di cancellazione, che agendo ricorsivamente può avere complessità
La Fig. 5.8 illustra un albero delle scelte per il problema di ordinare tre numeri a, b, c.
Per motivi di spazio, le operazioni parent(), left(), right(), read() e write() non sono20
©O(n).
Alberto Montresor
Poiché un qualsiasi algoritmo di ordinamento di n numeri deve fare una sequenza di scelte
mostrate; semplicemente, restituiscono il valore della variabile corrispondente.
Figura 5.9: Rappresentazione di un albero ordinato T con
un albero binario B.
Alberi binari: realizzazione
Alberi binari: realizzazione
T REE
T REE
Tree(I TEM v)
deleteLeft()
La sostanziale equivalenza di queste due realizzazioni non deve
poiché nel if left ⇥= nil then
T REE sorprendere,
t = new T REE
t.parent
nil
left.deleteLeft()
proporre quella per gli alberi ordinati si è implicitamente trasformato
l’albero
ordinato in uno
t.left
t.right
nil
left.deleteRight()
binario! Come illustrato nella Fig. 5.9, è sempre possibile rappresentare
un
albero
ordinato
T
t.value
v
delete left
t
left
nil
/ / B avente gli
/
/ / albero binario
/
con un
stessi nodi
e la stessa radice, in return
cui ogni
nodo di B ha come
insertLeft(T REE T )
figlio sinistro il primo figlio che ha in T e come figlio destro il fratello
successivo
che ha in TdeleteRight
.
()
T.parent
this
if right ⇥= nil then
leftcoincidono
T
È facile verificare che le
sequenze dei nodi esaminati
su
T
e
su
B
se
T
e
B
sono
right.deleteLeft()
/ /
/ /
Padre
insertRight
(T REE T )
right.deleteRight()
entrambi visitati in ordine anticipato, oppure se T è visitato in ordine
posticipato
e B è visitato
T.parent
this
Figlio
Figlio
delete right
Sinistro simmetrico.
Destro
in ordine
right
T
Nodo
right
nil
Utilizzando le operazioni introdotte, la visita di un albero binario viene effettuata molto
semplicemente da visitaProfondità(). La previsita si ottiene esaminando il nodo t soltanto nella
21 la invisita o la postvisita si hanno
riga (1) e ignorando le righe (2) e (3). Analogamente,
esaminando
ilprofondità
nodo t solo nella riga (2) o in (3), rispettivamente.
Alberi
binari: visite in
Semplici esercizi basati su visite
Per motivi di spazio, le operazioni parent(), left(), right(), read() e write() non sono mostrate; semplicemente, restituiscono il valore della variabile corrispondente.
© Alberto Montresor
© Alberto Montresor
visitaProfondità(T REE t)
(1)
(2)
(3)
if t = nil then
esame “anticipato” del nodo radice di t
visitaProfondità(t.left())
esame “simmetrico” del nodo radice di t
visitaProfondità(t.right())
esame “posticipato” del nodo radice di t
✦
Es. 5.1 - Dato un albero radicato T, calcolare la sua altezza
✦
Dato un albero radicato T, calcolare il numero totale di nodi
✦
Dato un albero radicato T, stampare tutti i nodi a profondità h
22
www.xkcd.com
5.6 Altre realizzazioni
© Alberto Montresor
23
© Alberto Montresor
24