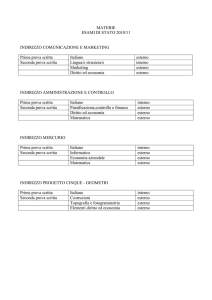
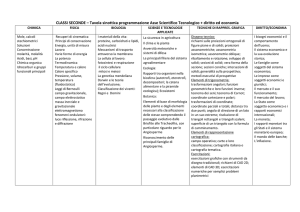
caricato da
tacca
Lezioni Di Topografia (Pdf)

R.Galetto A.Spalla - Lezioni di Topografia CAPITOLO I - TEORIA DEGLI ERRORI 1 1.1 1.2 1.2.1 1.2.2 1.2.3 1.2.4 1.2.5 1.2.6 1.2.7 1.2.8 1.3 1.4 1.4.1 1.4.2 1.4.3 Trattamento delle misure dirette. Considerazioni generali. Grandezze e quantità di grandezza. Prima definizione di grandezza. Seconda definizione di grandezza. Classi di grandezze. Classi di grandezze di divisibilità. Definizione di misura di una grandezza. La misura delle grandezze di divisibilità. Classi di grandezza la cui misura è riconducibile alla misura di una grandezza di divisibilità. Descrizione operazionale della misura di una grandezza di tipo quantitativo. Le misure e l'ambiente reale. Origine della dispersione delle misure. Sensibilità e precisione degli strumenti di misura. Influenza dell'ambiente. Definizione di errore accidentale 1.4.4 1.5 1.5.1 1.5.2 1.6 1.6.1 1.6.2 1.6.3 Lo sviluppo teorico della teoria degli errori. Variabili statistiche e variabili casuali. Variabile statistica. Variabile casuale discontinua. Determinazione della misura diretta di una quantità di grandezza. Analisi statistica dei risultati di n misure ripetute. Le popolazioni di misure possibili come variabili casuali normali. Determinazione dei valori approssimati dei parametri X e σ di una popolazione di misure possibili. 1.6.4 Caso in cui l'e.q.m. è noto “a priori”. 1.6.5 Differenza tra errore quadratico medio e tolleranza. 1.6.6 Media ponderata. 2. Trattamento delle misure indirette. 3. 3.1 3.2 3.3 3.4 3.5 3.6 Metodo delle osservazioni indirette. Impostazione del metodo. Linearizzazione delle equazioni generatrici. Applicazione del principio dei minimi quadrati. Iterazione dei calcoli. Valutazione della precisione dei risultati. Il problema dell'attribuzione dei pesi. CAPITOLO II - STRUMENTI TOPOGRAFICI 1 1.2 Le grandezze che sono oggetto delle misure. Dislivelli. Indice - pagina I R.Galetto A.Spalla - Lezioni di Topografia 1.3 1.4 2 Distanze. Strumenti con cui si effettuano le misure La materializzazione dei punti. 3 3 3.1 3.2 3.3 Il treppiede. Struttura. Modo d'impiego. Possibilità di posizione eccentrica del vitone. 4 4.1 4.2 4.2.1 4.2.2 Il cannocchiale topografico. Struttura. Funzionamento. Funzione del reticolo. Funzione della lente interna. 4.2.3 Funzioni della lente oculare. 4.2.4 Semplificazioni introdotte nelle spiegazioni date in questo paragrafo. 4.2.5 Posizione del primo fuoco nel cannocchiale topografico. 5 5.1 5.2 5.3 5.4 La basetta. Struttura. Uso delle viti calanti per rendere verticale un asse. Intercambiabilità tra teodolite e segnale. Piombino ottico. 6. 6.1. 6.2 6.3 6.3.1 6.3.2 6.3.3 6.3.4 Le livelle e il loro impiego. La livella torica. Sensibilità della livella torica. Funzione della livella torica negli strumenti topografici. Livella torica usata per rendere orizzontale un'asse. Livella torica usata per rendere verticale un asse. Uso combinato di due livelle toriche. Livella torica a coincidenza. 7 7.1 7.2 La livella sferica. Struttura. Uso della livella sferica per rendere verticale un asse. 8 8.1 8.2 8.3 8.4 La funzione della basetta. La basetta munita di livella sferica. La basetta usata come supporto di uno strumento topografico. La basetta usata come supporto di un segnale. Intercambiabilità tra strumento topografico e segnale. 9 9.1 9.2 9.3 Il teodolite. Premessa. Descrizione dello strumento. Misura degli angoli azimutali. Indice - pagina II R.Galetto A.Spalla - Lezioni di Topografia 9.4 9.5 9.6 9.6.1 9.6.2 9.6.3 9.7 Misura degli angoli zenitali. Condizioni di rettifica del teodolite. Errori che influenzano la determinazione degli angoli azimutali. Errore di eccentricità dell'alidada. Errori causati da srettifiche di costruzione. Errore di verticalità dell'asse primario. Errori che influenzano la determinazione degli angoli zenitali. 9.7.1 Srettifica dovuta alla presenza dello zenit strumentale (Z). 9.7.2 Errore dovuto all'eccentricità del cerchio verticale. 9.7.3 Errore residuo di verticalità. 10 Misura diretta delle distanze mediante distanziometri elettronici 10.1 Richiami sulle onde elettromagnetiche. 10.1.1 Periodo, frequenza, intensità istantanea 10.1.2 Fase. 10.1.3 Modulazione in ampiezza, 10.2 10.3 10.4 10.5 Schema di un distanziometro elettronico topografico. Funzionamento del distanziometro. Alcune considerazioni aggiuntive sui distanziometri. Strumenti che misurano angoli e distanze. 11 Misura indiretta di distanze mediante tacheometro. 11.1 Il metodo 11.2 Analisi della precisione del metodo. CAPITOLO III - IL SISTEMA CARTOGRAFICO NAZIONALE 1 1.1 1.2 1.2.1 1.2.2 1.2.3 1.2.4 1.3 1.4 1.5 1.6 1.7 Il problema cartografico. Impostazione generale La Terra, il geoide, lo sferoide, l’ellissoide La Terra Il geoide Lo sferoide L’ellissoide Quota ortometrica e quota ellissoidica Legame tra coordinate ellissoidiche geografiche e coordinate geocentriche Ellissoide geocentrico ed ellissoide nazionale La sfera locale Ricapitolazione sulla posizione del problema cartografico. 2 2.1 2.1.1 2.1.2 2.1.3 Rete di inquadramento planimetrica. Determinazione delle coordinate ellissoidiche dei vertici trigonometrici. Premessa Coordinate geografiche terrestri. Collegamento tra ellissoide e superficie fisica della Terra in un punto arbitrario. Indice - pagina III R.Galetto A.Spalla - Lezioni di Topografia 2.1.4 2.1.6 2.1.7 2.1.8 2.2 2.2.1 2.2.2 2.2.3 2.2.4 2.2.5 2.2.6 2.2.7 2.2.8 2.3 2.3.1 2.3.2 Scelta dei vertici trigonometrici. Calcoli eseguiti per la determinazione delle coordinate ellissoidiche. Suddivisione della porzione di ellissoide che riguarda l’Italia in due fusi Punto della situazione. La carta di Gauss. Criteri sui quali è basata la carta di Gauss. Motivo per il quale sono stati introdotti i due fusi ellissoidici. Introduzione del cilindro secante. Modulo di deformazione per elementi finiti. La proprietà della conservazione degli angoli e le sue implicazioni pratiche Trasformata, tangente e corda di un arco ellissoidico nella carta di Gauss Inserimento rigoroso di un angolo azimutale nella carta di Gauss Inserimento semplificato di un angolo azimutale nella carta di Gauss Inserimento delle distanze misurate sul terreno nel sistema cartografico nazionale. Definizione di distanza topografica. Semplificazione del problema mediante l'introduzione della sfera locale e di uno schema geometrico di comodo 2.3.3 Passaggio dalla distanza reale misurata alla distanza topografica. 2.3.4 Introduzione diretta delle misure di angoli e distanze nella proiezione di Gauss. CAPITOLO IV - LA CARTOGRAFIA TRADIZIONALE DISEGNATA 1 Generalità. 2 Le funzioni della cartografia 3 Il rapporto di scala della cartografia. 4 Esempi di cartografia alle diverse scale. CAPITOLO V - RILIEVO TOPOGRAFICO CLASSICO 1 Descrizione schematica della costruzione di una carta. 1.1 Impostazione concettuale della costruzione della planimetria. 1.2 Impostazione concettuale della costruzione dell’altimetria. 2 Funzione della rete di inquadramento. 3 3.1 3.1.1 3.1.2 3.2 3.2.1 3.2.2 3.3 3.3.1 3.3.2 3.3.3 3.4 3.4.1 Rilievo planimetrico. Triangolazioni. Rete di inquadramento Calcolo della rete. Applicazione del metodo delle osservazioni indirette a problemi topografici. Sviluppo del procedimento completo su un esempio. Generalizzazione del problema Intersezioni. Intersezione in avanti. Intersezione inversa. Osservazione importante sulla questione rete di base punti di infittimento. Poligonali. Poligonale ordinaria Indice - pagina IV R.Galetto A.Spalla - Lezioni di Topografia 3.4.2 Poligonale di precisione. 3.5 Celerimensura. 4 4.1 4.1.1 4.1.2 4.1.3 4.1.4 4.1.5 4.1.6 4.1.7 4.1.8 4.2 4.2.1 4.2.3 4.2.4 4.2.5 4.2.6 4.2.7 4.3 Rilievo altimetrico. Livellazione geometrica. Premessa. Principio del metodo. Descrizione del livello. Livelli ordinari e livelli di precisione: precisioni conseguibili Come valutare la precisione conseguibile nelle operazioni di livellazione geometrica Livellazione geometrica di precisione. Determinazione delle coordinate altimetriche nel rilievo topografico a grande e media scala mediante livellazione geometrica. Compensazione globale di un sistema a più poligonali mediante il metodo delle osservazioni indirette La livellazione trigonometrica ( L. T. ). Premessa. Schematizzazione del problema. Schematizzazione dell'operazione. Influenza della rifrazione atmosferica. Precisione del metodo. Impiego della livellazione trigonometrica. Livellazione tacheometrica. CAPITOLO VI- LA TECNICA TOPOGRAFICA NEI COLLAUDI E CONTROLLI DI GRANDI STRUTTURE 1 1.1 1.2 1.3 Considerazioni preliminari. Spostamenti assoluti e spostamenti relativi. Il metodo di misura variometrico e quello per differenza di posizione. Classificazione dei casi trattati. 2 2.1 2.1.1 2.1.2 2.1.3 2.2 2.3 2.4 Determinazione di spostamenti verticali. Impiego della livellazione geometrica. Metodologia classica Uso di stadiette di vetro Precisione conseguibile nella determinazione degli spostamenti verticali Impiego della livellazione trigonometrica. Impiego della livellazione idrostatica di precisione. Clinometro 3 3.1 3.2 3.3 Determinazione degli spostamenti orizzontali. Impiego della triangolazione. Uso del collimatore Uso dei distanziometri elettroottici Indice - pagina V R.Galetto A.Spalla - Lezioni di Topografia 3.3.1 Indicazioni di un metodo per l'eliminazione dell'errore dovuto alla precisione intrinseca dello strumento e applicazione del metodo per il controllo delle deformazioni di una diga con criterio variometrico. 3.3.2 Indicazione di un metodo per l'eliminazione dell'errore dovuto alla non perfetta conoscenza delle condizioni atmosferiche. CAPITOLO VII - IL SISTEMA GPS 1. La Geodesia classica e la Geodesia spaziale. 2. Struttura del sistema GPS. 3. La determinazione delle coordinate di un punto. 3.1 Il principio di base. 3.2. Dalle coordinate geocentriche alle coordinate ellissoidiche 4. 4.1 4.2 4.3 4.3.1 4.3.2 La prassi operativa. La tecnica differenziale Un uso riduttivo del sistema GPS: il GPS come distanziometro L’uso cinematico del GPS Utilizzazione nella tecnica fotogrammetrica Applicazioni in campo civile 5. La rete dei vertici trigonometrici GPS dell’IGMI CAPITOLO VIII - FOTOGRAMMETRIA 1 1.1 1.2 Concetti generali. Semplificazione del problema della rappresentazione cartografica del territorio. Il concetto di base della fotogrammetria. 1.3 1.3.1 1.3.2 1.3.3 1.3.4 1.3.5 1.4 1.4.1 1.4.2 1.4.3 1.4.4 Fotogrammetria analogica, analitica e digitale. Premessa: il fenomeno fisiologico della vista La fotogrammetria analogica. La fotogrammetria analitica La fotogrammetria digitale. Fotogrammetria aerea e fotogrammetria terrestre L’acquisizione del dato primario: i fotogrammi. Le fotografie aeree in uso nella fotogrammetria. La camera fotogrammetrica. I fotogrammi prodotti da una camera fotogrammetrica. Le onde elettromagnetiche dello spettro della luce visibile, dell'infrarosso vicino e dell'infrarosso termico. 1.4.5 Le pellicole fotografiche. 1.5 Schema di ripresa fotogrammetrica. 1.6 Le condizioni meteorologiche e le riprese da aereo. 2. 2.1 Fotogrammetria analitica. Il sistema di riferimento interno della camera da presa. Indice - pagina VI R.Galetto A.Spalla - Lezioni di Topografia 2.2 Lo strumento restitutore analitico. 2.3 La procedura di orientamento interno di un fotogramma. Dalle coordinate strumentali alle coordinate lastra 2.3.1 La procedura semplice. 2.3.2 La procedura che tiene conto della deformazione della pellicola 2.4 L’equazione di collinearità 2.4.1 Impostazione dell’equazione di collinearità 2.4.2 La matrice di rotazione tra il sistema (X,Y,Z) e il sistema (x,y,z) 2.4.3 Forma definitiva delle equazioni di collinearità per due raggi omologhi. 2.5 Sulla possibilità di utilizzare in diversi modi le equazioni di collinearità. 2.6 L’orientamento relativo di due fotogrammi. 2.6.1 Il concetto generale 2.6.2 Scelta del sistema di riferimento arbitrario 2.6.3 L’equazione di condizione per l’orientamento relativo 2.6.4 Calcolo delle coordinate dei punti del modello nel sistema arbitrario 2.7 L’orientamento assoluto del modello stereoscopico 2.8 La determinazione dei punti di appoggio con metodo topografico 2.9 La fase di restituzione 2.10 Rilievo fotogrammetrico e rilievo topografico 2.11 La triangolazione aerea a modelli indipendenti 2.11.1 Struttura del blocco, punti nadirali, di legame e di appoggio 2.11.2 Le operazioni di misura 2.11.3 Il programma di calcolo 2.11.4 Valutazione della precisione del calcolo del blocco 2.11.5 Uso dei risultati della triangolazione aerea 2.12 La triangolazione aerea a stelle proiettive con punti di appoggio e quella integrata da dati GPS 2.12.1 La triangolazione aerea a stelle proiettive con punti di appoggio 2.12.2 La triangolazione aerea a stelle proiettive con dati GPS 3. 3.1 Iter per la realizzazione di un rilievo con metodo fotogrammetrico. Progettazione ed allestimento del materiale necessario per la costruzione di una carta. 3.2 Restituzione fotogrammetrica. 3.3 La revisione sul terreno. 3.4.1 Editing cartografico 3.4.2 Il prodotto finale numerico 3.4.3 Il prodotto finale grafico 3.5 Schemi delle fasi di realizzazione di cartografia con metodo fotogrammetrico CAPITOLO IX - CARTOGRAFIA NUMERICA 1 1.1 Caratteristiche della cartografia numerica Schema concettuale Indice - pagina VII R.Galetto A.Spalla - Lezioni di Topografia 1.1.1 Cartografia tradizionale e cartografia numerica: analogia dei rispettivi schemi concettuali 1.1.2 Definizione della cartografia numerica 1.1.3 Tipologia della cartografia numerica 1.2 Scala nominale 1.3 Caratteristiche del contenuto planimetrico e altimetrico della cartografia numerica 1.3.1 Il contenuto planimetrico 1.3.2 Contenuto altimetrico della cartografia. 1.4 Funzione del sistema di codifica 2 2.1 2.2 Metodi di produzione Metodo fotogrammetrico numerico diretto Digitalizzazione di cartografia esistente 3 3.1 3.2 3.2.1 3.2.2 3.3 Intervento sui dati Editing cartografico Stazioni grafiche interattive Funzionalità Generalità sulle configurazioni hardware Differenze di esigenze fra sistemi per la produzione e sistemi per l'utilizzo della cartografia numerica 4 Aggiornamento della cartografia numerica 5 5.1 5.2 Organizzazione dei dati e loro trasferimento Struttura dei dati Formato di trasferimento della cartografia numerica 6 La cartografia numerica e i sistemi informativi territoriali (SIT) APPENDICI 1. Sistemi di misura degli angoli. 2. 2.1 2.2 Angoli di direzione. Definizioni e convenzioni L’angolo di direzione nel calcolo delle coordinate di un punto Indice - pagina VIII R.Galetto A.Spalla - Lezioni di Topografia CAPITOLO I TEORIA DEGLI ERRORI 1 Trattamento delle misure dirette. 1.1 Considerazioni generali. Lo studio degli errori di osservazione riveste una importanza fondamentale in tutte le scienze sperimentali, quando cioè si devono effettuare delle misure e si vogliono stabilire i criteri più opportuni per raggiungere una certa approssimazione, valutare le entità degli errori che si sono commessi o determinare i valori numerici da assumere per le grandezze misurate o per altre ad esse collegate da relazioni analitiche. Presenta un interesse notevole lo studio degli errori nelle misure topografiche, dal momento che la loro precisione deve essere spinta talvolta a limiti molto elevati che solo una scelta accurata di strumenti e di metodi, unita a particolari accorgimenti di osservazione, può consentire di ottenere. E' comunque il caso di sottolineare subito che la teoria degli errori non costituisce una guida indispensabile soltanto nelle misure di grande precisione, bensì in tutte le misure, in quanto occorre, caso per caso, scegliere i procedimenti più opportuni per raggiungere il risultato voluto con la massima economia di tempo e di mezzi e bisogna, inoltre, sapere che quel risultato è stato ottenuto cioè che si è raggiunta la desiderata approssimazione. 1.2 Grandezze e quantità di grandezza. 1.2.1 Prima definizione di grandezza. Una grandezza è una caratteristica che viene riconosciuta come comune in singole concretizzazioni di concetti che nascono dall’osservazione della realtà. Esempio. Sollevando oggetti diversi ne riportiamo una differente sensazione di sforzo; da questa osservazione nasce il concetto di peso; il peso è una caratteristica che riconosciamo come comune in singole concretizzazioni; il peso è una grandezza. 1.2.2 Seconda definizione di grandezza. Bertrand Russel così definisce una grandezza: “Esiste una certa coppia di relazioni indefinibili, maggiore o minore; queste relazioni sono simmetriche e transitive e sono incompatibili l’una con l’altra. Ognuna è inversa dell’altra nel senso che ogni volta che una è valida tra A e B e l’altra è valida tra B ed A. I termini che risultano suscettibili di queste relazioni sono grandezze. Capitolo I - Teoria degli errori pagina 1 R.Galetto A.Spalla - Lezioni di Topografia Ogni grandezza ha una certa relazione particolare con qualche concetto, espressa dicendo che essa è una grandezza di quel concetto. Due grandezze che hanno questa relazione col medesimo concetto si dicono dello stesso genere; essere dello stesso genere è la condizione necessaria e sufficiente per la relazione di maggiore e minore” 1.2.3 Classi di grandezze. Una classe di grandezze è l’insieme delle grandezze di uno stesso genere. Un chilometro, un metro, un millimetro sono concretizzazioni di un medesimo concetto, cioè del concetto di lunghezza, sono quindi grandezze di uno stesso genere; le grandezze di uno stesso genere formano una classe di grandezze. 1.2.4 Classi di grandezze di divisibilità. Consideriamo un tutto formato da un numero di parti semplici che lo compongono. Chiamiamo divisibilità il numero di parti che compongono il tutto. La divisibilità è una grandezza; infatti la divisibilità di un tutto sarà maggiore o minore a seconda del numero di parti che lo compongono. Tutti i fenomeni fisici che sono assimilabili ad un tutto scomponibile in parti semplici possiedono la grandezza di divisibilità. La divisibilità costituisce una classe di grandezze. Esempio Il numero di pezzi di cui è costituita una locomotiva è la divisibilità della locomotiva; il numero di pezzi di cui è costituita una penna a sfera è la divisibilità della penna a sfera. Se il numero di pezzi di cui è composta la locomotiva è maggiore di quello di cui è composta la penna a sfera si dirà che la grandezza di divisibilità della locomotiva è maggiore della grandezza di divisibilità della penna a sfera. 1.2.5 Definizione di misura di una grandezza. Definizione generale di misura di una grandezza secondo Russel. “Dicesi misura di una grandezza, nel senso più generale, qualsiasi metodo con cui si stabilisca una corrispondenza univoca e reciproca tra una grandezza di un determinato genere e un numero intero.” 1.2.6 La misura delle grandezze di divisibilità. La definizione di misura di una grandezza data da Russel è valida per grandezze di qualsiasi classe, ma si adatta particolarmente bene alla classe di grandezze di divisibilità. Capitolo I - Teoria degli errori pagina 2 R.Galetto A.Spalla - Lezioni di Topografia Infatti la misura di una grandezza di divisibilità si effettua semplicemente contando le parti che compongono il tutto ed associando tale numero alla quantità di grandezza. Inoltre quando due grandezze sono delle divisibilità, non soltanto possiamo misurarle con due numeri, ma la somma dei due numeri che le misurano darà direttamente la misura della grandezza che è la somma delle due grandezze di divisibilità. 1.2.7 Classi di grandezza la cui misura è riconducibile alla misura di una grandezza di divisibilità. Vi sono delle classi di grandezza chiamate di tipo quantitativo. Per una grandezza che appartiene a questa classe il valore zero della sua misura ha significato di non esistenza, mentre un valore non nullo della misura, che è sempre espresso da un numero positivo, ha significato di entità della grandezza, nel senso che tanto più è grande il numero che rappresenta la misura, tanto maggiore è l’entità della grandezza. La misura delle grandezze di tipo quantitativo, può essere ricondotta alla misura di una grandezza di divisibilità. 1.2.8 Descrizione operazionale della misura di una grandezza di tipo quantitativo. Oggetto di un’operazione di misura diretta è una quantità di grandezza, cioè un oggetto che concretizza nella realtà un concetto di grandezza. Stabilito ad esempio che la lunghezza è una grandezza, che le quantità di tale grandezza sono misurabili poiché tra esse ha senso il concetto di maggiore e minore, vediamo come viene eseguita la misura diretta della lunghezza di una quantità di lunghezza. Supponiamo si voglia misurare la lunghezza di un barra metallica L. Lo schema logico di esecuzione di una misura diretta è il seguente: • si stabilisce un’unità di misura U • si sommano tante unità di misura U fino a formare una quantità di grandezza G di paragone che giudichiamo uguale a L • si contano quante unità di misura U si sono sommate per formare G, cioè si misura la numerosità di G; • si assume come misura di L la numerosità di G. Molte volte non ci accorgiamo di applicare questa procedura, ma in realtà la misura diretta di una quantità di grandezza avviene sempre in questo modo. Esempio Quando misuriamo con una riga millimetrata lunga un metro la lunghezza di un oggetto, non ci rendiamo conto che parte dell’operazione di misura è già stata fatta da chi ha costruito il metro; e cioè: è stata scelta l’unità di misura millimetro e la si è sommata mille volte; quando noi effettuiamo la misura di un oggetto accostiamo lo zero della riga ad un’estremità dell’oggetto e guardiamo il punto in cui cade, sulla riga, l’altra estremità dell’oggetto; così facendo creiamo sulla riga una quantità di grandezza Capitolo I - Teoria degli errori pagina 3 R.Galetto A.Spalla - Lezioni di Topografia di paragone la cui lunghezza stimiamo uguale a quella dell’oggetto che vogliamo misurare; dopodiché leggiamo il valore della misura sulla riga, il che equivale a contare quanti millimetri è lunga la quantità di paragone; infine assumiamo come misura dell’oggetto il valore letto sulla riga, il quale corrisponde appunto alla numerosità della grandezza di paragone che abbiamo creato sulla riga. L’unica differenza tra l’esempio fatto e lo schema concettuale sopra esposto rispecchia il fatto che, molte volte, gli strumenti di misura offrono già una somma di unità di misura che permette di misurare quantità di grandezza che vanno da zero a un certo valore massimo; nell’esempio fatto questo valore massimo è appunto una lunghezza di un metro. La massima quantità di grandezza misurabile con uno strumento di misura è un parametro molto importante che, come vedremo tra poco, serve a definire la precisione dello strumento. Le misure delle grandezze di tipo quantitativo effettuate secondo lo schema descritto si dicono misure dirette. In realtà l’unica vera misura diretta è il conteggio, operazione nella quale consiste la misura delle grandezze di divisibilità. Tuttavia, per il fatto di adottare uno schema operazionale che riconduce la misura delle grandezze di tipo quantitativo alla misura di una grandezza di divisibilità, si dice appunto che le misure di grandezze di tipo quantitativo, effettuate secondo lo schema sopra descritto, sono misure dirette. 1.3 Le misure e l'ambiente reale. Quando si effettua la misura di una quantità di grandezza lo scopo dell’operazione è quello di associare in modo univoco un numero alla quantità di grandezza sottoposta all'operazione di misura. Quantità di grandezza e misure devono corrispondersi univocamente. Ad ogni quantità di grandezza deve cioè corrispondere una ed una sola misura e ad un numero deve corrispondere, nell'ambito della stessa classe di grandezza, una ed una sola quantità di grandezza. Si constata invece che, ripetendo più volte la misura di una stessa quantità di grandezza, variano i risultati che si ottengono. Diventa a questo punto necessario, per ridurre ad un unico valore la molteplicità di numeri che si riferiscono ad una stessa quantità di grandezza, cercare le cause che generano questa variabilità di risultati della misura ripetuta e definire delle modalità per ricavare un unico valore dalla molteplicità dei valori ottenuti mediante le operazioni di misura ripetute. Tali cause vengono individuate in due possibili categorie, una legata più propriamente ai limiti imposti dagli strumenti con cui le operazioni di misura vengono effettuate, l'altra legata all'ambiente in cui tali operazioni hanno luogo. Capitolo I - Teoria degli errori pagina 4 R.Galetto A.Spalla - Lezioni di Topografia 1.4 Origine della dispersione delle misure. 1.4.1 Sensibilità e precisione degli strumenti di misura. Si definisce sensibilità di uno strumento la più piccola quantità di grandezza misurabile univocamente con esso. Esempi: • per un righello millimetrato la sensibilità è 1 mm; • per una bilancia con scala graduata in grammi la sensibilità è 1 grammo. Si definisce precisione di uno strumento il rapporto tra la sensibilità dello strumento e la massima quantità di grandezza che lo strumento può misurare. La precisione è quindi un numero adimensionale; si dice che la precisione di uno strumento è tanto maggiore quanto minore è il numero che la esprime. Esempi: • una riga di 1 metro con suddivisione in millimetri ha una precisione di 1mm = 10−3 1000mm • una bilancia che può pesare una massa di entità massima di 10 kg e avente una graduazione in grammi ha un precisione di 1g −4 = 10 10000g Per il fatto di essere adimensionale, la precisione ci permette di confrontare l'accuratezza di misure di diverso tipo che intervengono nella determinazione di una grandezza misurata indirettamente. Una delle cause che crea la mancanza di univocità sui valori ottenuti nel ripetere la misura di una stessa quantità di grandezza, risiede nel fatto che generalmente noi usiamo gli strumenti pretendendo di aumentare con operazioni di stima la sensibilità, oppure con operazioni ripetitive la precisione. Ad esempio misuriamo una lunghezza con un righello millimetrato e stimiamo i decimi di millimetro se la lunghezza non risulta uguale ad un numero finito di millimetri. Oppure misuriamo una lunghezza di decine di metri riportando più volte una riga di un metro, commettendo delle imprecisioni. Questi due fatti, cioè • usare uno strumento al di fuori del suo campo di precisione, • pretendere di aumentarne la sensibilità con un'operazione di stima, introducono nell'operazione di misura dei fattori soggettivi, cioè dipendenti dal modo di eseguire la misura da parte dell'operatore; questi fattori non si mantengono costanti al ripetersi dell'operazione di misura. Capitolo I - Teoria degli errori pagina 5 R.Galetto A.Spalla - Lezioni di Topografia Questo causa una dispersione dei valori numerici che rappresentano il risultato delle misure. 1.4.2 Influenza dell'ambiente. Un altro elemento che genera la dispersione dei valori numerici ottenuti ripetendo le misure di una stessa quantità di grandezza, è dovuto all'influenza dell'ambiente nell'operazione di misura. L'ambiente in cui avviene la misura è infatti caratterizzato da parametri (temperatura, umidità, pressione atmosferica ecc.) che non hanno un valore costante, ma oscillano in un certo campo. Possiamo vedere quindi il numero X che rappresenta la misura eseguita in un certo istante come un particolare valore di una funzione f che dipende: • dalla quantità di grandezza G che si misura; • dall'unità di misura U che si adotta; • da parametri u, v, w,....t che caratterizzano l'ambiente; X = f (G/U, u, v, w,...t) Se durante un intervallo di tempo ripetiamo la misura, i valori dei parametri ambientali varieranno da misura a misura, e quindi si avranno diversi valori di X; pertanto nell'accingerci ad effettuare un'operazione di misura non dobbiamo pensare ad un solo risultato possibile, ma ad una molteplicità di risultati possibili. Poiché non vi è univocità nel valore della misura, il primo quesito a cui di deve dare risposta è: quale è, tra tutti i possibili valori che si potrebbero registrare, quello che potremmo assumere come misura vera della quantità di grandezza G? Si conviene di assumere come misura vera X della quantità di grandezza G, il valore di X che si avrebbe se effettuassimo la misura quando tutti i parametri ambientali assumono il loro valore medio: X = f (G/U, um, vm, wm,...tm) Si definisce inoltre come errore ε di una generica misura la differenza tra il valore X che corrisponde a quella misura e il valore X : ε = X - X = f(G/U, u, v, w,...t) - f (G/U, um, vm, wm,...tm) (2) 1.4.3 Definizione di errore accidentale Riprendiamo la (1) ed eseguiamo lo sviluppo in serie di Taylor della generica misura nell’intorno du, dv, dt, dw, ecc. dei valori medi dei parametri ambientali. Si avrà: ε =X - X= Capitolo I - Teoria degli errori pagina 6 R.Galetto A.Spalla - Lezioni di Topografia ∂ f ∂ f ∂f ∂ f du + dv + dw +..+ dt +R -f(G/U,um,vm,wm,...tm) ∂ u ∂ v ∂ w ∂ t f(G/U,um,vm,wm,...tm)+ e quindi: ∂ f ∂ f ∂f ∂ f ε = du + dv + dw +..+ dt +R ∂ u ∂ v ∂ w ∂ t Si dirà che la misura è affetta da soli errori accidentali se le variazioni du, dv, dt, dw, ecc. dei parametri ambientali nell’intorno dei valori medi sarà sufficientemente piccola che se ne possano trascurare le potenze superiori alla prima; in tal caso il resto R è trascurabile e l’errore sarà una combinazione lineare delle variazioni dei parametri ambientali. ∂ f ∂ f ∂f ∂ f ε = du + dv + dw +..+ dt ∂ u ∂ v ∂ w ∂ t La dizione sufficientemente piccola che se ne possano trascurare le potenze superiori alla prima significa questo: il resto R deve essere di entità numerica tale che andrebbe a modificare cifre non significative della misura. Ad esempio: se si sta misurando una lunghezza e si registrano i valori di misura fino ai millimetri, il resto R non deve superare come valore numerico qualche decimo di millimetro. 1.4.4 Lo sviluppo teorico della teoria degli errori. Partendo dall’impostazione esposta e utilizzando elementi molto avanzati di calcolo delle probabilità si può arrivare a dimostrare che gli errori di misura hanno un comportamento ben definito e quindi si possono determinare formule che, dalla molteplicità delle misure possibili, ci riconducono a un valore univoco da attribuire alla quantità di grandezza misurata e al modo di valutarne l’accuratezza. Poiché gli elementi molto avanzati di calcolo della probabilità necessari a questa trattazione non fanno parte del bagaglio culturale di chi segue questo corso, noi affronteremo il problema in modo un po’ diverso, che potremmo definire empirico; tale metodo ha il vantaggio di richiedere nozioni di statistica e di calcolo delle probabilità molto più limitate e inoltre, rifacendosi a ipotetici risultati di misura ottenuti in sede sperimentale, è più aderente a quella che è stata l’evoluzione del pensiero scientifico in questo settore. 1.5 Variabili statistiche e variabili casuali. 1.5.1 Variabile statistica. Si definisce: a) popolazione l'insieme di N individui (persone, cose, ecc.) che possiedono tutti una stessa caratteristica che si presenta in quantità differenti; b) attributo la caratteristica suddetta; Capitolo I - Teoria degli errori pagina 7 R.Galetto A.Spalla - Lezioni di Topografia c) valori argomentali i differenti valori dell'attributo che possono presentarsi negli individui della popolazione; d) frequenza assoluta il numero degli individui che hanno lo stesso valore argomentale; e) frequenza relativa il rapporto tra la frequenza assoluta ed il numero totale degli individui della popolazione. Esaminando una popolazione di N individui si può costruire una variabile statistica; essa risulta formata da due serie di numeri: 1. i valori argomentali X1 , X2 , ...Xi, Xm presenti nella popolazione (dove m è generalmente minore di N, perché più individui possono avere lo stesso valore argomentale); 2. le frequenze f1 , f2 , ...fi, fm dei suddetti valori argomentali, con Σfi = N; dai valori delle frequenze possiamo definire quelli delle frequenze relative f1 /N, f2 /N, ...fi/N , fm/N, con Σfi/N=1 Il tutto si schematizza come segue: X1 , X2 , ...Xi, Xm X f1 , f2 , . ..fi, fm con Σfi = N (2) o anche X1 , X2 , ...Xi, Xm X con Σfi/N=1 (3) f1 /N, f2 /N, ...fi/N , fm/N Per comodità, dopo aver eseguito l'esame di tutti i valori Xi presenti nelle popolazioni, i valori Xi vengono ordinati nelle (2) e (3) in valore crescente (X1 <X2 < ..<.Xi, <Xm). Per esprimere, in maniera sintetica, una variabile statistica si usano due parametri: la media e lo scarto quadratico medio (s.q.m.) che vengono così calcolati: m MX = ∑X fi i N 1 (4) s. q. m. = ± ∑ (x m 1 • • i − MX ) 2 fi N La media indica appunto il valore medio dell'attributo nella popolazione, lo s.q.m. indica se i valori argomentali sono più o meno dispersi intorno alla media. Una variabile statistica può essere rappresentata graficamente mediante l'istogramma. Per costruire un istogramma • si prendono in considerazione i valori argomentali della variabile statistica, che come abbiamo detto sono già ordinati in serie crescente, • si riportano su un asse delle ascisse il valore minimo X1 ed il valore massimo Xm ; • si suddivide tale intervallo in k intervalli parziali ∆x di uguale ampiezza; il numero k è arbitrario; in genere è tanto maggiore quanto più numerosi sono i valori argomentali; Capitolo I - Teoria degli errori pagina 8 R.Galetto A.Spalla - Lezioni di Topografia • • • si considera poi il valore X’1 = X1 +∆x e si sommano le frequenze relative di tutti i valori argomentali compresi tra X1 e X’1 ; si costruisce quindi nel grafico sul primo ∆x ,cioè su ∆x1 in figura, un rettangolo la cui area è proporzionale alla somma delle frequenze relative dei valori argomentali compresi tra X1 e X’1 ; si considera poi il valore X’2 = X’1 +∆x e si procede analogamente; e così via sino all'intervallo k. Poiché le diverse areole che insistono sui vari intervalli sono proporzionali alla frequenza relativa, l'area totale dell'istogramma, nella scala di rappresentazione, risulterà sempre uguale ad 1. Σfi/N X'1 X' 2 X'3 . . X'i . . . X'm figura 1 1.5.2 Variabile casuale discontinua. Consideriamo ancora una popolazione di individui e supponiamo che di essa sia possibile esaminare solo un individuo alla volta. Ogni individuo inoltre deve essere di volta in volta enucleato dalla popolazione mediante un'operazione di estrazione a caso, un'operazione cioè che non ha nessun criterio di scelta. Infine ogni individuo, dopo essere stato esaminato, deve essere reinserito nella popolazione prima di procedere ad una nuova estrazione. Esempio: in un sacchetto ci sono dei dischetti contrassegnati da numeri; si estrae un dischetto, se ne esamina il numero, lo si reinserisce quindi nel sacchetto prima di procedere ad un'altra estrazione. Questo tipo di operazione su una popolazione fa sì che ad essa possa considerarsi associata una variabile casuale; la variabile casuale è costituita da una doppia serie di numeri, che sono i valori argomentali e le probabilità ad essi associate. X1 , X2 , ...Xi, Xm X (5) Capitolo I - Teoria degli errori pagina 9 R.Galetto A.Spalla - Lezioni di Topografia p1 , p2 , ...pi, pm La probabilità pi che si presenti un valore argomentale prestabilito Xi data dal rapporto: numero dei casi favorevoli all' evento pi = numeri dei casi possibili Ogni singola probabilità pi sarà compresa tra i valori limiti 0 ed 1 (rispettivamente assenza dei casi favorevoli e cioè il valore Xi non compare nella popolazione; certezza del risultato, nella popolazione esiste cioè il solo valore Xi ). Non esistono possibilità negative. La somma di tutti i casi favorevoli è uguale al numero dei casi possibili, quindi ∑p =1 i Esempio: il classico dado da gioco può essere visto come una variabile casuale così composta: 123456 X 1/6 1/6 1/6 1/6 1/6 1/6 Lanciando il dado si esegue un'estrazione a caso; il reinserimento nella popolazione dell'individuo estratto, e cioè, nel caso del dado, la faccia rivolta verso l'alto, è in questo caso automatica. La probabilità di ogni numero è 1/6. Anche in una variabile casuale si possono definire la media e lo scarto quadratico medio. m media X= ∑X p i i 1 (6) m scarto quadratico medio σ=± ∑ (X − M) p i 2 i i =1 1.5.3 Variabile casuale continua. Una variabile casuale anziché essere composta da una serie discreta di valori argomentali e dalle rispettive probabilità, può essere definita con continuità in un intervallo a - b. Capitolo I - Teoria degli errori pagina 10 R.Galetto A.Spalla - Lezioni di Topografia a b figura 2 x x+dx a b figura 3 Esempio: il punto di arresto di una pallina che scivoli sul piano (vedi figura 2) In questo caso in tutto l'intervallo a - b esisterà una funzione f(x) in grado di definire la probabilità che un'estrazione a caso porti ad un valore compreso in un intervallo x - (x+dx) interno ad a - b. (vedi figura 3) Non potrà essere invece definita la probabilità che l'evento porti ad uno specifico valore x perché nell'intervallo a - b esistono infiniti valori e quindi la probabilità (intesa come rapporto tra casi favorevoli e casi possibili) risulta nulla. Per una variabile continua sarà: b pa,b= ∫ f(x) dx = 1 a (7) b X = ∫ f(x)x dx a (8) b σ=± ∫ (x - X) 2 f(x) dx a (9) 1.6 Determinazione della misura diretta di una quantità di grandezza. 1.6.1 Analisi statistica dei risultati di n misure ripetute. Supponiamo di ripetere la misura di una certa quantità di grandezza per un numero elevato di volte; siano: • • • • n il numero delle misure effettuate, X1 , X2 , ...Xi, Xm i valori numerici ottenuti, M la media aritmetica delle misure, a - b l'intervallo di dispersione delle misure. Capitolo I - Teoria degli errori pagina 11 R.Galetto A.Spalla - Lezioni di Topografia Le misure effettuate possono essere considerate come una variabile statistica; di esse si può costruire l'istogramma che risulta avere un andamento del tipo di quello riportato in figura 4. Facendo variare le quantità di grandezza sottoposte a misura e ripetendo, per ciascuna di esse, un certo numero di volte l'operazione di misura, si ottengono tante variabili statistiche ciascuna di media Mi , e di intervallo di dispersione ai- bi. Si verifica però che gli istogrammi costruiti con i risultati delle diverse misure hanno tutti lo stesso andamento, cioè sono del tipo di quelli rappresentati in figura 4. a1 X1 b1 a2 X2 b2 a3 X3 b3 figura 4 Tali istogrammi vengono costruiti riportando in ordinata le frequenze relative ed hanno quindi tutta la stessa area totale uguale ad 1; in ogni istogramma l'area totale rappresenta il 100% delle misure effettuate, mentre l'area di un generico rettangolino rappresenta la percentuale delle misure comprese nell'intervallo che ne costituisce la base. Quanto è maggiore quindi l'intervallo ai - bi di dispersione delle misure, tanto più schiacciato risulta l'istogramma; viceversa tanto più si restringe l'intervallo, tanto più ripido risulta l'istogramma. Ripetendo diverse serie di n misure su una stessa quantità di grandezza, si avrà che l'intervallo a - b di dispersione di valori numerici associati alle misure, sarà tanto minore quanto maggiore è l'accuratezza con cui si sono eseguite le operazioni di misura; di conseguenza un istogramma molto ripido, con una forte percentuale di misure raccolte nell'intorno del punto centrale dell'intervallo di dispersione, indica che le misure sono state fatte bene; e viceversa. Se prendiamo in considerazione un altro tipo di grandezza e sottoponiamo a misure ripetute varie quantità di essa, notiamo che l'andamento dei diversi istogrammi rimane ancora dello stesso tipo dei precedenti. Dall'esame quindi di tutti gli istogrammi così ottenuti, si possono ricavare le seguenti considerazioni. I. I risultati delle misure possono essere riguardati come estrazione a caso da una popolazione di misure possibili, rappresentabili mediante una variabile casuale. II. Più si aumenta il numero delle misure, più aumentano i valori argomentali che si verificano; l'intervallo a - b dell'asse delle ascisse sul quale si riportano i valori delle misure risulta sempre più fittamente popolato; ciò rende lecito introdurre l'ipotesi che la variabile casuale che costituisce la popolazione delle misure possibili sia di tipo continuo. Capitolo I - Teoria degli errori pagina 12 R.Galetto A.Spalla - Lezioni di Topografia III.L'andamento degli istogrammi costruiti su serie di misure ripetute rimane lo stesso, indipendentemente dalla grandezza considerata, dalla quantità di grandezza che si misura, dallo strumento di misura, dall'ambiente ecc.; si constata cioè che vi è un intervallo più o meno ampio in cui i valori sono compresi; • la frequenza dei valori argomentali è maggiore per i valori argomentali situati nella zona centrale dell'intervallo e diventa via via minore mano mano che ci si avvicina agli estremi dell'intervallo di dispersione; • l'istogramma è approssimativamente simmetrico rispetto al valore medio M delle misure effettuate. Vi è quindi una costante di comportamento nella popolazione delle misure possibili che ci permette di affermare che tutte le popolazioni di misure possibili sono pensabili come variabili casuali, in cui la distribuzione delle probabilità è definita da un unico tipo di funzione. • 1.6.2 Le popolazioni di misure possibili come variabili casuali normali. In seguito alle constatazioni esposte nel precedente paragrafo risulta lecito porsi il quesito di trovare un tipo di funzione f(x) che interpoli bene gli istogrammi e che possa essere considerata come la funzione della distribuzione delle probabilità della variabile causale di media X e varianza σ associabile ad una qualsiasi popolazione di misure possibili. La funzione f(x) che risulta più idonea a questo scopo, è la curva di Gauss, che ha la seguente espressione: ( f (x)= 1 ⋅e σ 2π 1 x−X − ⋅ 2 σ ) 2 (10) dove X e σ sono rispettivamente la media e la varianza della variabile casuale. La funzione (10) rappresenta una curva avente la forma di una campana più o meno schiacciata, simmetrica rispetto al punto X in cui l'ordinata delle funzioni di distribuzione della probabilità è massima (vedi figura 5). Affinché la (10) possa essere considerata l'espressione di una distribuzione di probabilità occorre che il suo integrale esteso ai limiti dell'intervallo di definizione della variabile casuale sia uguale ad 1; ciò si verifica per la (10) quando i limiti di tale intervallo si estendono a - ∞ e a + ∞. Possiamo pertanto concludere che: • • dati una certa quantità di grandezza da misurare, lo strumento di misura e l'ambiente in cui si opera, si genera una popolazione di misure possibili; questa popolazione di misure è rappresentabile con una variabile casuale continua, definita tra -∞ e + ∞, che ha una media X, uno scarto quadratico medio σ ed una distribuzione di probabilità definita dalla (10). Capitolo I - Teoria degli errori pagina 13 R.Galetto A.Spalla - Lezioni di Topografia -∞ +∞ X figura 5 L'essere giunti a questo risultato è importante. I. Siamo riusciti a stabilire una legge fisica che descrive bene il fenomeno delle misure ripetute. II. L'esistenza di un valore X rispetto al quale si ha uguale percentuale di misure ad esso inferiori o superiori, ci consente di assumere tale valore come il più rappresentativo della popolazione di misure e di dire pertanto che il valore che noi vorremmo associare alla quantità di grandezza misurata (in modo da avere univocità tra quantità di grandezza e numero che ne rappresenta la misura) è appunto X ; X è pertanto considerato il valore giusto della misura ed ogni altro valore xi ≠ X , appartenente alla popolazione delle misure possibili, è considerato affetto da errore essendo ε = xi - X l'errore. III.Degli unici due parametri X e σ che compaiono nella (10) è possibile (vedremo poi come) ricavare una media empirica (cioè un valore approssimato) in base ad un numero limitato di misure ripetute. IV.Possiamo dare un preciso significato al valore della varianza e cioè: consideriamo una variabile casuale a distribuzione normale di media X e varianza σ, la probabilità che un'estrazione a caso su questa variabile porti ad un risultato compreso tra due estremi a e b è data dalla relazione b pa ,b 1 x− X σ − 1 2 = e ∫ σ 2π a 2 dx (11) Volendo calcolare la probabilità che un'estrazione a caso porti ad un risultato compreso tra σ e +σ la (11) diventa +σ p−σ ,+ σ 1 x− X σ − 1 2 = e ∫ σ 2 π −σ 2 dx (12) Osservando la (12) sembrerebbe che il risultato numerico dell'integrale dipenda dalla variabile casuale in esame poiché nell'espressione dell'integrale compaiono X e σ, che sono valori numerici propri della variabile casuale in esame. Possiamo invece dimostrare che il risultato numerico della (12) è indipendente dalla variabile casuale considerata. x− X dx Infatti ponendo z = risulta dz = . σ σ Capitolo I - Teoria degli errori pagina 14 R.Galetto A.Spalla - Lezioni di Topografia Inoltre assumendo: per a x= X +σ risulta z=1 (13) x= X - σ risulta Sostituendo la nuova variabile indipendente z nella (12) si avrà per b +1 p− σ ,+ σ = z =-1 z2 − 1 2 dz = 0.683 ≅ 0.68 e ∫ 2π − 1 (14) Si ottiene cioè un risultato numerico indipendente dai valori X e σ della variabile casuale in esame, perchè nell'integrale compare solo la variabile indipendente z e le costanti e e π. Se operiamo questo cambiamento di variabile su una qualsiasi variabile casuale a distribuzione normale otteniamo sempre il risultato numerico della (14) perché appunto essa è indipendente dai parametri propri della variabile casuale a distribuzione normale. Questo risultato può essere così espresso: in ogni variabile a distribuzione normale l'area sottesa dalla gaussiana nell'intervallo - σ e +σ è costante e vale circa 0.68; ciò significa che in ogni popolazione di misure possibili il 68% circa delle misure stesse è compreso in un intervallo - σ e +σ nell'intorno di X o anche: in ogni popolazione di misure possibili un'estrazione a caso ha il 68% di probabilità di fornire un valore che differisce al massimo di ±σ dal valore X Consideriamo nuovamente la (11) e supponiamo che i limiti di integrazione a e b siano ora 2σ +2σ e -3σ +3σ . Effettuando sempre il cambiamento di variabile in z ed assumendo analogamente per a x = X + 2σ risulta z=2 per b x = X - 2σ per a x = X + 3σ risulta z=3 per b x = X - 3σ risulta z =-3 risulta z =-2 Risolvendo gli integrali relativi si avrà: +2 z2 +3 z2 p−2 σ ,+2 σ = − 1 2 dz = 0.954 ≅ 0.95 e 2π −∫2 p−3σ ,+3σ = − 1 e 2 dz = 0.997 ≅ 0.99 ∫ 2π − 3 il che appunto significa Capitolo I - Teoria degli errori pagina 15 R.Galetto A.Spalla - Lezioni di Topografia • • che il 95% delle misure possibili è compreso in un intervallo -2σ +2σ intorno ad X e che il 99% abbondante delle misure possibili è compreso in un intervallo -3σ +3σ intorno ad X . −σ +σ −2σ +2σ −3σ +3σ figura 6 Quindi anche se in teoria la variabile casuale normale è definita nell'intervallo -∞ + ∞ si vede che, in pratica, il semi-intervallo di dispersione di una popolazione di misure possibili è uguale a tre volte la varianza della popolazione stessa. 1.6.3 Determinazione dei valori approssimati dei parametri X e σ di una popolazione di misure possibili. Si è visto precedentemente che quando eseguiamo un'operazione di misura su una certa quantità di grandezza non ci troviamo di fronte ad un unico risultato possibile, ma davanti ad una popolazione di misure possibili; tale popolazione, come si è visto, si distribuisce simmetricamente rispetto ad un valore X in un intervallo di ampiezza -3σ +3σ. Trovandoci di fronte a tale molteplicità di valori, si è convenuto di privilegiare il valore X , punto centrale dell'intervallo di dispersione, assumendolo come il valore più significativo da associare alla quantità di grandezza sottoposta all'operazione di misura. −3σ +3σ figura 7 Per conoscere X dovremmo però eseguire infinite misure e quindi farne la media; poiché questo non è possibile dovremo accontentarci di trovare un valore approssimato di X . Il problema che dobbiamo risolvere è pertanto: • • come ricavare un valore empirico di X come valutare il suo grado di approssimazione. Capitolo I - Teoria degli errori pagina 16 R.Galetto A.Spalla - Lezioni di Topografia Cominciamo con il fare le seguenti constatazioni: • se eseguissimo una sola operazione di misura su una quantità di grandezza, otterremmo un valore X* che sarebbe già di per sé un valore approssimato di X . • questo unico valore non ci consentirebbe però di fare una valutazione empirica della varianza e quindi non potremmo avere neppure una vaga idea di quanto questo valore X* approssimi il valore X ; • non potremmo inoltre accorgerci né se la misura fatta è errata grossolanamente, né se essa sia o no affetta da errori sistematici. La popolazione di misure possibili segue infatti la legge di distribuzione della variabile casuale gaussiana solo se gli errori di misura sono accidentali. Quindi, solo esaminando l'istogramma costruito su numerose misure ripetute, il verificare che esso sia interpolabile da una gaussiana ci consente di escludere che le misure siano affette da errori sistematici. Per arrivare alla soluzione del problema che abbiamo enunciato imposteremo una trattazione empirica, in base alla quale risulterà giustificata la procedura che si segue per ricavare un valore di X e di σ partendo da un certo numero di misure ripetute. Supponiamo di operare sulla stessa quantità di grandezza e di eseguire diverse serie di misure ciascuna composta da n misure. Indichiamo con x1' , x2' ,... xn' la prima serie di misure e calcoliamo la media aritmetica M' = ∑x ' i n da una seconda serie x1" , x2" ,... xn" ricaviamo M"= ∑x " i n Procediamo analogamente per tutti i diversi gruppi di n misure. I valori delle medie così calcolate varieranno al variare dei gruppi di n misure, perché, essendo la popolazione delle misure possibili composta da infiniti valori, la probabilità che i gruppi siano composti dagli stessi valori di misura è praticamente nulla. Di conseguenza gli istogrammi relativi alle diverse serie di misure saranno fra loro simili, ma non coincidenti. Supponiamo di aver eseguito un numero r molto elevato di questi gruppi di n misure e di aver calcolato r volte le medie empiriche corrispondenti: se costruiamo l'istogramma delle r medie empiriche e lo sovrapponiamo a ciascuno degli r istogrammi relativi alle varie serie di misure notiamo quanto segue. M’ M” .. . . . . . X figura 8 Capitolo I - Teoria degli errori pagina 17 R.Galetto A.Spalla - Lezioni di Topografia I. Anche l'istogramma costruito con i valori delle medie empiriche è interpolabile con una gaussiana; possiamo quindi supporre che esista una popolazione delle medie empiriche alla quale sia associabile una variabile casuale continua con distribuzione gaussiana. II. Il punto di simmetria dell'istogramma della media è sempre molto prossimo al punto di simmetria di ciascuno degli istogrammi delle serie di misure; pertanto possiamo ritenere che, come la popolazione di misure possibili è distribuita normalmente intorno ad un valore X , così pure, intorno allo stesso valore X è distribuita normalmente la popolazione delle medie empiriche. III.L'intervallo di dispersione delle medie empiriche è più ristretto di quello delle varie serie di misure che hanno originato le medie empiriche stesse, e la gaussiana interpolante l'istogramma delle medie ha un andamento più ripido della gaussiana interpolante gli istogrammi delle misure. ab n a b figura 9 Queste constatazioni empiriche sono in accordo con la schematizzazione che del fenomeno dà la teoria degli errori in base alla quale è possibile dimostrare matematicamente che: data una variabile casuale normale, di media X e scarto quadratico medio σ, operando su di essa e facendone la media M, si ottiene un valore che può considerarsi estratto a caso da una variabile casuale normale, avente come valore centrale dell'intervallo di dispersione lo stesso X della variabile casuale di partenza e come s.q.m. quello della variabile casuale di partenza diviso per n e cioè: σ σM = n Quanto precedentemente esposto giustifica il comportamento abituale per il quale, volendo eseguire una misura con particolare accuratezza e ripetendola quindi più volte, sarà possibile assumere la media quale valore più significativo, che risulterà essere, con maggior probabilità, quello più prossimo ad X Si noti che, riferendosi al valore, si è affermato quello più prossimo ad X e non quello più vicino ad X ; non si può, infatti, escludere che uno o più degli n generici valori xi della serie di misure di cui si è calcolata la media sia più vicino ad X della media empirica M. Capitolo I - Teoria degli errori pagina 18 R.Galetto A.Spalla - Lezioni di Topografia Poiché l'intervallo di dispersione delle medie empiriche è n volte più ristretto di quello della popolazione delle misure possibili, si ritiene che la media empirica M abbia maggior probabilità di trovarsi più prossima ad X di quante ne abbia una generica misura xi . La media empirica è quindi un parametro di stima di X e avrà probabilità tanto maggiori di essere più prossima ad X , quanto maggiore sarà il numero n delle misure eseguite, poiché come abbiamo detto l'intervallo in cui essa può cadere è n volte minore di quello della popolazione delle misure possibili. Il valore di n tuttavia non potrà essere portato al di sopra di un certo limite perché il vantaggio che si ricaverebbe dalla diminuzione dell'intervallo di dispersione non giustificherebbe il suo costo in quanto l'intervallo di dispersione della media si restringe in funzione di n e non di n. A questo punto abbiamo risolto la prima metà del problema che ci eravamo posti, e cioè abbiamo visto come si ricava un valore approssimato di X ; ora vogliamo vedere come si può stimare il grado di approssimazione conseguito. Diremo allora, senza darne la dimostrazione, che, così come la media empirica M dà una stima di X , si ottiene una stima empirica di σ calcolando, in funzione delle n misure effettuate xi e della loro media M, il seguente valore m, che prende il nome di errore quadratico medio della serie delle n misure: n ∑(x i m=± i =1 − M) 2 n−1 (15) Mediante questo valore è possibile valutare empiricamente anche l'e.q.m. della media M; introducendo, infatti, la stima di σ, m, nella relazione σ σM = n si ha mM = m n (16) Il risultato di n misure di una stessa quantità di grandezza sarà pertanto sintetizzato da due valori: • la media M delle n misure, • il suo e.q.m. mM. Essi verranno scritti così: M ± m M. Esempio: ho eseguito una serie di n misure di una quantità di lunghezza da cui ho ricavato i seguenti valori: • • valore della media delle n misure M = 153.531 m; valore dell'e.q.m. della media ±2 mm . Il risultato si scrive così 153.531 m ± 2 mm. Il suo significato è il seguente: il valore "giusto" della quantità di lunghezza è un certo valore che non mi è noto; però il valore 153.531 che ho ricavato dalle n misure ne è una stima empirica; inoltre so che il valore Capitolo I - Teoria degli errori pagina 19 R.Galetto A.Spalla - Lezioni di Topografia 153.531 ha il 68% di probabilità di differire da X di non più di ± 2 mm, ha il 95% di probabilità di differire da X di non più di ± 4 mm e al massimo ne differirà di ± 6 mm. 1.6.4 Caso in cui l'e.q.m. è noto “a priori”. Associare ad una misura un e.q.m. può evidenziare due diverse situazioni. I Può essere che siano state eseguite un certo numero di misure e le si siano trattate come è stato precedentemente descritto. II Può però anche essere che si sia operato con uno strumento tale da consentire di valutare l'e.q.m. delle misure di una quantità di grandezza, anche se si è eseguita una sola misura. Se infatti operiamo diverse serie di misure sulla stessa quantità di grandezza con uno stesso strumento e, in condizioni ambientali medie, ne costruiamo le curve di distribuzione relative, se esse si disperdono in un intervallo costante, possiamo dire che utilizzando lo strumento in una situazione ambientale media, è noto lo scarto quadratico medio della popolazione di misure. Anche effettuando quindi un'unica misura saremo in grado di stabilirne l'accuratezza, semplicemente basandoci sul valore dell'e.q.m. fornito per lo strumento dalla casa costruttrice. Quanto detto vale tuttavia solo in condizioni ambientali medie di laboratorio e perde di significatività quando si opera, come accade al topografo, sulla realtà fisica del Territorio dove quindi risultano quanto mai variabili le condizioni ambientali, cosicché l'e.q.m. caratteristico dello strumento è da ritenersi solo indicativo, mentre il vero e.q.m. sarà determinabile operando una serie di misure e trattandole secondo la metodologia descritta in questo capitolo. 1.6.5 Differenza tra errore quadratico medio e tolleranza. Nei capitolati d'appalto per la costruzione delle carte vengono fissati dei limiti di precisione che devono venire rispettati dalle Ditte che eseguono i lavori. La precisione alla quale deve soddisfare il lavoro viene stabilita assegnando l'e.q.m. (errore quadratico medio) con il quale devono essere eseguite le misure, oppure assegnando un limite massimo d'errore che non deve essere superato e che viene indicato con il nome di tolleranza. In quale rapporto stanno tra di loro l'e.q.m. e la tolleranza? O meglio, che significa dire che una misura può essere affetta da un errore massimo prefissato? Per chiarire questo punto, bisogna ricordare che per errore di una misura si intende lo scostamento della misura dal valore M che è il valore centrale dell'intervallo di dispersione delle misure. Pertanto fissare una tolleranza significa fissare la massima quantità in cui una misura può discostarsi dal valore M ; in pratica significa fissare l'ampiezza dell'intervallo di dispersione Capitolo I - Teoria degli errori pagina 20 R.Galetto A.Spalla - Lezioni di Topografia delle misure. Poiché sappiamo che l'intervallo di dispersione contiene sei volte m (l'e.q.m.), possiamo dire che l'e.q.m. e la tolleranza stanno nel rapporto 1 a 3 (quello che interessa è infatti il semi-intervallo a sinistra o a destra di M ). Se pertanto viene richiesto di determinare una quota di un punto con la tolleranza di ±2 cm , questo significa che si dovrà operare con una metodologia tale per cui la popolazione di misure possibili sia tutta contenuta entro un intervallo che va da -2 cm a +2 cm nell'intorno del valore M , che possiamo chiamare quota esatta del punto in questione. Ma, per ottenere questo risultato, le operazioni dovranno essere effettuate con un metodo che consenta il conseguimento di un e.q.m. di un terzo di ± 2 cm. Generalmente di un metodo di misura o di uno strumento si dà l'e.q.m. a priori. Si dice ad esempio: con questo teodolite si possono misurare gli angoli con ± 2" di errore, intendendo con questo che si può sbagliare nella determinazione dell'angolo anche di 6". Imporre l'e.q.m. significa imporre anche le condizioni di accidentalità degli errori e della loro distribuzione gaussiana. Viceversa se si impone la tolleranza si deve accettare un lavoro anche se si constata che gli errori in esso presenti, pure essendo tutti inferiori alle tolleranze, sono tutti dello stesso segno e, come valore assoluto, tutti poco al di sotto della tolleranza. 1.6.6 Media ponderata. Quando è stato affrontato il problema delle misure dirette si è detto che ogni misura risulta funzione della quantità di grandezza dell'unità di misura e dei parametri ambientali e può quindi essere considerata un'estrazione a caso dalla popolazione di misure possibili relativa alle condizioni di esecuzione dell'operazione di misura. Il concetto di popolazione di misure possibili nasce infatti nel preciso istante in cui si stabilisce di procedere ad un'operazione di misura con particolari strumenti ed in precise condizioni ambientali. Se si considera quindi una stessa quantità di grandezza, misurata con strumenti diversi in ambienti diversi, si avranno valori estratti da popolazioni di misure possibili diverse. Supponiamo di avere a disposizione m serie di valori ottenuti per la stessa quantità di grandezza in m ambienti diversi. Ciascuna serie dovrà essere considerata appartenente ad una particolare popolazione che si distribuisce intorno ad un valore centrale in un intervallo di dispersione che sarà diverso per ciascuna popolazione. Il valore centrale sarà invece comune a tutte le popolazioni di misure possibili dal momento che esso rappresenta il valore della quantità di grandezza ricercato in ogni serie di misure. Per ogni serie di valori che si ricava dalle diverse popolazioni di misure possibili, si determinano la media empirica e l'e.q.m. della media secondo le relazioni Capitolo I - Teoria degli errori pagina 21 R.Galetto A.Spalla - Lezioni di Topografia Mi = mM i mi ∑x ni 1 =± =± ni ni con j=1,2...ni j ∑ (x j − Mi ) 2 ni − 1 i=1,2,...m Se le operazioni di misura sono state svolte in presenza di soli errori accidentali, gli e.q.m. avranno valori dello stesso ordine di grandezza. Si pone a questo punto il problema di stabilire tra le m medie empiriche, quale possa essere quella che più si avvicina al valore centrale X ricercato. Una possibile soluzione potrebbe essere quella di privilegiare la media caratterizzata da un e.q.m. minore. popolazione di misure n. 1 popolazione di misure n. 2 popolazione di misure m-esima popolazione di misure n-esima Tuttavia questa scelta ci indica solo che tale valore ha maggior probabilità degli altri di essere il valore ricercato e non che lo sia necessariamente; inoltre porta a trascurare le informazioni che sul valore X possono darci le altre serie di misure. Occorre quindi definire un criterio rigoroso che permetta di omogeneizzare i valori di cui si è in possesso, perché possano essere utilizzati tutti. Si procede in modo tale da porsi nella situazione in cui le diverse serie di misure insistano su uno stesso intervallo di dispersione, siano Capitolo I - Teoria degli errori pagina 22 R.Galetto A.Spalla - Lezioni di Topografia cioè tutte caratterizzate dallo stesso e.q.m. k; potranno essere così considerate tutte appartenenti alla stessa popolazione di misure possibili. Si impone a tale scopo che siano verificate le relazioni: k = m 2M p1 = m 2M p 2 = .... = m2Mii pi = mM2 m pm 1 (17) 2 dove i coefficienti pi dei quadrati degli e.q.m. delle medie sono detti pesi e hanno appunto la funzione di ridurre uguali tra loro gli e.q.m. . Perché la (17) sia verificata basta porre: 1 pi = 2 mM i In questo modo avranno peso maggiore le medie empiriche con e.q.m. minore. Verrà quindi considerata una popolazione di misure i cui valori argomentali sono Mipi e il cui e.q.m. è uguale a k. Come valore rappresentativo di tale popolazione, si assume una media detta ponderata, così definita: MP = M 1 p1 + M 2 p2 +.....+ M i pi + .....+ M m p m1 p1 + p2 +.....+ pi +.... pm dove i singoli valori Mi sono le medie empiriche delle m serie di ni misure. L'errore quadratico medio della media ponderata è (omettiamo la dimostrazione): m = 2 P m02 m ∑p i i =1 m dove : m02 = ∑ ( pi M i − M p ) 2 m −1 i =1 e cioè: ∑ p (M m mp = ± i= 1 i i − Mp ) 2 m ( m − 1)∑ pi i= 1 Il risultato da associare alla quantità di grandezza in esame sarà: Mp ± mp Capitolo I - Teoria degli errori pagina 23 R.Galetto A.Spalla - Lezioni di Topografia 2. Trattamento delle misure indirette. Una misura si definisce indiretta allorché viene ottenuta attraverso la misura diretta di altre grandezze legate da relazioni analitiche alla grandezza della quale ricerchiamo la misura. Risulta cioè: z = f(X1 , X2 , ... Xn) (18) dove: • z è la misura indiretta; • X1 , X2 , ... Xn sono le grandezze misurabili. Se sono a distribuzione normale le n popolazioni di misure possibili che si generano quando si sottopongono ad operazione di misura un certo gruppo di quantità di grandezza X1 , X2 , ... Xn , allora anche la popolazione dei possibili valori di z ha le caratteristiche di una variabile casuale a distribuzione normale. Z Si assume come valore più rappresentativo della grandezza z il valore medio teorico Z che è quello che si otterrebbe inserendo nella (18) i valori X 1 , X 2 ,.... X n che rappresentano i valori centrali dell'intervallo di dispersione delle popolazioni associate alle quantità di grandezza X1 , X2 , ... Xn Z =f ( X 1 , X 2 ,.... X n ) Tuttavia bisogna osservare che nella pratica non si conoscono tali valori, bensì soltanto i valori medi empirici. Introducendo questi ultimi si perviene ad un valore Z che potremo chiamare valore empirico della misura indiretta, cioe: Z=f (X1 , X2 , ... Xn) e che è quello con maggior probabilità più vicino a Z . La dispersione della popolazione dei valori possibili di Z sarà ancora data dall'indice mz , uguale ad 1/6 dell'intervallo di dispersione della variabile casuale associata alla popolazione di misure possibili. Al variare dei valori medi empirici , varia il valore empirico della misura indiretta; cioè i valori Zi oscillano intorno al valore medio teorico Z nell'intervallo -3 mz __ +3 mz. Si può dimostrare che un valore empirico di m si ottiene dalla seguente formula: Capitolo I - Teoria degli errori pagina 24 R.Galetto A.Spalla - Lezioni di Topografia 2 2 2 ∂Z ∂Z ∂Z m 2 + m 2 +....+ m 2 m =± z ∂X X ∂X X ∂X X 1 n 2 2 n n (19) Da quanto ora scritto risulta che gli e.q.m. delle misure dirette concorrono in modo diverso alla individuazione del valore m . E cioè il valore di mZ è funzione non solo degli e.q.m. delle X1 , X2 , ... Xn, , ma risulta anche funzione, attraverso le derivate parziali ∂X1, ∂X2, .. ∂Xn, che compaiono nella formula (19), del ruolo che ogni grandezza gioca nella funzione Z che definisce la misura indiretta. Ciò consente di valutare l'influenza dell'errore delle singole misure dirette sul valore finale di m e quindi di stabilire a priori dei criteri di scelta sulle misure dirette da eseguire. Esempio: supponiamo di dover determinare l'area S di un triangolo mediante la formula B b C S= a 1 a. b.senγ 2 A L'errore quadratico medio di S in funzione degli e.q.m. di a, b, e γ vale: 2 2 2 1 1 1 2 2 2 mS = ± b sen γ ma + a sen γ m b + ab cos γ mγ + 2 2 2 La formula, oltre a permettere il calcolo dell'e.q.m. di S in funzione degli e.q.m. di a, b e γ, mostra che se la misura affetta da un e.q.m. maggiore è quella dell'angolo, conviene misurare l'angolo più prossimo a π/2; se invece le misure affette da e.q.m. maggiori sono quelle dei lati conviene misurare quei lati che comprendono l'angolo più piccolo. Capitolo I - Teoria degli errori pagina 25 R.Galetto A.Spalla - Lezioni di Topografia 3. Metodo delle osservazioni indirette. 3.1 Impostazione del metodo. Il metodo delle osservazioni indirette è un algoritmo matematico che verrà trattato con particolare attenzione perché servirà da supporto alla risoluzione della quasi totalità dei problemi topografici che verranno proposti in questo corso. Le diverse operazioni topografiche si differenzieranno nelle metodologie di acquisizione dei dati, ma tali dati saranno tuttavia sempre inseriti nella stessa schematizzazione di calcolo, basata appunto sul metodo delle osservazioni indirette. Supponiamo di avere una funzione f che leghi dei parametri incogniti X1 ,X2 ,... X m a delle grandezze misurabili P1 , P2 ,... P s f (X1 ,X2 ,... X m; P1 , P2 ,...P s) = 0 (20) l'equazione (20) viene soddisfatta quando, rimanendo costanti i valori X1 ,X2 ,... X m, variano, congruentemente fra loro, i valori delle grandezze P1 , P2 ,... P s. Esempio: l'equazione di una retta y + mx + c = 0 può essere riguardata come una funzione f (m,c; x,y) = 0 (21) che lega i parametri m e c, costanti, alle grandezze x e y, variabili; esistono cioè infinite coppie di valori (x,y) che soddisfano la (21) e che rappresentano tutti i punti della retta. Il problema che ci poniamo è quello di determinare i valori dei parametri incogniti disponendo di un certo numero di gruppi di misure delle grandezze P1 , P2 ,... P s. Avendo cioè n gruppi di valori noti P1i , P2i , . . .Psi con i = 1, 2, ... n potremo scrivere n volte l'equazione (20) e cioè fi (X1 ,X2 ,... X m; P1i , P2i , . . .Psi ) = 0 (22) Come abbiamo già detto i valori dei parametri X1 ,X2 ,... X m delle (22) rimangono costanti al variare dei gruppi di misure delle grandezze P1i , P2i , . . .Psi Le equazioni (22) costituiscono cioè un sistema di n equazioni nelle m incognite Xj (con j = 1,m). Se viene eseguito un numero strettamente necessario di gruppi di misure delle P1i , P2i , . . .Psi cioè se m è uguale ad n, il sistema risulta sì risolvibile, però, nella determinazione dei valori dei parametri incogniti, non si è in grado: • • • di mediare, l'effetto degli errori accidentali di cui sono affette le misure, di valutare l'e.q.m. con il quale vengono determinati i valori di X1 ,X2 ,... X m, di verificare o meno la presenza di errori grossolani nelle misure effettuate. Si deve quindi eseguire un numero sovrabbondante di gruppi di misure. Capitolo I - Teoria degli errori pagina 26 R.Galetto A.Spalla - Lezioni di Topografia Considerando però m degli n gruppi di misure e risolvendo il sistema di di m equazioni in m incognite, i valori ricavati per le incognite non saranno tali da annullare le restanti (n - m) equazioni. La (20) infatti, che prende il nome di equazione generatrice, schematizza un fenomeno in linea teorica; quando invece sottoponiamo a misura un gruppo di quantità di grandezza P1 , P2 ,... P s siamo calati in una realtà fisica che implica due conseguenze: • • la schematizzazione rappresentata dalla (20) non ha riscontro esatto nella realtà; i valori numerici che vengono inseriti nella (20) al posto delle grandezze P1 , P2 ,... Ps, sono dei valori ottenuti misurando delle quantità di grandezza e, come sappiamo, le misure sono sempre affette da errori (accidentali). Per i due motivi suddetti, e cioè per il fatto che le quantità misurabili sono affette da errori di misura e per il fatto che operiamo su un ambiente fisico reale nel quale i parametri incogniti non possono corrispondere alla loro schematizzazione ideale, non è lecito pensare una m-pla di valori X1 ,X2 ,... X m, che soddisfi rigorosamente le n equazioni. Le equazioni del sistema (22) vanno pertanto riscritte nella seguente forma: f i (X*1 ,X* 2 ,... X* m ; P1i , P2i , . . .Psi ) = vi (23) dove abbiamo introdotto, per ciascuna equazione, lo scarto che deve essere aggiunto affinché l'espressione matematica traduca con fedeltà il fatto fisico che vuole esprimere. Più precisamente, gli scarti presentati dalle (23) saranno tanto maggiori, quanto meno sarà aderente alla realtà fisica del fenomeno la schematizzazione scelta e quanto maggiori saranno gli errori di misura. Abbiamo inoltre introdotto le notazioni X*1 ,X* 2 ,... X* m per sottolineare il fatto che la m-pla ricavata è di tipo empirico e non potrà soddisfare rigorosamente tutte le n equazioni. Naturalmente, con l'introduzione degli scarti vi , il sistema (23) da impossibile diventa indeterminato, perché gli n scarti, oltre alle m incognite X*i , sono incogniti: abbiamo cioè un sistema di n equazioni in (n + m) incognite. Il sistema viene reso determinato imponendo che la sua soluzione conduca alla determinazione di un valore delle incognite, tale per cui risulti minima la sommatoria degli scarti vi elevati al quadrato (principio dei minimi quadrati). La condizione che viene imposta è la seguente: Σvi2 = min i = 1,n (24) Tale condizione traduce il fatto che i valori finali delle incognite saranno quelli che renderanno, in massimo grado, tra loro compatibili le misure eseguite. Essa indica cioè che si preferisce una soluzione che, oltre a produrre scarti mediamente piccoli, li dia anche tra loro omogenei, al fine di non privilegiare serie di misure rispetto ad altre, se non in base a criteri che saranno esposti in seguito. Prima di vedere come si pervenga alla determinazione delle incognite associando al sistema (23) la condizione (24) dobbiamo constatare che le equazioni generatrici, nei problemi topografici, sono generalmente di tipo trascendente. Capitolo I - Teoria degli errori pagina 27 R.Galetto A.Spalla - Lezioni di Topografia Nell'algoritmo delle osservazioni indirette si formula invece l'ipotesi di trattare equazioni lineari: sarà perciò necessario procedere alla linearizzazione delle equazioni (23). 3.2 Linearizzazione delle equazioni generatrici. Per operare la linearizzazione delle equazioni generatrici, si rende necessario conoscere il valore assunto dalla funzione f almeno in un punto: ci occorre cioè una m-pla di valori approssimati delle incognite che si ricava o analiticamente, considerando m delle n equazioni e risolvendole nelle m incognite, o con costruzione grafica, quando la risoluzione analitica del sistema risulta eccessivamente gravosa. Consideriamo X10 , X 02 , .. , X 0m valori approssimati di X1* , X *2 , .. , X *m Avendo introdotto dei valori approssimati delle incognite, dobbiamo ridefinire le incognite stesse; d’ora in poi le incognite sono x1 , x2 ,... xm, che rappresentano le correzioni da apportare ai valori approssimati per ottenere la m-pla ricercata. X1* = X 01 + x 1 X*2 = X 02 + x 2 . . X *m = X 0m + x m Sviluppiamo ora in serie di Taylor la generica funzione i-esima del sistema (23), nell'intorno x1 , x2 ,... xm dei valori approssimati X10 , X 02 , .. , X 0m avremo: fi ( X1* , X *2 , .. , X *m ; P1i , P2i , . . .Psi ) = fi ( X10 , X 02 , .. , X 0m ; P1i , P2i , . . .Psi ) + 0 0 0 ∂f ∂f ∂f x1 + x 2 +... xm + R ∂X1 i ∂X 2 i ∂X m i dove nel resto R sono compresi tutti i termini dello sviluppo in serie in cui gli incrementi (le differenze cioè fra il punto in cui viene eseguito lo sviluppo e un generico punto) sono superiori alla prima potenza. Si fa a questo punto la seguente ipotesi: che i valori x1 , x2 ,... xm siano sufficientemente piccoli da rendere il valore del resto R inferiore di un ordine di grandezza agli errori di misura e quindi trascurabile. Questa ipotesi equivale a dire che i valori approssimati X10 , X 02 , .. , X 0m sono così vicini ad X1* , X *2 , .. , X *m che le correzioni x1 , x2 ,... xm sono dello stesso ordine di grandezza degli errori di misura. L'ipotesi fatta è semplificativa e generalmente non risulta mai verificata, ma rappresenta l'unico modo per realizzare la linearizzazione delle equazioni generatrici. Si vedrà successivamente come, nello svolgimento dell'algoritmo stesso, in effetti poi si ovvii alla arbitrarietà dell'ipotesi. Ponendo a questo punto: Capitolo I - Teoria degli errori pagina 28 R.Galetto A.Spalla - Lezioni di Topografia li = f i ( X10 , X 02 , .. , X 0m ; P1i , P2i , . . .Psi ) 0 ∂f a i = x1 ∂X 1 i 0 0 ∂f b i = x2 ∂X 2 i ∂f mi = xm ∂X m i il sistema (23) potrà essere scritto nella forma più semplice a i x1 + b i x2 +....+ m i xm + li = vi (25) i = 1, 2, ... n dove i coefficienti a i , b i , .., m i ed il termine noto li sono calcolati in funzione dei valori approssimati X10 , X 02 , .. , X 0m e delle misure P1i , P2i , . . .Psi . Le equazioni (25) scritte in forma lineare prendono il nome di equazioni generate. Prima di procedere all'applicazione del principio dei minimi quadrati, premettiamo due generalizzazioni del metodo. I. Per la costruzione del sistema di equazioni generate potranno essere utilizzati contemporaneamente più tipi di funzioni che leghino però le stesse incognite alle stesse quantità di grandezza. Infatti se consideriamo il sistema (25) delle n equazioni generate, vediamo che in esse le funzioni generatrici compaiono solo in forma di derivate calcolate con i valori delle misure e dei valori approssimati e cioè come coefficienti numerici. Trovandoci quindi ad esaminare il sistema (25) non siamo in grado di stabilire da che tipo di funzione sia generata ciascuna equazione perché, a sviluppo di Taylor avvenuto, le equazioni sono tutte nella stessa forma, e cioè lineari nelle incognite. II. Nelle equazioni generatrici non devono necessariamente comparire sempre tutte le incognite x1 , x2 ,... xm e tutte le quantità misurabili P1 , P2 ,... P s . 3.3 Applicazione del principio dei minimi quadrati. Affinché la funzione v sia minima deve essere nullo il suo differenziale totale; deve cioè risultare: . Σv i dv i = 0 i = 1, n (26) Ma poiché lo scarto v i può essere riguardato come una funzione delle x1 , x2 ,... xm risulta: dv i =a i dx1 + b i dx2 +....+ m i dxm e quindi la (26) diventa: . Σv i (a i dx1 + b i dx2 +....+ m i dxm) )= 0 i = 1, n (27) Sviluppando i prodotti e applicando le Σ ai vari prodotti si ha: . . . Σv i a i dx1 +Σv i b i dx2 +....+ Σv i m i dxm= 0 (28) Affinché la (28) sia identicamente nulla per qualsiasi valore degli incrementi occorre che tutti i coefficienti degli incrementi infinitesimi dx1 , dx2 ,dxm siano nulli, e quindi la (28) si trasforma in un sistema di m equazioni: Capitolo I - Teoria degli errori pagina 29 R.Galetto A.Spalla - Lezioni di Topografia . Σv i a i =0 . Σv i b i=0 . Σv i m i=0 ... (29) Sostituendo a v i l'espressione data dalla (25) si ha: . Σ(a i x1 + b i x2 +....+ m i xm + li) a i = 0 . Σ(a i x1 + b i x2 +....+ m i xm + li) b i = 0 . . . . Σ(a i x1 + b i x2 +....+ m i xm + li) m i = 0 (30) i = 1, n Sviluppando i prodotti: Σa i a i x1 + Σa i b i x2 +....+ Σa i m i xm+ Σa i l i =0 Σa i b i x1 + Σb i b i x2 +....+ Σb i m i xm+ Σb i l i = 0 . i=1,n (31) . Σa i m i x1 +Σm i b i x2 +....+ Σm i m i xm+ Σm i l i = 0 Il sistema (31) è un sistema di m equazioni nelle m incognite x1 , x2 ,... xm e si definisce sistema normale. Riepilogando quindi le diverse fasi del metodo, diciamo che dal sistema iniziale di n equazioni generatrici siamo passati, linearizzando le funzioni, ad un sistema di n equazioni generate: in entrambi i sistemi però il numero delle equazioni è inferiore a quello delle incognite ed essi risultano indeterminati. Associando quindi al sistema delle equazioni generate la condizione dei minimi quadrati si arriva alla definizione del sistema normale di m equazioni nelle m incognite x1 , x2 ,... xm Una volta ricavati i valori degli incrementi x1 , x2 ,... xm , risaliamo alla m-pla X*1 , X *2 , .. ,X *m ricercata. X1* = X 01 + x 1 X*2 = X 02 + x 2 ... (32) * 0 Xm = Xm + x m 3.4 Iterazione dei calcoli. I valori dati dalle (32) non devono però in generale venire assunti come valori definitivi delle incognite. Infatti nell'operare la linearizzazione dalle equazioni generatrici (23) per ottenere le equazioni generate (25) abbiamo trascurato tutti i termini dello sviluppo in serie di Taylor contenenti le correzioni x1 , x2 ,... xm elevate al quadrato, al cubo e così via. Questo fatto non avrebbe alcuna conseguenza pratica se i valori x1 , x2 ,... xm , (cioè le differenze tra i valori approssimati X10 , X 02 , .. , X 0m , ed i valori finali X1* , X *2 , .. , X *m ), fossero dello stesso ordine di grandezza degli errori di misura delle quantità misurate (omettiamo la dimostrazione di quanto appena asserito). Capitolo I - Teoria degli errori pagina 30 R.Galetto A.Spalla - Lezioni di Topografia Viceversa molte volte, specialmente quando i valori approssimati sono ottenuti per via grafica, i valori approssimati X10 , X 02 , .. , X 0m differiscono dai valori X1* , X *2 , .. , X *m di quantità ben superiori, come ordine di grandezza, agli errori di misura delle quantità misurate. Ne consegue che, per giungere alla determinazione della m-pla incognita X1* , X *2 , .. , X *m , bisogna iterare più volte la soluzione del sistema (28) nel seguente modo. Si inizia con risolvere il sistema una prima volta; indichiamo con x’1 , x’2 ,... x’ m le correzioni determinate . Calcoliamo i valori: X1' = X01 + x1' X'2 = X02 + x '2 ... X = X0m + x'm ' m Sostituiamo questi valori nelle equazioni (25) e ricaviamo in ogni equazione lo scarto vi; con i vi calcoliamo la Σvi2 che indichiamo con (Σvi2)’ Poi, anzichè ritenere i valori X1' , X '2 , .., X 'm come definitivi, li consideriamo come nuovi valori approssimati. Ricalcoliamo quindi i coefficienti a i ,b i, m i e i termini noti li con i nuovi valori X1' , X '2 , .., X 'm Risolvendo nuovamente il sistema (31) otteniamo una nuova serie di correzioni x”1 , x”2 ,... x”m . Mediante questi valori otteniamo: X1" = X 1' + x 1 X "2 = X2' + x 2 ... X "m = X 'm + x m Reintroduciamo questi valori nella (25) e ricalcoliamo i nuovi scarti vi e la (Σvi2)". Ora confrontiamo (Σvi2)" con (Σvi2)' . Se (Σvi2)" è molto diminuita rispetto a (Σvi2)' vuol dire che non abbiamo ancora raggiunto la condizione di minimo della Σvi2 , e che quindi dobbiamo procedere ad un'altra iterazione. Σ vi2 fine delle iterazioni | 1| 2 | 3 .... numero iterazioni Capitolo I - Teoria degli errori pagina 31 R.Galetto A.Spalla - Lezioni di Topografia Praticamente interrompiamo le iterazioni quando vediamo che la Σvi2 relativa all'ultima iterazione non diminuisce più in modo apprezzabile da quella relativa alla penultima. Sottolineiamo il fatto che se le espressioni generatrici (23) fossero di forma lineare, la prima soluzione sarebbe già quella definitiva, cioè già la prima soluzione del sistema (31) porterebbe alla condizione Σvi2 = min. 3.5. Valutazione della precisione dei risultati. Abbiamo detto che uno dei vantaggi che ci offre l'applicazione del metodo delle osservazioni indirette è quello di permetterci una valutazione rigorosa della precisione conseguita nella determinazione delle incognite. Omettiamo la dimostrazione delle formule che diamo qui di seguito perché appesantirebbe il discorso. Per calcolare l'errore quadratico medio delle incognite si procede nel modo seguente. 1. Si calcola un primo coefficiente che è funzione degli scarti finali delle equazioni generatrici. Sostituendo cioè i valori finali delle incognite nelle equazioni (25) si calcolano gli scarti vi ; in funzione di questi scarti si calcola un errore quadratico medio delle equazioni: m 20 = Σ v 2i n-m (33) Esso risulta tanto più piccolo quanto più precise sono le misure effettuate e quanto maggiore è il numero delle misure esuberanti. 2. Si calcolano gli elementi diagonali della matrice inversa della matrice costituita dai coefficienti delle incognite del sistema (31). Ricordiamo che data una matrice a11 a A = 21 . a1m a12 a 22 . a 2m . a1m . a 2m . . . a mm La matrice inversa A-1 si ottiene sostituendo a un generico elemento ai,k , il minore Ai,k del termine ai,k diviso per il valore A della matrice: A −1 A11 A A21 = A . A1m A A12 A A22 A . A2m A . . . . A1m A A2 m A . Amm A Per i nostri calcoli interessano solo i termini della diagonale principale: Capitolo I - Teoria degli errori pagina 32 R.Galetto A.Spalla - Lezioni di Topografia A11 A A −1 = . . . . . A22 A . . . . . . . Amm A . A11 A22 Amm , , si ottengono gli errori quadratici medi delle A A A incognite dalle relazioni: Calcolati gli elementi m0 A11 A m0 A22 A m0 Amm A mX* 1 = ± mX* 2 = ± . . mX* m 3.6. = ± Il problema dell'attribuzione dei pesi. Lo scarto vi che introduciamo nell'equazione generata (25) è dovuto, come si è detto, al fatto che le misure P1i , P2i , . . .Psi delle quantità di grandezza P1, P2 , Ps sono affette da errore. L'influenza degli errori di misura sulle equazioni generate assume un valore significativo solo nel termine noto dell'equazione generata; infatti l'effetto di tali errori nei restanti termini della (25) può ritenersi trascurabile, poiché i coefficienti ai ,bi.,.. mi , in cui gli errori sono presenti, sono moltiplicati per le correzioni dei valori approssimati x1, x2,..xm che sono quantità piccole. Questo fatto si sintetizza dicendo che gli scarti vi, delle equazioni generate sono dovuti all'influenza degli errori di misure nei termini noti li . I termini noti li possono essere riguardati come funzione delle misure P1i , P2i , . . .Psi , e quindi si può calcolare il loro e.q.m. in funzione dell'e.q.m. delle misure dirette P1i , P2i , . . .Psi che in essi compaiono, applicando ad essi la formula dell'e.q.m. delle misure indirette. Sarà cioè, indicando con mli l'e.q.m. del generico termine noto li : 2 2 2 ∂f ∂f ∂f mli = ± i ⋅ m2P1 + i ⋅ m2P2 +...+ i ⋅ m2Pm ∂ P1 0 ∂ P2 0 ∂ Pm 0 (34) dove l'indice( )0 sta a significare che nelle derivate compaiono i valori approssimati delle incognite, e m 2P1 , m 2P2 , ....m 2Pm sono gli errori quadratici delle misure dirette. Capitolo I - Teoria degli errori pagina 33 R.Galetto A.Spalla - Lezioni di Topografia Applicando la (34) alle n equazioni generate dal sistema della (25), si possono ricavare gli n e.q.m. degli n termini noti li . Essi risulteranno in generale differenti tra di loro. In seguito a questa constatazione ci poniamo allora il problema di come fare per far sì che le equazioni, il cui termine noto ha e.q.m. minore, abbiano più importanza nella determinazione di x1, x2,..xm , di quanta ne abbiano quelle con termine noto avente e.q.m. maggiore. Si segue il criterio già visto per la media ponderata e cioè si impone che gli e.q.m. di tutti i termini noti diventino uguali tra di loro con l'applicazione di un coefficiente moltiplicativo, detto peso; si impone cioè la seguente condizione: m 2l1 ⋅ p1 = m 2l2 ⋅ p2 = ... = m 2lm ⋅ p m dove i valori p1 ,p2, ...ps verranno calcolati con la relazione: 1 pi = 2 m li (35) (36) essendo gli m 2li calcolati mediante la (34). L'introduzione dei pesi viene fatta perché si vuol realizzare il seguente scopo: il principio dei minimi quadrati deve minimizzare gli scarti delle equazioni generate, privilegiando gli scarti delle equazioni che hanno e.q.m. del termine noto minori. Cioè anziché applicare il principio: Σvi2 = min si applica il principio i = 1,n 2 . Σvi pi= min i = 1,n (24) (37) Per realizzare la (37), anziché la (24), è sufficiente moltiplicare ogni equazione del sistema (25) per la radice quadrata del peso del suo termine noto: pi a i x1 + pi b i x2 +....+ pi m i xm + pi li = pi vi i = 1, 2, ... n (38) Si procede quindi come indicato al precedente paragrafo. Con l'introduzione dei pesi la (33) diventa: Σpi v 2i m = n-m 2 0 (39) Capitolo I - Teoria degli errori pagina 34 R.Galetto A.Spalla - Lezioni di Topografia CAPITOLO II STRUMENTI TOPOGRAFICI 1 Le grandezze che sono oggetto delle misure. Gli strumenti topografici si dividono fondamentalmente in tre categorie: teodoliti, livelli, distanziometri elettronici. In ciascuna categoria esistono moltissimi tipi di strumenti che si differenziano per: • principio di funzionamento; • struttura; • livello tecnologico; • grado di precisione; • campo di applicazione. È ovviamente impossibile fare, in questo Corso, una casistica completa degli strumenti topografici; ci limiteremo pertanto a prendere in considerazione, per ciascuna categoria, il tipo di strumento più diffuso, o meglio quello che fa più capire le funzioni che con esso vengono svolte. Le operazioni topografiche hanno come scopo la misura di: • angoli; • dislivelli; • distanze. 1.1 Angoli. Gli angoli possono essere: azimutali o zenitali. Angoli azimutali. Consideriamo tre punti sul terreno A, B e C (vedi figura 1) πC πΒ B C A figura 1 V è la verticale passante per A; Capitolo II - Strumenti topografici pagina 35 R.Galetto A.Spalla - Lezioni di Topografia π B è il piano definito dalla verticale V e dalla congiungente AB; π C è il piano definito dalla verticale V e dalla congiungente AC; chiamiamo angolo azimutale l'angolo diedro definito dai due piani π B e π C e che ha per spigolo la verticale V . Angoli zenitali. Dato un punto A ed un punto B, l'angolo zenitale ζ è l'angolo formato dalla verticale per il punto A e dalla congiungente i punti A e B (vedi figura 2). ζ figura 2 1.2 Dislivelli. Come vedremo in seguito in modo più approfondito, definiamo quota di un punto la sua distanza da una superficie di riferimento misurata sulla verticale per il punto stesso; la superficie di riferimento sarà il geoide che può essere approssimato alla superficie del mare in quiete, supposta estesa anche al di sotto delle terre emerse (vedi figura 3). vA vB A mare qA B qB figura 3 Considerando il punto A, di quota qA ed il punto B a quota qB , il problema sarà quello di stabilire la differenza di quota, o dislivello, fra i punti, cioè la differenza qA - qB. In particolare, le verticali passanti per due punti, distanti fra loro meno di 100 metri, possono essere considerate parallele e la superficie del geoide può essere approssimata da un piano ad essa tangente; il dislivello può allora essere così schematizzato (vedi figura 4). Capitolo II - Strumenti topografici pagina 36 R.Galetto A.Spalla - Lezioni di Topografia B ∆ A q q B A figura 4 1.3 Distanze. In Topografia sono oggetto di misura le distanze reali intese come segmenti congiungenti in linea retta i punti in esame (vedi figura 5). B d* A figura 5 Per convenzione vengono indicate con d*; con la sola dizione distanza (d) si indica invece la distanza topografica, che verrà più avanti definita. 1.4 Strumenti con cui si effettuano le misure Tutte le operazioni topografiche hanno come scopo la misura delle classi di grandezze che abbiamo appena esaminato. Gli strumenti adottati per queste operazioni saranno: • il teodolite, per la misura di angoli azimutali e zenitali; • il livello, per la misura delle differenze di quota; • il distanziometro elettronico, per la misura diretta delle distanze. Il teodolite ed il livello potranno essere inoltre usati anche per la misura indiretta di distanze brevi (< 100 m) che debbano essere determinate con scarsa precisione (10 -3). Capitolo II - Strumenti topografici pagina 37 R.Galetto A.Spalla - Lezioni di Topografia 2 La materializzazione dei punti. Nel definire le grandezze che sono oggetto di misure da parte del topografo, abbiamo fatto riferimento, in modo generico, a punti A, B, C .... del terreno; occorre chiarire come questi punti, là considerati come astrazioni geometriche, siano materializzati nella realtà. Prendiamo in considerazione, a questo scopo, la misura di un angolo azimutale; la misura verrà eseguita mettendosi con uno strumento, il teodolite, sul punto A e osservando, mediante il cannocchiale topografico, che fa parte del teodolite, gli altri due punti B e C. Il punto A sul quale ci si mette con lo strumento, si chiama punto di stazione, mentre i punti B e C sono i punti collimati. Il punto di stazione può essere costituito da una borchia metallica infissa nella pavimentazione stradale (vedi figura 6-1), da un cilindretto di metallo cementato in una piccola gettata di calcestruzzo (vedi figura 6-2.), dall'incrocio di due tratti disegnati sulla testa di un picchetto (vedi figura 6-3.), da una borchia cementata in un piccolo pilastrino di cemento armato (vedi figura 6-4.), da un punto non materializzato di proposito ma ben individuabile, come ad esempio l'incrocio di due assi stradali (vedi figura 6-5.). I punti collimati possono essere materializzati in due modi: • • punti di strutture artificiali esistenti (punta di un campanile, spigolo di una casa, un punto caratteristico di un edificio, ecc.); punti del tipo di quelli su cui si fa stazione e che vengono resi visibili da lontano con opportuni segnali (vedi paragrafo 8.3.). Per fare un esempio, una traduzione in termini reali dello schema in figura 1 potrebbe essere la seguente (figura 7.): il punto A è materializzato da una borchia infissa in un pilastrino; il punto B è la punta di un campanile ed il punto C è un picchetto in legno sul quale è stato posto un segnale. figura 6-3 P P figura 6-1 P figura 6-2 figura 6-4 P Via Tosi P figura 6-5 Capitolo II - Strumenti topografici pagina 38 R.Galetto A.Spalla - Lezioni di Topografia B C A figura 7 3 Il treppiede. 3.1 Struttura. Come vedremo in seguito, per misurare angoli e distanze occorre mettersi con lo strumento di misura su uno dei punti che definiscono l'angolo o la distanza; così pure occorrerà mettere un segnale per rendere visibile da lontano gli altri punti, qualora questi non lo siano già; ad esempio, nel caso della figura 7, il punto B è visibile di per sé, mentre sul punto C occorrerà mettere un segnale, ossia un qualcosa che lo renda visibile da lontano (le caratteristiche del segnale saranno descritte al paragrafo 8.3.). figura 8 Per sostenere lo strumento di misura ed i segnali si usa il treppiede (vedi figura 8); esso è formato da tre gambe allungabili che sono incernierate ad una piastra che chiameremo piastra di appoggio; vista dall'alto la piastra ha una forma di triangolo ad angoli smussati (figura 9) Capitolo II - Strumenti topografici pagina 36 R.Galetto A.Spalla - Lezioni di Topografia con foro centrale; nella figura le tre forme oblunghe tratteggiate indicano l'attacco a cerniera delle tre gambe del treppiede. Nel foro centrale passa una grossa vite, detta vitone; mediante il vitone si fissa al treppiede un dispositivo intermedio tra il treppiede stesso e lo strumento (o il segnale), che si chiama basetta. figura 9 3.2 Modo d'impiego. Quando si vuole effettuare una misura, la prima operazione da fare è quella di mettere il treppiede in stazione sul punto; il che vuol dire posizionare il treppiede in modo che il centro del foro della piastra di appoggio sia approssimativamente sulla verticale passante per il punto e la piastra sia approssimativamente orizzontale; questa operazione sebbene sembri facile, in realtà non lo è, perché quando si lavora in campagna su terreno accidentato, e non su strada asfaltata e piana, le irregolarità del terreno stesso e la presenza di vegetazione richiedono alle gambe del treppiede lunghezze diverse e posizioni strane (figura 10). figura 10 Per raggiungere lo scopo bisogna pertanto sfruttare il fatto che le gambe del treppiede sono a lunghezza variabile, indipendenti l'una dall'altra; per verificare che la posizione della piastra d'appoggio sia abbastanza centrata sul punto si potrà usare un filo a piombo (figura 11) mentre per mettere approssimativamente orizzontale la piastra d'appoggio si potrà usare una comune livella da muratore (figura 12). P figura 11 figura12 Capitolo II - Strumenti topografici pagina 37 R.Galetto A.Spalla - Lezioni di Topografia 3.3 Possibilità di posizione eccentrica del vitone. Il vitone non è fisso al centro della piastra d'appoggio, ma può scorrere in una specie di collare oblungo fatto come illustrato in figura 13, il quale è incernierato ad una estremità sotto la piastra di appoggio. Facendo ruotare il collare (freccette a, b della figura 13) e facendo traslare il vitone nel collare (freccette c, d della figura 13) si può portare il vitone qualsiasi punto del foro centrale della piastra (vedi figura 14). a d c b figura 13 figura 14 Questo speciale attacco del vitone alla piastra di appoggio del treppiede, permette di posizionare la basetta sulla piastra d'appoggio in modo che il centro C della basetta stia sul punto di stazione anche se il centro K della piastra di appoggio non è esattamente nel punto di stazione (figura 15). C K P figura 15 Quanto detto in questo paragrafo può essere per ora un po' oscuro, quindi si consiglia di ritornare su questo punto dopo aver visto la parte che segue sino al punto 5.4. compreso. E' importante aver capito che non è possibile posizionare il treppiede sul punto di stazione P in modo che: • • il centro del foro della piastra d'appoggio sia esattamente sulla verticale per P; la piastra d'appoggio sia perfettamente orizzontale. Capitolo II - Strumenti topografici pagina 38 R.Galetto A.Spalla - Lezioni di Topografia 4 Il cannocchiale topografico. 4.1 Struttura. Abbiamo visto che, nel definire gli angoli (azimutali e zenitali) e le distanze, abbiamo preso in considerazione la retta che congiunge dei punti del terreno; le operazioni di misura delle grandezze esaminate al punto 1 implicano, come vedremo in seguito, che la retta che congiunge idealmente i punti venga opportunamente materializzata. N2 a.c. a.o. t p L2 R L3 C k L1 l lo cm. 20 M figura 16 Questa funzione viene svolta dal cannocchiale di cui tutti gli strumenti topografici sono dotati. Il cannocchiale topografico è composto (vedi figura 16): • da un corpo metallico tubolare; • da una lente obiettiva L1 , che è in genere una lente convergente; • da una lente interna L2 , che è in genere una lente divergente; • da un reticolo R che è una lastrina di vetro con sopra incisa una crocetta; • da una lente oculare L3 , che è in genere una lente convergente. Le lenti L1 e L2 sono delimitate da superfici sferiche i cui centri Ci devono essere tutti allineati su una retta (figura 17). asse ottico C 1 C C 2 3 C 4 figura 17 Questa retta si chiama asse ottico del cannocchiale. Capitolo II - Strumenti topografici pagina 39 R.Galetto A.Spalla - Lezioni di Topografia La condizione suddetta deve essere realizzata in sede di montaggio delle lenti nel cannocchiale. Si chiama invece asse di collimazione la retta che congiunge il centro della lente obiettiva, con il centro del reticolo (figura 18). asse di collimazione figura 18 Nel cannocchiale l'asse ottico e l'asse di collimazione devono essere coincidenti; questa condizione viene realizzata nel momento del montaggio del reticolo nel cannocchiale. La distanza l0 tra la lente L1 ed il reticolo è fissa; invece la distanza tra la lente L1 e la lente L2 è variabile perché la lente L2 può essere traslata lungo l'asse ottico ruotando il bottone M esterno al cannocchiale. Ruotando il bottone M si fa ruotare il pignoncino p, il quale fa traslare la cremagliera t, che è un unico pezzo con il collare K in cui è inserita la lente L2. La meccanica interna del cannocchiale, cioè l'insieme manopola M-pignoncino p-collare Kcremagliera t, deve essere molto curata poiché bisogna che, al traslare della lente L2, l'asse di collimazione resti coincidente con l'asse ottico. D'ora in avanti, quando parleremo degli strumenti topografici, supporremo che sia sempre verificata la condizione di coincidenza tra asse ottico del cannocchiale e asse di collimazione per qualsiasi posizione della lente L2 . 4.2 Funzionamento. 4.2.1 Funzione del reticolo. Collimare un punto P con il cannocchiale significa puntare il cannocchiale sul punto P in modo che esso si trovi sull'asse ottico del cannocchiale (figura 19). Capitolo II - Strumenti topografici pagina 40 R.Galetto A.Spalla - Lezioni di Topografia P figura 19 Poiché l'asse ottico coincide con l'asse di collimazione, la condizione di cui sopra è verificata quando il puntamento viene effettuato in modo che l'immagine del punto P si formi sul reticolo, proprio in coincidenza dell'incrocio dei due tratti che formano il reticolo stesso (figura 20). figura 20 Per poter collimare un punto P occorre quindi fare una prima operazione che consiste nel far formare l'immagine del punto sul piano del reticolo (figura 21) e poi posizionare il cannocchiale in modo che il punto P risulti coincidente con l'incrocio del reticolo stesso. figura 21 Capitolo II - Strumenti topografici pagina 41 R.Galetto A.Spalla - Lezioni di Topografia 4.2.2 Funzione della lente interna. Se ci fosse solo la lente L1 (figura 22) di focale f 1 , l'immagine di un punto P, alla distanza D dalla lente, si formerebbe nello spazio immagine ad una distanza d dalla lente data dalla relazione: f ⋅D d= 1 4.2.2.(1) D − f1 L1 R P1 f1 D d l0 figura 22 In generale d risulterebbe diversa da l0 e quindi l'immagine di P non si formerebbe sul reticolo R. La funzione della lente L2 è proprio quella di ottenere questo risultato, cioè di far formare l'immagine di P sul piano del reticolo; infatti l'insieme delle due lenti L1 ed L2 costituisce un sistema ottico la cui focale risultante è data dalla relazione: f = f1 f2 f1 + f 2 − l 4.2.2.(2) essendo f 2 la focale di L2 ed l la distanza tra le due lenti (figura 16); variando la distanza l si può quindi variare il valore di f. Pertanto, considerando l'insieme delle due lenti L1 ed L2 , può essere resa uguale a l0 la distanza d, dalla prima lente L1 dell'immagine di un punto P posto alla distanza D. Ciò avviene facendo variare opportunamente la distanza l tra le due lenti sino a che si realizza la condizione: f1 f2 D f1 + f 2 − l d = l0 = 4.2.2.(3) f1 f 2 D− f1 + f2 − l La relazione 4.2.2.(3) è stata ottenuta introducendo la 4.2.2.(2) nella 4.2.2.(1). Capitolo II - Strumenti topografici pagina 42 R.Galetto A.Spalla - Lezioni di Topografia 4.2.3 Funzioni della lente oculare. La lente oculare (L3 in figura 16) serve come lente d'ingrandimento, per vedere ingranditi sia l'immagine che si forma sul reticolo, sia il reticolo stesso, in modo da poter fare la collimazione con la necessaria accuratezza. Se la lente L3 è divergente, oltre ad ingrandire l'immagine, la capovolge; poiché l'insieme delle due lenti L1 ed L2 dà sul piano del reticolo un'immagine capovolta, osservando quest'ultima attraverso l'oculare, che la capovolge a sua volta, la si vede diritta. La lente L3 può essere leggermente avvicinata (allontanata) al reticolo mediante avvitamento (o svitamento), in modo da sopperire ad eventuali difetti di vista dell'operatore; il movimento della lente oculare non è critico, come quello della lente interna L2 , perché la lente L3 non viene coinvolta nel procedimento di formazione dell'immagine sul reticolo; essa inoltre non concorre a definire né l'asse ottico, né l'asse di collimazione e non può pertanto influenzare il posizionamento dell'immagine di un punto, rispetto ad essi. 4.2.4 Semplificazioni introdotte nelle spiegazioni date in questo paragrafo. In realtà nei cannocchiali topografici non esistono solo le lenti L1, L2 e L3,, ma ciascuna di esse è formata da un pacchetto di lenti al fine di correggere le aberrazioni. Inoltre il raddrizzamento dell'immagine viene generalmente realizzato con un sistema di prismi posto tra la lente L2 ed il reticolo. 4.2.5 Posizione del primo fuoco nel cannocchiale topografico. Quando consideriamo una lente semplice, i due fuochi della lente stanno dalle parti opposte di essa; uno nello spazio oggetto e uno nello spazio immagine (figura 23). F1 F2 figura 23 Nel cannocchiale topografico invece il sistema ottico costituito dalle lenti L1 ed L2 viene progettato in modo che il primo fuoco F1 del sistema cada all'interno del cannocchiale stesso (figura 24). Capitolo II - Strumenti topografici pagina 43 R.Galetto A.Spalla - Lezioni di Topografia l F1 spazio oggetto K K 1 2 figura 24 Poiché la focale f del sistema varia con la distanza l tra le due lenti, anche la posizione del primo fuoco non è costante, ma varierà in un intervallo K1 ÷ K2 la cui ampiezza è dell'ordine di 1 ÷ 2 mm. Vedremo in seguito che, per poter dare al cannocchiale delle rotazioni azimutali e zenitali, nei tre tipi di strumenti topografici che prendiamo in considerazione (teodoliti, livelli, distanziometri), esso sarà montato su un asse rotante m (vedi figura 25), sostenuto da un supporto U che è a sua volta sorretto da un basamento B; il supporto U può ruotare intorno ad un asse r. r m C m U B r figura 25 L'asse di rotazione r è detto asse primario; l'asse m è detto asse secondario. L'asse m e l'asse r dovranno essere complanari ed ortogonali; il cannocchiale dovrà essere montato nello strumento in modo che l'asse di collimazione passi per un punto C, intersezione dei due assi m ed r, che viene detto centro dello strumento. Il sistema di lenti L1 ed L2 viene progettato in modo che l'intervallo K1 ÷ K2 in cui può cadere il suo primo fuoco F sia centrato sul punto C, intersezione dei tre assi. Capitolo II - Strumenti topografici pagina 44 R.Galetto A.Spalla - Lezioni di Topografia 5 La basetta. 5.1 Struttura. Come abbiamo già detto la basetta è un dispositivo che deve essere interposto tra il treppiede e lo strumento (o il segnale); essa si compone di tre parti (vedi figura 26): • una piastra di base b; • una piastra basculante b'; • tre viti calanti, che uniscono la piastra basculante alla piastra di base. La piastra di base viene fissata per mezzo del vitone alla piastra di appoggio del treppiede come si vede in figura 5.1.-1 che rappresenta la sezione frontale della figura 27. Le viti calanti hanno la funzione di permettere il basculamento rispetto alla piastra di base. La piastra basculante ha la funzione di fare da supporto o allo strumento di misura, o al segnale. Nella piastra basculante ci sono tre fori (vedi figura 28) nei quali vanno ad infilarsi i tre piedini di cui sono muniti gli strumenti di misura ed i segnali. Si chiama centro della basetta il centro del cerchio ideale passante per i centri dei tre alloggiamenti. Nella figura 29 si vede, in sezione, come sono fatte le viti calanti e come funzionano; si vede cioè che la testa della vite è prigioniera nella piastra di base. Quando si ruota la vite mediante l'apposito anello zigrinato, si provoca (a seconda del senso di rotazione) l'allontanamento o l'avvicinamento della parte della piastra basculante che contiene la testa filettata, dalla parte della piastra di base che contiene la testa. b v c V figura 26 figura 28 b a v b figura 27 figura 29 Capitolo II - Strumenti topografici pagina 45 R.Galetto A.Spalla - Lezioni di Topografia 5.2 Uso delle viti calanti per rendere verticale un asse. Per capire come vengono usate le viti calanti schematizziamo la basetta come in figura 30. A 2 1 c B 3 r1 1 r2 2 1=2 2 1=2 3 3 r1 1 3 r2 3 r2 r1 1 2 1 3 2 c 3 r2 r1 vista da A vista da B figura 30 Nella figura si vede come ruotando le viti 1 e 2 in senso contrario, si può far ruotare la piastra basculante intorno ad un asse ideale r1 che congiunge il centro della basetta con la vite 3; mentre ruotando la vite 3 in un senso e le viti 1 e 2 nello stesso senso si può far ruotare la piastra basculante intorno ad un asse ideale r2 che è ortogonale al precedente e passa per il centro della basetta. Supponiamo ora che sulla piastra basculante sia stata innestata una piastra circolare munita di piedini (vedi figura 31) alla quale sia stata saldata ortogonalmente un'asta. Supponiamo che inizialmente questa asta sia verticale. Ripetendo il ragionamento appena fatto si vede che, con la rotazione in senso opposto delle viti 1 e 2, l'asta R può essere fatta ruotare nel piano π 2 di un generico angolo v2 (vedi figura 32); Capitolo II - Strumenti topografici pagina 46 R.Galetto A.Spalla - Lezioni di Topografia π2 figura 31 V1 V2 π1 figura 32 quindi con la rotazione della vite 3 si può far ruotare l'asta nel piano π 1 di un generico angolo v1 . A questo punto l'asta non sarà più verticale, ma formerà con la verticale un generico angolo v . Facciamo ora il ragionamento inverso: se con le viti calanti posso rimuovere l'asta dalla sua posizione di verticalità, con le viti calanti posso anche riportare l'asta nella posizione di verticalità quando essa non è verticale. Ed è proprio per questo che noi, come vedremo, useremo le viti calanti; sarà però necessario disporre anche dell'ausilio di una livella torica o sferica, come vedremo al punto 6. 5.3 Intercambiabilità tra teodolite e segnale. Abbiamo già detto che nella piastra basculante ci sono tre alloggiamenti, cioè tre fori, nei quali si infilano e rimangono prigionieri per mezzo di un apposito dispositivo, comandato da una levetta, i tre piedini del teodolite (o del segnale). Il teodolite ed il segnale sono fatti in modo che possano essere fissati al treppiede con lo stesso tipo di basetta; ossia si possono mettere sulla stessa basetta dapprima il teodolite, successivamente, dopo aver rimosso lo strumento, il segnale. Al punto 8.4. riprenderemo in esame questo argomento che per le operazioni topografiche di precisione è molto importante. 5.4 Piombino ottico. Nella basetta, e precisamente nella piastra basculante, esiste un dispositivo, che si chiama piombino ottico, che serve per centrare la basetta sul punto di stazione (figura 33). Il piombino ottico è formato da un piccolo cannocchiale, costituito da una lente obiettiva, da un reticolo e da un oculare; il cannocchiale è a fuoco fisso, cioè la distanza tra la lente obiettiva ed il reticolo è invariabile; non c'è bisogno di lente interna perché la distanza del terreno dalla basetta è all'incirca sempre uguale (1.20-1.30 m) e quindi la distanza alla quale va posto il reticolo dalla lente può essere fissata una volta per tutte. L'oculare, come nel cannocchiale topografico, serve a vedere ingrandita l'immagine sul reticolo. Capitolo II - Strumenti topografici pagina 47 R.Galetto A.Spalla - Lezioni di Topografia m 1,20 - 1,30 figura 33 Davanti alla lente obiettiva c'è un prisma che rimanda in senso orizzontale le immagini che provengono dal basso verso l'alto lungo la verticale. Il piombino ottico è montato e tarato in modo tale che quando il centro C della basetta si trova sulla verticale passante per il punto P, il punto P risulta collimato sul reticolo, ossia l'immagine P' di P si trova in corrispondenza dell'incrocio dei tratti del reticolo. A questo punto risulta chiaro perché al paragrafo 3 abbiamo detto che il vitone che fissa la basetta al treppiede deve essere cavo; attraverso ad esso deve esserci la visuale libera per centrare, con il piombino ottico, la basetta sul punto di stazione. Capitolo II - Strumenti topografici pagina 48 R.Galetto A.Spalla - Lezioni di Topografia 6. Le livelle e il loro impiego. 6.1. La livella torica. La livella torica è costituita da una fiala cilindrica di vetro la cui parte superiore è internamente lavorata a forma di superficie torica. È una superficie torica quella generata dalla rotazione di un cerchio C intorno ad un centro O (figura 34). figura 34 C R V1 V2 V1 V2 figura 35 O La fiala è inserita in una custodia metallica che viene fissata agli strumenti mediante due viti V1 e V2 (vedi figura 35). Sulla parte superiore della fiala è incisa una graduazione a tratti, distanziati di 2 mm, simmetrica rispetto ad uno zero centrale. La tangente t al punto centrale della graduazione si chiama tangente centrale della livella (t.c.). La fiala contiene un liquido abbastanza volatile (ad esempio alcool) che è in parte allo stato gassoso e quindi forma una bolla. Consideriamo la sezione mediana della livella (figura 36): la risultante F delle forze fi che agiscono sulla superficie di separazione tra la parte liquida e quella gassosa è diretta secondo la verticale passante per k, punto intermedio tra gli estremi A e B della bolla. Capitolo II - Strumenti topografici pagina 49 R.Galetto A.Spalla - Lezioni di Topografia A t K B t f i f i f f f f f i fi i i i i figura 36 La tangente t alla sezione circolare nel punto k è ortogonale alla direzione della forza F è quindi orizzontale. Pertanto quando si vuole disporre orizzontale la tangente centrale (t.c.) di una livella, occorre posizionare la livella stessa in modo che la bolla si disponga con le estremità equidistanti dal punto zero della graduazione (figura 37). 3 2,5 2 1,5 1 0,5 0 0,5 1 1,5 2 2,5 t.c. 3 figura 37 6.2 Sensibilità della livella torica. Si chiama sensibilità di una livella l'angolo, espresso in secondi sessagesimali, che sottende un tratto di graduazione (figura 38); la sensibilità si esprime pertanto come secondi/millimetri. Una livella consente una maggior accuratezza nel disporre gli assi verticali ed orizzontali, quanto più è sensibile. Una livella torica molto buona, che si usa cioè in strumenti di elevata precisione, deve avere una sensibilità variabile tra 10"/2 mm e 20"/2 mm. Si noti che nella figura 38 il raggio R della sezione meridiana della livella è puramente indicativo; infatti in una livella con sensibilità di 10"/mm il raggio R vale 40 metri. Capitolo II - Strumenti topografici pagina 49 R.Galetto A.Spalla - Lezioni di Topografia 3 2 1 0 1 2 3 ε R figura 38 Per avere un'idea di cosa significhi costruire una livella da 10"/2 mm calcoliamo quale è lo scostamento della tangente centrale della sezione circolare della superficie torica dopo 10 tratti di graduazione; se ε = 10", l'angolo corrispondente a 10 tratti vale 100" (vedi figura 39); l'angolo δ varrà: d sarà quindi dato da: δ=ε/2 = 50" 50" d = 50" . 20 mm = 20.000 = 5 µm 200.000 0 t.c. 15 10 5 5 10 15 10" = ε d δ figura 39 6.3 Funzione della livella torica negli strumenti topografici. La livella torica può essere usata per rendere orizzontale o verticale un asse. 6.3.1 Livella torica usata per rendere orizzontale un'asse. Consideriamo il dispositivo D della figura 40. Esso consiste in una piastra P sulla quale è fissata la sbarretta S che porta una linea di traguardo materializzata dalle due crocettine C1 e C2 . C1 C2 o O V S CR P figura 40 figura 41 Capitolo II - Strumenti topografici pagina 50 R.Galetto A.Spalla - Lezioni di Topografia O l.t. O figura 42 t.c. figura 43 La sbarretta S è vincolata alla piastra P da una vite calante V e da una cerniera CR; ruotando la vite calante, la sbarretta S ruota attorno al centro O della cerniera CR. Si vuole poter disporre la linea di traguardo secondo l'orizzontale anche quando la piastra P è appoggiata su un piano non orizzontale (vedi figura 41). Si procede così: si prende il dispositivo D e si fa in modo di rendere orizzontale la linea di traguardo; ad esempio traguardando, attraverso i centri C1 e C2 delle crocette, il pelo libero di un liquido in due vasi comunicanti (vedi figura 42). A questo punto si prende una livella torica e, senza muovere il dispositivo, la si avvita sulla sbarretta S in modo che la bolla risulti centrata; ossia con la t.c. orizzontale (vedi figura 43). Ora, tutte le volte che vorremo rendere orizzontale la linea di traguardo, non dovremo far altro che centrare la livella mediante la vite calante; però la linea di traguardo sarà orizzontale soltanto se si sarà mantenuta la condizione di parallelismo tra la t.c. della livella e la linea di traguardo, cioè la linea ideale che unisce i centri dei due crocicchi. 6.3.2 Livella torica usata per rendere verticale un asse. Si consideri quanto rappresentato in figura 44 . Vediamo una basetta fissata sulla piastra di un treppiede; nella figura la piastra di appoggio del treppiede è stata disegnata volutamente non orizzontale. r1 P1 B P1 T figura 44 figura 45 Prendiamo ora in considerazione il pezzo cilindrico P1 munito di piedini (figura 46) che si può incastrare nella basetta; il pezzo P1 ha una cavità cilindrica di diametro ϕ1 che può ricevere un perno cilindrico. Capitolo II - Strumenti topografici pagina 51 R.Galetto A.Spalla - Lezioni di Topografia r2 r2 s1 s2 P2 s1 r2 s2 P2 s1 P2 figura 46 Consideriamo il pezzo P2 (figura 46) costituito da una piastra a disco che inferiormente è dotata di un perno cilindrico di diametro ϕ2 e superiormente di due supporti verticali (questi ultimi non interessano ai fini del discorso che stiamo facendo; spiegheremo nella nota 1, in fondo al paragrafo, perché li prendiamo in considerazione). Inseriamo il pezzo P1 nella basetta ed il pezzo P2 nel pezzo P1 (figura 47). Ora facciamo la seguente ipotesi: che ϕ1 differisca così poco da ϕ2 che si possano considerare i due pezzi privi di gioco, pur potendo il pezzo P2 ruotare in P1 ; potremo allora considerare i due assi r1 e r2 coincidenti in un unico asse r. Si vuole rendere verticale l'asse r tutte le volte che è necessario, indipendentemente dall'assetto della piastra di appoggio del treppiede. Per far questo si prende il pezzo P2 e si va in officina; qui lo si dispone con l'asse r2 verticale; ciò può essere fatto, ad esempio, verificando che i punti su una stessa generatrice del perno siano equidistanti da un filo verticale ed eseguendo questa operazione in due piani ortogonali (figura 48). r _r _r 1 2 δ r t.c. t.c. figura 49 figura 47 Capitolo II - Strumenti topografici pagina 52 R.Galetto A.Spalla - Lezioni di Topografia δ r c d filo a piombo d d d figura 48 P2 (ruotato diπ /2) basetta 3 1 3 P1 1 2 2 P1 (fisso) P2 figura 50 figura 51 A questo punto, senza ovviamente muovere il pezzo, che deve essere bloccato in questa posizione, si fissa sulla faccia superiore del disco una livella torica e la si avvita in modo che la tangente centrale della livella risulti orizzontale, e cioè in modo che la bolla sia centrata (vedi figura 49). In questo modo abbiamo realizzato la seguente condizione di rettifica: la tangente centrale della livella è ortogonale all'asse r2 del perno cilindrico del pezzo P2 . Ora possiamo rinfilare il pezzo P2 nel pezzo P1 e agire come detto al paragrafo 5.2.: • • • • ruoteremo cioè P2 in P1 sino a che la livella sarà parallela a due viti calanti, ad esempio la 1 e la 2 in figura 50; ruotando le due viti calanti in senso contrario centreremo la livella, portando così l'asse r a giacere in un piano verticale passante per la terza vite; ruotiamo allora il pezzo P2 in P1 sino a che la livella si disponga lungo la congiungente il centro della basetta con la vite 3 (vedi figura 51); notiamo che con questa ultima operazione non spostiamo l'asse r, poiché ruotiamo il pezzo P2 intorno ad r che sta fermo; a questo punto ricentriamo la livella con la vite 3; abbiamo così reso verticale l'asse r, scomponendo idealmente la sua deviazione v dalla verticale in due componenti v1 e v2 su due piani tra loro ortogonali ed eliminando v1 con la rotazione delle viti 1 e 2 e v2 con la rotazione della vite 3. Capitolo II - Strumenti topografici pagina 1 R.Galetto A.Spalla - Lezioni di Topografia v1 v v2 figura 52 nota 1: i pezzi P1 e P2 sono simili, anche se molto semplificati, a due pezzi fondamentali del teodolite la cui struttura è già stata introdotta al punto 4.2.5. (figura 25); il pezzo P1 rappresenta cioè il basamento B e il pezzo P2 rappresenta la parte ruotante U che sostiene l'asse di rotazione m del cannocchiale: il pezzo P2, che nel teodolite si chiama alidada, è stato preso con la forma che ha, proprio per evidenziare che sui due supporti S1 ed S2 si appoggerà il perno di rotazione del cannocchiale (figura 53). r C a.c. m figura 53 I tre assi r, m e a.c. si incontrano in un punto C detto centro dello strumento. Allora quale è la finalità vera del discorso che abbiamo fatto in questo paragrafo ? La finalità è la seguente: per mezzo della livella torica posta sull'alidada, è possibile rendere verticale l'asse del basamento sul quale l'alidada ruota e quindi anche l'asse di rotazione dell'alidada stessa; l'asse r viene fatto coincidere cioè con la verticale v passante per il punto di stazione e materializza lo spigolo degli angoli azimutali, oppure la direzione di riferimento, nella misura degli angoli zenitali (figura 4). nota 2: errore residuo di verticalità. Si è detto che, con l'uso della livella torica e delle viti calanti, è possibile rendere verticale un asse. In realtà questa affermazione non è esatta. Infatti non si riesce Capitolo II - Strumenti topografici pagina 53 R.Galetto A.Spalla - Lezioni di Topografia mai a rendere perfettamente verticale un asse a causa degli inevitabili giochi meccanici degli strumenti e del fatto che, anche usando livelle molto sensibili, non si riesce ad agire sulle viti calanti con un'abilità manuale che sfrutti in pieno la sensibilità della livella. Vi è sempre quindi, quando si mette verticale un asse con la prassi illustrata, un errore residuo di verticalità la cui influenza sui risultati della misura dovrà essere minimizzata con opportuni accorgimenti. 6.3.3 Uso combinato di due livelle toriche. Abbiamo visto che per rendere verticale un asse con la livella torica occorre (figura 54): • • • disporre la livella torica parallelamente a due viti calanti e centrarla; ruotare l'elemento ruotante di π/2 disponendo la livella torica in posizione ortogonale alla precedente; ricentrare la livella torica. basetta 2 2 3 3 1 1 elemento mobile figura 54 Non occorrerebbe ruotare l'elemento mobile se su di esso ci fossero due livelle toriche tra loro ortogonali, anziché una sola (vedi figura 55); in tal caso sarebbe infatti sufficiente disporre una livella parallela a due viti calanti; l'altra livella sarebbe automaticamente disposta secondo una parallela alla congiungente la terza vite con il centro del perno ruotante. Sarebbe allora sufficiente centrare la livella a con le rotazioni delle viti 1 e 2, e, senza ruotare nulla, centrare la livella b con la rotazione della vite 3. 3 1 b a 2 figura 55 Abbiamo accennato a questo possibile uso delle due livelle toriche non perché sia importante in sé, ma per questi motivi: Capitolo II - Strumenti topografici pagina 54 R.Galetto A.Spalla - Lezioni di Topografia • • • per cercare di dare un ulteriore chiarimento sull'impiego della livella torica usata per rendere verticale un asse; perché, quando nel successivo paragrafo parleremo della livella sferica, se ne comprenderà meglio il funzionamento immaginandola come l'insieme di due livelle toriche ortogonali; perché in effetti su alcuni strumenti si trovano ancora due livelle toriche; negli strumenti moderni tuttavia c'è un'unica livella torica. 6.3.4 Livella torica a coincidenza. Abbiamo visto che per centrare la bolla nella livella torica a graduazione, occorre far assumere alle due estremità della bolla una posizione simmetrica rispetto allo zero centrale della graduazione; poiché nella generalità dei casi la bolla non ha lunghezza uguale ad un numero intero e pari di unità di graduazione, il centramento viene effettuato stimando che i due tratti siano uguali (vedi figura 56). Per evitare questa operazione di stima, è stato realizzato un tipo di livella per la quale il centramento avviene in modo completamente diverso. εA ε A B B figura 56 Innanzitutto la livella non ha graduazione; sopra di essa vi è un telaietto (vedi figura 57) che porta alle due estremità due prismi; i due prismi sono messi in modo da raccogliere solo la metà dell'immagine delle due estremità della bolla; le due immagini delle due metà della bolla vengono portate ad un oculare nel quale le si vedono accostate. Facendo scorrere il telaietto avanti ed indietro lungo la direzione indicata dalla doppia freccia, si può trovare una posizione in cui si vedono le due estremità della bolla coincidenti, come se si trattasse di un'unica estremità della bolla. L'operazione di giudicare che le due estremità sono in coincidenza viene fatta con precisione molto superiore all'operazione di stima di uguaglianza dei tratti. A B A B figura 57 Per tarare una livella a coincidenza in modo che con essa si possa disporre orizzontale un asse, si procede come segue. Prendiamo in considerazione il caso relativo al dispositivo illustrato in figura 58; come là spiegato si dispone orizzontale l'asse di collimazione, poi si prende la livella a coincidenza e la si fissa sullo strumento; quindi si fa scorrere il telaietto con i due prismi sino a che, nell'apposito oculare, le due estremità appaiono coincidenti; a questo punto si fissa Capitolo II - Strumenti topografici pagina 55 R.Galetto A.Spalla - Lezioni di Topografia rigidamente il telaietto sulla livella; così facendo si realizza questa condizione: che l'asse di collimazione dello strumento è orizzontale e le due estremità della bolla sono coincidenti. figura 58 Allora ogni volta che si vorrà disporre orizzontale l'asse di collimazione sarà sufficiente posizionare lo strumento in modo che le due estremità della bolla risultino coincidenti. Gli strumenti che richiedono la miglior precisione possibile nel disporre orizzontalmente l'asse di collimazione sono i livelli, pertanto, in essi, viene usata la livella a coincidenza. Nota: nella livella torica a coincidenza risulta diversa la definizione di tangente centrale della livella; in quella a graduazione si era detto infatti che la tangente centrale della livella è la tangente al punto centrale della graduazione; nella livella a coincidenza la graduazione non c'è, quindi la definizione di tangente centrale diventa la seguente: la tangente centrale delle livelle a coincidenza è la tangente al punto di mezzo della bolla quando le due estremità della bolla compaiono coincidenti nel dispositivo di osservazione. 7 La livella sferica. 7.1 Struttura. La livella sferica è costituita da un piccolo tronco di cilindro di vetro del diametro di circa 2 cm con la faccia inferiore piana e quella superiore a forma di calotta sferica (vedi figura 59); sulla calottina sferica è inciso un cerchietto. La livella sferica, come quella torica, è piena, ma non completamente, di un liquido volatile; c'è quindi anche qui una bolla costituita da parte del liquido volatilizzato. La bolla è di dimensioni tali che può essere inscritta nel cerchietto inciso sulla calottina sferica. figura 59 Capitolo II - Strumenti topografici pagina 56 R.Galetto A.Spalla - Lezioni di Topografia La sensibilità della livella sferica è molto inferiore a quella delle livelle toriche; essa è in genere compresa tra 4'/2 mm e 8'/2 mm, ed è quindi 40-50 volte meno sensibile di una livella torica. Essa viene quindi impiegata quando si possono tollerare errori residui di verticalità dell'ordine di 10'. Diciamo che una livella sferica è centrata quando la bolla è inscritta nel cerchietto inciso sulla calottina sferica; in questa condizione il piano tangente alla calotta sferica nel punto centrale O del cerchietto è orizzontale e la normale n in O al piano tangente è verticale (vedi figura 60). n=v figura 60 7.2 Uso della livella sferica per rendere verticale un asse. Prendiamo in considerazione una basetta ed una livella torica; appoggiamo la livella torica sulla basetta come indicato in figura 61. 3 1 2 3 + figura 61 = 1 3 2 1 2 figura 62 Ruotando in senso opposto le viti 1 e 2 possiamo far spostare la bolla nella livella; ma se ruotiamo la vite 3 non possiamo provocare nessuno spostamento della bolla. E viceversa se poniamo la livella sulla basetta come in figura 62 potremo far spostare la bolla nella livella torica solo con rotazioni della vite 3, e con rotazioni congiunte della 1 e della 2. Immaginiamo invece ora di appoggiare sulla basetta una livella sferica C (vedi figura 63); supponiamo che essa risulti centrata. Noi vediamo che ruotando la vite 3 possiamo far spostare la bolla nel senso di avvicinarla o allontanarla dalla vite stessa (vedi figura 64) a seconda del senso in cui ruotiamo la vite calante. Capitolo II - Strumenti topografici pagina 57 R.Galetto A.Spalla - Lezioni di Topografia 3 1 2 3 + = 3 1 2 3 1 figura 63 2 1 figura 64 Se invece ruotiamo le viti 1 e 2 possiamo portare la bolla o verso sinistra o verso destra (facendo riferimento al disegno di figura 65). Combinando la rotazione della vite 3 con le rotazioni delle viti 1 e 2 possiamo portare la bolla in una qualsiasi posizione (vedi figura 66). 3 1 3 2 1 A 3 2 1 2 B figura 65 figura 66 Facciamo allora il ragionamento inverso e cioè: se, partendo con la livella centrata, è possibile portare la bolla in una qualsiasi posizione mediante la rotazione della vite 3 e delle viti 1 e 2, ciò vuol dire che quando la livella non è centrata, cioè la bolla è in una posizione generica, possiamo centrare la livella, ossia portare la bolla ad essere inscritta nel cerchietto, ruotando opportunamente la vite 3 e le viti 1 e 2. Vediamo ora cosa vuol dire l'opportunamente inserito nella frase precedente. 3 3 1 2 1 2 A figura 67 3 1 2 B figura 68 Capitolo II - Strumenti topografici pagina 58 2 R.Galetto A.Spalla - Lezioni di Topografia 3 1 2 figura 69 Quando la bolla si trova in una posizione generica (vedi figura 67), per centrarla bisogna operare come se ci fossero sulla basetta due livelle toriche ortogonali tra di loro, e cioè: con la rotazione combinata delle due viti 1 e 2 si porta la bolla in una posizione per la quale si trovi allineata con il centro del cerchietto inciso sulla calottina sferica (posizione a o b di figura 68). Poi, con la rotazione della vite 3, si porta la bolla nel centro della calotta (vedi figura 69). Notiamo che per centrare la livella non occorre ruotare la basetta, cosa che sarebbe inoltre impossibile fare perché la basetta è fissata con il vitone al treppiede. 8 La funzione della basetta. 8.1 La basetta munita di livella sferica. Per quanto viene esposto e trattato in queste dispense, possiamo dire che la livella sferica viene utilizzata in due applicazioni, e cioè: • unita alla basetta; • unita alle stadie; (per ora non sappiamo ancora cosa siano le stadie; vedremo quindi più avanti questa seconda applicazione). Prima di prendere in considerazione la prima applicazione facciamo un riepilogo su come è fatta la basetta; completando quello che è stato detto al punto 5.1. la basetta è composta da (vedi figura 70): • una piastra di base; • una piastra basculante; • tre viti calanti; • una livella sferica; • un piombino ottico. Capitolo II - Strumenti topografici pagina 59 R.Galetto A.Spalla - Lezioni di Topografia V1 V2 L.S. P.O. L1 V3 p. basculante V1 V2 P.O. p. di base figura 70 Ciò detto, vediamo la funzione della livella sferica della basetta in due casi: quando sulla basetta si mette uno strumento topografico e quando ci si mette un segnale. 8.2 La basetta usata come supporto di uno strumento topografico. Quando la basetta è usata come supporto di uno strumento topografico, la funzione della livella sferica è quella di dare un assetto alla piastra basculante della basetta tale per cui, quando si mette lo strumento topografico su di essa, l'asse primario di rotazione (vedi figure 25 e 52) si trovi in posizione prossima alla verticale. Pertanto, per montare in maniera corretta la livella sferica nella basetta, bisogna seguire un procedimento del tipo di quello descritto al punto 6.3.2.: e cioè una volta che è stato reso verticale l'asse r dell'insieme dei due pezzi P1 e P2 , si unisce la livella sferica alla basetta in modo che la bolla sia nel centro del cerchietto inciso sulla sommità della calottina sferica della livella (vedi figura 71). L'operatore topografico, dopo aver fissato la basetta al treppiede, centrerà la livella sferica della basetta; in tal modo quando innesterà su di essa lo strumento topografico, questo risulterà avere l'asse di rotazione primario r, molto prossimo alla verticale; con la livella torica posta sull'alidada, seguendo il procedimento descritto in 6.3.2., l'operatore migliorerà quindi l'assetto di verticalità dell'asse r, sino a lasciare solo l'inevitabile errore residuo di verticalità (vedi nota 2 al punto 6.3.2.). Capitolo II - Strumenti topografici pagina 60 R.Galetto A.Spalla - Lezioni di Topografia figura 71 L'ordine di grandezza dell'accuratezza che si può conseguire nel mettere verticale l'asse r è il seguente: • con la livella sferica della basetta: circa 5'; • con la livella torica sull'alidada dello strumento: circa 5" - 10". 8.3 La basetta usata come supporto di un segnale. Occorre innanzitutto spiegare come è formato un segnale, del quale abbiamo già ricordato la funzione al paragrafo 2. Il segnale è costituito da una piastra metallica sottile di forma rettangolare o quadrata ben collimabile, avente un asse di simmetria s; ad esempio un segnale come quello riprodotto in figura 72 soddisfa al requisito detto perché il centro O del segnale si collima agevolmente mettendo il tratto orizzontale del reticolo in corrispondenza dei vertici dei due triangoli piccoli, ed il filo verticale in corrispondenza del vertice del triangolo grande (vedi figura 73). figura 74 figura 72 Capitolo II - Strumenti topografici pagina 61 R.Galetto A.Spalla - Lezioni di Topografia figura 73 figura 75 Sul lato inferiore del segnale è saldato un alloggiamento cilindrico che permette di infilare il segnale su un supporto del tipo di quello rappresentato in figura 74; questo supporto ha tre piedini mediante i quali può essere inscritto in una basetta e termina, nella parte superiore, con un perno cilindrico sul quale viene inserito il segnale mediante l'apposito alloggiamento cilindrico saldato al suo lato inferiore (vedi figura 75). Quando il segnale è montato sul supporto, l'asse di simmetria s del segnale coincide con l'asse t del perno cilindrico terminale del supporto; inserendo quindi il supporto con il segnale sulla basetta, è possibile rendere verticale l'asse di simmetria del segnale mediante le viti calanti e la livella sferica della basetta (vedi figura 75). 8.4 Intercambiabilità tra strumento topografico e segnale. Il fatto che il segnale sia realizzato come è stato descritto al precedente punto 8.3., permette di sostituire il segnale a uno strumento topografico messo in stazione su un punto, con una approssimazione elevata, cioè con un errore inferiore al decimo di millimetro. r s o c d d P figura 76 P figura 77 Capitolo II - Strumenti topografici pagina 63 R.Galetto A.Spalla - Lezioni di Topografia L'operatore, infatti, dopo aver messo in stazione lo strumento topografico su un punto P ed aver eseguito le misure necessarie (vedi figura 76), può togliere lo strumento dalla basetta ed inserire su di essa un segnale; l'asse di simmetria s del segnale passerà anch'esso sulla verticale passante per il punto P; inoltre il topografo usa strumenti topografici e segnali costruiti da una stessa Casa Costruttrice di strumenti, la quale ha cura di dimensionare il supporto del segnale stesso, in modo che la distanza d dal punto O del segnale dal piano d'appoggio della piastra basculante della basetta (vedi figura 77), sia uguale a quella del centro dello strumento C sempre dal piano di appoggio della basetta. (Per la definizione di centro dello strumento si veda al punto 4.2.5. ed alla nota 1 del punto 6.3.2.). Questa intercambiabilità tra strumento e segnale viene indicata con l'espressione centramento forzato, che significa appunto la possibilità di centrarsi su un punto alternativamente con strumento e segnale, con elevata precisione. Vedremo in seguito le operazioni topografiche che devono venire eseguite applicando il centramento forzato. Capitolo II - Strumenti topografici pagina 64 R.Galetto A.Spalla - Lezioni di Topografia 9 Il teodolite. 9.1 Premessa. Con il teodolite può venire effettuata la misura diretta di angoli azimutali e zenitali. Consideriamo la figura 78: B ζ B ζC A α C figura 78 l'angolo azimutale α è individuato dalle congiungenti A-B, A-C; l'angolo zenitale ζB è individuato dalla verticale vA e dalla congiungente A-B; l'angolo zenitale ζC è individuato dalla verticale vA e dalla congiungente A-C. La misura di tali angoli è possibile con uno strumento che possieda • organi che consentano la materializzazione degli angoli stessi, materializzando le rette che li definiscono, • e organi di misura degli angoli materializzati. Vedremo nei paragrafi successivi attraverso quali organi avvenga nel teodolite la materializzazione e la misura degli angoli azimutali e zenitali. 9.2 Descrizione dello strumento. Il teodolite, nella sua struttura è visibile alla figura 80. Esso presenta inferiormente un basamento munito di tre piedini che vanno ad inserirsi in una basetta solidale al terreno mediante un treppiede (vedi figura 79). figura 79 Capitolo II - Strumenti topografici pagina 65 R.Galetto A.Spalla - Lezioni di Topografia Il basamento presenta internamente una cavità cilindrica detta collare; l'asse del collare viene detto asse primario del teodolite. Nel collare si innesta il perno dell'alidada, dispositivo a due bracci che ruota intorno all'asse primario. I due bracci dell'alidada portano le sedi di un perno che sostiene un cannocchiale topografico del tipo descritto al capitolo 4. La congiungente le due sedi, che materializza l'asse intorno al quale ruota il cannocchiale, è l'asse secondario del teodolite. Sull'alidada è montata una livella torica che viene usata per rendere verticale l'asse primario. Quando infatti si dispone lo strumento in stazione sul punto A, collimandolo con il piombino ottico (vedi paragrafo 5.4.), l'asse primario viene a trovarsi in una posizione del tutto generica; agendo sulle viti calanti secondo la prassi operativa descritta al paragrafo 6.3.2. sarà possibile correggere la deviazione della verticale dell'asse primario che potrà quindi essere considerato la materializzazione della retta vA (vedi figura 78). figura 80 Capitolo II - Strumenti topografici pagina 66 R.Galetto A.Spalla - Lezioni di Topografia r m C m U B r figura 81 Lo strumento può dunque essere schematizzato come in figura secondo tre assi: r m asse primario, reso verticale, intorno al quale ruota l'alidada; asse secondario, perpendicolare ad r, orizzontale, intorno al quale ruota il cannocchiale. L’asse primario e l’asse secondario sono di tipo meccanico. a.o. asse terziario, di tipo ottico. E' l'asse del cannocchiale stesso, è solidale con le rotazioni degli altri due assi e può avere rotazioni indipendenti nel piano verticale. Sono stati esaminati a questo punto gli organi che consentono la materializzazione degli angoli azimutali e zenitali. Abbiamo visto infatti come si possa far coincidere l'asse primario dello strumento con la verticale per il punto di stazione A e come le rette congiungenti A-B e A-C siano, ad ogni collimazione, coincidenti con l'asse terziario. Occorre ora descrivere quali organi del teodolite consentano la misura degli angoli materializzati. 9.3 Misura degli angoli azimutali. Come si vede in figura 80, calettato sul collare del basamento c'è un cerchio graduato; in fase di lettura un indice montato sull'alidada segnerà un valore del cerchio. Supponendo quindi di aver collimato il punto B, ad asse primario perfettamente verticale, l'indice di lettura, solidale con l'alidada, definirà, sul cerchio graduato, un certo valore l1 ; collimiamo ora il punto C mediante rotazioni dell'alidada intorno all'asse primario e del cannocchiale intorno al secondario: leggeremo sul cerchio l2. L'angolo azimutale sarà allora: α= l2 - l1 Capitolo II - Strumenti topografici pagina 67 R.Galetto A.Spalla - Lezioni di Topografia Questo vale però solo in condizioni di rettifica dello strumento, quando cioè gli assi sono fra loro ortogonali e il centro della graduazione del cerchio coincide con la traccia dell'asse primario sul piano di rotazione dell'alidada. 9.4 Misura degli angoli zenitali. Innestato sullo stesso perno che porta il cannocchiale e solidale ad esso, c'è un secondo cerchio graduato il cui centro coincide con la traccia dell'asse secondario; l'indice di lettura è solidale con l'alidada. Se è realizzata la condizione che, a cannocchiale perfettamente verticale l'indice segni zero, in fase di collimazione, quando cioè ruoteremo il cannocchiale per mirare il punto B, potremo leggere sul cerchio l'angolo di cui il cannocchiale è dovuto ruotare per portarsi dalla verticale per A sulla congiungente A-B, che è appunto l'angolo zenitale. 9.5 Condizioni di rettifica del teodolite. Esaminiamo ora le condizioni che devono essere verificate perché si possa realizzare con il teodolite lo schema di misura di angoli azimutali e zenitali precedentemente esaminato. Condizioni intrinseche dello strumento. Le condizioni di rettifica intrinseche dello strumento sono le seguenti 1. Si ipotizza che l'asse del perno dell'alidada coincida con il centro del collare (asse primario). 2. L'asse primario, intorno al quale ruota il perno dell'alidada deve essere ortogonale all'asse secondario, intorno al quale ruota il cannocchiale. 3. L'asse di collimazione del cannocchiale (asse terziario) deve a sua volta essere ortogonale all'asse secondario. 4. I tre assi strumentali devono intersecarsi in uno stesso punto che viene definito centro dello strumento. 5. Il centro della graduazione del cerchio orizzontale deve coincidere con la traccia dell'asse primario sul piano che contiene il cerchio stesso, così come il centro della graduazione del cerchio verticale deve coincidere con la traccia dell'asse secondario sul suo piano. 6. Quando il cannocchiale è disposto con l'asse di collimazione coincidente con l'asse primario, si deve leggere zero al cerchio verticale. Condizione in fase di misura. Ponendo lo strumento in stazione su un punto, l'asse primario deve coincidere con la verticale passante per quel punto. Nota. Dobbiamo chiarire che tutte le condizioni sopra elencate non sono mai rigorosamente verificate perché lo strumento viene realizzato con dispositivi Capitolo II - Strumenti topografici pagina 68 R.Galetto A.Spalla - Lezioni di Topografia meccanici che sono sì caratterizzati da precisioni molto elevate (dell'ordine del µm) ma, proprio perché meccanici, devono presentare particolari giochi. Per poter seguire la schematizzazione di misura descritta, dovremo pertanto adottare opportune metodologie operative che consentano di rendere trascurabile l'influenza delle srettifiche sulle misure. 9.6 Errori che influenzano la determinazione degli angoli azimutali. 9.6.1 Errore di eccentricità dell'alidada. Perché l'alidada abbia la possibilità di ruotare nel collare è indispensabile che ci sia un certo gioco che determina la non coincidenza fra il centro del cerchio graduato e la traccia dell'asse primario sul piano del cerchio. L0 B α' A ε L1 D C figura 82 Vediamo come l'eccentricità dell'alidada influenza le misure. Supponiamo di collimare il punto B; l'indice di lettura solidale con l'alidada sia nella direzione dell'eccentricità: avremo L0 . Collimando ora il punto D e leggendo L1 determineremo, per differenza, un angolo: α’= L1 - L0 che differisce dal valore effettivo α dell'angolo di ε = e r Se il raggio del cerchio graduato è di 6 cm (60.000 µm ) e l'eccentricità è di 6 µm : 6 1 1 ε= = radianti ε = 200.000 = 20" secondi 60.000 10.000 10.000 E' necessario a questo punto operare una distinzione fra i diversi tipi di teodolite in base alla precisione con essi conseguibile. Si definiscono • tacheometri • teodoliti gli strumenti che consentono di eseguire misure con e.q.m. di ± 20" gli strumenti che consentono di eseguire misure con e.q.m. di ± 1". In base a questa distinzione, poiché nei tacheometri l'errore dovuto all'eccentricità è dello stesso ordine di grandezza della precisione che si vuol conseguire nella misura, in tale tipo di strumenti l'errore di eccentricità potrà essere trascurato. Ciò non sarà invece possibile nei teodoliti. Capitolo II - Strumenti topografici pagina 69 R.Galetto A.Spalla - Lezioni di Topografia Nella parte ottica dei teodoliti, infatti, si riesce ad ottenere una precisione anche di 0,5" : un errore quindi di 20" non è assolutamente tollerabile. D'altra parte, il gioco non può essere eliminato senza bloccare la rotazione dell'alidada attorno al perno; si cercherà di ridurne l'entità con opportuni accorgimenti costruttivi, ad esempio con cuscinetti a sfera che mantengono stabile il perno nel collare. Tuttavia l'influenza dell'errore dovuto all'eccentricità dell'alidada si elimina completamente soltanto con il procedimento di lettura simultanea alle parti opposte del cerchio. Come si vede infatti in figura, siano L1 ed L2 i valori letti alle parti opposte del cerchio quando si collima il punto A. Tali valori saranno l'uno maggiore, l'altro minore rispetto ai valori che si avrebbero in condizioni ideali di centramento (L e L + π): assumendo pertanto la media dei valori L1 ed L2 si elimina l'influenza del decentramento. 0 1 2 .. . L L1 e L+ π L2 figura 83 I teodoliti si distinguono quindi dai tacheometri perché, mentre nei teodoliti esistono due indici di lettura, esiste cioè la possibilità di eseguire la lettura simultanea alle parti opposte del cerchio, nei tacheometri si può fare una sola lettura che risulta quindi affetta dall'errore di eccentricità. 9.6.2 Errori causati da srettifiche di costruzione. Per ovviare agli errori causati: • dalla non ortogonalità fra asse primario e secondario, • dalla non ortogonalità fra asse secondario e terziario, • dalla non coincidenza dei centri dei cerchi di graduazione orizzontale e verticale con le tracce degli assi rispettivamente primario e secondario sui piani relativi, si segue la prassi operativa della regola di Bessel che è così schematizzabile: 1. si collima il punto in esame (supponiamo che durante questa operazione il cerchio verticale dello strumento sia sulla destra dell'operatore) 2. si esegue la lettura simultanea alle parti opposte del cerchio, descritta al paragrafo precedente, e si ottiene un valore LD; 3. si ruota quindi l'alidada e si ricollima il punto (il cerchio verticale sarà ora sulla sinistra dell'operatore), 4. si riesegue la lettura simultanea alle parti opposte del cerchio e si ottiene un valore LS Capitolo II - Strumenti topografici pagina 70 R.Galetto A.Spalla - Lezioni di Topografia Se si assume come valore della misura la media di LD ed LS , si elimina l'influenza che sulla lettura hanno tutte le srettifiche intrinseche dello strumento. Tali srettifiche, infatti, causano, nelle due diverse condizioni di cerchio verticale a sinistra e cerchio verticale a destra, errori di segno opposto che sommati si elidono. 9.6.3 Errore di verticalità dell'asse primario. La condizione che viene richiesta, in fase di misura, è la coincidenza dell'asse primario dello strumento con la verticale passante per il punto di stazione. I dispositivi che consentono, in fase operativa, di avvicinarci il più possibile a questa condizione ideale sono le livelle (vedi paragrafo 6.3.2.). Ricordiamo che, in fase di costruzione, si realizza la condizione che ad asse primario reso verticale la livella sia centrata. Perché ciò si verifichi, si parte dal presupposto che sia possibile rendere verticale l'asse primario, in laboratorio, con particolari metodi e dispositivi diversi dalle livelle. Viene successivamente montata l'alidada che porta una livella torica. Agendo sulle viti di rettifica della livella se ne centra la bolla in modo che risulti simmetrica rispetto alla graduazione: si realizza così la condizione essenziale richiesta che ad asse primario verticale la livella sia centrata. In fase operativa pertanto tutte le volte che verrà centrata la livella si realizzerà conseguentemente la verticalità dell'asse primario. Naturalmente la perfetta verticalità non può venire realizzata: l'errore di verticalità sarà infatti strettamente connesso coi limiti di precisione della livella, né si potrà pensare di montare su un teodolite una livella la cui sensibilità sia superiore a 10", perché in fase di misura anche minime vibrazioni del terreno, trasmesse allo strumento attraverso il treppiede, impedirebbero di mantenere la bolla ferma in posizione centrata per il tempo necessario alla misura (vedi anche nota 2 paragrafo 6.3.2.). Oltre alle srettifiche intrinseche dello strumento, ci sarà quindi questa ulteriore srettifica che influenzerà le misure. Mentre però gli errori dovuti alle srettifiche di costruzione si possono eliminare seguendo la metodologia di Bessel, perché generano errori il cui segno varia nel caso di lettura con il cerchio a sinistra o con il cerchio a destra, non c'è nessuna possibilità di eliminare l'errore residuo di verticalità con letture coniugate. Consideriamo infatti i punti A e B e la retta verticale v della figura 84; α sarà l'angolo azimutale. Se ora consideriamo l'asse di rotazione v' deviato di un certo errore di verticalità rispetto a v, l'angolo azimutale α’ relativo agli stessi punti A e B sarà maggiore di α Anche ruotando l'alidada di π, poiché la rotazione avviene intorno a v', l'errore non cambierà di segno. Bisogna però anche considerare che, nella determinazione dell'angolo azimutale AB, nella condizione della figura 85, la non verticalità dell'asse primario porta a leggere un valore minore del valore reale. Capitolo II - Strumenti topografici pagina 71 R.Galetto A.Spalla - Lezioni di Topografia α A α' α A α' B B figura 84 figura 85 L'errore residuo di verticalità può dunque influire positivamente o negativamente sulla misura dell'angolo azimutale a seconda che ci si trovi nelle condizioni di figura 84 o di figura 85: ripetendo quindi molte volte la misura dell'angolo, ogni volta scentrando e rimettendo in bolla lo strumento, si opereranno misure nelle due diverse situazioni e si renderà accidentale l'influenza dell'errore di verticalità. 9.7 Errori che influenzano la determinazione degli angoli zenitali. Abbiamo visto sinora come eliminare l'influenza delle diverse srettifiche sulla misura degli angoli azimutali. Vediamo ora quali srettifiche influiscono sulla determinazione degli angoli zenitali. Le ipotesi di rettifica strumentale dalle quali si parte nella schematizzazione della misura degli angoli zenitali sono tre, due intrinseche allo strumento ed una, la condizione di verticalità, da realizzare in fase operativa. 1) Quando si posiziona l'asse del cannocchiale coincidente con l'asse primario, si deve leggere zero sulla graduazione del cerchio verticale, 2) il centro della graduazione del cerchio verticale deve coincidere con la traccia dell'asse secondario sul piano del cerchio, 3) l'asse primario deve coincidere con la verticale per il punto di stazione. Il fatto che non si verifichi la condizione 1) in fase di costruzione dello strumento, fa sì che, quando si posiziona l'asse di collimazione secondo l'asse di rotazione primario, si legga un valore angolare che sarà definito come zenit strumentale. Sulle misure degli angoli zenitali incide poi anche l'errore residuo di verticalità dovuto al fatto che non si realizzi l'ipotesi 3). Per spiegare come venga eliminata dalle misure l'influenza dello zenit strumentale e dell'errore residuo di verticalità, si considerano separatamente i due errori che, essendo piccoli, possono essere trattati indipendentemente. Capitolo II - Strumenti topografici pagina 72 R.Galetto A.Spalla - Lezioni di Topografia 9.7.1 Srettifica dovuta alla presenza dello zenit strumentale (Z). È già stata data la definizione di zenit strumentale come di quel valore angolare Z che si leggerebbe, invece del valore zero, qualora si riuscisse a posizionare l'asse di collimazione perfettamente verticale (vedi figura 86 dove l'indice di lettura è stato disegnato esternamente per semplicità). III 300 300 IV 0 0 200 II 200 z I 100 I indice 100 figura 86 I è l’indice di lettura. la graduazione, espressa in gradi centesimali, cresce ruotando il cannocchiale in senso antiorario. Per vedere come la presenza di Z influisce sulla misura degli angoli zenitali, supponiamo di dover collimare un punto A e di dover determinare l'angolo z che la retta CA forma con la verticale A (angolo zenitale). Eseguiamo l'operazione mantenendo il cerchio verticale sulla nostra sinistra (vedi figura 87) A Z Z+z 300 0 z I 200 100 figura 87 Partendo dalla posizione di figura 87 e ruotando il cannocchiale dell'angolo z, anche il cerchio verticale, che è solidale con il cannocchiale, ruoterà di z. Capitolo II - Strumenti topografici pagina 73 R.Galetto A.Spalla - Lezioni di Topografia Poiché però a cannocchiale verticale la lettura che si esegue non è S = 0, ma bensì S = Z, all'indice I si leggerà ora il valore: S=Z+z (1) Per quantificare il valore Z e per eliminarne l'influenza sulle misure, si segue il metodo delle letture coniugate. Dopo aver eseguito la lettura con il cerchio a sinistra si ruota l'alidada di 200g portando il cerchio verticale a destra (vedi figura 88). 2z Z+z Z 300 0 z I 200 100 figura 88 La graduazione cresce ora ruotando il cannocchiale in senso orario. Il cannocchiale viene a trovarsi rispetto alla verticale in posizione simmetrica alla congiungente AC; né il cannocchiale, né il cerchio graduato, solidale con esso, subiscono rotazioni nel piano verticale; all'indice I si legge ancora il valore S. Sempre dalla figura 88 si nota che per ricollimare il punto A occorre ruotare il cannocchiale in senso antiorario di un angolo 2z. Supponiamo di poter dare questa rotazione in due tempi: ruotiamo cioè il cannocchiale in un primo tempo solo dell'angolo z. Il cannocchiale si troverà in posizione verticale, il cerchio graduato sarà ruotato anch'esso in senso antiorario di z (vedi figura 89). All'indice I si leggerà: D=Z A 2z z 300 0 I 200 Z 100 figura 89 Capitolo II - Strumenti topografici pagina 74 R.Galetto A.Spalla - Lezioni di Topografia Collimiamo ora il punto A ruotando il cannocchiale sempre in senso antiorario di z (vedi figura 90). Il cerchio graduato ruoterà anch'esso di z e l'indice di lettura segnerà un valore che sarà: D = - (z - Z) (2) z 300 200 z-Z 0 100 z Z figura 90 Nella espressione (2), il segno " - " esprime il fatto che la lettura viene eseguita nel senso decrescente della graduazione; per ovviare a questo fatto occorrerà riscrivere la (2) come D = 400g - (z - Z) = 400g - z + Z (3) Il valore dell'angolo zenitale esente dalla srettifica provocata dallo zenit strumentale si ottiene sottraendo alla (1) la (3): S - D = z + Z - 400g + z - Z S − D + 400 g z= 2 (4) Il valore dello zenit strumentale si ottiene sommando la (1) e la (3) e cioè: S + D = Z + z +400g - z + Z S + D − 400g Z= 2 (5) Si è visto dunque come la presenza di uno zenit strumentale non influisca sulla determinazione degli angoli zenitali se si segue la prassi operativa delle letture coniugate: Z è presente sia in S che in D con lo stesso segno e viene quindi eliminato per differenza. Sempre allo scopo di rendere trascurabile l'influenza dello zenit strumentale, è anche possibile, quando si eseguono misure speditive di scarsa precisione, eseguire la prima misura di un angolo zenitale con il metodo delle letture coniugate e determinare Z con la (5). Capitolo II - Strumenti topografici pagina 75 R.Galetto A.Spalla - Lezioni di Topografia Per le successive misure basterà poi eseguire una sola lettura e corregerne il valore dello zenit strumentale calcolato. 9.7.2 Errore dovuto all'eccentricità del cerchio verticale. Le stesse considerazioni che sono state fatte al paragrafo 9.6.1. sull'eccentricità dell'alidada, valgono anche per l'eccentricità del cerchio verticale. L'influenza di tale srettifica sulle misure può venire completamente eliminata, negli strumenti di precisione e cioè in quegli strumenti forniti di due indici di lettura anche al cerchio verticale, eseguendo la lettura simultanea agli indici opposti e prendendone la media. Si effettuano cioè, in posizione di cerchio a sinistra, due letture simultanee ai due indici , se ne fa la media che fornirà il valore S. In posizione di cerchio a destra la media delle letture simultanee fornirà il valore D. I valori S e D inseriti nella (4) consentiranno di determinare il valore dell’angolo zenitale esente dall'influenza dell'eccentricità del cerchio verticale. 9.7.3 Errore residuo di verticalità. L'errore residuo di verticalità, l'errore cioè dovuto al fatto che non sia possibile rendere l'asse primario perfettamente coincidente con la verticale, si corregge con dispositivi compensatori automatici il cui principio di funzionamento può essere schematizzato come segue. A z 0 0 I z figura 91 Capitolo II - Strumenti topografici pagina 76 R.Galetto A.Spalla - Lezioni di Topografia L'indice di lettura al cerchio verticale non sia più solidale all'alidada, ma sia montato su essa con un dispositivo a pendolo. Collimando il punto A in condizioni ideali di assenza di errore residuo di verticalità, si legge all'indice il valore z dell'angolo zenitale (vedi figura 91). Supponiamo ora di essere in presenza di un errore residuo di verticalità v. L'angolo che l'asse di collimazione forma con l'asse primario è, come si vede in figura 92, z + v. z v z+v figura 9 2 Ad un indice solidale con l'alidada, il valore di lettura sarebbe proprio z + v. Adottando invece un dispositivo pendolare, l'indice si dispone sempre parallelamente alla verticale passante per il centro dello strumento, e come si vede in figura 93, il valore angolare che esso segna sul cerchio graduato è proprio l'angolo zenitale esente da errore residuo di verticalità. z v z+v figura 93 Capitolo II - Strumenti topografici pagina 77 R.Galetto A.Spalla - Lezioni di Topografia 10 Misura diretta delle distanze mediante distanziometri elettronici Analizzando in seguito i vari tipi di operazioni topografiche, vedremo che alcune di esse richiedono misure di distanza. In alcune operazioni le distanze da misurare hanno entità variabile tra pochi metri sino a 50÷100 m con un grado di approssimazione di ±10 cm circa (precisione 10-3 ). Altre operazioni richiedono invece che vengano misurate distanze di entità variabile da qualche decina di metri a 1÷2 Km o più; il grado di approssimazione richiesto è di circa ± 1÷2 cm (precisione 10-5 ). Per le distanze del primo tipo (brevi e richiedenti precisioni non elevate) viene impiegato il metodo basato sull'uso del tacheometro e della stadia; per le seconde si usano i distanziometri elettronici. I distanziometri elettronici sono strumenti di recente introduzione; contrariamente al teodolite, al tacheometro o al livello, che sono in uso da secoli, i distanziometri elettronici hanno fatto la loro comparsa da circa 20÷30 anni. Essi, proprio perché basati sull'elettronica, hanno subito un'evoluzione rapidissima e hanno dato luogo ad una vasta diversificazione di modelli. I diversi modelli si basano su principi diversi, specialmente in funzione dell'entità delle distanze che essi sono in grado di misurare. Date le non poche cognizioni di elettronica richieste per la comprensione del loro funzionamento, ci limiteremo a prendere in considerazione i distanziometri elettronici che si impiegano nelle misure topografiche cioè quelli aventi una portata massima di 1÷2 Km. Prima di affrontare la descrizione della struttura e del funzionamento di un distanziometro richiamiamo per comodità alcune nozioni sulle onde elettromagnetiche. 10.1 Richiami sulle onde elettromagnetiche. 10.1.1 Periodo, frequenza, intensità istantanea Un'onda elettromagnetica è caratterizzata dai seguenti parametri: • T (sec) periodo dell'onda, ossia intervallo di tempo nel quale l'intensità dell'onda compie un ciclo completo; • f (1/sec) frequenza, numero di cicli al secondo; • I intensità istantanea: I = I 0 sen(2π t ) T La rappresentazione del valore istantaneo dell'intensità dell'onda è la seguente: Capitolo II - Strumenti topografici pagina 78 R.Galetto A.Spalla - Lezioni di Topografia Ι Ι ° ϕ = 2π t T La frequenza f si misura in Herzt; se cioè un'onda impiega 1 secondo a compiere un ciclo la sua frequenza è 1 Hz; se impiega 1/1000 di secondo la sua frequenza è 1000 Hz ( 1 KHz, 1 chiloerz); se impiega 1/1.000.000 di secondo la sua frequenza è 1.000.000 di Hz (1 MHz, 1 megaerz). Si indica inoltre con λ la lunghezza dell'onda, cioè lo spazio percorso dall'onda nel propagarsi, corrispondente ad un periodo T; λ è legata alla frequenza T dalla relazione: c λ=cT= f essendo c la velocità della luce nel vuoto. Esempi. La luce visibile ha una lunghezza d'onda variabile tra 0,4 µm e 0,7 µm con frequenza variante tra 75 . 10 MHz e 45 . 10 MHz. Le onde elettromagnetiche che seguono immediatamente nello spettro quelle della luce visibile sono dette onde infrarosse e hanno lunghezza d'onda variabile tra 0,7 µm e 1,1 µm. 10.1.2 Fase. Indichiamo con ϕ (fase) l'argomento del seno dell'intensità di un'onda: t I = I 0 sen(2π ) = I 0 senϕ T Quando t = 0 lo spazio di propagazione dell'onda è zero; quando t = T lo spazio di propagazione è λ; per un tempo t compreso tra 0 e T lo spazio d percorso dall'onda sarà legata a ϕ dalla relazione: ϕ d=λ 2π Questo significa che ad una certa intensità dell'onda I corrisponde una fase ϕ, e da questa possiamo ricavare la distanza d percorsa dall'onda dall'istante t = 0 all'istante t. Capitolo II - Strumenti topografici pagina 79 R.Galetto A.Spalla - Lezioni di Topografia Ι ϕ" I" I' ϕ' ϕ Più in generale dal confronto di due intensità I' e I" possiamo risalire ai valori di fase ϕ' e ϕ" che ad esse corrispondono e quindi alla distanza d di propagazione dell'onda tra il verificarsi dei due valori di intensità. La differenza di fase ∆ϕ tra ϕ' e ϕ" si chiama sfasamento. Succede però che uno stesso valore di sfasamento si presenta ciclicamente ad ogni periodo T. I ∆ϕ ϕ' ∆ϕ + 4π ∆ϕ + 2π ϕ" ϕ" ϕ Quindi se emettiamo un'onda da un emettitore ed in un certo momento misuriamo l'intensità I' e l'intensità I" registrata da un ricevitore che riceve l'onda riflessa da un prisma, non siamo in grado di determinare la distanza di propagazione dell'onda dallo sfasamento corrispondente ai valori I' e I". D emettitore I' I" prisma ricevitore Possiamo solo dire che la distanza 2D (andata e ritorno) è uguale alla distanza di propagazione corrispondente allo sfasamento, più un numero indeterminato k di lunghezze d'onda: ∆ϕ 2D= λ + kλ 2π 10.1.3 Modulazione in ampiezza, Un'onda può essere modulata in ampiezza (se ne fa cioè aumentare e diminuire ciclicamente l'ampiezza massima), per ottenere da essa un'onda di lunghezza d'onda maggiore. La prima onda si chiama onda portante o onda modulata; la seconda onda modulante. Capitolo II - Strumenti topografici pagina 80 R.Galetto A.Spalla - Lezioni di Topografia L'onda modulante è data dall'inviluppo dei massimi dell'onda modulata. Con l'operazione di modulazione si possono ottenere onde di lunghezza d'onda lunghissime, modulando onde di lunghezza d'onda molto corta. Ad esempio, un'onda elettromagnetica infrarossa di 1 µm di lunghezza d'onda può essere modulata in modo da ottenere onde con λ= 20 m o λ= 2000 m. ' λ=4λ λ Per esemplificare riportiamo un grafico da cui si può comprendere come da un'onda se possa ottenere un'altra di lunghezza d'onda 4 volte superiore. 10.2 Schema di un distanziometro elettronico topografico. Un distanziometro elettronico si compone delle seguenti parti. a) Un generatore di corrente continua (batteria). b) Un generatore di frequenza (quarzo piezoelettrico). c) Un diodo (all'arseniuro di Gallio) che percorso da corrente emette luce infrarossa con intensità proporzionale alla corrente che lo attraversa. Mediante questi tre primi componenti, il distanziometro può emettere luce infrarossa modulata; si ottiene questo effetto, applicando ai capi del diodo una tensione variabile, direttamente ricavata dal circuito del quale fa parte l'oscillatore a quarzo (il quarzo piezoelettrico). La frequenza del quarzo piezoelettrico è detta frequenza fondamentale del distanziometro. Questa frequenza è in genere di 15 MHz ; ne consegue che la luce infrarossa emersa dal distanziometro è modulata e genera un'onda modulante di lunghezza d'onda: Capitolo II - Strumenti topografici pagina 81 R.Galetto A.Spalla - Lezioni di Topografia λ'= 300.000m / sec = 20m 15.000.000periodi / sec Il distanziometro si completa con i seguenti altri componenti. d) Nel circuito è possibile inserire un divisore elettronico di frequenza, cioè un componente che può dividere per cento la frequenza del quarzo piezoelettrico; quando il divisore elettronico è inserito nel circuito, la frequenza dell'onda modulante diventa cento volte più piccola della frequenza fondamentale, cioè diviene, nel caso fatto, di 150 KHz . A questa frequenza, detta frequenza secondaria, corrisponde una lunghezza d'onda dell'onda modulante: 300.000m / sec λ" = = 2000m 150.000periodi / sec e) Un apparato ricevente, in grado di captare l'onda emessa dal distanziometro e riflessa verso di esso da un prisma posto a distanza. f) Un misuratore di fase che è un dispositivo in grado di misurare lo sfasamento corrispondente a due diversi valori di intensità dell'onda, e di risalire alla distanza di propagazione corrispondente a tale valore. Il misuratore di fase ha una precisione di 10-3 , cioè misura la distanza d di propagazione corrispondente allo sfasamento, con e.q.m. uguale a: d ± 1000 10.3 Funzionamento del distanziometro. Le caratteristiche principali di un distanziometro sono due: la portata, cioè la massima distanza misurabile, e l' e.q.m. con il quale tale distanza viene misurata. La portata è (e vedremo il perché) inferiore alla metà della lunghezza d'onda modulante, ottenuta modulando la portante con la frequenza secondaria. La precisione è invece uguale a ±1/1000 della lunghezza dell'onda modulante ottenuta modulando la portante con la frequenza fondamentale (vedremo il perché). A D B Sia da misurare la distanza D tra i punti A e B. Si mette in stazione il distanziometro sul punto A e si mette un prisma riflettente su B. Si emette dal distanziometro la luce infrarossa modulata con la frequenza secondaria e ad uno stesso istante t viene effettuata sul distanziometro la misura dell'intensità I' dell'onda modulante emessa e l'intensità I" dell'onda modulante ricevuta. Se lo strumento è usato correttamente, cioè se la distanza D non è superiore alla portata dello strumento, la differenza di fase Capitolo II - Strumenti topografici pagina 82 R.Galetto A.Spalla - Lezioni di Topografia corrispondente ai due valori I' ed I" calcolata dal misuratore di fase, ci fornisce la distanza D in modo univoco: ∆ϕ 1 ∆ϕ 2D = λ" e cioè D = λ" (6) 2π 2 2π Poiché però lo sfasamento ∆ϕ è misurato con precisione di 10-3, ne segue che il valore di D così ricavato ha un e.q.m. di ±1/1000 di D; vi è cioè proporzionalità diretta tra l'errore in ϕ e quello in D; infatti, applicando la formula dell'e.q.m. delle misure indirette si ha: 1 λ"2 2 mD2 = m (7) 16 π 2 ∆ϕ ricavando λ”2 dalla (6): 16π 2 D 2 λ"2 = ∆ϕ 2 sostituendo nella (7) 16π 2 D 2 mD2 = m∆2ϕ ∆ϕ 2 16π 2 e cioè m2D m2 ∆ϕ = D2 ∆ϕ 2 Il che significa che quando un distanziometro ha portata 1 Km, e quindi occorre che λ” sia uguale a 2 Km, l'e.q.m. di D, misurato con lo sfasamento dell'onda ottenuta con la frequenza secondaria, è ± 1 m. Infatti la precisione di 10-3 nella misura dello sfasamento di λ” = 2000 m, porta ad un errore di ± 2 m nella misura di 2D e quindi ad un errore di ± 1 m nella misura di D. Precisione naturalmente insufficiente. Abbiamo però la possibilità di usare l'onda modulante corrispondente alla frequenza fondamentale λ’. Inviando allora il fascio di luce infrarossa modulata con la frequenza fondamentale λ’, misuriamo nuovamente a un tempo t lo sfasamento tra l'intensità dell'onda modulante emessa e quella dell'onda ricevuta per riflessione dal prisma. La misura della distanza D in funzione di ∆ϕ è: 1 ∆ϕ D= λ '+ kλ ' 2 2π con k incognito. A noi però non interessa la quantità k, poiché sappiamo già quanto approssimativamente vale D; ci interessa solo il valore: ∆ϕ 2D = λ' 2π Poiché λ’ è di 20 m e poiché il valore di 2D viene ricavato con un e.q.m. di ±1/1000 , e cioè ±2 cm, D ha un e.q.m. di + ±1 cm. Ciò significa che la prima misura ci fornisce la distanza sino alle decine di metri; ad es.: D = 84.... m e la seconda misura permette di completarne il valore sino ai centimetri: Capitolo II - Strumenti topografici pagina 83 R.Galetto A.Spalla - Lezioni di Topografia D = 847,15 m In pratica, le due misure non vengono eseguite in successione dall'operatore, ma tutto il procedimento è eseguito automaticamente dallo strumento che fornisce in pochi secondi il risultato definitivo completo su un visore digitale. 10.4 Alcune considerazioni aggiuntive sui distanziometri. 1) L'impiego della luce infrarossa è giustificato dai seguenti motivi: • • • • il diodo che la genera richiede un'alimentazione limitata; quindi la batteria non appesantisce molto lo strumento; il diodo (che emette la luce infrarossa) si presta ad una modulazione diretta molto semplice; il sensore che riceve la luce infrarossa rimandata dal prisma essendo sensibile solo all'infrarosso non risente della luce diurna; non vi è cioè rumore di fondo nella ricezione del segnale; la luce infrarossa penetra la foschia (quella leggera); ne risulta che il distanziometro è usabile anche in condizioni atmosferiche non ideali. 2) Oltre ai distanziometri elettronici topografici, (cioè del tipo di quello che abbiamo esaminato) che hanno una portata variabile tra 500 metri e 2÷3 Km e misurano le distanze con un'approssimazione di ± 0,5 - ± 1 cm, vi sono altri distanziometri atti a misurare distanze sino a 50 Km, con precisione dell'ordine di 10-6 . Vi sono poi altri distanziometri con portata dello stesso ordine di grandezza di quelli topografici, ma aventi precisione più elevata e cioè di 10-6, che vengono impiegati per i controlli di grandi strutture (dighe) o per rilevamenti topografici di grande precisione. 3) Per quanto riguarda le cause di errore nella misura con i distanziometri, accenniamo di sfuggita al fatto che, solo per quelli di precisione dell'ordine di 10-6 , possono avere una certa influenza le condizioni ambientali. Infatti la velocità di propagazione delle onde elettromagnetiche nell'aria dipende dalle condizioni atmosferiche (pressione, temperatura); e quindi su distanze lunghe e con strumenti di elevata precisione intrinseca, si deve tener conto di questo per evitare errori che possano portare ad una precisione di 10-5 nella misura della distanza (anziché di 10-6 come la precisione intrinseca dello strumento permette). 10.5 Strumenti che misurano angoli e distanze. Da quanto esposto nei paragrafi precedenti risulta che un distanziometro elettronico è essenzialmente un misuratore di distanze. Tuttavia, poiché, come vedremo, le operazioni topografiche principali si basano sulla misura di angoli e distanze, si è trovato opportuno realizzare degli strumenti che fossero allo stesso tempo misuratori di angoli e di distanze. Questi strumenti vengono realizzati seguendo due principi: Capitolo II - Strumenti topografici pagina 84 R.Galetto A.Spalla - Lezioni di Topografia • • il primo è quello di realizzare dei distanziometri che siano accoppiabili a teodoliti; e cioè una Casa che costruisce strumenti topografici e che ha già in produzione i teodoliti, studia e realizza un distanziometro in modo che si possa unire al teodolite; il secondo è quello di costruire ex-novo degli strumenti integrati nei quali il teodolite ed il distanziometro sono inscindibili e per così dire si fondono in un unico strumento (total station). La prima soluzione è generalmente adottata per i distanziometri topografici. La seconda fu adottata inizialmente solo per gli strumenti più precisi e di portata maggiore; ora però viene utilizzata sempre più frequentemente anche per la costruzione di strumenti ordinari. Quando si usa un distanziometro unito ad un teodolite, il segnale di collimazione deve essere costituito da due parti; ossia dal prisma che riflette il raggio inviato dal distanziometro e da un segnale (mira) collimabile esattamente mediante il reticolo per la misura degli angoli. vB vA B d* ζ A d0 Notiamo che con un distanziometro unito ad un teodolite possiamo misurare la distanza reale d* e l'angolo zenitale ζ, e possiamo ricavare quindi immediatamente la distanza d0 , cioè la proiezione di d* sul piano orizzontale passante per il punto di stazione del distanziometro: d0 = d*.senζ Gli strumenti total station sono particolarmente agevoli da utilizzare perché evitano i lavori di lettura e di trascrizione dei risultati delle misure, che sono spesso fonte di errori grossolani. Infatti i risultati delle misure vengono memorizzati direttamente sulle memorie di massa presenti negli strumenti stessi, in forma poi elaborabile da software dedicati, residenti su comuni personal computer. In questi strumenti anche le misure degli angoli, oltre che le misure delle distanze, vengono eseguite automaticamente. I cerchi orizzontale e verticale hanno qui graduazioni codificate; opportune le elettroniche di conteggio sanno interpretare le codifiche, così da eseguire automaticamente le misure. La funzione che, negli strumenti classici, svolgevano gli indici è svolta da sensori che scandiscono i cerchi codificati. I problemi connessi con le srettifiche strumentali degli strumenti classici sono attuali anche in questi strumenti. Ad esempio all’errore, che l’eccentricità dell’alidada induce nella misura degli angoli azimutali, si ovvia sempre con la lettura simultanea ai lembi opposti del cerchio, solo che, in questi strumenti, la lettura viene eseguita anziché dall’operatore che legge ai due indici sul cerchio graduato, dal firmware di conteggio dello strumento, sulla base degli input che gli provengono Capitolo II - Strumenti topografici pagina 85 R.Galetto A.Spalla - Lezioni di Topografia da due sensori posti alle parti opposte del cerchio codificato. La presenza dei due sensori sarà anche in questo caso garanzia delle migliori prestazioni dello strumento, così come la presenza dei due indici lo era negli strumenti tradizionali. Capitolo II - Strumenti topografici pagina 86 R.Galetto A.Spalla - Lezioni di Topografia 11 Misura indiretta di distanze mediante tacheometro. 11.1 Il metodo Con il tacheometro possono essere realizzate, oltre che operazioni di misura diretta di angoli, anche misure indirette di distanze. Ciò è reso possibile dalla presenza sul reticolo di collimazione di due tratti detti distanziometrici. h Consideriamo la figura: L1 F h f H d' L2 Sebbene il primo fuoco del sistema obiettivo sia, come sappiamo, interno allo strumento e coincidente con l'intersezione degli assi strumentali, lo consideriamo per semplicità di descrizione esterno. Consideriamo quel particolare raggio che nello spazio immagine passa per uno dei tratti distanziometrici, interseca parallelamente all'asse di collimazione il sistema obiettivo e, passando per il primo fuoco interseca nello spazio oggetto la stadia in L1 . Il raggio passante per l'altro tratto distanziometrico intersecherà la stadia in L2 . Se indichiamo con H la lunghezza del tratto L1-L2 , con f la focale del sistema obiettivo, con d' la distanza della stadia dal primo fuoco, con h la distanza fra i tratti distanziometrici, per la similitudine dei triangoli, potremo scrivere: f d' = h H Se è possibile quindi realizzare tra due punti una linea di collimazione e disporre la stadia verticale, possiamo determinare la distanza d' tra i due punti come: f d' = H h f C= si definisce costante distanziometrica e viene generalmente assunta uguale a 100 (il h che implica, ad esempio, che se un obiettivo ha una focale di 30 cm i tratti distanziometrici siano a 3 mm). Per estendere la schematizzazione semplificativa della figura precedente al caso più generale, dovremo tener presente che: Capitolo II - Strumenti topografici pagina 87 R.Galetto A.Spalla - Lezioni di Topografia • la focale di un cannocchiale a lunghezza costante è data da: f1 f 2 f = f1 + f 2 − D • che non è richiesta la distanza della stadia dal 1° fuoco, ma dal centro dello strumento; • che non è generalmente possibile realizzare una linea di collimazione orizzontale. Il fatto che f non sia rigorosamente costante implica che la relazione d' = C .H sia valida solo per quella distanza d per cui C = 100; quando vengono collimati punti a distanze diverse da d’ si generano quindi degli errori. Essi sono però trascurabili perché essendo dell'ordine dei 2÷3 cm su battute di 100 m, sono inferiori, come vedremo, all'errore del procedimento stesso. Per quanto riguarda il secondo punto, ricordiamo che nei cannocchiali a lunghezza costante il 1° fuoco è portato, per costruzione, a coincidere con il centro strumentale per cui la distanza calcolata è già la distanza richiesta. Se la visuale non è orizzontale occorre modificare la formula d = C .H in modo d'avere la proiezione sull'orizzontale della distanza misurata; ciò si ottiene moltiplicando il prodotto C . H per cos2α, essendo α il complemento dell'angolo zenitale. α d* α L1 L1 - L2 = H ← H* ∼ H cos α L2 d° Il motivo, per il quale si moltiplica per cos2α, è il seguente: • • si moltiplica una prima volta per cosα per ottenere il valore H* (in prima approssimazione); la relazione d = C .H precedentemente vista vale infatti quando la stadia è ortogonale all'asse di collimazione; questo primo prodotto C . H . cosα ci dà la distanza d*, per ridurre d* a d occorre moltiplicarlo un'altra volta per cosα. In definitiva si ha quindi: d = C . H . cos2α Questo metodo di misura consente di misurare distanze comprese tra 2÷100 m con un e.q.m. variabile tra ±15 cm. Capitolo II - Strumenti topografici pagina 88 R.Galetto A.Spalla - Lezioni di Topografia 11.2 Analisi della precisione del metodo. Volendo determinare a priori il grado di approssimazione che si consegue, occorrerà applicare la relazione (19) del capitolo I*) alla relazione: d = C . H . cos2α si avrà cioè: ∂ d 2 ∂ d 2 md = ± m + m ∂ H H ∂ a α 2 2 poiché d è in funzione di H e α, non di C, che è una costante strumentale e non una quantità misurata. Le derivate parziali valgono: ∂d = C cos2 α ∂H ∂d = −2CH sen α cos α = −2 d ⋅ tgα ∂α La seconda derivata si ottiene nella forma 2 d . tgα, moltiplicando e dividendo per cosα l'espressione 2 C . H . senα.cosα e ricordando che d = C . H . cos2α. Per valutare numericamente md , dobbiamo attribuire ad α e a d dei valori; possiamo però già notare che il coefficiente di mH è max per α= 0, mentre il coefficiente di mα è nullo per α= 0 ed è tanto maggiore quanto più grande è l'angolo α. Per un'esauriente analisi della precisione di d in funzione dell'e.q.m. di misura di H e di α valutiamo prima separatamente quale dei due errori è maggiore. Dobbiamo innanzitutto conoscere mH e mα ; poiché H viene letto su una stadia graduata in centimetri, nella migliore delle ipotesi il suo e.q.m. è ± 1 mm (cioè nell'ipotesi che chi fa la misura abbia l'accortezza di far coincidere un tratto distanziometrico con il bordo di uno scacco della stadia, e poi abbia l'abilità di stimare con l'approssimazione del millimetro la porzione di scacco sul quale cade il secondo tratto distanziometrico). Infine, poiché si usa un tacheometro, si avrà mα = + 30". ∂d Per valutare numericamente l'espressione mα occorre però inserire mα in radianti; ∂α ricordando che: 1 1" = 200.000 *) Z=f(X1 , X2 , ... Xn) 2 2 2 ∂Z ∂Z ∂Z 2 2 m m m 2 m =± + + ....+ z ∂ X X ∂X X ∂X X n 2 n 1 2 n Capitolo II - Strumenti topografici pagina 89 R.Galetto A.Spalla - Lezioni di Topografia si ha mα =±30" 1 =± 15 . 10-5 200.000 Valutiamo allora dapprima separatamente i due termini: ∂d ∂d mH mα ∂H ∂α Si avrà per il primo termine ∂d m H = C cos 2 αm H ∂H e, ponendo α= 0 per massimizzarlo, si ha ∂d m H = 100 ⋅ 1 ⋅ (±1mm ) ∂H Per il secondo termine si avrà: ∂d mα = −2d ⋅ tgα ⋅ mα ∂α ponendo per massimizzarlo d = 100 m e α= 45° , cioè tg α= 1, si avrà: ∂d mα = 2 ⋅ (100m) ⋅ 1 ⋅ ±15 ⋅ 10− 5 = ±30mm ∂α Si vede che l'errore in H è più nocivo di quello in α ( ) Volendo ora valutare globalmente md in funzione dei valori massimi trattati, dobbiamo applicare la formula rigorosa e combinare i quadrati dei valori trovati: mα = ± ( ±100mm) 2 + ( ±30mm) = ±104mm = ±10cm 2 Naturalmente questo è l'e.q.m. con il quale si misura d nel 68% dei casi; per un certo numero di misure (il 27%) si potrà avere anche un errore doppio; e, come sappiamo, solo nel 5% delle misure un errore triplo. Capitolo II - Strumenti topografici pagina 90 R.Galetto A.Spalla - Lezioni di Topografia CAPITOLO III IL SISTEMA CARTOGRAFICO NAZIONALE 1 Il problema cartografico. 1.1 Impostazione generale Il problema cartografico consiste nel dare una rappresentazione in un unico sistema di riferimento, di tutta la superficie del territorio nazionale. Esso è stato risolto dividendolo in due parti e cioè dando una rappresentazione del territorio suddivisa in planimetria e altimetria. Per la rappresentazione planimetrica, la soluzione è stata quella di mettere in relazione i punti della superficie fisica della Terra con i punti di un sistema cartesiano piano, detto proiezione cartografica di Gauss-Boaga; il passaggio tra superficie fisica della Terra e proiezione cartografica Gauss-Boaga non è diretto, ma, come vedremo si avvale di una superficie matematica intermedia di passaggio che è l’ellissoide. L’impostazione della rappresentazione altimetrica è stata quella di attribuire ad ogni generico punto P della superficie fisica della Terra una quota, che è la sua distanza, lungo la verticale v passante per esso, da una superficie di riferimento detta geoide. 1.2 La Terra, il geoide, lo sferoide, l’ellissoide 1.2.1 La Terra La superficie esterna della Terra è di forma irregolare, non rappresentabile da una superficie matematica; inoltre la densità della massa all’interno di tale superficie non è omogenea. Per mettere in corrispondenza mediante relazioni analitiche i punti della superficie fisica della Terra con quelli di un sistema cartesiano piano i geodeti dovettero affrontare il problema di definire una superficie matematica della Terra, cioè di una superficie non coincidente con la superficie fisica, ma ad essa prossima ed esprimibile in termini matematici. Come sistema di riferimento rispetto al quale riferire le coordinate di questa superficie matematica fu scelta una terna cartesiana ortogonale (X,Y,Z) definita come segue: • origine della terna nel baricentro della massa terrestre, • asse Z coincidente con l’asse di rotazione terrestre, • asse X giacente nel piano contenente l’asse di rotazione e un punto arbitrario della superficie terrestre (Greenwich). Il sistema di riferimento così definito prende il nome di sistema geocentrico. Capitolo III - Realizzazione del Sistema Cartografico Nazionale pagina 90 R.Galetto A.Spalla - Lezioni di Topografia Dato un punto P sulla superficie fisica della Terra, si definisce piano del meridiano terrestre passante per P il piano contenente l’asse di rotazione terrestre ed il punto P. Z superficie fisica della terra v P GREENWICH ϕ ZP XP YP Y X π G λ πP sistema geocentrico latitudine e longitudine terrestri figura 1 Ogni punto P della superficie terrestre è individuabile in doppio modo e cioè: • in funzione delle sue coordinate X,Y,Z nel sistema geocentrico, • in funzione di una coppia di coordinate geografiche terrestri che sono la latitudine terrestre e la longitudine terrestre. La latitudine terrestre è l’angolo che la verticale passante per il punto P forma con un generico piano ortogonale all’asse di rotazione terrestre, in particolare col piano equatoriale; la longitudine terrestre è l’angolo che il piano π P contenente il punto P e l’asse di rotazione terrestre forma con un piano di riferimento della longitudine π G, che è quello definito dall’asse di rotazione terrestre e dal piano contenente l’asse X, ovverosia il piano meridiano passante per Greenwich. 1.2.2 Il geoide I geodeti definirono l’espressione matematica della Terra prendendo come dato di partenza il suo campo gravitazionale. In ogni punto della Terra esiste la forza di gravità, che è la risultante della forza di attrazione Newtoniana e della forza centrifuga. Stante la non omogeneità della densità della massa terrestre e l’irregolarità della sua forma, le linee di forza del campo della gravità sono linee gobbe; esse prendono il nome di linee verticali. La tangente in un punto P a una linea verticale prende il nome di verticale. Capitolo III - Realizzazione del Sistema Cartografico Nazionale pagina 91 R.Galetto A.Spalla - Lezioni di Topografia I geodeti assunsero come superficie matematica della Terra una superficie che è sempre perpendicolare alle linee di forza del campo gravitazionale; poiché di queste ne esistono infinite, la resero univoca imponendo che fosse quella passante per un determinato punto fisico della Terra, costituito dal livello medio del mare in un ben preciso punto del porto di Genova. Questa superficie si chiama geoide. Con grossolana approssimazione possiamo dire che il geoide è la superficie che si otterrebbe prolungando al di sotto delle terre emerse la superficie del mare in quiete passante per il punto di riferimento di cui sopra. P ν mare q P geoide P' figura 2 Il geoide è quindi una superficie che ha un riscontro nella realtà fisica; inoltre è possibile determinare le quote dei punti della superficie fisica della Terra partendo appunto dal livello del mare (vedremo come); per questi motivi il geoide fu assunto come superficie di riferimento per l’altimetria. Questa superficie, che presenta questi vantaggi ed è suscettibile di una definizione molto rigorosa in termini fisica, ha però lo svantaggio di non essere rappresentabile da un’equazione matematica operativa. L'equazione del geoide si ottiene infatti come integrale del vettore forza di gravità esteso a tutta la massa terrestre. Per risolvere tale integrale occorrerebbe però conoscere con esattezza la densità della massa della Terra in ogni suo punto. Poiché tale dato è noto solo con una certa approssimazione, l’integrale del vettore forza di gravità non può essere calcolato e quindi in definitiva l'equazione del geoide non è operativa. Il geoide non può quindi essere preso come superficie di passaggio tra la superficie fisica della Terra e il piano della proiezione cartografica, poiché, anche se fossimo in grado di mettere in corrispondenza i punti della superficie fisica della Terra con quelli del geoide, non saremmo poi in grado di mettere in corrispondenza i punti del geoide con quelli di un sistema cartesiano piano. Per chiarire come si è proceduto per arrivare alla soluzione del problema, procediamo ora con una esemplificazione molto elementare di alcuni concetti che sarebbe difficile trattare in modo matematico rigoroso. Stante la definizione data, il geoide è una superficie che, sezionata con piani contenenti l’asse di rotazione, genera linee chiuse di andamento irregolare, non riconducibili a entità geometriche semplici come cerchi o ellissi, e tutte diverse tra loro (v. fig. 3); lo stesso accade per le linee Capitolo III - Realizzazione del Sistema Cartografico Nazionale pagina 92 R.Galetto A.Spalla - Lezioni di Topografia che si ottengono con sezioni ortogonali all’asse di rotazione. Nella figura queste irregolarità sono state esagerate all’ennesima potenza per tradurre questo concetto. Z Z b a Y X Geoide Y X Sferoide figura 3 1.2.3 Lo sferoide Per cominciare a semplificare il problema, i geodeti supposero, ipotesi poi confermata in tempi recenti dalla geodesia spaziale, che la massa interna della Terra fosse distribuita mediamente in modo simmetrico rispetto all’asse di rotazione Z; questa semplificazione portò alla trasformazione del geoide in uno sferoide, cioè in un solido di rotazione (vedi figura 3). Per lo sferoide succede questo: se lo sezioniamo con un qualsiasi piano contenente l’asse di rotazione otteniamo ancora una linea chiusa irregolare, che però resta la stessa per qualsiasi piano del fascio che ha per sostegno l’asse Z; di conseguenza se lo sezioniamo con piani ortogonali all’asse Z otteniamo dei cerchi. Nello sferoide possiamo quindi definire un raggio a del cerchio che giace nel piano equatoriale, e un valore b della distanza tra il piano equatoriale e i poli. 1.2.4 L’ellissoide Anche lo sferoide non aveva però un’equazione operativa. I geodeti introdussero quindi un’ultima semplificazione, assumendo, come superficie di passaggio tra la superficie fisica della Terra e la sua rappresentazione cartografica, l’ellissoide che è la superficie generata dalla rotazione di un’ellisse di semiassi a e b uguali a quelli dello sferoide, intorno all’asse Z. Capitolo III - Realizzazione del Sistema Cartografico Nazionale pagina 93 R.Galetto A.Spalla - Lezioni di Topografia Z b meridiano per P P a Y X piano meridiano per P figura 4 Dato un punto P sulla superficie dell’ellissoide, si definisce piano meridiano di P il piano contenente l’asse di rotazione Z ed il Punto P; si definisce meridiano di P l’intersezione di detto piano con la superficie dell’ellissoide. Vedremo tra poco che l'ellissoide ha un'espressione matematica semplice e quindi si presta bene alla soluzione del problema di mettere in corrispondenza i suoi punti con quelli di un sistema di coordinate cartesiane piane. Più complesso è il problema di mettere in corrispondenza i punti della superficie fisica della Terra con quelli dell’ellissoide; infatti, essendo l'ellissoide una superficie teorica, non è semplice stabilirne la posizione rispetto alla superficie fisica della Terra. Vedremo più avanti come il problema è stato risolto dai geodeti. Con riferimento al sistema geocentrico (X,Y,Z) precedentemente definito, l’equazione dell’ellissoide è la seguente: X 2 + Y 2 Z2 + 2 = 1 a2 b (1) dove: semiasse equatoriale dell'ellissoide semiasse polare dell'ellissoide a = 6378388 m b = 6356912 m a2 − b2 eccentricità dell’ellissoide e = =0.006722... a2 Si definisce inoltre schiacciamento s il rapporto tra la differenza di lunghezza dei due assi e la lunghezza dell’asse maggiore: a −b 1 s= = = 0.003367...... a 297 La determinazione dei valori a e b dello sferoide, che vengono poi assunti come semiassi dell’ellissoide, implica misure accuratissime astronomiche e di gravità, ed è stato un compito 2 Capitolo III - Realizzazione del Sistema Cartografico Nazionale pagina 94 R.Galetto A.Spalla - Lezioni di Topografia molto arduo affrontato più volte dai geodeti nel corso del tempo. A mano a mano che progredivano le tecniche di misura e di calcolo si perveniva a nuovi e più precisi valori. I valori di a e di b sopra riportati sono quelli determinati dal geodeta Hayford nel 1909; l’ellissoide con tali semiassi prende il nome di ellissoide internazionale. Tale ellissoide è stato assunto di riferimento di geodeti italiani per il calcolo delle coordinate geografiche ϕ e λ dei vertici trigonometrici. Vedremo che il sistema GPS (Global Positioning System), di cui parleremo più avanti, e che costituisce il più moderno metodo per l’esecuzione di misure geodetiche basato sull’uso di satelliti , utilizzerà invece dei nuovi parametri ellissoidici denominati WGS’84 (World Geodetic System 1984) che sono i seguenti: a = 6378137 m b = 6356752.314 m a2 − b2 e = = 0.000669..... a2 a−b 1 s= = = 0.00335281........ a 298.25722.... La posizione di un punto P sull'ellissoide può essere definita in doppio modo e cioè: • in funzione delle sue coordinate nel sistema geocentrico • in funzione di una coppia di coordinate ellissoidiche, che sono la latitudine ellissoidica ϕ e la longitudine ellissoidica λ. 2 Z n ZP P b λ=0 ϕ a YP Y XP X λ figura 5 La latitudine di un punto P è l'angolo che la normale n all'ellissoide in P forma con il piano equatoriale dell'ellissoide o con qualsiasi altro piano perpendicolare all'asse Z. Capitolo III - Realizzazione del Sistema Cartografico Nazionale pagina 95 R.Galetto A.Spalla - Lezioni di Topografia La longitudine è l'angolo, in senso antiorario, che il piano (XZ), piano meridiano di Greenwich, forma con il piano meridiano di P. La latitudine ϕ è un valore assoluto, mentre la longitudine λ è un valore relativo, perché dipende dalla scelta del piano meridiano di riferimento. Se cioè per definire il sistema geocentrico si scegliesse un punto diverso da Greenwich per definire il piano (XZ), cambierebbe il piano di riferimento della longitudine e quindi cambierebbe il valore della longitudine per ogni generico punto P. Abbiamo introdotto precedentemente al punto 1.2.1 la latitudine terrestre e la longitudine terrestre; d’ora in avanti quando vorremo fare riferimento ad esse useremo sempre l’aggettivo terrestre; mentre quando vorremo riferirci alla latitudine ellissoidica e alla longitudine ellissoidica ometteremo, in generale, l’aggettivo ellissoidica. 1.3 Quota ortometrica e quota ellissoidica Abbiamo precedentemente detto che la quota ortometrica (o semplicemente la quota) qP di un punto P della superficie fisica della Terra è la distanza di P dal geoide misurata lungo la verticale ν passante per esso (segmento PP’ in figura). Possiamo analogamente definire, per un generico punto P della superficie terrestre, una quota ellissoidica hP ( e in questo caso l’aggettivo ellissoidica è di rigore) che è la distanza del punto P dall’ellissoide misurata lungo la normale all’ellissoide passante per P (segmento PP’’ in figura). v n superficie fisica del terreno P geoide ellissoide hP qP P' P" PP' = q P PP" = q P quota ortometrica quota ellissoidica figura 6 Facciamo notare che i geodeti erano in grado di determinare la quota ortometrica di un punto, ma non la quota ellissoidica, e proprio per questo avevano scelto il geoide come riferimento delle quote. Vedremo in seguito come sia possibile ricavare le quote ortometriche in funzione di quelle ellissoidiche. Capitolo III - Realizzazione del Sistema Cartografico Nazionale pagina 96 R.Galetto A.Spalla - Lezioni di Topografia 1.4 Legame tra coordinate ellissoidiche geografiche e coordinate geocentriche Esistono delle relazioni che mettono in corrispondenza un punto di coordinate geografiche ϕ,λ e quota ellissoidica h, con le coordinate X,Y,Z che tale punto ha nel sistema cartesiano geocentrico (X,Y,Z) a cosϕ cos λ X = + h 2 2 1 − e sen ϕ a cos ϕ sen λ Y = + h 2 2 1 − e sen ϕ (2) ( ) Z = a 1 − e 2 sen2 ϕ + h sen ϕ E, viceversa, esistono le relazioni inverse che consentono di determinare le coordinate ϕ,λ e la quota ellissoidica h di un punto P avente coordinate ellissocentriche X,Y,Z. Stante la natura trascendente delle relazioni soprascritte non vi sono però relazione dirette che danno ϕ,λ ed h di un punto P in funzione delle sue coordinate X,Y,Z. Esse comunque possono essere ricavate mediante un procedimento iterativo. Come vedremo questo passaggio da X,Y,Z a ϕ,λ ed h sarà molto utile per la determinazione delle coordinate dei punti mediante il GPS. 1.5 Ellissoide geocentrico ed ellissoide nazionale Abbiamo già fatto cenno al fatto, e torneremo sull’argomento al punto 2 che segue, che l’ellissoide è la superficie di passaggio tra la superficie fisica della Terra e la sua proiezione cartografica. L’ellissoide che abbiamo sopra descritto, e che chiameremo geocentrico, ha, come si è visto, l’asse di rotazione che lo genera, coincidente con l’asse di rotazione terrestre e quindi coincidente con l’asse Z del sistema di coordinate cartesiane geocentriche, e il piano in cui giace il cerchio generato dalla rotazione del semiasse maggiore a coincidente col piano (X,Y) della terna geocentrica (piano equatoriale). Inoltre attribuendo all’ellissoide i semiassi a e b, si ottiene una specie di condizione di tangenza, ai poli e all’equatore, tra ellissoide e geoide. Quest’ultimo fatto minimizza lo scostamento tra ellissoide e geoide ai poli e all’equatore, ma lo rende invece massimo proprio alle latitudini europee, ed in particolare alla latitudine media italiana. Poiché nei tempi passati non era neppure immaginabile una visione globale mondiale del problema geodetico del tipo ora possibile in virtù del GPS, i geodeti delle varie nazioni, per minimizzare le deformazioni che si introducono nel proiettare la superficie fisica della Terra sull’ellissoide, decisero di adottare non l’ellissoide geocentrico, ma un ellissoide nazionale di Capitolo III - Realizzazione del Sistema Cartografico Nazionale pagina 97 R.Galetto A.Spalla - Lezioni di Topografia uguale dimensione e forma di quello geocentrico, ma leggermene ruotato e traslato rispetto al sistema geocentrico, in modo da realizzare la condizione di tangenza al geoide in un punto baricentrico del territorio nazionale. Per l’Italia, i geodeti italiani scelsero di realizzare questa coincidenza tra ellissoide nazionale e geoide in corrispondenza dell’Osservatorio di Monte Mario a Roma. Noi però nel seguito non parleremo di ellissoide nazionale, e, allo scopo di rendere più semplice la trattazione che seguirà e soprattutto per non complicare ancor più le figure, noi considereremo nel seguito che l’ellissoide utilizzato dai geodeti sia quello geocentrico. Questa ipotesi non ha infatti nessuna grave conseguenza concettuale da un punto di vista didattico e evita invece di complicare il discorso, soprattutto quando poi si parlerà del GPS. L’ipotesi che facciamo è resa lecita dal fatto che esistono relazioni che mettono in corrispondenza le coordinate geografiche di un ellissoide nazionale con quelle dell’ellissoide geocentrico e pertanto, da un punto di vista pratico, riferirsi alle une o alle altre è del tutto indifferente. Nel seguito non faremo più differenza tra i due ellissoidi, quello geocentrico e quello nazionale, e considereremo di aver sempre a che fare con quello geocentrico, che chiameremo quindi nel seguito solo ellissoide, omettendo l’aggettivo geocentrico. 1.6 La sfera locale Abbiamo visto che lo schiacciamento, ha per l’ellissoide terrestre, un valore molto contenuto (per questo, a volte, per descrivere la forma della Terra, si usa l’espressione semplificata di sfera leggermente schiacciata ai poli); da questo fato deriva che, per estensioni che rientrano in certi limiti, la forma della la superficie dell'ellissoide è uguale a quella di una sfera. E precisamente si può dimostrare che, preso un generico punto P dell’ellissoide di latitudine ϕ, la calotta ellissoidica di 100 km di raggio nell'intorno di P, che prende il nome di campo geodetico, coincide, come forma, a meno di quantità trascurabili, con quella di una sfera avente come raggio R il valore: R= a 1 − e2 1 − e 2 sen 2 ϕ (3) essendo appunto ϕ latitudine del punto considerato, a il valore del semiasse equatoriale ed e2 l’eccentricità. La sfera di raggio R si chiama sfera locale in P. L'aggettivo locale significa appunto che il suo raggio varia a seconda della latitudine del punto considerato. Anche la forma del geoide, nell’ambito del campo geodetico, può essere considerata coincidente con quella della sfera locale, a meno di anomalie locali, dovute a forti variazione di densità della massa terrestre. Quando si prendono in considerazione zona della superficie fisica della Terra che hanno un’estensione pari a quella di una calotta sferica di 100 km di diametro, si ha pertanto questa Capitolo III - Realizzazione del Sistema Cartografico Nazionale pagina 98 R.Galetto A.Spalla - Lezioni di Topografia notevolissima semplificazione: la forma delle superfici del geoide e dell’ellissoide possono essere ritenute coincidenti tra di loro ed entrambi coincidenti con quelle della sfera locale. Questa semplificazione fu particolarmente utile per i geodeti, che per eseguire i calcoli per la determinazione delle distanze tra i vertici trigonometrici, poterono usare formule di trigonometria sferica anziché ellissoidica. Per quanto riguarda gli argomenti che verranno trattati in queste dispense utilizzeremo più volte il concetto di sfera locale; in particolare nel problema della riduzione delle distanze misurate a distanze topografiche (punto 2.3 di questo capitolo), e nel problema della livellazione trigonometrica (punto 4.2 del capitolo V). In tale formule potrà essere inserito un valore approssimato del raggio della sfera locale; in funzione del valore della latitudine della zona in cui si opera si potrà cioè assumere il valore medio di R riportato nella tabella che segue: Raggio della sfera media locale alle latitudini italiane (in km) ϕ 36 37 38 39 40 41 42 43 44 45 46 47 R 6371.7 6372.4 6373.2 6373.9 6374.6 6375.4 6376.1 6376.9 6377.6 6378.4 6379.1 6379.9 1.7 Ricapitolazione sulla posizione del problema cartografico. In base a quanto esposto ai punti precedenti possiamo concludere con quanto segue. La Geodesia (che è una scienza che sta a monte della Topografia) stabilisce in che modo mettere in corrispondenza biunivoca i punti della superficie fisica della Terra con quelli dell'ellissoide. E cioè di come far corrispondere ad ogni punto P del terreno un punto P' sull'ellissoide, individuato attraverso due coordinate ellissoidiche, che sono la latitudine ϕ e la longitudine λ. Punto P sul terreno Ellissoide P P' (ϕ,λ) Punto P' sull'ellissoide figura 7 - Geodesia: da P a P’ La Cartografia stabilisce invece in che modo mettere in corrispondenza biunivoca un generico punto P’ della superficie ellissoidica, dato in termine di coordinate geografiche ϕ e λ, con un punto P’’ di coordinate N,E nel sistema della proiezione cartografica Gauss-Boaga. Capitolo III - Realizzazione del Sistema Cartografico Nazionale pagina 99 R.Galetto A.Spalla - Lezioni di Topografia Z P' N ϕ Y λ N = f (ϕ,λ) P" E = g (ϕ,λ) P" NP" P" X E P" E figura 8 - Cartografia: da P’ a P’’ In definitiva il problema della rappresentazione cartografica della superficie terrestre è stato risolto con un’impostazione rigorosa, che nel seguito chiameremo procedimento canonico, che prevederebbe che per ogni punto da riportare in cartografia si operasse nel seguente modo: a) Costruzione della planimetria Mediante operazioni di misura e di calcolo molto complesse, cioè di tipo geodetico, ad ogni punto P della superficie fisica della Terra, se ne fa corrispondere uno P' sull'ellissoide di coordinate geografiche ϕ e λ (rispettivamente latitudine e longitudine). Le coordinate ϕ e λ del punto P’ dell'ellissoide vengono trasformate, vedremo come, in una coppia di coordinate cartesiane piane N,E nel sistema cartografico Gauss-Boaga. b) Costruzione dell'altimetria A partire da un punto che materializza la superficie del geoide, costituita dalla superficie del mare in quiete in un punto ben preciso nel porto di Genova, si determina la sua quota ortometrica (o semplicemente quota), che è la sua distanza dal geoide misurata lungo la verticale. Sarebbe però impensabile, perché implicherebbe tempi interminabili e costi impossibili da affrontare, costruire una cartografia applicando questo procedimento ad ogni punto della superficie fisica del terreno che deve essere riportato in cartografia, come elemento della planimetria o dell’altimetria. In realtà il procedimento canonico è stato applicato dai geodeti solo per riportare, nella proiezione cartografica Gauss-Boaga, una serie di punti planimetrici (i vertici trigonometrici) e di punti altimetrici (caposaldi di livellazione) che inquadrano tutto il territorio nazionale. Vedremo come appoggiandosi ai vertici trigonometrici e ai caposaldi di livellazione i topografi e i fotogrammetri possono costruire le cartografie del territorio con procedure molto più semplici. Capitolo III - Realizzazione del Sistema Cartografico Nazionale pagina 100 R.Galetto A.Spalla - Lezioni di Topografia 2 Rete di inquadramento planimetrica. 2.1 Determinazione delle coordinate ellissoidiche dei vertici trigonometrici. 2.1.1 Premessa Come già abbiamo accennato in precedenza, l’inquadramento cartografico nazionale planimetrico è stato realizzato dai geodeti e dai cartografi costruendo una rete di punti, detti vertici trigonometrici, materializzati da punti fisici del territorio, e calcolandone la posizione prima sull’ellissoide e quindi nella proiezione cartografica di Gauss-Boaga. In questo paragrafo diamo pertanto un breve cenno, senza scendere nei particolari, su come furono determinate, con la geodesia classica, le coordinate ellissoidiche dei vertici trigonometrici; in quello seguente vedremo come di essi ne furono calcolate le coordinate nella proiezione cartografica nazionale. 2.1.2 Coordinate geografiche terrestri. Abbiamo visto in precedenza (vedi punto 1.2.1 di questo Capitolo) che per ogni generico punto P della superficie fisica della Terra è possibile determinare, mediante misure astronomiche, una coppia di coordinate geografiche terrestri che sono simili a quelle geografiche ellissoidiche. Esse sono dette latitudine terrestre e longitudine terrestre, proprio per indicare che si riferiscono a un punto fisico della superficie terrestre e che vengono misurate con riferimento alla verticale passante per il punto stesso. 2.1.3 Collegamento tra ellissoide e superficie fisica della Terra in un punto arbitrario. Per mettere in corrispondenza biunivoca i punti della superficie terrestre e quelli dell'ellissoide è stato necessario innanzitutto far corrispondere arbitrariamente un punto della superficie fisica della Terra a un punto dell’ellissoide; ciò è stato fatto nel seguente modo: • si è scelto come punto arbitrario della superficie terrestre un punto P* dell’Osservatorio di Monte Mario a Roma • di tale punto P* è stata misurata la latitudine geografica terrestre; • si è imposto che il corrispondente di P* sull’ellissoide fosse un punto P avente come valore di latitudine ellissoidica lo stesso valore di latitudine geografica terrestre di P* e avesse valore di longitudine λ=0. Questa operazione corrisponde al fatto, descritto al punto precedente, di aver sostituito all’ellissoide geocentrico un ellissoide nazionale. Con questa operazione si è stabilito un punto di partenza, o di origine, per calcolare le posizioni sull'ellissoide di tutti i vertici trigonometrici. Indicheremo nel seguito con ϕ0, e λ0 le coordinate ellissoidiche di questo punto P di partenza situato a Monte Mario a Roma, ricordando che λ0=0. Capitolo III - Realizzazione del Sistema Cartografico Nazionale pagina 101 R.Galetto A.Spalla - Lezioni di Topografia 2.1.4 Scelta dei vertici trigonometrici. La seconda operazione, come schema logico e non temporale, è stata quella di scegliere su tutto il territorio nazionale i punti fisici che avrebbero materializzato i vertici trigonometrici. I vertici trigonometrici si suddividono in quattro ordini di importanza. Quelli del primo ordine sono i più importanti e sono stati scelti in modo tale che congiungendoli con dei segmenti ideali si ottiene su tutto il territorio nazionale una rete di triangoli equilateri di circa 30 km di lato (vedi figura 9). figura 9 Triangolazione italiana del 1° ordine (per gentile concessione IGMI) Capitolo III - Realizzazione del Sistema Cartografico Nazionale pagina 102 R.Galetto A.Spalla - Lezioni di Topografia I vertici trigonometrici del primo ordine sono materializzati da punti fisici della superficie terrestre che offrono elevate garanzie di indistruttibilità (ad es. un punto della Madonnina del Duomo di Milano, campanili di chiese, ecc.). Dove non esistono punti che offrono questa garanzia, ad esempio in montagna, i vertici trigonometrici sono materializzati da appositi pilastrini di cemento armato, con plinto di fondazione. Oltre ai vertici trigonometrici del primo ordine vi sono quelli di secondo, terzo e quarto ordine. I vertici di secondo ordine formano dei triangoli all'interno di ciascun triangolo di vertici del primo ordine. Quelli di terzo ordine formano triangoli all'interno dei triangoli aventi per vertici i punti del secondo ordine. I vertici di quarto ordine infittiscono ulteriormente la rete così creata. La suddivisione sui vari ordini è stata fatta per diversi motivi; citiamo i più importanti: • la costruzione della rete di vertici trigonometrici è stata realizzata quando ancora non esistevano i calcolatori elettronici, e risultava quindi impossibile elaborare tutte le misure relative ai vertici dei quattro ordini nel loro insieme; • operando sui quattro ordini separatamente si è potuto differenziare la precisione delle misure da eseguire. Le misure geoidiche sono consistite principalmente in misura di angoli; cioè facendo stazione su ogni vertice trigonometrico venivano collimati tutti i vertici trigonometrici adiacenti (si pensi alla difficoltà di collimare punti a 30 km di distanza con errori di misura di pochi secondi!). Non esistendo ovviamente negli anni in cui fu costruita la rete (seconda metà dell’ottocento) i distanziometri elettronici, non si procedette alla misura di distanza tra i vertici trigonometrici, ma furono misurate solo otto basi, lunghe ognuna circa una decina di km, distribuite su tutto il territorio nazionale. I calcoli basati sulle misure angolari tra i vertici e su quelle delle basi, portarono alla determinazione di tutte le distanze tra i vertici trigonometrici e dell’azimut di ogni direzione collegante due qualsiasi vertici trigonometrici contigui. L’azimut di un arco ellissoidico s congiungente due punti P e Q è l’angolo, misurato in senso orario, che va dal meridiano passante per P, all’arco s. meridiano per P α Q s P figura 10 Indicheremo nel seguito un generico valore di distanza tra due vertici trigonometrici con s e con α il suo azimut. E' per l’esecuzione di questi calcoli che i geodeti si servirono del concetto di sfera locale; poiché infatti ogni singolo triangolo formato da tre vertici trigonometrici era compreso nel campo geodetico, per calcolarne i lati i geodeti poterono usare formule di trigonometria sferica, anziché ricorrere alla trigonometria ellissoidica. Capitolo III - Realizzazione del Sistema Cartografico Nazionale pagina 103 R.Galetto A.Spalla - Lezioni di Topografia 2.1.6 Calcoli eseguiti per la determinazione delle coordinate ellissoidiche. La terza operazione è stata quella di calcolare le coordinate ellissoidiche dei vertici trigonometrici. Per far questo sono state introdotte delle formule di trigonometria ellissoidica. Queste formule consentono di calcolare le coordinate ellissoidiche ϕk e λk di un punto k dell’ellissoide in funzione: • delle coordinate ϕi, λi, di un altro punto i • dell’arco s di ellissoide che congiunge i due punti • dell’azimut α della direzione che congiunge il vertice i al vertice k. Risulta chiaro ora perché al punto precedente si è detto che i calcoli eseguiti dai geodeti portarono alla determinazione di tutti gli archi s e degli azimut di tutte le direzioni. Le formule usate sono dette di trasporto delle coordinate, proprio a sottolineare il fatto che le coordinate ϕ e λ di un generico punto sono ricavate in funzione delle coordinate ϕ e λ di un altro in precedenza determinate e ad esso adiacente; per adiacente si intende che i due vertici siano collegati da un unico arco s. Indichiamo con F e G le due relazioni (che sono in realtà molto complesse), che forniscono rispettivamente i valori di ϕ e λ di un punto. Per un generico vertice trigonometrico i, immediatamente adiacente al vertice origine di Monte Mario, le coordinate ϕi e λi sono date dalle funzioni F e G in cui, come coordinate del punto precedentemente determinato, si inseriscono quelle ϕ0 e λ0 del vertice origine di Monte Mario: ϕi = F(ϕ0, λ0, a, b, α, s) λi = G(ϕ0, λ0, a, b, α, s) essendo a e b i semiassi dell’ellissoide, ed α ed s i valori dell’azimut e dell’arco che congiunge i due punti. Per un generico vertice k non adiacente al vertice origine si avrà: ϕk = F(ϕi, λi, a, b, α, s) λk = G(ϕi, λi, a, b, α, s) essendo ϕi e λi le coordinate precedentemente determinate di un vertice i adiacente a al vertice k, ed α ed s i valori dell’azimut e dell’arco che congiunge i due punti. 2.1.7 Suddivisione della porzione di ellissoide che riguarda l’Italia in due fusi La zona di ellissoide su cui erano sparsi i vertici trigonometrici del territorio italiano aveva un’ampiezza di circa 120 di longitudine; tenendo conto che, come meridiano origine di valore λ=0, era stato assunto quello passante per Monte Mario, le longitudini dei vertici trigonometrici, calcolati mediante le formule di cui al precedente punto, variavano approssimativamente tra λ=-60 e λ=+60. Capitolo III - Realizzazione del Sistema Cartografico Nazionale pagina 104 R.Galetto A.Spalla - Lezioni di Topografia Vedremo più avanti che, usando la proiezione di Gauss, la deformazione lineare di un arco s di ellissoide proiettato sul piano, è tanto più grande quanto maggiore è la sua distanza dal meridiano che è stato assunto come origine delle longitudini. Per contenere l’entità di tali deformazioni, i geodeti decisero allora di suddividere la zona di ellissoide in cui cadevano i vertici trigonometrici in due parti, in modo da non avere un unico meridiano origine e valori di longitudine varianti tra λ=-60 e λ=+60, ma due meridiani origine e valori di longitudine varianti tra λ=-30 e λ=+30. Le due parti di ellissoide in cui fu divisa la calotta ellissoidica che comprendeva tutti i vertici furono detti fusi; ciascun fuso risultò quindi avere 60 di ampiezza. Tenuto conto che il meridiano passante per Monte Mario era approssimativamente situato a una longitudine di λ=120 a Est di Greenwich, i meridiani centrali dei due fusi furono scelti come segue. Al fuso a Ovest di Monte Mario, detto fuso Ovest, fu dato come meridiano origine il meridiano situato a 9° Est di Greenwich; a tale meridiano fu dato il valore convenzionale di longitudine λ=0. Al fuso a Est di Monte Mario, detto fuso Est, fu dato come meridiano origine il meridiano situato a 15° Est di Greenwich; anche a tale meridiano fu dato il valore convenzionale di longitudine λ=0. Con questa impostazione le longitudini dei vertici trigonometrici variano, in entrambi i fusi, tra i valori di λ=-30 e λ=+30 rispetto al valore λ=0 dei rispettivi meridiani centrali. La trasformazione delle longitudini dei vertici trigonometrici dai valori calcolati con le precedenti formule nei nuovi valori, fu ottenuta semplicemente sommando alla longitudine dei vertici che cadevano a Ovest di Monte Mario il valore +30 e a quelli che cadevano a Est di Monte Mario il valore -30. Sia il meridiano centrale del fuso Ovest che quello del fuso Est verranno nel seguito indicati entrambi col nome di meridiano centrale. meridiano di Greenwich meridiano di Monte Mario ellissoide λ = 12° 27’ 09,40” Est di Greenwich meridiano centrale del fuso Est 15° EG meridiano centrale del fuso Ovest 9° EG figura 11 Capitolo III - Realizzazione del Sistema Cartografico Nazionale pagina 105 R.Galetto A.Spalla - Lezioni di Topografia figura 12 materializzazione di un vertice del 1° ordine della rete geodetica italiana figura 13 Scheda di identificazione di un vertice trigonometrico del IV ordine della rete geodetica italiana. Si noti che sono riportate le coordinate ellissoidiche (con la longitudine riferita a Monte Mario) e le coordinate della proiezione di Gauss-Boaga Capitolo III - Realizzazione del Sistema Cartografico Nazionale pagina 106 R.Galetto A.Spalla - Lezioni di Topografia 2.1.8 Punto della situazione. Con le operazioni descritte ai precedenti paragrafi si è conseguito il risultato di far corrispondere ai vertici trigonometrici, che appartengono alla superficie terrestre, che è una superficie irregolare e non matematicamente rappresentabile, dei punti appartenenti all'ellissoide, cioè a una superficie esprimibile matematicamente in forma semplice. E' necessario, a questo punto, per portare a termine il problema, che ricordiamo era quello di mettere in corrispondenza i punti dell'ellissoide con quelli di un sistema di coordinate cartesiane piane, stabilire delle formule di corrispondenza tra punti sull'ellissoide e punti su un sistema di coordinate cartesiane piane. La soluzione di questa ultima parte del problema viene descritta nel paragrafo che segue. Il paragrafo è intitolato La Carta di Gauss poiché, delle infinite formule che si possono adottare per mettere in corrispondenza i punti dell'ellissoide con quelli di un piano, sono state scelte delle relazioni introdotte dal matematico Gauss. La proiezione viene anche detta Gauss-Boaga poiché negli anni ’50 il Prof. Giovanni Boaga, fu il promotore di un nuovo calcolo delle coordinate dei vertici trigonometrici nella proiezione di Gauss. I nuovi valori calcolati sono quelli ora ufficiali per i vertici trigonometrici. Capitolo III - Realizzazione del Sistema Cartografico Nazionale pagina 107 R.Galetto A.Spalla - Lezioni di Topografia 2.2 La carta di Gauss. 2.2.1 Criteri sui quali è basata la carta di Gauss. Quando parliamo di Carta di Gauss intendiamo un sistema di coordinate cartesiane piane N ed E e due funzioni f e g che mettono in relazione un generico punto P dell'ellissoide, dato in coordinate ellissoidiche ϕ e λ, e il punto corrispondente P' del sistema cartesiano. meridiano origine ellissoide N P Q ϕ equatore E=g ( ϕ , λ ) P' λ N= f ( ϕ , λ ) E figura 14 Le formule di trasformazione f e g **) per passare dal sistema ellissoidico , ad un sistema piano N, E sono state ricavate da Gauss imponendo le seguenti condizioni: 1. il meridiano ellissoidico assunto come origine delle longitudini deve trasformarsi nell'asse delle ordinate N; 2. l'equatore ellissoidico deve trasformarsi nell'asse delle ascisse E; 3. un arco di lunghezza m sul meridiano origine deve trasformarsi in un segmento di uguale lunghezza sull'asse delle ordinate N; 4. l'angolo α formato da due direzioni uscenti da un punto sull'ellissoide deve mantenersi uguale a quello delle corrispondenti direzioni riportate nella carta; 5. il coefficiente di deformazione, pur variando da punto a punto, deve essere uguale in tutte le direzioni uscenti da un punto. **) Le formule di corrispondenza tra ellissoide e piano di rappresentazione, che per semplicità abbiamo chiamato f e g, sono le seguenti Nsenϕcosϕ Nsenϕcos3ϕ 2 2 Nord = B + sen λ + (5 + 9η2 + 4η4 ) sen 4 λ4 2 24 Nsenϕcos5ϕ + ( 61 + 58t 2 + t 4 + 270η2 + 330η2t 2 ) sen6 λ6 +.... 720 Ncos5ϕ 2 Est = coordinata convenzionale del fuso + Ncos ϕseλ + (1 + t 2 + η2 ) sen 3 λ3 + 6 Ncos5ϕ + (5 + 18t 2 + t 4 + 14η2 + 58η 2t 2 ) sen5 λ5 +.... 120 • • • • dove N è il valore della gran normale alla latitudine ϕ, B rappresenta la lunghezza dell’arco di meridiano centrale del fuso dall’equatore alla latitudine ϕ, rappresenta la differenza di longitudine tra il meridiano del punto considerato e il meridiano centrale del fuso espressa in radianti, t=tgϕ η= e2 cos ϕ , essendo e l’eccentricità dell’ellissoide. 1 − e2 Capitolo III - Realizzazione del Sistema Cartografico Nazionale pagina 108 R.Galetto A.Spalla - Lezioni di Topografia Da queste condizioni analitiche si hanno funzioni f e g che applicate alle coordinate , generano una proiezione analoga a quella che si otterrebbe proiettando i punti dell'ellissoide, dal centro dell'ellissoide, su un cilindro tangente all'ellissoide lungo il meridiano origine delle longitudini; cioè su un cilindro orizzontale avente per direttrici ellissi di semiassi a e b, uguali ai semiassi ellissoidici. Ricordiamo che proiettare i punti dell'ellissoide su un cilindro equivale a proiettarli su un piano, in quanto il cilindro è una superficie che può svolgere su un piano. N Q* P E R* S N Q* Q m' P b m R R* b __equatore O λ S s' 1 s1 s 2 s 3 s4 s 5 s'2 s'3 s'4 direttrice del cilindro s'5 E a meridiano di tangenza tra ellissoide e cilindro λ=0 figura 15 Dalla figura 15 si vede infatti che proiettando i punti dell'ellissoide dal centro O sul cilindro si ottiene che: 1. i punti giacenti sul meridiano origine rimangono coincidenti con la direttrice di tangenza, la quale, sviluppando il cilindro sul piano, si trasforma nell'asse delle ordinate N; 2. i punti dell'equatore vengono proiettati sulla generatrice tangente all'equatore, la quale sviluppando il cilindro sul piano, si trasforma nell'asse delle ascisse E; 3. un generico arco m di meridiano, giacente sul meridiano origine, mantiene la sua lunghezza sull'asse N delle ordinate; 4. un arco meridiano m su un meridiano di longitudine si deforma assumendo sul cilindro il valore m'; lo stesso avviene per qualsiasi generico arco di sezione normale congiungente due punti avente longitudine diversa da zero; 5. la deformazione della carta cresce con l'aumentare della longitudine, come si vede confrontando gli archi di equatore s1 ,s2..., s5 con le loro proiezioni sull'asse E, s’1,s’2, ...s’5. Capitolo III - Realizzazione del Sistema Cartografico Nazionale pagina 109 R.Galetto A.Spalla - Lezioni di Topografia Dalle funzioni di corrispondenza tra le coordinate ellissoidiche ϕ e λ, e quelle N, E del piano della Carta, si ricava l'espressione del coefficiente di deformazione µ della carta. Questo coefficiente è tale che dato un elemento infinitesimo dm di arco di sezione normale sull'ellissoide si ottiene la sua lunghezza dm' sulla carta dal prodotto: dm' = µ. dm Abbiamo parlato di elemento infinitesimo dm, poiché, come è stato detto, il coefficiente di deformazione µ varia con continuità da punto a punto in funzione delle coordinate ϕ e λ del punto considerato. E' però stata data anche un'espressione di µ da applicarsi a lunghezze finite. Inoltre, questa espressione di µ è funzione, come vedremo, non di coordinate ellissoidiche ma di coordinate N, E le quali vengono chiamate coordinate Gauss. Prima però di prendere in considerazione la formula di µ per elementi finiti dobbiamo fare alcune considerazioni. 2.2.2 Motivo per il quale sono stati introdotti i due fusi ellissoidici. Abbiamo detto precedentemente che le longitudini dei vertici trigonometrici sono state riferite a due meridiani origine in modo che ogni vertice trigonometrico abbia una longitudine che in valore assoluto, non superi i 3°. Diamo ora la spiegazione di questo fatto. Osserviamo ancora la figura 15 e prendiamo in considerazione gli archi di equatore s1, s2..., s5 ; notiamo che i segmenti sull'asse E corrispondenti a tali archi si deformano (in particolare aumentano) a mano a mano che ci si allontana dal meridiano origine. Questo avviene ovviamente non solo per gli archi di equatore, ma per qualsiasi arco s dell'ellissoide; e cioè la proiezione s' di un arco s situato vicino al meridiano origine è meno deformata di quella di un arco più lontano. Al fine dunque di limitare le deformazioni della carta, si è ritenuto opportuno proiettare i vertici trigonometrici su due cilindri tangenti: uno tangente al meridiano centrale del fuso Ovest, e uno tangente al meridiano centrale del fuso Est. Le proiezioni dei vertici trigonometrici dell'ellissoide sul piano hanno quindi luogo in due sistemi cartesiani; entrambi questi sistemi hanno, come asse delle ascisse E, l'equatore. L'asse N delle ordinate è invece il meridiano a 9° E.G. per il fuso Ovest e a 15° E.G. per il fuso Est. In entrambi i sistemi i punti situati sull'asse N dovrebbero avere coordinata E = 0; ciò deriva dal fatto che introducendo il valore λ= 0 nella funzione g si ottiene E = 0. Ugualmente introducendo valori negativi di λ si ottengono valori negativi di E. Per evitare di avere a che fare con coordinate E negative, si è sommato un valore costante alle coordinate E dei due fusi Alle coordinate del fuso Ovest è stato sommato il valore 1500 km. A quelle del fuso Est il valore 2520 km. In tal modo i meridiani origine hanno rispettivamente coordinate 1500 km e 2520 km. Capitolo III - Realizzazione del Sistema Cartografico Nazionale pagina 110 R.Galetto A.Spalla - Lezioni di Topografia 2.2.3 Introduzione del cilindro secante. Prendiamo nuovamente in considerazione nella figura 15 gli archi s1 ,s2..., s5 sull'equatore; abbiamo già detto che la deformazione dei corrispondenti tratti sull'asse E cresce allontanandosi dal meridiano origine. Per comodità di esposizione consideriamo la figura 2.2.3-1 dove il piano del disegno coincide con quello equatoriale. Vediamo che, le deformazioni sono sempre dello stesso segno, cioè sempre positive, ma grandi per archi lontani del meridiano origine e piccole per quelli vicini. Come concetto generale è meglio invece avere deformazioni positive e negative (anziché solo positive) e più contenute in valore assoluto. O centro dell'ellissoide equatore s s s 6 s s s 1 s' 1 4 5 3 2 s' 2 s' 3 s' 4 s' 5 s' 6 generatrice equatoriale del cilindro figura 16 - Sezione nel piano equatoriale della figura 15 Per conseguire questo scopo i due fusi sono stati proiettati anziché su due cilindri tangenti ai meridiani origine, su due cilindri secanti l'ellissoide. Cioè su due cilindri aventi come direttrici un'ellisse di semiassi a’ e b' minori di quelli dell'ellissoide. Ciò si è ottenuto molto semplicemente. Infatti nelle formule f e g che trasformano le coordinate ϕ e λ, in coordinate N , E, compaiono i valori dei semiassi a e b dell'ellissoide. Per ottenere la proiezione sui cilindri secanti è stato sufficiente introdurre nelle espressioni f e g i valori ridotti a' e b' al posto dei valori a e b. I semiassi a' e b' sono stati ridotti dello 0,4 °/°° (0,4 per mille) rispetto ai semiassi ellissoidici; essi valgono cioè: a' = a . 0,9996 b' = b . 0,9996 meridiano origine, l'asse N è la sua trasformata nel sistema Gauss-Boaga sistema ellissocentrico m' l" m" b' a' l' figura 17 m’, m” sono i meridiani limite del fuso l’,l” sono i luoghi di deformazione nulla Capitolo III - Realizzazione del Sistema Cartografico Nazionale pagina 111 R.Galetto A.Spalla - Lezioni di Topografia Pertanto con questa variazione non è più verificata la prima condizione imposta per ottenere le funzioni f e g, e cioè che gli archi di meridiani origine vengono riprodotti in vera grandezza sugli assi delle ordinate; o, che è lo stesso, che per gli archi giacenti sul meridiano origine la deformazione è nulla. Succede invece che, per ogni fuso, la deformazione è nulla lungo due linee di intersezione del cilindro con l'ellissoide; gli archi di ellissoide giacenti sulla parte dell'ellissoide compresa tra queste due linee, e quindi esterna al cilindro, risultano contratti nella loro posizione sul cilindro (deformazione negativa); mentre gli archi di ellissoide compresi tra le due linee di intersezione e i margini del fuso risultano dilatati nella loro proiezione sul cilindro (deformazione positiva). Per chiarire, riprendiamo in esame quanto accade sul piano equatoriale con l'adozione dei cilindri secanti; come si vede nella figura 18, la generatrice del cilindro, la quale giace sul piano equatoriale, non è più tangente all'equatore, ma lo interseca in due punti; gli archi di equatore s1 ,s2, s3 risultano contratti nella loro proiezione sulla generatrice del cilindro; mentre l'arco s4 risulta dilatato (e così pure s5 e s6). centro dell'ellissoide equatore cilindro secante asse del cilindro centro dell'ellissoide - - - + + + - - asse del cilindro + cilindro secante figura 18 - contrazione per µ < 1 + dilatazione per µ > 1 Riprendiamo ora il discorso sul modulo di deformazione per elementi finiti, ricordando che d'ora in avanti considereremo sempre la proiezione di Gauss sui cilindri secanti. 2.2.4 Modulo di deformazione per elementi finiti. Abbiamo detto che le funzioni di trasformazione f e g sono tali per cui il coefficiente di deformazione µ varia da punto a punto; ciò del resto è chiaro se si considera l'equivalente geometrico della proiezione dell'ellissoide sul cilindro. E cioè (considerando ancora per semplicità di illustrazione quanto avviene sul piano equatoriale) dividendo in elementi infinitesimi ds ogni arco s precedentemente preso in considerazione, si vede che, nelle proiezioni sul cilindro, la deformazione è diversa per ogni elemento infinitesimo. Tuttavia, proprio per il particolare tipo di proiezione prescelta, il Capitolo III - Realizzazione del Sistema Cartografico Nazionale pagina 112 R.Galetto A.Spalla - Lezioni di Topografia coefficiente di deformazione µ varia molto lentamente, con l'aumentare della longitudine, cosicché è possibile dare un coefficiente di deformazione medio per elementi finiti. La formula di questo coefficiente di deformazione è data in funzione delle coordinate N, E dei vertici trigonometrici. Questo significa che, quando il topografo si trova ad operare in una data zona, in funzione delle coordinate di due vertici trigonometrici esistenti in quella zona (o nelle sue vicinanze) può calcolare un coefficiente di deformazione medio da applicare alle distanze misurate (o calcolate) per inserire tali valori direttamente sulla carta (chiariremo meglio con un esempio nel prossimo paragrafo questo concetto). centro dell'ellissoide equatore proiezioni ds'i L" archetti infinitesimi ds i generatrice equatoriale del cilindro secante L° s1 figura 19 La formula del coefficiente di deformazione medio in una zona della carta è data in funzione delle coordinate di due vertici trigonometrici in essa compresi o ad essi vicini ed è la seguente: µ = 0.9996 ⋅ 1 + F ⋅ E *2m ( ) dove, se N1 , E1 e N2 , E2 sono le coordinate dei vertici trigonometrici, si calcola: a) E1* = E1 - coord. convenzionale E del meridiano origine E2* = E2 - idem E* = 1/2.( E1* + E2* ) . 10-6 (E* è cioè la coordinata media dei due punti riferita al meridiano centrale) b) N* = 1/2.( N1* + N2* ) c) per F si prende il valore corrispondente all'N più vicino a N*, nella tabella riportata nel seguito. Notiamo alcune cose: • • nella formula compaiono le coordinate E* dei vertici cioè le coordinate depennate del valore convenzionale attribuito al meridiano centrale; solo così infatti si tiene conto della vera posizione dei punti rispetto al meridiano centrale; il fatto che il coefficiente F sia tabellato ogni 100 km indica che il coefficiente di deformazione varia poco per il variare della latitudine, mentre è più influenzato dalla posizione dei punti rispetto al meridiano origine, infatti il valore E* compare al quadrato; Capitolo III - Realizzazione del Sistema Cartografico Nazionale pagina 113 R.Galetto A.Spalla - Lezioni di Topografia se i due punti giacciono sul meridiano centrale, si ha E*=0 e quindi µ= 0,9996; cioè il coefficiente assume il valore minimo (e cioè massima contrazione delle distanze da riportare sulla carta); • • quando invece i punti giacciono in prossimità della linea di intersezione ellissoide-cilindro il valore F.E* si avvicina a 0,0004 e quindi µ tende a 1 (deformazione nulla); quando i punti sono all'esterno del fuso, F.E* si avvicina a 0,0008 e quindi µ tende al valore 1,0004 (e cioè massima dilatazione delle misure reali da rispettare nella carta). tabella per il calcolo di µ N(km) F 4.000 4.100 4.200 4.300 4.400 3.(1) 4.600 4.700 4.800 4.900 5.000 5.100 5.200 5.300 0,012325 0,012323 0,012320 0,012318 0,012315 0,012312 0,012310 0,012307 0,012305 0,012302 0,012299 0,012297 0,012294 0,012292 9° 15° N N E E 1500 km 2520 km figura 20 - I due fusi ellissoidici della proiezione di Gauss 2.2.5 La proprietà della conservazione degli angoli e le sue implicazioni pratiche Si indica con il nome di trasformata di un arco di ellissoide sulla carta di Gauss, la linea che si otterrebbe sulla carta applicando, a tutti gli infiniti punti dell'arco di ellissoide, le formule di trasformazione f e g . La trasformata di un arco di ellissoide è una linea curva e non è cioè il segmento che congiunge i due punti sulla carta. ellissoide N B' B A' A E figura 21 Quando abbiamo elencato, tra le condizioni poste per ricavare le formule f e g, la condizione che la carta di Gauss mantiene l’uguaglianza degli angoli, intendevamo quanto segue. Capitolo III - Realizzazione del Sistema Cartografico Nazionale pagina 114 R.Galetto A.Spalla - Lezioni di Topografia B N B α C α C A A E a) b) figura 22 Consideriamo tre punti sull'ellissoide (A, B, C in figura 22a ) e i corrispondenti tre punti nella carta di Gauss; la proprietà di conservazione degli angoli fa sì che: l’angolo α formato tra le tangenti agli archi ellissoidici AB, AC rimanga uguale all’angolo α formato tra le tangenti alle trasformate nella proiezione cartografica. Uno dei motivi che hanno portato alla scelta della proiezione di Gauss come proiezione cartografica nazionale, consiste proprio nel fatto che tale proiezione ha questa proprietà. Infatti fino a tempi molto recenti, i topografi misuravano prevalentemente angoli, ed era quindi utile usare una proiezione cartografica che avesse tra le sue proprietà quella di consentire di poterli inserire nella cartografia senza doverli modificare. Con riferimento alla figura 22 b dobbiamo però notare che questa proprietà vale tra l’angolo formato tra gli archi ellissoidici e le corrispondenti trasformate; ma il topografo non misura l’angolo formato tra gli archi ellissoidici, bensì l’angolo azimutale BAC tra i tre punti che, sul terreno, corrispondono agli estremi degli archi ellissoidici (vedi figura 23 a). Questa proprietà non avrebbe quindi alcun valore pratico se non si verificasse questo fatto molto importante: che l'angolo azimutale BAC misurato sul terreno facendo stazione in A e collimando due punti B e C, è uguale (entro i limiti di errore delle misure topografiche di precisione) all'angolo formato dalle tangenti agli archi di ellissoide che congiungono le proiezioni dei punti sull'ellissoide. vA B a) (BAC) C A B' A' α b) C' figura 23 Capitolo III - Realizzazione del Sistema Cartografico Nazionale pagina 115 R.Galetto A.Spalla - Lezioni di Topografia In conseguenza di ciò possiamo pertanto dire che la proprietà di conservazione degli angoli può considerarsi valida anche tra gli angoli azimutali tra due direzioni sul terreno e l’angolo formato dalle tangenti alle trasformate di tali direzioni nella carta di Gauss. 2.2.6 Trasformata, tangente e corda di un arco ellissoidico nella carta di Gauss Come è evidenziato dalla figura 24, un arco ellissoidico tra due punti A e B dà luogo, nella proiezione cartografica, a tre diverse entità: la sua trasformata, la tangente alla trasformata e la corda, ovvero la congiungente i due punti nella proiezione cartografica. N (AB) A ε B t E figura 24 Esiste una formula che permette di calcolare l'angolo ε tra la corda e la tangente di una trasformata. Questa formula serve per ricavare l’angolo di direzione della tangente alla trasformata in funzione dell’angolo di direzione della corda, o viceversa. Ad esempio: se abbiamo due punti A e B di coordinate N,E note e vogliamo ricavare l’angolo di direzione della tangente alla trasformata che li unisce, dobbiamo calcolare l’angolo di direzione (AB) in funzione delle coordinate N,E dei due punti e l’angolo ε e quindi possiamo ricavare l’angolo di direzione della tangente alla trasformata come (AB)+ ε. 2.2.7 Inserimento rigoroso di un angolo azimutale nella carta di Gauss Tenendo conto della validità del principio di conservazione degli angoli anche per angoli azimutali tra due direzioni sul terreno e angoli tra le corrispondenti trasformate, affrontiamo il seguente problema: • siano note le coordinate N,E di due punti A e B • si sia misurato sul terreno l’angolo azimutale α tra la direzione AB e la direzione AC • si voglia calcolare l’angolo di direzione AC nella proiezione cartografica. Per ricavare l'angolo di direzione relativo al punto C si deve (vedi figura 25) • calcolare l'angolo di direzione (AC) in funzione delle coordinate N,E di A e di B; • calcolare le differenze ε’ ed ε” tra corde e tangenti alle trasformate • calcolare l'angolo di direzione (AC) come somma di (AB) + ε’ + α - ε” Capitolo III - Realizzazione del Sistema Cartografico Nazionale pagina 116 R.Galetto A.Spalla - Lezioni di Topografia N B (AB) ε' (AC) α C ε" A E trasformate corde tangenti alle trasformate figura 25 Il calcolo delle correzioni ε’ ed ε” è però abbastanza complicata e vanificherebbe, per il topografo, il vantaggio di non dover correggere gli angoli misurati per inserirli nei calcoli relativi alla costruzione della cartografia. Vediamo al punto che segue che in realtà per il topografo questa complicazione può essere evitata. 2.2.8 Inserimento semplificato di un angolo azimutale nella carta di Gauss Si può dimostrare che per archi di ellissoide lunghi sino a 5 km l'angolo formato tra la trasformata e la corda (cioè il segmento congiungente i punti sulla carta) è < 1", e quindi inferiore all’e.q.m. con cui vengono normalmente misurati gli angoli azimutali anche nelle operazioni topografiche più accurate. Pertanto ai fini delle operazioni topografiche in cui si misurano distanze lunghe sino a 5 km, possiamo considerare che le trasformate degli archi di ellissoide coincidano con le corde, cioè con le congiungenti dei punti sulla carta. Questo fa sì che il problema posto al punto precedente si risolva sommando direttamente all’angolo di direzione (AB) l'angolo azimutale misurato : (AC) = (AB) + α N B (AB) (AC) C α A E figura 26 Possiamo generalizzare il concetto esposto dicendo che: Capitolo III - Realizzazione del Sistema Cartografico Nazionale pagina 117 R.Galetto A.Spalla - Lezioni di Topografia • la trasformata di un arco ellissoidico che congiunge due punti A e B distanti sul terreno meno di 5 km coincide, a meno di quantità trascurabili, con il segmento (corda) che congiunge i due A e B nella proiezione di Gauss • se le distanze AB e AC tra i punti che definiscono sul terreno l’angolo azimutale ∧ α= BA C , sono entrambe inferiori a 5 km, l’angolo α può essere ritenuto uguale, a meno di quantità trascurabili, con la differenza (AC)-(AB) tra i due angoli di direzione individuati dai tre punti A* , B* , C* nella proiezione cartografica. Capitolo III - Realizzazione del Sistema Cartografico Nazionale pagina 118 R.Galetto A.Spalla - Lezioni di Topografia 2.3 Inserimento delle distanze misurate sul terreno nel sistema cartografico nazionale. 2.3.1 Definizione di distanza topografica. Da quanto detto precedentemente, e cioè che l'ellissoide è la superficie di riferimento per la planimetria, discende anche il fatto che tale superficie è usata per definire in modo rigoroso ed univoco la distanza tra due punti. E precisamente si chiama distanza topografica tra due punti A e B della superficie fisica della Terra, l'arco di ellissoide che congiunge le proiezioni A' e B' dei due punti sull'ellissoide. In pratica in Topografia quando si parla di distanza si intende sempre la distanza topografica e quindi l'aggettivo topografico viene omesso. Si aggiunge invece un aggettivo quando si indica una distanza che non è quella topografica; ad esempio distanza reale d* è la distanza in linea d'aria tra i due punti. Mentre la distanza ridotta all'orizzontale d0 è la distanza reale, moltiplicata per il seno dell'angolo zenitale tra i due punti. vA vB θ B d* A q d° qA A* A" A' B* d B' B geoide ellissoide figura 27 Si noti che la figura mette in evidenza una cosa molto importante, e cioè che la proiezione A' di A sull’ellissoide non è data dall'intersezione della verticale passante per A con l'ellissoide; sappiamo infatti che le coordinate ϕ, λ di A' vengono determinate con il procedimento canonico illustrato ai precedenti capitoli; e altrettanto dicasi per B e B'. Nel disegno si è volutamente esagerata la distanza tra A", intersezione della verticale per A con l'ellissoide, e A', posizione di A sull'ellissoide determinata per procedimento canonico, proprio per evidenziare questo fatto. Nella figura vi sono inoltre rappresentate le quote di A e B, che sono i segmenti di verticale tra i punti e il geoide. 2.3.2 Semplificazione del problema mediante l'introduzione della sfera locale e di uno schema geometrico di comodo Si è detto in uno dei precedenti paragrafi, che si può dimostrare che: per ogni punto P della superficie terrestre, per una calotta di 100 km centrata su di esso, detta campo geodetico, l’ellissoide ed il geoide coincidono, come forma, con quella della sfera locale. Capitolo III - Realizzazione del Sistema Cartografico Nazionale pagina 119 R.Galetto A.Spalla - Lezioni di Topografia Al solo scopo di poterci riferire ad uno schema geometrico che ci consenta di ricavare agevolmente alcune formule operative, potremo prendere in considerazione una situazione fittizia, ma lecita per lo scopo dichiarato, in cui, con riferimento alla figura 27, facciamo passare per il punto A* , non solo la sfera locale, ma anche l’ellissoide. Ipotizzando questa coincidenza, non solo come forma, ma anche come posizione, tra ellissoide e geoide (che, ripetiamo non è vera, ma non inficia il discorso per la quale la supponiamo) si avrà che (figura 28): • la distanza tra A e A* resta la quota qA del punto A • la distanza tra B e la sua proiezione B* sulla sfera locale sarà uguale alla quota qB di B • l'arco di circonferenza A* B* sarà uguale all’arco di sezione normale ellissoidico A'B', cioè alla distanza topografica • le verticali per A e B coincideranno con le normali alla sfera locale e si incontreranno quindi nel suo centro O. vB n vA n B d* ζ A q b d A' A* B' B* R figura 28 δ O Se da un punto A, di quota qA nota e di coordinate NA , EA note, vogliamo determinare la quota qB di un punto B e la sua distanza topografica da A, con riferimento a questo schema geometrico di comodo, possiamo procedere nel seguente modo: • misuriamo l'angolo zenitale ζ tra A e B (con un teodolite); • misuriamo la distanza reale d* tra A e B (con un distanziometro); • calcoliamo il valore del raggio R della sfera locale in A; • calcoliamo (vedremo come tra poco) la lunghezza dell'arco di cerchio ds , che potrà essere assunta rigorosamente uguale alla distanza topografica; • calcoliamo la lunghezza del segmento B-B*, che potrà essere assunto rigorosamente come quota qB del punto B, col metodo della livellazione trigonometrica ( punto 4.2 del capitolo V). Utilizzando questo schema geometrico di comodo, possiamo quindi ricavare agevolmente la distanza topografica tra A e B e la quota qB, ma non possiamo determinare la posizione B' sull'ellissoide in termini di coordinate ellissoidiche ϕ, λ. Questo però non è rilevante. Infatti, supponendo che A sia un punto di coordinate N,E note, in funzione della distanza Capitolo III - Realizzazione del Sistema Cartografico Nazionale pagina 120 R.Galetto A.Spalla - Lezioni di Topografia topografica A-B, il topografo sarà in grado, come vedremo, di determinare le coordinate N,E del punto B nella proiezione di Gauss, senza dover conoscere le coordinate ellissoidiche ϕ, λ di B. 2.3.3 Passaggio dalla distanza reale misurata alla distanza topografica. a) Formula rigorosa Con riferimento alla precedente figura 27 vediamo che il problema del passaggio dalla distanza reale misurata alla distanza topografica può essere posto in questo modo: • avendo misurato d* e ζ e nota la quota qA • determinare la distanza topografica d tra A e B. Una volta determinata d, vedremo come inserirla direttamente nella carta di Gauss. Il problema è di immediata soluzione; infatti, noti d* e ζ, applicando il teorema di Carnot al triangolo ABO si ricava: OB = d * 2 +( R A + q A ) − 2 ⋅ d * ⋅( R A + q A ) ⋅ cos(π − ζ ) 2 e quindi: OB d* = sen(π − ζ ) senδ da cui δ = arcsen d * ⋅ sen(π − ζ ) OB ed infine: d = RA ⋅δ essendo RA il raggio della sfera locale in A. Vi è però un grave inconveniente da un punto di vista operativo, e cioè: per ottenere una sufficiente precisione nel calcolo di d, il valore di RA non può essere un valore approssimato, quale è quello desumibile ad esempio dalla tabella riportata al punto 1.6, ma deve essere ricavato con la formula rigorosa, che implica la conoscenza della latitudine del punto e la conoscenza dei parametri ellissoidici (coi quali molti topografi non hanno dimestichezza); inoltre i calcoli devono essere obbligatoriamente fatti in doppia precisione (16 cifre significative) e non con normali calcolatrici portatili. È quindi opportuno dare una formula più operativa, valida per distanze inferiori a 5 km, che sono poi quelle che interessano il topografo. b) Il campo topografico Dimostriamo innanzitutto che, per distanze inferiori a 5 km, la distanza d può essere sostituita da d’. Capitolo III - Realizzazione del Sistema Cartografico Nazionale pagina 121 R.Galetto A.Spalla - Lezioni di Topografia B ζ d* δ A qA d' f ε d° R figura 29 δ O Si ha : d’ = R.tgδ e d = R.δ Sottraendo membro a membro si ha: d’ - d = R.( tgδ - δ ) Sostituendo a tgδ i primi due termini del suo sviluppo in serie di Taylor si ha: d’ - d = R.( δ + δ 3/3 - δ ) = R. δ 3/3 Ponendo d = 5 km e assumendo per R un valore medio di 6.300 km si ha δ = 5 e quindi 6300 δ3 ∼ 0.001 m 3 valore inferiore all’errore di misura che si commette nelle misure di tipo topografico, e quindi trascurabile. d’ - d = R Quando la distanza tra due punti A e B è inferiore a 5 km possiamo pertanto assumere come loro distanza topografica il valore d’ anziché d. Considerando un generico punto P su cui il topografo fa stazione, si chiama campo topografico la zona di terreno compresa in un cerchio di raggio pari a 5 km con centro in P; nel campo topografico le distanze topografiche coincidono, a meno di quantità trascurabili, con la loro proiezione sul piano tangente alla sfera locale in P. c) Formula semplificata Supponendo di operare nel campo topografico si avrà quindi (figura 29): d' = d °−ε = d * senζ − (q A + d * cosζ ) ⋅ tgδ Poiché, per d<5 km, δ è inferiore a 1/1000 di radiante, e poiché inoltre tgδ si trova in un termine correttivo che, sempre per d<5 km, non supera (come vedremo più avanti) qualche decimetro, possiamo sostituire nella relazione precedente δ a tgδ; si avrà quindi: Capitolo III - Realizzazione del Sistema Cartografico Nazionale pagina 122 R.Galetto A.Spalla - Lezioni di Topografia d' = d°− ε = d * sen ζ − ( q A + d * cosζ ) ⋅ δ Sempre in virtù del fatto che δ entra nella determinazione di un fattore correttivo di piccola entità possiamo calcolarlo in funzione di d0 e di un valore approssimato di R0A quale possiamo ricavare dalla già citata tabella riportata la punto 1.6: d° δ = 0 RA In definitiva si ha: d = d' = d * senζ − (q A + d * cos ζ ) ⋅ d * ⋅ senζ 0 RA Questa formula sembra a prima vista più complicata di quella rigorosa precedentemente trovata, ma in realtà è più semplice dal punto di vista operativo poiché non richiede di eseguire calcoli in doppia precisione e consente di usare un valore approssimato del raggio della sfera locale, quale quello ricavabile dalla tabella riportata al punto 1.6. d) Ordine di grandezza del fattore correttivo ε Abbiamo detto più volte che ε è un fattore correttivo di d0 di modesta entità; non ci si deve infatti far trarre in inganno dalla figura 29 in cui ε sembra avere un valore comparabile a d0; in realtà ε vale al massimo qualche decina di centimetri. Ad esempio: supponendo di effettuare una misura di distanza di 3 km da un punto di quota qA pari a 200 m, collimando un punto B a quota 500 m (situazione abbastanza eccezionale per misure topografiche eseguite dal topografo per scopi cartografici), il valore di ε risulta di 24 cm. Se invece supponiamo di operare in terreni pianeggianti, a quote medie intorno ai 100 m, anche per distanze fino a 5 km, ε resta sempre inferiore ai 10 cm. Infine, per distanze brevi dell’ordine dei 100 m, misurate con metodi tacheometrici, si può trascurare del tutto il termine correttivo ε e calcolare la distanza topografica con al formula: d = d° = d* . senζ 2.3.4 Introduzione diretta delle misure di angoli e distanze nella proiezione di Gauss. Siano dati due punti A e B di coordinate note; e un punto C di coordinate incognite. Supponiamo di aver misurato l'angolo azimutale θ= BAC, l'angolo zenitale ζ e la distanza reale d* tra A e C. Supponiamo che sia d*≤5 km e quindi che ci si trovi nel campo topografico. Capitolo III - Realizzazione del Sistema Cartografico Nazionale pagina 123 R.Galetto A.Spalla - Lezioni di Topografia θ N B B NB (AB) ζ C d* A NA A EA EB E figura 30 Situazione di partenza A e B sono punti di coordinate note nella proiezione di Gauss-Boaga. Ci proponiamo di calcolare le coordinate di C nella proiezione di Gauss-Boaga . Poiché l'angolo azimutale θ misurato sul terreno tra due direzioni si mantiene uguale (entro l'approssimazione dell'ordine di quella delle misure topografiche) a quello formato dalle direzioni congiungenti i punti sulla carta, possiamo subito determinare l'angolo di direzione incognito (AC). N B (AB) θ C (AC) A E Risulterà infatti: (AC) = (AB) + θ = arctg EB − EA +θ NB − NA Dobbiamo innanzitutto passare dalla distanza reale d* alla distanza d° ridotta all'orizzontale: d° = d* . senζ Da questa passiamo alla distanza d' (sul piano tangente) attraverso la relazione seguente, valida per il campo topografico. d° d' = d °−ε = d°− f ⋅ δ = d °−( q A + d * ⋅ cosζ ) ⋅ R Dobbiamo ora applicare a d' il coefficiente di deformazione della carta che compete alla zona in cui si trovano i vertici trigonometrici A e B . Capitolo III - Realizzazione del Sistema Cartografico Nazionale pagina 124 R.Galetto A.Spalla - Lezioni di Topografia Ricordiamo che la formula del modulo di deformazione è : ( µ = 0.9996 ⋅ 1 + F ⋅ E *2m ) dove E *m = E *A +E *B ⋅ 10 −6 2 E*A = EA -E° E*B = EB -E° essendo E A ed EB le coordinate Est di A e di B ed E° la coordinata convenzionale del meridiano centrale del fuso; ricordiamo che E° vale 1500 km per il fuso Est e 2520 km per il fuso Ovest. Il valore di F si determina invece, mediante la tabella riportata al paragrafo 2.2.4, in funzione N + NB del valore N* = A . 2 In pratica si entra nella tabella col valore N più prossimo a N* e si determina il valore di F da prendere in considerazione. Determinando F ed E* si calcola µ e quindi il valore dc della distanza d’ riportata nella carta di Gauss. dc = µ . d' A questo punto possiamo calcolare le coordinate del punto B nella carta di Gauss mediante le relazioni: NC = NA + dc cos (AC) EC = EA + dc sen (AC) Abbiamo conseguito questo importantissimo risultato: siamo passati dalle misure sul terreno d*, ζ, θ,direttamente alle coordinate carta di C, senza doverne determinare con misure e calcoli geodetici le coordinate ellissoidiche , e calcolare in funzione di queste le coordinate carta applicando le formule della carta di Gauss. Capitolo III - Realizzazione del Sistema Cartografico Nazionale pagina 125 R.Galetto A.Spalla - Lezioni di Topografia CAPITOLO IV CARTOGRAFIE PER LA PIANIFICAZIONE E LA PROGETTAZIONE TERRITORIALE 1 Esigenze di cartografie tecniche di base Negli ultimi anni si è assistito ad un notevole aumento di richiesta di cartografia tecnica e tematica da parte di Enti pubblici con competenze territoriali. Questo accresciuto interesse è dovuto al fatto che le carte tecniche e tematiche rappresentano un mezzo efficace per rappresentare, in forma sintetica, i dati di conoscenza territoriale necessari ai diversi enti per adempiere, ai diversi livelli, ai compiti istituzionali specifici. Per dare un'idea dell'importanza che ha il disporre di dati in forma sintetica per la pianificazione ai diversi livelli, consideriamo l’esempio della pianificazione urbanistica. Fino a non pochi anni fa la pianificazione urbanistica avveniva a livello quasi esclusivamente comunale. Chi esercitava scelte di governo del territorio aveva, nella maggior parte dei casi, conoscenza diretta degli argomenti su cui deliberava. Da quando la pianificazione urbanistica viene regolata a livello regionale, chi delibera non ha conoscenza, in prima persona, dei problemi su cui e chiamato a prendere decisioni, ma deve acquisire questa conoscenza esaminando dei dati. Ma i dati, solo in quanto tali, possono non servire, se non sono aggregati così da costituire delle informazioni. Perché le decisioni di governo possano essere prese in maniera corretta deve cioè svolgersi il processo: • acquisizione di dati, • sintesi dei dati in informazioni utili, • decisioni sulla base delle informazioni desunte. Al pianificatore che è chiamato a prendere decisioni nel campo dell'edilizia scolastica, ad esempio, non serve poter disporre di tutte le schede personali dei singoli studenti, ma potrà essere per lui di utilità conoscere quanti studenti frequentano le medie inferiori; quanti i licei, quanti gli istituti tecnici. Il pianificatore infatti non usa i dati così come vengono acquisiti, ma si avvale di sintesi di dati, di dati cioè aggregati in informazioni. I dati che sono necessari per una corretta pianificazione territoriale sono molteplici. Una delle convenzioni più usate porta a suddividere il territorio in quattro componenti: suolo, popolazione, infrastrutture e attività. Ciascuna delle quattro componenti può essere osservata in relazione ad un suo aspetto: ad esempio il suolo può essere visto sotto gli aspetti geologico, morfologico, pedologico, ecc.; la popolazione può essere riguardata dal punto di vista della composizione, del reddito, ecc.. La pianificazione e la gestione del territorio richiedono che tali aspetti vengano dapprima rilevati e quindi analizzati, singolarmente o in modo incrociato, per conoscere i fenomeni che si manifestano sul territorio e poterne così studiare le correlazioni e le interazioni. Capitolo IV - Descrizione del materiale cartografico esistente in Italia. pagina 126 R.Galetto A.Spalla - Lezioni di Topografia Il mezzo più diffuso per il riporto e per la successiva analisi di questi dati è costituito dalle carte tematiche; nelle carte tematiche i vari aspetti del territorio sono trascritti mediante simboli qualitativi e quantitativi su un fondo, o supporto, costituito da una carta topografica, più o meno semplificata. Le carte tematiche rappresentano un efficace mezzo di rappresentazione di dati territoriali, infatti: • esse forniscono una sintesi visiva dei dati relativi ai vari aspetti del territorio, • in esse, ad ogni fenomeno che è stato rilevato sul territorio viene data una precisa collocazione spaziale. Altre fonti di informazione territoriali, oltre alle cartografie tecniche, tematiche e catastali, sono costituite da archivi, quali gli archivi anagrafici, gli archivi catastali, gli archivi delle Camere di Commercio, ecc. Tutti i dati conoscitivi che si riferiscono ad uno stesso territorio ne costituiscono il patrimonio informativo. Quando alcuni o tutti i dati del patrimonio informativo di un territorio sono organizzati sistematicamente in modo tale da essere facilmente accessibili e consultabili dagli organi preposti alla gestione di quel territorio si parla di sistema informativo territoriale. Un sistema informativo territoriale può essere: • in forma cartacea, cioè organizzato come insieme di archivi tradizionali; • in forma numerica, e cioè organizzato come insieme di dati archiviati in forma numerica, su supporti elaborabili mediante calcolatore. E’ ormai invalso l'uso però , quando si parla di sistema informativo territoriale, SIT, di considerare un sistema informativo in cui i dati siano memorizzati su memorie di massa e siano gestibili mediante calcolatori elettronici. In definitiva un Sistema Informativo Territoriale è un insieme di dati e di procedure atte alla loro elaborazione, di cui un Ente, avente giurisdizione territoriale, si fornisce per ottenere quelle informazioni che gli sono necessarie per effettuare le scelte decisionali dalle quali dipende la corretta realizzazione dei compiti istituzionali che gli sono propri. E in particolare, mutuando la terminologia dal lessico anglosassone, • si parla di GIS (Geographical Information System) quando si considerano sistemi informativi a supporto di decisioni con grado di dettaglio regionale • si parla di LIS (Land Information System) quando si considerano sistemi informativi gestionali con elevato grado di dettaglio che gestiscono generalmente reti di distribuzione dei servizi (acqua, gas, ecc.) Perché un sistema informativo territoriale possa essere gestito in maniera ottimale da un suo servizio di elaborazione dati deve presentare alcune caratteristiche peculiari. I dati gestiti dai SIT devono essere organizzati in archivi (data base), e cioè : • tutti i dati devono essere memorizzati in forma numerica su supporti elaborabili mediante calcolatore elettronico • i dati devono essere organizzati in banche di dati, cioè in archivi tra loro correlati e correlabili. II SIT deve avere una strutturazione dinamica e la sua potenzialità non consisterà tanto nel disporre di grandi quantità di dati, ma nella possibilità di elaborare tali dati con tecniche più o meno sofisticate. Capitolo IV - Descrizione del materiale cartografico esistente in Italia. pagina 127 R.Galetto A.Spalla - Lezioni di Topografia Il SIT deve garantire una sufficiente flessibilità e cioè pur avendo una struttura dettata dalle finalità cui deve assolvere, non deve essere chiuso, ma deve essere tale da consentire un suo continuo sviluppo, sia per ampliamenti delle banche dati originarie, sia per l’inserimento di nuove banche dati. Il SIT deve offrire rapidità di risposta e cioè deve fornire gli elementi necessari alle scelte decisionali in modo che queste ultime non vengano condizionate dal tempo che intercorre tra la richiesta dell’informazione e la sua disponibilità effettiva. I risultati delle elaborazioni devono essere di facile interpretazione, devono essere presentati in forme diagrammatiche o mediante carte tematiche, in forme cioè che abbiano un forte potere di sintesi e siano al tempo stesso di lettura facile e immediata. I punti di accesso all'informazione devono essere il più possibile decentrati, in modo da consentire l’utilizzazione dei dati del sistema ad un'utenza numerosa, per ottimizzare il rapporto costo/beneficio del sistema. Poiché l'impianto e la gestione di sistemi informativi comportano sempre un considerevole impegno di risorse, è auspicabile che i SIT non nascano come iniziative isolate e a sé stanti, ma possano essere concepiti secondo quadri organici così da non rendere impossibile il flusso dei dati da archivi periferici ad archivi centrali. Una condizione irrinunciabile perché questo flusso di dati possa verificarsi correttamente è che il sistema di riferimento spaziale sia univoco. E’ indispensabile cioè che il sistema di riferimento fornisca in maniera indiscutibile la collocazione spaziale del dato perché solo a questa condizione i dati, pur provenendo da archivi diversi, resi identificabili unicamente dall'univocità del sistema di riferimento, potranno essere aggregati ed elaborati in maniera corretta. Dalla considerazione che esistono più livelli di governo del territorio, i quali implicano scelte decisionali basate su informazioni più o meno dettagliate e quindi su una conoscenza più o meno approfondita del territorio, discende l’esigenza di dotare gli organi tecnici di ciascun livello di una cartografia adeguata al grado di risoluzione delle indagini conoscitive che sono alla base delle loro scelte tenendo conto, per ottimizzare il rapporto tra il costo della cartografia e i benefici che derivano dal suo impiego, delle esigenze di cartografia proprie dei vari livelli. Oggi è ormai invalso l'uso di non fare distinzioni che dipendono dalla scala o dalla tipologia della carta e di indicare col termine cartografia di base tutte le carte che riguardano un certo territorio, purché costruite con tecniche topografiche o fotogrammetriche secondo i principi rigorosi della cartografia. In altre parole, volendo tentare una definizione, si può dire che si può considerare come cartografia di base di un territorio ogni sua rappresentazione cartografica realizzata con metodi topografici o fotogrammetrici rigorosi, inquadrata nel sistema di riferimento planimetrico e altimetrico nazionale e che si presenta nella consueta forma di carta disegnata classica o in forma di cartografia numerica. Capitolo IV - Descrizione del materiale cartografico esistente in Italia. pagina 128 R.Galetto A.Spalla - Lezioni di Topografia 2 Le funzioni della cartografia di base E’ spesso difficile, e talvolta anche fuorviante, inquadrare in uno schema troppo rigido un problema che si presenta con contorni ampi e sfumati quale l’elencare e definire le funzioni che la cartografia di base svolge nel contesto del governo del territorio, in particolare quando esso implica scelte decisionali guidate da informazioni prodotte da un sistema informativo che si avvale di una gestione dei dati basata su tecniche informatiche. E tuttavia, poiché i tipi di prodotto che l'industria topografica e fotogrammetrica propone per soddisfare la domanda di cartografia di base sono tra loro molto diversi e non equivalenti, occorre che coloro che hanno la responsabilità della scelta abbiano ben chiare le operazioni che devono potersi compiere su una cartografia di base e valutare quindi se tutte, o solo alcune di esse, potranno essere effettuate sul prodotto che verrà fornito. Si osserverà quindi il problema delle funzioni della cartografia di base nel governo del territorio in modo da formulare un numero limitato, ma sufficiente, di paradigmi di comportamento nella scelta della scala e della tipologia di una carta di base. Ciò premesso, le funzioni della cartografia di base sono fondamentalmente le seguenti: • fornire informazioni di tipo qualitativo; e cioè consentire di ricavare sia una visione d'insieme del territorio rappresentato sia l’esistenza, la dimensione e la forma dei particolari naturali e artificiali del terreno; • fornire informazioni di tipo metrico, e cioè premettere di ricavare la distanza topografica e la differenza di quota tra due qualsiasi punti su di essa rappresentati; • costituire, opportunamente semplificata, la base topografica per la formazione delle carte tematiche; • fornire le coordinate di tutti gli elementi topografici che costituiscono l’ossatura portante del sistema informativo; è infatti proprio il riferimento spaziale 1'anello di saldatura tra i dati del sistema informativo, i quali, in quanto relativi alle varie componenti del territorio, sono disomogenei e perciò, senza un riferimento topografico, non avrebbero quella pienezza di significato che è alla base dello studio delle interazioni e delle correlazioni dei vari fenomeni che avvengono sul territorio; • consentire il riporto su di essa dei progetti che costituiscono il risultato della pianificazione e della progettazione. Per le prime due funzioni risulta determinante la giusta scelta del rapporto di scala, il quale, come vedremo, condiziona in modo sostanziale il grado di dettaglio e la risoluzione di una carta; esso dovrà pertanto essere scelto in modo da realizzare un soddisfacente compromesso tra la necessità di sintesi e quella d'analisi dell'utilizzatore. Nei casi dubbi, cioè quando l’aspetto tecnico lascerà spazio a soluzioni differenti, converrà prendere in considerazione l’aspetto economico e quello dei tempi di realizzazione; i costi di una carta di base, .e anche i suoi tempi di realizzazione, crescono infatti in progressione geometrica con l’aumentare della scala della carta. E’ importante tenere presente che l’informazione, qualitativa e metrica, ricavata da una carta di base non deve lasciare all'utente dubbi d'interpretazione; con ciò si vuol dire che natura, forma e posizione di un particolare naturale o artificiale del terreno riportato dalla carta devono essere interpretati nello stesso modo da tutti i suoi utiIizzatori, e così pure la misura delle Capitolo IV - Descrizione del materiale cartografico esistente in Italia. pagina 129 R.Galetto A.Spalla - Lezioni di Topografia distanze o della differenza di quota tra due qualsiasi punti rappresentati sulla carta deve portare a un unico risultato, prescindendo da chi esegue la misura. Il fatto che la cartografia di base debba potere essere presa come supporto delle carte tematiche significa poi che si deve poter alleggerire il suo contenuto d'informazioni non necessarie alla comprensione e all'utilizzazione della carta tematica, e che anzi ne renderebbe difficoltoso l’allestimento; questa contiene infatti altri tipi di informazioni, che consistono molto spesso nell'individuazione del perimetro di aree omogenee rispetto a un determinato fenomeno (es. una carta della destinazione d'uso del suolo agricolo con indicate le aree con lo stesso tipo di coltura); l’evidenziazione in genere è effettuata mediante la campitura con retini delle aree omogenee e per facilitarne la lettura è opportuno quindi eliminare dalla cartografia di base quanto non utile all'utilizzatore della carta tematica, lasciando solo i particolari planimetrici e altimetrici necessari per definire la posizione delle diverse aree. L'utilizzazione della cartografia di base come supporto di tutte informazioni spaziali del sistema informativo implica la trasformazione in forma numerica di parte le informazioni planimetriche e altimetriche in essa contenute in forma grafica, per poterle elaborare mediante il calcolatore elettronico: le caratteristiche della cartografia di base dovranno quindi essere tali da rendere possibili le varie fasi di lavoro richieste dalla tecnica che si intende utilizzare per la digitalizzazione della carta. Infine sulla cartografia di base devono essere riportati gli studi quali è servita; anche per questo dovrà quindi essere possibile sfoltire la carta di base di tutti i particolari d'ostacolo alla facile comprensione dell'elaborato. Ad es. per la stesura d'un piano regolatore un centro urbano potrà convenire disporre di una cartografia di base in cui non siano campiti con retini gli edifici rappresentati sulla carta. Nello scegliere la scala e la tipologia di una carta di base occorre dunque tener presente i diversi usi a cui è destinata e verificare se la soluzione adottata è quella ottimale. Naturalmente in taluni casi non si potrà prendere in considerazione esclusivamente l’aspetto tecnico del problema, risultando più vincolanti problemi di costo o di tempo di realizzazione; anche in questa ipotesi tuttavia l’inevitabile compromesso tra carta ideale e carta realizzabile dovrà essere raggiunto tenendo conto di quanto detto. 3 Cartografia tradizionale 3.1 Influenza del rapporto di scala sulla precisione e sul grado di dettaglio di una carta di base Il contenuto d'informazioni di tipo qualitativo di una carta di base e la precisione delle misure su di essa eseguibili dipendono dal suo rapporto di scala, cioè dal rapporto di riduzione con il quale vengono rappresentate le grandezze lineari; si dice che la scala di una carta e tanto più piccola quanto più piccole sono, rispetto alla realtà, le dimensioni di ciò che essa rappresenta. Le carte di base si possono suddividere, in funzione del loro rapporto di scala , come segue: • carte a grandissima scala 1:500, 1:200 • carte a grande scala 1:2.000, 1:1.000 Capitolo IV - Descrizione del materiale cartografico esistente in Italia. pagina 130 R.Galetto A.Spalla - Lezioni di Topografia • • carte a media scala carte a piccola scala 1:10.000, 1:5.000 1:100.000, 50.000, 1:25.000. Dalla scala della carta dipendono i due parametri che la caratterizzano dal punto di vista metrico: 1. il suo grado di risoluzione, cioè a dimensione lineare del particolare più piccolo rappresentabile sulla carta; è dato dal minimo spessore del tratto grafico con cui la carta viene disegnata e che viene assunto, per convenzione, uguale a 0,2 mm, moltiplicato per il fattore di riduzione; ad esempio per una carta alla scala 1:10.000 il grado di risoluzione e di 2 m e cioè non è possibile rappresentare sulla carta particolari del terreno inferiori a tale grandezza; 2. l'errore massimo che si commette nel rilevare da essa la posizione di un punto: si conviene che esso debba essere inferiore al prodotto di 0,5 mm per il rapporto di riduzione della carta; per una carta alla scala 1:10.000 ad es. l’errore massimo di posizionamento di un punto vale 5 m. I particolari artificiali e naturali del terreno che devono essere riportati su una carta perché ne sia una rappresentazione valida (case, strade, fiumi, ecc.) hanno in generale una dimensione che, se divisa per il rapporto di riduzione delle carte a grande e media scala, è superiore a 0,2 mm e possono quindi essere rappresentati nel giusto rapporto in carte di grandezza di scala opportuna. Ad esempio una strada larga 10 m può venire rappresentata correttamente su una carta alla scala 1:10.000 con due linee di 0,2 mm di spessore tra loro distanziate di 1 mm; chi utilizza la carta misurando su di essa la larghezza di quella strada ne ricaverà cioè la larghezza reale di 10 m moltiplicando la larghezza di 1 mm misurata sulla carta per il rapporto di riduzione che è 1:10.000; la stessa strada non può venire invece rappresentata nel giusto rapporto di riduzione su una carta alla scala 1:50.000, poiché in questo caso dovrebbe avere larghezza di 0,2 mm; essa viene pertanto rappresentata sulla carta con un segno convenzionale, cioè con un simbolismo che indica l’esistenza, la posizione e il grado di importanza ma che ne altera le dimensioni; ad es. la si rappresenta con due linee: una continua e una a tratto, distanziate di 1 mm. Ne consegue che, mentre da un punto di vista d'impostazione generale non vi è differenza fra le carte a media e a grande scala, esiste invece una diversità notevole tra le carte a grande e media e quelle a piccola scala; nelle prime le dimensioni reali di quanto rappresentato possono essere ricavate moltiplicando la misura presa sulla carta per il suo coefficiente di scala; nelle seconde questo procedimento può portare a errori notevoli perché, essendo il rapporto di riduzione molto elevato, la realizzazione delle carte richiede che vengano impiegati in larga misura segni convenzionali, cioè una serie di simboli che non stanno nel giusto rapporto con le dimensioni reali degli oggetti. Al diminuire della scala della carta, cioè con l’aumentare del rapporto di riduzione, si ha quindi un minor contenuto d'informazione in termini qualitativi e metrici; d'altra parte però con il diminuire della scala si produce sulla carta una specie di semplificazione, che cancella quanto ne costituisce la tessitura minuta ed esalta i tratti più importanti del territorio; inoltre aumenta, a parità di dimensioni del foglio, la zona reale di territorio rappresentata. Pertanto, se è vero che le grandi scale consentono un grado di lettura molto fine del territorio, è anche vero che quelle a piccola scala permettono una visione di insieme che le prime non danno. Capitolo IV - Descrizione del materiale cartografico esistente in Italia. pagina 131 R.Galetto A.Spalla - Lezioni di Topografia In particolare riprendendo la suddivisione delle carte in carte a piccola, media, grande e grandissima scala, i relativi ambiti di utilizzazione sono i seguenti. Le carte a piccola scala (1:100.000, 50.000, 1:25.000), che dànno una visione di sintesi del territorio che rappresentano, sono generalmente carte nazionali che vengono utilizzate come base di progetti di programmazione di larga massima. Le carte a media scala (1:10.000, 1:5.000) sono le carte regionali. Esse devono avere, per contenuto qualitativo e metrico, il grado di dettaglio che consenta di ricavare tutti gli elementi conoscitivi necessari per la pianificazione a livello regionale. Le carte a grande scala (1:2.000, 1:1.000) descrivono il territorio con il grado di dettaglio necessario ad una sua pianificazione a livello comunale. Infatti esse vengono utilizzate come base per stendere i PRG, i PPA , ecc. Le carte a grandissima scala (1:500, 1:200), stante il loro costo elevato, non vengono generalmente realizzate per l’intero territorio di un comune, ma per particolari zone, ad esempio per centri storici, e vengono utilizzate come base di strumenti molto specifici come piani di recupero, PEEP, ecc. Capitolo IV - Descrizione del materiale cartografico esistente in Italia. pagina 132 R.Galetto A.Spalla - Lezioni di Topografia 3.2 Tipologia delle carte topografiche tradizionali Per avere un’idea del contenuto qualitativo delle cartografie alle diverse scale, si riportano alcuni esempi di cartografie dello stesso territorio realizzate a scale differenti. fig. 3. -1 Esempio di cartografia alla scala 1:25.000 Capitolo IV - Descrizione del materiale cartografico esistente in Italia. pagina 133 R.Galetto A.Spalla - Lezioni di Topografia fig. 3. - 2 Esempio di cartografia alla scala 1:10.000 Capitolo IV - Descrizione del materiale cartografico esistente in Italia. pagina 134 R.Galetto A.Spalla - Lezioni di Topografia fig. 3. - 3 Esempio di cartografia alla scala 1:2.000 Capitolo IV - Descrizione del materiale cartografico esistente in Italia. pagina 135 R.Galetto A.Spalla - Lezioni di Topografia fig. 3. - 4 Esempio di cartografia alla scala 1:500 Capitolo IV - Descrizione del materiale cartografico esistente in Italia. pagina 136 R.Galetto A.Spalla - Lezioni di Topografia 3.2 Cartografie numeriche La cartografia numerica è un prodotto che pur mantenendo le funzioni della cartografia tradizionale, ha caratteristiche molto peculiari. Al successivo capitolo VIII queste caratteristiche vengono descritte diffusamente. Si rimanda perciò ad esso per le definizioni sulle differenti tipologie di cartografie numeriche con differenti gradi di dettaglio. 4 Indicazioni sulle cartografie esistenti in italia 4.1 La cartografia dell’Istituto geografico militare 4.1.1 Carte classiche Di tutto il territorio nazionale esiste: • • • • la carta alla scala 1:200.000 la carta alla scala 1:100.000 la carta alla scala 1:50.000(non completa) la carta alla scala 1:25.000 Quella fondamentale può ritenersi la carta alla scala 1:25.000 in quanto le altre scale sono per lo più da essa ricavate per riduzione. Tutta la cartografia su elencata è stata prodotta dall'I.G.M. (Istituto Geografico Militare) il quale con la costruzione della carta alla scala 1:25.000 non si prefiggeva di fornire un prodotto cartografico per la progettazione di ingegneria civile, bensì quello di dare una rappresentazione di tutto il territorio nazionale in un tempo ragionevolmente breve (la costruzione di una cartografia nazionale prima dell'avvento della fotogrammetria era impresa veramente impegnativa anche per un organismo istituito apposta per realizzarla) e ad una scala che potesse servire, oltre che ad usi militari, anche ad una gamma più vasta possibile di usi civili. E in effetti per molti problemi di progettazione, soprattutto in fase di progetto preliminare (di strade, di urbanistica ecc.) ci si può servire della carta 1:25.000; quando la si usa bisogna però tener presente quanto segue: • alla scala 1:25.000 1 mm equivale a 25 m sul terreno; il tratto di stampa che delimita i particolari del terreno e che ha la dimensione media di 0,2 mm equivale pertanto a 5 m; non ha senso quindi pretendere di ricavare dalla carta alla scala 1:25.000 delle misure di distanza con precisione superiore ad una decina di metri. • per quanto riguarda la determinazione dei dislivelli tra due punti del terreno, ricavati (i dislivelli) mediante i dati riportati alla carta, si può dire che non si può ottenere una precisione superiore a 2 m, e che se anziché da punti quotati i dislivelli si ricavano dalle curve di livello si può facilmente sbagliare anche di 5 o 10 m (specialmente in terreni a forte pendenza). Capitolo IV - Descrizione del materiale cartografico esistente in Italia. pagina 137 R.Galetto A.Spalla - Lezioni di Topografia Oltre alle carte alle scale 1:200.000, 1:100.000, 1:50.000, e 1:25.000, l'I.G.M. ha eseguito anche il rilievo alla scala 1:10.000 di alcune Regioni (Calabria, Sardegna). Queste ultime sono già delle vere carte tecniche 4.1.2 Prodotti non convenzionali: carte numeriche, spaziocarte. Avvalendosi di tecnologie che si basano sull’uso di immagini da satellite, IGM sta realizzando i nuovi fogli alla scala 1:100.000 in forma di spaziocarte. Le spaziocarte sono ricavate da immagini rilevate dal sensore Thematic Mapper (TM), montato sui satelliti LANDSAT 5. Tali immagini sono georeferenziate, cioè orientate geometricamente, sul sistema cartografico UTM. Su di esse sono riportate informazioni topografiche relative alla viabilità, alla toponomastica, ai limiti amministrativi, ecc, al fine di facilitare la lettura e l’utilizzazione. L’IGM fornisce dati cartografici numerici desunti, per digitalizzazione dalla cartografia tradizionale, in particolare fornisce: • dati orografici: ottenuti dalla digitalizzazione delle curve di livello e dei punti quotati riportati sulla cartografia alla scala 1:25.000, organizzati in file • dati idrografici: ottenuti dalla digitalizzazione dei particolari idrografici sempre riportati sulla cartografia alla scala 1:25.000, • file dei limiti amministrativi desunti dalla cartografia alla scala 1:100.000. 4.2 La cartografia catastale. Per tutto il territorio nazionale esiste la carta del Catasto alle scale 1:4.000 o 1:2.000. Il carta catastale consta di circa 300.000 fogli. Il Catasto ha affrontato e sta risolvendo il problema di trasporre questi fogli dalla forma tradizionale alla forma numerica. Sono infatti già stati prodotti in forma numerica circa un terzo dei fogli esistenti. Questo significa che per un terzo del territorio nazionale è possibile ottenere copia dei fogli di mappa oltre che sul consueto supporto cartaceo, anche su supporto magnetico, secondo formati standard di trasferimento. La trasposizione in forma numerica non si limita al solo aspetto cartografico, ma investe anche la componente descrittiva degli archivi catastali. E’ in atto quindi un imponente lavoro di informatizzazione che prevede anche l’acquisizione mediante il sistema satellitare GPS di vaste reti di punti “fiduciali” sui quali inquadrare la cartografia trasposta. Capitolo IV - Descrizione del materiale cartografico esistente in Italia. pagina 138 R.Galetto A.Spalla - Lezioni di Topografia 4.3 Carte tecniche regionali e provinciali. Molti Comuni ed alcune Provincie, dovendo risolvere problemi connessi con la progettazione urbanistica, stradale, delle fognature, ecc., hanno ritenuto indispensabile (come in effetti lo è) far costruire una nuova carta del territorio Comunale (o Provinciale) alla scala 1:2.000. La scala 1:2.000 si ritiene infatti la più idonea, e nello stesso tempo di costo sostenibile, per risolvere i problemi di un ufficio tecnico provinciale o comunale. Generalmente poi dalla carta si ricava per riduzione una carta alla scala 1:5.000 e una carta alla scala 1:10.000. Naturalmente il procedimento di riduzione non consiste in un lavoro di pura riduzione fotografica, ma implica un lavoro di semplificazione del disegno. Dal 1971, in seguito alla creazione delle Regioni a statuto ordinario, molte altre Regioni hanno dato inizio alla costruzione della Carta Tecnica Regionale; alcune Regioni hanno scelto di costruirla alla scala 1:5.000 (ad es. Liguria, Emilia Romagna, Friuli-Venezia Giulia); altre alla scala 1:10.000 (ad es. Lombardia, Marche, Toscana). 4.4 Cartografie a grande e grandissima scala Generalmente l’obiettivo che si intende raggiungere con la realizzazione di cartografie a grande e grandissima scala è avere una conoscenza puntuale dell’edificato da sfruttare a fini di pianificazione urbanistica o di gestione dei servizi. In particolare, le cartografie a grande e grandissima scala (1:2.000. 1:1.000, 1:500), soprattutto se realizzate in forma numerica anziché nella consueta forma tradizione, soddisfano le esigenze di pianificazione a livello comunale e sovracomunale e di gestione dei servizi perché: • forniscono informazioni dettagliate sull’edificato • dànno la possibilità di individuare l’insieme di edifici afferenti ad uno stesso numero civico • sono l’ossatura spaziale di analisi specifiche sullo stato di degrado, sulla destinazione d’uso, sulla tipologia edilizia degli edifici • sono la base su cui studiare e progettare interventi di recupero edilizio • sono di supporto nell’automatizzazione del rilascio delle concessioni edilizie, • sono un supporto cartografico aggiornato su cui riportare le planimetrie catastali, • sono l’ossatura dei sistemi informativi territoriali. Queste cartografie che vengono prodotte dall’Industria Fotogrammetrica, hanno come committenti i Comuni e le Aziende municipalizzate di distribuzione dei servizi. *** Capitolo IV - Descrizione del materiale cartografico esistente in Italia. pagina 139 R.Galetto A.Spalla - Lezioni di Topografia Considerando un territorio comunale, la condizione di dotazione cartografica ideale per realizzare ogni tipo di intervento tecnico dovrebbe essere la seguente: • • • disporre di una C.T.R. (carta tecnica regionale) a media scala (1:5.000 1:10.000) per tutto il territorio comunale disporre di una cartografia alla scala 1:2.000, sempre per tutto il territorio comunale disporre di cartografie a grandissima scala , 1:500, 1:200, per quelle zone di rilevante interesse storico, su cui si rendono necessari interventi di ampio respiro. Questo patrimonio cartografico, oltre ad essere di recente realizzazione, dovrebbe anche essere in forma numerica per venire incontro alle esigenze più diversificate dei tecnici. In queste condizioni l'ingegnere civile avrebbe il supporto di base per stendere i suoi progetti ai differenti livelli (da progetto di massima a progetto esecutivo). Viceversa i Comuni che hanno provveduto a darsi una cartografia valida e recente sono pochi, e quindi quando l'ingegnere di costruzioni stradali deve stendere un progetto di una strada ha bisogno prima di tutto di far costruire una carta sulla quale stendere il progetto, e così per l'urbanista e per l'ingegnere idraulico che deve progettare una diga o un acquedotto. Ecco dunque la necessità per l'ingegnere di sapere come si ordina la costruzione di una carta, come ci si può assicurare che la Ditta chiamata a costruirla sia veramente in grado di farlo ed infine come si fa a controllarne la bontà sia dal punto di vista metrico che qualitativo. Capitolo IV - Descrizione del materiale cartografico esistente in Italia. pagina 140 R.Galetto A.Spalla - Lezioni di Topografia CAPITOLO V RILIEVO TOPOGRAFICO CLASSICO Premessa La produzione della cartografia viene oggi di regola eseguita col metodo fotogrammetrico; inoltre la maggior parte di essa non viene prodotta in forma grafica, cioè come un disegno, ma in forma numerica, come verrà più avanti illustrato. Il rilievo topografico classico a scopo cartografico viene oggi impiegato solo per rilievi di limitate estensioni (ad esempio frazionamenti catastali o rilievi per la rappresentazioni di zone su cui devono essere realizzate grandi opere di ingegneria) oppure come integrazioni del lavoro fotogrammetrico. Le operazioni topografiche sono invece ancora molto usate per realizzare le reti di inquadramento o di infittimento, in appoggio ai lavori di cartografia fotogrammetrica; anche in questo settore la loro applicazione verrà però presto ridotta dall’uso sempre crescente del GPS e, in futuro, probabilmente anche dai sistemi inerziali. Quanto esposto ai punti 1 e 2 di questo Capitolo, che, come ripetiamo, si riferisce alla produzione di cartografia tradizionale disegnata, realizzata col rilievo topografico classico, ha lo scopo di illustrare, con un esempio banale e con una terminologia semplice, la complessa filosofia che sta alla base della rappresentazione cartografica della superficie fisica della terra. 1 Descrizione schematica della costruzione di una carta. 1.1 Impostazione concettuale della costruzione della planimetria. Tenendo presente: • che i geodeti hanno provveduto a coprire tutto il territorio nazionale con una rete di vertici trigonometrici; • che dei vertici trigonometrici sono state calcolate le coordinate planimetriche nella proiezione cartografica di Gauss, inquadrando così una volta per tutte l’intero territorio nazionale in un unico sistema di riferimento di coordinate cartesiane piane; • che una distanza reale può essere inserita direttamente sulla carta di Gauss una volta che sia stata ridotta a distanza topografica e corretta del coefficiente di deformazione; • che gli angoli azimutali si introducono senza correzione nella carta di Gauss; ne deriva che il topografo, per dare una rappresentazione cartografica planimetrica della superficie fisica della terra, può operare come se essa scorresse parallelamente al piano della proiezione di Gauss (figura 1). Dicendo parallelamente si intende che, in questa finzione, i punti della superficie fisica della terra assumono, rispetto al piano della rappresentazione di Gauss, la quota che essi hanno rispetto al geoide. Capitolo V - Rilievo topografico classico pagina 141 R.Galetto A.Spalla - Lezioni di Topografia P V2 V3 V1 π proiezione ortogonale figura 1 Tenuto conto infine del fatto che l’estensione del territorio interessato dalle misure che il topografo esegue da una stazione di rilevamento è limitata al campo topografico (vedi capitolo III punto 2.3.3), per la costruzione della planimetria di una carta il topografo può operare come se, in ogni stazione di rilevamento, gli elementi caratteristici naturali ed artificiali della superficie terrestre dovessero essere proiettati direttamente nel piano della proiezione di Gauss, la quale viene idealmente fatta coincidere col piano tangente alla sfera locale nei vari punti di stazione. Supponiamo ad esempio che il territorio da rilevare sia quello rappresentato in figura 1 e che i punti V1, V2, V3 siano vertici trigonometrici (in realtà in un territorio così poco esteso non ce ne sarebbero così tanti). In questo nostro esempio questi vertici trigonometrici hanno la funzione di costituire i punti della rete di inquadramento (e di infittimento) del rilievo; facendo riferimento a questi punti si effettuano le operazioni topografiche che portano al rilevamento di tutti i punti che sono necessari alla costruzione della carta; più avanti vedremo che la rete di inquadramento del rilievo sarà realizzata creando tutta una serie di punti dei quali si determinano le coordinate in funzione dei vertici trigonometrici esistenti nella zona da rilevare. Per rilevare un generico punto che serve alla costruzione della planimetria, ad esempio il punto P in figura, il topografo potrà fare stazione ad esempio sul punto V1 e assumendo come direzione di riferimento quella al punto V2 misurerà l’angolo V1PV2, la distanza reale V1-P e l’angolo zenitale della direzione V1-P; quindi in funzione di queste misure e delle coordinate dei vertici V1 e V2 sarà in grado di ricavare le coordinate di P nella proiezione di Gauss (vedi l’esempio al punto 2.3.3 del capitolo III). Capitolo V - Rilievo topografico classico pagina 142 R.Galetto A.Spalla - Lezioni di Topografia z P V2 y V2V1P x V1 figura 2 Nota. Non prendiamo in considerazione tutta la problematica connessa alla reale esecuzione delle misure, poiché il discorso esula dai nostri fini didattici; ma, solo per averne un’idea, si consideri che quando diciamo che il topografo fa stazione sul vertice V1 ipotizziamo in realtà una cosa impossibile, poiché egli non può piazzarsi col teodolite sulla punta di un campanile! Facendo stazione nei vari vertici trigonometrici e applicando il procedimento sopra descritto si determinano e si inseriscono nella cartografia tutti i punti del terreno che servono a darne una rappresentazione planimetrica. Ad esempio, per riportare sulla carta un edificio si determina mediante misura di angoli e distanze la posizione dei suoi spigoli rispetto ad uno o più punti di inquadramento vicini; si riportano sulla carta questi punti e li si congiungono con tratto continuo. Naturalmente, oltre che la posizione planimetrica, si dovrà determinare anche la posizione altimetrica dei punti. Alla fine si arriverebbe alla produzione di un elaborato del tipo di quello riportato nella figura 3. L’esempio fatto dovrebbe ancora una volta chiarire il concetto già esposto e cioè che il lavoro dei geodeti ha messo in grado i topografi di realizzare una rappresentazione del territorio inserita nella proiezione nazionale Gauss-Boaga seguendo uno schema concettuale molto semplice (altra cosa come detto sono le difficoltà operative) e utilizzando semplici formule di trigonometria piana. Ricordiamo ancora l’utilità di alcune approssimazioni lecite nel campo topografico, quali l’approssimazione della distanza topografica alla sua proiezione sul piano tangente alla sfera locale e il poter assumere come coincidenti, nella proiezione di Gauss, trasformata, corda e tangente congiungenti due punti aventi distanza inferiore a 5 km. Capitolo V - Rilievo topografico classico pagina 143 R.Galetto A.Spalla - Lezioni di Topografia Comune di .... Legenda segni convenzionali ..... +++ ''''' Ditta esecutrice ....... Data del rilievo ....... scala 1:n figura 3 Ciò detto occorre subito chiarire che in realtà il rilievo topografico non avviene passando direttamente dai vertici trigonometrici alle misure che portano al disegno della carta, ma richiede i seguenti passi: • reperimento dei vertici trigonometrici • costruzione della rete di inquadramento • costruzione della rete di infittimento • esecuzione di poligonali • esecuzione di livellazioni per l’inquadramento altimetrico • esecuzione del rilievo di dettaglio (rilievo celerimetrico). 1.2 Impostazione concettuale della costruzione dell’altimetria. Nell’elaborato è stata rappresentata anche l’altimetria che è costituita dai punti quotati e dalle curve di livello. I punti quotati sono dei punti del terreno dei quali viene data la distanza rispetto ad una superficie di riferimento, che come abbiamo visto, è il geoide. La quota dei punti quotati viene determinata con tre metodi (che verranno descritti più avanti): Capitolo V - Rilievo topografico classico pagina 144 R.Galetto A.Spalla - Lezioni di Topografia • • • la livellazione geometrica - la procedura operativa di questo tipo di livellazione tiene automaticamente conto della curvatura terrestre; la livellazione trigonometrica - in questo metodo, usato su distanze abbastanza grandi, si tiene conto della curvatura terrestre nella fase di calcolo ; la livellazione tacheometrica - in questo metodo, usato nel rilievo di dettaglio, non si tiene conto della curvatura terrestre poiché il metodo è di modesta precisione, e pertanto la curvatura terrestre dà un effetto che non è apprezzabile. Le curve di livello sono invece delle linee che indicano la posizione planimetrica dei punti aventi tutti la stessa quota, cioè la stessa distanza dalla superficie di riferimento (figura 4). Queste linee vengono tracciate ad intervalli regolari e costanti di differenza di quota; l'intervallo altimetrico tra le curve di livello viene chiamato equidistanza. In genere l’equidistanza corrisponde ad un numero di millimetri uguale al denominatore del rapporto di scala di una carta; ad esempio: in una carta alla scala 1:2000 l’equidistanza delle curve di livello è pari a 2 metri (2000 millimetri). Geoide + 131.2 π 125 figura 4 L'insieme della planimetria e della altimetria permettono all’utente di cartografia di effettuare analisi qualitative e metriche sul territorio cartografato. 2 Funzione della rete di inquadramento. Se un solo punto fosse preso come origine delle misure per la costruzione della planimetria di una carta e tutto il rilievo si sviluppasse a partire da esso, si avrebbero due gravi inconvenienti: • una sensibile perdita di precisione per un continuo accumularsi di piccoli errori, • la precisione di determinazione dei diversi particolari non sarebbe omogenea per tutti del rilievo Spieghiamo meglio il concetto. Come illustrato al precedente punto 1.1 le operazioni topografiche di rilievo possono essere sommariamente descritte come la determinazione plano-altimetrica dei punti rispetto ad altri punti presi come riferimento; in queste operazioni di determinazione della posizione di punti rispetto ad altri, che consistono in operazioni di misura, si commettono degli errori; non consideriamo ovviamente gli errori grossolani (cioè gli sbagli), ma gli errori accidentali dovuti all’influenza dell’ambiente sulle operazioni di misura e alle limitazioni di precisione intrinseche dei metodi di misura usati. Capitolo V - Rilievo topografico classico pagina 145 R.Galetto A.Spalla - Lezioni di Topografia Se si partisse da un punto e da questo si procedesse per eseguire tutto il rilievo, ad ogni determinazione di un nuovo punto, sulla posizione di esso graverebbero tutti gli errori precedentemente commessi. Per contenere questo progressivo accumularsi di errori si dovrebbero impiegare metodi di misura molto onerosi, senza tuttavia evitare il progressivo decadimento della precisione. Pertanto i punti di inquadramento di un rilievo, oltre a costituire una rete di punti di vincolo che garantiscono una precisione uniforme al rilievo, evitano di dover operare, anche nella fase del rilievo di dettaglio, con metodi di misura onerosi . Per la funzione che devono assolvere e per il fatto di essere alquanto distanti tra di loro, le misure che riguardano la determinazione della posizione dei punti di inquadramento vengono eseguite con strumenti più precisi di quelli che vengono usati per determinare la posizione di tutti i punti che costituiscono la carta. Come verrà descritto al successivo punto 3, nella costruzione della rete di inquadramento la funzione dei vertici trigonometrici è fondamentale, poiché essi assolvono a una duplice funzione: inserire correttamente il rilevo cartografico nel contesto nazionale, consentire di costruire la rete senza dover effettuare misure di distanza. Questa seconda funzione è oggi meno rilevante, ma quando non esistevano i distanziometri elettronici era di enorme aiuto per i topografi. E’ ancora molto importante invece la prima funzione, cioè quella di inserire una cartografia nel contesto nazionale. Il compito di costruire carte a grande scala viene infatti generalmente assolto, a seconda dei casi, da Comuni, Province, Consorzi od altri Enti pubblici o privati. Quando uno di questi Enti costruisce la cartografia del territorio di sua competenza lo fa appunto (per motivi economici, burocratici ecc.) limitatamente ad esso. Ma quando poi i tecnici eseguono studi di pianificazione e progettazione sentono la necessità di esaminare anche i territori che circondano il Comune; e può darsi che alcuni o tutti i Comuni limitrofi si siano anch'essi dati una cartografia. Risulta allora molto più agevole utilizzare queste cartografie, se sono tutte impostate su uno stesso sistema di riferimento e quindi hanno una precisione omogenea (a parità di scala) e presentano discrepanze nelle zone di contatto. Capitolo V - Rilievo topografico classico pagina 146 R.Galetto A.Spalla - Lezioni di Topografia 3 Rilievo planimetrico. 3.1 Triangolazioni. Come abbiamo visto, il primo passo per un rilievo è la costruzione della rete di inquadramento, che si appoggia alla rete dei vertici trigonometrici esistenti. Costruire la rete di inquadramento significa determinare le coordinate N, E e la quota di un certo numero di punti del terreno. Questo viene fatto in due tempi: • con operazioni di misura mediante le quali è possibile ricavare la posizione reciproca dei punti, • con operazioni di calcolo che ci forniscono le coordinate N , E in funzione delle misure eseguite. La costruzione della rete di inquadramento avviene mediante l'operazione topografica che prende il nome di triangolazione tecnica. Nella triangolazione tecnica possiamo distinguere due casi tipici: quello basato su sole misure angolari e quello basato su misure di angoli e distanze. In quest'ultimo caso occorrerà disporre di strumenti atti alla misura delle distanze con distanziometri elettronici. Nota: oggi (1997) si può eseguire una triangolazione tecnica anche mediante il solo uso del GPS (v. Cap. VII). Noi qui non prenderemo in considerazione tale metodo. 3.1.1 Rete di inquadramento Prendiamo in considerazione lo schema di triangolazione tecnica riportato nella figura che segue. Per inquadrare il territorio da cartografare si sono reperiti due vertici trigonometrici (punti 1 e 5 in figura) e si sono scelti altri sei vertici di cui determinare le coordinate N,E. N 2 1 3 9 4 α 8 7 6 5 E punti trigonometrici esistenti dei quali è possibile conoscere le coordinate N, E (ed eventualmente la quota), che vengono fornite dall'I.G.M. vertici della triangolazione figura 5 Capitolo V - Rilievo topografico classico pagina 147 R.Galetto A.Spalla - Lezioni di Topografia Il numero e la posizione dei vertici incogniti sono determinati da queste due esigenze: • ricoprire omogeneamente tutta la zona del rilievo • avere distanze tra i vertici non troppo grandi e cioè tali che le operazioni di misura e di calcolo eseguiti per collegarli possano usufruire delle semplificazioni ammesse per il campo topografico. Per i rilievi cartografici a grande scala la distanza media tra i vertici varierà tra 1 o 2 km, mentre per i rilievi a media scala essa potrà arrivare anche a 4 o 5 km. Con riferimento al fatto che nella rete sono inclusi dei vertici trigonometrici possono essere eseguite solo misure angolari, esse verranno eseguite utilizzando un teodolite di buona precisione, (con e.q.m. di lettura di una direzione pari a ±1” ). Nella figura 6 i segmenti che congiungono i vertici stanno ad indicare le direzioni osservate. Ad esempio: dal vertice 8 si è fatta stazione con il teodolite e si sono eseguite le letture al cerchio orizzontale (comunque posizionato), collimando i vertici 1,2,9,7. Nel vertice 2 si è fatta stazione e si sono collimati i punti 1,8,9,3. Facendo la differenza tra le letture al cerchio si ricavano gli angoli tra le congiungenti i vertici, ad esempio l'angolo α sarà dato dalla differenza tra lettura al C.O. (cerchio orizzontale) eseguita collimando il punto 1 dal vertice 8, e quella eseguita al C.O., sempre dal punto 8 collimando il vertice 2. Se alcuni vertici della triangolazione sono dei trigonometrici, come è nel nostro esempio, non sarebbe necessario eseguire misure di distanza, perché il dimensionamento della rete, cioè la sua grandezza reale, ci viene fornita dalla distanza tra i trigonometrici, che è nota (dal momento che dei vertici trigonometrici sono note le coordinate) Ciò nonostante è buona regola eseguire ugualmente delle misure di distanza, allo scopo di dare una maggiore rigidità alla rete. Supponiamo che, nel nostro esempio, si sia misurata con un distanziometro elettronico di elevata precisione (10-6) la distanza tra i vertici 7 e 8. Vediamo ora: • quale è lo scopo della triangolazione; • quante sono le misure necessarie; • quali sono i calcoli da eseguire. Lo scopo della triangolazione è quello di fornire le coordinate N,E di tutti i vertici della triangolazione, ad eccezione ovviamente dei vertici trigonometrici in essa inclusi; nel nostro esempio dovranno quindi essere determinate le coordinate N, E dei punti 2, 3, 4, 6, 7, 8. Se n è il numero dei vertici dei quali si devono determinare le coordinate, le misure necessarie sono 2n; con riferimento all’esempio saranno quindi necessarie almeno 12 misure; esse possono essere: • tutte misure angolari, • misure di distanza e misure angolari, • tutte misure di distanza. Il numero delle misure eseguite deve tassativamente essere superiore a quello strettamente necessario, in modo da poter verificare di non aver fatto errori grossolani, di compensare l’influenza degli errori accidentali sulla determinazione delle coordinate incognite e di poter valutare l’e.q.m. con cui esse sono state determinate. Capitolo V - Rilievo topografico classico pagina 148 R.Galetto A.Spalla - Lezioni di Topografia Non basta però che le misure siano in numero maggiore di quello strettamente necessario, ma devono essere tra di loro indipendenti e comunque devono permettere di determinare tutte le incognite. Per chiarire il senso di quanto detto consideriamo che la nostra triangolazione consista semplicemente di quattro vertici dei quali due di coordinate note: le misure necessarie per determinare la rete sono 2 n= 4. 2 1 α1 α2 α4 3 α3 4 figura 6 Ma se si misurano gli angoli α 1, α 2, α 3, α 4 segnati in figura 6 ovvio che, pur facendo quattro misure, non si raggiunge lo scopo, perché si ha una misura sovrabbondante per determinare il punto 4, ma risulta indeterminato il punto 2. Il miglior modo per vedere se le misure sono sufficienti a determinare la rete, è quello di provare a costruirla graficamente; questo è del resto necessario per proseguire al calcolo della rete stessa, come viene in seguito spiegato. 3.1.2 Calcolo della rete. Con una scala di disegno arbitraria si riportano nel sistema di assi N, E i vertici trigonometrici; quindi, riferendosi ad essi e sfruttando alcune delle misure eseguite, si costruisce graficamente la rete, cioè si riportano sul disegno tutti i vertici di coordinate non note. N 2 1 α1 α5 α2 α6 α8 4' α10 α 12 4 9 α7 8 3 α4 α3 α11 α9 7 5 6 E figura 7 Indicando con la notazione Li-j la lettura al cerchio orizzontale fatta stando in i e collimando il punto j si ha: Capitolo V - Rilievo topografico classico pagina 149 R.Galetto A.Spalla - Lezioni di Topografia I) II) III) IV) V) VI) α 1 = L1-9 - L1-2 α 2 = L9-2 - L9-1 α 3 = L9-2 - L9-3 α 4 = L2-3 - L2-9 α 5 = L1-9 - L1-2 α 6 = L9-1 - L9-8 α 7 = L8-9 - L8-7 α 8 = L9-8 - L9-7 α 9 = L7-9 - L7-6 α 10= L3-9 - L3-6 α 11 = L5-6 - L5-4 α 12= L3-6 - L3-4 misure per la determinazione del punto 2 misure per la determinazione del punto 3 misure per la determinazione del punto 8 misure per la determinazione del punto 7 misure per la determinazione del punto 6 misure per la determinazione del punto 4 Come si vede sfruttando soltanto 12 delle misure eseguite si possono determinare le coordinate dei 6 punti incogniti; naturalmente la costruzione grafica può anche essere sostituita da un calcolo analitico. Se le misure fossero però nello stretto numero di 12 non ci potremmo accorgere di eventuali errori grossolani: se ad esempio la lettura L3-4 fosse errata di 10° , ricaveremmo l'angolo errato di 10° e posizioneremmo il punto 4 in 4', senza peraltro accorgerci dell'errore. La costruzione grafica della rete, o il suo calcolo analitico, eseguita in base al minimo numero di misure, ci permette di controllare che la rete sia determinata e di ricavare dei valori approssimati delle coordinate dei vertici le cui coordinate sono incognite. Si parla di coordinate approssimate perché, per determinarle, non si sono sfruttate tutte le misure eseguite. Nel nostro esempio tali coordinate saranno quelle dei vertici 2,3,4,6,7,8 che indichiamo con E02 ,N 02 , E03 , N 03 ,....... E08 ,N80 Si procede quindi per via analitica al calcolo di compensazione della rete; con la parola compensazione si intende quell'operazione che permette di calcolare le correzioni da apportare ai valori approssimati, in funzione di tutte le misure eseguite, cioè anche di quelle che sono già state usate per la determinazione delle coordinate approssimate. Il calcolo di compensazione si basa sul metodo delle osservazioni indirette e viene descritto nel successivo paragrafo 3.2. . 3.2 Applicazione del metodo delle osservazioni indirette a problemi topografici. L'applicazione del metodo delle osservazioni indirette consente una ampia generalizzazione dei calcoli topografici. Capitolo V - Rilievo topografico classico pagina 150 R.Galetto A.Spalla - Lezioni di Topografia Nel paragrafo che segue tratteremo operazioni topografiche mediante le quali si costruisce la planimetria di una carta; esse sono: la triangolazione tecnica, le intersezioni, le poligonali; queste operazioni differiscono per gli strumenti impiegati nelle misure e nello schema di attuazione, ma da un punto di vista generale servono tutte alla soluzione dello stesso tipo di problema che può essere così enunciato: dato un certo numero di punti di posizione nota, dei quali si conoscono le coordinate in un certo sistema di riferimento, che supponiamo sia quello della carta di Gauss, si devono determinare le coordinate di altri punti di posizione non nota, collegati ai precedenti da misure di angoli e distanze. Come già detto più volte il numero di misure di angoli e distanze deve essere superiore a quello strettamente necessario alla soluzione del problema. Questo sia per ovviare al fatto che le schematizzazioni geometriche ideali non corrispondono alla effettiva realtà fisica, sia perché le misure stesse risultano affette da errori accidentali. Il numero sovrabbondante di misure offre quindi la possibilità di mediare l'effetto degli errori accidentali, di verificare la precisione di determinazione delle coordinate, di cautelarsi da eventuali errori grossolani. Note quindi le coordinate di alcuni punti ed i valori misurati di angoli e distanze, per determinare i valori delle coordinate incognite con il metodo delle osservazioni indirette, occorre individuare i tipi di equazioni generatrici che legano fra loro coordinate note, coordinate incognite e misure effettuate. 3.2.1 Sviluppo del procedimento completo su un esempio. Per fissare le idee consideriamo l'esempio molto semplice rappresentato in figura 8, n cui i punti C, D, di coordinate incognite, sono stati collegati ai punti A e B, di coordinate note, mediante la misura di angoli e distanze. N B d3 A α2 α1 d2 α4 α3 C d1 D E figura 8 α 1, α 2, α 3, α 4 angoli misurati d1 , d2 , d3 distanze misurate Capitolo V - Rilievo topografico classico pagina 151 R.Galetto A.Spalla - Lezioni di Topografia Per determinare le coordinate incognite EC , NC , ED , ND, verranno utilizzati due tipi di equazioni dei quali • uno lega coordinate note, coordinate incognite e misure di angoli; • l'altro coordinate note, coordinate incognite e misure di distanze. Il primo tipo di equazione generatrice deriva dalla definizione stessa di angolo di direzione (vedi APPENDICE ); N (AC) C (AD) A α1 D E figura 9 se infatti consideriamo lo schema di figura 9 vediamo che possiamo legare le coordinate dei tre punti all'angolo misurato tra le due direzioni AC e AD con la relazione : (AD) - (AC) = α 1 (1) da cui l'equazione generatrice : f = (AD) - (AC) - α 1 =0 Inserendo l'espressione dell'angolo di direzione in funzione delle coordinate dei punti si ottiene: f = arctg ED − E A E − EA + π- arctg C - α1 = 0 ND − NA NC − N A (2) (vedi APPENDICI ) Riscriviamo questa equazione secondo le notazioni viste nell’esposizione del metodo delle Osservazioni Indirette (Capitolo I ) ED − EA * f 1 (N A ,EA ,N C,E C,N D,E D; α 1)=arctg * * * * N *D − N A - arctg E *C − E A N *C − N A - α 1= v1 (3) dove le notazioni asteriscate indicano che i valori calcolati per le coordinate incognite saranno di tipo empirico e non soddisferanno rigorosamente l'equazione (3) nella quale sarà presente uno scarto v1. Per seguire l'iter del metodo delle Osservazioni Indirette dovremo linearizzare l'equazione generatrice (3) sviluppandola in serie di Taylor negli intorni dei valori approssimati delle incognite. I valori approssimati delle incognite vengono calcolati o analiticamente o con costruzione grafica sfruttando, fra tutte le misure eseguite, solo quelle strettamente necessarie alla soluzione del problema geometrico: i valori così ottenuti, sono quelli che nella trattazione del paragrafo 3.2. del capitolo I abbiamo chiamato valori approssimati. Capitolo V - Rilievo topografico classico pagina 152 R.Galetto A.Spalla - Lezioni di Topografia Le incognite del problema sono pertanto, come sappiamo, le correzioni che a questi valori approssimati devono essere apportate per trovare i valori finali che realizzano la condizione Σ v i2 = min. Avremo quindi : E *C = E 0C + eC N *C = N 0C + nC E *D = E 0D + e D N *D = N 0D + n D dove i valori caratterizzati dall'apice zero rappresentano i valori approssimati delle coordinate, i valori asteriscati rappresentano i valori finali e i valori ec, nc, ed, nd le correzioni, incognite, da apportare ai valori approssimati per ottenere i valori finali. L'equazione generata risulta: f 1 (N A,EA,N C,E C,N D,E D; α 1) = arctg * * * * E 0D + eD − E A N 0D + n D − N A -arctg E 0C + eC − E A N 0C + nC − N A - α 1= v1 (4) Occorre a questo punto determinare i coefficenti delle incognite, che sono dati dalle derivate della funzione f 1 rispetto alle relative incognite. 0 ∂ f1 = ∂ eC 1 E0 − EA 1 + C0 NC − NA 2 ⋅ N 0C − N A 1 = 2 N 0C − N A N 0C − N A + E 0C − E A ( ) ( ) 2 =− N 0C − N A (d ) 2 0 AC Il denominatore della relazione soprascritta rappresenta la distanza fra i punti A e C calcolata per i valori approssimati delle coordinate. 0 ∂ f1 N0 − NA = a1 = − C 2 ∂ eC d 0AC 0 ∂ f1 = ∂ nC 1 ( ) −( E − E ) ⋅ = (N − N ) (N 0 C E 0C − E A A E 0C − E A = 2 2 2 2 2 0 0 0 E 0C − E A − N + E − E d 0AC C A C A C A 1+ 0 NC − N A Gli altri coefficienti delle incognite per l'equazione generata si ricavano analogamente e saranno: ) ( ) ( ) 0 ∂ f1 N 0D − N A = − = c1 2 0 ∂ eD d AD ( ) 0 ∂ f1 E0 − E = − D 0 2A = d 1 ∂ nD d AD ( ) Capitolo V - Rilievo topografico classico pagina 153 = b1 R.Galetto A.Spalla - Lezioni di Topografia Il termine noto l1 sarà dato dal valore che l'espressione generatrice (2) assume per i valori approssimati delle incognite e cioè : ED − EA E C − EA 0 l1 = arctg N 0D − N A 0 -arctg N 0C − N A - α1 (5) L'equazione generata data dalla (4) sviluppata in serie diventa pertanto : a1 eC + b1 nC + c1 eD + d1 nD + l1 = v1 (6) dove l'indice l indica che l'equazione angolare appena scritta che congiunge i punti A, C, D, è una delle quattro equazioni di questo tipo che si possono scrivere. Le altre tre saranno scritte per gli angoli α 2, α 3, α 4 (vedi figura 8) Per quanto riguarda gli angoli, avremo perciò queste quattro equazioni generate : a1 eC + b1 nC + c1 eD + d1 nD + l1 = v1 a2 eC + b2 nC + 0 eD + 0 nD + l2= v2 a3 eC + b3 nC + c3 eD + d3nD + l3 = v3 (7) a4 eC + b4 nC + 0 eD + 0 nD + l4= v4 I coefficienti c2 ,d2 e c4 ,d4 delle incognite eD, nD sono nulli perché nella seconda e nella quarta equazione generatrice il punto D non è coinvolto. Consideriamo ora le equazioni che si possono scrivere sfruttando le misure di distanze. La funzione che lega le coordinate dei punti alle distanze misurate è molto semplice, si basa sul Teorema di Pitagora N C D E figura 10 L'equazione generatrice sarà pertanto : (N C − N D ) + ( E C − E D ) − d C,D = 0 2 2 Da cui si ricava l'equazione generata : (N * C − N *D ) + (E 2 * C − E *D ) 2 − d C,D = v 5 (8) dove Nc*, Ec*, Nd* , Ed* sono le coordinate incognite dei due punti C e D e dC,D è la loro distanza misurata. Capitolo V - Rilievo topografico classico pagina 154 R.Galetto A.Spalla - Lezioni di Topografia Anche in questo caso considereremo incognite le correzioni da dare ai valori approssimati per ottenere i valori finali; avremo cioè : E *C = E 0C + eC N *C = N 0C + nC E *D = E 0D + e D N *D = N 0D + n D Introducendo i valori approssimati nella (8) l'equazione generata diventa : (N g5 (N *C,E*C,N*D,E*D; dC,D) = 0 C ) + (E 2 + n C − N 0D + nD 0 C + eC − E 0D + e D ) 2 - dC,D = v5 (9) Le derivate della funzione g sono : 0 ∂ g5 E 0C − E D = a5 = ∂ eC d 0CD ( ) 0 ∂ g5 N 0C − N D = b5 = ∂ nC d 0CD ( ) 0 ∂ g5 E 0C − E D = c5 = ∂ eD d 0CD ( ) (10) 0 ∂ g5 N 0C − N D = d5 = ∂ nD d 0CD ( ) Ricordiamo che le distanze che compaiono nelle (8), (9) e (10) sono distanze topografiche, riferite cioè alla proiezione cartografica sul piano (N,E) e che si ottengono da quelle misurate con la metodologia indicata al capitolo III. L'equazione generata (9) diventa quindi ∆E ∆N ∆E ∆N eC + 0 nC + 0 eD + 0 nD + ( d 0C,D − d C,D ) = v5 0 d C,D d C,D d C,D d C,D o anche con la solita notazione : a5 eC + b5 nC + c5 eD + d5 nD + l5 = v5 (11) Ci serviremo a questo punto delle altre due distanze misurate (dBC e dAC ) per costruire altre due equazioni dello stesso tipo della (11) seguendo lo stesso procedimento. Alle quattro equazioni angolari (7) se ne aggiungono pertanto le seguenti tre ricavate dalle misure di distanze a5 eC + b5 nC + c5 eD + d5 nD + l5= v5 a6 eC + b6 nC + 0 eD + 0 nD + l6 = v6 (12) a7 eC + b7 nC + 0 eD + 0 nD + l7= v7 Capitolo V - Rilievo topografico classico pagina 155 R.Galetto A.Spalla - Lezioni di Topografia A questo punto le (7) e le (12) vengono a costituire il sistema delle equazioni generate; da esso si ricava il sistema normale (come indicato al paragrafo 3.3. del capitolo I) Σa i a i eC + Σa i b i nC +Σa i c i eC + Σa i d i nC + Σa i l i =0 Σa i b i eC + Σb i b i nC +Σb i c i eC + Σb i d i nC + Σb i l i =0 Σa i c i eC + Σb i c i nC +Σc i c i eC + Σc i d i nC + Σc i l i =0 Σa i d i eC + Σb i d i nC +Σc i d i eC + Σd i d i nC + Σa i l i =0 la cui soluzione fornisce i valori incogniti. In realtà, come abbiamo visto al paragrafo 3.4 del cap. I, occorrerà seguire un procedimento iterativo. Resta ora da considerare il problema dell'attribuzione dei pesi alle (7) e alle (12). Consideriamo dapprima le equazioni (7) e calcoliamo l'espressione dell'e.q.m. del termine noto di una generica di esse*. 2 ∂f ml1 = ± 1 ⋅ m2α1 = ± mα 1 ∂ α 1 0 essendo ∂ f1 = −1 ∂ α1 Analogamente per le equazioni relative alle misure α 2, α 3, α 4 si ricava : ml1 = ± mα 1 ml2 = ± mα 2 ml3 = ± mα 3 Poiché l'e.q.m. con cui si misurano gli angoli non varia da un angolo all'altro in quanto tutti vengono misurati con lo stesso strumento e nelle stesse condizioni ambientali risulta m α1 = m α 2 = m α 3 = m α 4 e quindi per applicare la 37del capitolo I, è sufficiente porre p1 = p2 = p3 = p4 = 1 il che vuol dire che non si applica alcun peso alle equazioni perché sono già ridotte allo stesso peso. Questo risultato può essere generalizzato dicendo che quando nel termine noto compare una sola quantità misurata, non inserita in alcun tipo di funzione e con coefficiente unitario, le equazioni sono automaticamente ridotte allo stesso peso, a patto che rimanga costante per tutte le misure l'e.q.m. . Per brevità, diremo che la misura compare in forma bruta nell'equazione generatrice, quando appunto compare in essa non inserita in alcun tipo di funzione e con coefficiente uguale a + 1 o a - 1. Consideriamo ora l'equazione (12). Anche nelle equazioni generatrici relative alle misure di distanze, il termine noto è costituito dalla misura della distanza in forma bruta. Non possiamo * ) Si utilizza questa espressione illustrata nel capitolo I, al paragrafo 3.6 2 2 2 ∂f ∂f ∂f mli = ± i ⋅ m2P1 + i ⋅ m 2P2 +...+ i ⋅ m2Pm ∂P1 0 ∂P2 0 ∂Pm 0 Capitolo V - Rilievo topografico classico pagina 156 R.Galetto A.Spalla - Lezioni di Topografia però considerare tutte le equazioni di questo tipo automaticamente ridotte allo stesso peso perché gli e.q.m. di misure di distanze effettuate con il distanziometro elettronico, non possono essere considerate sempre costanti. Nel caso generale infatti l'e.q.m. di una distanza misurata con distanziometro elettronico è dato dalla relazione md = ± (k1 + k2 d ) (13) in cui il primo addendo è fisso e l'altro invece è proporzionale alla distanza misurata secondo un coefficiente k2 che è dell'ordine di 10-6 . Tuttavia la (13) vale per distanziometri che hanno portata geodetica; a noi invece interessano distanziometri con portata topografica cioè che sono in grado di misurare direttamente distanze di 3 km al massimo. Per tali distanziometri l'e.q.m. della misura può essere invece espresso dalla relazione : md = ± k1 dove k1 per la maggior parte degli strumenti è compreso fra mezzo centimetro e un centimetro. Possiamo pertanto dire che anche le equazioni (12) sono già automaticamente ridotte alla stesso peso. Questa asserzione potrebbe eventualmente non essere vera solo se le distanze misurate fossero di entità molto diversa fra di loro, perché allora bisognerebbe tenere conto del fatto che le distanze più lunghe danno un maggior contributo di stabilità geometrica alla triangolazione; ad esempio se osserviamo la figura 11 in cui si suppone si siano misurate le distanze d1 , d2 , d3 si può intuire che ai fini del dimensionamento della rete la misura d3 ha minor importanza delle misure d1 e d2 , N d1 d2 d3 E figura 11 Questo caso è però del tutto eccezionale e non lo prendiamo in considerazione perché ci obbligherebbe a fare un ulteriore discorso sulla metodologia di attribuzione dei pesi. 3.2.2 Generalizzazione del problema L'esempio fatto si riferisce ad un caso molto semplice; volendo invece porre il caso generale occorrerà considerare il problema in questi termini . Si abbiano: m1 punti di coordinate note m2 punti di coordinate incognite Capitolo V - Rilievo topografico classico pagina 157 R.Galetto A.Spalla - Lezioni di Topografia Si siano effettuate: n1 misure di angoli n2 misure di distanze Innanzitutto dovrà essere: n1+n2 > 2 m2 affinché si possano avere più equazioni che incognite nel sistema di equazioni generatrici. Le n1 misure angolari consentiranno descrivere n1 equazioni del tipo (5); in questo tipo di equazioni potremo avere 2, 4 o 6 incognite a seconda che le due direzioni che definiscono l'angolo misurato colleghino rispettivamente : • un punto incognito e due noti • due punti incogniti e uno noto • tre punti incogniti Le n2 misure di distanze consentiranno di scrivere n2 equazioni di tipo (8); in questo tipo di equazione potremo avere 2 o 4 incognite a seconda che la distanza sia stata misurata fra : • un punto noto ed uno incognito • due punti incogniti. Il procedimento sopra descritto viene eseguito di regola mediante un apposito programma di calcolo elaborato su calcolatore elettronico. Esistono in commercio vari programmi che possono servire allo scopo; in genere possiamo dire che essi utilizzano come dati di input i seguenti: • • • • Dati generali e cioè : • il numero dei punti incogniti, • il numero dei punti noti, • il numero delle equazioni che consentono al programma stesso di dimensionare il problema e liberare lo spazio di memoria necessario; dati relativi ai vertici e cioè : • il numero di identificazione di ciascun punto e le relative coordinate, • l'indicazione se il punto sia noto (e quindi le sue coordinate non debbano essere compensate) oppure incognito (e quindi con coordinate approssimate da compensare in fase di calcolo); dati relativi alle misure angolari e cioè : • il numero di identificazione dei tre punti che definiscono ciascun angolo misurato (punto di stazione e punti collimati) • le misure angolari relative; dati relativi alle misure di distanze e cioè : • il numero di identificazione dei punti fra i quali sono state misurate le distanze • le distanze relative. In base a questa serie di dati il programma determina i valori delle coordinate compensate e i relativi scarti quadratici medi sfruttando il principio dei minimi quadrati, che è stato descritto precedentemente. Capitolo V - Rilievo topografico classico pagina 158 R.Galetto A.Spalla - Lezioni di Topografia 3.3 Intersezioni. Le operazioni mediante le quali si infittisce la rete dei punti noti della triangolazione di base sono l'intersezione in avanti multipla e l'intersezione inversa multipla. 3.3.1 Intersezione in avanti. Spieghiamo prima che cos'è l'intersezione in avanti semplice. N P b θ(AP) α γ β θ(AB) A B d E figura 12 Da due punti A e B di coordinate note si eseguono le letture al cerchio orizzontale del teodolite, in particolare dal punto A si effettuano le letture LAP e LAB dal punto B si effettuano le letture LBA e LBP Si ricavano: α= LAB -LAP La distanza d tra i due punti è nota: ricavare b: sen β b= d sen γ essendo β= LBA -LBP d= (E B − E A ) 2 + ( N B − N A ) , quindi è possibile 2 γ=π -α-β Noto b si avrà: N P = N A + b cosθ P E P = E A + bsenθ P essendo θP = θAB - α e θAB = = arctg EB − E A NB − N A Il metodo esposto è quello classico dell'intersezione in avanti semplice. Però se commettiamo un errore nelle letture al cerchio e quindi un errore in α o in β, non abbiamo modo di accorgercene. Dal momento, invece, che i nostri punti di appoggio devono essere degni del migliore affidamento, dovremo ricorrere sempre all'intersezione in avanti multipla: Capitolo V - Rilievo topografico classico pagina 159 R.Galetto A.Spalla - Lezioni di Topografia N P α1 α 2 A1 α α3 4 A2 α5 α6 A4 A3 E figura 13 Lo schema scolastico di questa operazione è rappresentato dalla figura precedente e cioè: da n punti di coordinate note, si collima tante volte il punto P in modo da avere misure sovrabbondanti. Per ritornare allo schema di calcolo della triangolazione occorre procedere in questo modo: si ricavano graficamente, sfruttando due sole misure (ad esempio α 1, α 2) le coordinate approssimate del punto P. Si possono quindi scrivere equazioni generate del tipo (7) e calcolare i valori finali delle coordinate di P seguendo l'algoritmo delle osservazioni indirette come descritto al paragrafo 3.2. E' chiaro che l'intersezione multipla in avanti richiede di fare stazione in più punti noti, dai quali si collima il punto incognito. 3.3.2 Intersezione inversa. Lo schema dell'intersezione inversa è quello riportato nella figura seguente. N A2 A3 A1 β1 β 2 P E figura 14 Capitolo V - Rilievo topografico classico pagina 160 R.Galetto A.Spalla - Lezioni di Topografia Dal punto P incognito si collimano almeno tre punti noti; ci sarebbe un metodo di calcolo per ricavare le coordinate di P,in funzione delle coordinate di A1 , A2 , A3 e degli angoli β 1 , β 2, ma a noi non interessa perché anche l'intersezione inversa deve essere multipla per controllare la precisione delle coordinate di P; quindi il nostro schema sarà sempre quello della figura seguente. N A2 A3 A1 An As β1 β2 E P figura 15 Per il calcolo si deve procedere in questo modo. a) Si determinano per via grafica delle coordinate di P sfruttando tre letture, con il metodo della carta trasparente. Questo metodo consiste nel riportare tre semirette uscenti da un punto O su un foglietto di carta trasparente; quindi si sovrappone tale foglietto al foglio parametrato sul quale sono riportati i punti A1 , A2 .... An e si fa in modo che le semirette si sovrappongano ad A1 , A2 , A3 ; quando si è riusciti nell'impresa (piuttosto agevole), la posizione del punto O va riportata sul foglio parametrato e fornisce le coordinate approssimate di P. β1 β2 O b) Si procede con il calcolo analitico come per l'intersezione multipla in avanti (par. 3.3.1.). L'intersezione inversa è più economica di quella in avanti perché si fa stazione solo sul punto incognito anziché su tutti i punti noti; il punto P è scelto in posizione comoda per farvi stazione, mentre i punti noti potrebbero presentare la riguardo delle difficoltà. L'intersezione in avanti da, però, risultati migliori, cioè è più rigida, a parità di precisione nelle misure. Di solito le ditte che fanno rilievi preferiscono eseguire intersezioni inverse; bisogna allora che esse siano appoggiate su tanti punti (almeno cinque) in modo che sia bene valutabile l'errore con cui vengono determinate le coordinate di P. Capitolo V - Rilievo topografico classico pagina 161 R.Galetto A.Spalla - Lezioni di Topografia 3.3.3 Osservazione importante sulla questione rete di base punti di infittimento. Ci si potrebbe chiedere: perché se il tipo di misure e il metodo di calcolo della rete di base e quello dei punti di infittimento è lo stesso, non si considerano anche i punti di infittimento come vertici della triangolazione di base e non si calcola tutto insieme? I motivi di tenere separate le due operazioni sono i seguenti: • se la rete è troppo complessa, nel caso si sia commesso qualche errore di misura è difficile andarlo ad individuare, perché l'effetto di tale errore viene ripartito su più vertici e quindi è meno evidente il punto che incriminato; • la precisione delle due categorie di punti è diversa e quindi anche dando un peso diverso alle equazioni relative ai vertici di base ed a quelle relative ai punti di infittimento è difficile ottenere un risultato ottimo, nel senso che il calcolo per minimizzare gli scarti nei punti di infittimento, fa introdurre degli errori nei punti della rete di inquadramento. • i vertici della triangolazione di base devono essere materializzati meglio dei punti di infittimento perché devono rimanere nel tempo e consentire quindi eventuali il riferimento per rilievi successivi; i punti di infittimento hanno invece un carattere più provvisorio. 3.4 Poligonali. Al termine del rilievo svolto per mezzo delle triangolazioni e delle intersezioni, è possibile dare una rappresentazione dei punti rilevati. Ad esempio, mediante un plotter o su un video grafico, possiamo vedere la posizione di tali punti. ¤ ¤ σ ¤ σ Comune di ..... ¤ ¤ ¤ ¤ N E σ vertici trigonometrici ¤ punti di infittimento figura 16 Nel caso di una cartografia a grande scala la distanza media tra tali punti sarà,come già detto di circa 1 o 2 km. Per eseguire il rilievo di dettaglio occorre invece disporre di un reticolato di punti noti la cui distanza media sia di circa 100 m. Capitolo V - Rilievo topografico classico pagina 162 R.Galetto A.Spalla - Lezioni di Topografia N S L P A N R M G H F E figura 17 Le metodologie del rilievo di dettaglio consentono infatti elevata rapidità ed economia di esecuzione delle misure e sufficiente precisione, soltanto se si opera in un raggio di 100 metri dal punto di stazione dello strumento. Operando quindi dai soli punti della rete di inquadramento non si potrebbe rilevare tutto il territorio oggetto della cartografia. Perché sia invece possibile il rilievo di dettaglio, cioè la determinazione di ciascun punto comunque collocato sul terreno, occorrerà provvedere ad infittire la rete dei punti di appoggio, in modo cioè che la distanza fra essi diventi tale che i cerchi tracciati nel modo visto prima (e che esemplificano il campo d'azione del tacheometro) coprano tutto il territorio da rilevare. Per raggiungere questo scopo si scelgono opportunamente sul terreno dei nuovi punti e se ne determinano le coordinate con un'operazione topografica che si chiama poligonale. 3.4.1 Poligonale semplice. Col termine di poligonale semplice intendiamo quell’operazione topografica mediante la quale si determinano le coordinate dei punti intermedi di una spezzata formata da n lati e il cui primo e ultimo punto coincidono con due punti della rete di infittimento. Lo schema operativo della poligonale semplice consiste nel determinare le coordinate dei suoi vertici intermedi mediante la misura delle loro distanze reciproche e degli angoli formati dai segmenti che li congiungono. Per fare una poligonale tra due punti M e N della rete di inquadramento occorre pertanto, in primo luogo, scegliere sul terreno e materializzare i punti A, B, C, D, E, F che ne costituiscono i vertici. E' bene osservare che, poiché questi punti devono rimanere solo per il tempo della realizzazione del rilievo, la loro materializzazione avverrà: • in territorio urbano, infiggendo degli speciali chiodi nel manto stradale o in altri manufatti • in territorio extraurbano (campagna), con semplici picchetti in legno infissi nel terreno. Materializzati i vertici , si procede alla misura degli angoli e delle distanze. La poligonale semplice può essere ordinaria se le misure angolari vengono eseguite con il tacheometro e la lunghezza dei lati viene determinata con metodo tacheometrico; in questo caso si pone in stazione lo strumento su ciascun vertice, mentre sui due adiacenti si collocano delle stadie. Capitolo V - Rilievo topografico classico pagina 163 R.Galetto A.Spalla - Lezioni di Topografia Si eseguono le letture alla stadia e quelle ai cerchi orizzontale e verticale, e si ricavano: • gli angoli azimutali dalla differenza delle letture al cerchio orizzontale • le distanze con il metodo della misura indiretta (v. Cap. II punto 11.1) • i dislivelli mediante la formula della livellazione tacheometrica (v. Cap. V, punto 4.3). La poligonale semplice sarà invece di precisione se le misure angolari vengono eseguite con il teodolite e le misure di distanza vengono fatte mediante distanziometro elettronico. Ad esempio, utilizzando una stazione totale, al posto delle stadie si collocheranno dei prismi riflettenti. Per ogni lato della poligonale la distanza reali sarà misurate in modo diretto e da questa, in funzione dell’angolo zenitale, si ricaverà la distanza topografica tra i due punti che costituiscono gli estremi del lato e, mediante la formula semplificata della livellazione trigonometrica (v. Cap. V punto 4.2.4 formula (9)), il dislivello tra i due punti. N L F (ML) D B N (MA) (AB) α M a b β E C A E figura 18 Il calcolo della poligonale viene eseguito partendo dal punto iniziale di coordinate note e applicando semplici formule di trigonometria piana. Con riferimento alla figura 19, si opererà come segue: NA = NM + a . cos (MA) essendo (MA) = (ML) + α EA = EM + a . sen (MA) Allo stesso modo NB = NA + b . cos (AB) dove (AB) = (MA) + π + β - 2π EB = EA + b . sen (AB) Capitolo V - Rilievo topografico classico pagina 164 R.Galetto A.Spalla - Lezioni di Topografia L N N (ML) M α (MA) β M A a B (AB) b A E E figura 19 Proseguendo in tal modo si completa l'operazione di rilievo, giungendo a trovare le coordinate dell'ultimo vertice N. Esse, però, sono già note per il fatto che N è, a sua volta, un punto della rete di inquadramento. Il confronto delle coordinate di N, calcolate mediante le coordinate di M e le misure fatte nell'esecuzione della poligonale, con quelle già note, permette di giudicare la bontà delle misure effettuate e garantisce che la posizione dei punti A, B, C, ecc. (cioè dei vertici della poligonale) sia stata ben determinata. Consideriamo la figura 20 che segue, nella quale si è indicata la posizione vera dei vertici con A, B, ecc. e con A’, B’, ecc. quella che risulta in funzione delle misure eseguite. N L B' D F' D' F C' B M N* E E' C A A' N E figura 20 Supponiamo che il punto N sia finito, una volta risolta la poligonale, nella posizione N* (figura 20). Per valutare se la differenza di posizione S tra N e N*, che prende il nome di errore di chiusura laterale, sia accettabile, ci si basa su un criterio empirico, e cioè: si valuta quale sia l’e.q.m. di determinazione di un vertice della poligonale rispetto al precedente preso come riferimento in funzione della precisione con cui si misurano gli angoli e le distanze; detto mp tale e.q.m. l’errore di chiusura laterale dovrà risultare: S < 3 . mp n Capitolo V - Rilievo topografico classico pagina 165 R.Galetto A.Spalla - Lezioni di Topografia dove n è il numero dei lati della poligonale. Ad esempio: se l’e.q.m. nella determinazione di un punto è di ±.2 cm e la poligonale è composta da 16 vertici (escludendo quello iniziale e includendo quello finale) l’errore di chiusura laterale dovrà risultare inferiore a 24 cm. Se l’errore di chiusura laterale risulta accettabile si provvede ad una compensazione empirica della poligonale, che consiste nel ripartire l’errore di chiusura in modo proporzionale su tutti i vertici. Sia n il numero dei lati della poligonale, e quindi anche quello dei vertici successivi a quello di partenza; siano Ei* e Ni* le coordinate del vertice i-esimo non compensate; siano inoltre: SE = E *N − EN SN = N*N − N N le componenti sui due assi E e N dell’errore di chiusura laterale S; sia ancora li la lunghezza del lato i-esimo della poligonale. Le coordinate compensate Ei e Ni del vertice i-esimo saranno date dalle relazioni: Ei = E*i − l i SE n ∑ li i= 1 Ni = N i − l i * SN n ∑l i =1 i Esiste anche il modo di valutare l’errore di chiusura angolare di una poligonale, che qui non prendiamo in considerazione. Sono sconsigliabile poligonali costituite da un numero elevato di lati (superiore a dieci, per intenderci) dal momento che sarebbe da temere una sensibile propagazione degli errori di misura, dovuto al fatto che un errore commesso su un lato o su un angolo si ripercuote su tutti i lati successivi. 3.4.2 Rete di poligonali. Oltre allo schema della poligonale semplice si può avere lo schema della rete di poligonali; questo caso si verifica quando una o più poligonali semplici hanno punti intermedi in comune, come indicato nella figura che segue. Capitolo V - Rilievo topografico classico pagina 166 R.Galetto A.Spalla - Lezioni di Topografia D Nella figura con A, B, C, D si sono indicati i punti della rete di inquadramento, e con P1 e P2 i punti in comune tra le poligonali. P1 P2 A C B figura 21 In pratica, nell’esempio riportato in figura, possiamo considerare di avere tre poligonali semplici: una che va da A a B, una che va da B a P1, ed una che va da D a P2. Nel loro complesso le tre poligonali formano una rete di poligonali in cui P1 e P2 sono i punti comuni. Quando si ha il caso della rete di poligonali occorre effettuare un calcolo approssimato delle poligonali, scomponendo la rete in poligonali semplici e risolvendole in un qualsiasi ordine di priorità; quindi si deve procedere ad una compensazione rigorosa utilizzando lo stesso programma di calcolo usato per la compensazione delle reti di inquadramento. Ad esempio, con riferimento alla figura precedente, si può prima procedere la calcolo della poligonale A-C; quindi assumendo come dato noto le coordinate di P1 e di P2 ricavate dal calcolo della poligonale A-C si calcolano le poligonali B-P1 e D-P2; quindi si compensa la rete assumendo come coordinate approssimate dei vertici delle poligonali quelle precedentemente calcolate; anche le coordinate precedentemente calcolate per P1 e per P2 vengono considerate coordinate approssimate. 3.5 Celerimensura. Costituisce l'ultima fase del procedimento di rilievo, in quanto, con essa, si individuano i punti di dettaglio. Come si è appena visto, il foglio su cui viene tracciata la carta presenta ormai punti di coordinate note distanti non più di 100 - 200 metri; si tratta appunto dei vertici di poligonale che vengono a costituire la rete di appoggio del rilievo di dettaglio o celerimetrico. Facendo stazione sui vertici delle poligonali si rilevano per coordinate polari tutti i punti da riportare in cartografia: Come nel caso delle poligonali, le misure potranno essere eseguite con tacheometro e stadia o con stazioni totali e prismi riflettenti, a seconda della precisione che si vuole ottenere e anche in funzione della rapidità ed efficienza che si vuole conseguire. Non dimentichiamo infatti che l’uso della stazione totale o di strumenti analoghi consente la misura automatica di angoli e distanze e la loro registrazione su supporti elaborabili direttamente da personal computer. Quindi l’uso di strumenti moderni può essere consigliabile non solo per conseguire più elevate precisioni, ma anche per rendere il rilievo di dettaglio più economico. Supponendo allora di avere come rete di appoggio la poligonale rilevata precedentemente, poniamoci con il tacheometro sul punto C (vertice di poligonale). Capitolo V - Rilievo topografico classico pagina 167 R.Galetto A.Spalla - Lezioni di Topografia D 5 3 1 4 2 d1 B α5 α4 α3 α2 d5 d3 d2 d4 α1 C figura 22 Supponendo di dover effettuare il rilievo dell'edificio tratteggiato in figura, si misurano gli angoli azimutali α 1, α 2, α 3, α 4, α 5 per la misura dei quali si è considerata come direzione di riferimento il lato di poligonale precedente CB, si misurano le distanze d1, d2, d3, d4, d5 e i dislivelli ∆C1, ∆C2,......... In base a tali misure e alle coordinate dei vertici B e C della poligonale, si determineranno le coordinate dei punti 1, 2, 3, 4, e 5. Per quanto riguarda l’altimetria, dove il terreno presenta un cambiamento di pendenza, si determina la quota di un punto al suolo; l’insieme di questi punti, per i centri urbani, costituisce l’altimetria della carta. In territorio extraurbano, specialmente se collinare o montuoso, i punti quotati rilevati dovranno consentire di tracciare le curve di livello. Nell'eseguire il rilievo di dettaglio bisogna avere cura di scegliere convenientemente i punti da riportare poi sulla carta, in modo che essi diano, sia come numero, sia soprattutto, come accorta distribuzione, un'idea efficace e convincente dell'effettivo andamento planimetrico e altimetrico del terreno. 3.6 Considerazioni sul rilievo cartografico col metodo topografico. E’ importante sottolineare, a conclusione di questo argomento, quanto sia onerosa la costruzione di una cartografia con il metodo topografico. Consideriamo a titolo di esempio una delle possibili procedure operative. In genere una squadra che effettua il rilievo si compone di un caposquadra, di un operatore allo strumento di misura e di un secondo operatore che posiziona la stadia o il prisma sui punti da collimare. Mentre l’operatore allo strumento mette in stazione lo strumento sul vertice di poligonale, il caposquadra traccia rapidamente uno schizzo della parte di territorio da rilevare da quel vertice; quindi, quando l’operatore che effettua le misure è pronto, manda l’operatore con la stadia (o il prisma) su un punto da rilevare, viene fatta la misura, e così via fino a che sono stati rilevati tutti i punti da collimare da quel vertice di poligonale: Quindi si cambia vertice di poligonale e così via. Naturalmente ci devono essere buone condizioni atmosferiche. Inoltre se si è in città si è ostacolati dal traffico; se si è in campagna si è ostacolati dalle accidentalità del terreno nello Capitolo V - Rilievo topografico classico pagina 168 R.Galetto A.Spalla - Lezioni di Topografia spostarsi e dalla vegetazione che impedisce la collimazione della stadia o del prisma dal punto di stazione. E così via. Quanto sopra per far vagamente comprendere che i problemi del rilievo topografico non stanno nell’esecuzione dei calcoli, che peraltro sono anch’essi lunghi e laboriosi, ma soprattutto nella fase di esecuzione delle misure. Si deve inoltre considerare che una Ditta che lavora in questo settore dovrà inviare i suoi operatori a lavorare in località distanti dalla sua sede; questo implica costi di albergo e di trasferta per gli operatori e quindi costi rilevanti per lo svolgimento del lavoro. Questo è ovviamente un discorso che nulla ha a che fare con gli aspetti tecnici e scientifici dell’argomento, ma bisogna invece tener presente che nel mondo del lavoro molte volte gli aspetti economici determinano le scelte tecniche. E’ a causa di questi elevati costi (e lunghi tempi) di esecuzione che i rilievi cartografici vengono oggi di regola eseguiti col metodo fotogrammetrico, mentre il rilievo topografico viene usato solo per scopi particolari, come indicato all’inizio del Capitolo. Capitolo V - Rilievo topografico classico pagina 169 R.Galetto A.Spalla - Lezioni di Topografia 4 Rilievo altimetrico. 4.1 Livellazione geometrica. 4.1.1 Premessa. La livellazione geometrica è un'operazione che consente di misurare la differenza di quota, o dislivello, fra i punti della superficie fisica della terra. La livellazione geometrica può essere ordinaria o di precisione. I casi tipici in cui si utilizza la livellazione ordinaria sono: a) determinazione delle quote dei punti di inquadramento altimetrico di rilievi a grande scala effettuati sia con metodo topografico sia fotogrammetrico; b) integrazione altimetrica di rilievi fotogrammetrici a grande e media scala di carattere speciale; c) rilevamento di tracciati di opere di ingegneria (strade, ferrovie, canalizzazioni, ecc.). Si adotta invece generalmente la livellazione di precisione: a) per la determinazione delle quote dei caposaldi di livellazione della rete generale di inquadramento altimetrico; b) per valutare assestamenti del suolo che coinvolgono aree molto estese (decine o centinaia di km); c) per il controllo di grandi strutture; d) per il controllo dell'orizzontalità dei grossi impianti industriali. 4.1.2 Principio del metodo. Per determinare il dislivello fra due punti A e B mediante livellazione geometrica, si ricorre al livello che, come vedremo al paragrafo successivo, deve soddisfare essenzialmente la sola condizione di poter disporre orizzontale l'asse di collimazione del cannocchiale in qualsiasi direzione si effettui il puntamento. Lo schema della livellazione geometrica è il seguente: B ∆AB A qB qA s figura 4.1.2.-1 Si considerano due punti A e B distanti circa 100 m. A tale distanza le verticali passanti per i due punti possono essere considerate parallele e la superficie di riferimento delle quote è perciò assimilabile ad un piano orizzontale perpendicolare alle verticali stesse (vedi cap. III). Capitolo V - Rilievo topografico classico pagina 170 R.Galetto A.Spalla - Lezioni di Topografia Il dislivello fra i punti A e B sarà la differenza fra le distanze dei punti A e B della superficie di riferimento s . Per misurare il dislivello si procede nel seguente modo: 1) Si dispone una stadia graduata su ciascuno dei punti A e B. Le più comuni stadie verticali sono stecche di legno lunghe 3 m e larghe circa 10 cm . Recano generalmente una graduazione in cm la cui origine è il punto di appoggio sul terreno. Collimando la stadia e facendo la lettura ad un tratto orizzontale del reticolo si leggono i dm, si contano i cm e si stimano i millimetri (vedi figura 4.1.2.-2). Le stadie vengono disposte secondo la verticale con l'ausilio di una livella sferica montata su ciascuna di esse dalla parte opposta rispetto alla graduazione. 2 1 0 9 8 figura 4.1.2.-2 2) Si rendono verticali le stadie centrandole con le livelle sferiche montate su di esse; 3) si fa stazione con il livello su un punto O equidistante da A e B, ma non necessariamente allineato con essi; B A AO=OB O figura 4.1.2.-3 4) si collima dapprima la stadia posta in A, avendo resa orizzontale la linea di mira del livello con l'ausilio della livella di precisione posta sul livello stesso (vedi paragrafo successivo) e si esegue la lettura LA ; si ruota quindi il cannocchiale sino a collimare la stadia posta in B, si ricentra la livella e si esegue la lettura LB . Il dislivello sarà allora: ∆AB = LB - LA perché le visuali realizzate collimando le stadie in A ed in B sono orizzontali e perciò parallele alla superficie di riferimento. Capitolo V - Rilievo topografico classico pagina 171 R.Galetto A.Spalla - Lezioni di Topografia Quando si deve misurare il dislivello fra punti la cui distanza sia superiore ai 100 m o fra punti non visibili fra loro si eseguono più battute di livellazione. Si divide cioè la loro distanza in tratti per ciascuno dei quali si esegue una battuta dal mezzo. B ∆5 ∆4 ∆3 A ∆ AB ∆2 ∆1 superficie di riferimento delle quote figura 4.1.2.-4 La misura del dislivello risulta: ∆ΑΒ=∆1 + ∆2+ ...... ∆n 4.1.2.(1) 4.1.3 Descrizione del livello. Il livello è costituito da una piastra di base che è parte dello strumento stesso. Nella base sono prigioniere le tre viti calanti che sono collegate superiormente ad un collare su cui si innesta un'alidada ridotta libera di ruotare intorno all'asse del collare stesso. All'alidada è collegato un cannocchiale mediante un sistema costituito da una cerniera e da una speciale vite calante (vite di elevazione). Questo tipo di collegamento consente al cannocchiale di ruotare di angoli molto piccoli nel piano verticale. Sul cannocchiale è poi montata una livella torica a coincidenza. La condizione di rettifica richiesta per il livello è che la tangente centrale sia parallela all'asse di collimazione del cannocchiale. In fase costruttiva si centra l'asse di collimazione con particolari dispositivi ottici (i collimatori); viene poi centrata, sempre in laboratorio, la livella agendo sulle sue viti di rettifica. Si realizza così la condizione che ad asse di collimazione orizzontale sia orizzontale anche la tangente centrale della livella. In fase operativa allora, tutte le volte che verrà centrata la livella, sarà garantita l'orizzontalità dell'asse di collimazione. Capitolo V - Rilievo topografico classico pagina 172 R.Galetto A.Spalla - Lezioni di Topografia L 1 lente obbiettiva L 2 lente di messa a fuoco L 3 lente oculare R reticolo L1 L2 R L3 oculare di osservazione della R livella a coincidenza vite di elevazione viti calanti L3 R L2 L 1 figura 4.1.3-1 Dovendo quindi determinare con lettura dal mezzo il dislivello fra due punti, si mette in stazione lo strumento dapprima con la livella sferica (anch'essa montata sul livello ) che consente di arrivare a disporre l'asse di collimazione con una deviazione dall'orizzontale tale da rientrare nel campo di sensibilità della livella torica; si centra quindi la livella torica con la vite di elevazione e si procede finalmente alla lettura delle stadie. Naturalmente per il livello, come per il teodolite, le condizioni ideali di rettifica non possono essere realizzate costruttivamente, soprattutto non si mantengono indefinitamente con l'uso dello strumento e quindi la tangente centrale non sarà generalmente parallela all'asse di collimazione in maniera assoluta. Questa srettifica comporta l'insorgere di errori di misura. L1 L0 B ∆ AB A figura 4.1.3.-2 Capitolo V - Rilievo topografico classico pagina 173 R.Galetto A.Spalla - Lezioni di Topografia Nella determinazione del dislivello ∆ΑΒ infatti, se collimiamo la stadia in B avendo posizionato lo strumento in A (vedi figura 4.1.3-2) si nota che l'errore di srettifica fa sì che si legga il valore L1 invece del valore L0 . Se ci poniamo però con lo strumento ad eguale distanza dai due punti ed eseguiamo la lettura dal mezzo, poiché l'errore di srettifica può essere ritenuto costante nel breve arco di tempo necessario per eseguire le misure e poiché le distanze fra punto e stadie sono uguali, l'errore di lettura sarà uguale per ambedue le stadie. B ∆ A Nel calcolare il dislivello per differenza tale errore sarà quindi eliminato. La metodologia operativa della lettura dal mezzo consente dunque di correggere piccoli errori di srettifica. Ogni volta che si deve eseguire una lunga livellazione o comunque una livellazione che deve essere accurata, bisogna verificare l'effettivo stato di rettifica dello strumento. Si effettua allora una prova consistente nel misurare il dislivello fra due punti A e B mediante una battuta dal mezzo e una battuta eccentrica (figura 4.1.3-3). B ∆ A figura 4.1.3.-3 Se i valori del dislivello misurati con le due diverse metodologie coincidono, o differiscono della stessa entità della precisione intrinseca dello strumento, allora lo strumento può considerarsi rettificato; se la differenza fra i valori determinati è notevole si può valutare, in base ad essa, l'entità della srettifica strumentale ed eventualmente correggerla, se si è capaci, o comunque portare lo strumento in officina a farlo rettificare. 4.1.4 Livelli ordinari e livelli di precisione: precisioni conseguibili Capitolo V - Rilievo topografico classico pagina 174 R.Galetto A.Spalla - Lezioni di Topografia Nell'errore di determinazione di un dislivello concorrono errori dovuti a cause diverse (meccanica dello strumento, precisione della livella, ecc.); tuttavia la causa fondamentale è l'errore di stima che si commette, dal momento che è possibile leggere direttamente sulle stadie solo il cm. Poiché l'errore di stima è generalmente del decimo dell'intervallo di suddivisione, ogni lettura sarà affetta da un e.q.m. di ± 1 mm. Ciò comporta che, su una battuta di 100 m, con letture affette da ± 1 mm di errore, l'e.q.m. di determinazione del dislivello risulti ± 1 2 . Tale errore è preponderante rispetto a quelli generati dalle srettifiche strumentali. Occorrerà quindi studiare la possibilità di eliminare l'operazione di stima. Notiamo che non si può procedere semplicemente effettuando una suddivisione più fine delle stadie perché, alla distanza a cui esse sono generalmente poste, tale suddivisione non sarebbe più possibile, se non con cannocchiali molto potenti e, anche in questo caso, il filo del reticolo, ingrandito notevolmente, coprirebbe comunque alcuni tratti di suddivisione. Si procede invece aggiungendo al livello il dispositivo di lastra pianparallela che è costituito da una lastra a facce parallele che ha la possibilità di ruotare intorno ad un asse orizzontale perpendicolare all'asse di collimazione. figura 4.1.4.-1 Supponiamo che l'asse di collimazione segni sulla stadia una posizione intermedia fra due tacche. La rotazione della lastra pianparallela offre la possibilità di deviare, come in figura 4.1.4.-1, il percorso ottico; ruotando cioè la lastra si vede l'immagine della tacca sulla stadia scendere ( o salire ) sino a portarsi sul filo medio del reticolo. Lo spostamento sul piano verticale è proporzionale alla rotazione della lastra. La rotazione della lastra pianparallela viene realizzata nel seguente modo (vedi figura 4.1.4.-2). Si ruota una manopola alle cui estremità è fissato un ingranaggio che è innestato in una cremagliera incisa su un'asticella; la rotazione dell'ingranaggio provoca la traslazione dell'asticella; questa asticella è incernierata, ad una estremità, ad un dispositivo che trasforma il suo movimento di traslazione in un movimento rotatorio della lastra pianparallela; inoltre all'altra estremità porta una scaletta in vetro con una graduazione che va da 0 a 100. Capitolo V - Rilievo topografico classico pagina 175 R.Galetto A.Spalla - Lezioni di Topografia figura 4.1.4.-2 L'immagine della scaletta viene portata da un dispositivo a prisma su un vetrino con un traguardo di lettura, osservabile da apposito oculare. Il dispositivo quindi provoca contemporaneamente la traslazione dell'immagine della graduazione sul vetrino e la rotazione della lastra pianparallela; a sua volta la rotazione della lastra pianparallela provoca la traslazione dell'immagine della stadia sul reticolo del cannocchiale vero e proprio del livello. Il tutto è costruito e tarato in modo che, quando il movimento dell'asticella fa scorrere l'immagine della graduazione da 0 a 100 sul vetrino, la rotazione della lastra pianparallela provoca la traslazione di 1 cm di graduazione alla stadia sul reticolo del cannocchiale. Potremo pertanto leggere il cm sulla stadia e le sue frazioni sul micrometro della lastra 1 pianparallela. L'e.q.m. di lettura sarà pertanto ± del tratto graduato. 100 Naturalmente quando si adotta un livello così preciso da essere corredato dal dispositivo di lastra pianparallela, sarà indispensabile prevedere l'uso di stadie particolari indeformabili, nelle quali la graduazione è incisa su un nastro di invar; le comuni stadie di legno sarebbero infatti facilmente soggette alle deformazioni causate da variazioni di temperatura, umidità, ecc. . Lo schema delle stadie di precisione è il seguente: il nastro di invar che porta una graduazione al mezzo centimetro è saldamente vincolato solo alla parte inferiore del supporto esterno ed è montato superiormente con un dispositivo a molla in modo tale da rimanere comunque in posizione fissa anche per avvenute deformazioni del supporto. Capitolo V - Rilievo topografico classico pagina 176 R.Galetto A.Spalla - Lezioni di Topografia 4.1.5 Come valutare la precisione conseguibile nelle operazioni di livellazione geometrica ∆AB = LB - LA Consideriamo la relazione L'e.q.m. del dislivello per ogni battuta si ricava sfruttando la relazione già descritta al cap. I1 2 2 ∂ ∆ AB ∂ ∆ AB m∆ = ± ⋅ m 2LA + ⋅ m2LB ∂ LA ∂ LB Le letture LA ed LB sono eseguite con la stessa accuratezza e perciò mLA = mLB = mL m ∆ = ± 2 ⋅ m 2L = ± m L 2 Con mL viene indicato il generico e.q.m. di stima della lettura alla stadia; il suo valore è ± 1 10 dell'intervallo di suddivisione della graduazione; se la stadia è graduata al cm mL = ± 1 mm m ∆ = ± m L 2 = ± 1 ⋅ 2 = 1,4 mm Se per la misura del dislivello fra due punti sono necessarie n battute di livellazione, l'e.q.m. del dislivello sarà m 2DAB = m 2∆1 + m 2∆ 2 + ...+m 2∆n Poiché le battute vengono assunte di lunghezza uguale m 2∆AB = n ⋅ m 2∆ m ∆AB = ± n ⋅ m ∆ Se consideriamo ad esempio una livellazione ordinaria di 10 battute, si ha un e.q.m. m ∆AB = ± 10 ⋅ 1,4 mm = ± 4,47 mm ≈ 4 ,5 mm Se consideriamo di operare con stadie di 3 m, il massimo dislivello misurabile ad ogni battuta sarà di circa 2..50 m e quindi il dislivello massimo misurabile con 10 battute sarà di circa 25 m. 3.00 metri B ∆ 3.00 metri 2.50 metri A 1 Si utilizza questa espressione illustrata nel capitolo I, al paragrafo 3.6 2 2 2 ∂ f ∂ f ∂f mli = ± i ⋅ m 2P1 + i ⋅ m 2P2 +...+ i ⋅ m2Pm ∂P1 0 ∂P2 0 ∂Pm 0 Capitolo V - Rilievo topografico classico pagina 177 R.Galetto A.Spalla - Lezioni di Topografia La precisione del metodo, intesa come rapporto fra sensibilità e massima quantità misurabile ±4,5 mm sarà allora: = 1,8 ⋅ 10− 3 25 m Quanto detto indica come la livellazione geometrica sia un'operazione veloce che consente il conseguimento di precisioni notevoli con uno strumento, il livello, relativamente facile da usare anche da operatori non altamente specializzati. 4.1.6 Livellazione geometrica di precisione. Qualora occorrano precisioni di determinazione delle quote maggiori di quelle conseguibili con il metodo della livellazione ordinaria, e cioè volendo definire il piano del ferro di una ferrovia o volendo controllare i cedimenti di una struttura in condizioni di carico ecc. , si adotta la livellazione geometrica di precisione, per la quale si utilizza il livello di precisione precedentemente descritto. Con la livellazione geometrica di precisione si ottiene un e.q.m. nelle misure del dislivello di ± 1 mm / km. Poiché l'e.q.m. di determinazione del dislivello di una livellazione geometrica ordinaria è dovuto essenzialmente all'errore di stima nella lettura alla stadia, in fase di livellazione geometrica di precisione si adotteranno accorgimenti per rendere tale errore di ordine inferiore. Il livello di precisione avrà allora una meccanica più precisa, un cannocchiale con possibilità di maggiori ingrandimenti e soprattutto sarà dotato del già descritto dispositivo di lastra pianparallela. Sulla graduazione portata dal bottone che comanda il dispositivo di lastra pianparallela si legge il centesimo della graduazione della stadia. Le stadie adottate per la livellazione geometrica di precisione sono di tipo indeformabile a nastro di invar recanti generalmente una graduazione al mezzo centimetro. L'e.q.m. di ogni battuta sarà quindi m ∆ = ± 2 ⋅ 0,05 mm = ± 0,07 mm Riferendoci, come per la livellazione geometrica ordinaria, al dislivello massimo misurabile con 10 battute, che è dell'ordine dei 25 m, la precisione conseguibile con la livellazione geometrica di precisione risulta 0,07 mm 10 ⋅ = 8,8 ⋅ 10- 6 25 m Capitolo V - Rilievo topografico classico pagina 178 R.Galetto A.Spalla - Lezioni di Topografia 4.1.7 Determinazione delle coordinate altimetriche nel rilievo topografico a grande e media scala mediante livellazione geometrica. Si consideri la figura 4.1.7.-1 nella quale si sono indicati con σ i caposaldi della livellazione nazionale e l con i punti di cui si vogliono determinare le quote; questi punti potrebbero, ad esempio, essere i vertici delle poligonali impostate per la costruzione della planimetria. l l l l l l l figura 4.1.7.-1 Per determinare le coordinate altimetriche dei punti λ si procede ad operazioni di livellazione geometrica ripetendo l'andamento della poligonale e misurandone i dislivelli fra i vertici. Le livellazioni potranno andare da un punto di quota nota ad un altro di quota nota, oppure richiudersi ad anello. Il controllo delle livellazioni che congiungono punti di quota nota (livellazione A-B in figura) è immediato, basterà infatti verificare che la somma dei dislivelli parziali delle battute tra A e B sia uguale alla differenza tra le due quote note QA e QB e cioè Σ∆i = QB - QA 4.1.7.(1) Un altro modo di controllare la bontà dell'esecuzione è di partire da un punto e richiudere ad anello la livellazione su esso (livellazione B-B vedi figura 4.1.7.-1). Si controlla che la somma dei dislivelli sia nulla e cioè Σ∆i = 0 4.1.7.(2) Sia la 4.1.7.(1) sia la 4.1.7.(2) non saranno in genere soddisfatte ma presenteranno uno scarto v detto errore di chiusura. La valutazione dell'errore di chiusura permette di stabilire se l'operazione di livellazione sia stata eseguita con l'accuratezza necessaria. Viene infatti stabilito un errore di chiusura massimo ammissibile, tolleranza, dove m∆ è l’e.q.m. di battuta del metodo di livellazione impiegato. t =± m∆ . n . 3 Se dobbiamo eseguire una livellazione geometrica ordinaria di 20 battute, sapendo che m∆ % ± 1,4 mm, possiamo avere una tolleranza pari a Capitolo V - Rilievo topografico classico pagina 179 R.Galetto A.Spalla - Lezioni di Topografia t =± m∆ . 20 . 3 =± 1,4 mm . 20 . 3 = =± 18,79 mm Se l'errore di chiusura supera tale valore limite, significa che l'operazione di livellazione non è stata svolta correttamente, è cioè affetta da errori grossolani. In tal caso occorre rieseguire la livellazione. Se invece l'errore di chiusura rientra nei limiti imposti dalla tolleranza si procede ad una compensazione empirica distribuendo l'errore di chiusura sui dislivelli parziali. 4.1.8 Compensazione globale di un sistema a più poligonali mediante il metodo delle osservazioni indirette Il metodo di compensazione empirica descritto risulta valido quando ci si trova nella condizione di dover compensare un'unica poligonale od un unico anello di livellazione. Quando invece si debba eseguire un rilievo in cui le livellazioni siano numerose e collegate fra loro da punti comuni, il problema della compensazione non può essere risolto semplicemente compensando ciascuna poligonale separatamente secondo il metodo visto al precedente paragrafo; infatti si introdurrebbe in questo caso come fattore del tutto arbitrario la priorità di compensazione sulle diverse poligonali, il che comporterebbe l'impossibilità di compensare le quote dei punti comuni già compensate come appartenenti ad una poligonale, in base all'errore di chiusura di un'altra. Occorre quindi prendere in esame un metodo più rigoroso per eseguire una compensazione globale delle livellazioni che tenga conto di tutte le misure. Verrà applicato anche ni questo caso il metodo delle osservazioni indirette. Le incognite saranno le coordinate altimetriche di quei punti su cui convergono più anelli di livellazione; i loro valori approssimati saranno anche in questo caso determinati sfruttando il numero di misure strettamente necessario. L'equazione generatrice che lega le incognite Qi alle quantità misurate ∆i è Qi - Qi+1-∆i = 0 Indicando con Q°i i valori approssimati delle incognite e con qi le correzioni da apportare ad essi per ottenere i valori finali, l'equazione generata risulta: Q°i + qi - Q°i+1 - qi+1 - ∆i = vi 4.1.7.(3) o anche qi - qi+1 +(Q°i -Q°i+1 - ∆i )= vi che si presenta già in forma lineare. Nell'applicazione del metodo delle osservazioni indirette alla compensazione di più poligonali, occorre prestare particolare attenzione all'attribuzione di pesi diversi a equazioni relative a poligonali diverse. Consideriamo infatti lo schema in figura: Capitolo V - Rilievo topografico classico pagina 180 R.Galetto A.Spalla - Lezioni di Topografia A D C B figura 4.1.7.-2 si sono eseguite livellazioni che hanno portato alla determinazione dei dislivelli: ∆AB , ∆AC , ∆ΑD, ∆BC, ∆BD, ∆CD fra i punti A, B, C, D In base a tali dislivelli devono essere determinate e compensate le quote dei punti suddetti. Il sistema di equazioni generate è per j=1,3, i=j+1,4 k=1,6 Qi - Qi-∆ij =vk qi - qj +(Q°i -Q°j - ∆ij )= vk 4.1.7.(4) L'e.q.m. di un'equazione dipende essenzialmente dall'e.q.m. del termine noto: esaminiamo dunque il termine noto della 4.1.7.(4). In esso è presente il dislivello ∆ij che risulta dalla somma dei dislivelli parziali relativi alle diverse battute che congiungono i punti i e j. Ora, proprio perché i dislivelli fra i diversi punti vengono determinati con livellazioni geometriche composte nelle quali è di volta in volta diverso il numero di battute, poiché l'errore di determinazione del dislivello è funzione della radice quadrata del numero di battute, ne consegue che i dislivelli vengono determinati con precisioni diverse. Esempio Nell’esempio di figura 4.1.7- 2 m∆AB = ± 4 mδ m∆BC = ± 3mδ ( mδ è l'e.q.m. di ogni singola battuta). Il peso delle 4.1.7.(4) è diverso. Per omogeneizzarle realizzando la condizione che gli e.q.m. di ciascuna equazione risultino uguali fra loro, si attribuisce un peso pi ad ognuna di esse. In tal modo il risultato da conseguire non è più la minimizzazione della somma degli scarti al quadrato Σvi2=min, ma Σvk2 pk =min Ciascun termine delle 4.1.7.(4) viene moltiplicato per il coefficiente pk che viene assunto come 1 pk = n i, j dove n i, j è il numero di battute della livellazione composta operata fra i punti i e j. Una volta attribuiti i pesi delle equazioni generatrici relative ai diversi punti la soluzione dell'algoritmo delle Osservazioni Indirette si presenta semplificata rispetto al Capitolo V - Rilievo topografico classico pagina 181 R.Galetto A.Spalla - Lezioni di Topografia caso generale perché le equazioni generatrici sono per questo tipo di problema già in forma lineare. Il sistema normale si costruisce quindi in base alle 4.1.7.(3) e la sua soluzione fornisce le correzioni da apportare ai valori approssimati delle incognite per ottenerne i valori finali senza che occorra iterare il procedimento. Capitolo V - Rilievo topografico classico pagina 182 R.Galetto A.Spalla - Lezioni di Topografia 4.2 La livellazione trigonometrica ( L. T. ). 4.2.1 Premessa. Abbiamo già detto alcune volte, e qui lo ripetiamo, che in queste dispense prendiamo in considerazione le operazioni topografiche che vengono eseguite dai topografi per la costruzione di carte topografiche a grande e media scala e sappiamo che le operazioni che a tal fine un topografo esegue richiedono che egli debba collegare, in ogni singola operazione di misura, punti la cui distanza reciproca non supera in genere i 5 km. Anche nel trattare la livellazione trigonometrica (L.T.) ci metteremo in questa ipotesi, e pertanto nell'esporre questo tipo di operazione potremo sostituire il geoide con la sfera locale. 4.2.2 Definizione di L. T. La L.T. è un'operazione topografica che permette di determinare la differenza di quota fra due punti A e B mediante misure angolari eseguite con il teodolite; l'operazione richiede che sia nota la distanza topografica tra i punti. Purché la visuale tra i due punti sia libera, essi possono essere anche molto distanti fra loro (qualche chilometro) e tra di essi può esservi anche un forte dislivello (centinaia o anche migliaia di metri). Se eseguita con cura, questa operazione può avere una discreta sensibilità e permette di raggiungere un'elevata precisione (vedremo in seguito di quantificare queste espressioni). 4.2.3 Schematizzazione del problema. Consideriamo la figura 4.2.3.-1. In essa sono rappresentati due punti: A di quota nota qA, B di quota non nota qB vB CS Β vA q B CT qA d Α R A δ fig. 4.2.3.-1 Capitolo V - Rilievo topografico classico pagina 183 R.Galetto A.Spalla - Lezioni di Topografia Per l'ipotesi fatta sulla distanza topografica d fra i due punti, che consideriamo inferiore od uguale a 5 km, possiamo sostituire alla superficie di riferimento delle quote, che è il geoide, la sfera locale di raggio RA ; ne segue che possiamo supporre le due verticali vA e vB , passanti per A e per B rispettivamente complanari ed intersecantesi nel centro O della sfera locale. Abbiamo detto inoltre che la visuale tra i due punti A e B deve essere libera, il che significa che facendo stazione in A con un teodolite si deve poter osservare un segnale posizionato sul punto B (nella figura il teodolite ed il segnale sono ovviamente rappresentati in una scala molto maggiore di tutto il resto del disegno). Con l'operazione di L.T. si determina in realtà il dislivello tra il centro CT del teodolite posto in stazione in A e il centro CS del segnale posto in stazione in B; poiché però è nota sia l'altezza strumentale h (distanza fra CT ed A) sia l'altezza del segnale (distanza fra CS e B), determinare il dislivello fra CT e CS equivale a determinare il dislivello fra i due punti A e B. Pertanto nelle figure che seguiranno si considererà che l'asse di collimazione del cannocchiale del teodolite coincida con la distanza AB. 4.2.4 Schematizzazione dell'operazione. Ponendosi in stazione con il teodolite sul punto A si misura l'angolo zenitale ZA ; sono noti come già detto la quota qA e la distanza topografica (vedi figura 4.2.4.-1). B qB A d qA RA δ O figura 4.2.4.-1 E' importante conoscere la distanza d perché, come vedremo, per la determinazione di qB occorre sia noto l'angolo δ; essendo noto il valore di d e potendosi calcolare il valore RA2, si ricava immediatamente d δ= 4.2.4.(1) R 2 a 1− e 2 RA = 1 − e 2 sen 2 ϕ A Questa relazione e il significato dei suoi termini sono esposti al paragrafo 1.2 del capitolo II Capitolo V - Rilievo topografico classico pagina 184 R.Galetto A.Spalla - Lezioni di Topografia Per ricavare la formula che ci dà il valore di qB, disponendo di ZA e qA, occorre richiamare il teorema di Nepero che mette in relazione due lati di un triangolo con i due angoli opposti (vedi figura 4.2.4.-2). b−a = b+a 1 (β − α) 2 1 tg ( β + α ) 2 tg 4.2.4.(2) B α c A β b a γ C figura 4.2.4.-2 Confrontando le figure 4.2.4.-1 e 4.2.4.-2 si vede che: β = π- ZA 4.2.4.(3) α = π -[(π- ZA) + δ ] = ZA - δ Sostituendo le 4.2.4.(3) nelle 4.2.4.(2) si ricava: β - α = π - ZA - ZA + δ=π -2 ZA + δ= β +α=π -δ e quindi: π δ − tg ZA − 1 1 π δ 2 2 tg ( β − α ) = tg (π − 2 ZA + δ ) = tg − ZA − = = 2 2 2 2 1 + tg π tg Z − δ A 2 2 tg δ tg Z A − 2 1− π tg 1 δ 2 = = = cotg Z A − 1 δ δ 2 + tg Z A − tg Z A − π 2 2 tg 2 Analogamente: 4.2.4.(4) Capitolo V - Rilievo topografico classico pagina 185 R.Galetto A.Spalla - Lezioni di Topografia 1 tg 1 (β + α ) 2 1 = tg 1 (π − δ ) 2 = .....= 1 δ = tg 1 2 δ tg 2 4.2.4.(5) E quindi tenendo conto che: b = qB + R a = qA + R la 4.2.4.(2) diventa: qB + R − qA − R δ δ = co tg Z A − ⋅ tg qB + R + qA + R 2 2 δ δ q B − q A = ( q B + q A + 2R)cotg Z A − ⋅ tg 2 2 da cui e quindi δ δ q B = q A + ( q B + q A + 2R)cotg Z A − ⋅ tg 2 2 4.2.4.(6) Naturalmente la 4.2.4.(6) sembra non risolvere il problema perché anche a destra dell'uguale compare qB ; si deve notare però che qB è comunque una quantità piccola rispetto a 2R; il che permette di ricavare qB in questo modo: • si calcola un primo valore di q’B mettendo al posto della quota qB che compare a destra dell'uguale un valore qB° , approssimato (anche stimato ad occhio in maniera grossolana): δ δ ' 0 q B = q A + ( q B + q A + 2R)cotg Z A − ⋅ tg 2 2 si calcola quindi il valore di qB definitivo mettendo, al posto di qB a destra dell'uguale, il valore q'B ricavato: δ δ ' q ' = q A + ( q B + q A + 2R)cotg Z A − ⋅ tg B 2 2 4.2.4.(7) Questa formula non è però quella definitiva. Innanzitutto possiamo sostituire nelle 4.2.4.(7) tg ha: δ δ δ con ; infatti sviluppando in serie tg si 2 2 2 δ2 δ δ tg = 1 + + ........ 12 2 2 δ2 d2 52 = = ≅ 5.10−8 2 2 12 12 ⋅ R 12 ⋅ 6378 δ δ quantità trascurabile rispetto all'unità e quindi possiamo considerare tg ≅ 2 2 δ δ Sostituendo tg con nelle 4.2.4.(7) si ha: 2 2 Per d = 5 km, assumendo R = 6378 km, risulta: Capitolo V - Rilievo topografico classico pagina 186 R.Galetto A.Spalla - Lezioni di Topografia d d q B = q A + ( q 'B + q A + 2R)cotg Z A − ⋅ 2R A 2R A e quindi qB = qA + ( q 'B + q A 2R A d + 1)cotg Z A − ⋅d 2R A 4.2.4.(8) Introduzione di un valore medio di R. Nelle 4.2.4.(8) compare il valore RA ,raggio della sfera locale nel punto A; sembrerebbe pertanto necessario calcolare per ogni battuta di livellazione trigonometrica il valore del raggio della sfera locale mediante la relazione esposta al paragrafo 1.2 del capitolo II, il che implica tra l'altro la conoscenza della latitudine del punto di stazione. In realtà nella 4.2.4.(8), si può utilizzare sempre un valore R* costante per tutta l'Italia, calcolato per la latitudine media italiana che è ϕm = 41° . Il valore di R* vale : R* = 6.375.000 m Il valore esatto del raggio della sfera locale varia in Italia in funzione della latitudine massima e minima che possiamo assumere rispettivamente uguali a 46° e 37° ; a tali valori corrispondono i due raggi delle sfere locali Rmin e Rmax che valgono Rmax = 6.378.871 Rmin = 6.372.228 ϕ= 46 per per ϕ= 37 Assumendo pertanto sempre il valore R* = 6.375.000 si commette un errore che vale al massimo ∆R = 3800 m Introducendo nella 4.2.4.(8) R* anzichè il valore esatto di R si commette un errore q − qA percentuale del termine B che vale 2R ∆R 3.800 = = ±6 ⋅ 10 −4 R * 6.375.000 Poiché il termine (q'B + qA ) vale al massimo 10.000 m (valore che si ottiene quando sia il punto A sia il punto B si trovano in alta montagna), la quantità (q'B + qA)/2R* varrà al massimo: qB − qA 10.000 = = 7.8 ⋅ 10 −4 2R 2 ⋅ 6.375.000 ∆R Applicando a tale valore l'errore percentuale precedentemente calcolato si ha un errore R* assoluto ε nella quantità (q'B + qA)/2R* che vale: ε = ± (6.10-4) . (7.8 . 10-4) = ± 4.7 .10-7 Capitolo V - Rilievo topografico classico pagina 187 R.Galetto A.Spalla - Lezioni di Topografia Ne deriva che, anche ipotizzando che il dislivello incognito ∆AB = qB - qA che deve essere determinato, abbia un valore molto elevato, ad esempio 2000 m, commettendo un errore di ± 4.7 .10-7 nel calcolo di (q'B + qA)/2R* si commette un errore nel dislivello pari a : ε = ± ∆AB 4.7 .10-7 ≅ mm che può essere considerato trascurabile, data la precisione del metodo (vedi successivo paragrafo 4.2.6.). d Vediamo ora se anche nel rapporto che compare come argomento della cotangente, si 2R può introdurre sempre il valore R* al posto del valore RΑ relativo alla latitudineϕΑ del punto A di stazione. d Per fare questo calcoliamo il valore γ = per i valori Rmin e Rmax; sempre prendendo in 2R considerazione la distanza massima di 5 km; si ha rispettivamente: d 5.000 γmin= = ⋅ 206.264 = 80",92 2R min 2 ⋅ 6.372.229 γmax= d 5.000 = ⋅ 206.264 = 80" ,83 2R min 2 ⋅ 6.378.871 Come si vede la differenza del valore γ calcolata per i punti di latitudine minima e massima è di ∆γ= 0",09 e quindi del tutto trascurabile in quanto Z viene misurato, nella migliore delle ipotesi, con un e.q.m. = ± 5" . d Pertanto anche nel termine si può assumere sempre 2R R = R* = 6375 km . La 4.2.4.(8) diventa pertanto: qB = qA + ( q 'B + q A 2R * d + 1)cotg Z A − ⋅d 2R * 4.2.4.(9) La 4.2.4.(8) non è ancora la formula definitiva perché in essa occorre introdurre una correzione del valore Z dovuta alla influenza della rifrazione atmosferica. 4.2.5 Influenza della rifrazione atmosferica. Poiché la densità dell'aria diminuisce con l'aumentare della quota, i raggi luminosi che si originano da un punto si propagano nell'atmosfera secondo delle traiettorie curve e non secondo delle semirette. Questo fenomeno non è avvertibile per distanze brevi, ma diventa sensibile su distanze di centinaia di metri o di chilometri. In particolare nello schema delle L.T. questo fenomeno fa sì che quando si collima da A il punto B l'asse di collimazione (a.c. in figura 4.2.5.-1) si dispone non secondo la congiungente A - B, ma secondo la tangente della traiettoria del raggio ottico che da B arriva in A. Capitolo V - Rilievo topografico classico pagina 188 R.Galetto A.Spalla - Lezioni di Topografia Ne consegue che l’angolo zenitale Z'A che viene letta al cerchio verticale deve venire corretta dell'angolo ε tra tangente e corda. I geodeti hanno dimostrato teoricamente e poi verificato sperimentalmente che l'angolo è proporzionale alla distanza secondo la relazione d ε=k 4.2.5.(1) 2r dove k è detto coefficiente di rifrazione. Il valore di k varia in funzione del luogo e dell'ora del giorno; i geodeti, in base a sperimentazioni condotte nell'arco di decine di anni, hanno determinato il valore di k per tutto il territorio italiano, ed in particolare i valori che k assume durante le varie ore della giornata, per ogni giorno dell'anno. Inoltre i geodeti hanno anche determinato diverse formule per il calcolo di k in funzione della temperatura, della pressione atmosferica ecc. . Per la precisione che si vuole conseguire nelle operazioni topografiche, si può però evitare di fare ogni volta il calcolo di k ed assumere per esso un valore medio k*=0.13; pertanto la 4.2.4.(9) assume la seguente espressione: qB = qA + ( q 'B + q A 2R * d d + 1)cotg Z A + k * − 2R * 2R * ⋅d 4.2.5.(2) e introducendo k*=0.13 ed R*=6.375.000 si ha in definitiva : q 'B + q A 0,87 q B = q A + + 1 cotg Z A − ⋅d 12.750.000 12.750.000 4.2.5.(3) N.B. : d, qA . q'B vengono introdotti in metri. vΑ asse collimazione vΑ ζΑ Β ε d Α figura 4.2.5.-1 Capitolo V - Rilievo topografico classico pagina 189 R.Galetto A.Spalla - Lezioni di Topografia 4.2.6 Precisione del metodo. Diamo per verificate le tre condizioni che seguono: I. Per eseguire la L.T. bisogna usare un teodolite di buona precisione, cioè del tipo WILD T2, che ha una precisione intrinseca di ± 1". Utilizzando un teodolite di questo tipo si può pensare di misurare l'angolo Z con un e.q.m. di + 5"; la differenza fra questo e.q.m. e quello nominale di + 1" è dovuta come sappiamo, all'influenza dell'ambiente reale sull'operazione di misura. II. La distanza d sia ricavata da misure con distanziometro elettronico oppure ricavata dalle coordinate note dei punti A e B; in ogni caso essa sia affetta da e.q.m. di ± 20 cm al massimo. III.Utilizzando per k il valore k* = 0.13 si commette un e.q.m. in k pari ad mk = + 0.016; questo dato deriva da verifiche sperimentali eseguite dai geodeti. Dati dunque per verificati questi tre assunti, deriva che l'e.q.m. nella determinazione di qB vale: m qB = ± 1 cm per d = 500 m m qB = ± 2 cm per d = 1000 m m qB = ± 8 cm per d = 5000 m Il calcolo di questi e.q.m. viene effettuato applicando alla 4.2.5.(2) la 2.(2) del capitolo I ed assumendo mZA = ± 5" mK = ± 0.018 mAq = ± 0.20 cm Con un tale procedimento si può calcolare l'e.q.m. di qB per qualsiasi distanza d . 4.2.7 Impiego della livellazione trigonometrica. La livellazione trigonometrica viene usata per determinare le quote dei punti delle reti di inquadramento nei rilievi sia topografici sia fotogrammetrici. Per poter applicare la L.T. occorre che le visuali tra i punti che si vogliono collegare siano libere; quindi la L.T. si applica male in pianura ed in particolare nei territori urbani. Si usa molto invece quando il territorio da rilevare è molto esteso, i punti della rete di inquadramento sono molto distanti tra di loro (qualche chilometro) ed il terreno è un po' mosso, in modo che presenti punti dominanti su cui posizionare i punti di inquadramento. Non conviene fare tuttavia battute più lunghe di 5 km altrimenti la precisione del metodo decade notevolmente; questo anche se la rete di inquadramento potrebbe in teoria essere costituita da punti collocati a distanza maggiore; in tal caso è bene infittire i punti in modo da non dover superare mai, con una sola battuta di L.T., la distanza di 5 km. La L.T. viene inoltre impiegata, come vedremo, per il controllo di grandi strutture; in tal caso le battute sono molto brevi, dell'ordine delle decine o di poche centinaia di metri, e i dislivelli vengono determinati con e.q.m. rispettivamente di pochi decimi di millimetro o di pochi millimetri. Capitolo V - Rilievo topografico classico pagina 190 R.Galetto A.Spalla - Lezioni di Topografia 4.3 Livellazione tacheometrica. Si esegue impiegando il tacheometro e consente di determinare il dislivello tra due punti distanti all'incirca 100 metri. La distanza fra i punti (che pure deve essere nota) viene determinata indirettamente con il cannocchiale distanziometrico e la stadia (paragrafo 11 del capitolo II) Lo schema si può evincere dalla figura 4.3-1. l ϕ B h A ∆ AB d figura 4.3-1 Con semplici considerazioni geometriche si ricava per il dislivello tra i due punti la formula: ∆AB = d . cotgϕ + h - l dove : d distanza topografica tra i due punti; ϕ lettura al cerchio verticale del tacheometro; h altezza strumentale; H lettura alla stadia in corrispondenza al filo medio del reticolo. Siccome d = CHsen2ϕ la formula precedente diviene: ∆AB = CHsen2ϕ. cotgϕ + h - l = CHsenϕ+ h - l Su una distanza appunto dell'ordine dei ±100 metri la precisione risulta di + 10÷20 cm. Valutiamo ora la precisione del metodo. 2 ∂ ∆ ∂ ∆ ∂ ∆ ∂ ∆ 2 2 2 2 m∆ = ± ⋅ mh + ⋅ md + ⋅ mϕ + ⋅ ml ∂ h ∂ d ∂l ∂ ϕ 2 2 2 Essendo mh = ml = ± 10-3 m e le relative derivate di valore unitario, possiamo trascurare l'errore dovuto alla misura dell'altezza strumentale e alla misura della stadia. 1. Errore dovuto alla misura della distanza. ∂∆ a= ⋅ md = cot gϕ ⋅ m d ∂d dove md = ± 0,15 m nel caso di misura della distanza con il metodo tacheometrico e md = ± 0,01 m con l'uso del distanziometro. Capitolo V - Rilievo topografico classico pagina 191 R.Galetto A.Spalla - Lezioni di Topografia Valutiamo questo errore per diversi valori dell'angolo zenitale. ϕ=100 ϕ=90 ϕ=70 ϕ=60 ϕ=50 per md = ± 0,15 m a = cotg ϕ . md 0 2,4 7,6 11 15 per md = ± 0,01 m a = cotg ϕ . md 0 0,15 0,5 0,7 1 tabella 1 - analisi dell’errore dovuto alla misura della distanza; i valori di a sono espressi in cm 2. Errore dovuto alla misura dell'angolo zenitale. ∂∆ d b= ⋅ mϕ = mϕ ∂ϕ sen 2 ϕ Supponiamo mϕ = 50” e d = 100 m, abbiamo: b ϕ=100 ϕ=90 ϕ=70 ϕ=60 ϕ=50 1,5 1,5 1,9 2,8 3 ϕ=100 ϕ=90 ϕ=70 ϕ=60 ϕ=50 Essendo m∆ = ± a 2 + b 2 si ottiene nei due casi: m∆ = ± a 2 + b 2 per md = ± 0,15 m 1,5 2,8 7,8 11,3 15,3 m∆ = ± a 2 + b 2 per md = ± 0,01 m 1,5 1,5 2 2,8 3,3 Si possono notare i due ordini di precisione da utilizzare in relazione alla scala della carta. Si tenga anche presente che gli errori con il metodo distanziometrico, dipendendo essenzialmente dalle misure dell'angolo zenitale, si possono ridurre notevolmente con un teodolite da 1" . In questo caso, praticamente, rimane solo l'errore dovuto alla misura della distanza. Capitolo V - Rilievo topografico classico pagina 192 R.Galetto A.Spalla - Lezioni di Topografia CAPITOLO VI LA TECNICA TOPOGRAFICA NEI COLLAUDI E CONTROLLI DI GRANDI STRUTTURE 1 Considerazioni preliminari. 1.1 Spostamenti assoluti e spostamenti relativi. Il problema del collaudo e del controllo delle grandi strutture viene sottoposto al topografo sotto l'aspetto della determinazione di spostamenti, deformazioni o inclinazioni della struttura. Spostamento, deformazione, inclinazione sono parole che fanno parte della terminologia corrente: riteniamo però che prima di accingersi ad impostare le operazioni di misura, il topografo debba tradurre queste espressioni in termini di spostamenti assoluti e di spostamenti relativi, siano essi verticali che orizzontali. Prima di definire che cosa intendiamo per spostamento assoluto e spostamento relativo di un punto e di mettere in relazione queste espressioni e quelle di uso più corrente di spostamento, deformazione e inclinazione, occorre introdurre il concetto di spostamento reale di un punto, dove per reale si intende effettivamente avvenuto. Spostamento reale Quando si sottopone la struttura ad un controllo o ad un collaudo, si vuole in pratica determinare il comportamento rispetto ad una certa zona di terreno che la circonda. Sia i punti della struttura sia i punti del terreno di questa parte di Terra che avvolge la struttura, hanno una certa posizione che potrebbe essere univocamente definita mediante un opportuno sistema di riferimento. Si dirà che un punto della struttura o del terreno che la circonda, subisce uno spostamento reale, quando, a causa di un certo stato di sollecitazione, il punto cambia di posizione rispetto all'insieme di tutti gli altri. Spostamento assoluto Si dirà che si determina lo spostamento assoluto di un punto A di una struttura, quando se ne determina il cambiamento di posizione riferendosi ad uno o più punti di essa che abbiano la caratteristica di non subire spostamenti reali della stessa natura e dello stesso ordine di Capitolo VI - La tecnica topografica nei collaudi e controlli di grandi strutture pagina 193 Lezioni di Topografia grandezza di quelli sui quali stiamo indagando riguardo la struttura in esame. I punti rispetto ai quali si determinano gli spostamenti assoluti e che hanno caratteristica suddetta, prendono il nome di caposaldi. Pertanto quando le operazioni di misura portano alla determinazione dello spostamento assoluto di un punto, ciò significa che esso ha subito uno spostamento reale. La richiesta della determinazione di spostamenti assoluti deve essere validamente motivata dal collaudatore o da chi è preposto al controllo della struttura, perché può essere fonte di gravi difficoltà per il topografo reperire il caposaldo o i caposaldi necessari. Quanto al numero dei caposaldi, esso deve essere sempre in numero maggiore a quello strettamente necessario; occorre infatti che delle opportune operazioni di misura, anche non necessarie ai fini del collaudo o del controllo, confermino l'ipotesi fatta in sede dell'organizzazione delle misure, e cioè che i punti rispetto ai quali si determinano gli spostamenti assoluti siano effettivamente dei caposaldi. Spostamento relativo Si dirà che si determina lo spostamento relativo di un punto A di una struttura, quando se ne determina il cambiamento di posizione rispetto ad uno o più punti che possono anch'essi subire un cambiamento di posizione rispetto alla totalità degli altri punti che costituiscono il mondo esterno alla struttura. Spostamento relativo è quindi sinonimo di differenza di spostamenti reali. La determinazione dello spostamento relativo di un punto A di una struttura, rispetto ad un punto B può infatti essere dovuto ad uno dei seguenti casi: • il punto A ha subito uno spostamento reale ed il punto B non si è mosso; • il punto B ha subito uno spostamento reale ed il punto A non si è mosso; • entrambi i punti hanno subito uno spostamento reale. La causa di questa indeterminazione risiede nel fatto che il punto B non è un caposaldo, e naturalmente questa indeterminazione rispetto a B dovrebbe essere data per scontata. Accade però a volte che, eseguite le misure, si cerchi di ricavare dai risultati delle informazioni che non è possibile avere. È bene perciò chiarire sempre, in fase di impostazione, i limiti di una operazione di misura intesa a determinare degli spostamenti relativi ed in particolare è opportuno ricordare che un punto che denunci uno spostamento relativo può anche non aver subito alcun spostamento reale. Possiamo ora prendere in esame il problema della corrispondenza tra terminologia corrente e quella ora introdotta, premettendo che essa non ha ovviamente nessun carattere di ufficialità, ma viene suggerita dalla personale esperienza, acquisita nel campo dei collaudi e controlli di grandi strutture. Possiamo dire nella maggior parte dei casi: • quando la richiesta riguarda la determinazione di spostamenti, si intende la misura di spostamenti assoluti; Capitolo VI - La tecnica topografica nei collaudi e controlli di grandi strutture pagina 194 Lezioni di Topografia • quando la richiesta riguarda la determinazione di deformazioni della struttura si intende la misura di spostamenti relativi e generalmente le misure dello spostamento di alcuni punti della struttura rispetto ad uno o più punti della struttura stessa; • quando la richiesta riguarda la determinazione di inclinazione si intende la misura di eventuali rotazioni in un piano verticale intorno ad un asse orizzontale non determinato; queste rotazioni vengono messe in evidenza misurando lo spostamento relativo, orizzontale o verticale, tra due punti della struttura, posti approssimativamente su uno stesso piano orizzontale o su una stessa linea verticale. La misura di inclinazioni rientra pertanto nel problema della determinazione di spostamenti relativi. Ed è del resto significativo che il committente, anche quando dice che desidera conoscere le inclinazioni di una struttura, non chiede che il risultato gli venga dato sotto forma di una quantità angolare, ma come misura dello spostamento della verticale o come variazione altimetrica, di due punti appartenenti alla struttura. In seguito a queste considerazioni i metodi topografici usati per il collaudo ed il controllo delle grandi strutture, che saranno in seguito prese in considerazione, verranno divisi in due categorie: • strumenti e metodologie atti alla determinazione di spostamenti verticali, • strumenti e metodologie atti alla determinazione di spostamenti orizzontali. Tali spostamenti saranno assoluti o relativi a seconda che i punti rispetto ai quali verranno determinati, saranno o no caposaldi. 1.2 Il metodo di misura variometrico e quello per differenza di posizione. Nei problemi del collaudo e del controllo delle grandi strutture il topografo si trova a dover risolvere un problema di misura in cui non è necessario determinare la posizione assoluta della struttura, ma semplicemente la variazione di forma o di posizione rispetto ad una posizione iniziale. Questa considerazione ha la conseguenza che, non appena sia possibile, il topografo, il quale nelle operazioni di collaudo ha appunto il compito di misurare gli spostamenti di quei punti della struttura che permettono di determinarne lo stato di deformazione, l'inclinazione o il cambiamento di posizione, deve ricorrere a sistemi di misura basati sul metodo variometrico. I problemi di collaudo e di controllo richiedono infatti che le misure siano eseguite con grande precisione; tali precisioni sono praticamente raggiungibili solo se il campo della misura è limitato, come appunto avviene se si imposta il problema sul criterio della misura diretta dello spostamento dei punti sotto controllo, e non come determinazione degli spostamenti come differenza di due operazioni di misura che ne determinano la posizione. Capitolo VI - La tecnica topografica nei collaudi e controlli di grandi strutture pagina 195 Lezioni di Topografia A M Distingueremo pertanto i metodi per la determinazione degli spostamenti in due categorie: metodi variometrici e metodi per differenza di posizione. Per chiarire la differenza tra i due metodi prendiamo in considerazione il seguente esempio: si voglia determinare lo spostamento verticale assoluto del punto A della struttura M sotto l'effetto del carico Q. Supponiamo che, in prossimità della struttura M, si disponga di una piattaforma sulla quale appoggiare un livello e che tale base d'appoggio non subisca variazioni di quota, sia cioè un caposaldo. Supponiamo inoltre, che l'operazione di caricamento della struttura avvenga in tempo molto breve, in modo cioè che durante tale intervallo di tempo l'assetto dell'asse di collimazione del livello non cambi. Per la determinazione dello spostamento del punto A si potrà allora operare come segue: • si dispone il livello in stazione sulla piattaforma e si pone una stadia in A; si esegue quindi la lettura alla stadia; • si procede al caricamento della struttura e si esegue la nuova lettura alla stadia; • la differenza delle due letture ci fornisce lo spostamento verticale del punto A. Se viceversa la piattaforma è lontana dal manufatto occorrerà eseguire una vera e propria livellazione tra un punto B della piattaforma ed il punto A e ricavare lo spostamento verticale del punto A come differenza della sua quota rispetto a B prima e dopo l'applicazione del carico Q. Il primo metodo di misura è un metodo variometrico, il secondo è un metodo per differenza di posizione. Dall'esempio fatto traiamo le seguenti conclusioni: • nel metodo variometrico non è necessario fissare un sistema di riferimento nel quale determinare la posizione del punto controllato (nell'esempio fatto il punto B) essendo il riferimento costituito dalla posizione originaria, non nota, del punto da controllare; • nel metodo variometrico si misura direttamente lo spostamento verticale di A, mentre con il secondo metodo esso viene determinato come differenza tra i due dislivelli; • nel metodo variometrico sono tollerabili errori di tipo sistematico, purché restino costanti; ad esempio nel primo caso un errore di srettifica del livello non ha alcuna influenza negativa sulla determinazione dello spostamento del punto A; Capitolo VI - La tecnica topografica nei collaudi e controlli di grandi strutture pagina 196 Lezioni di Topografia • nell'esempio fatto si ottiene una maggiore precisione con il primo metodo di misura che con il secondo, ed in genere questo avviene quasi sempre quando si impostano le misure su metodi variometrici anziché su metodi per differenza di posizione. 1.3 Classificazione dei casi trattati. In questa nota vengono prese in considerazione le operazioni topografiche che vengono più comunemente usate nei collaudi e controlli delle grandi strutture, considerandone l'applicazione più corrente. Nella trattazione verrà dato più spazio a quegli argomenti che trattano strumenti e metodologie che vengono usati da studi professionali o ditte che eseguono lavori topografici in genere; degli strumenti e dei metodi che, pur avendo importanza nei problemi di collaudo e di controllo, non rientrano tra quelli abitualmente impiegati dal topografo, faremo solo breve cenno. Bisogna tenere presente del resto che alcuni problemi, come ad esempio il problema delle dighe, richiederebbe già di per sé, una trattazione molto più lunga e complessa. Diamo qui di seguito l'elenco delle operazioni topografiche che verranno prese in considerazione, suddivise nei due differenti tipi di problemi: a) determinazione di spostamenti verticali: • livellazione geometrica; • livellazione trigonometrica; • livellazione idrostatica; • clinometro. b) determinazione di spostamenti orizzontali: • triangolazione; • collimatore; • distanziometri elettroottici. 2 Determinazione di spostamenti verticali. 2.1 Impiego della livellazione geometrica. 2.1.1 Metodologia classica L'impiego più frequente della livellazione geometrica lo si ha per i collaudi dei ponti, quando per l'impraticabilità dello spazio sottostante il ponte (corsi d'acqua, strade che non possono essere chiuse al traffico, ecc.), non è possibile l'impiego dei flessimetri. Capitolo VI - La tecnica topografica nei collaudi e controlli di grandi strutture pagina 197 Lezioni di Topografia Vista Pianta battute di livellazione punti controllati caposaldi figura 3 - schema di livellazione geometrica per il collaudo di un ponte a travate Consideriamo il ponte a travata della figura 3; il collaudatore può richiedere che le misure gli permettano di conoscere le deformazioni della travi e cioè la freccia sotto carico; oppure può richiedere che si determini anche l'abbassamento delle spalle dell'appoggio delle travi. Consideriamo questo secondo caso, che, anche se non molto frequente, ci permette di richiamare l'attenzione su alcuni accorgimenti che devono essere tenuti presenti al fine di non incorrere in errori di interpretazione delle misure. Le operazioni si svolgono generalmente attraverso i seguenti passi. a) Si effettua un sopralluogo con il collaudatore durante il quale si stabilisce il numero e la posizione dei punti in esame per la ricostruzione della deformata delle travi. Si deve fare attenzione essenzialmente a due cose: • che i punti siano accessibili, cioè ci si possa appoggiare la stadia, anche nella situazione più gravosa di carico, ossia quando sul ponte vengono immessi i camion o i compressori; • in secondo luogo bisogna accertarsi che la materializzazione dei punti in esame avvenga con chiodi di opportuna fattura (consigliabili degli spezzoni prismatici a testa sferica di ottone) i quali devono essere ancorati nella struttura portante, e quindi se, come generalmente accade, il ponte è già stato asfaltato, occorre far predisporre dei pozzetti fino a raggiungere la struttura in cemento armato. La dimensione dei pozzetti deve essere sufficiente a permettere l'appoggio delle stadie sui chiodi. Capitolo VI - La tecnica topografica nei collaudi e controlli di grandi strutture pagina 198 Lezioni di Topografia figura 4 - Ancoraggio del chiodo alla struttura Per la determinazione dell'abbassamento delle spalle i chiodi vanno fissati all'esterno delle travi; infatti l'abbassamento del bordo della trave che appoggia sulla spalla potrebbe essere dovuto allo schiacciamento dei cuscinetti d'appoggio e non ad un reale cedimento delle spalle. Inoltre dovranno essere predisposti dei caposaldi in numero minimo di due, in modo da consentire un loro reciproco controllo; si avrà cura di ubicarli non solo in una zona non immediatamente prospiciente il ponte, ma anche lontani dalla zona in cui potrebbero trovarsi a manovrare i veicoli impiegati per il controllo del ponte. b) Le operazioni di collaudo richiedono che vengano eseguiti come minimo tre cicli di misure: uno iniziale a vuoto, uno a carico ed uno finale a vuoto per accertare il ritorno della struttura alla forma originale. Le precauzioni da adottare sono le seguenti (oltre naturalmente a tutte quelle solite inerenti all'operazione di livellazione di precisione). • occorre eseguire con la massima cura soprattutto la prima misura, ossia quella iniziale a vuoto (a ponte scarico), ripetendo tre volte le letture anziché le solite due; infatti se i risultati che si ottengono nella situazione di ponte carico destano qualche preoccupazione occorre essere in grado di garantire nel modo più assoluto la bontà delle misure; ma mentre le misure in condizioni di carico sono sempre ripetibili, la misura per conoscere l'assetto originario della struttura è ovviamente irripetibile. • Un'altra precauzione da tenere presente è quella di lasciar passare un po' di tempo tra il caricamento della struttura e l'inizio delle operazioni di misura in modo che la struttura abbia il tempo di subire completamente la deformazione dovuta ai carichi; la stessa precauzione bisogna avere prima di eseguire l'ultima livellazione per controllare il ritorno della struttura. c) Lo schema della livellazione per la determinazione della deformazione della struttura ha di solito la forma di anello semplice; nel caso però che il ponte sia di larghezza ragguardevole ed il collaudatore voglia conoscerne le deformazioni anche in una o più sezioni trasversali, la livellazione assumerà forme più complesse. Quando è necessario ricorrere a metodi di compensazione rigorosi, i calcoli richiedono tempo e calma, quindi in sede di collaudo si provvederà ad accertarsi della bontà delle misure solo mediante l'esame degli errori di chiusura dei singoli anelli. Capitolo VI - La tecnica topografica nei collaudi e controlli di grandi strutture pagina 199 Lezioni di Topografia Per la determinazione dell'abbassamento delle spalle d'appoggio si potrà seguire lo schema di livellazione indicato alla figura 3, controllando che ad ogni livellazione la quota relativa dei due caposaldi rimanga costante, o che le sue variazioni siano di ordine di grandezza inferiore a quelle che si devono determinare per il controllo della struttura. 2.1.2 Uso di stadiette di vetro Nel caso che si debba tenere sotto controllo un edificio che richieda il ripetersi periodico di operazioni di livellazione, è consigliabile utilizzare stadiette in vetro, anziché normali stadie di invar da 3 m, che risultano spesso di impiego difficoltoso in ambienti chiusi. I punti da controllare vengono materializzati da apposite squadrette d'acciaio che vengono fissate alla struttura o mediante collanti o con zanche; a queste squadrette, vengono applicate stadiette, del tipo rappresentato in figura 5, che aderiscono ad esse mediante una testina magnetica o con altri metodi. figura 5 - una stadietta di vetro per livellazione di precisione Tali stadiette possono essere vantaggiosamente impiegate solo quando i punti da controllare si trovano tutti pressappoco alla medesima quota; il loro uso presenta molti vantaggi in quanto sono maneggevoli e non richiedono canneggiatori esperti (al limite può essere lo stesso operatore che sistema le stadiette e poi esegue le misure); inoltre è più facile materializzare i punti da controllare e può essere conseguite una maggior precisione 2.1.2 Precisione conseguibile nella determinazione degli spostamenti verticali La precisione che si può raggiungere nella determinazione del dislivello tra due punti mediante una singola battuta di livellazione dipende da molti fattori; comunque si può dire che oscilla da un errore medio di ± 0,05 mm per battute in ambiente chiuso e con stadiette in vetro del tipo a cui si è accennato, a ± 0,07 mm all'aperto con stadie invar di 3 m e per battute abbastanza lunghe. In base a questi dati è possibile valutare a priori la precisione con la quale si può determinare lo spostamento verticale di un punto inserito in una linea di livellazione. Il metodo che esponiamo qui di seguito porta ad una valutazione grossolana e prudenziale dell'errore quadratico medio con il quale si eseguono le misure; la reale precisione raggiunta potrà essere ricavata solo a posteriori applicando metodi di calcolo rigorosi. Prendiamo ad esempio la Capitolo VI - La tecnica topografica nei collaudi e controlli di grandi strutture pagina 200 Lezioni di Topografia livellazione della fig.3; supponiamo che il calcolo delle quote dei sei punti controllati sul ponte, parta dal punto 1, al quale viene data una quota arbitraria. Supponiamo inoltre che la ripartizione dell'errore di chiusura non modifichi sostanzialmente l'errore medio del dislivello misurato tra due punti; l'errore medio della quota di un generico punto sarà dato dall'errore medio di una battuta, moltiplicato per la radice quadrata del minimo numero di battute che lo separano dal punto di partenza; nel caso della figura 3, il punto più lontano da quello di partenza è il n.3; pertanto l'errore medio m q,3 , nella determinazione della sua quota vale: m q,3 = ± 0,07 mm √3 avendo assunto pari a + 0,07 mm l'errore quadratico medio di una singola battuta. Ricordiamo però che lo spostamento verticale lo si ottiene come differenza tra due quote determinate con due successive operazioni di livellazione; pertanto l'errore medio m s,3 nella determinazione dello spostamento verticale del punto più lontano vale: m s,3 = m s,3. √2 = ± 0,07 . √3 √2 mm = ± 0,17 mm In base a questo semplice calcolo è pertanto possibile farsi un'idea della precisione che si può ottenere. Sarà inoltre opportuno che anche nel consegnare gli elaborati di calcolo, non vengano forniti dei risultati di misura con delle cifre decimali che hanno scarso significato, o non ne hanno per niente. 2.2 Impiego della livellazione trigonometrica. Sui viadotti delle autostrade vengono talvolta eseguiti dei controlli aventi lo scopo di accertare che non ci siano variazioni di quota tra i plinti di fondazione. I plinti di fondazione si trovano però molto spesso in posizione ravvicinata, ma a quote molto diverse e pertanto l'impiego della livellazione geometrica non risulta conveniente sia per ragioni economiche che di precisione, poiché si dovrebbero seguire itinerari lunghi e tortuosi per congiungere i punti interessati al controllo. figura 6 - schema del controllo delle variazioni di quota mediante livellazione trigonometrica E' preferibile ricorrere allora alla livellazione trigonometrica; infatti la piccola distanza tra i plinti fa sì che non intervengano gli errori dovuti alla rifrazione atmosferica, che sono quelli che più compromettono la precisione di questo metodo; le distanze tra il punto di stazione ed i punti da controllare potranno essere misurate con un distanziometro elettroottico (a sé stante o Capitolo VI - La tecnica topografica nei collaudi e controlli di grandi strutture pagina 201 Lezioni di Topografia integrato al teodolite). Ricordiamo inoltre che un piccolo errore nella misura della distanza ha influenza sulla determinazione dei dislivelli, ma non sulla loro variazione. Applicando questo metodo, se le distanze tra i punti sono dell'ordine di qualche decina di metri, si possono determinare le variazioni di dislivello tra i punti con una approssimazione di qualche decimo di millimetro. 2.3 Impiego della livellazione idrostatica di precisione. Qualora si debba tenere sotto controllo una struttura per un periodo di tempo molto lungo (da qualche anno sino a tutto il periodo di esistenza della struttura) può essere conveniente l'impiego della livellazione idrostatica. I vantaggi dell'impiego della livellazione idrostatica sono i seguenti: • • • • • • possibilità di far eseguire le misure da personale non necessariamente esperto in operazioni di misure di precisione; possibilità di far eseguire le misure in breve tempo (a paragone di quello richiesto dalla livellazione geometrica) e quindi di poter ripetere le operazioni di misura ad intervalli brevi di tempo; possibilità di collegare tra di loro punti che non sarebbe possibile collegare con i metodi di livellazione; possibilità di determinare quasi simultaneamente il dislivello tra più punti; possibilità di rendere automatiche e registrabili a distanza le misure; aumento della sensibilità delle misure. D'altra parte l'impiego della livellazione idrostatica ha lo svantaggio di richiedere la costruzione di un impianto fisso per il collegamento degli strumenti che vengono vincolati ai punti da controllare; ed inoltre anche il costo degli strumenti di misura, che devono consentire la lettura del livello del liquido in appositi bicchieri con la precisione del centesimo di millimetro, non è indifferente. Pertanto possiamo dire che l'impiego della livellazione idrostatica è consigliabile per il controllo di strutture di grande importanza, che necessitino di continui ed accurati controlli; in tal caso, sia per la natura della struttura sotto controllo, sia perché la ripetizione di livellazioni geometriche da parte di personale specializzato è pur sempre onerosa, risulta giustificata la spesa per l'impianto e per l'acquisto degli strumenti. Il metodo della livellazione idrostatica è stato applicato negli anni ‘70 per il controllo della statica di parte del Duomo di Milano; per tale impianto è stato anche realizzato un sistema automatico di lettura degli strumenti e di trasmissione dei dati a distanza. Una realizzazione di questo tipo risulta di grande utilità per il controllo degli assestamenti delle dighe, in cui la possibilità di avere un sistema centralizzato di controllo riveste particolare carattere di importanza. Capitolo VI - La tecnica topografica nei collaudi e controlli di grandi strutture pagina 202 Lezioni di Topografia 2.4 Clinometro I tipi di clinometro comunemente usati per il controllo ed il collaudo delle grandi strutture, sono costruiti sullo schema riportato in figura 7 in base al quale la rotazione di una struttura viene determinata in funzione dello spostamento verticale relativo di due suoi punti: ad un supporto munito di due (o tre) piedini è fissato a cerniera un braccio orizzontale sul quale è montata una livella torica di grande sensibilità; il braccio orizzontale è incernierato ad un estremo e può venire fatto ruotare nel piano verticale per mezzo di un dispositivo a vite micrometrica che è vincolato all'altro estremo; disponendo di un clinometro sulla struttura per mezzo di una apposita base di appoggio è possibile centrare la livella torica facendo ruotare il braccio orizzontale per mezzo della vite. Alla vite è collegato un tamburo graduato; la rotazione della vite può tradurre su tale tamburo o la quantità angolare della quale ruota il braccio orizzontale o lo spostamento verticale dell'estremo del braccio orizzontale vincolato alla vite. figura 7 - schema del clinometro Il clinometro viene usato nel seguente modo: • • • • si appoggia il clinometro sulla base d'appoggio e si centra la livella torica con la vite V; si esegue la lettura iniziale al tamburo; ad ogni ciclo successivo di misure si dispone nuovamente il clinometro sulla base di appoggio e si centra la livella torica; se la parte di struttura alla quale è vincolata la base di appoggio ha subito una rotazione, la posizione dell'estremità del braccio orizzontale sulla vite sarà diversa e al tamburo si farà una lettura differente da quella originaria; la differenza delle letture eseguite al tamburo può fornire l'angolo di rotazione del braccio orizzontale o la differenza degli spostamenti verticali s dei punti di appoggio, a seconda del tipo di graduazione incisa sul tamburo. Alcuni tipi di clinometro consentono la misura diretta degli spostamenti verticali relativi di due punti posti alla distanza di un metro con la precisione di 0,01 mm. Capitolo VI - La tecnica topografica nei collaudi e controlli di grandi strutture pagina 203 Lezioni di Topografia figura 7 bis - impiego del clinometro con base di prolunga per il controllo delle dighe Il clinometro viene generalmente impiegato per determinare le rotazioni di strutture particolarmente rigide; solo in questo caso infatti lo spostamento verticale relativo di due punti della struttura può essere interpretato come dovuto ad una rotazione di tutta la struttura e non ad un fatto locale, limitato cioè alla zona alla quale è ancorata la base di appoggio del clinometro. Esso trova largo impiego nel controllo delle dighe (vedi figura 7 bis), nel controllo dei plinti di fondazione, nel controllo di ciminiere o strutture simili; inoltre nei collaudi di strutture in cemento armato viene impiegato per la determinazione della rotazione di sezioni di travi o dell'estremità di mensole. 3 Determinazione degli spostamenti orizzontali. 3.1 Impiego della triangolazione. Premettiamo che daremo qui solo alcuni cenni sull'impiego della triangolazione per i collaudi delle grandi strutture, principalmente per due motivi: in primo luogo la trattazione del metodo dovrebbe vertere soprattutto sulle metodologie riguardanti le operazioni che concernono le triangolazioni di elevata precisione per cui si rimanda al capitolo V; inoltre i metodi di collaudo e di controllo sono oggi orientati verso metodologie che consentono di ottenere risultati in tempi brevi, in modo da essere ripetibili anche ad intervalli brevi di tempo, che consentano l'automatizzazione dei procedimenti di misura e che non necessitino di personale specializzato in operazioni topografiche così delicate e complesse quali sono quelle riguardanti le triangolazioni di alta precisione. Possiamo dire che in generale l'uso della triangolazione per la determinazione degli spostamenti orizzontali è applicato principalmente per il controllo delle dighe. Il metodo è basato sulla determinazione della posizione di un certo numero di vertici dei quali alcuni sono caposaldi al di fuori della struttura ed altri sono i punti che si vogliono tenere sotto controllo (punti sul coronamento della diga o sul paramento di valle). Ripetendo le operazioni di misura si determina lo spostamento dei punti controllati come variazione di posizione dei punti stessi. Il metodo rientra pertanto nei metodi di misura per differenza di posizione . Capitolo VI - La tecnica topografica nei collaudi e controlli di grandi strutture pagina 204 Lezioni di Topografia E' necessario che le operazioni di misura siano effettuate con la maggior precisione possibile, avendo cura di rendere costanti gli eventuali errori di tipo sistematico, e che già in fase di impostazione dei lavori si abbia la precauzione di realizzare degli schemi geometrici ottimali. pilastro di osservazione di riferimento base di triangolazione figura 8 - schemi di triangolazione a valle di una diga In generale lo schema di triangolazione a valle della diga è fatto in modo che i vertici della triangolazione si trovino in zone che non subiscano le sollecitazioni del carico idrostatico. La conformazione della rete deve prevedere una distribuzione dei vertici in modo che risulti composta da triangoli approssimativamente equilateri, che si inseriscano in uno schema a quadrilateri. Il dimensionamento della rete avverrà attraverso la misura di una o più basi; in genere le basi vengono misurate con precisione geodetica, o mediante i classici dispositivi a fili o nastri di invar, o mediante i distanziometri elettroottici di precisione Conviene sottolineare il fatto che una elevata precisione nella misura delle basi non sarebbe di per sé necessaria per la determinazione degli spostamenti, risulta infatti affetta dallo stesso errore relativo di quello commesso nella misura della base, e quindi un errore di qualche centimetro nella misura di quest'ultima non ha praticamente influenza sulla precisione nella determinazione degli spostamenti. La precisione nella misura delle basi ha invece la funzione di garantire la stabilità dei vertici. Qualora la stabilità dei vertici venga controllata con altri metodi (fili a piombo rovesci, telemisuratori ecc.) si può pertanto procedere alla misura delle basi con minor precisione. I calcoli della triangolazione vanno eseguiti con metodi di compensazione rigorosi in modo da poter ricavare ogni volta l'errore quadratico medio delle coordinate dei vertici. L'errore medio nella determinazione degli spostamenti risulta, nella maggior parte dei casi, di circa 1 mm. 3.2 Uso del collimatore Il principio del metodo, basato sull'uso del collimatore, consiste nella realizzazione di una linea di mira fissa ed invariabile mediante un collimatore ed un apposito segnale posto su due caposaldi alle estremità opposte della diga. Capitolo VI - La tecnica topografica nei collaudi e controlli di grandi strutture pagina 205 Lezioni di Topografia figura 9 - collimatore su diga a gravità e su diga ad arco (Fondelli,1991) Ai punti che devono essere tenuti sotto controllo vengono collegati dei segnali che hanno la caratteristica di poter subire delle piccole traslazioni orizzontali rispetto al supporto che li vincola alla struttura. All'inizio delle operazioni di controllo, i centri dei segnali vengono portati in corrispondenza della linea di mira fissa e se ne legge la posizione rispetto al supporto su una scaletta graduata al millimetro, con nonio al decimo di millimetro. Ripetendo l'operazione di allineamento dei segnali con la linea di mira in tempi successivi, si determinano gli spostamenti dei punti controllati come differenza di letture alle scalette graduate. Se il segnale è costruito in maniera opportuna è possibile determinare anche gli spostamenti verticali dei punti controllati. a) b) figura 10 - segnale e collimatore (Galetto,1971) Il metodo di misura degli spostamenti basato sull'uso del collimatore è pertanto un metodo variometrico che ha il vantaggio di fornire direttamente gli spostamenti cercati e che si basa su uno schema di misura estremamente semplice; tuttavia perché sia garantita la buona riuscita delle operazioni di controllo, occorre che siano verificate le ipotesi di partenza e cioè che la linea di mira fissa resti effettivamente invariata nel tempo. Questo implica che i pilastrini sui quali vengono fissati il collimatore ed il segnale di riferimento devono essere dei caposaldi; inoltre le misure di allineamento devono essere fatte seguendo una procedura ben determinata e bisogna accertarsi della stabilità dei pilastrini. L'uso del collimatore è generalmente adottato nel controllo delle dighe in terra o più in generale a gravità, in dighe cioè ad andamento prevalentemente rettilineo e nelle quali il carico idrostatico che grava sulla diga viene trasmesso all'imposta in quantità trascurabile; pertanto collimatore e segnale di riferimento possono essere ubicati in prossimità del coronamento senza pregiudizio per la loro stabilità. Capitolo VI - La tecnica topografica nei collaudi e controlli di grandi strutture pagina 206 Lezioni di Topografia mire di riferimento punto controllato collimatore figura 11 Il metodo del collimatore è però usato anche per il controllo delle dighe ad arco, quando la sezione di imposta della diga dà sufficienti garanzie di stabilità; per il controllo degli spostamenti di alcuni punti del coronamento di una diga ad arco, è necessario predisporre più di una linea di mira fissa di riferimento (vedi figura 11), secondo delle direzioni tangenti al coronamento. Quando una delle spalle d'appoggio non offre garanzie di stabilità, si può seguire, in via eccezionale, lo schema d'impianto che prevede l'installazione del collimatore e del segnale di riferimento da uno stesso estremo della diga; in questo modo si ha infatti un decadimento della precisione e pertanto si deve ricorrere ad esso solo in caso di estrema necessità. 3.3 Uso dei distanziometri elettroottici Oltre che per la misura delle basi di triangolazione nel controllo delle dighe, i distanziometri possono essere impiegati secondo schemi nuovi, che sfruttino cioè la loro possibilità di determinare degli spostamenti come variazione di distanze, secondo metodi variometrici. Sia nell'uno che nell'altro caso però, per rimanere nei limiti di errore indicati occorre apportare, alla misura eseguita, delle correzioni che sono funzioni delle condizioni atmosferiche; da un punto di vista rigoroso bisognerebbe conoscere il valore della temperatura e della pressione lungo tutto il percorso del raggio ottico. L'impossibilità di conoscere con esattezza questi dati fa sì che l'errore globale dal quale risulta affetta la misura, possa essere maggiore di quello prevedibile. Per raggiungere veramente delle elevate precisioni dobbiamo pertanto risolvere questi problemi: • eliminazione dell'influenza sulle misure dell'errore dovuto alla struttura interna dello strumento (per gli strumenti nei quali esso è superiore al millimetro); • eliminazione dell'errore dovuto alla non perfetta conoscenza delle condizioni atmosferiche (per entrambi i tipi di strumenti). Capitolo VI - La tecnica topografica nei collaudi e controlli di grandi strutture pagina 207 Lezioni di Topografia 3.3.1 Indicazioni di un metodo per l'eliminazione dell'errore dovuto alla precisione intrinseca dello strumento e applicazione del metodo per il controllo delle deformazioni di una diga con criterio variometrico. Per comprendere correttamente il principio del metodo conviene ricordare che, impiegando un distanziometro, la distanza da misurare equivale ad un certo numero intero di lunghezze d'onda, più una certa frazione di lunghezze d'onda; nei distanziometri elettronici la parte equivalente alla frazione di lunghezza d’onda viene ricavata convertendo in termini metrici la differenza tra due letture: una funzione del raggio riflesso da un riflettore interno. E' proprio questa operazione di confronto tra le due letture e la traduzione in equivalente metrico della loro differenza, la causa principale della parte costante dell'errore nella misura della distanza. B' B A C figura 12 Il metodo proposto da A.L. Allan per la misura di una certa base (circa 300 m) con elevata precisione mediante l'impiego del distanziometro Geodimetro, evita il confronto delle letture al riflettore interno ed esterno. Il metodo è il seguente: si voglia misurare la base AB, procedendo come segue: • si dispone il Geodimetro in C (vedi fig.12), un riflettore in A ed uno in B; • si esegue a lettura al riflettore posto in A; • • si collima al riflettore posto in B e lo si sposta sino a dare la stessa lettura che si è ottenuta collimando al riflettore posto in A; il riflettore posto in B passerà quindi nella posizione di B'; si ottiene la misura della distanza AB' mediante una relazione in cui le letture ai riflettori posti in A ed in B' entrano come differenza, e poiché esse sono state prese uguali si annullano e non devono essere convertite nei rispettivi equivalenti metrici. Se invece di spostare il riflettore posto in B, quest'ultimo ed il Geodimetro vengono fissati su due caposaldi, applicando il principio esposto si possono determinare gli spostamenti di un punto a cui venga collegato il riflettore A; il collegamento del riflettore al punto da controllare dovrà essere realizzato in modo da permettere delle piccole traslazioni, misurabili con precisione, lungo l'allineamento AC (ad esempio ruotando il riflettore su un dispositivo a slitta). Da confronti tra i risultati ottenuti mediante il metodo tradizionale della triangolazione con quelli ottenuti applicando il Geodimetro ed il metodo variometrico esposto, si è visto che i risultati sono stati coincidenti su tutti i punti controllati e la precisione dei due metodi uguale, pari a ± 1 mm; ma il tempo richiesto per le operazioni di misura e l'esecuzione dei calcoli è risultato con il metodo geodimetrico di quindici volte più breve. Capitolo VI - La tecnica topografica nei collaudi e controlli di grandi strutture pagina 208 Lezioni di Topografia 3.3.2 Indicazione di un metodo per l'eliminazione dell'errore dovuto alla non perfetta conoscenza delle condizioni atmosferiche. Supponiamo ora di disporre di uno strumento di elevata sensibilità, in cui l'errore dovuto al metodo di misura dello sfasamento sia contenuto nei limiti di un millimetro, e vediamo come si possono evitare, per la misura degli spostamenti di punti di grossi manufatti, gli errori dovuti alla non perfetta conoscenza delle condizioni atmosferiche. Esponiamo qui di seguito il principio su cui si basa un interessante metodo realizzato per la determinazione delle deformazioni di una diga. Supponiamo di dover controllare gli spostamenti di una serie di punti di una struttura e di disporre di due caposaldi uno dei quali ubicato in prossimità dei punti da controllare (vedi fig.13); supponiamo inoltre che le condizioni atmosferiche, pur potendo variare nel tempo, siano abbastanza omogenee nell'area in cui sono compresi i caposaldi e la struttura sotto controllo. figura 13 In tal caso si può fare l'ipotesi che le condizioni ambientali influenzino allo stesso modo la misura delle distanze tra il punto di stazione del distanziometro, posto su un caposaldo, ed i punti sotto controllo, e la misura della distanza tra il punto di stazione del distanziometro ed il secondo caposaldo (quello posto in prossimità dei punti da controllare). Ogni volta che viene effettuata la misura della distanza dei punti sotto controllo, si esegue anche la misura della distanza tra i due caposaldi; poiché in realtà tale distanza rimane invariata (non si trascurerà però di accertarsene con i soliti dispositivi), la differenza che può registrarsi in tempi successivi è da imputarsi al cambiamento delle condizioni atmosferiche. In funzione della variazione della misura di questa distanza, vengono corrette le misure delle distanze dei punti sotto controllo. In questo modo si evita di dover conoscere, sia al ciclo iniziale delle misure che ai successivi, la distanza tra il caposaldo su cui è posto il distanziometro ed i punti sotto controllo, con la stessa precisione con la quale devono essere determinati gli spostamenti. Infatti in ogni ciclo di misure le condizioni atmosferiche influenzano in modo diverso le distanze rilevate; ma queste ultime, mediante la ripetizione della misura della distanza al caposaldo di riferimento, verranno riportate al valore che si sarebbe determinato in condizioni atmosferiche uguali a quelle che si avevano quando è stato effettuato il primo ciclo di misure; e pertanto gli spostamenti dei punti vengono ricavati come differenze di distanze affette da un errore costante, in quanto misurate in un ambiente stabile nel tempo. Capitolo VI - La tecnica topografica nei collaudi e controlli di grandi strutture pagina 209 R.Galetto A.Spalla - Lezioni di Topografia CAPITOLO VII IL SISTEMA GPS 1. La Geodesia classica e la Geodesia spaziale. Al Capitolo III abbiamo visto come i Geodeti abbiano dovuto trovare una soluzione alquanto complessa al problema di mettere in relazione spaziale i punti della superficie fisica della Terra, al fine di darne poi una rappresentazione cartografica. La loro situazione era in un certo senso simile a quella di una formichina che, posta su una mongolfiera, ne avesse dovuto determinare la forma assumendo un sistema di riferimento in qualche modo materializzato dalla mongolfiera stessa, senza avere la possibilità di collegarsi ad un sistema di riferimento esterno. Essi introdussero una superficie matematica di riferimento, l’ellissoide, poiché avevano individuato la possibilità di mettere in corrispondenza i punti della superficie fisica della Terra con i punti dell’ellissoide e di mettere poi in corrispondenza i punti dell’ellissoide con quelli della proiezione cartografica di Gauss. Anche se non ci siamo soffermati molto sulla descrizione delle operazioni geodetiche mediante le quali si passava dalla superficie fisica della Terra all’ellissoide, ne abbiamo messo in evidenza la grande complessità e soprattutto la necessità di eseguire misure di angoli e distanze con grande precisione. Proprio per evitare ai topografi la necessità di eseguire misure di natura geodetica e calcoli complessi, i geodeti si presero cura di creare la rete dei vertici trigonometrici, che consente ai topografi, riferendosi ad essi, di determinare la posizione dei punti della superficie fisica della Terra nella proiezione di Gauss, senza determinare la loro posizione sull’ellissoide. Poiché l’ellissoide è una superficie matematica riferita al sistema geocentrico cartesiano (X,Y,Z), è possibile ricavare le coordinate X,Y,Z di un punto P della superficie fisica della Terra in tale sistema, in funzione delle sue coordinate geografiche ellissoidiche ϕ, λ e della sua quota ellissoidica h (non di quella ortometrica riferita al geoide!) (formule (2) al Capitolo III). Un procedimento di calcolo inverso consente di ricavare le coordinate ϕ, λ e la quota ellissoidica h di un punto, in funzione delle sue coordinate X,Y,Z. Ma questo procedimento di calcolo inverso non è mai stato di grande interesse pratico per i geodeti, poiché, non esistendo un modo di ricavare in maniera diretta le coordinate geocentriche X,Y,Z dei punti della superficie fisica della Terra, non era possibile ricavare le coordinate geografiche ϕ, λ e la quota ellissoidica h di un punto, in funzione delle sue coordinate X,Y,Z. L’avvento e l’evoluzione della tecnologia satellitare ha permesso finalmente di invertire i termini del problema; col sistema GPS (Global Positioning System , cioè Sistema di Posizionamento Globale) è infatti possibile ricavare direttamente le coordinate X,Y,Z dei punti della superficie fisica della Terra nel sistema geocentrico e di passare quindi alle loro coordinate ϕ, λ, h mediante il procedimento di calcolo inverso a cui si è prima accennato. Capitolo VII - Il Sistema GPS pagina 210 R.Galetto A.Spalla - Lezioni di Topografia Il vantaggio di aver invertito i termini del problema sta nel fatto che la fase di misura consistente nella determinazione delle coordinate X,Y,Z di un punto mediante la tecnica GPS è molto semplice, ed il passaggio dalle coordinate X,Y,Z alle corrispondenti ϕ, λ, h e quindi alle coordinate N,E e q nella proiezione di Gauss viene eseguita da programmi di calcolo senza alcun intervento di rilievo da parte dell’operatore; di conseguenza sono diventate alla portata di ogni topografo operazioni che, prima dell’avvento del GPS, erano possibili solo per i geodeti e per i più esperti topografi. Sbaglieremmo però se considerassimo il sistema GPS solo da questo punto di vista; il metodo infatti non consente solo di conseguire più agevolmente e con una nuova impostazioni risultati che erano comunque già ottenibili con le operazioni geodetiche e topografiche classiche, ma offre soluzioni prima impensabili per la determinazione della posizione spaziale dei punti, quale ad esempio la determinazione della posizione spaziale di punti in movimento. L’avvento del GPS segna quindi il passaggio dalla geodesia e dalla topografia classica, basata su misure di angoli di distanze eseguite a Terra con teodoliti e distanziometri, alla geodesia e alla topografia spaziale, nelle quali le operazioni di misura consistono essenzialmente nella determinazione del tempo impiegato da un segnale emesso da un satellite per giungere a un’antenna di ricezione terrestre. 2. Struttura del sistema GPS. Le componenti fondamentali del sistema GPS sono: • 24 satelliti che ruotano su orbite fisse attorno alla Terra ad una quota di circa 20.000 km • 5 stazioni di controllo a terra • un sistema di trasmissione di segnali da parte dei satelliti • gli strumenti di ricezione di tali segnali (antenne di ricezione). figura 1 L’orbita di ogni satellite è nota, in quanto calcolata matematicamente prima del lancio del satellite stesso. Capitolo VII - Il Sistema GPS pagina 211 R.Galetto A.Spalla - Lezioni di Topografia Poiché però un satellite può avere delle piccole deviazioni dalla sua orbita nominale, vi sono cinque stazioni di monitoraggio a terra (vedi figura 2) che rilevano con continuità la posizione dei satelliti e sono in grado di determinarne l’orbita reale. Colorado Springs Hawaii Ascencion Diego Garcia Kwajalein figura 2 Possiamo pertanto dire che, per ogni satellite, è nota in ogni istante la posizione in termini di coordinate geocentriche X*,Y*,Z* (vedi figura 3). Z satellite Z* Y* Y X* X figura 3 La posizione delle orbite dei satelliti e il periodo di rotazione intorno alla Terra di ogni satellite, sono stati studiati in modo tale che da un generico punto della superficie fisica della Terra siano quasi sempre visibili più di tre satelliti. Capitolo VII - Il Sistema GPS pagina 212 R.Galetto A.Spalla - Lezioni di Topografia antenna GPS Su ogni satellite esiste un orologio di altissima precisione; tutti gli orologi sono sincronizzati sulla stessa ora. I satelliti emettono con continuità dei segnali, in forma di onde elettromagnetiche; ogni segnale trasporta delle informazioni; una di esse è l’istante di emissione del segnale. Questi segnali possono essere ricevuti da un apposito apparato di ricezione, che si compone di un antenna, in grado di ricevere i segnali dai satelliti, di una componentistica elettronica in grado di elaborare i segnali e di programmi di supporto all’esecuzione delle misure. Lo strumento ricevente contiene anche un orologio di precisione, sincronizzato con quelli ubicati sui satelliti. figura 4 La figura 4 mostra uno strumento di ricezione montato su un treppiede messo in stazione sul punto di cui si vogliono determinare le coordinate. Esistono vari tipi di strumenti di ricezione che si differenziano tra di loro per la capacità di ricevere tutti o in parte i segnali emessi dai satelliti e per la capacità di elaborarli. 3. La determinazione delle coordinate di un punto. 3.1 Il principio di base. Volendo determinare la posizione di un punto P mediante il sistema GPS, si mette in stazione un treppiede con l’antenna ricevente, sul punto P; dal punto P devono essere visibili* almeno tre satelliti. Durante una sessione di misure, che dura mediamente da mezz’ora a un’ora, lo strumento registra i segnali provenienti dai tre satelliti. Lo strumento ricevente determina, per ogni satellite Si, lo sfasamento ∆Ti tra l’ora che risulta dall’orologio interno dello strumento e l’ora che viaggia col segnale ricevuto dal satellite Si. Poiché l’orologio di ogni satellite è in sincronia con quello dello strumento ricevente, moltiplicando la velocità V di propagazione delle onde elettromagnetiche per lo sfasamento * Con il termine visibili non si intende che i satelliti siano visibili nel senso ottico della parola; si intende che essi abbiano un’altezza sull’orizzonte di almeno 15°, in modo che le onde elettromagnetiche possano essere captate dall’antenna. Occorre inoltre che l’antenna non si trovi circondata da ostruzioni che ostacolino il ricevimento delle onde elettromagnetiche. Capitolo VII - Il Sistema GPS pagina 213 R.Galetto A.Spalla - Lezioni di Topografia ∆Ti dell’ora di emissione e quella di ricezione del segnale, si ricava la distanza Di tra il satellite Si e l’antenna ricevente. Avendo determinato le tre distanze Di si può scrivere un sistema di tre equazioni del tipo Di = (X P − X i*) 2 + (YP − Yi* ) 2 + (Z P − Zi* ) 2 nelle quali sono incognite le coordinate XP,YP,ZP del punto P e sono note le distanze Di e le coordinate X*i, Y*i, Z*i, dei satelliti. Z D1 D2 P D3 Y X figura 5 Risolvendo il sistema si ricavano le coordinate XP,YP,ZP del punto P. Come per ogni altra operazione topografica, è però opportuno non effettuare un numero di misure strettamente necessario alla determinazione delle incognite, al fine di mediare l’effetto di errori accidentali sul risultato finale. Ciò significa che è opportuno utilizzare più di tre satelliti per determinare la posizione di un punto. Appositi programmi, che vengono venduti insieme agli strumenti riceventi, consentono di conoscere, fissata la località nella quale si intende operare e il giorno nel quale si vogliono effettuare le misure, la configurazione della costellazione dei satelliti e cioè quanti satelliti saranno visibili e quale sarà la loro altezza sull’orizzonte, nell’arco delle 24 ore. E’ pertanto possibile progettare la sessione delle operazioni di misura in modo da operare quando sono visibili più di tre satelliti. Se si opera correttamente si può arrivare a determinare le coordinate dei punti con e.q.m. di pochi centimetri. Per raggiungere queste precisioni occorre però completare le elaborazioni dei segnali che vengono fatte al momento della misura, con altri calcoli che tengono conto anche delle informazioni, fornite dalle stazioni di monitoraggio a terra, riguardanti le deviazioni dei satelliti dalle orbite teoriche nel periodo di tempo in cui le misure sono state eseguite. Capitolo VII - Il Sistema GPS pagina 214 R.Galetto A.Spalla - Lezioni di Topografia 3.2 Dalle coordinate geocentriche alle coordinate ellissoidiche Abbiamo detto precedentemente che esiste una procedura di calcolo che consente di ricavare dalle coordinate geocentriche XP,YP,ZP di un punto P le use coordinate geografiche ellissoidiche ϕ, λ e la quota ellissoidica h. Dalle coordinate ellissoidiche ϕ, λ si possono ricavare direttamente le coordinate N,E nella proiezione di Gauss, e quindi il problema planimetrico può considerarsi risolto*. superficie fisica del terreno v P geoide ellissoide hP q P' P" figura 6 P n Vi è invece un problema da risolvere per quanto riguarda l’altimetria. Al punto 1.3 del capitolo III abbiamo infatti visto (vedi figura 6) che quella che viene detta quota di un punto P, e che viene in genere indicata con la lettera minuscola q, è la sua distanza, lungo la verticale v, dal geoide; questa quota è detta anche quota ortometrica. La quota ellissoidica di un punto P, che viene generalmente indicata con la lettera minuscola h, è invece la sua distanza dall’ellissoide, lungo la normale all’ellissoide. Vi è quindi il problema di trasformare la quota ellissoidica in quota ortometrica. Sempre al capitolo III abbiamo detto che, nell’ambito del campo geodetico** , l’ellissoide coincide, come forma, con quella della sfera locale; e abbiamo detto che anche il geoide, a meno di irregolarità dovute a variazione di densità della massa terrestre, coincide con la sfera locale, sempre come forma e non come posizione, e quindi con l’ellissoide. Se dunque non ci fossero irregolarità di distribuzione della densità della massa terrestre nella zona in cui si opera, che supponiamo compresa nel campo geodetico, sarebbe sufficiente conoscere la quota ortometrica di un punto, misurare col metodo GPS la quota ellissoidica del medesimo punto e quindi ricavare la costante δ che ci permette di passare dalle quote ellissoidiche alle quote ortometriche. In realtà il geoide non ha quasi mai un andamento regolare, ma presenta delle ondulazioni, dovute appunto alla non uniforme densità della massa terrestre, che genera irregolarità nel campo gravitazionale e quindi nel geoide che, ricordiamo è la superficie sempre ortogonale alle linee di forza di tale campo. * In realtà il problema è un po’ più complicato, poiché il sistema GPS fornisce le coordinate geografiche ϕ, λ riferite all’ellissoide geocentrico WGS84, e quindi, prima di passare alla trasformazione da ϕ, λ a N,E bisogna trasformare le coordinate ϕ, λ a quelle che sono le loro corrispondenti sull’ellissoide nazionale (vedi capitolo III), tutto questo viene però fatto automaticamente da programmi di calcolo in dotazione con lo strumento ricevente e quindi non crea problemi all’operatore. ** Ricordiamo che si intende per campo geodetico nell’intorno di un punto P una zona circolare della superficie terrestre con centro in P di diametro di 100 km. Capitolo VII - Il Sistema GPS pagina 215 R.Galetto A.Spalla - Lezioni di Topografia superficie fisica del terreno geoide Nella figura 7 abbiamo messo in evidenza, esagerandole di moltissimo, tali ondulazioni. ellissoide Le ondulazioni del geoide sono invece molto morbide; per cui misurando la quota ellissoidica mediante il GPS su un figura 7 certo numero di punti di quota ortometrica nota, distribuiti nella zona da rilevare con una densità di uno ogni 5÷10 kmq, si possono determinare i parametri per passare dalle quote ellissoidiche alle quote ortometriche per tutti gli altri punti rilevati col GPS. In varie Nazioni, tra cui l’Italia, per una certa parte del territorio nazionale, è stato determinato, mediante misure geodetiche speciali (astronomiche e di gravità), lo scostamento del geoide dall’ellissoide; in tal caso non occorre avere il doppio valore di quota su un certo numero di punti campione, ma si può passare direttamente dalle quote ellissoidiche alle quote ortometriche. Si può ipotizzare che in un futuro molto prossimo l’andamento del geoide, e cioè il suo scostamento dall’ellissoide, sarà noto con sufficiente precisione per tutto il territorio nazionale. 4. La prassi operativa. Nei paragrafi precedenti abbiamo dato una descrizione molto semplificata del sistema GPS; ci siamo cioè limitati ad esporre i concetti di base del metodo, senza prendere in considerazione tutti gli aspetti che concernono le modalità di trasmissione dei segnali dai satelliti alle antenne riceventi, le cause di errore da cui possono essere affette le misure e i vari modi con cui si può operare per la determinazione delle coordinate dei punti. Non entreremo in tutti questi dettagli poiché lo spazio che possiamo dedicare all’argomento, nell’economia del corso, non lo consente. Chi volesse approfondire l’argomento potrà consultare, per quanto riguarda gli aspetti teorici, i molti articoli apparsi in questi ultimi anni sulla rivista della SIFET (Società Italiana di Fotogrammetria e Topografia) e per quanto riguarda i metodi operativi, i manuali delle case costruttrici degli strumenti. Tuttavia daremo sinteticamente almeno qualche nozione su quella che è la prassi operativa, e cioè il modo di utilizzare il GPS che viene generalmente seguito nella pratica. 4.1 La tecnica differenziale L’effetto di molte cause d’errore del sistema GPS (imperfetta conoscenza delle orbite reali dei satelliti, errori nella misura del tempo da parte degli orologi sui satelliti, imperfetta conoscenza della velocità di trasmissione delle onde elettromagnetiche a causa della variabilità della densità dell’atmosfera, ecc.) può essere eliminato applicando la tecnica della misura differenziale. Capitolo VII - Il Sistema GPS pagina 216 R.Galetto A.Spalla - Lezioni di Topografia Essa consiste in questo. Dovendo determinare la posizione di un certo numero di punti, ad esempio per costruire la rete di inquadramento di un rilievo cartografico, non si opera con un solo strumento ricevente determinando la posizione di un punto alla volta; si usano invece simultaneamente due strumenti riceventi, uno posizionato su un punto di riferimento, detto punto principale, e uno su uno degli altri punti. Si effettuano quindi le misure facendo stazione su questi due punti di cui si determinano le coordinate. Ciò fatto si procede posizionando di volta in volta i due ricevitori uno su un nuovo punto da determinare e uno su un punto di cui già si sono determinate le coordinate; e così via fino a determinare le coordinate di tutti i punti della rete. Realizzare una triangolazione col metodo GPS è quindi molto più facile che realizzarla con i metodi topografici classici, basati sull’uso di misure angolari effettuate col teodolite e di misure di distanza effettuate con distanziometri elettronici. L’operatore che usa un ricevitore GPS non deve infatti possedere una particolare capacità operativa, ma deve solo attenersi a quelle che sono le prescrizioni d’uso, e cioè effettuare le misure con una corretta situazione della costellazione dei satelliti, evitare di fare stazione in zone in cui esistono ostruzioni al ricevimento delle onde elettromagnetiche e così via. E’ anche vero però che per ottenere buoni risultati occorre saper predisporre un buon progetto della campagna di misure e sapersi destreggiare nell’uso di programmi di calcolo che richiedono per lo meno una buona capacità nel saper valutare criticamente i risultati ottenuti. Non è proprio semplice, tenuto conto che il GPS ricava i dati nel sistema WGS84, arrivare alle coordinate nel nostro sistema nazionale Gauss-Boaga. Operando correttamente si arriva a ricavare le coordinate dei punti con un e.q.m di pochi centimetri. 4.2 Un uso riduttivo del sistema GPS: il GPS come distanziometro Il sistema GPS è stato concepito per determinare le coordinate di punti; tuttavia esso può essere usato anche in maniera più riduttiva, come semplice misuratore di distanze. Quando si fa stazione su due punti con la tecnica differenziale il dato che si ottiene direttamente, che non ha cioè bisogno di calcoli particolari per essere reso disponibile, è la distanza reale tra i due punti su cui si è fatta stazione. Si può pertanto riguardare l’insieme delle due antenne riceventi come un distanziometro elettronico di grande potenzialità. Rispetto ad un distanziometro elettronico tradizionale l’uso delle due antenne GPS con tecnica differenziale consente di misurare distanze molto maggiori (10÷20 km), ma soprattutto non richiede che i due punti siano tra loro visibili. Il distanziometro elettronico tradizionale richiede infatti di collimare, dal punto di stazione dello strumento, un prisma riflettente posto sull’altro punto che determina la distanza da misurare. Usando il GPS i due punti possono invece essere anche dalle parti opposte di una collina; l’unica condizione è che abbiano la visibilità dei satelliti (visibilità nel senso che abbiamo prima definito). Capitolo VII - Il Sistema GPS pagina 217 R.Galetto A.Spalla - Lezioni di Topografia 4.3 L’uso cinematico del GPS Una delle applicazioni più interessanti della tecnica GPS è quella che riguarda la determinazione di punti in movimento. 4.3.1 Utilizzazione nella tecnica fotogrammetrica In questo senso l’applicazione più interessante che riguarda il nostro settore disciplinare è l’uso del GPS per determinare le coordinate del centro dell’obbiettivo di una macchina fotografica montata su un aeroplano, nell’istante in cui viene scattata una fotografia del territorio sorvolato. Vedremo infatti che la fotogrammetria è la tecnica che consente di ricostruire un modello della superficie fisica del terreno, quando di esso se ne hanno due immagini prese da due diverse posizioni dello spazio. Da questo modello (che non è un modello fisico, ma è costituito da un numero di punti di cui sono note le coordinate in un sistema di riferimento arbitrario) si ricava poi la cartografia del territorio. Ma per giungere a questo risultato la fotogrammetria necessita del supporto della topografia, per conoscere le coordinate di un certo numero di punti del modello, che servono per completare le informazioni che si ricavano dalle immagini fotografiche. Vedremo che la possibilità di determinare quelli che, nella terminologia fotogrammetrica, vengono detti punti di presa dei fotogrammi, riduce praticamente a zero la necessità di eseguire queste operazioni topografiche di supporto. 4.3.2 Applicazioni in campo civile Le applicazioni del GPS sono però numerosissime anche in altri settori, anche senza considerare quello militare e tutti i campi della navigazione per i quali il GPS è stato esplicitamente progettato e realizzato, come si evince dall’acronimo completo del sistema che è NAVSTAR GPS, ossia: NAVigation Satellite Timing And Ranging Global Positioning System). Citiamo due applicazioni che riguardano la determinazione di veicoli in movimento. Una riguarda la realizzazione di un sistema di controllo in tempo reale della posizione degli autobus del servizio di trasporto urbano; collocando cioè su ogni autobus un’antenna GPS si può determinare la loro posizione in ogni istante e controllarne il corretto svolgimento del servizio da una postazione centralizzata. Un’altra applicazione riguarda la possibilità di conoscere la posizione di grossi mezzi di trasporto (ad es. TIR) che siano soggetti a furti; un’antenna GPS collocata sul mezzo rileva con continuità la sua posizione, e la trasmette via radio a una centrale di controllo; in caso di furto del mezzo è quindi possibile vedere dove esso viene portato e recuperarlo. Queste applicazioni sono rese possibili dal fatto che le antenne riceventi sono abbastanza costose quando devono consentire precisioni centimetriche nella determinazione dei punti, ma hanno costi assai più modesti quando è sufficiente determinare la posizione dei punti con Capitolo VII - Il Sistema GPS pagina 218 R.Galetto A.Spalla - Lezioni di Topografia qualche decina di metri di approssimazione. Inoltre quando non occorrono precisioni centimetriche nella determinazione dei punti, si può operare senza applicare la tecnica di misura differenziale e si può elaborare solo una parte del segnale che viene inviato dai satelliti senza procedere alla fase di calcolo più raffinata che tiene conto della correzione da apportare all’orbita teorica dei satelliti. 5. La rete dei vertici trigonometrici GPS dell’IGMI L’IGMI (Istituto Geografico Militare Italiano) ha utilizzato il sistema GPS per realizzare una nuova rete di vertici trigonometrici. La nuova rete dei vertici trigonometrici realizzata col sistema GPS costituisce in pratica una nuova rete di vertici trigonometrici paragonabile, come importanza e funzioni, alla vecchia rete dei vertici trigonometrici del primo ordine. La nuova rete di vertici trigonometrici è stata denominata IGM95. Mentre la vecchia rete del primo ordine di vertici trigonometrici si componeva di circa 360 punti, la nuova rete IGM95 si compone di 1150 vertici, con una densità media sul territorio italiano di circa un vertice ogni 10 kmq (vedi figura 8). Ciò significa che la nuova rete IGM95 non solo si sostituisce alla vecchia rete del primo ordine, ma rimpiazza automaticamente anche le reti di ordine inferiore. figura 8 - La rete IGM95 Applicando infatti la tecnica differenziale cui si è prima fatto cenno, assumendo come stazione di riferimento un vertice IGM95, è facile realizzare reti di inquadramento in qualsiasi zona del territorio italiano e ottenere le coordinate dei punti nel sistema di riferimento nazionale. Dal punto di vista operativo vi è inoltre il vantaggio che i nuovi vertici sono stazionabili, al contrario dei vecchi vertici trigonometrici, i quali, per essere collimabili da lontano, erano materializzati da particolari fisici non stazionabili (cime di campanili, ecc.). Capitolo VII - Il Sistema GPS pagina 219 R.Galetto A.Spalla - Lezioni di Topografia CAPITOLO VIII FOTOGRAMMETRIA 1 Concetti generali. 1.1 Semplificazione del problema della rappresentazione cartografica del territorio. Trattando il problema della riduzione delle distanze misurate a distanze topografiche, abbiamo visto che la distanza topografica d tra due punti A e B della superficie fisica della terra, tra i quali vi è una distanza reale in linea d’aria d* inferiore 5 km, può essere ritenuta uguale, a meno di quantità trascurabili, alla sua proiezione d’ sul piano tangente alla sfera locale. B d* ζ A qA B° ε κ d' d° q B R O figura 1 Abbiamo visto inoltre che, sempre per valori di d* inferiori a 5 km, la differenza ε tra la distanza topografica d’ e la distanza reale proiettata sull’orizzontale do, vale al massimo una ventina di centimetri, anche quando si hanno valori di qA e della differenza qB-qA che tendono a massimizzare ε . La differenza κ tra la quota qB di B ed il segmento che va da B a Bo, intersezione della verticale per B col piano tangente, è di pochi centimetri, per d* inferiore ad 1 km, ma aumenta più sensibilmente all’aumentare di d* . Vedremo però nel seguito che la fotogrammetria realizza la cartografia di un territorio comunque vasto, scomponendolo in tanti tasselli rettangolari di dimensioni limitate, il cui lato maggiore, nel caso della cartografia a grande scala, non supera i 2 km, e operando separatamente su ciascuno di essi. Capitolo VIII – Fotogrammetria pagina 220 R.Galetto A.Spalla - Lezioni di Topografia Vedremo tra poco che ognuno di questi tasselli sarà costituito da un modello stereoscopico, cioè da una stessa zona di superficie di terreno riprodotta su due fotografie prese da due punti diversi dello spazio. Vedremo poi che, anche per la cartografia a grande scala, il metodo fotogrammetrico non consente di determinare le coordinate plano-altimetriche di un punto con un errore quadratico medio inferiore a 15÷20 cm. Se quindi consideriamo entrambi i fatti e cioè: il fatto di cartografare il territorio scomponendolo in tasselli di limitata estensione e la precisione conseguibile col metodo fotogrammetrico, possiamo ritenere trascurabili, nell’ambito di un modello stereoscopico sia ε che κ. Ne consegue che, quando parliamo di realizzazione di cartografia col metodo fotogrammetrico e prendiamo in considerazione un’estensione di territorio compresa in un modello stereoscopico, possiamo dare una definizione semplificata di cosa intendiamo per rappresentazione cartografica della superficie fisica del terreno, che è la seguente: considerando di realizzare una cartografia fotogrammetrica con la precisione mediamente conseguibile nel campo della produzione commerciale e operando nell’ambito di un modello stereoscopico, la rappresentazione planimetrica della superficie fisica del terreno può essere assimilata alla sua proiezione ortogonale sul piano tangente alla sfera locale nel punto approssimativamente baricentrico del modello stereoscopico e la quota dei punti è assimilabile alla loro distanza da detto piano. C B A q qA A' q B B' C C' piano tangente sfera locale rappresentazione cartografica semplificata figura 2 1.2 Il concetto di base della fotogrammetria. La fotogrammetria è quella tecnica che consente la ricostruzione della forma e delle dimensioni di un oggetto quando si hanno di esso due immagini fotografiche riprese da due punti diversi. In particolare, se l'oggetto è il terreno e se le fotografie sono state riprese da un aereo, secondo particolari accorgimenti che saranno definiti nel seguito, la fotogrammetria consente: • di ricostruire la forma e le dimensioni della porzione di terreno ripresa, di formare cioè il modello del terreno; Capitolo VIII – Fotogrammetria pagina 221 R.Galetto A.Spalla - Lezioni di Topografia • di passare, attraverso la proiezione ortogonale del modello, alla sua rappresentazione cartografica. Per chiarire il perché servano due fotografie di una stessa zona del terreno per realizzarne la rappresentazione cartografica e non ne basti invece una, si considerino le figure seguenti. C B A O B A C figura 3 La fotografia aerea (vedi figura 3) fornisce un'immagine del terreno che geometricamente si definisce una proiezione centrale, poiché i raggi che generano sulla fotografia le immagini del terreno passano tutti per uno stesso punto che è il centro dell'obbiettivo (più avanti sarà data spiegazione del concetto di centro dell’obbiettivo). Ne consegue che, se riproiettassimo l’immagine, dal punto dello spazio O da cui è stata ripresa, sul piano tangente alla sfera locale passante per il punto centrale della zona fotografata (vedi figura 4), otterremmo una rappresentazione della superficie del terreno che ci dà un'immagine deformata, e che quindi non può essere utilizzata come una carta topografica, la quale deve essere, come abbiamo visto in premessa, la proiezione ortogonale della superficie del terreno piano tangente alla sfera locale. C B A O B A A' C A" B' B" C' C" P sfera locale figura 4 Capitolo VIII – Fotogrammetria pagina 222 R.Galetto A.Spalla - Lezioni di Topografia Quando invece si hanno due fotografie che riprendono una stessa zona del terreno (vedi figura 5), il generico punto A della superficie comune ripresa, genera la sua immagine A' sulla fotografia 1 e la sua immagine A" sulla fotografia 2; i raggi r1 ed r2che generano dal punto A i punti A' e A" sulle lastre 1 e 2 si definiscono raggi omologhi. A" A' r' r" A figura 5 Supponendo che la superficie fisica del terreno scompaia (il fatto è espresso dall’aver disegnata tratteggiata nella figura 6 la superficie del terreno) e che le fotografie rimanessero posizionate nello spazio così come al momento della presa, risulterebbe possibile, ricostruendo con percorso inverso i raggi omologhi, individuare ciascun punto del terreno come intersezione dei raggi omologhi ad esso relativi (vedi figura 4). a' a" b' b" c' c" raggi omologhi b' b" c" c' a' a" A B C sfera locale figura 6 Capitolo VIII – Fotogrammetria pagina 223 R.Galetto A.Spalla - Lezioni di Topografia La proiezione delle intersezioni dei raggi omologhi sul piano tangente alla sfera locale fornirebbe la rappresentazione cartografica planimetrica del terreno; inoltre la distanza dei punti dal piano tangente fornirebbe la quota dei punti. In questo pertanto consiste il concetto di base della fotogrammetria; nel poter riprodurre la forma di un oggetto attraverso due sue immagini riprese da punti diversi dello spazio. L’applicazione pratica del concetto di base implica che vengano risolti tre tipi di problemi: 1. la ripresa delle immagini aeree; 2. la ricostruzione, per intersezione dei raggi omologhi, del modello del terreno; 3. l’individuazione delle intersezioni dei raggi omologhi di un generico punto P e il desumere dalla posizione spaziale di detta intersezione la rappresentazione cartografica di P. Le operazioni di cui al punto 1 riguardano il momento dell’acquisizione delle immagini, cioè il momento della presa; lo strumento base di questa fase operativa è la camera da presa fotogrammetrica. Le operazioni di cui ai punti 2 e 3 riguardano la fase di restituzione; con questo termine (restituzione) si intende l’insieme delle operazioni che portano alla ricostruzione di un modello (analogico o analitico del terreno) e delle operazioni di misura che portano alla determinazione delle coordinate dei punti del modello e quindi alla rappresentazione cartografica del terreno. Lo strumento di base in questa fase operativa è lo strumento restitutore fotogrammetrico, detto semplicemente restitutore. 1.3 Fotogrammetria analogica, analitica e digitale. 1.3.1 Premessa: il fenomeno fisiologico della vista Vale la pena di ricordare di sfuggita, senza entrare in particolari, che in pratica la fotogrammetria riproduce qualcosa di molto simile al meccanismo fisiologico della vista umana. Tale meccanismo è basato sul fatto che quando guardiamo una scena, di questa scena se ne formano sulle nostre retine due immagini, che sono un po’ diverse l’una dall’altra, poiché i punti di osservazione di ciascuna di esse, costituiti dal centro del cristallino (centri di presa), sono situati in due punti diversi dello spazio. Le immagini sulle retine sono il dato di partenza con cui poi il nostro cervello ricostruisce il modello tridimensionale della scena; il corretto posizionamento nello spazio di ogni singolo punto della scena viene calcolato dal cervello in funzione della differente posizione sulle due retine delle due immagini di ogni punto. Possiamo dire che il cervello misura la posizione dei due punti immagine riferite ad uno stesso punto oggetto sulle due retine, e quindi calcola la posizione del punto oggetto nello spazio. La posizione del punto nello spazio viene ricavata quindi con un procedimento di calcolo del cervello e non come intersezione di due raggi che, partendo dalle immagini delle retine e passando per il centro dei cristallini, vadano a creare un punto di intersezione nello spazio coincidente con la posizione del punto oggetto. Possiamo dire quindi che la parte concreta del fenomeno della vista fisiologica si ha solo nella ricezione delle immagini, cioè per usare un termine fotogrammetrico, solo nella presa delle immagini, mentre il fenomeno della Capitolo VIII – Fotogrammetria pagina 224 R.Galetto A.Spalla - Lezioni di Topografia ricostruzione dell’immagine, la restituzione con termine fotogrammetrico, è solo un fatto mentale. La fotogrammetria analogica e quella analitica non si differenziano per la fase di presa, che è la stessa per entrambe, ma per la fase di restituzione. 1.3.2 La fotogrammetria analogica. La fotogrammetria analogica, a partire dalle due fotografie aeree, per ogni punto di cui vuole determinare la posizione nello spazio, ricostruisce con dei dispositivi fisici i raggi che proiettano nello spazio i due punti immagine relativi a quel punto, e determina la posizione spaziale del punto con un’operazione di misura su tale punto di intersezione; l’operazione di misura, nella fotogrammetria analogica, avviene quindi, sul modello del terreno costituito dall’insieme dell’intersezione di tutti i raggi omologhi. Gli strumenti restitutori analogici ripetono fisicamente all’inverso, con dispositivi ottici o meccanici, il fenomeno della presa: la ricostruzione dei raggi omologhi ha cioè in essi un riscontro fisico che è analogo al fenomeno della presa. L’individuazione dell’intersezione dei raggi omologhi avviene mediante dispositivi ottici o meccanici e la determinazione della loro posizione rispetto ad un sistema di riferimento strumentale avviene con dispositivi meccanici. L’operazione di misura avviene cioè in uno spazio oggetto, fisicamente compreso nell’ambito dello strumento, dove si forma idealmente un modello della superficie del terreno e tale operazione consiste appunto nel determinare le coordinate dei punti di intersezione dei raggi omologhi rispetto a un sistema di riferimento strumentale. proiettori a' a" b' b" raggi c' c" omologhi b' b" c" c' a' a" A B dispositivo C carta da disegno tracciante piano di restituzione figura 7 Ad esempio uno dei primi di tipi di strumenti analogici, che lavoravano sul principio di ricostruire l’analogia del fenomeno della presa con metodo ottico, era essenzialmente costituito da due proiettori in cui si inseriva la coppia di diapositive, e da un piano su cui si appoggiava la carta da disegno e che simulava la posizione del piano tangente alla sfera locale al momento della presa; un particolare dispositivo (non facile da spiegare sinteticamente e di cui perciò tralasciamo la descrizione) consentiva di individuare l’intersezione dei raggi omologhi e di Capitolo VIII – Fotogrammetria pagina 225 R.Galetto A.Spalla - Lezioni di Topografia proiettarne l’intersezione sulla carta da disegno (che diventava poi la cartografia del terreno ripreso); la distanza dell’intersezione dei raggi omologhi dal piano del disegno, eventualmente corretta dall’effetto della curvatura terrestre, forniva la quota dei punti (vedi figura 7). figura 7.bis Si noti questo fatto molto importante: come indicato nella figura 7, nello strumento analogico le due camere di restituzione erano poste a una distanza molto ravvicinata rispetto a quelle che esse avevano al momento della presa; del resto non sarebbe stato certo possibile costruire strumenti delle dimensioni di centinaia di metri! Ma in effetti si davano due fortunate coincidenze: • avvicinando le due camere da presa l’una all’altra lungo la base di presa mediante una traslazione pura (figura 7.bis) i raggi omologhi continuano ad intersecarsi; ciò significa che tale traslazione non distrugge il modello del terreno, ma ne crea uno di dimensioni ridotte; Capitolo VIII – Fotogrammetria pagina 226 R.Galetto A.Spalla - Lezioni di Topografia • il cartografo non vuole rappresentare il terreno nella scala 1:1, ma in scala ridotta, quindi doveva appunto realizzare un modello del terreno in scala ridotta per poi proiettarlo sul piano dello strumento. Questi due fatti congiunti rendevano possibile la restituzione fotogrammetrica analogica; se ad esempio si voleva realizzare una carta alla scala 1:5000 si effettuavano le riprese aeree in modo che la base di presa (distanza media tra i punti di presa di due fotogrammi consecutivi), divisa per 5000, fosse orientativamente uguale alla base di restituzione, cioè alla distanza delle due camere di restituzione nello strumento che poi si intendeva usare nella fase di restituzione; la base di restituzione poteva subire nello strumento restitutore modeste variazioni di grandezza per compensare le inevitabili irregolarità della base di presa in modo da realizzare il modello stereoscopico nella esatta scala voluta . Il tipo più diffuso di strumento analogico, ancor oggi utilizzato nell’industria fotogrammetrica, si basa invece su un’analogia meccanica; in pratica le coppie dei raggi omologhi vengono di volta in volta materializzate da due bacchette metalliche che sono incernierate con due snodi sferici nei due punti che corrispondono ai centri di proiezione dello strumento ottico sopra descritto. Le altre due parti terminali delle due bacchette, opposte a quelle incernierata nella posizione assimilabile a quella dei centri di proiezione, sono unite tra di loro in un punto mediante un altro snodo sferico, il quale rappresenta il punto di intersezione dei raggi omologhi quando le due bacchette coincidono con due raggi omologhi. Non entriamo qui nel dettaglio di come l’operatore potesse giudicare che le due bacchette coincidessero con due raggi omologhi. Anche se gli strumenti analogici a proiezione meccanica vengono ancora talvolta usati nella produzione della cartografia, noi non prenderemo in considerazione la fotogrammetria analogica, che appunto sull’uso di tali strumenti si basa, poiché tali strumenti possono oggi (anno 1996) considerarsi in via di estinzione. 1.3.3 La fotogrammetria analitica La fotogrammetria analitica opera invece misurando direttamente sulle due fotografie la differente posizione delle due immagini di uno stesso punto e, con sole operazioni di calcolo (donde il nome di analitica), calcola la posizione spaziale del punto; il procedimento è quindi molto simile, in linea di principio, a quello della vista fisiologica, poiché anche nella fotogrammetria analitica il fenomeno è concreto solo nella fase di acquisizione, mentre consiste solo in una fase di calcolo in quello della restituzione. Lo strumento restitutore usato nella fase di restituzione nella fotogrammetria analitica è lo strumento restitutore analitico. Una sua parte integrante e fondamentale è il calcolatore elettronico (tipo Personal Computer) dedicato all’esecuzione dei calcoli. E’ anche dovuto alla necessità di disporre di una potenza di calcolo notevole inclusa nello strumento restitutore che fa sì che la fotogrammetria analitica divenga operativa solo a partire dalla metà degli ’70; Non ci dilunghiamo oltre sulla fotogrammetria analitica poiché essa costituisce appunto l’argomento principale del corso, che verrà trattato diffusamente più avanti. Capitolo VIII – Fotogrammetria pagina 227 R.Galetto A.Spalla - Lezioni di Topografia 1.3.4 La fotogrammetria digitale. Ultima arrivata sulla scena è la fotogrammetria digitale, divenuta operativa solo a partire dei primi anni ’90. La fotogrammetria digitale si caratterizza fondamentalmente per due aspetti: • uso di immagini digitali (donde il nome); anziché usare come immagini del terreno le diapositive in forma di pellicola usa delle immagini digitali ottenute sottoponendo a scansione le pellicole; queste vengono trasformate in matrici numeriche. La fotografia viene cioè idealmente suddivisa in un grigliato di piccoli quadratini (pixel); ogni quadratino viene messo in corrispondenza con un elemento di una matrice; il valore numerico di un generico elemento della matrice corrisponde all’intensità di grigio (se la pellicola è in bianco e nero) o al colore (se la pellicola è a colori) che è presente nel quadratino che gli corrisponde. • eliminazione dello strumento restitutore fotogrammetrico, che viene sostituito dal computer. A parte queste due caratteristiche, dal punto di vista concettuale la fotogrammetria digitale è simile alla fotogrammetria analitica, poiché anch’essa adotta il principio di effettuare l’operazione di misura sulle immagini e di ricavare per via analitica le coordinate dei punti oggetto. Attualmente (anno 1996) la fotogrammetria digitale è stata adottata da alcuni importanti centri europei di produzione cartografica; in Italia, per ora, non trova ancora impiego nel mondo della produzione. Si può prevedere però che in un futuro molto prossimo (dieci anni?) col progredire della tecnologia del computer che renderà disponibili memorie di massa sempre più a buon mercato per memorizzare le immagini digitali e maggior potenza di calcolo per elaborarle, la fotogrammetria digitale soppianterà ogni altro tipo di fotogrammetria. Riteniamo quindi essenziale dare qualche cenno anche di questa nuova tecnica (paragrafo 4 di questo stesso capitolo) 1.3.5 Fotogrammetria aerea e fotogrammetria terrestre Per illustrare l’argomento abbiamo finora supposto che le immagini fotografiche da cui origina il processo fotogrammetrico fossero riprese da una camera fotografica (in realtà fotogrammetrica come vedremo tra poco) situata a bordo di un aereo. In questo caso, di prese effettuate da aereo, dovremmo però specificare che siamo nel campo della fotogrammetria aerea; infatti esiste anche una fotogrammetria terrestre, che è quella che si ha quando le prese vengono fatte da terra con apparati fotografici simili a quelli con cui si fa della fotografia amatoriale. La fotogrammetria terrestre trova largo impiego in tanti settori, dal rilevamento architetturale, al rilevamento di pezzi nel settore meccanico (largo impiego nel settore automobilistico), al settore, al settore medico, ecc. ecc.. Nella trattazione che segue, quando parleremo di fotogrammetria, intenderemo la fotogrammetria aerea, anche se molti dei concetti, delle apparecchiature e delle metodologie di lavoro, possono intendersi riferite anche alla fotogrammetria terrestre. Capitolo VIII – Fotogrammetria pagina 228 R.Galetto A.Spalla - Lezioni di Topografia 1.4 L’acquisizione del dato primario: i fotogrammi. 1.4.1 Le fotografie aeree in uso nella fotogrammetria. Le fotografie aeree che vengono utilizzate per la produzione di cartografia devono presentare requisiti ben precisi che dipendono: • dalle caratteristiche geometriche delle camere di presa; • dai metodi di attuazione delle riprese; • dalle emulsioni fotografiche adottate. Le fotografie che hanno queste particolari caratteristiche, che saranno definite in dettaglio nel seguito, si definiscono fotogrammi e vengono utilizzate tanto in strumenti di tipo analogico come per fotogrammetria analitica. 1.4.2 La camera fotogrammetrica. Una camera fotogrammetrica è una camera fotografica molto complessa e di notevoli dimensioni e peso. Le sue caratteristiche più salienti sono: • • • • • il formato dell'immagine, di forma quadrata, ha il lato di 230 mm e quindi la sua area è sessanta volte maggiore di quella del negativo che si ottiene con una comune macchina fotografica amatoriale di formato (24 x 36) mmq; la macchina è dotata di un grande magazzino porta pellicola, che può contenere pellicole lunghe sino a 250 piedi (circa 80 m), e di dispositivi che consentono un'elevata automazione delle operazioni di ripresa; le immagini che da essa si ottengono sono metricamente corrette perché la distorsione dell'obbiettivo è praticamente nulla; la camera possiede dei riferimenti geometrici intrinseci alla sua struttura che materializzano un sistema di riferimento rispetto al quale è possibile definire la posizione dei punti immagine in termine di coordinate cartesiane; poiché la quota di volo di un aereo che esegue riprese fotogrammetriche è, come minimo, di alcune centinaia di metri, il terreno è sempre molto lontano dalla camera da presa (a distanza iperfocale); essa è quindi a fuoco fisso e la sua focale è, in generale, di 150 mm; solo da pochi anni, e limitatamente a rilevamenti speciali, vengono impiegate anche camere con focali maggiori (220 e 300 mm). a) Schematizzazione della camera da presa L’ottica di una camera fotogrammetrica è molto complessa e viene definita in funzione di diversi parametri; per non appesantire la trattazione verrà qui usata una schematizzazione semplificata della geometria interna della camera da presa, che, oltre ad essere sufficiente alla comprensione della trattazione che segue, non si discosta molto dalla realtà. Capitolo VIII – Fotogrammetria pagina 229 R.Galetto A.Spalla - Lezioni di Topografia asse ottico piano focale pellicola A P' marche fiduciali distanza focale f α' spazio immagine telaio conico che sostiene l'obbiettivo O corpo esterno della camera α P spazio oggetto figura 8 Adottando questa schematizzazione semplificata possiamo dire(vedi figura 8) che: • esiste un centro dell’obbiettivo O, che assumeremo come punto di simmetria tra stella di raggi oggetto (cioè quelli che vengono riflessi dal terreno e colpiscono l’obbiettivo) e stella di raggi immagine (cioè quelli che, dopo aver attraversato l’obbiettivo, vanno a impressionare la pellicola); • esiste un asse ottico dell’obbiettivo che è costituito dalla retta su cui giacciono i centri di tutte le calotte sferiche che delimitano la forma di tutte le lenti semplici da cui l’obbiettivo è formato; • l’asse ottico dell’obbiettivo è ortogonale al piano su cui giace la pellicola da impressionare, piano che a sua volta coincide con il piano focale della camera da presa; • l’obbiettivo ha una focale f che assumiamo essere la distanza del centro dell’obbiettivo dal piano focale; • la distanza p del piano della pellicola dal centro dell’obbiettivo è detta distanza principale; poiché la camera da presa è a fuoco fisso, la distanza principale ha un valore costante, coincidente con quello della distanza focale f; • l’angolo α formato tra un raggio che proviene da un punto P dello spazio oggetto e l’asse ottico, è uguale a quello α’ formato dal raggio immagine e dall’asse ottico, il che significa che assumeremo l’obiettivo come esente da qualsiasi tipo di distorsione. All’interno della base quadrata del tronco di cono che sostiene l’obbiettivo, si trova una cornice, che serve d’appoggio alla pellicola; su tale cornice vi trovano quattro forellini; al momento della presa della fotografia la luce passa attraverso i quattro forellini, che quindi appariranno come quattro piccoli puntini bianchi su fondo nero, sulla diapositiva ottenuta sviluppando il negativo. Il diametro dei puntini è di qualche decimo di millimetro. Questi forellini (e anche le loro immagini sui fotogrammi) sono detti marche fiduciali e servono a materializzare un sistema di riferimento interno della camera da presa. Sempre adottando una visione semplificata della geometria interna della camera da presa possiamo dire che: • l’asse ottico dell’obbiettivo interseca il piano focale in un punto A, detto punto principale, che coincide con l’intersezione dei due segmenti ideali che congiungono le due coppie di marche fiduciali. Capitolo VIII – Fotogrammetria pagina 230 R.Galetto A.Spalla - Lezioni di Topografia Nelle camere da presa le marche possono trovarsi in posizione mediana dei quattro lati del telaio su cui si appoggia la pellicola, oppure in corrispondenza degli angoli del telaio, o in entrambi le posizioni contemporaneamente, e in tal caso se ne avranno otto. A A A figura 9 Nel seguito si supporrà di trovarsi nel primo caso, per il semplice fatto che sarà più evidente la funzione delle marche come elemento fisico che materializza il sistema di riferimento interno della camera da presa. b) Parti che costituiscono la camera da presa. Le parti delle quali è costituita una camera per effettuare riprese aeree fotogrammetriche, sono indicate nella figura 10 figura 10 • la camera propriamente detta o cono (1) costituita possibilmente in monoblocco ed avente il compito di collegare nel modo più rigido possibile l'obbiettivo (2), al quadro (3) della camera, cioè al piano della prospettiva, sul quale sono fissati i quattro indici che servono a Capitolo VIII – Fotogrammetria pagina 231 R.Galetto A.Spalla - Lezioni di Topografia definire il punto principale e che, illuminati dalla luce che attraversa l'obbiettivo nel momento dell'esposizione, verranno registrati sulla superficie sensibile. Fanno inoltre parte del cono l'otturatore, li diaframma e gli strumenti di registrazione (4), cioè l'orologio, la livella, l'altimetro ed il contafotogrammi, che vengono riprodotti sul bordo del fotogramma ad ogni esposizione: l'utilizzatore potrà quindi conoscere l'assetto della camera mediante l'immagine della livella sferica, l'ora in cui è avvenuta l'esposizione, la quota di volo assoluta ed il numero progressivo di ogni fotogramma. • • Il dispositivo di sospensione (7), mediante il quale la camera è fissata elasticamente al pavimento (8) del veicolo, con tamponi di gomma (9), sopra la botola (10). Il quadro interno della sospensione può essere livellato secondo due direzioni perpendicolari fra di loro agendo su due manopole di comando. Il magazzino del film (11), che viene collegato rigidamente al cono nella sua parte superiore, la scatola del magazzino contiene il rocchetto di alimentazione (12), sul quale è avvolto il film vergine, il rocchetto ricevitore (13) ed il piatto di spianamento (14) del film con il dispositivo depressore. Il trascinamento del film avviene mediante un motore (15), che ad ogni impulso elettrico proveniente da una scatola di comando, mette in rotazione il rocchetto ricevitore e trascina quindi una porzione di film pari al formato del quadro sul quale si adagia. In un istante successivo il piatto di spianamento, sollevato durante il movimento di trascinamento, si abbassa sul dorso del film e fa sì che il lato emulsionato venga a diretto contatto con il quadro del cono. La superficie del piatto a contatto con il dorso del film è provvista di scanalature o di fori, attraverso i quali, con un dispositivo a pompa (16), si crea una depressione che mantiene il film aderente al piatto stesso sino a che non è avvenuta l'esposizione. • • • L'ottica di osservazione (17). Rigidamente collegato al telaio della camera vi è di solito un cannocchiale, mediante il quale il fotografo osserva sulla verticale il terreno durante la ripresa e controlla, con un traguardo appositamente dimensionato contenuto nel campo visivo, che la zona fotografata corrisponda a quella stabilita in sede di progetto del volo. L'intervallometro (18). Per ottenere una copertura fotografica regolare che riproduca omogeneamente tutta la regione in studio secondo le necessità fotogrammetriche, bisogna imporre alla camera una cadenza di esecuzione dei fotogrammi. Mediante l'intervallometro, senza bisogno di misurare tempi o eseguire calcoli, l'osservatore impone la cadenza di ripresa desiderata. Il pannello di comando della camera (19). L'azionamento della camera viene effettuato agendo su manopole appartenenti ad un pannello di comando che può far parte della camera ma che in diversi casi è separato da essa. I comandi principali servono per la messa in azione e l'arresto della camera (20), per l'esecuzione di fotogrammi singoli o di fotogrammi in serie con diverse cadenze (21), per la regolazione della cadenza di scatto (22). 1.4.3 I fotogrammi prodotti da una camera fotogrammetrica. Capitolo VIII – Fotogrammetria pagina 232 R.Galetto A.Spalla - Lezioni di Topografia L'immagine fotografica ottenuta mediante una camera fotogrammetrica si definisce fotogramma. Un fotogramma è dal punto di vista geometrico una proiezione centrale. L'immagine del terreno ripresa ha una scala media che dipende dalla distanza principale della camera da presa e dalla quota di volo; detta Q la quota di volo assoluta e q la quota media del terreno, entrambe espresse in metri, e assunta pari a 0,150 m la focale della camera da presa, la scala media del fotogramma risulta dalla relazione: 1 0.150 = σ f Q − qm Si parla di scala media di un fotogramma e non semplicemente di scala poiché la scala alla quale il terreno è rappresentato può variare all'interno di un unico fotogramma. Si consideri infatti il caso in cui la porzione di terreno fotografata comprenda una valle incassata tra due pareti; il fondo valle sarà la zona di terreno più lontana dalla macchina da presa, e quindi la sua immagine sarà a scala più piccola delle creste dei monti che delimitano la valle, le quali, trovandosi a quota maggiore, saranno più vicine alla camera da presa e saranno pertanto a scala maggiore. Se, ad esempio, la quota di volo assoluta Q è di 2500 metri, il fondovalle è a quota 500 metri e le creste dei monti che delimitano la valle sono a 1300 metri, si avrà per il fondovalle la seguente scala: 1 0.150 1 = = σ f 2500 − 500 13000 mentre per le creste dei monti si avrà: 1 0.150 1 = = σ f 2500 − 1300 8000 Al momento dello scatto dell'otturatore, oltre alle quattro marche fiduciali, vengono impressionati su fotogramma, lungo uno dei suoi lati: • • • un numero progressivo di contatore, utile per ricostruire la sequenzialità dei fotogrammi; infatti mentre il negativo viene conservato in rotolo, le diapositive, o le stampe su carta, vengono stampate singolarmente nel formato 240 x 240 mm (230 x 230 mm utili); l'immagine di un altimetro indicante con un margine di errore di ± 100 m, la quota assoluta di volo dell'aereo; dal lato dell'altimetro, nota la quota media del terreno ripreso, si può ricavare una buona stima della scala media del fotogramma; un datario, cioè una finestrella con la data in cui il fotogramma è stato ripreso; è compito del fotografo di bordo scrivere al momento dell'inizio delle riprese, la data del giorno nel datario, in modo che la sua immagine risulti sui fotogrammi. La presenza della data sul fotogramma permette di controllare che le riprese siano state fatte nell'intervallo di tempo previsto dal contratto; consente inoltre di conoscere quando le foto sono state scattate nel caso di impiego in tempi successivi da persone che non ne conoscono con esattezza l'origine. é importante però che la data presente sul bordo del fotogramma risulti anche sul negativo del fotogramma e non solo sulla diapositiva o sulla stampa su carta, il che indicherebbe che la data è stata stampata sulla diapositiva o sulla stampa su carta successivamente alla ripresa aerea e che quindi è scarsamente attendibile; Capitolo VIII – Fotogrammetria pagina 233 R.Galetto A.Spalla - Lezioni di Topografia • • • l'immagine di un orologio indicante l'ora in cui il fotogramma è stato ripreso; l'ora è sempre quella solare, anche quando si è in regime di ora legale. Anche questa indicazione è importante perché le ore utili per le riprese aeree vengono fissate nel capitolato; l'immagine di una livella sferica, che permette di giudicare se l'aereo al momento della ripresa del fotogramma avesse un assetto regolare di volo; il valore della distanza principale della camera fotogrammetrica. 1.4.4 Le onde elettromagnetiche dello spettro della luce visibile, dell'infrarosso vicino e dell'infrarosso termico. Un'onda elettromagnetica è un flusso di energia che viene originato da una sorgente e si propaga nello spazio. Il sole è una sorgente di onde elettromagnetiche che producono l'effetto fisiologico chiamato luce. Quando la luce del sole ci giunge direttamente, essa non ha alcun colore particolare (si dice che è luce bianca); l'insieme di tutte le onde elettromagnetiche che compongono la luce bianca si chiama spettro della luce visibile, o anche semplicemente spettro; le onde elettromagnetiche dello spettro hanno una lunghezza d'onda variabile. La luce solare nel suo complesso è assimilabile al suono che proviene da un'orchestra, nella quale coesistono toni acuti, medi e bassi; come con appositi dispositivi è possibile assorbire parte del suono e mettere in evidenza i vari toni, così con opportuni filtri ottici si può filtrare la luce solare e osservare separatamente parti limitate dello spettro; queste si differenziano perché sono composte da onde elettromagnetiche che hanno diversa lunghezza d'onda e assumono varie tonalità di colore (dal blu, al verde, al rosso ) mano a mano che aumenta la lunghezza d'onda delle onde che compongono la parte di spettro considerata. Quando la luce solare cade su un oggetto, questo agisce come un filtro; parte della luce viene assorbita dall'oggetto stesso e parte viene riflessa; poiché però gli oggetti assorbono la luce solare in quantità differenti e in parti diverse dello spettro, la luce che riflettono non è bianca ma colorata; per questo noi diciamo che gli oggetti hanno un colore; in realtà il loro colore è quello della parte dello spettro della luce bianca che essi non assorbono. In particolare un oggetto ci appare bianco quando riflette tutte le onde dello spettro e nero quando le assorbe tutte. Come nel campo delle onde acustiche esistono gli ultrasuoni, cioè onde che hanno le stesse caratteristiche di quelle sonore, ma che non sono percepibili dall'orecchio umano, così abbiamo onde elettromagnetiche che hanno caratteristiche simili a quelle dello spettro della luce solare, sono emesse dal sole e sono in parte assorbite e in parte riflesse dalle superfici sulle quali incidono, ma non sono visibili dall'occhio umano; esse sono dette dell'infrarosso vicino; la parola infrarosso deriva dal fatto che tali onde elettromagnetiche hanno lunghezza d'onda un po' più grande di quella parte dello spettro della luce visibile che, singolarmente presa, assume colorazione rossa; la parola vicino indica che esse, come lunghezza d'onda, vengono subito dopo quelle dello spettro visibile. Le onde dell'infrarosso vengono più o meno riflesse dalle superfici sulle quali incidono a seconda della natura di queste ultime. In particolare è interessante il comportamento della vegetazione nel riflettere tali onde: l'intensità di riflessione delle onde infrarosse da parte delle foglie di una pianta o dell'erba o di una coltivazione agricola in genere è, infatti, funzione non solo del tipo di vegetale, ma anche Capitolo VIII – Fotogrammetria pagina 234 R.Galetto A.Spalla - Lezioni di Topografia del suo livello di crescita, dello stato di salute, della composizione litologica del suolo sul quale si trova, dello stato di umidità del suolo e di altri fattori. Valutando quindi su una fotografia, mediante un opportuno codice cromatico, la quantità di onde infrarosse riflesse dalla vegetazione, è possibile ottenere una quantità di informazioni utili non solo agli agronomi o ai forestali, ma anche ai geologi, agli idrologi ed in generale ai tecnici preposti alla sistemazione del suolo ed alla salvaguardia dell'ambiente. Un terzo gruppo interessante è quello delle onde elettromagnetiche dell'infrarosso termico. A differenza di quelle dei primi due gruppi, le onde dell'infrarosso termico non provengono dal sole e non vengono riflesse dagli oggetti, ma vengono emesse dagli oggetti stessi in funzione della loro temperatura (da qui l'aggettivo termico). Anch'esse hanno lunghezza d'onda superiore alle onde dello spettro della luce visibile che danno la sensazione del rosso, e perciò vengono dette dell'infrarosso. La loro lunghezza d'onda è superiore anche a quella delle onde dell'infrarosso vicino e come queste ultime non sono visibili all'occhio umano; inoltre, a differenza delle onde dell'infrarosso vicino, non sono neppure in grado di impressionare le emulsioni fotografiche (esistono tuttavia opportuni strumenti in grado di rilevarle e metodi per visualizzarle). Poter visualizzare le onde dell'infrarosso termico è utile tutte le volte che si vuol rilevare un fenomeno che si evidenzia soltanto dal suo stato termico; si pensi, ad esempio, al problema dell'individuazione di sorgenti di acqua dolce in mare lungo una costa: l'affioramento dell'acqua della sorgente nell'acqua marina non è rilevabile visivamente, però provoca localmente una variazione di temperatura. Poter rilevare rapidamente, da un mezzo aereo, vaste superfici di mare con uno strumento in grado di captare le onde dell'infrarosso termico permette quindi d'accertare la presenza delle sorgenti. Indicheremo nel seguito con la sigla IR le onde elettromagnetiche dell'infrarosso vicino e con quella IRT quelle dell'infrarosso termico; abbrevvieremo inoltre in OE il termine onde elettromagnetiche ed in LdO quello lunghezza d'onda. 1.4.5 Le pellicole fotografiche. Le pellicole attualmente disponibili per le riprese aeree sono le seguenti: bianco e nero negativo; colore negativo; colore invertibile; infrarosso bianco e nero negativo; infrarosso falso colore invertibile. Le pellicole negative sono quelle che, sviluppate, si presentano in forma di negativo, dalle quali si ottiene poi, con un secondo passaggio di stampa su altra pellicola o su carta, il positivo. Le pellicole invertibili sono invece quelle che, una volta sviluppate, si presentano in forma di diapositiva; per ottenere da queste altre copie si deve effettuare una stampa o su pellicola invertibile o su carta invertibile. Generalmente quando la ripresa aerea è effettuata per ricavare i fotogrammi per la costruzione di una cartografia, si utilizza la pellicola bianco e nero negativa, dalla quale si ottengono poi alcune serie di stampe in bianco e nero ed una serie di diapositive per la restituzione fotogrammetrica. Quando invece la ripresa aerea è effettuata per fotointerpretare particolari aspetti del territorio, si utilizza la pellicola a colori (negativa o invertibile). Capitolo VIII – Fotogrammetria pagina 235 R.Galetto A.Spalla - Lezioni di Topografia Dal punto di vista della qualità, la pellicola invertibile a colori è superiore a quella negativa; quest'ultima però consente la produzione di stampe a colori con minor costo. Pertanto se si prevede di dover effettuare una distribuzione in più copie delle foto aeree, è meglio scegliere la pellicola a colori negativa, mentre se l'impiego delle fotografie è limitato alla restituzione fotogrammetrica o ad uno studio di fotointerpretazione da parte di un solo ente, è meglio utilizzare quella invertibile. Le pellicole all'infrarosso bianco e nero ed all'infrarosso falso colore vengono impiegate per scopi speciali, quando cioè si deve effettuare un'indagine fotointerpretativa per studiare fenomeni connessi alla vegetazione, all'idrologia, ecc.. Pellicola in bianco e nero (b&n) E' costituita da uno strato di emulsione steso su un supporto di base, sensibile a tutte le onde elettromagnetiche dello spettro, ma non a quelle dell'IR. sensibilità LdO in micron 0,4 0,5 0,6 0,7 0,8 0,9 figura 11.a - curva sensitometrica di una pellicola in b&n Pellicola all'infrarosso in b&n L'emulsione è sensibile a tutte le OE dello spettro ed anche alle OE dell'IR vicino; la curva sensitometrica è rappresentata in figura 11.b. sensibilità LdO in micron 0,4 0,5 0,6 0,7 0,8 0,9 figura 11.b - curva sensitometrica di una pellicola all’infrarosso b&n Pellicola a colori Ha tre strati di emulsione: uno sensibile alle OE comprese tra 0,4 - 0,5 micron, uno sensibile alle OE di LdO comprese tra 0,5 - 0,6 micron ed uno alle OE di LdO comprese tra 0,6 - 0,7 micron. Poiché le OE comprese in questi tre campi danno rispettivamente la sensazione di luce blu, verde, rossa, si dice che nella pellicola a colori vi è uno strato sensibile al blu, uno al verde ed uno al rosso. La curva sensitometrica è pertanto composta da tre curve, una per ogni strato (vedi figura 11.c). Capitolo VIII – Fotogrammetria pagina 236 R.Galetto A.Spalla - Lezioni di Topografia sensibilità strato sensibile al blu strato sensibile al verde strato sensibile al rosso LdO in micron 0,4 0,5 0,6 0,7 0,8 0,9 figura 11.c - curva sensitometrica di una pellicola a colori Il meccanismo mediante il quale avviene la riproduzione a colori di una immagine mediante l'uso delle pellicole a colori è abbastanza complesso ed esula dai nostri interessi; brevemente si può dire che la luce riflessa da un oggetto sensibilizza in modo diverso i tre strati della pellicola; questa, una volta sviluppata, quando viene illuminata da luce bianca, assorbe parte di questa luce in modo che il colore dell'immagine dell'oggetto riprodotto sulla fotografia sia uguale a quella dell'oggetto che l'ha generata. L'impiego principale delle pellicole a colori si ha nella fotointerpretazione. Pellicola all'infrarosso falso colore (Irfc) Ha tre strati di emulsione • uno sensibile alle OE 0,5 - 0,6 micron (verde) • uno alle OE 0,6 -0,7 micron (rosso) • uno alle OE 0,7 - 0,9 micron (IR); tutti gli strati sono inoltre sensibili alle OE 0,4 - 0,5 micron (blu), che vengono eliminate anteponendo all'obbiettivo all'atto della presa un filtro giallo: ciò che ha colore blu appare quindi nero su una pellicola all'IRfc. La curva sensitometrica della pellicola è rappresentata nella figura 11.d strato sensibile al verde sensibilità strato sensibile al rosso strato sensibile all'infrarosso LdO in micron 0,4 0,5 0,6 0,7 0,8 0,9 figura 11.d - curva sensitometrica di una pellicola all’infrarosso falso colore Durante lo sviluppo, la colorazione dei tre strati viene ottenuta in modo che l'intensità di riflessione dell'IR si manifesti con il colore rosso perché l'occhio umano distingue le sue sfumature meglio di quelle del blu o del verde, di conseguenza, essendo questa pellicola impiegata per indagini sulla vegetazione, si è ritenuto opportuno utilizzare lo strato di emulsione che si trasforma in colore rosso per registrare le OE dell'IR. La composizione chimica della pellicola è, inoltre, fatta in modo che gli oggetti rossi compaiono di colore verde, e quelli verdi di colore blu. Capitolo VIII – Fotogrammetria pagina 237 R.Galetto A.Spalla - Lezioni di Topografia Come già detto, questa pellicola è particolarmente adatta alla fotointerpretazione, in particolare per indagini che riguardano la vegetazione (classificazione di colture, esame del loro stato di sviluppo per previsione di produzione; rilevamento tempestivo di casi di infestazione, ecc.). 1.5 Schema di ripresa fotogrammetrica. l f H R L L 0,4 L 0,6 L figura 12.a L'aereo sorvola il terreno ad una quota relativa H; vengono riprese delle fotografie del terreno in modo che ogni punto del terreno compaia su due fotografie; ciò si ottiene facendo sì che ogni fotografia ricopra al 60% la parte di terreno che compare sulla precedente. Nelle figure L è il lato della zona di terreno (all'incirca quadrata) ripresa sul fotogramma; R è il ricoprimento longitudinale che è uguale al 60% di L; l è il lato del fotogramma (230 mm); f è la focale della camera di ripresa (in genere 150 mm). L'aereo sorvola il terreno eseguendo delle strisciate di fotogrammi secondo lo schema illustrato alle successive figure 12.b e 13. L'interasse i tra due strisciate viene scelto in modo che le strisciate si ricoprano per il 20%(r = ricoprimento trasversale) questo sempre per garantire la totale copertura fotografica del terreno da cartografare. Capitolo VIII – Fotogrammetria pagina 238 R.Galetto A.Spalla - Lezioni di Topografia i r L 0,4L L i figura 12.b. Supponiamo che la zona da rilevare sia l'area contornata in figura dalla linea tratteggiata; il percorso dell'aereo sarà quello indicato dalla linea continua; i tratti rettilinei all'interno della zona da rilevare costituiscono gli assi delle strisciate. figura 13.a - schema di volo Capitolo VIII – Fotogrammetria pagina 239 R.Galetto A.Spalla - Lezioni di Topografia figura 13.b - copertura fotogrammetrica A causa del ricoprimento longitudinale del 60% e di quello trasversale del 20%, il numero di fotogrammi di una copertura fotogrammetrica è molto superiore a quello che sarebbe necessario per una semplice copertura fotografica. 1.6 Le condizioni meteorologiche e le riprese da aereo. In un intero anno solare il numero di giornate utili a riprese fotografiche aeree per la costruzione di cartografia di base è limitato dalle condizioni meteorologiche e dai periodi stagionali. Per l'esecuzione di una ripresa aerofotogrammetrica è necessaria infatti: • l'assenza di nubi, che creano zone cieche se al di sotto della quota di volo, oppure di ombra se al di sopra; • l'assenza di foschia, che impedisce la navigazione a vista e provoca un decadimento non tollerabile nella qualità dell'immagine fotografica; • l'assenza di vento forte, che non permette di mantenere l'aereo in assetto di volo regolare; • un'inclinazione sull'orizzonte dei raggi del sole non inferiore ai 30 ; un'inclinazione inferiore provoca ombre troppo lunghe e troppo intense che ostacolano la corretta interpretazione dei fotogrammi. Oltre a queste condizioni meteorologiche occorre poi scartare per le zone in pianura il periodo estivo, nel quale la vegetazione è molto sviluppata e copre molti particolari del terreno, e, per quelle di montagna, il periodo dell'innevamento. Per rendere l'idea di quali sarebbero le condizioni ideali per una ripresa aerea fotogrammetrica, potremmo dire che il tempo ideale si avrebbe nelle ore a cavallo del mezzogiorno di una serena giornata di giugno, con l'aria tersa come in una ventosa giornata di marzo, ma senza il vento che c'è generalmente in questo mese; inoltre lo stato di sviluppo della vegetazione dovrebbe essere quello di febbraio. Da questo paradossale esempio si può ricavare che le giornate utili per le riprese fotogrammetriche sono poche nell'arco di un intero anno solare. In Italia non sono mai state fatte statistiche al riguardo, ma si può ipotizzare, in base all'esperienza che, presa a caso una zona sul territorio nazionale, non si registrano per essa più di 30 giornate utili per la sua ripresa aerofotogrammetrica. Capitolo VIII – Fotogrammetria pagina 240 R.Galetto A.Spalla - Lezioni di Topografia Questo elemento vincolante, non è generalmente noto ai committenti, che pensano quindi di poter realizzare lavori di cartografia di base nell'arco di qualche mese mentre nella maggior parte dei casi passano già alcuni mesi dal momento in cui viene stipulato il contratto d'appalto a quello in cui si verificano le condizioni idonee alla ripresa aerea. Vi sono invece più giornate utili per i voli quando le riprese aeree fotografiche vengono eseguite per la costruzione di cartografia tematica. Infatti, pur rimanendo validi tutti gli altri vincoli, cade quello riguardante il limitato sviluppo della vegetazione; anzi, per una delle indagini più frequentemente richieste per la pianificazione del territorio, quella sulla destinazione d'uso del suolo e la classificazione delle colture, può convenire che la coltura sia in avanzato stato di sviluppo. Risulta quindi utile, ai fini delle riprese aeree, anche tutto il periodo estivo, il più favorevole sotto il profilo meteorologico. Capitolo VIII – Fotogrammetria pagina 241 R.Galetto A.Spalla - Lezioni di Topografia 2. Fotogrammetria analitica. Come detto precedentemente la fotogrammetria analitica è basata sul principio di determinare la posizione spaziale di un punto di cui se ne abbiamo le immagini su due fotogrammi, direttamente in termini di coordinate, attraverso operazioni di calcolo che hanno, come dati di input fondamentale, le coordinate delle due immagini del punto espresse in un sistema di riferimento materializzato nella camera da presa e che quindi rimane costante per tutti i fotogrammi. 2.1 Il sistema di riferimento interno della camera da presa. La fotogrammetria analitica richiede che la posizione dei punti immagine sui fotogrammi venga espressa in termini di coordinate cartesiane tridimensionali rispetto ad un sistema di riferimento materializzato da elementi fisici della camera da presa stessa, che chiameremo nel seguito sistema di riferimento interno. Con riferimento alla schematizzazione semplificata della camera da presa che è stata data al punto 1.41 di questo capitolo, il sistema di riferimento interno è così definito: • origine del sistema coincidente con il centro dell’obbiettivo; • asse z coincidente con l’asse ottico dell’obbiettivo; • assi x ed y paralleli alle congiungenti delle marche fiduciali; viene assunto come asse x quello che congiunge le marche che si trovano sui due lati del fotogramma che sono approssimativamente paralleli alla direzione di volo. Poiché la pellicola giace nel piano focale, detta f la focale dell’obbiettivo, la coordinata z di un generico punto immagine è uguale ad f se si considera l’immagine negativa e pari a -f se si considera l’immagine positiva. Nel seguito si considererà sempre l’immagine positiva del fotogramma, poiché in effetti sono le diapositive ottenute dal negativo che vengono utilizzate negli strumenti restitutori; pertanto il valore z dei punti immagine sarà sempre assunto pari a -f. z O asse ottico dell'obbiettivo y P x -f P figura 14 Capitolo VIII – Fotogrammetria pagina 242 R.Galetto A.Spalla - Lezioni di Topografia Notiamo infine che nel seguito si commetterà spesso un’imprecisione, per motivi di praticità; e cioè in alcuni grafici di supporto alla trattazione si disegneranno gli assi x ed y del sistema di riferimento interno, come giacenti nel piano dell’immagine positiva, come appunto indicato in figura 15.a); mentre per l’esattezza in tale piano gli assi dovrebbero essere indicati con la simbologia //x e //y come in figura 15.b), per evidenziare che in tale piano non giacciono gli assi x ed y del sistema di orientamento interno, ma degli assi ad essi paralleli. O -f O -f y // y x // x a) b) figura 15 2.2 Lo strumento restitutore analitico. Lo strumento restitutore analitico si compone: • di una struttura ottico-meccanica finalizzata alla misura delle coordinate x,y dei punti immagine su una coppia di fotogrammi • di un calcolatore elettronico, sul quale risiedono i programmi che costituiscono il software di gestione dello strumento, e che esegue i calcoli previsti da tali programmi; il calcolatore, di tipo personal computer, è dotato di monitor che serve come interfaccia strumentooperatore e per la visualizzazione della cartografia che viene prodotta nella fase di restituzione fotogrammetrica • di un plotter che traccia su carta il risultato della restituzione; questa periferica è però ormai raramente inclusa nelle componenti del restitutore poiché la produzione su carta avviene fuori linea (cioè dopo la fase di restituzione) dopo che il risultato della restituzione ha subito delle elaborazioni che sono il risultato della fase di ricognizione e di editing (il significato di questi due termini verrà spiegato più avanti). La parte ottico-mecanica dello strumento è costituita da due strutture gemelle, ciascuna delle quali composta come illustrata nella figura 16. Vi sono due guide fisse vincolate alla struttura esterna dello strumento, esse sono indicate in figura con le lettere A1 e A2; su queste due guide fisse è appoggiato un primo carrello C1 che può traslare lungo di esse; su questo carrello si trovano due guide, indicate in figura con le lettere B1 e B2; su queste due guide trasla un secondo carrello C2, detto carrello portalastra, poiché su di esso si appoggia una delle due diapositive (le diapositive vengono a volte impropriamente chiamate lastre poiché una volta dal negativo si ricavavano le diapositive su vetro, non disponendosi di supporti indeformabili per la stampa delle diapositive). Due motori, comandati tramite pulsanti dall’operatore, consentono di far traslare i due carrelli C1 e C2 sulle rispettive coppie di guide. Capitolo VIII – Fotogrammetria pagina 243 R.Galetto A.Spalla - Lezioni di Topografia A2 A1 C2 B1 LV P B2 C1 LU figura 16 Fissa al telaio dello strumento vi è una graduazione elettronica LV su cui scorre un sensore di lettura automatica della graduazione solidale al carrello C1; solidale al carrello C2 vi è una seconda guida elettronica su cui scorre un sensore di lettura automatica della graduazione LU. Queste due guide materializzano il sistema di riferimento strumentale (U,V) per la lettura delle coordinate della diapositiva di sinistra* . Sopra a questi dispositivi, in posizione mediana rispetto al campo di escursione dei due carrelli (figure 17.a e 17.b) vi è un traguardo di lettura fisso, costituito da una lente con un puntino nero inciso su di essa, detto marca di collimazione o semplicemente marca, di circa un decimo di millimetro di diametro (non si confonda la marca stereoscopica con le marche fiduciali della camera da presa!). * Nella trattazione useremo la terminologia fotogramma di sinistra e fotogramma di destra; deve essere chiaro che questa terminologia è strettamente funzionale alla spiegazione della materia. In realtà una ripresa fotogrammetrica si compone di decine o centinaia di fotogrammi, ripresi secondo lo schema a strisciate indicato al punto 1.3.5 di questo Capitolo. Quindi sarebbe più corretto ogni volta dire: consideriamo due qualsiasi fotogrammi consecutivi di una strisciata e indichiamoli con i ed i+1, ecc. ecc. Per brevità di esposizione li chiamiamo invece fotogramma di sinistra e fotogramma di destra e differenziamo i parametri ad essi relativi con i pedici 1 e 2 anziché i e 1+1. Capitolo VIII – Fotogrammetria pagina 244 R.Galetto A.Spalla - Lezioni di Topografia LV LV LV 0 0 0 VP 0L U max a) 0L U max b) max UP 0 L U c) figura 17 Facendo traslare la diapositiva, mediante il movimento dei due carrelli C1 e C2, sotto la marca nelle due direzioni U,V, è possibile portare in corrispondenza della marca stereoscopica qualsiasi punto della diapositiva. Il sistema è calibrato in modo che, in ogni istante, vengano attribuite al punto che si trova in corrispondenza della marca, le coordinate UP, VP che vengono lette dai due sensori sulle graduazioni elettroniche LU ed LV. (figura 17.c) Nella figura 17 si sono indicate tre posizioni dei carrelli che portano sotto la marca di collimazione tre diversi punti del fotogramma. Il dispositivo descritto viene detto a ottica fissa e lastra mobile, poiché appunto l’ottica di osservazione sta ferma e si muove la lastra mediante i carrelli C1 e C2 . Da un punto di vista concettuale potrebbe sembrare più semplice realizzare un dispositivo a lastra fissa e a ottica mobile in cui la diapositiva sta ferma e la marca stereoscopica si muove sopra di essa. In realtà non è così; infatti la parte di diapositiva che cade sotto la lente su cui è incisa la marca deve venir portata all’occhio dell’operatore attraverso un complicato sistema di lenti e di prismi; nel sistema a ottica mobile questo sistema ottico in movimento sarebbe molto costoso da realizzare e da tenere rettificato; è meno costoso invece realizzare la parte meccanica che fa muovere la lastra (i carrelli) e tenerla rettificata. Tra poco vedremo come, dalle coordinate strumentali UP,VP di un generico punto P della diapositiva. sia possibile passare alla determinazione delle sue coordinate lastra xP,yP nel sistema interno della camera da presa Nello strumento restitutore analitico vi sono due apparati come quello appena descritto, affiancati l’uno all’altro; su uno viene posto il fotogramma di sinistra e sull’altro quello di destra. Questi due apparati ottico meccanici, costituiscono la parte di misura dello strumento fotogrammetrico analitico. Le coordinate strumentali di un generico punto P del terreno che appare sulla diapositiva di sinistra e sulla diapositiva verranno indicate rispettivamente con la seguente notazione: (UP,VP)S e (UP,VP)D. Capitolo VIII – Fotogrammetria pagina 245 R.Galetto A.Spalla - Lezioni di Topografia RESTITUTORE ANALITICO diapositiva 1 diapositiva 2 LV LV VP VP UP x,y P' UP LU LU COMPUTER x,y P" ARCHIVIO DATA-BASE PLOTTER figura 18 Per ognuno dei due apparati, un sistema ottico trasporta l’immagine della marca, e della porzione di diapositiva che cade sotto la lente su cui la marca è incisa, ad uno degli occhi dell’operatore; in pratica l’operatore appoggia gli occhi ad una specie di binocolo che gli consente di vedere la diapositiva di sinistra con il solo occhio sinistro e la diapositiva di destra col solo occhio destro. Per mezzo di questo artificio, l’operatore non ha la sensazione di osservare due distinte immagini del terreno, ma vede un’immagine tridimensionale del terreno; infatti il nostro apparato fisiologico visivo rimane ingannato dall’artificio e ricrea nel nostro cervello un’immagine tridimensionale del terreno come se guardassimo il territorio dall’alto e si formassero sulle due retine due diverse immagini di esso. Senza entrare troppo nel particolare, sottolineiamo il fatto che l’effetto di tridimensionalità con cui l’operatore vede il modello dl terreno, è molto esasperato rispetto a una visione diretta dall’alto. Ciò è dovuto al fatto che la distanza tra i punti di presa dei due fotogrammi è dello stesso odine di grandezza della distanza dell’oggetto (il terreno) che viene fotografato; poiché la distanza tra i punti di presa è assimilabile alla distanza interpupillare nella visione fisiologica, l’aumento di effetto stereoscopico è paragonabile a quello che si avrebbe nella visione diretta se guardassimo la realtà che ci circonda con una distanza interpupillare di qualche metro! Inoltre (e anche di questo fatto tralasciamo la spiegazione perché troppo complicata e ininfluente sulla trattazione che segue) quando di uno stesso punto P del terreno, l’immagine P’ sul fotogramma di sinistra si trova sotto la marca di sinistra e l’immagine P’’ sul fotogramma di destra si trova sotto la marca di destra, l’operatore vede la marca come un unico puntino nero appoggiato sul punto P del modello stereoscopico del terreno. Capitolo VIII – Fotogrammetria pagina 246 R.Galetto A.Spalla - Lezioni di Topografia figura 19 - un operatore allo strumento. Da ciò ne consegue che: quando l’operatore vuole collimare un punto, il che significa portare le due immagini P’ e P’’ in corrispondenza delle marche di sinistra e di destra rispettivamente, egli deve muovere i due carrelli portalastra mediante gli appositi dispositivi di comando, fino a che la marca gli appare come un puntino nero appoggiato sul punto P del modello del terreno. Questo procedimento è detto collimazione stereoscopica; la collimazione stereoscopica è il metodo più veloce e preciso per effettuare la collimazione di un punto. La collimazione stereoscopica di due punti omologhi non è l’unica possibile; si potrebbe fare anche una collimazione monoscopica di due punti omologhi portando separatamente ciascuno di essi a sovrapporsi alla sua marca, e giudicando, per ciascuno di essi, la coincidenza tra punto e marca con una semplice operazione di traguardo. Ad esempio durante le esercitazioni del corso di fotogrammetria, poiché gli studenti non sono esperti nella collimazione stereoscopica, li si invita a procedere come segue: 1. “chiuda l’occhio destro e, muovendo con gli appositi comandi solo il carrello portalastra di sinistra, porti la marca di sinistra su un punto del fotogramma di sinistra (ad esempio lo spigolo di una casa)”; a rigor di termini si dovrebbe dire “porti un punto sotto la marca”, perché chi si muove è il fotogramma; ma poiché l’effetto visivo che si ha quando si sposta il carrello portalastra è quello di veder scorrere la marca sul fotogramma, si usa la dizione precedente ; ciò fatto: 2. “chiuda l’occhio di sinistra e, muovendo con gli appositi comandi solo il carrello portalastra di destra, porti la marca di destra sullo stesso punto sul fotogramma di destra”; Capitolo VIII – Fotogrammetria pagina 247 R.Galetto A.Spalla - Lezioni di Topografia 3. “apra entrambi gli occhi e dica cosa vede”; 4. la risposta è: “vedo la marca sullo spigolo della casa”. Lo studente ha cioè eseguito due collimazioni monoculari anziché una sola collimazione stereoscopica; entrambi i metodi sono validi; vedremo infatti che anche l’operatore userà la collimazione monoculare per una certa operazione in cui non ne può fare a meno; solo che, come detto, la collimazione stereoscopica è più precisa e più rapida. Più precisa significa che, nella collimazione stereoscopica, le due marche vengono sovrapposte ai due punti omologhi con maggior precisione di quanto venga fatto nella collimazione monoculare; poiché collimare un punto significa prelevare le sue coordinate (UP,VP)S e (UP,VP)D dalle graduazione elettroniche quando giudichiamo che le immagini P’ e P’’ di tale punto stiano sotto le due marche, è chiaro che quanto più è accurata l’operazione di sovrapposizione delle marche sui punti omologhi, tanto maggiore è la precisione con cui si determinano le coordinate strumentali (UP,VP)S e (UP,VP)D dei medesimi. La qualità di uno strumento restitutore analitico dipende principalmente dalla qualità del suo sistema ottico meccanico (che ne è la componente di costo maggiore); altri fattori che ne determinano la qualità sono il software di assistenza alla restituzione e la disponibilità di altri dispositivi, tra i quali specialmente quello che consente la superimposizione (vedremo più avanti in cosa consiste). Nei migliori strumenti basati sul sistema ottico-meccanico descritto, e usando la collimazione stereoscopica, è possibile determinare le coordinate strumentali UP e VP di un punto con un e.q.m di +/- 2 micron su ciascuna coordinata. Per concludere la descrizione del restitutore veniamo ora la PC (personal computer) ad esso associato; su di esso risiede il software che gestisce lo strumento e che elabora i dati. Attraverso il monitor, che fa da interfaccia, guida l’operatore nell’esecuzione delle varie operazioni, gestisce i dati che vengono prelevati dalle graduazioni elettroniche, esegue calcoli e visualizza sul monitor il disegno della cartografia ottenuta dai dati numerici . Le sue funzioni verranno chiarite più avanti a mano a mano che descriveremo i vari passi attraverso i quali si arriva alla costruzione della cartografia. 2.3 La procedura di orientamento interno di un fotogramma. Dalle coordinate strumentali alle coordinate lastra 2.3.1 La procedura semplice. Eseguire la procedura di orientamento interno di un fotogramma significa eseguire una serie di operazioni che portano alla determinazione dei parametri che sono necessari per passare dalle coordinate strumentali UP,VP di un punto immagine, alle sue coordinate xP,yP nel sistema di riferimento interno della camera da presa. Nella trattazione indicheremo le coordinate strumentali con UP,VP e le coordinate lastra con xP,yP senza usare il pedice S o D, poiché la trattazione è la medesima per ciascuno dei due fotogrammi. Considerando che il fotogramma viene appoggiato sul carrello portalastra in una posizione casuale, con i lati solo approssimativamente paralleli agli assi U,V materializzati dalle Capitolo VIII – Fotogrammetria pagina 248 R.Galetto A.Spalla - Lezioni di Topografia graduazioni elettroniche LU ed LV, possiamo dire che la relazione che lega le coordinate di un punto immagine P nel sistema strumentale (U,V) alle coordinate del medesimo punto nel sistema di riferimento interno (x,y) sono le seguenti: xP = x0 + UP cosα + VP senα (1) yP = y0 - UP senα + VP cosα dove x0 e y0 sono le coordinate dell'origine del sistema (U,V) nel sistema (x,y), α è l'angolo che si origina dal fatto che il fotogramma è posizionato solo approssimativamente con i lati paralleli al sistema (U,V), è cioè l’angolo formato dall’asse x con l’asse U, positivo in senso antiorario. Come è stato al precedente punto 1, quando una Ditta che produce cartografia ordina l’esecuzione delle riprese aeree a una Ditta specializzata in questa attività, riceve, con i fotogrammi, anche copia del certificato di taratura della camera da presa, sul quale sono riportate le coordinate delle quattro marche fiduciali nel sistema interno x,y che esse stesse materializzano. Sono quindi note le coordinate xi, yi delle quattro marche fiduciali della camera da presa con la quale sono stati ripresi i fotogrammi; sul certificato di taratura è anche riportata la distanza focale f che verrà usata per successivi calcoli. Ciò premesso, quando l’operatore deve eseguire la procedura di orientamento interno, lancia tale procedura con comandi dalla tastiera del PC, dopo di che è il software di gestione che lo guida nei passi successivi. Seguendo la procedura prevista dal software di gestione, l’operatore collima monocularmente una dopo l’altra le quattro marche fiduciali impresse sul fotogramma all’atto della presa; ad ogni collimazione il software di gestione preleva le coordinate strumentali Ui, Vi e le memorizza. A questo punto l’operatore lancia una procedura di calcolo che, utilizzando le (1) per le quattro coppie di valori misurati Ui, Vi, e delle quattro coppie di valori noti xi, yi precedentemente inserite da tastiera nel PC, genera un sistema di 8 equazioni nelle 3 incognite x0, y0 ,α. La procedura di calcolo, risolvendo il sistema delle 8 equazioni con il metodo delle osservazioni indirette, determina i valori delle 3 incognite x0, y0 ,α e li memorizza per applicarli nelle procedure che seguono. Ricordiamo che la procedura viene eseguita per il fotogramma di sinistra e poi per quello di destra, e quindi al termine della procedura si avranno i tre valori x0, y0 ,α per il fotogramma di sinistra e i tre valori x0, y0 ,α per il fotogramma di destra. A questo punto, dopo aver cioè eseguito quanto sopra per i due fotogrammi, l’operatore chiude la procedura dell’orientamento interno. Il software di gestione ne prende atto e da questo momento in poi, ogni volta che l’operatore collimerà un punto P sul modello stereoscopico (il che equivale a dire collima due punti omologhi sui due fotogrammi), il software di gestione utilizzando le 1, e le due triplette di valori x0, y0 ,α precedentemente memorizzate, trasformerà le due coppie di coordinate strumentali (UP,VP)S e (UP,VP)D nelle due coppie di coordinate (xP,yP)S e (xP,yP)D . Capitolo VIII – Fotogrammetria pagina 249 R.Galetto A.Spalla - Lezioni di Topografia La procedura di orientamento interno deve essere eseguita, come prima operazione, ogni volta che si mette un fotogramma sul carrello portalastra; infatti tutti i successivi calcoli prevedono di operare sulle coordinate dei punti immagine espresse nel sistema interno della camera da presa (anche dette coordinate lastra); ed è appunto la procedura dell’orientamento interno che consente il passaggio tra i due sistemi: quello strumentale e quello interno della camera da presa. Ricordiamo che, parlando della struttura della camera da presa, abbiamo detto che esistono anche camere da presa con otto marche fiduciali; in questo caso l’operatore potrà collimarle tutte otto e avere una miglior determinazione dei parametri di rototraslazione. In realtà però il vero motivo per cui è utile avere otto marche anziché quattro sarà più chiaro dopo aver letto quanto riportato al punto che segue. 2.3.2 La procedura che tiene conto della deformazione della pellicola Dobbiamo aprire a questo punto una parentesi per evidenziare questo fatto: l’immagine riprodotta sul fotogramma non è mai esattamente quella che è stata generata, come immagine latente, all’atto della presa. Ricordiamo che l’immagine latente è quella che si forma nella pellicola a seguito dell’esposizione; essa è formata dagli alogenuri d’argento sensibilizzati che durante il procedimento di sviluppo si trasformeranno in toni di grigi o in colore, a seconda del tipo di pellicola. Noi supponiamo che l’immagine latente sia un’immagine del terreno geometricamente corretta perché abbiamo supposto nulla la distorsione dell’obbiettivo (e non consideriamo eventuali effetti di distorsione dovuti alla rifrazione atmosferica); ma non dobbiamo dimenticare che, dopo la presa, la pellicola negativa subisce un trattamento chimico di sviluppo, durante il quale può deformarsi. Ad esempio: per effetto dell’azione di trazione che i rulli di trascinamento esercitano sulla pellicola nel farla passare da un bagno chimico all’altro, si può avere un effetto di allungamento della pellicola stessa nella direzione della sua lunghezza e un effetto di restringimento in senso trasversale alla lunghezza medesima. Successivamente si ha la stampa del negativo sulla pellicola diapositiva, la quale a sua volta in fase di sviluppo può subire ulteriori deformazioni. Bisogna subito precisare che queste deformazioni sono sempre piccole, se rapportate alle dimensioni del fotogramma; in generale su una diapositiva la distanza tra due marche fiduciali opposte differisce dal valore nominale riportato sul certificato di taratura di quantità inferiori al decimo di millimetro. Inoltre queste deformazioni, o almeno la parte apprezzabile di esse, variano linearmente dal centro del fotogramma verso il bordo, sia nella direzione x che nella direzione y del sistema di riferimento interno. Ipotizzando allora che l’effetto di queste deformazioni sia correggibile con una deformazione affine dei fotogrammi, nella procedura dell’orientamento interno si utilizza una espressione modificata delle formule (1), e precisamente si inseriscono in esse due coefficienti di correzione λx e λy che devono correggere l’effetto della deformazione della pellicola; le (1) diventano: xP = x0 + λx .UP cosα + λy.VP senα (2) Capitolo VIII – Fotogrammetria pagina 250 R.Galetto A.Spalla - Lezioni di Topografia yP = y0 - λx .UP senα + λy .VP cosα La procedura dell’orientamento interno dovrà allora determinare 5 incognite per ciascun fotogramma anziché 3; ciò è possibile disponendo delle solite quattro marche fiduciali, ma nel caso se ne abbiano 8, e cioè 4 in posizione mediana dei lati e 4 negli angoli, si ha una maggior probabilità di correggere meglio la deformazione della pellicola. Ovviamente, in questo caso, saranno le (2) ad essere utilizzate, dopo la procedura dell’orientamento interno, per trasformare le coordinate strumentali dei punti omologhi in coordinate lastra. 2.4 L’equazione di collinearità 2.4.1 Impostazione dell’equazione di collinearità Come è stato detto precedentemente, nella fotogrammetria analitica la ricostruzione dei raggi che proiettano i punti omologhi avviene in modo analitico; infatti abbiamo visto che nello strumento restitutore non vi è alcun dispositivo, né ottico né meccanico che riproduca fisicamente i raggi ottici che hanno generato le immagini dei punti del terreno sui fotogrammi, ma vi sono solo dei dispositivi per misurare le coordinata lastra dei punti omologhi sui due fotogrammi di una coppia stereoscopica. Un generico raggio ottico che, al momento della presa, partendo da un punto P del terreno e passando attraverso il centro O dell’obbiettivo abbia generato il punto immagine P’ su un fotogramma, viene ricostruito nella fase di restituzione, con una retta che esprime questa condizione: al momento della presa il punto P del terreno, il centro O dell’obiettivo e l’immagine latente del punto immagine P’ di P sul negativo, erano allineati su una stessa retta. L’espressione di questa retta prende di equazione di collinearità. Scrivendo l’equazione delle due rette che esprimono il concetto della collinearità per due raggi omologhi e determinandone il punto di intersezione, si ricava la posizione del punto oggetto che ha generato i due punti omologhi che ne costituiscono la sue immagine sui due fotogrammi. Il problema che ci si pone è quello di scegliere il sistema di riferimento nel quale scrivere l’equazione di collinearità. Adottando il concetto semplificato di rappresentazione cartografica esposto al punto 1.1 di questo capitolo, il sistema di riferimento assoluto nel quale attribuire le coordinate ai punti del terreno per una zona di territorio compresa nell’ambito di un modello stereoscopico può essere così definito: • gli assi N,E della proiezione di Gauss, supposti giacere nel piano tangente alla sfera locale in un punto baricentrico R della zona • un asse Q ortogonale al piano tangente parallelo alla direzione della verticale nel punto R. In tale sistema (N,E,Q) ad ogni punto del terreno è associabile una terna di coordinate del tipo di quelle che esso avrebbe in una terna tridimensionale ortogonale (X,Y,Z); le coordinate cartografiche N,E sono assimilabili alle coordinate X,Y, mentre la quota Q è assimilabile al valore Z. Capitolo VIII – Fotogrammetria pagina 251 R.Galetto A.Spalla - Lezioni di Topografia Q P N piano tangente sfera locale E figura 20 Sembrerebbe pertanto logico assumere il sistema (N,E,Q), come sistema di riferimento nel quale scrivere le due equazioni di collinearità. Tale sistema, che è quello che viene adottato nella pratica operativa, dove le approssimazioni, purché ininfluenti sulle qualità del prodotto, vengono sempre accettate, o per meglio dire ignorate, non è però idoneo ad esser preso come sistema di riferimento per impostare un discorso rigoroso di geometria analitica. Sceglieremo quindi, per scrivere l’equazione di collinearità, un ideale sistema cartesiano tridimensionale ortogonale (X,Y,Z) così definito: • asse X parallelo alla direzione media di volo della strisciata • piano (X,Y) coincidente con il piano tangente alla sfera locale in un punto approssimativamente baricentrico alla zona di terreno ripresa su entrambi i fotogrammi Capitolo VIII – Fotogrammetria pagina 252 R.Galetto A.Spalla - Lezioni di Topografia Z P Y piano tangente X figura 21 Tale sistema (X,Y,Z) sarà dunque il sistema di riferimento rispetto al quale verrà ricavata l’equazione di collinearità. La figura 22 riproduce in termini di geometria analitica lo schema a cui ci riferiamo per determinare le equazioni di collinearità di due raggi omologhi. Nella figura il sistema di riferimento esterno(X,Y,Z) nel quale verranno scritte le equazioni è quello appena definito; non si è disegnata la camera da presa nelle due posizioni di presa, ma solo il suo sistema di riferimento interno (x,y,z) all’atto dei due istanti di presa; dei due fotogrammi si è riportata l’immagine positiva. I due sistemi di riferimento sono stati disegnati con gli assi (x,y,z) non paralleli agli assi della terna (X,Y,Z); così pure i due punti di presa O1 e O2 non hanno valore Y e Z uguali; ciò sta a significare che durante la ripresa dei fotogrammi, tra un fotogramma ed il successivo si ha un diverso assetto angolare dell’aereo e una traiettoria non perfettamente rettilinea e a quota non costante ( per motivi di turbolenza atmosferica ed altri). Capitolo VIII – Fotogrammetria pagina 253 R.Galetto A.Spalla - Lezioni di Topografia z Z z O2 y O1 y y" x" x x y' x' P" P' Y P ZP YP XP X figura 22 Nelle due posizioni O1 e O2 le due terne non avranno gli assi paralleli agli (X,Y,Z), né saranno paralleli tra di loro. Inoltre l’origine della terna del sistema di riferimento interno avrà coordinate X01 , Y10 , Z10 al momento della presa del fotogramma di sinistra e coordinate X02, Y02, Z02 al momento della presa del fotogramma di destra. Si tenga presente che nella figura 22 gli assetti angolari delle due terne e le variazioni in Y e Z dei due punti di presa sono stati enfatizzati rispetto ai valori che si hanno nella realtà per esigenze di chiarezza della spiegazione. Si noti infine che nella figura è presente un’imprecisione, alla quale abbiamo già fato cenno in precedenza, e che consiste nell’aver rappresentato gli assi x,y del sistema di riferimento interno nel piano delle diapositive, anziché in un piano ad esse parallelo e passante per il punto di resa O. Affrontiamo ora il problema di scrivere l’equazione di collinearità per il raggio omologo che si riferisce al punto immagine sul fotogramma di sinistra. Con riferimento a quanto detto indicheremo con: X01 , Y10 , Z10 le coordinate del punto di presa O1 nel sistema (X,Y,Z) XP, YP, ZP le coordinate di un generico punto P del terreno nel sistema (X,Y,Z) x', y', z' le coordinate di P’, immagine di P sul fotogramma 1 nel sistema (x,y,z) X', Y', Z' le coordinate di P' nel sistema (X,Y,Z) L’equazione di collinearità deve esprimere, come già detto, il fatto che i tre punti P,P’ ed O1 siano allineati su una retta. Dobbiamo quindi scrivere l’equazione della retta r passante per i punti P,P’,O1. Capitolo VIII – Fotogrammetria pagina 254 R.Galetto A.Spalla - Lezioni di Topografia Consideriamo la proiezione della retta r sui due piani (XZ) ed (YZ) (vedi figura 23). Z Z° Z O1 Z° 1 O1 1 Z' Z' rxz ZP r yz ZP P X°1 X' X X P Y°1 Y' P Y Y P figura 23 Dalle due proiezione rXZ e rYZ si ricavano immediatamente le relazioni analitiche che esprimono la collinearità fra i punti O1 , P' e P: XP − X01 X'− X01 = ZP − Z01 Z'− Z01 YP − Y10 Y'−Y10 = ZP − Z10 Z'− Z10 (3) Per analogia possiamo ricavare immediatamente le equazioni che esprimono la collinearità per il raggio omologo relativo al punto immagine del fotogramma di destra: XP − X02 X'− X02 = ZP − Z02 Z'− Z02 YP − Y20 Y'−Y20 = Z P − Z02 Z'− Z02 Possiamo notare che nelle equazioni di collinearità che abbiamo appena ricavato, compaiono le coordinate dei punto immagine X’,Y’,Z’ e X’’,Y’’,Z’’ nel sistema di riferimento esterno X,Y,Z; a noi interessa invece che le coordinate dei punti immagine, nell’equazione di collinearità, siano le loro coordinate lastra, che siamo appunto in grado di misurare mediante lo strumento restitutore analitico. Dobbiamo allora cercare di esprimere le coordinate X’,Y’,Z’ e X’’,Y’’,Z’’ in funzione delle corrispondenti coordinate lastra x’,y’ e x’’,y’’. 2.4.2 La matrice di rotazione tra il sistema (X,Y,Z) e il sistema (x,y,z) Capitolo VIII – Fotogrammetria pagina 255 R.Galetto A.Spalla - Lezioni di Topografia Chiamiamo [M] la matrice di rotazione che trasforma le coordinate lastra di un punto immagine espresse nel sistema interno (x,y,z) nel sistema esterno (X,Y,Z) precedentemente definito. La matrice [M] avrà ovviamente la stessa espressione sia per il fotogramma di destra [M1] che per il fotogramma di sinistra [M2]. Noi la ricaveremo quindi in una forma generica e vedremo dopo come specificare quando essa si riferisce al fotogramma di sinistra e quando si riferisce al fotogramma di destra. Indicando con X’,Y’,Z’ le coordinate di un punto immagine P’ della lastra nel sistema (X,Y,Z), con X01,Y01,Z01 le coordinate del punto di presa del fotogramma di sinistra e con x’,y’,z’ le coordinate del punto immagine P’ nel sistema di riferimento interno (x,y,z), [M1] dovrà soddisfare la relazione: X' −X 01 x' Y' −Y10 = M 1 ⋅ y' Z'−Z 01 z' (4) [ ] Mentre indicando con X’’,Y’’,Z’’ le coordinate di un punto immagine P’’ della lastra nel sistema (X,Y,Z), con X02,Y02,Z02 le coordinate del punto di presa del fotogramma di destra e con x’’,y’’,z’’ le coordinate del punto immagine P’’ nel sistema di riferimento interno (x,y,z), [M2]. dovrà soddisfare la relazione: X"− X 02 x" 0 Y"−Y2 = M 2 ⋅ y" Z"− Z 02 z" (5) [ ] La matrice [M] , scritta in funzione dei coseni direttori tra le due terne (X,Y,Z) e (x,y,z) ha la seguente espressione: cos( xX ) cos( yX ) cos( zX ) [ M] = cos( xY ) cos( yY ) cos( zY ) cos( xZ ) cos( yZ ) cos( zZ ) I nove coseni direttori possono essere espressi in funzione di tre sole rotazioni indipendenti. Per fissare queste tre rotazione assumiamo che la terna (x,y,z) abbia inizialmente gli assi paralleli a quelli della terna (X,Y,Z) e imponiamo che essa assuma la sua generica posizione nello spazio (X,Y,Z) che ha al momento della presa del fotogramma, mediante le seguenti tre successive rotazioni: • ω, positiva in senso antiorario, intorno all’asse x • ϕ, positiva in senso antiorario, intorno all’asse y dopo che la terna ha subito la rotazione omega • κ, positiva in senso antiorario, intorno all’asse z dopo che la terna ha subito le due precedenti rotazioni. Per ricavare [M] in funzione delle tre rotazioni ω, ϕ, κ si scrivono le tre matrici che esprimono le tre rotazioni della terna (x,y,z) intorno ad x, y e z e se ne esegue il prodotto: Capitolo VIII – Fotogrammetria pagina 256 R.Galetto A.Spalla - Lezioni di Topografia [M] = [Mω ] . [Mϕ] .[Mκ ] Rotazione primaria ω (intorno a x) zω z ω [ Mω ] = yω ω 1 0 0 0 cosω − sen ω 0 sen ω cos ω y x Rotazione secondaria ϕ, (intorno a yω , dove si è portato l’asse y a seguito della rotazione primaria ω) z ωϕ zω [M ] = ϕ ϕ X x ϕ cos ϕ 0 0 sen ϕ 1 0 − sen ϕ 0 cos ϕ yω ϕ Rotazione terziaria κ (intorno a zω ϕ , dove si è portato l’asse z a seguito delle due rotazioni ω e ϕ; l’asse zω ϕ , avendo subito due rotazioni coincide già con Z) yω cosκ Y=yωκ [ M k ] = senκ κ 0 κ Z=z ωϕ − senκ 0 cosκ 0 0 1 X=x ϕκ xϕ Capitolo VIII – Fotogrammetria pagina 257 R.Galetto A.Spalla - Lezioni di Topografia Dal prodotto delle tre matrici, relative alle tre rotazioni, ricaviamo quindi la matrice [M]: cos ϕ cosκ senκ cosκ 0 − sen ϕ cosκ sen κ sen ϕ cosϕ [Mϕ] x [Mκ ]= 1 0 [M]= 0 cosω 0 sen ω − sen κ cos ϕ sen ϕ 0 cos ϕ cosκ − sen ω x senκ cos ω − sen ϕ cosκ − sen κ cos ϕ sen ϕ cosκ 0 sen κ sen ϕ cosϕ e infine: cos ϕ cosκ − sen κ cosϕ [M]= cos ω senκ + sen ω sen ϕ cosκ sen ω sen κ − sen ϕ cosω cosκ sen ϕ cosω cosκ − sen ω sen κ sen ϕ sen ω cos κ + cos ω sen κ sen ϕ − sen ω cos ϕ (6) cos ω cos ϕ Quando nella (6) i valori di ω ϕ κ si riferiscono al fotogramma di sinistra li indicheremo con ω1 ϕ1 κ1 ; quando invece saranno riferiti al fotogramma di destra li indicheremo con ω2 ϕ2 κ2. Nel seguito della trattazione, quando la matrice [M] conterrà i valori ω1 ϕ1 κ1 del fotogramma di sinistra la indicheremo con [M1] e indicheremo i suoi elementi con aij; quando invece la matrice [M] conterrà i valori ω2 ϕ2 κ2 del fotogramma di destra la indicheremo con [M2] e indicheremo i suoi elementi con bij . a11 [M1] = a12 a13 a21 a22 a23 a31 a23 a33 b11 b21 [M2]= b12 b22 b13 b23 b31 b23 b33 (7) Sostituendo le (7) nelle (4) e nelle (5) si ottiene: X’ = X01 + a11 x’ + a12 y’ + a13 z’ Y’ = Y01 + a21 x’ + a22 y’ + a23 z’ Z’ = Z01 + a31 x’ + a32 y’ + a33 z’ (8) X’’ = X02 + b11 x’’ + b12 y’’ + b13 z’’ Y’’ = Y02 + b21 x’’ + b22 y’’ + b23 z’’ Z’’ = Z02 + b31 x’’ + b32 y’’ + b33 z’’ Capitolo VIII - Fotogrammetria pagina 258 R.Galetto A.Spalla - Lezioni di Topografia 2.4.3 Forma definitiva delle equazioni di collinearità per due raggi omologhi Sostituendo le (8) nelle (3) si ottiene: X P − X10 (X 10 + a11 x'+ a12 y'+a13 z' ) − X10 = 0 Z P − Z10 (Z1 + a31 x'+a 32 y'+ a33 z' ) − Z10 YP − Y10 (Y10 + a21 x'+a 22 y'+ a23 z' ) − Y10 = Z P − Z10 (Z01 + a 31x '+a 32 y'+ a33 z') − Z10 XP − X02 (X 02 + b11x"+b12y"+b13 z") − X02 = 0 ZP − Z02 (Z2 + b31x"+b32y"+b33z") − Z02 YP − Y20 (Y20 + b21x"+b22 y"+b23z") − Y20 = Z P − Z02 (Z02 + b31x '+b32 y' +b33z' ) − Z02 E semplificando: X P − X10 a11 x'+ a12 y'+a13 z' = a31 x'+a 32 y'+ a33 z' Z P − Z10 YP − Y10 a21x '+a 22 y'+a 23z ' = Z P − Z01 a31x '+a 32 y'+a 33z ' (9) XP − X b x" b y"+b13 z" = 11 12 b31x"+b32 y"+b33 z" ZP − Z 0 2 0 2 YP − Y b x"+b22 y"+b23 z" = 21 b31x"+b32 y"+b33 z" ZP − Z 0 2 0 2 Le (9) esprimono la condizione di collinearità fra un punto P del terreno e le sue due immagini P’ e P’’ sui fotogrammi di sinistra e di destra. Le (9) esprime quindi il legame fra: • le coordinate di un generico punto P nel sistema (X,Y,Z); • i parametri che definiscono le posizioni delle terne O1(x,y,z) e O2(x,y,z) nel sistema (X,Y,Z); tali parametri sono le coordinate X01, Y01, Z01 e X02, Y02, Z02 delle origini delle terne O1 e O2 ed i loro valori angolari d'assetto ( ω1 ϕ1 κ1 ) e ( ω2 ϕ2 κ2 ) contenuti negli elementi aij e bij rispettivamente; • le coordinate x’,y’ e x’’,y’’ dei punti P' e P", immagini di P sui fotogrammi 1 e 2. 2.5 Sulla possibilità di utilizzare in diversi modi le equazioni di collinearità. Ora che abbiamo determinato la relazione analitica fondamentale sulla quale si regge tutta la fotogrammetria analitica, e cioè l’equazione di collinearità, potremmo procedere in vari modi per arrivare alla soluzione che ci interessa, che è quella di dare una rappresentazione cartografica del terreno, ricavando le coordinate N,E,Q dei punti del modello stereoscopico in funzione delle coordinate dei punti immagine. Tenuto conto tuttavia della necessità di contenere l’argomento entro i limiti imposti dalle esigenze del corso, prenderemo in considerazione solo la soluzione classica, che ancor oggi viene in genere seguita da tutte le Ditte fotogrammetriche che producono cartografia con strumenti analitici. Questa soluzione è tradotta nella realtà operativa da un programma, che risiede sul PC che fa parte del restitutore, e che guida l’operatore ad eseguire le varie fasi del lavoro. Capitolo VIII - Fotogrammetria pagina 259 R.Galetto A.Spalla - Lezioni di Topografia Abbiamo infatti precedentemente visto che l’operatore, dopo aver appoggiato sui due carrelli portalastre le due diapositive che formano un modello stereoscopico, lancia dalla tastiera del PC il programma di orientamento interno e seguendo i comandi che appaiono sul monitor esegue le varie operazioni da esso previste. La soluzione classica prevede che, dopo che l’orientamento interno è terminato, l’operatore lanci una seconda procedura, che si compone di due parti: l’orientamento relativo e l’orientamento assoluto. L’operazione di orientamento relativo ha lo scopo di determinare la posizione reciproca che i due fotogrammi avevano al momento della presa, senza prendersi cura di determinare quale fosse la posizione dei fotogrammi rispetto al sistema di riferimento assoluto N,E,Q. Vedremo che sarà sufficiente conoscere la posizione reciproca dei due fotogrammi in un sistema arbitrario per calcolare i punti di intersezione dei raggi omologhi, il che equivale a dire a formare il modello stereoscopico del terreno. Successivamente, dopo aver creato il modello del terreno con l’orientamento relativo, con l’orientamento assoluto lo si metterà in scala, lo si ruoterà e lo si traslerà in modo che le coordinate dei punti di intersezione dei raggi omologhi, calcolate nel sistema di riferimento arbitrario, si trasformino in coordinate terreno N,E,Q. 2.6 L’orientamento relativo di due fotogrammi. 2.6.1 Il concetto generale Richiamiamo il concetto di base dell’orientamento relativo: eseguire l’orientamento relativo di due fotogrammi significa saperne determinare, in un sistema di riferimento arbitrario, la posizione che uno aveva rispetto all’altro al momento della presa. Poiché al momento della presa le due immagini P’ e P’’ di un punto P si originano da uno stesso punto P del terreno, se noi rimettiamo (analiticamente) i due fotogrammi nella stessa posizione reciproca che essi avevano al momento della presa, anche se essi hanno nell’insieme una posizione qualsiasi nello spazio, i due raggi omologhi che proiettano (analiticamente) P’ e P’’ dai punti di presa O1 e da O2 rispettivamente, si incontreranno nuovamente in un punto che corrisponde a P. Noi non sappiamo quale fosse l’assetto dei due fotogrammi nel loro insieme rispetto al sistema assoluto al momento della presa (e, come si è detto, in questo momento non ci importa di saperlo) e quindi, li posizioneremo l’uno rispetto all’altro nella stessa posizione reciproca che avevano al momento della presa, ma, nel loro insieme, in una posizione qualsiasi nello spazio; il che significa che la terna di riferimento (X,Y,Z) che sceglieremo per esprimere i parametri che ne determinano la posizione reciproca dell’uno rispetto all’altro sarà una terna arbitraria. Di conseguenza, una volta determinati i parametri dell’orientamento relativo, le coordinate di P (e di ogni altro punto del modello stereoscopico) le ricaveremo in questa terna arbitraria; in un secondo tempo, come già detto, le trasformeremo in N,E,Q con l’operazione di orientamento assoluto. Capitolo VIII - Fotogrammetria pagina 260 R.Galetto A.Spalla - Lezioni di Topografia 2.6.2 Scelta del sistema di riferimento arbitrario Per comprendere quale sia il sistema di riferimento arbitrario (X,Y,Z) nel quale determineremo i parametri di orientamento relativo dei due fotogrammi, consideriamo come abbiamo costruito il disegno riportato in figura 24: • in un punto arbitrario dello spazio posizioniamo l’origine O del sistema di riferimento arbitrario (X,Y,Z); • facciamo coincidere con O l’origine O1 della terna del sistema interno di riferimento (x,y,z) nella posizione di presa del fotogramma di sinistra, indicandone gli assi con x’,y’,z’; abbiamo scelto il piano del disegno in modo che esso contenga l’asse z’; gli altri due assi x’ e y’, in generale, non giaceranno nel piano del disegno; • scegliamo l’asse X del nostro sistema di riferimento arbitrario in modo che passi per il secondo punto di presa O2 e disegniamolo nel piano del disegno; il punto di presa O2 si troverà dunque sull’asse X ed avrà un valore di ascissa X02 pari alla base di presa b; tale valore è in realtà incognito, ma noi lo supponiamo per il momento noto; vedremo che esso verrà determinato nella fase di orientamento assoluto; • disegniamo quindi, con la notazione x’’,y’’,z’, la terna di riferimento interna (x,y,z) con l’origine in O2, e supponiamo che essa abbia, rispetto alla terna x’,y’,z’, la stessa posizione angolare che essa aveva al momento della presa; questo significa che il disegno rappresenta i due fotogrammi correttamente orientati in senso relativo l’uno rispetto all’altro; • disegniamo poi due generici raggi omologhi, che proiettano due punti omologhi P’ e P’’; poiché abbiamo supposto che le due terne siano correttamente orientate l’una rispetto all’altra come al momento della presa, i due raggi omologhi si incontrano in un punto P che è l’equivalente del punto terreno che ha generato i punti omologhi P’ e P’’; • nel disegno abbiamo quindi evidenziato con linea a trattini le proiezioni dei due raggi omologhi nei piani (X,Z) e (Y,Z); • i due raggi omologhi nel piano (X,Z) escono dai punti O1 e O2 che giacciono nel piano (X,Z) si incontrano nel punto di ascissa X* e di ordinata Z*; • i due raggi omologhi nel piano (Y,Z) risulteranno invece sovrapposti, poiché devono entrambi passare per il punto di coordinate Y*,Z* e per le proiezioni di O1 e O2 sul piano (Y,Z), proiezioni che coincidono entrambe con l’origine O della terna (X,Y,Z). Capitolo VIII - Fotogrammetria pagina 261 R.Galetto A.Spalla - Lezioni di Topografia Z Y z' z" y' O 1 y" O2 b x' X x" y" y' P" P' x" x' r1 r2 P Y Z* Y* X X* figura 24 2.6.3 L’equazione di condizione per l’orientamento relativo Riprendiamo ora le equazioni di collinearità e per semplicità di notazione poniamo: a x' +a12 y'+a13 z' b x"b y"+b13z" Tx1 = 11 Tx2 = 11 12 a31x'+ a32 y'+ a33z ' b31x"+b32y"+b33z" (10) Ty1 = a21x'+ a22 y'+ a23z ' a31x'+ a32 y'+ a33z ' Ty2 = b21x"+b22y"+b23z" b31x"+b32y"+b33z" Le equazioni dei raggi omologhi risultano rispettivamente: XP − X10 − Tx1 = 0 ZP − Z10 XP − X02 − Tx2 = 0 ZP − Z02 (11) YP − Y10 − Ty1 = 0 ZP − Z10 YP − Y20 − Ty2 = 0 Z P − Z02 Supponiamo ora di scrivere le equazioni assumendo come riferimento la terna (X,Y,Z) che abbiamo definito al punto 2.6.2 precedente; nelle (11) possiamo porre: X 01 = Y10 = Z 01 = 0 Y20 = Z 02 = 0 X 02 ≠ 0 Inoltre sostituiamo X*,Y*,Z* alle generiche coordinate del punto P. Capitolo VIII - Fotogrammetria pagina 262 R.Galetto A.Spalla - Lezioni di Topografia Le equazioni di collinearità assumono allora la seguente espressione: X* Y* = T = Ty1 x1 Z* Z* (12) X * − X02 Y* = T = Ty2 x2 Z* Z* (13) Come già si evince dalla figura precedente, nelle (12) i primi termini dell’uguaglianza, e cioè i Y* rapporti * sono uguali e quindi devono essere uguali anche i rispettivi secondi termini delle Z due uguaglianze, e cioè: Ty2=Ty1; da cui si ricava: Ty2-Ty1=0 (14) che è l’equazione che deve essere soddisfatta per ogni coppia di punti omologhi quando i due fotogrammi sono correttamente orientati relativamente. Riscriviamo la relazione (14) esplicitando le coordinate lastra dei punti omologhi e gli elementi aij e bij delle due matrici di orientamento: b21x"+b22 y"+b23 z" a 21 x'+a 22 y '+a 23 z' − =0 b31x"+b32 y"+b33 z" a 31 x'+a 32 y '+a 33 z' (15) dove i termini della matrice [M1 ] = [ai,j] sono funzione dei valori di assetto angolare κ1, ϕ1, ω1 del sistema O1(x,y,z) rispetto al sistema (X,Y,Z) ed i termini della matrice [M2 ] = [bi,j] sono funzione dei valori d'assetto angolare κ2,ϕ2, ω2 del sistema O2(x,y,z) sempre rispetto al sistema arbitrario (X,Y,Z). Determinare i parametri dell’orientamento angolare dei due fotogrammi significa determinare i valori angolari ω1 ϕ1 κ1,, e ω2,ϕ2 κ2, che sono contenuti negli elemento aij e bij. Per far questo bisogna scrivere un sufficiente numero di equazioni di tipo 14, misurando sufficiente numero di coordinate x’,y’ e x’’,y’’ di coppie di punti omologhi e risolverle rispetto alle incognite ω1 ϕ1 κ1,, e ω2,ϕ2 κ2. Da quanto detto sembrerebbe che i parametri dell’orientamento relativo fossero 6, cioè appunto i sei valori angolari ω1 ϕ1 κ1, e ω2,ϕ2 κ2. Invece vediamo subito che essi sono solo 5. E questo è un conseguenza del fatto di aver scelto l’asse X della terna di riferimento (X,Y,Z) complanare all’asse z’ della terna di riferimento interna nella posizione O1; scelta di cui non si era finora data ragione. Ricordiamoci infatti che quando abbiamo definito la matrice di rotazione [M1] tra il sistema interno (x,y,z) e quello (X,Y,Z) avevamo fissato i tre angoli ω1 ϕ1 κ1, come primario, secondario e terziario, assumendo che la terna (x,y,z) avesse originariamente gli assi paralleli alla terna (X,Y,Z) e che le tre rotazioni, applicate in successione, la portassero nella posizione generica. Capitolo VIII - Fotogrammetria pagina 263 R.Galetto A.Spalla - Lezioni di Topografia Z z" Y z y O1 O2 y" x" X x vettori contenuti nel piano del foglio vettori ortogonali al piano del foglio vettori nè ortogonali al piano del foglio nè contenuti in esso Facciamo ora il ragionamento inverso e cioè riportiamo la terna (x,y,z) dalla posizione generica ad avere gli assi paralleli alla terna (X,Y,Z). Dovremo allora applicare all’inverso la sequenza di rotazioni κ1, ϕ1, ω1;.procediamo come segue: • consideriamo la terna (x,y,z) nella posizione O1 cioè riferita al primo fotogramma; • diamo una rotazione κ1 alla terna (x,y,z) intorno all’asse z fino a portare il suo asse x nel piano del disegno e quindi a giacere nel piano (X,Y) della terna (X,Y,Z); Z κ1 Y z O1 y O2 X x • a questo punto sia il piano (x,z) che il piano (X,Z) giacciono nel piano del foglio, e quindi gli assi y e Y saranno entrambi ortogonali al piano del foglio e quindi coincidenti; • diamo adesso la rotazioneϕ1 intorno all’asse y fino a portare l’asse z coincidente con Z e conseguentemente x coincidente con X; Z ϕ1 z Y y x O2 X O1 • a questo punto le due terne coincidono senza che ci sia bisogno di dare alcuna rotazione ω1;.cioè, assumendo come sistema di riferimento per determinare i parametri dell’orientamento relativo quello sopra descritto, possiamo porre sempre nelle (14) ω 1=0 e quindi le incognite dell’orientamento relativo sono in effetti solo le seguenti 5: κ1, ϕ 1, κ2, ϕ 2, ω 2 Capitolo VIII - Fotogrammetria pagina 264 R.Galetto A.Spalla - Lezioni di Topografia Per realizzare l'orientamento relativo sarebbe pertanto sufficiente, in teoria, scrivere l'equazione (15) cinque volte, considerando 5 coppie di raggi omologhi proiettanti 5 coppie di punti omologhi sulle due lastre. In realtà quando l’operatore deve eseguire l’operazione di orientamento relativo non si accontenta di collimare 5 coppie di punti omologhi, ma ne collima molte di più, almeno 12. Questo è dovuto a due fatti. Uno è comune ad ogni problema di determinazione di incognite per mezzo di operazioni di misura, e, come abbiamo visto nella trattazione delle osservazioni indirette, riguarda l’esigenza di ridurre l’influenza degli errori di misura sulla determinazione delle incognite. Ma in questo caso specifico vi è un’altra esigenza, che è quella di mediare, sulla determinazione delle incognite, gli effetti dovuti a eventuali residui di deformazione della pellicola, non corretti in fase di orientamento interno, in quanto non correggibili dalla trasformazione affine ivi applicata. Scegliendo quindi un numero sovrabbondante di punti omologhi , opportunamente distribuiti nel modello, si ha una migliore determinazione delle incognite. Dobbiamo infatti ragionare in questo modo: per quanto accuratamente si esegua l’operazione, dopo l’orientamento relativo non si avrà comunque mai una perfetta intersezione dei raggi omologhi per le n coppie di punti omologhi osservate; il che, matematicamente parlando, significa che la quintupletta di valori determinati κ1, ϕ 1, κ2, ϕ 2, ω 2 non sarà in grado di annullare tutte le n equazioni in base alle quali sono stati determinati (metodo delle osservazioni indirette docet!). E’ vero però che, utilizzando appunto un numero sovrabbondante di coppie di punti omologhi per determinare i parametri incogniti, la distanza tra due generici raggi omologhi, in corrispondenza del loro punto ideale di intersezione, sarà ridotta mediamente a una quantità molto piccola, cioè dell’ordine dell’errore di misura delle coordinate lastra dei punti omologhi, cioè di pochi micron. Dobbiamo infine notare a questo proposito, che aumentare il numero n di coppie di punti omologhi per migliorare l’orientamento relativo, e cioè eseguire l’orientamento relativo con 12 o con 20 coppie di punti, anziché le 5 strettamente necessarie, è irrilevante sul piano economico. Ciò infatti comporta unicamente che l’operatore impieghi 4 o 5 minuti di tempo in più per scegliere nel modello un po’ di coppie ben collimabili e che le collimi; il tempo di calcolo poi, stante l’apposito programma di calcolo sul PC, è trascurabile. Questo è il motivo fondamentale (cioè quello economico) per cui nella prassi ordinaria, per ricavare le coordinate N,E,Q dalle x’,y’ e x’’,y’’, si è spezzato il procedimento in due parti: • l’orientamento relativo, in cui è opportuno usare tanti punti per formare bene il modello stereoscopico e questo può essere fatto perché intanto i punti in più costano poco • l’orientamento assoluto, in cui invece i punti che occorrono costano molto (o almeno una volta era così, ora, anno 1996, un po’ meno) ma possono essere contenuti nel numero. 2.6.4 Calcolo delle coordinate dei punti del modello nel sistema arbitrario Dopo aver completato la fase di collimazione dei punti omologhi, l’operatore lo segnala al PC tramite tastiera, e il software procede allora a calcolare i parametri di orientamento di relativo ϕ1, κ1, ω2, ϕ2, κ2, col metodo delle osservazioni indirette. Da questo punto in poi ogni volta che l’operatore collimerà sui due fotogrammi le due immagini Pi’ e Pi’’ di un punto Pi, la procedura residente sul PC eseguirà automaticamente le seguenti operazioni: Capitolo VIII - Fotogrammetria pagina 265 R.Galetto A.Spalla - Lezioni di Topografia • • le due coppie di coordinate strumentali (Ui,Vi)1 e (Ui,Vi)2 vengono trasformate in (x'i,y'i)1 e (x"i,y"i)2 dalla routine dell'orientamento interno; dalle due coppie di coordinate (x' i,y'i) e (x"i,y"i) si passa alle coordinate (X i,Y i,Z i) nel sistema di riferimento arbitrario mediante la routine di orientamento relativo. I calcoli di cui ai due punti precedenti avvengono naturalmente in una frazione di secondo; e cioè in minor tempo di quello che l'operatore impiega a passare da un punto collimato al successivo. Il calcolo delle coordinate di ogni coppia di punti omologhi nello spazio arbitrario (X,Y,Z) viene eseguito con le formule che seguono. Riesaminiamo l’espressione semplificata delle equazioni di collinearità (13) X* = Tx1 Z* Y* = Ty1 Z* equazione del raggio omologo r1 (13.a) X * − X02 = Tx2 Z* Y* = Ty2 Z* equazione del raggio omologo r2 (13.b) Dalla prima delle prime due si ricava X* = Tx1 Z* Dalla prima delle altre due si ricava Z* = (16.a) X * − X 02 Tx2 (16.b) Sostituendo nella 16.a il valore di Z* ricavato nella 16.b, si ottiene X * = Tx1 X* − X * X * − X 02 Tx2 Tx1 Tx2 da cui = − X 02 Tx1 Tx2 Tx - Tx1 T = − X 02 x1 X* 2 Tx2 Tx2 da cui Tx Tx X* 1 − 1 = − X02 1 Tx2 Tx 2 da cui X * = − X 02 Tx1 Tx2 - Tx1 Sostituendo X* nella (16.b) si ricava Z* − X 02 Z = * Tx1 Tx2 - Tx1 Tx2 − X02 1 1 − X 02 Tx1 + Tx2 - Tx1 Tx1 X 02 = =− Tx2 Tx2 T + T -T X 02 x2 x1 x1 =− T T T Tx2 - Tx1 x2 x1 x1 ( ) ( ) Per ricavare Y* si può usare la seconda equazione delle 13.a o della 13.b ; ne calcoliamo quindi il valore definitivo come media dei due valori possibili: Y = * Z *Ty1 + Z*Ty 2 2 =Z * Ty1 + Ty2 2 ( ( X 02 Ty1 + Ty2 = 2 T −T x1 x2 ) ) Come già detto prima a X02 possiamo dare un qualsiasi valore arbitrario, ad esempio 1m Il fatto di dare un valore arbitrario ad X02 si traduce nel fatto di costruire, con l’orientamento relativo, non solo un modello riferito ad un sistema di riferimento arbitrario, ma anche in un Capitolo VIII - Fotogrammetria pagina 266 R.Galetto A.Spalla - Lezioni di Topografia rapporto di scala arbitrario; ciò non ci deve preoccupare, poiché anche il fattore di scala verrà messo a posto nella fase di orientamento assoluto. Dopo aver eseguito l’orientamento relativo, prima di passare alla fase di orientamento assoluto, l’operatore collima i punti che gli serviranno per l’orientamento assoluto del modello. L’operatore ha infatti davanti a se una copia a stampa su carta di uno dei due fotogrammi che formano la coppia stereoscopica e su questa stampa vi sono segnati i punti che dovranno essere utilizzati nell’orientamento assoluto; di essi ne riparleremo tra poco. Per ora ci basti sapere che l’operatore li collima e quindi, come già detto, la procedura ne calcola le coordinate nel sistema (X,Y,Z) e le memorizza per utilizzarle nella fase di orientamento assoluto. 2.7 L’orientamento assoluto del modello stereoscopico L'orientamento assoluto è quell'operazione mediante la quale il modello stereoscopico, viene portato ad una scala fissata ed orientato in un sistema di riferimento assoluto. Come abbiamo visto al punto 1 del capitolo V il sistema di riferimento assoluto al quale si deve ricondurre il modello stereoscopico, è definito in planimetria dal sistema cartografico Gauss-Boaga ed in altimetria dal geoide. Immaginiamo di vedere la porzione di terreno relativa al modello stereoscopico inserita nel sistema di riferimento assoluto (vedi figura 25) ne abbiamo tracciato il perimetro con linea a tratti per indicare che in realtà la sua rappresentazione non l’abbiamo e la dobbiamo ottenere in funzione del modello stereoscopico ottenuto dai fotogrammi. Nello stesso disegno appare anche il modello stereoscopico nel suo sistema di riferimento arbitrario e in una scala arbitraria; nel disegno questi due concetti sono rappresentati dal fatto che il modello stereoscopico, più piccolo rispetto alle dimensioni reali del terreno e vincolato al sistema arbitrario (X,Y,Z) svolazza in un punto generico del sistema di riferimento assoluto. Abbiamo inoltre evidenziato nel disegno 5 punti del terreno, detti punti di appoggio del modello stereoscopico, che hanno coordinate note N,E,Q; per ore supponiamo che tali coordinate siano state determinate con un rilievo topografico a terra a partire dai vertici trigonometrici e dai caposaldi di livellazione. I punti di appoggio sono quelli che vengono utilizzati per eseguire l’orientamento assoluto e dei quali, come si è detto al paragrafo precedente, l’operatore ha determinato le coordinate nel sistema arbitrario (X,Y,Z,). Eseguire l'orientamento assoluto significa dare un fattore di scala Λ al modello stereoscopico, dargli tre rotazioni Ω ,Φ ,Κ e tre traslazioni N0, E0, Q0 in modo che i cinque punti che appartengono ad esso e corrispondono ai 5 punti di orientamento assoluto, vadano a coincidere con i corrispondenti cinque punti di coordinate note nel sistema assoluto. Per determinare i parametri dell’orientamento assoluto è sufficiente scrivere le formule di rototraslazione e di messa in scala, che sono le seguenti: E = E 0 + Λ( Xcos(XE) + Ycos(YE) + Zcos(ZE)) N = N 0 + Λ( Xcos(XN) + Ycos(YN) + Zcos(ZN)) (16) Q = Q 0 + Λ( Xcos(XQ) + Ycos(YQ) + Zcos(ZQ)) Capitolo VIII - Fotogrammetria pagina 267 R.Galetto A.Spalla - Lezioni di Topografia Z O1 Y YP XP ZP O2 P Q X P Q N NP EP E figura 25 Per ognuno dei cinque punti di appoggio si potranno scrivere le tre equazioni precedenti, ottenendo così un sistema di quindici equazioni nelle sette incognite N0, E0, Q0 , Κ, Φ , Ω e Λ, la cui determinazione viene eseguita dal software del sistema applicando il solito algoritmo delle osservazioni indirette. In realtà per eseguire l’orientamento assoluto sarebbe sufficiente conoscere le coordinate N,E,Q di due punti di appoggio e la quota Q di un terzo. Infatti il modello stereoscopico può essere visto come un corpo rigido nello spazio del quale dobbiamo vincolare sei gradi di libertà (tre traslazioni e tre rotazioni indipendenti)e a cui dobbiamo attribuire un fattore di scala. Pertanto: • conoscendo le coordinate (N,E,Q) di due punti e le relative coordinate nel sistema arbitrario (X,Y,Z) è possibile calcolare la distanza d tra i due punti nel sistema (X,Y,Z) e la D distanza D nel sistema (N,E,Q); il rapporto Λ= (coefficiente di scala) rappresenta il d coefficiente di cui deve essere variata la dimensione del modello, affinché esso venga rappresentato nel sistema (N,E,Q); • imponendo che i due punti modello in esame assumano le corrispondenti coordinate (N,E,Q) vengono vincolate le tre traslazioni del corpo rigido (cioè del modello) nonché due rotazioni; l'ultima labilità del corpo rigido è costituita dalla possibile rotazione intorno alla congiungente i punti scelti; • tale rotazione viene bloccata imponendo che un terzo punto, non allineato con i precedenti, abbia una quota fissata Q. La scelta di utilizzare 5 punti di appoggio invece dei tre strettamente necessari è dovuta, come già abbiamo detto, all’esigenza di ridurre l’influenza degli errori di misura sulla determinazione dei parametri di orientamento assoluto. Tali errori sono sia quelli dovuti alle precedenti misure Capitolo VIII - Fotogrammetria pagina 268 R.Galetto A.Spalla - Lezioni di Topografia eseguite allo strumento, sia all’errore con cui sono state determinate le coordinate N,E,Q dei punti di appoggio. E’ importante osservare che in questa fase si è molto più parchi, rispetto alla fase dell’orientamento relativo, nell’aumentare il numero dei punti esuberanti, perché in questa fase aumentare il numero dei punti non vuol dire semplicemente aumentare le collimazioni alo strumento, che non sarebbe niente, ma aumentare le operazioni di misura topografiche a terra per determinare più punti!!! Operazioni molto costose! Per valutare correttamente questo fatto si pensi che, prima dell’avvento della triangolazione aerea (operazione che è entrata nella prassi operativa delle Ditte verso la fine degli anni ’80 e di cui parleremo nel seguito e che serve appunto a determinare con metodo fotogrammetrico e non topografico i punti di appoggio dei modelli stereoscopici) il solo lavoro topografico per determinare i punti di appoggio era pari al 25% del costo totale di un rilievo cartografico fotogrammetrico! Questo spiega quindi perché l’impostazione originariamente data dai fotogrammetri è stata quella di tenere separata l’operazione di orientamento relativo da quella dell’orientamento assoluto; nell’orientamento relativo, che è una fase molto delicata, perché è quella in cui si ricostruisce la forma del terreno, si può operare con grande sovrabbondanza di punti, poiché non occorre conoscerne le coordinate assolute, ma basta collimarli allo strumento; una volta formato il modello, nella fase di orientamento assoluto, in cui bisogna preventivamente determinare le coordinate N,E,Q dei punti di appoggio, si può operare con un numero meno consistente di punti esuberanti. In nota sono riportate le funzioni che realizzano gli orientamenti interno, relativo ed assoluto, secondo le notazioni esposte nella trattazione teorica del metodo delle Osservazioni Indirette * Applicazione dell'algoritmo delle Osservazioni Indirette. Orientamento interno: xi - x0 +(Ui cosα+Vi senα)λ= v 1i f1i(x0*,α*,λ*;Ui,Vi) = v 1i y i - y 0 +(Ui senα+Vi cosα)λ= v 2i f2i(y 0*,α*,λ*;Ui,Vi) = v 2i le equazioni generatrici sono 2, le incognite sono 4 (x0*,y 0*,α*,λ*); i deve essere > di 2. Orientamento relativo: Assumendo le semplificazioni introdotte nella definizione dell'equazione della parallasse κ 2 x i "− y i "+ω 2 z i " κ x '+ y i ' − 1 i = vi −ϕ 2 x i "+ω 2 y i "+ z i " −ϕ 1x i '+ z i ' fi(κ1*,ϕ1*,κ2*,ϕ2*,ω2*;x’i,y’i,z’i, x” i,y”i,z” i,) = v 1i l'equazione generatrice è una, le incognite sono 5 κ1*,ϕ1*,κ2*,ϕ2*,ω2*. i deve essere > di 5. Orientamento assoluto: E = E0 + Λ( Xcos(XE) + Ycos(YE) + Zcos(ZE)) N = N 0 + Λ( Xcos(XN) + Ycos(YN) + Zcos(ZN)) Q = Q 0 + Λ( Xcos(XQ) + Ycos(YQ) + Zcos(ZQ)) ricordando che ai 9 coseni direttori corrispondono 3 sole rotazioni indipendenti, che chiamiamo Φ,Ω,Κ risulta: f1i(E0*,Λ*,Φ*,Ω*,Κ*;Xi,Yi,Zi) = v 1i f2i(N0* ,Λ*,Φ*,Ω*,Κ*;Xi,Yi,Zi) = v 2i f3i(Q0*,Λ*,Φ*,Ω*,Κ*;Xi,Yi,Zi) = v 3i le equazioni generatrici sono 3, le incognite sono 7 (E0*,N0*,Q0*,Λ*,Φ*,Ω*,Κ*); i deve essere > di 3. Capitolo VIII - Fotogrammetria pagina 269 R.Galetto A.Spalla - Lezioni di Topografia 2.8 La determinazione dei punti di appoggio con metodo topografico Nel trattare l’argomento dell’orientamento assoluto abbiamo visto che occorrono mediamente 5 punti di appoggio (cioè di coordinate N,E,Q note) per poter orientare il modello stereoscopico, e abbiamo anche detto che provvedere alla determinazione delle coordinate di questi punti incide non poco nell’economia generale del rilievo fotogrammetrico. Distratti dalle formule che abbiamo via via sciorinato nel corso del Capitolo, non dobbiamo infatti pensare che un rilievo fotogrammetrico si componga di due fotogrammi, ma come abbiamo visto al punto 1.3.5 di questo steso Capitolo e come vedremo al successivo punto 3, una copertura fotografica per un rilievo può essere composta da centinaia di fotogrammi e quindi da centinaia di modelli stereoscopici. Non dobbiamo però pensare che se n sono i modelli stereoscopici i punti di appoggio da determinare siano nx5. Il numero effettivo dei punti di appoggio, pur elevato, sarà però molto inferiore a questo valore teorico. Infatti poiché i modelli stereoscopici si ricoprono tra di loro in senso longitudinale alla direzione di volo di circa il 10% e le strisciate si ricoprono, trasversalmente alla direzione di volo, del 10-20%, scegliendo opportunamente buona parte dei punti di appoggio in queste zone di ricoprimento si ha una notevole riduzione dei punti di appoggio rispetto al valore teorico. Tanto per dare un’idea possiamo dire che i punti di appoggio siano nx3 anziché nx5 (ricordiamo che entrambi questi valori sono orientativi). Resta il fatto che un rilievo cartografico di una città di medie dimensioni richiede centinaia di punti di appoggio. Prima dell’avvento della tecnica della triangolazione aerea, che descriveremo tra poco, il rilievo topografico dei punti di appoggio consisteva in una serie di fasi di lavoro molto simili a quelle che, nel rilievo topografico classico (vedi capitolo V), precedono il rilevo di dettaglio; e cioè, una volta eseguito il volo ed essendo disponibili le fotografie aeree, si sceglievano su di esse i punti di appoggio e quindi si partiva per le operazioni topografiche in campagna che si svolgevano come segue: • mediante triangolazione topografica tecnica si creava una rete di inquadramento del rilievo appoggiata ai vertici trigonometrici esistenti nella zona del rilevo; • tale rete veniva ulteriormente infittita mediante operazioni di intersezioni multiple in avanti ed inverse; • analogamente a partire dai caposaldi di livellazione si creava una rete di inquadramento e di infittimento altimetrica; • mediante poligonali, appoggiate ai punti delle reti di inquadramento e di infittimento planimetriche ed altimetriche, si determinavano le coordinate dei punti d'appoggio necessari per l'orientamento assoluto di ciascun modello. Possiamo dire che questo metodo, completamente topografico, per la determinazione delle coordinate dei punti di appoggio, ormai è usato molto raramente, poiché tutte le Ditte fotogrammetriche ricorrono alla triangolazione aerea (che è descritta al successivo punto 2.11). Capitolo VIII - Fotogrammetria pagina 270 R.Galetto A.Spalla - Lezioni di Topografia 2.9 La fase di restituzione Riprenderemo al successivo punto 3 l’argomento della restituzione fotogrammetrica; solo per concludere la trattazione matematica del problema, sarà sufficiente dire per ora che: • una volta eseguita la procedura dell’orientamento assoluto per il modello stereoscopico, il programma memorizza i parametri di orientamento N0, E0, Q0 , Κ, Φ, Ω e Λ che sono appunto stati determinati in questa fase; • ogni volta che l’operatore collima un punto sul modello stereoscopico la catena di calcoli descritta al punto 2.6.4 si allunga di una passo, e cioè: • le coordinate Xi,Yi,Zi nel sistema arbitrario del generico punto Pi di cui si sono collimati i punti omologhi sui fotogrammi, vengono trasformate mediante le 2.5.(1) in coordinate assolute Ni, Ei, Qi . Dopo l’orientamento assoluto inizia quindi la fase vera e propria della restituzione fotogrammetrica, durante la quale l’operatore interpreta il modello del terreno che osserva stereoscopicamente nel restitutore, scegliendo quali punti restituire, per dare una rappresentazione planimetrica e altimetrica del terreno che sia congruente alla scala della carta che deve produrre. 2.10 Rilievo fotogrammetrico e rilievo topografico Sulla fase di restituzione si tornerà più avanti; merita però fare subito una riflessione sul motivo per cui la fotogrammetria ha, in pratica, soppiantato la topografia come metodo di costruzione della cartografia. A chiusura della descrizione della costruzione della cartografia col metodo topografico (v. Cap. V) abbiamo sottolineato l’onerosità di tale metodo, che implica che squadre di operatori si rechino sul terreno da rilevare e rilevino ogni singolo punto ponendo preventivamente su di esso una stadia o un prisma riflettente; abbiamo inoltre sottolineato come il lavoro del topografo sia condizionato dagli eventi atmosferici, dalle asperità della natura o dall’interferenza del traffico, e infine come sia costoso implicando la trasferta di operatori in luoghi lontani dalla sede della Ditta. Con la fotogrammetria invece l’unico collo di bottiglia è rappresentato dalla ripresa aerea e dalla determinazione dei punti di appoggio (ma vedremo tra poco che questa fase viene oggi molto sveltita dall’uso della triangolazione aerea); per il resto si tratta essenzialmente di svolgere un lavoro d’ufficio davanti al restitutore e senza allontanarsi dalla sede della Ditta. Nel rilievo topografico ogni punto rilevato in campagna aveva un costo enormemente superiore a quello di un punto ottenuto per collimazione sul modello stereoscopico; il topografo doveva quindi limitare al massimo il numero di punti da rilevare sul terreno per stare in limiti di costi accettabili; l’operatore al restitutore non ha questo problema e può quindi abbondare nel restituire punti e quindi produrre con facilità una carta più dettagliata. Vi è poi un altro fatto: nel rilievo topografico la fase delle misure sul terreno per acquisire gli elementi per costruire la carta e quella della costruzione della carta vera e propria, erano due momenti separati: il topografo doveva infatti rilevare i punti sul terreno e quindi, dopo esser rientrato in sede dalla zona delle operazioni di campagna (l’una dall’altra potevano distare anche centinaia di km), procedeva all’esecuzione dei calcoli e al disegno della carta; se nella Capitolo VIII - Fotogrammetria pagina 271 R.Galetto A.Spalla - Lezioni di Topografia fase di disegno qualcosa non tornava, non vi era la possibilità di effettuare un controllo sul terreno, perché ciò avrebbe implicato un viaggio aggiuntivo sul luogo del rilievo, e quindi si cercava, con l’esperienza, di sanare la lacuna. Il restitutista può invece controllare continuamente la corrispondenza della carta che via via produce, col modello del terreno che ha sempre sott’occhio e questo va a vantaggio di una maggior completezza e di una miglior qualità della carta. Questi sono solo alcuni dei motivi che rendono il rilievo cartografico fotogrammetrico più rapido, più economico e più completo del rilievo topografico classico, e che quindi hanno portato la fotogrammetria a soppiantare la topografia nel rilievo cartografico. C’è da dire però che, per i rilievi a grandissima scala, il rilievo topografico sopravvive ancora, perché è in grado di dare precisioni metriche superiori a quelle che la fotogrammetria può dare. Inoltre l’esistenza degli strumenti topografici total station con la registrazione automatica delle misure, l’immissione automatica dei dati di misura nel PC, l’uso del PC per l’esecuzione dei calcoli delle coordinate dei punti e, a partire da queste, il tracciamento automatico della carta mediante plotter, ha reso la produzione di cartografia mediante il rilievo topografico molto più rapida ed economica di quello che fosse qualche decina d’anni addietro. 2.11 La triangolazione aerea a modelli indipendenti La triangolazione aerea è una tecnica fotogrammetrica che ha lo scopo di fornire le coordinate dei punti di appoggio per i modelli stereoscopici di un rilievo fotogrammetrico. La triangolazione aerea ha origini antiche, nel senso che già nei primi anni ’50, quando ancora esisteva solo la fotogrammetria analogica, già esistevano metodi per realizzare la triangolazione aerea con gli strumenti analogici, tanto era fin d’allora l’interesse a ridurre il costo delle operazioni topografiche a terra. Dalla triangolazione aerea analogica si passò poi a quella semianalitica a metà degli anni sessanta, e da questa si è originato il metodo di triangolazione aerea analitica che, tra tutti quelli realizzati, è stato quello più usato fino ad oggi (1996) e che va sotto il nome di triangolazione aerea a modelli indipendenti. 2.11.1 Struttura del blocco, punti nadirali, di legame e di appoggio Prima di procedere alla descrizione della triangolazione aerea a modelli indipendenti ricordiamo (vedi punto 1.5 di questo Capitolo, figure . 12.a e 12.b) che ogni fotogramma si sovrappone col precedente e col seguente di almeno il 60%; pertanto un generico modello stereoscopico ha una striscia di sovrapposizione del 10% a sinistra col modello precedente e una striscia di sovrapposizione del 10% a destra col modello seguente. Inoltre poiché le strisciate si sovrappongono tra di loro di un 15-20% ogni modello stereoscopico ha anche una striscia di sovrapposizione in alto e una striscia di sovrapposizione in basso con i modelli delle due strisciate contigue a quella a cui appartiene. (Abbiamo messo in corsivo le dizioni a sinistra, a destra, in alto e in basso poiché esse si riferiscono a come viene disegnato il modello stereoscopico nella trattazione che andiamo facendo). Capitolo VIII - Fotogrammetria pagina 272 R.Galetto A.Spalla - Lezioni di Topografia I punti del terreno che si trovano in tali zone di sovrapposizione sono collimabili in più di un modello stereoscopico. S 1 3 1 i i-1 2 S2 D S 3 1 i+1 D 3 D 2 4 Si dicono punti nadirali di sinistra tre punti del modello stereoscopico i che si trovano nella striscia di sovrapposizione col modello i-1; tali punti sono indicati con S1, S2 e S3 nella figura 26 si dicono punti nadirali di destra tre punti del modello i che si trovano nella striscia di sovrapposizione col modello 1+1; tali punti sono indicati con D1, D2 ,D3 nella figura 26. figura 26 Ovviamente, poiché i punti nadirali di sinistra stanno nella zona di sovrapposizione col modello i-1, essi saranno collimabili dall’operatore non solo quando esso sta osservando il modello i, ma anche quando nello strumento vi saranno i fotogrammi che formano il modello i-1; e ugualmente poiché i punti nadirali di destra stanno nella zona di sovrapposizione col modello i+1, essi saranno collimabili dall’operatore non solo quando esso sta osservando il modello i, ma anche quando nello strumento vi saranno i fotogrammi che formano il modello i+1. LA LB Indichiamo poi col termine di punti di legame i punti che si trovano nelle zone di sovrapposizione tra due modelli di strisciate diverse (vedi figura 27) cioè nelle zone di sovrapposizione del modello che abbiamo definito alta e bassa; anche questi punti potranno essere collimati più volte, e cioè tante volte quanti sono i modelli stereoscopici in cui cadono. Vi sono infine nel territorio da rilevare, cioè quello ricoperto dalle strisciate di fotogrammi, dei punti di coordinate note; la triangolazione aerea fa infatti diminuire il numero di punti a terra dei quali determinare le coordinate, ma, almeno nella triangolazione aerea a modelli indipendenti, non li può eliminare del tutto. L’esperienza (basata su innumerevoli studi di ricerca nazionali e internazionali) ha dimostrato che occorre figura 27 determinare almeno un punto in planimetria e in altimetria nel primo e nell’ultimo modello stereoscopico di ogni strisciata, e poi delle file di punti, noti anche solo in altimetria , posti nelle zone di ricoprimento trasversale tra le strisciate; tali file di punti debbono avere andamento ortogonale alla direzione delle strisciate e devono cadere ogni quattro o cinque modelli (vedi figura 27) . L’insieme di questi punti costituiscono i punti di appoggio del blocco di strisciate o, più semplicemente, del blocco. 2.11.2 Le operazioni di misura Capitolo VIII - Fotogrammetria pagina 273 R.Galetto A.Spalla - Lezioni di Topografia Le operazioni di misura necessarie all’esecuzione della triangolazione aerea a modelli indipendenti di un blocco di strisciate sono le seguenti: • si esegue l’orientamento relativo di tutti i modelli stereoscopici di tutte le strisciate, cioè di tutti i modelli che compongono il rilievo; • per ogni generico modello stereoscopico i , l’operatore, dopo aver formato il modello, memorizza: ∗ le coordinate dei punti di presa, ∗ le coordinate dei tre punti nadirali di sinistra, ∗ le coordinate dei tre punti nadirali di destra, ∗ le coordinate dei punti di legame ∗ le coordinate dei punti di appoggio del blocco (ovviamente solo per i modelli in cui ce ne sono!). Il metodo si chiama a modelli indipendenti proprio perché, nella fase di lavoro che riguarda ciascun modello, le coordinate dei punti sopra elencati vengono determinate nel sistema di coordinate arbitrario di ciascun modello!. Tutte le misure effettuate vengono memorizzate in modo tale che siano elaborabili da un programma di calcolo. Sottolineiamo che le operazioni di misura per effettuare la triangolazione aerea non hanno nulla che fare con quelle che si eseguono in fase di restituzione, in quanto vengono effettuate in una fase precedente del lavoro; anzi sarà opportuno ricordare che nelle Ditte fotogrammetriche molte volte la triangolazione aerea viene fatta su uno strumento analitico più preciso di quelli che poi vengono usati per la fase di restituzione vere e propria. punti planoaltimetrici punti altimetrici figura 28 Capitolo VIII - Fotogrammetria pagina 274 R.Galetto A.Spalla - Lezioni di Topografia Cioè l’organizzazione del lavoro nelle Ditte, almeno i quelle di una certa dimensione, è quella di avere uno strumento analitico sul quale viene fatta la triangolazione aerea per determinare i punti di appoggio di diversi blocchi, la cui restituzione avviene su diversi altri strumenti. 2.11.3 Il programma di calcolo Dopo aver eseguito questa fase di misure si esegue il calcolo del blocco, mediante un apposito programma di calcolo (ne esistono diversi, tutti basati sullo stesso concetto di base). Il programma si basa su questo concetto: bisogna determinare per ogni modello una rototraslazione e una variazione di scala in modo che siano soddisfatte queste due condizioni: • applicando alle coordinate (X,Y,Z) di un generico punto di appoggio osservato nel modello i i parametri di rototraslazione e variazione di scala determinati dal programma per tale modello, si devono ottenere le coordinate N,E,Q del punto di appoggio nel sistema di riferimento assoluto; • un generico punto nadirale o di legame, comune a due modelli i e j, dovrà avere le stesse coordinate assolute, sia che esse siano ottenute applicando alle coordinate arbitrarie X,Y,Z del punto nel modello i i parametri di rototraslazione e di variazione di scala del modello i, sia che esse siano ottenute applicando alle coordinate arbitrarie X,Y,Z del punto nel modello j i parametri di rototraslazione e di variazione di scala del modello j. La prima condizione si realizza applicando per tutti i punti di appoggio la seguente relazione: Ei = A k + Λ k (a11 X i,k + a12 Y i,k + a13 Z i,k ) Ni = B k + Λ k (a21 X i,k + a22 Y i,k + a23 Z i,k ) (17) Qi = C k + Λ k (a31 X i,k + a32 Y i,k + a33 Z i,k ) nella quale: • Ei,Ni,Qi sono le coordinate note del punto di appoggio i nel sistema assoluto • X i,k, Y i,k, Z i,k, sono le coordinate del punto determinate nel sistema arbitrario di riferimento del modello k • le traslazioni A k,B k,C k, gli elementi aij della matrice di rotazione (che contengono le rotazioni Ω,Φ,Κ ) e il coefficiente di scala Λ k, sono quelli del modello k nel quale sono state osservate le coordinate X i,k, Y i,k, Z i,k, del punto di appoggio i. Se il punto di appoggio i fosse stato osservato anche nel modello m, perché situato in una zona di sovrapposizione tra il modello i ed il modello m, le (17) dovrebbero essere anche per il modello m; in pratica nelle (17) al pedice k si dovrebbe sostituire il pedice m. Notiamo inoltre che se il punto di appoggio fosse noto solo in planimetria, per esso si dovrebbero scrivere solo le prime due delle (17); mentre se di esso fosse nota solo la quota si dovrebbe scrivere solo la terza. Per i punti nadirali o di legame le equazioni da scrivere sono le seguenti (dove con i si è indicato un generico punto nadirale o di legame situato in una zona di sovrapposizione tra due modelli e k e j ): Ak + Λk (a11k X i,k + a12k Y i,k + a13k Z i,k ) = Aj + Λj (a11j X i,j + a12j Y i,j + a13j Z i,j ) Bk + Λk (a21k X i,k + a22k Y i,k + a23k Z i,k ) = Bj + Λj (a21j X i,j + a22j Y i,j + a23j Z i,j ) (18) Ck + Λk (a31k X i,k + a32k Y i,k + a33k Z i,k ) = Cj + Λj (a31j X i,j + a32j Y i,j + a33j Z i,j ) Capitolo VIII - Fotogrammetria pagina 275 R.Galetto A.Spalla - Lezioni di Topografia Nelle (18) le espressioni a sinistra dell’uguale rappresentano le coordinate del punto i rilevate nella fase di orientamento relativo del modello k, trasformate nel sistema assoluto in funzione degli elementi di rototraslazione e variazione di scala del modello j. Le espressioni a destra dell’uguale rappresentano le coordinate del medesimo punto i rilevate nella fase di orientamento relativo del modello j, trasformate nel sistema assoluto in funzione degli elementi di rototraslazione e variazione di scala del modello j. Al pedice del generico elemento delle matrici aij si è aggiunto un k o un j per indicare che, nelle equazioni a sinistra dell’uguale esse contengono le rotazioni Ω,Φ,Κ del modello k e, nelle equazioni a destra dell’uguale contengono le rotazioni Ω,Φ,Κ del modello j. Un stesso punto nadirale o di legame può generare anche più di una tripletta di equazioni (18); si consideri ad esempio il caso (vedi figura 29) in cui un punto venga usato come punto nadirale alto in due modelli di una strisciata, e venga usato come punto nadirale basso in due modelli della strisciata adiacente; esso darà luogo addirittura a quattro triplette di equazioni (18). h h+1 P i E’ detta molteplicità di un punto nel blocco il numero di modelli in cui cade quel punto. In genere i punti nadirali hanno molteplicità due o tre; ma possono avere anche molteplicità maggiore. Nel caso appena fatto, ad esempio, il punto ha molteplicità 4. i+1 Sulla base dei concetti esposti sono stati sviluppati diversi programmi di calcolo dei blocchi di strisciate; tutti sono in pratica basati sulla determinazione delle incognite col metodo delle osservazioni indirette. Ciò che li differenzia è il modo di gestire i dati di input. Si tenga presente infatti che i problemi difficili da risolvere in un programma di questo genere non sono certo il calcolare le figura 29 derivate parziali delle (17) o delle (18), o impostare una volta per tutte i coefficienti del sistema normale; la difficoltà è studiare il modo di numerare i modelli e i punti nei modelli in modo che siano riconoscibili in modo univoco; e ancora: individuare in quanti modelli cade uno stesso punto, e così via. Altra difficoltà risiede nel risolvere il sistema normale, che molto spesso ha dimensioni ragguardevoli. Infatti se n sono i modelli del blocco, le incognite saranno 7.n e quindi le dimensioni della matrice del sistema normale saranno (7.n)2 . Ad esempio in un blocco di trecento modelli (dimensione abituale e non tra le maggiori di un blocco) le dimensioni della matrice sarebbero di 21002. Al termine delle elaborazioni il programma determina quindi i 7 parametri incogniti per ciascun modello; in funzione di essi, applicando le (17), è possibile ricavare le coordinate dei punti nadirali e dei punti di legame nel sistema assoluto. Poiché tutti i punti hanno almeno molteplicità due, essi possono essere calcolati con i parametri di almeno due modelli; se ne calcola perciò le coordinate nei vari modelli e se prende come valore definitivo la media. Capitolo VIII - Fotogrammetria pagina 276 R.Galetto A.Spalla - Lezioni di Topografia 2.11.4 Valutazione della precisione del calcolo del blocco La precisione del calcolo del blocco può venir valutata in modi più o meno raffinati, sui quali qui non entriamo nel merito. Ricordiamo solo, a titolo d’esempio, che uno dei modi più semplici, ma anche più significativi, per valutare la precisione del calcolo del blocco è quello di calcolare gli scarti residui dopo la determinazione delle incognite delle (17) e delle (18). Gli scarti delle (17) rappresentano la differenza tra le coordinate note dei punti di appoggio e quelle che si ricavano applicando alle loro coordinate modello i rispettivi parametri determinati dal programma; Gli scarti delle (18) rappresentano le discrepanze tra le coordinate di uno stesso punto nadirale , o di legame, quando vengono calcolate con i parametri di due diversi modelli. 2.11.5 Uso dei risultati della triangolazione aerea Il risultato dell’operazione della triangolazione aerea è quello di aver calcolato, in funzione dei pochi punti di appoggio del blocco, le coordinate dei punti nadirali e di legame di tutti i modelli del blocco di strisciate nel sistema di riferimento assoluto N,E,Q. Cioè, a seguito della triangolazione aerea , si hanno sei punti, almeno, di coordinate note per eseguire l’orientamento assoluto dei modelli stereoscopici. Pertanto, dopo l’esecuzione della triangolazione aerea , inizierà la fase di restituzione vera e propria; e cioè ogni coppia di fotogrammi verrà rimessa nello strumento restitutore, verrà rieseguito l’orientamento interno, quello relativo e infine quello assoluto basato appunto sui punti nadirali di sinistra e di destra del modello, le cui coordinate, lo ripetiamo ancora, sono state appunto determinate mediante la triangolazione aerea . Dopo aver eseguito queste operazioni l’operatore procede alla fase di restituzione. 2.12 La triangolazione aerea a stelle proiettive con punti di appoggio e quella integrata da dati GPS Abbiamo descritto al precedente punto 2.11 la triangolazione aerea a modelli indipendenti, che come abbiamo detto è ancor oggi (anno 1996) il metodo di triangolazione aerea più usato. Il progredire degli studi nel campo della triangolazione aerea e i risultati del progresso tecnologico stanno però portando all’attenzione delle Ditte fotogrammetriche altri modi di effettuare la triangolazione aerea, che probabilmente costituiranno in futuro delle valide alternative alla triangolazione aerea a modelli indipendenti. Descriviamo qui brevemente il metodo a stelle proiettive in due sue versioni e cioè quello basato sui tradizionali punti di appoggio e quello basato sui dati GPS. 2.12.1 La triangolazione aerea a stelle proiettive con punti di appoggio Capitolo VIII - Fotogrammetria pagina 277 R.Galetto A.Spalla - Lezioni di Topografia Questo metodo di triangolazione aerea è così chiamato perché prende in considerazione come elemento del blocco non il modello stereoscopico, ma il singolo fotogramma, o meglio il fascio di raggi che, dal punto di presa, proiettano i punti immagine del fotogramma.; è appunto questo ideale fascio di raggi, inteso come stella di direzioni proiettanti i punti che dà origine al nome di questo tipo triangolazione aerea . La base teorica del metodo della triangolazione aerea a stelle proiettive è semplice; basta considerare l’equazione di collinearità per un generico punto Pi di un generico fotogramma j del blocco: Xi − X0j a11 j xij + a12 j yij + a13 j zij = Zi − Z0j a 31 j xij + a32 j yij + a33 j zij Yi − Yj0 a21 j xij + a22 j yij + a23 j zij = Zi − Z0j a31 j xij + a32 j yij + a33 j zij vediamo che essa contiene: • le coordinate Xi,Yi,Zi del punto P nel sistema assoluto; queste coordinate saranno per la maggior parte dei punti non note; saranno note solo per i punti di appoggio del blocco • le coordinate lastra xi,j,yi,j del punto immagine di Pi sul fotogramma j • i parametri di orientamento del fotogramma X0j , Yj0 , Z0j , ωj, ϕj, κj Consideriamo ora la situazione generica di un blocco di strisciate quale l’abbiamo descritta nel metodo di triangolazione aerea a modelli indipendenti; ci riferiamo cioè al fatto di avere punti del terreno che danno la loro immagine su più fotogrammi, e di avere punti noti che servono per appoggiare il blocco nel suo complesso. Per tutti questi punti possiamo scrivere l’equazione di collinearità riferita ; otterremo un grande sistema di equazioni di collinearità nel quale: • in tutte le equazioni saranno note le coordinate xi,j,yi, del punto immagine • in ogni equazione saranno incogniti i parametri di orientamento del fotogramma X0j , Yj0 , Z0j , ωj, ϕj, κj • nella maggior parte delle equazioni saranno incognite anche le coordinate assolute dei punti Xi,Yi,Zi ; esse saranno note solo per i punti di appoggio del blocco. Anche se in questo metodo di triangolazione aerea prendiamo in considerazione i fotogrammi e non i modelli stereoscopici, possiamo ancora ricorrere al concetto di molteplicità di un punto; diremo cioè che un punto ha molteplicità due se la sua immagine esiste su due fotogrammi del blocco, ha molteplicità tre se esiste su tre fotogrammi e in genere avrà molteplicità n se compre su n fotogrammi. Per ogni punto, concettualmente corrispondente a quello che era un punto o nadirale o di legame della triangolazione aerea a modelli indipendenti, che ha molteplicità n, potremo scrivere n equazioni di collinearità, dove saranno sempre le stesse, anche se incognite, le coordinate Xi,Yi,Zi assolute del punto. Anche per un generico punto di appoggio del blocco, se n è la sua molteplicità, potremo scrivere n equazioni di collinearità, dove saranno però note le coordinate assolute Xi,Yi,Zi del punto. Capitolo VIII - Fotogrammetria pagina 278 R.Galetto A.Spalla - Lezioni di Topografia Scrivendo dunque tutte queste possibili equazioni, si ottiene un sistema in cui si hanno simultaneamente come incognite i parametri di orientamento X0j , Yj0 , Z0j , ωj, ϕj, κj di ogni fotogramma e le coordinate assolute Xi,Yi,Zi di ogni punto nadirale o di legame. Con riferimento alla figura 30 si vede come, ad esempio, il punto P abbia molteplicità 5, in quanto la sua immagine compare sui fotogrammi 2,3,4,6 e 7, dando luogo a 5 equazioni di collinearità. 5 1 6 P6 2 P2 7 P7 3 P3 8 4 P4 P figura 30 Nel sistema le equazioni relative ai punti del tipo nadirali o di legame, hanno esclusivamente la funzione di ricreare l’orientamento relativo dei fotogrammi, mentre le equazioni relative ai punti di appoggio posizionano correttamente il blocco di fotogrammi nel sistema assoluto. La soluzione del sistema porta alla determinazione delle coordinate dei punti nadirali e di legame e quindi danno la possibilità di procedere all’orientamento assoluto dei modelli, come avveniva con la triangolazione aerea a modelli indipendenti. La differenza tra il metodo a stelle proiettive e quello a modelli indipendenti, consiste più che altro in un diverso approccio concettuale al problema, ma dal punto di vista pratico non vi è Capitolo VIII - Fotogrammetria pagina 279 R.Galetto A.Spalla - Lezioni di Topografia gran differenza in quanto entrambi richiedono la determinazione di un certo numero di punti di appoggio del blocco. 2.12.2 La triangolazione aerea a stelle proiettive con dati GPS Abbiamo visto al capitolo VII che con la tecnologia GPS è possibile determinare anche la posizione di punti in movimento ed in particolare la posizione della camera da presa al momento della presa di un fotogramma, o per meglio dire le coordinate assolute dell’origine della terna del sistema di riferimento interna della camera da presa. Consideriamo allora di aver eseguito le riprese di un blocco di fotogrammi ed aver determinato, mediante il metodo del GPS cinematico, le coordinate dei punti di presa X0j , Yj0 , Z0j , di tutti i fotogrammi. Impostando nuovamente la soluzione del blocco con la metodologia delle stelle proiettive avremmo la sostanziale differenza di conoscere per ogni fotogramma le coordinate assolute dell’origine della terna del sistema di riferimento interno per ogni fotogramma. Nelle equazioni di collinearità, come parametri incogniti di orientamento di ogni fotogramma, rimarranno solo i parametri angolari ωj, ϕj, κj. I punti di presa saranno quindi già posizionati in maniera corretta nel sistema di riferimento assoluto, sostituendosi, nel calcolo del blocco, alla funzione svolta dai punti di appoggio, mentre il sistema delle equazioni di collinearità porterà alla determinazione dell’orientamento relativo dei fotogrammi e alla determinazione delle coordinate dei punti nadirali e di legame. L’innovazione introdotta da questo metodo è quindi quello di eliminare la necessità di determinare punti di appoggio a terra. In realtà, per controllo, si usano ancora quattro soli punti di appoggio a terra situati nei quattro spigolo del blocco. Volendo ridimensionare la portata innovativa di questo metodo si possono fare delle considerazioni e cioè: • che la tecnica del GPS cinematico è tecnologicamente molto avanzata e richiede particolari capacità operative • che la determinazione dei punti di appoggio a terra è anch’essa molto più agevole da quando le operazioni topografiche classiche possono essere integrate, o addirittura sostituite, dall’uso del GPS per la determinazione delle coordinate dei punti del terreno • che esistono comunque nella nostra realtà italiana, e potremmo dire europea, molti punti a terra di coordinate note, e quindi è un peccato non usarli. In effetti queste considerazioni hanno la loro validità. Possiamo allora concludere dicendo che il metodo di triangolazione aerea a stelle proiettive integrato dall’uso del GPS cinematico trova la sua massima validità di impiego proprio quando si deve operare in territori dove non esistono, o sono diventate obsolete, le reti nazionali di vertici trigonometrici, o dove le operazioni sul terreno sono rese molto complesse per la natura del territorio. Si pensi ad esempio al caso di dover rilevare vaste zone di nazioni africane mai inquadrate in sistemi cartografici nazionali e coperte da fitta vegetazione che ostacola i movimenti sul terreno. Capitolo VIII - Fotogrammetria pagina 280 R.Galetto A.Spalla - Lezioni di Topografia 3. Iter per la realizzazione di un rilievo con metodo fotogrammetrico. 3.1 Progettazione ed allestimento del materiale necessario per la costruzione di una carta. Si suppone di dover eseguire il rilievo fotogrammetrico alla scala 1 : n di una certa zona. Poiché esistono tabelle che danno l'altezza relativa ottimale di volo in funzione del fattore di scala della carta che si vuole costruire, noto il fattore 1 :n è anche definito il valore H. Dal valore di H si risale alla scala media del fotogramma tramite la relazione: 1 0.150 = σf H essendo 0.150 il valore, espresso in metri, della distanza principale. Tenuto conto che il formato standard dei fotogrammi per fotogrammetria aerea è 0.23 m x 0.23 m, una volta imposto σf, si calcola la dimensione reale L del lato di ciascun fotogramma L = 0.23 . σf (in metri) Ci si procura a questo punto della cartografia ufficiale, ad esempio della cartografia IGM alla scala 1:100.000, sulla quale si riporta il contorno della zona da rilevare. Si calcola il valore che il lato del fotogramma ha alla scala 1:100.000 L' = L / 100000 I figura 31 Avendo scelto di riprendere tale zona con strisciate ad andamento Est-Ovest, si traccia il bordo superiore della prima strisciata; esso dovrà ovviamente essere tracciato esternamente al limite della zona da cartografare almeno del 20% della dimensione del lato L'. Si traccia l'asse della prima strisciata distanziato di L'/2 dal bordo tracciato. Si calcola quindi il valore dell’interasse I fra le strisciate I = 0.8 . L' dove il fattore 0.8 tiene conto del fatto che le strisciate, ciascuna di dimensione trasversale L', devono sovrapporsi del 20%. Si riportano quindi gli assi di tutte le strisciate parallelamente al primo e distanziati di I. Capitolo VIII - Fotogrammetria pagina 281 R.Galetto A.Spalla - Lezioni di Topografia Accanto a ciascun asse si scrive la quota effettiva di volo alla quale la strisciata dovrà essere ripresa. La quota effettiva di volo si ottiene sommando ad H la quota media del terreno. L'elaborato così costruito si definisce piano di volo . Il piano di volo viene consegnato alla Ditta esecutrice dei voli, che, non appena si verificano le condizioni meteorologiche favorevoli, può effettuare, sulla base di esso, le riprese aeree e fornire i fotogrammi relativi alla zona richiesta, alla scala media stabilita. Nel frattempo la sezione topografica della Ditta cui è affidata la costruzione della carta, procede alle operazioni di costruzione della rete di inquadramento del rilievo, reperendo i vertici trigonometrici esistenti nella zona, infittendoli mediante triangolazione tecnica, infittendoli ulteriormente mediante intersezioni in avanti ed inverse. Eseguite le riprese aeree sulla base dei fotogrammi è possibile realizzare il quadro d'unione di essi; il quadro d'unione si ottiene riportando sulla cartografia alla scala 1:100.000 l'effettivo contorno dei fotogrammi. Definito il quadro d'unione, si scelgono sui fotogrammi i punti d'appoggio necessari per la determinazione dell'orientamento assoluto di ciascun modello; questi punti devono essere ben visibili sui fotogrammi e ben disposti nel modello. La sezione topografica della Ditta, cui è affidata la costruzione della carta, completa il suo lavoro reperendo i punti fotografici sul terreno, collegando tali punti, mediante poligonali, ai punti della rete precedentemente realizzata e determinando le coordinate (N,E,Q) di questi punti fotografici che serviranno per l'appoggio dei modelli. 3.2 Restituzione fotogrammetrica. Perché si possa procedere alla fase di restituzione fotogrammetrica deve essere disponibile il seguente materiale: • copia diapositiva su materiale indeformabile trasparente (generalmente poliestere) dei fotogrammi; • copia a stampa su carta dei fotogrammi sui quali sono stati evidenziati i punti di appoggio scelti; • tabulati sui quali sono riportate le coordinate (N,E,Q) dei punti d'appoggio. Nel diagramma a blocchi n.2 vengono riepilogate sinteticamente le operazioni che si effettuano nella fase di restituzione fotogrammetrica, quando si costruisce cartografia mediante fotogrammetria analitica. Le operazioni che vengono eseguite per la restituzione fotogrammetrica sono le seguenti: 1. inserimento dei due fotogrammi adiacenti nello strumento restitutore; 2. determinazione dei parametri dell'orientamento interno: l'operatore esegue la collimazione delle quattro marche di ciascun fotogramma; è così in possesso di quattro coppie di coordinate strumentali per ciascun fotogramma U'i,V' i e U"i,V"i ; il calcolatore connesso allo stereorestitutore mediante la routine dell'orientamento interno, note le U'i,V' i e U"i,V"i delle marche sui due fotogrammi e note le coordinate nominali delle marche per la camera da presa (che sono riportate sul certificato di taratura Capitolo VIII - Fotogrammetria pagina 282 R.Galetto A.Spalla - Lezioni di Topografia della camera stessa), determina i valori dei parametri di passaggio dai sistemi (U',V') e (U",V") ai sistemi (x',y'), (x",y"); 3. determinazione dei parametri dell'orientamento relativo: l'operatore esegue la collimazione stereoscopica di un certo numero di n punti omologhi, (n = 10-12). Il calcolatore, mediante la routine dell'orientamento relativo, note le coordinate x'i,y'i e x"i,y"i dei punti collimati determina i parametri dell'orientamento relativo e cioè κ1, ϕ1, κ2, ϕ2, ω2; 4. determinazione dei parametri dell'orientamento assoluto: l'operatore esegue la collimazione stereoscopica di quei punti fotografici d'appoggio dei quali sono note le coordinate Gauss-Boaga; il calcolatore, mediante la routine dell'orientamento assoluto, determina appunto i parametri dell'orientamento assoluto Κ, Φ, Ω, N0, E0, Q0, Λ di passaggio fra il sistema arbitrario dell’orientamento relativo e il sistema Gauss-Boaga; 5. restituzione di tutti i punti che devono essere riportati in cartografia: • • • • l'operatore collima le coppie di punti omologhi, dei quali automaticamente vengono acquisite dal calcolatore le coordinate U' i,V' i e U"i,V"i; le coppie di coordinate U' i,V' i e U"i,V"i vengono inserite nelle formule di rototraslazione dove compaiono i parametri dell'orientamento interno x'0, y'0, α', λ' e x"0, y"0, α", λ" determinati nella fase 2; si ottengono le coppie di coordinate x' i , y'i e x"i,y"i; le coppie x' i , y'i e x"i,y"i vengono inserite nelle formule dove compaiono i parametri dell'orientamento relativo κ1, ϕ1, κ2, ϕ2, ω2 determinati nella fase 3; si ottengono le coordinate Xi, Yi, Zi del modello stereoscopico; le coordinate Xi, Yi, Zi vengono introdotte nelle formule di rototraslazione dove compaiono i parametri dell'orientamento assoluto Κ, Φ, Ω, N0, E0, Q0, Λ determinati nella fase 4; si ottengono le coordinate Ei, Ni, Qi; i punti di coordinate Ei, Ni, Qi; vengono memorizzati sulle memorie di massa del calcolatore che gestisce le operazioni di restituzione; la loro rappresentazione viene eseguita automaticamente o mediante plotter, su carta da disegno oppure su video grafico. Si deve notare che la sequenza delle operazioni di applicazione dei parametri di orientamento interno, relativo ed assoluto (fase 5) è molto veloce (perchè eseguita da elaboratore elettronico); essa avviene in un lasso di tempo minore di quello impiegato dall'operatore per spostarsi da un punto al successivo. I dati memorizzati a seguito di queste operazioni trovano collocazione nei file di restituzione. L'elaborato grafico prodotto a partire da tali dati si chiama minuta di restituzione. 3.3 La revisione sul terreno. Con l'operazione di restituzione l'operatore riporta sulla minuta di restituzione tutti i particolari naturali ed artificiali del terreno che sono visibili sulle fotografie e che devono essere riprodotti in conformità alla scala della carta. Può capitare, tuttavia, che alcuni particolari che devono essere riportati sulla carta non siano ben visibili, perché coperti dalle chiome degli alberi, o Capitolo VIII - Fotogrammetria pagina 283 R.Galetto A.Spalla - Lezioni di Topografia perché defilati alla vista dall'effetto prospettico delle fotografie; oppure può capitare che l'operatore non riesca a distinguere la natura di un elemento del terreno (ad esempio non riesce a distinguere se un certo "oggetto" è un muro o una siepe). In questi casi il restitutista, cioè l'operatore che effettua la restituzione, indica sulla minuta di restituzione che quel particolare deve essere rivisto a terra. Pertanto, dopo le operazioni di restituzione, deve essere effettuata una ricognizione sul terreno in modo da completare la restituzione stessa, risolvendo i punti dubbi ed integrando la carta con quelle informazioni che non sono visibili dalle fotografie (ad esempio linee interrate di oleodotti o metanodotti). Con la revisione sul terreno l'originale di restituzione viene completato e con questa fase si conclude l'operazione di costruzione della cartografia per quello che riguarda il suo contenuto qualitativo e quantitativo. Come ultima operazione la carta viene completata con i toponimi, cioè con tutte quelle scritte che consentono l'individuazione delle località, dei fiumi, dei torrenti e, se richiesta, l'individuazione di ogni via o piazza delle zone urbanizzate. 3.4 L'elaborato finale. 3.4.1 Editing cartografico Con il termine di editing si intende quella fase del lavoro di realizzazione della cartografia fotogrammetrica numerica diretta durante la quale si interviene sull'archivio di dati che costituisce la cartografia numerica, se ne visualizza il contenuto su video grafico e si procede ad eventuali correzioni e aggiornamenti dell'archivio. Idealmente, nella fase di editing deve essere possibile la realizzazione di tutti quei tipi di intervento che nella restituzione fotogrammetrica tradizionale vengono attuati sulla minuta di restituzione e nella fase di ridisegno finale della carta. Si interviene sui dati memorizzati: • per integrare o correggere la codifica dei particolari restituiti, • per riportare le integrazioni, le correzioni e gli aggiornamenti individuati grazie alle operazioni di ricognizione sul terreno o per acquisizione di dati da altra fonte • per ricostruire le congruenze geometriche, ove necessario, • per introdurre la toponomastica. Si controlla che spezzate che definiscono entità campibili siano poligoni chiusi. Vengono inoltre effettuate tutte le operazioni di intervento atte a migliorare l'aspetto estetico delle visualizzazioni nella cartografia numerica, quali ad esempio eventuali ricollocazioni delle scritte indicanti la quota dei punti quotati e delle di gronda, realizzazione di ortogonalizzazioni e parallelismi in strutture artificiali, ecc. Sempre in questa fase si procede alla ricostruzione delle congruenze geometriche che consiste in interventi volti ad attribuire coordinate identiche a punti memorizzati che si riferiscono ad uno stesso punto fisico, ma che in fase di restituzione sono stati acquisiti più volte come afferenti ad entità diverse. Capitolo VIII - Fotogrammetria pagina 284 R.Galetto A.Spalla - Lezioni di Topografia Le operazioni di editing non vengono eseguite quando le nuove coordinate che dovrebbero assumere i vertici delle spezzate originarie per costituire spezzate soddisfacenti le condizioni di ortogonalizzazione, parallelismo e/o allineamento causerebbero spostamenti dei vertici dalla posizione originaria alla posizione finale superiori alla tolleranza planimetrica della carta. Sempre nella fase di editing viene realizzato il riporto della integrazioni numeriche derivanti dalle operazioni di ricognizione. Tali integrazioni potranno essere inserite nell'archivio dei dati: • introducendo direttamente le coordinate plano-altimetriche del particolare rappresentato, • integrando con il disegno tradizionale il disegno ottenuto al plotter dal file di restituzione, e trasformando i dati integrativi in forma numerica mediante digitalizzazione; al dato planimetrico acquisito per digitalizzazione, dovrà essere associata la quota relativa. 3.4.2 Il prodotto finale numerico Una volta realizzata la pulizia e il completamento dei dati mediante la fase di editing, la cartografia fotogrammetrica numerica può essere considerata compiuta e deve quindi essere consegnata al Committente. Nei capitolati che regolano la produzione di lavori di questo tipo sono generalmente descritti i formati in cui i dati devono essere scritti e i supporti magnetici su cui devono essere memorizzati. Di solito si mantiene, anche per quanto riguarda gli archivi numerici, la stessa suddivisione per fogli da sempre utilizzata per la cartografia tradizionale. D’altra parte poiché comunque viene sempre anche effettuata la consegna di un prodotto grafico, organizzato in fogli, è comodo anche la banca dati è strutturata in pseudofogli. Gli elaborati numerici vengono dunque consegnati per blocchi di file, ciascun blocco relativo ad uno pseudofoglio numerico. Ogni pseudofoglio numerico si riferisce ad uno dei fogli grafici, ma il suo perimetro, di andamento irregolare, non coincide con il perimetro, rettangolare, del foglio grafico a cui si riferisce. Il perimetro degli pseudofogli numerici viene stabilito in modo da non dividere entità con sviluppo superficiale che si trovano a cavallo di due fogli. 3.4.3 Il prodotto finale grafico A partire dai dati memorizzati nella cartografia numerica vengono prodotti automaticamente gli elaborati grafici mediante plotter elettrostatici e termici. Sempre nei capitolati che regolano la realizzazione di questo genere di lavori, sono descritte dettagliatamente le norme di rappresentazione dei differenti contenuti per i quali è previsto il rilievo (repertorio dei contenuti e delle codifiche) Nel prodotto grafico vengono rappresentate con grafia opportuna tutte le entità memorizzate e differenziate per codice nella cartografia numerica. (Vedi anche capitolo IX) Capitolo VIII - Fotogrammetria pagina 285 R.Galetto A.Spalla - Lezioni di Topografia L'elaborato grafico viene generalmente realizzato in doppia copia (con e senza campitura degli edifici). La quota in gronda degli edifici viene riportata solamente sulla copia senza campitura. Il formato dei fogli, le legende, le titolazioni e i cartigli vengono concordati con la Committenza e la Direzione Lavori. 3.5 Schemi delle fasi di realizzazione di cartografia con metodo fotogrammetrico Sono nel seguito riportati due schemi a blocchi; lo schema 1 descrive sinteticamente tutte le fasi di costruzione di una carta fotogrammetrica; lo schema 2 riepiloga tutte le operazioni relative alla sola fase della restituzione fotogrammetrica. Capitolo VIII - Fotogrammetria pagina 286 R.Galetto A.Spalla - Lezioni di Topografia schema 1 PRODUZIONE DI CARTOGRAFIA MEDIANTE FOTOGRAMMETRIA Acquisizione cartografia esistente (IGM, CTR, altro) con le seguenti funzioni : 1. individuazione della zona da rilevare 2. reperimento vertici trigonometrici e caposaldi livellazione 3. progetto rete di inquadra mento 4. progetto piano di volo Determinazione con metodi topografici (GPS;triangolazioni, intersezioni) delle coordinate dei punti della rete di inquadramento a partire dai vertici trigonometrici e dai caposaldi di livellazione Esecuzione del volo Copia a stampa dei Produzione dei fotogrammi fotogrammi Copia su poliestere dei fotogrammi (diapositiva) Determinazione coordinate dei punti d'appoggio dei modelli stereoscopici mediante metodi topografici (livellazioni, poligonali) e/o mediante triangolazione aerea Produzione della carta mediante strumento restitutore ( vedi schema 2 ) Minuta di restituzione Ricognizione sul terreno Minuta di restituzione corretta Editing fotogrammetrico Produzione di elaborati grafici nelle forme richieste Traduzione dei dati cartografici secondo i formati standard di trasferimento Consegna degli elaborati grafici e numerici Capitolo VIII - Fotogrammetria pagina 287 R.Galetto A.Spalla - Lezioni di Topografia schema 2 RESTITUZIONE FOTOGRAMMETRICA MEDIANTE RESTITUTORE ANALITICO Introduzione nel calcolatore associato al restitutore delle coordinate delle 4 marche della camera da presa e del Introduzione di una coppia di fotogrammi nello strumento restitutore valore della distanza principale analitico Collimazione delle marche sui due fotogrammi determinazione dei parametri per passare dal sistema di riferimento del restitutore al sistema di riferimento materializzato alle marche fiduciali *) Collimazione di n punti (n>5) sul modello Determinazione dei parametri di orientamento relativo **) Introduzione nel calcolatore delle coordinate terreno di m punti di appoggio (m>5) Determinazione dei parametri di orientamento assoluto del modello ***) per ogni punto da riportare in cartografia • Si collima stereoscopicamente il punto e si imposta la codifica del punto stesso, vengono automaticamente misurate le coordinate strumentali sui fotogrammi • Il calcolatore opera le seguenti trasformazioni: a) da coordinate strumentali a coordinate lastra mediante i parametri dell'orientamento interno *) b) da coordinate lastra a coordinate modello mediante i parametri dell'orientamento relativo **) c) da coordinate modello a coordinate terreno mediante i parametri dell'orientamento assoluto ***) • Si visualizza il punto restituito sul dispositivo grafico associato al restitutore analitico, (video grafico o plotter). • Si procede alla memorizzazione della codifica e delle coordinate del punto. Capitolo VIII - Fotogrammetria pagina 288 R.Galetto A.Spalla - Lezioni di Topografia CAPITOLO IX CARTOGRAFIA NUMERICA 1 Caratteristiche della cartografia numerica 1.1 Schema concettuale 1.1.1 Cartografia tradizionale e cartografia numerica: analogia dei rispettivi schemi concettuali Consideriamo una generica carta tecnica tradizionale a grande scala (nel seguito indicata col semplice termine di carta tradizionale) e vediamo di delinearne le caratteristiche qualitative e metriche. Possiamo dire che essa è costituita da un disegno del territorio che vuole rappresentare e che tale disegno, suddiviso in tavole e completato con opportune cornici e parametratura, viene realizzato in un sistema di coordinate cartesiane piane i cui punti sono in corrispondenza biunivoca, in funzione di precise relazioni di tipo geometrico e/o matematico, con quelli della superficie fisica del territorio rappresentato; aggiungiamo poi che la rappresentazione viene realizzata secondo uno schema che prevede due categorie di informazioni: la planimetria e l'altimetria; la prima costituita dalla proiezione nel piano del disegno dei particolari naturali e artificiali del terreno e la seconda dai punti quotati e dalle curve di livello; la planimetria è sempre presente, mentre l'altimetria può non esserci e in questo caso la carta è solo planimetrica. Altri elementi caratteristici che fanno del disegno una carta sono il rapporto di scala 1:n, essendo n il numero di volte di cui risulta ridotta sulla carta la distanza topografica tra due punti, e la legenda, che fornisce la chiave di lettura della carta in funzione di tipi di linee, retinature, simboli, segni convenzionali, ecc.. Infine il contenuto metrico dovrà essere conforme a delle tolleranze, che stabiliscono i massimi scostamenti che si possono verificare tra le distanze e i dislivelli ricavabili dalla carta e i corrispondenti nella realtà. L'elemento più caratterizzante della carta è senza dubbio il rapporto di scala; esso infatti determina, per convenzione ormai consolidata, il grado di dettaglio della carta, la sua precisione, l'equidistanza delle curve di livello e il grado di impiego di segni convenzionali. Le funzioni base che questo disegno assolve, vale a dire gli scopi principali per cui esso viene realizzato e impiegato sono: • • • fornire una conoscenza del territorio basata sia sull'osservazione puntuale di ogni singolo oggetto, sia come visione generale di insieme paragonabile a quella che si avrebbe osservando il territorio in direzione nadirale da conveniente altezza; consentire di sviluppare processi logici di tipo deduttivo e induttivo in funzione di relazioni di concomitanza, di vicinanza, di frequenza, ecc. ecc.; costituire il supporto di base, anche in senso fisico, per i lavori di classificazione, di pianificazione, di progettazione e di gestione del territorio. Capitolo IX - Cartografia numerica pagina 289 R.Galetto A.Spalla - Lezioni di Topografia Tutte le caratteristiche qualitative e metriche che sono state elencate indicano a quali aspetti formali un disegno del territorio debba soddisfare e quali contenuti debba avere, affinché corrisponda in termini tecnici ad una carta. Ma affinché questo disegno sia, come in effetti vuol essere, un elemento di conoscenza del territorio, oltre a qualificarsi come il prodotto di applicazioni tecniche che si richiamano a discipline scientifiche quali la Geodesia, la Cartografia, la Topografia e la Fotogrammetria, esso deve avere dei requisiti generali che sono quelli che gli conferiscono la sua impronta genetica di strumento di Informazione. Questi requisiti generali sono: • la congruenza, in base alla quale una qualsiasi informazione contenuta nella carta non deve essere in contraddizione con alcuna delle altre; • • la leggibilità, che deve garantire l'univocità di interpretazione, la quale deriva oltre che dalla similitudine fra la realtà e il disegno, anche dagli elementi di autocertificazione della carta stessa (rapporto di scala, cornice, legenda, ecc.); la veridicità, cioè la corrispondenza al vero dell'informazione qualitativa, che costituisce un vincolo anche più severo delle stesse tolleranze metriche. Mentre gli aspetti formali, i contenuti e le funzioni base della cartografia, hanno subito delle evoluzioni nel corso dei tempi, questi requisiti generali, anche se sottintesi, hanno sempre permeato la sua intima essenza. Lo schema concettuale della cartografia tradizionale si basa quindi su: • requisiti generali • aspetti formali • contenuti • funzioni base. Da esso emerge chiaramente cosa sia una carta tradizionale senza che si sia detta una parola su come essa venga prodotta. La tipologia della carta deriva dai suoi aspetti formali, dai suoi contenuti o dalle particolari funzioni che essa deve assolvere. Il modo con cui la carta deve venire realizzata sarà invece oggetto di norme di Capitolato, le quali hanno lo scopo di fornire alla Committenza degli elementi di garanzia aprioristici sul prodotto che essa vuole ottenere; di creare i presupposti necessari perché si possa effettuare l'affidamento dei lavori secondo determinate procedure di Legge; di creare, come di fatto è avvenuto, degli standard di produzione che semplificano il rapporto domanda-offerta. Per definire le caratteristiche qualitative e metriche della cartografia numerica ci atterremo allo schema concettuale sopra esposto, poiché non ci sono, allo stato attuale, motivi e ragioni per introdurne uno diverso 1.1.2 Definizione della cartografia numerica Seguendo la stessa impostazione metodologica con la quale è stata definita al precedente paragrafo la cartografia tradizionale, e cioè tenendo conto dei requisiti principali, degli aspetti formali, dei contenuti e delle funzioni base, elenchiamo gli elementi distintivi fondamentali che nel loro insieme costituiscono la definizione di cartografia numerica. Capitolo IX - Cartografia numerica pagina 290 R.Galetto A.Spalla - Lezioni di Topografia • • • • • • • • La cartografia numerica fornisce le informazioni qualitative e metriche proprie di una cartografia sotto due aspetti: in forma di dati numerici (coordinate che descrivono la geometria degli oggetti cartografati e codifiche che ne indicano la tipologia), memorizzati su supporto magnetico elaborabile da calcolatore elettronico, e in forma di visualizzazioni su video-grafico o su supporto cartaceo mediante plotter, simili nell'aspetto alla cartografia tradizionale; la cartografia numerica costituisce pertanto un'immagine speculare della cartografia tradizionale, in quanto quest'ultima è un prodotto cartografico in forma di disegno che contiene in forma implicita gli stessi dati sotto forma di coordinate; mentre la cartografia numerica è costituita da un archivio di coordinate che contiene in forma implicita la sua visualizzazione sotto forma di disegno; la visualizzazione costituisce quindi parte integrante della cartografia numerica, e deve essere insita in essa, così come parte integrante di una carta tradizionale sono la cornice, i riferimenti cartografici e la parametratura che consentono di ricavare le coordinate di ogni punto rappresentato. La cartografia numerica consente di trasformare il dato cartografico in informazione non solo in funzione di processi logici di un operatore umano che ne utilizzi una delle sue possibili visualizzazioni, ma anche in funzione di elaborazioni basate su logiche programmate ed effettuate mediante il calcolatore elettronico. La cartografia numerica sostituisce la cartografia tradizionale e quindi, nonostante la diversità di aspetto formale, ne deve mantenere i requisiti principali, deve possederne almeno tutti i contenuti, e deve assolverne almeno le stesse funzioni base. La cartografia numerica conferisce una totale univocità al contenuto metrico della cartografia poiché elimina sia gli elementi di soggettività che affliggono le operazioni di misura mediante le quali nella cartografia tradizionale si passa dal disegno alle coordinate, sia le conseguenze della deformabilità e deteriorabilità dei supporti cartacei; l'univocità risulta inoltre totale anche dal punto di vista del contenuto qualitativo, essendo l'interpretazione del disegno sostituita dalla lettura della codifica. La cartografia numerica consente di estendere la tipologia della cartografia, affiancando alla cartografia solo planimetrica e a quella plano-altimetrica con punti quotati e curve di livello, altre tipologie di cartografia in funzione di un incremento dell'informazione altimetrica, che è reso possibile dal fatto che, sotto l'aspetto formale, non vi è più differenza tra informazione planimetrica e informazione altimetrica, poiché ad ogni punto della carta possono essere associate oltre alle coordinate planimetriche anche quella altimetrica. La cartografia numerica consente di utilizzare la geometria e la posizione topografica degli oggetti cartografati e la codifica ad essi associata come attributi in base ai quali effettuare operazioni computerizzate di classificazione, di selezione, di calcoli statistici, ecc.. La cartografia numerica consente di utilizzare la cartografia come comune denominatore di riferimento nei sistemi informativi territoriali o in qualsiasi banca dati per i quali sia significativa la collocazione spaziale. La cartografia numerica considerata come prodotto finito, deve essere paragonabile a quello che, nella cartografia tradizionale, rappresenta il fotoinciso finale. Capitolo IX - Cartografia numerica pagina 291 R.Galetto A.Spalla - Lezioni di Topografia L'utente potrà poi, se vorrà, manipolare, modificare o ristrutturare la cartografia numerica che gli viene consegnata, per adattarla al tipo di gestione proprio del Sistema Informativo Territoriale (SIT) di cui costituisce il riferimento spaziale, ma tali eventuali interventi devono essere considerati estranei al processo produttivo. La cartografia numerica non è quindi semplicemente un archivio di dati numerici dai quali sono deducibili delle geometrie che opportunamente interpretate e ricomposte possono dar luogo ad entità a loro volta identificabili attraverso un sistema di codifica, ma ne costituiscono parte integrante anche tutti i dati, anch'essi formanti un archivio numerico, necessari a realizzarne la visualizzazione completa di linee speciali, campiture, simboli, toponomastica, ecc. sia su video-grafico che su supporto cartaceo mediante plottaggio. 1.1.3 Tipologia della cartografia numerica Per quanto riguarda la tipologia della cartografia numerica è imperativo che essa non sia correlata al metodo di produzione che porta a classificarla come cartografia numerica digitalizzata e cartografia numerica diretta. Un'impostazione corretta del problema deve invece prevedere una casistica articolata come nel seguito. • • • 1.2 Cartografia numerica solo planimetrica; in essa esiste solo gli elementi che sono caratteristici del contenuto planimetrico di una carta, che vengono dati attraverso le sole coordinate planimetriche. Cartografia numerica con planimetria e altimetria; è una carta numerica dove, analogamente a quanto avviene per la cartografia tradizionale, vi è una planimetria, descritta mediante coordinate soltanto planimetriche, e un'altimetria, consistente in punti quotati e curve di livello, descritta mediante le coordinate planimetriche e la quota. Cartografia numerica tridimensionale; in questo tipo di cartografia alle coordinate planimetriche di ogni punto che descrive particolari planimetrici viene associata anche la quota. Continua ad esistere anche l'altimetria tradizionale data mediante curve di livello e punti quotati. Ai punti che de scrivono particolari artificiali deve essere attribuita la quota al piede, cioè al livello del suolo, del particolare cui appartengono. Scala nominale Uno degli aspetti più fortemente innovativi, nel contesto della tradizione cartografica, è costituito dal fatto che per la cartografia numerica sembrerebbe superato il concetto di rapporto di scala, poiché, a meno del fattore di deformazione della proiezione cartografica adottata, il teorema di Pitagora applicato alle coordinate planimetriche di due punti ne dà direttamente la distanza topografica; il rilievo è cioè memorizzato in forma di coordinate assolute e perciò è sempre e comunque in scala 1:1. Sembrerebbe pertanto improprio parlare di scala di una carta numerica; tuttavia si ritiene che non si debba abbandonare questo riferimento soprattutto in considerazione del fatto che i dati Capitolo IX - Cartografia numerica pagina 292 R.Galetto A.Spalla - Lezioni di Topografia di cartografia numerica possono essere visualizzati, mediante plotter o su video grafici, con rimpicciolimenti ed ingrandimenti esasperati. Ciò significa che una cartografia numerica realizzata seguendo gli stessi canoni cartografici che porterebbero alla realizzazione di una carta tradizionale alla scala 1:2000, potrebbe essere facilmente visualizzata o portata a scale maggiori, ad esempio alla scala 1:500 o anche 1:200, e ingenerare nell'utente l'equivoco di possedere una precisione che invece non le è propria. L'utente invece deve avere chiaro il concetto che una cartografia numerica ha un contenuto di precisione metrico ben preciso, dovuto alle procedure di costruzione della carta, dettato dai canoni della fotogrammetria classica; pertanto pensare di acquisire maggiori informazioni operando su visualizzazioni a scale maggiori di quella nominale equivale all'errore dell'utilizzatore di cartografia tradizionale che crede di aumentarne il contenuto informativo e metrico facendone un ingrandimento fotografico. Si conviene pertanto che si debba mantenere il concetto di rapporto di scala anche per la cartografia numerica e che si debba intendere per rapporto di scala di una cartografia numerica quella che corrisponde al massimo rapporto di scala a cui si può riprodurre una carta numerica mediante plotter, in modo che essa abbia i requisiti qualitativi e metrici di una carta tradizionale avente la stessa scala. Anche per la cartografia numerica il rapporto di scala definisce quindi il grado di precisione metrica e il contenuto qualitativo. Per correttezza formale sarà tuttavia opportuno usare, per la cartografia numerica, il termine di scala nominale, intendendo con tale espressione il rapporto di scala che avrebbe una carta tradizionale di corrispondente precisione metrica e contenuto qualitativo. A parziale rettifica di quanto esposto in merito alle operazioni di ingrandimento della cartografia numerica in rapporti di scala superiori a quella nominale, conviene tuttavia prendere atto che la visualizzazione su video-grafico consente, o per meglio dire invoglia, a rappresentare la cartografia numerica a scala superiore a quella nominale; pertanto, fermo restando che ogni ingrandimento superiore alla scala nominale della carta deve essere considerato a rischio dell'utente, sarebbe tuttavia sbagliato considerare la visualizzazione su video-grafico ad una scala superiore a quella nominale alla stregua dell'esecrato ingrandimento fotografico della carta tradizionale; la facilità di produrre automaticamente su video-grafico o mediante plotter, visualizzazioni della cartografia numerica in rapporti di scala maggiori di quello nominale va vista come una ulteriore possibilità offerta dalla cartografia numerica per leggere non di più di quella che essa in effetti contiene, ma di leggerlo meglio. Capitolo IX - Cartografia numerica pagina 293 R.Galetto A.Spalla - Lezioni di Topografia 1.3 Caratteristiche del contenuto planimetrico e altimetrico della cartografia numerica 1.3.1 Il contenuto planimetrico L'utente della cartografia tradizionale, osservando la carta, individua entità che sono oggettivamente riportate nella carta stessa: riconosce una casa, una strada, altri particolari. Tuttavia il potere di analisi consentito dalla visione diretta della cartografia, gli consente anche di evincere altre informazioni: osservando ad esempio una pista aeroportuale, le recinzioni della zona aeroportuale, le infrastrutture dell'areoporto, ecc., l'utilizzatore è in grado di riconoscere tutta la zona che è asservita a questo particolare tipo di infrastruttura. E ancora: l'osservatore, guardando la carta può ricavare l'informazione dello spazio occupato da un nodo stradale, anche se un nodo stradale su una carta tradizionale è semplicemente uno spazio bianco, non contraddistinto da alcun segno particolare. E' il potere di aggregazione logica che deriva dalla consuetudine all'osservazione della carta a permettere all'utilizzatore di distinguere entità che in realtà sulla carta non sono rappresentate, ma che costituiscono la concretizzazione di concetti. Nella elaborazione della cartografia numerica mediante logiche programmate, questa componente dovuta all'osservazione dell'operatore non è più possibile. E' necessario perciò che le entità, riconoscibili nella utilizzazione tradizionale della cartografia grazie ad operazioni soggettive eseguite di volta in volta dall'operatore, vengano invece oggettivizzate come entità realmente esistenti e che sia associato ad esse un codice per permetterne il riconoscimento nel contesto generale. Per rifarsi all'esempio della struttura aeroportuale, oltre ad essere differenziabile la pista aeroportuale con un suo codice, l'areostazione, con un suo codice, deve anche essere evidenziato un perimetro come linea ideale, o come linea reale a seconda che esista o no una reale delimitazione dell'area aeroportuale, e la superficie delimitata da perimetro, ideale o reale, dovrà essere contraddistinto da un codice che definisce la tipologia "area aeroportuale". Per portare un altro esempio, nella memorizzazione di una realtà urbana, non sarà sufficiente dare i perimetri delle case o di quelle strutture superficiali che definiscono il perimetro di un isolato, ma per una corretta gestione della cartografia occorrerà che le strade, rappresentate nella cartografia tradizionale da spazi bianchi, siano opportunamente perimetrate e memorizzate, ad esempio secondo una struttura di tronchi e di nodi, dove appunto una sede stradale è un tronco, quando scorre tra un perimetro di due edifici, oppure un nodo in quelle zone in cui più strade si intersecano tra di loro. Occorre, in pratica, che tutte le superfici rappresentate nella cartografia siano in qualche modo sempre contraddistinte da un codice di tipologia. Così come un utente di cartografia tradizionale, se, con procedimento casuale, individua con la punta di una matita un punto della carta, non corrispondente ad alcun segno grafico, valutando la rappresentazione dei particolari che sono in un intorno di questo punto, riesce a stabilire che esso appartiene ad esempio ad un'area a seminativo, o ad un bosco, oppure che questo punto è interno ad un edificio, così pure l'utente della cartografia numerica, considerando un punto individuato da una coppia di coordinate casuali, deve poter ricavare come informazione diretta e non come risultato di Capitolo IX - Cartografia numerica pagina 294 R.Galetto A.Spalla - Lezioni di Topografia un'elaborazione, il dato di appartenenza di questo punto ad una superficie codificata rispettivamente con un codice di limite di coltura agraria a seminativo, ovvero con un codice di limite di bosco o ancora, per seguire l'esempio portato per la carta tradizionale, con un codice di edificio. In altri termini si può dire che nella cartografia numerica non debbono esistere superfici non codificate. Mentre cioè la carta tradizionale è costituita riportando segni grafici di tipo puntuale, lineare ed areale su uno sfondo bianco, nella cartografia numerica non può esistere uno sfondo non codificato; le entità puntuali e lineari potranno essere interne ad entità areali o coincidere con i vertici o il perimetro di esse, ma non potranno appartenere o intersecare uno sfondo non codificato. 1.3.2 Contenuto altimetrico della cartografia. Come già visto al paragrafo 1.1.2, un elemento fortemente caratterizzante della cartografia numerica è la possibilità che essa offre di superare la divisione fra il dato planimetrico e il dato altimetrico. Infatti utilizzando una carta tradizionale si possono ricavare con operazioni di misura relative alla parametratura le coordinate planimetriche di tutti i punti della carta; per ricavare invece la quota di un generico punto è necessario ricorrere a procedimenti di interpolazione che forniscono il dato quota in funzione delle informazioni altimetriche rappresentate dai punti quotati e dalle curve di livello. Nella cartografia numerica invece il contenuto altimetrico può essere costituito da quattro categorie di entità: • punti quotati, intesi nell'usuale significato cartografico; • curve di livello; • quota di ogni punto di descrizione di particolari planimetrici naturali o artificiali; • quota delle unità volumetriche alla linea di gronda, intendendosi per unità volumetrica di un edificio ogni parte dell'edificio omogenea dal punto di vista della quota di gronda. Non ci soffermeremo nel seguito sulla descrizione delle categorie punti quotati e curve di livello perché la definizione di quali punti del territorio debbano essere quotati (centri di incroci, piazze, cortili, infrastrutture viarie, ecc.) e di come debbano essere realizzate le curve di livello rientra nei canoni della Cartografia classica. Si ritiene invece opportuno sottolineare i contenuti delle altre due categorie, perché peculiari della cartografia numerica. Quote dei punti di descrizione di particolari planimetrici I punti che costituiscono la cartografia numerica sono memorizzati nella banca dati con una quadrupletta di numeri e cioè: un codice e le tre coordinate E,N,q del punto. Sia che il particolare planimetrico abbia oppure no estensione in altezza, la quota dei punti che lo descrivono nella cartografia numerica deve essere quella del terreno. Ad esempio i punti che descrivono l'andamento planimetrico di una struttura artificiale che si estende in altezza al di sopra del piano di calpestio, (ad esempio. il perimetro di un edificio, un Capitolo IX - Cartografia numerica pagina 295 R.Galetto A.Spalla - Lezioni di Topografia muro, ecc.) deve essere attribuita la quota al piede della struttura, cioè quella che corrisponde all'intersezione della struttura con il piano di calpestio ad essa adiacente. Questa regola ammette alcune eccezioni; per esempio: per tralicci e pali della luce dovrà essere data la quota al piede, mentre all'entità che definisce la linea elettrica da essi portata, dovrà essere associata la quota propria della linea stessa. Quota di gronda delle unità volumetriche. Ad ogni unità volumetrica deve essere attribuita la quota della linea di gronda; tale informazione può essere costituita da un'entità puntuale avente coordinate planimetriche interne al perimetro dell'unità volumetrica e quota uguale alla quota della linea di gronda. A chiarimento di quanto sopra esposto si propongono i seguenti esempi. figura 1 Esempio di contenuto planimetrico e altimetrico proprio della cartografia numerica Nella figura 1, la quota del punto 1 sarà la quota del suolo al livello A; la quota del punto 2 sarà la quota del punto B. Ugualmente i punti 3 e 4 avranno come quota la quota del punto B. La quota di gronda dell'edificio sarà la quota di A+H; la quota di gronda del box sarà la quota di B+h. La quota del punto 5, piede del muro, sarà la quota del punto C. I punti 6,7,8 e 9 che descrivono il perimetro del traliccio avranno la quota del punto C; il punto centrale avrà la quota della linea elettrica (C+L). L'edificio rappresentato in figura 2 dovrà essere memorizzato nella cartografia numerica con quattro entità: il perimetro totale P dell'intero edificio, che non avrà quota di gronda e il perimetro delle tre unità volumetriche A, B, C con le rispettive quote di gronda. La quota dei vertici delle spezzate chiuse che rappresentano i quattro perimetri sarà pari alla quota al suolo (160.2 nell'esempio in figura 2). Capitolo IX - Cartografia numerica pagina 296 R.Galetto A.Spalla - Lezioni di Topografia figura 2 Suddivisione di un edificio in unità volumetriche. 1.4 Funzione del sistema di codifica Solo l'attribuzione di un codice ad ogni entità memorizzata nella cartografia numerica, può consentire all'utente la possibilità di una sua lettura, oltre che per osservazione diretta della sua visualizzazione, anche con elaborazioni effettuate mediante calcolatore elettronico. Lo studio e la scelta del sistema di codifica sono quindi momenti essenziali nella costruzione della cartografia numerica perché l'articolazione del sistema di codifica ne definisce il contenuto qualitativo. Per creare un sistema di codifica occorre innanzitutto stabilire l'elenco degli oggetti che si vogliono tenere differenziati nell'ambito della cartografia numerica . Per fare questo, tenuto conto della scala nominale della cartografia numerica ci si può ricondurre allo stesso tipo di differenziazione degli oggetti che viene fatto in una cartografia tradizionale di pari scala. Poiché, come esposto in premessa, ci si riferisce fondamentalmente a cartografia numerica a grande scala nominale, l'elenco degli oggetti che devono essere tenuti differenziati può essere desunto dai capitolati redatti a suo tempo dalla Commissione Geodetica Italiana per le cartografie tradizionali appunto a grande scala. In tali capitolati sono descritte le norme tecniche da seguire per la realizzazione di lavori di cartografia e sono riportati gli elenchi dei contenuti qualitativi che le carte devono assicurare. Questi elenchi suddividono per grandi categorie, come idrografia, orografia, edificato, ecc, tutti gli oggetti che devono essere rappresentati nella cartografie. Essi possono quindi venire assunti come elenchi degli oggetti cartografici che devono essere tenuti differenziati nella cartografia numerica; in particolare si può mantenere valida la suddivisione esistente in grandi categorie. Capitolo IX - Cartografia numerica pagina 297 R.Galetto A.Spalla - Lezioni di Topografia Effettuata questa prima operazione di definizione dei contenuti, integrando eventualmente gli elenchi citati per tener conto delle considerazioni esposte nei paragrafi precedenti, si passa alla successiva fase di scelta del tipo di codice da attribuire a ciascun oggetto cartografico. I codici possono essere di tipo alfanumerico o numerico, con lunghezza fissa o variabile. Generalmente negli strumenti restitutori per produzione di cartografia numerica, sia analitici, sia analogici encoderizzati, viene riservato al codice un campo costituito da un numero di caratteri fisso; in molti strumenti questo campo è di 8 caratteri. Dovendo rispettare il vincolo della lunghezza fissa del codice, per avere comunque un sistema di codifica flessibile, che consenta di realizzare selezioni sugli oggetti cartografati in funzione delle categorie cui afferiscono, è opportuno adottare codifiche che si basano su articolazioni ad albero Vediamo come le 8 cifre di un codice possano essere sfruttate per creare una codifica con strutturazione ad albero in modo tale cioè che le prime due cifre del codice indichino l'appartenenza dell'oggetto a una delle grandi categorie cui prima si è fatto riferimento, le seconde due cifre del codice indichino la tipologia dell'oggetto, e le altre cifre del codice specifichino maggiormente la tipologia dell'oggetto nell'ambito di una determinata classe. A scopo illustrativo si consideri la figura 3; in essa è rappresentata un'area aeroportuale con delle strutture tipiche di essa e cioè le piste, gli edifici dell'aerostazione, il perimetro della zona aeroportuale ecc. Come si vede un tipo di codifica numerica strutturata secondo un codice di 8 cifre potrebbe prevedere che appunto con il primo gruppo di 2 cifre 03 si indichi la grande categoria costituita da edifici e costruzioni, che il secondo gruppo di due cifre 05, indica che nell'ambito della categoria edifici e costruzioni la sottocategoria costruzioni speciali che il terzo gruppo di 2 cifre 05 indica che i, nell'ambito della sottocategoria costruzioni speciali l'ulteriore sottocategoria aeroporti e che l'ultimo gruppo di 2 cifre serva a differenziare nel dettaglio gli oggetti afferenti alla categoria aeroporti. codifica 03****** 0305**** 030505** definizione EDIFICI E COSTRUZIONI costruzioni speciali areoporti 03050501 03050502 03050503 03050504 perimetro di areoporto edifici areoportuali piste di decollo assi delle piste di decollo rappresentazione grafica 03050503 03050504 03050502 03050501 figura 3 Capitolo IX - Cartografia numerica pagina 298 R.Galetto A.Spalla - Lezioni di Topografia Esempio relativo ai tipi di oggetti da memorizzare per descrivere compiutamente un aeroporto. sono stati completati con asterischi i codici che non possono essere associati a nessuna entità in quanto incompleti. 2 Metodi di produzione Esistono tre differenti metodi per produrre cartografia numerica: • mediante rilievo diretto sul terreno con strumentazione topografica; • mediante restituzione fotogrammetrica diretta; • mediante digitalizzazione di cartografia esistente. In questo capitolo non si descriverà la produzione di cartografia in forma numerica mediante rilievo diretto sul terreno con strumentazione topografica perché dell’argomento si è già trattato al capitolo V. 2.1 Metodo fotogrammetrico numerico diretto La realizzazione di cartografia numerica con metodo fotogrammetrico numerico diretto differisce sostanzialmente dalla realizzazione mediante restituzione fotogrammetrica di cartografia tradizionale, in quanto i particolari naturali e artificiali, che vengono desunti dalla osservazione stereoscopica delle fotografie aeree e acquisiti per far parte della cartografia, vengono acquisiti direttamente in forma numerica. Per quanto riguarda quindi la fase di presa, di inquadramento e determinazione di punti di appoggio dei modelli, non vi è differenza fra realizzazione di cartografia numerica o cartografia tradizionale. La differenza subentra nel momento in cui si attua la fase di restituzione. Innanzi tutto devono essere utilizzati strumenti in grado di memorizzare su memorie di massa le coordinate dei punti via via collimati e quindi: o strumenti di tipo analitico, oppure strumenti analogici encoderizzati. Per quanto attiene il dato che viene acquisito in restituzione, questo può essere: la traduzione numerica del dato di tipo tradizionale, se viene richiesta un cartografia solo planimetrica, oppure planimetrica con altimetria, ma nella quale comunque gli elementi della planimetria vengono tenuti distinti da quelli dell'altimetria, come avviene per la cartografia tradizionale; il dato cartografico tridimensionale, quando si richiede che per ogni punto cartografato siano memorizzate, oltre che le coordinate planimetriche, anche la quota. Nel primo caso avremo l'acquisizione degli elementi della planimetria mediante le sole coordinate x,y e degli elementi plano-altimetrici (punti quotati e curve di livello) mediante coordinate x,y a cui viene associato il valore z della quota. Nel secondo caso invece, in cui si richiede che la cartografia numerica sia di tipo tridimensionale, la coordinata z, dovrà essere acquisita per tutti i punti che concorrono alla determinazione di tutti i particolari planimetrici. Durante la fase di restituzione l'operatore può seguire il procedere del suo lavoro in due modi diversi: Capitolo IX - Cartografia numerica pagina 299 R.Galetto A.Spalla - Lezioni di Topografia • • se associato allo strumento restitutore c'è un tavolo tracciatore, può essere prodotta, in linea alla restituzione, una minuta di tipo tradizionale; se allo strumento restitutore è associato un video grafico, la cartografia numerica può essere direttamente visualizzata sul video in funzione delle coordinate che vengono via via memorizzate sulle memorie di massa e che costituiranno l'archivio della restituzione numerica. Nel caso in cui la restituzione fotogrammetrica numerica diretta avvenga con l'ausilio di video grafico e senza la produzione di una vera e propria minuta di restituzione, dovrà comunque essere ricavato dal dato numerico, mediante tracciamento automatico al plotter, un elaborato grafico a documentazione della restituzione che dovrà essere utilizzato per la ricognizione e anche per costituire un documento sul lavoro eseguito, qualora richiesto dai capitolati con cui vengono affidati i lavori. Le differenze però fra cartografia tradizionale e cartografia numerica che hanno maggiori implicazioni di natura operativa sono sostanzialmente le seguenti. • • • Il restitutista che realizza cartografia numerica deve attribuire un codice ai vari oggetti cartografici che via via osserva stereoscopicamente e memorizza. Questa operazione di attribuzione di codifica, che è peculiare della cartografia numerica, può essere realizzata, all'atto della restituzione già in maniera, oppure può essere parziale: in tal caso verrà definitivamente completata durante la fase di editing. La scelta di impiegare più tempo al momento della restituzione per codificare tutti gli elementi restituiti, o di demandare alla fase di editing questa operazione, dipende dalla organizzazione operativa della ditta esecutrice dei lavori. Il restitutista deve tenere presente che la cartografia numerica realizzata con il suo lavoro di restituzione, è costituita da archivi di dati che hanno una loro strutturazione. Per poter fornire le entità che rappresentano nella cartografia numerica gli oggetti cartografici, eseguirà la fase di restituzione applicando dei criteri logici che in generale, nella produzione della restituzione fotogrammetrica avente lo scopo di produrre cartografia tradizionale, non sono necessari. Infatti, mentre nella cartografia tradizionale la restituzione può avvenire passando continuamente da un tipo di particolare a un altro senza porre attenzione a ricostruire oggetti cartografici completi, nella cartografia numerica si cercherà, anche in restituzione, di ricostruire nella loro interezza questi oggetti cartografici, in modo da ridurre al minimo le operazioni di editing necessarie al perfezionamento questo tipo di strutturazione dei dati. Quando si deve produrre una cartografia numerica tridimensionale il restitutista cerca di determinare in sede di restituzione la quota la piede del maggior numero di particolari naturali e artificiali che deve restituire. Infatti mentre nella cartografia tradizionale i particolari planimetrici vengono riprodotti soltanto secondo la loro planimetria e quindi possono essere collimati, al momento della restituzione, a una quota anche arbitraria, (si consideri il caso tipico in cui si percorre il perimetro di una casa secondo la linea di gronda e non secondo la linea al piede), in una cartografia numerica tridimensionale occorrerà porre particolare cura per cercare di individuare la corretta quota dei punti restituiti. Capitolo IX - Cartografia numerica pagina 300 R.Galetto A.Spalla - Lezioni di Topografia • In una cartografia numerica tridimensionale tutte le strutture artificiali devono essere date con la loro quota la piede: a ogni punto deve cioè essere associata la quota del piano di calpestio che è la quota del punto di distacco della struttura artificiale dal suolo. Molti punti non possono essere collimati al suolo perché, a causa dell'effetto prospettico dei fotogrammi, non sono visibili stereoscopicamente. All'impossibilità di determinare in restituzione la quota di tali punti si può ovviare: • • determinando le quote mancanti in sede di ricognizione, applicando particolari accorgimenti operativi, uno dei quali può consistere nel restituire punti al livello del suolo che siano prossimi al punto di cui non si vede la quota la piede; successivamente in fase di editing al punto sarà attribuita una quota determinata in funzione delle quote dei punti restituiti appositamente per questo scopo. Un'ulteriore differenza che si può riscontrare nella fase di restituzione tra la produzione della cartografia tradizionale e quella della cartografia numerica fotogrammetrica diretta, è che, quando la cartografia numerica viene realizzata utilizzando strumenti dotati di dispositivi di superimposizione, l'operatore può essere facilitato nell'eseguire il lavoro di restituzione poiché ha un confronto diretto fra ciò che è già stato acquisito e ciò che deve essere acquisito per costituire la cartografia finale . Finora sono state esaminate le implicazioni di natura operativa causate, sulla fase di restituzione fotogrammetrica, dal dovere realizzare cartografia numerica anziché cartografia tradizionale. Esaminiamo ora il prodotto della restituzione numerica fotogrammetrica. Il prodotto della restituzione numerica diretta è un file di dati strutturato in maniera semplice: è un file a record fissi dove ciascun record ha generalmente non più di cinque campi. Un campo è riservato al codice, tre campi sono necessari per la memorizzazione della coordinate x,y,z; un ulteriore campo è talvolta riservato alla memorizzazione del tipo di operazione eseguita in restituzione. Devono infatti essere dati dei criteri per far comprendere quando una sequenza di record si riferisca ad un'unica entità e quando questa sequenza di record debba ritenersi interrotta perché inizia la descrizione di una nuova entità. Vi sono diversi modi di dare questa informazione, uno dei più diffusi consiste nel restituire due volte l'ultimo punto di un entità, memorizzandone quindi due volte le coordinate; quando però è disponibile nella struttura dei record l'ulteriore campo riservato al codice numerico , in questo campo possono venire memorizzati valori diversi per indicare appunto l'inizio di una nuova entità, la sua tipologia e altro. Come nella realizzazione di cartografia tradizionale, anche nella realizzazione di cartografia numerica, dopo aver eseguito la fase di restituzione di dovrà procedere alla fase di ricognizione; questa viene svolta secondo criteri tradizionali, avendo però cura di porre particolare attenzione all'aspetto altimetrico qualora la cartografia sia di tipo tridimensionale. Successivamente si procederà alla correzione della cartografia numerica per tener conto dei risultati della ricognizione. Queste operazioni di inserimento della cartografia numerica vengono eseguite generalmente contestualmente alla fase di editing, nella quale oltre all'inserimento delle integrazioni di ricognizione , vengono anche eseguite le operazioni di correzione delle congruenze geometriche, di inserimento della toponomastica e di completamento del sistema di codifica. I dati della ricognizione potranno essere inseriti direttamente grazie a opportuni so- Capitolo IX - Cartografia numerica pagina 301 R.Galetto A.Spalla - Lezioni di Topografia ftware che gestiscono il sistema grafico, oppure potranno essere riportati in maniera tradizionale sulla minuta di restituzione e rinumerizzati mediante procedimento di digitalizzazione. 2.2 Digitalizzazione di cartografia esistente La digitalizzazione di una carta si realizza, nella maggior parte dei casi, con il digimetro che è uno strumento misuratore di coordinate gestito da un calcolatore elettronico. Il digimetro è costituito da: • • un tavolo elettronico su cui si dispone la carta da digitalizzare; un organo per la collimazione del punto da memorizzare; tale organo viene chiamato cursore ed è costituito da una lente su cui è inciso un reticolo per la collimazione e da una tastiera; premendo i tasti della tastiera vengono inviate al calcolatore: • • • le coordinate del punto posto sotto il centro del reticolo inciso sulla lente di collimazione; un codice di indicazione del tipo di tasto premuto sulla tastiera; una linea che consente la trasmissione delle coordinate e della codifica del punto collimato al calcolatore che memorizza le informazioni provenienti dal digimetro in un'opportuna banca di dati. Nella pratica operativa la digitalizzazione avviene come descritto nel seguito. • • • L'operatore posiziona la carta sul digimetro collegato al calcolatore e dà l'avvio al programma che consente al calcolatore la gestione del digimetro. La prima operazione prevista da qualsiasi software di digitalizzazione di carte è l'operazione di orientamento della carta. L'operatore per attuare questa operazione collima alcuni punti sulla carta di cui siano note le coordinate-carta e ne misura le relative coordinate nel sistema di riferimento del digimetro; quindi imposta, al calcolatore, le corrispondenti coordinate carta al fine di calcolare i parametri di corrispondenza fra il sistema digimetro e il sistema carta. A seconda dell'architettura di memorizzazione dei dati che il software di gestione realizza, l'operatore viene guidato a collimare quei punti che devono essere memorizzati e ad impostarne le relative codifiche. Volendo fare un esempio, possiamo descrivere come potrebbe avvenire la digitalizzazione di una carta eseguita al fine di realizzare una banca di dati. Il software di gestione dovrà prevedere l'esecuzione delle fasi operative nel seguito elencate. • • Fase preliminare di calcolo dei parametri di orientamento della carta. Richiesta della codifica dell'entità da digitalizzare. L'operatore potrà comunicare la risposta al calcolatore impostandola o dalla tastiera del calcolatore o dalla tastierina del cursore oppure digitalizzando un punto su quello che si definisce menu. Capitolo IX - Cartografia numerica pagina 302 R.Galetto A.Spalla - Lezioni di Topografia Il menu è una zona del digimetro riservata, sulla quale non viene disposta la carta: questa zona è divisa in caselle e ad ogni casella si fa corrispondere, da software, una risposta particolare; quando l'operatore, per rispondere ad una domanda che gli viene posta dal programma, digitalizza un punto appartenente ad una casella del menu, il programma di gestione individua che le coordinate del punto che gli vengono inviate non sono di un punto della carta, ma appartengono alla zona riservata e, in particolare, a quella certa casella per la quale è già stata memorizzata una precisa risposta. Impostare da menu le risposte ai programmi di gestione consente una discreta economia di tempo all'operatore. • Fase di collimazione dei punti che descrivono il perimetro dell'entità in esame. L'operatore, guidato dal software di gestione, digitalizza i punti secondo la logica prevista dal programma, ad esempio percorrendo il perimetro in senso orario e richiudendo il perimetro sul punto iniziale: un sistema di contatori provvederà ad attribuire ad ogni punto la sua codifica e opportuni test sui valori delle coordinate, indicheranno quali punti siano già stati digitalizzati e quindi non debbano essere memorizzati più volte. Con questo metodo di digitalizzazione, all'atto della numerizzazione vera e propria, possono essere eseguite anche altre operazioni, e cioè: • • • si seleziona ciò che si vuole digitalizzare, cioè si numerizza solo ciò che deve essere inserito nella banca dati topografici; si può procedere contemporaneamente alla strutturazione della banca dati poiché si associano le codifiche dell'oggetto digitalizzato alle coordinate dei punti atti a descriverlo, individuando al tempo stesso quali siano questi punti; si può già dare un ordine logico ai punti che descrivono un oggetto in modo che la sua geometria resti definita. Altre caratteristiche del metodo sono il basso costo dello strumento e il breve tempo di addestramento necessario per la formazione degli operatori. L'operazione di digitalizzazione di tipo manuale ha come svantaggio il fatto di non essere, o almeno di non apparire, veloce; questo avviene perché spesso si confonde l'operazione di trascrizione di una carta in banca dati, con una sola delle sue fasi e cioè appunto la digitalizzazione; se però consideriamo l'insieme delle operazioni che l'operatore compie e non solo la digitalizzazione, possiamo dire che il metodo manuale non è così lento come potrebbe apparire, quando lo si confronta con il metodo a inseguimento di linee e con il metodo automatico che verranno descritti nei prossimi paragrafi. 3 Intervento sui dati 3.1 Editing cartografico Quale che sia la fonte dei dati della cartografia numerica, sia cioè che venga realizzata con metodo topografico classico, o per restituzione numerica diretta o per digitalizzazione di Capitolo IX - Cartografia numerica pagina 303 R.Galetto A.Spalla - Lezioni di Topografia cartografia esistente, il prodotto che viene realizzato è sempre costituito da uno o più file di dati opportunamente strutturati. Su tali dati devono essere possibili interventi di varia natura, che si definiscono interventi di editing cartografico. Un editing cartografico generalizzato deve prevedere le seguenti funzioni: • correzione di errori grossolani commessi in acquisizione; • integrazione con eventuali dati di aggiornamento; • pulizia dei dati di acquisizione e di aggiornamento mediante ricostruzione delle congruenze geometriche. • inserimento della toponomastica e degli elementi di vestizione, • ecc. Per chiarire che cosa significhino le funzioni suddette, consideriamo ad esempio il caso della cartografia numerica prodotta per restituzione fotogrammetrica diretta. L'editing cartografico sui dati di restituzione numerica diretta deve permettere la realizzazione di tutte quelle operazioni di correzione che nella restituzione fotogrammetrica tradizionale vengono attuate sulla minuta di restituzione e nella fase di ridisegno finale della carta. Sulla minuta di restituzione infatti vengono riportate sia le correzioni di errori grossolani commessi in restituzione, sia i dati di ricognizione e di aggiornamento. Successivamente alla fase di restituzione viene infatti effettuata, una ricognizione sul terreno per valutare se l'interpretazione del restitutista sia stata corretta e per rilevare eventuali dati di aggiornamento; i dati acquisiti vengono riportati sulla minuta di restituzione. Il disegnatore cartografico eseguendo il ridisegno finale della carta: • darà la stessa veste grafica ai particolari di restituzione, di ricognizione e di aggiornamento; • nei limiti dello spessore del tratto grafico (0.2 mm), ricostruirà la continuità geometrica di entità a sviluppo lineare ( realizzerà ad esempio con un unico segmento il disegno di uno stesso bordo stradale restituito con due segmenti consecutivi i cui estremi distino meno di 0.2 mm sulla carta); • saprà valutare se rappresentare come perfettamente rettangolari poligoni che sulla minuta di restituzione lo sono solo approssimativamente; • saprà valutare se rappresentare come rigorosamente parallele linee che sulla minuta di restituzione lo sono solo approssimativamente; • saprà valutare se spezzate aperte debbano essere effettivamente tali o se non lo siano perché il restitutista ha dimenticato di tracciare un lato; • ecc. Per mantenere il parallelo che è stato ipotizzato fra le operazioni sopra descritte e gli interventi sui file di restituzione, l'operatore alla stazione grafica dovrà effettuare le operazioni nel seguito descritte. • Individuazione degli errori propri della restituzione numerica diretta che nella maggior parte dei casi sono: • errori nell'attribuzione del codice di una data entità; • omissioni di segnalazione di fine di un'entità. Capitolo IX - Cartografia numerica pagina 304 R.Galetto A.Spalla - Lezioni di Topografia Mentre il riscontro degli errori del secondo tipo è generalmente agevole (in quanto la mancanza di segnalazione della fine di un'entità ne determina di solito automaticamente la visualizzazione perché viene unita all'entità successiva mediante uno spostamento a "penna giù" ), l'esame della congruenza dei codici impostati non è immediato. Con elaborazioni batch è possibile stabilire se siano stati attribuiti alle entità solo codici presenti in elenchi e tabelle di definizione; per entità di codici particolari potranno anche essere fatte altre verifiche, sempre batch ( ad esempio le serie di punti, con il codice corrispondente a fabbricato e che descrivono una stessa entità, dovranno essere tali da realizzare graficamente poligoni chiusi). Tuttavia solo una visione selettiva delle entità relative ai singoli codici potrà fornire il mezzo di individuazione di eventuali errori di codifica. • • 3.2 Riporto dei dati di ricognizione e di aggiornamento Ricostruzione delle congruenze geometriche con procedure in parte batch in parte di tipo interattivo. Stazioni grafiche interattive 3.2.1 Funzionalità Le funzioni descritte al paragrafo precedente sono realizzabili mediante le stazioni grafiche interattive. Dal punto di vista dell' hardware, una stazione grafica interattiva atta a realizzare i diversi tipi di interventi necessari per dell'editing cartografico, deve essere costituita, nella sua configurazione minima da: • un calcolatore; • unità hard_disk; • un video grafico di alta risoluzione, a colori, per facilitare l'individuazione di entità con codici diversi; • una tavoletta grafica; • un digimetro per l'acquisizione dei dati di aggiornamento; • un plotter; • una stampante. Il software di gestione deve essere particolarmente dedicato a problemi di tipo cartografico, data la loro estrema specificità. Tale software dovrà essere composto di programmi di elaborazione di tipo batch e programmi di elaborazione di tipo interattivo. Il software di tipo propriamente interattivo dovrà riportare sullo schermo grafico la rappresentazione della cartografia memorizzata e guidare l'operatore nella ricerca e nella correzione delle incongruenze geometriche e degli errori visualizzati. Nella maggior parte dei casi queste operazioni di ricerca e di correzione si svolgono come descritto nel seguito. Capitolo IX - Cartografia numerica pagina 305 R.Galetto A.Spalla - Lezioni di Topografia • • L'operatore stabilisce la zona di cui vuole la rappresentazione sullo schermo e, se il software lo prevede, sceglie se preferisce operare sulla totalità dei dati memorizzati per la zona prescelta, o se selezionare entità di codici particolari, ad esempio solo edifici, solo viabilità, ecc. L'operatore esplora sistematicamente quanto viene visualizzato sullo schermo; • • • • se trova errori o incongruenze, seleziona sul menu, posto sulla tavoletta grafica, la unzione o le funzioni necessarie ad eseguire la correzione; a seconda della funzione attivata mediante il menu, il software di gestione guida l'operatore nell'esecuzione delle operazioni elementari necessarie alla correzione; eseguite queste operazioni, i dati corretti vengono memorizzati nell'archivio; l'operatore passa all'esame di altre entità a codici particolari o all'esame di un'altra zona. Le funzionalità di un software dedicato al trattamento post restituzione della cartografia numerica sono in generale le seguenti: • modifiche di codici; • traslazione di vertici; • squadratura di un singolo angolo formato da due segmenti; • squadratura per un'intera spezzata, aperta o chiusa, di tutti gli angoli prossimi, entro una certa tolleranza, ad angoli retti; • modifica di una spezzata, aperta o chiusa, per spostamento di uno o più vertici o per aggiunta di uno o più lati; • realizzazione di condizioni di parallelismo tra segmenti di entità diverse; • infittimento dei vertici di una spezzata mediante operazioni di spline; • realizzazione di congruenze geometriche mediante operazioni che ricostruiscono la continuità fra spezzate interrotte nelle zone di riattacco tra modelli fotogrammetrici; • operazioni di integrazione della restituzione mediante la creazione di punti ottenuta con l'inserimento diretto delle misure effettuate in sede di ricognizione; • inserimento della toponomastica; • completamento della cartografia numerica con tutti gli elementi di vestizione necessari a produrre gli elaborati grafici da essa derivati; • ecc. Le operazioni interattive di editing vengono effettuate visualizzando la cartografia numerica sul video grafico, catturando le entità da correggere e applicando ad esse una o più delle funzioni sopra elencate. Per dare un'idea di come sia possibile realizzare una procedura di questo tipo diamo una descrizione molto semplice e schematica di due operazioni che stanno alla base delle procedure interattive e cioè la visualizzazione della cartografia numerica su un video grafico e la cattura di un'entità. Per questa descrizione prendiamo in considerazione una configurazione hardware in cui al calcolatore, che supponiamo di tipo personal evoluto, sia collegata una tavoletta digitalizzatrice. Capitolo IX - Cartografia numerica pagina 306 R.Galetto A.Spalla - Lezioni di Topografia La tavoletta è, a tutti gli effetti, un piccolo digitizer, e cioè trasmette in ogni istante al calcolatore le coordinate u, v dell'organo di collimazione ad essa collegato, purché esso venga mantenuto nell'area utile della tavoletta (figura 4); l'organo di collimazione può essere l'incrocio di un reticolo. figura 4 - Principio di utilizzazione di una tavoletta grafica. Le tavolette di più comune impiego sono di 12" (circa 30cm x 30 cm) di area utile e sono connesse in linea al calcolatore. L'elettronica della tavoletta fornisce in ogni istante le coordinate dell'organo di collimazione in un sistema di riferimento u, v. La zona utilizzabile della tavoletta è divisa in due parti: una è dedicata al menu di funzioni possibili, l'altra serve a emulare sul video gli spostamenti dell'organo di collimazione. E' possibile mettere in corrispondenza la posizione dell'organo di collimazione della tavoletta nel sistema di riferimento u, v, con un punto sul video-grafico nel sistema x, y; il punto sul video-grafico che corrisponde all'organo di collimazione della tavoletta è materializzato con una figura geometrica opportuna, che chiamiamo cursore. Il cursore può essere una piccola crocetta o una freccetta o altro. Il cursore consente di prendere in considerazione un'entità geometrica presente sul videografico; ciò avviene portando il cursore in prossimità dell'entità considerata ed attivando la funzione di cattura che verrà più avanti descritta. Le traslazioni del cursore sul video per effettuare l'operazione di cattura vengono realizzate mediante le traslazioni dell'organo di collimazione sulla tavoletta. Perché ciò sia possibile, la posizione dell'organo di collimazione viene trasmessa al calcolatore con frequenza elevata e continua o, come si dice, in real-time, per cui ad ogni cambiamento di posizione dell'organo di collimazione sulla tavoletta, il calcolatore corrispondentemente sposta il cursore sul video. La zona del menu è divisa in varie caselle, su ognuna delle quali è raffigurato un simbolo indicante una funzione grafica interattiva: posizionando l'organo di collimazione della tavoletta su una casella e dando un opportuno comando, il programma esegue la funzione corrispondente alla casella su cui si trova l'organo di collimazione.. Capitolo IX - Cartografia numerica pagina 307 R.Galetto A.Spalla - Lezioni di Topografia Anche il video è diviso in due zone: una parte dedicata alla grafica nella quale compare il disegno e può essere spostato il cursore, ed un'altra parte dedicata ai messaggi diretti dal calcolatore all'operatore o all'introduzione dei dati da parte di quest'ultimo. Se il video del calcolatore è grafico, è possibile mettere in corrispondenza un generico punto P dalle coordinate numeriche con un punto P' del piano x, y di punti illuminabili del video. Se ad esempio il video ha una risoluzione di 1280x1024 punti, ciò significa che la superficie del tubo catodico può essere considerata come un'area rettangolare i cui punti sono definiti in un sistema x, y, dove la coordinata x varia, per valori interi, da 0 a 1280 e la coordinata y varia, per valori interi, da 0 a 1024. Indichiamo con Emin, Nmin, Emax, Nmax le coordinate dei due vertici opposti del rettangolo che inscrive tutti i punti che costituiscono la cartografia numerica, e supponiamo di volerli rappresentare tutti sul video-grafico. (figura 5). N Emax Nmax Zona rilevata Emin Nmin E O figura 5 - Rettangolo di inscrizione di una zona rilevata Se la risoluzione del video-grafico è, come ipotizzato, di 1280x1024 N − N min 1024 si pone L = max per N Max − N min ) > ⋅ ( E Max − E min ) ( 1024 1280 oppure E -E 1024 si pone L = max min per N Max − N min ) < ⋅ ( E Max − E min ) ( 1280 1280 Quindi si calcolano le coordinate di ogni punto della cartografia numerica nel sistema di riferimento x, y del video con le relazioni: x = valore intero di (Ei-Emin) x L y = valore intero di (Ni-Nmin) x L Illuminando i pixel corrispondenti alla coppia di coordinate x, y di tutti i punti si ha la visualizzazione sul video di tutti i punti che costituiscono la cartografia numerica. Capitolo IX - Cartografia numerica pagina 308 R.Galetto A.Spalla - Lezioni di Topografia E' possibile, con istruzioni di programma molto semplici, far si che, se due punti devono essere congiunti con un segmento, vengano illuminati tutti i pixel che congiungono i corrispondenti punti sul video; in tal modo si ottiene la rappresentazione della cartografia numerica sul videografico. 3.2.2 Generalità sulle configurazioni hardware Per effettuare le operazioni descritte ci si può affidare a configurazioni hardware diverse. Il mercato della strumentazione dedicata al CAD/CAM, cioè al trattamento di dati grafici mediante calcolatore, è estremamente sviluppato e possono essere reperite strumentazioni di capacità molto differenziate che hanno come cuore del sistema sia calcolatori di piccola potenza, sia calcolatori di grande potenza. Un ulteriore elemento di differenziazione per le stazioni grafiche interattive, disponibili oggi sul mercato, è costituito dalle caratteristiche del video grafico di cui la stazione è dotata. Il trattamento di un disegno da video è infatti tanto più agevole e più immediato quanto maggiore è la risoluzione del video. Il video deve quindi garantire almeno una risoluzione di 1024 per 780 punti; la risoluzione ottimale potrebbe essere 1280 per 1024 punti. Oltre al grado di risoluzione, un'altra caratteristica importante è costituita dal fatto che il video sia consentito l'uso di molti colori. Infatti un elemento identificativo fondamentale delle entità che costituiscono un archivio di dati, che traduce numericamente un prodotto cartografico, è costituito dal sistema di codifica che viene utilizzato per separare, in livelli diversi, i vari oggetti che vengono rappresentati. Questa rappresentazione risulta ovviamente potenziata se avviene attraverso colori differenti che guidano l'operatore nella fase di intervento su entità a codice diverso. La gestione di un video grafico ad elevata risoluzione a colori richiede peraltro calcolatori di elevata potenza e componenti hardware dedicate alla gestione del video grafico. A causa della rapida evoluzione che caratterizza tutto il settore della strumentazione informatica, e particolarmente quello dei calcolatori elettronici compresi nella fascia dei personal computer e delle work-station, non si ritiene utile dare delle configurazioni standard per le stazioni hardware per l'edit della cartografia numerica. Infatti, sia per quanto riguarda le velocità di elaborazione dei microprocessori, sia per quello che riguarda la possibilità di memorizzazione dei dati su dischi fissi tradizionali o su dischi ottici, che sono in questo momento in fase di grande sviluppo, sia infine per la risoluzione degli schermi su cui viene realizzata la cartografia, è difficile dare una configurazione che possa, anche per pochi anni, rappresentare una soluzione ottimale. Allo stato attuale (1995) una possibile configurazione hardware potrebbe prevedere un calcolatore della fascia dei personal computer ( microprocessore INTEL 486 o Pentium) che utilizzi hard-disk di tipo tradizionale di capacità variabile tra 600 Mb e 1 Gb, che sia ovviamente dotato di coprocessore matematico e che utilizzi schermi video a colori di alta risoluzione. Capitolo IX - Cartografia numerica pagina 309 R.Galetto A.Spalla - Lezioni di Topografia Tenuto conto del fatto che generalmente chi opera su queste stazioni video-grafiche per l'editing della cartografia numerica non ha necessità di essere collegato in rete con altri calcolatori si può inoltre ipotizzare che il sistema operativo nell'ambito del quale operare possa ancora essere il sistema MS/DOS, con evoluzione verso WINDOWS Questa configurazione di hardware, basata sull'utilizzazione di personale computer, può apparire vantaggiosa anche dal punto di vista del contenimento dei costi; infatti la fase dell'editing cartografico incide notevolmente nella produzione di cartografia numerica, ed è quindi opportuno che il costo della struttura hardware sia contenuto. Tuttavia si sta assistendo ad un notevole contenimento dei costi dei calcolatori che rientrano nella fascia delle work-station, basati su tecnologia RISC e operanti con sistema operativo UNIX. Si stanno quindi diffondendo hardware di questo tipo. Come periferiche di memorizzazione dei dati si sta sempre maggiormente ricorrendo alla tecnologia dei dischi ottici. 3.3 Differenze di esigenze fra sistemi per la produzione e sistemi per l'utilizzo della cartografia numerica La scelta del sistema per la produzione della cartografia numerica deve comunque essere fatta in maniera oculata, in quanto il processo produttivo presenta delle problematiche, quale, ad esempio, quella dell'editing dei dati acquisiti in restituzione, completamente diverse da quelle che riguardano la fase di gestione della cartografia numerica da parte dell'utente. Il giusto dimensionamento della stazione hardware e software per il trattamento della cartografia numerica è un problema che deve essere affrontato avendo ben chiara la differenza tra strumentazioni necessarie alla produzione della cartografia e strumentazioni necessarie per la gestione della cartografia stessa. Spesso si confondono le operazioni che devono essere fatte da chi fa parte del mondo della produzione della cartografia con le operazioni di gestione della cartografia da parte dell'utente. In particolare, volendo vedere una differenziazione di questi compiti, possiamo dire che le stazioni grafiche interattive per la produzione di cartografia non necessitano in generale di elaboratori molto potenti poiché l'editing e l'elaborazione dei dati può essere fatta operando separatamente su quantità ridotte di cartografia numerica. Viceversa l'utente avrà non solo la necessità di gestire la cartografia nella sua completezza, ma dovrà inoltre incrociare questo dato cartografico ad altri dati; l'utente vedrà cioè la cartografia numerica come uno scheletro su cui poi appoggiare informazioni specifiche di altro tipo, che sono generalmente quelle che per cui la cartografia numerica è stata richiesta. Infatti, nella pratica, la cartografia numerica viene usata molte volte dall'utente non tanto per sfruttare il dato topografico in senso stretto, ma per dare un ordinamento spaziale a dati d'altro genere. Un esempio tipico di utilizzazione di cartografia numerica è quello nel quale la cartografia numerica è vista come supporto di distribuzione di reti di servizio o di reti tecnologiche. Capitolo IX - Cartografia numerica pagina 310 R.Galetto A.Spalla - Lezioni di Topografia A causa quindi del diverso tipo di utilizzazione dei dati archiviati, dovranno essere previsti sistemi che operino sullo stesso tipo di dati, ma con funzioni e con mezzi diversi, a seconda vengano utilizzati per la realizzazione o per la gestione dei dati di cartografia numerica. In particolare nelle stazioni grafiche interattive dedicate alla produzione, dovrà essere previsto un software molto articolato, per tipi di interventi volti a modificare la cartografia numerica per correggerne errori, per modificarne il contenuto secondo determinati criteri, ecc. Le stazioni grafiche interattive destinate agli utenti invece, dovranno privilegiare la velocità di elaborazione dei dati, la capacità di disporre di grandi memorie di massa e la rapidità di visualizzazione del dato grafico sul video, caratteristica quest'ultima essenziale per una stazione grafica interattiva gestita dall'utenza per la quale è un'esigenza primaria la capacità di consentire rapide visualizzazioni di determinate aree del territorio, con tutte le informazioni che vengono via via aggiunte. 4 Aggiornamento della cartografia numerica L'aggiornamento della cartografia numerica non si differenzia in linea di principio dall'aggiornamento di una cartografia di tipo tradizionale; infatti le operazioni di aggiornamento devono sia per l'uno sia per l'altro caso ricondurre la situazione quale appare su una cartografia, realizzata in tempo più o meno remoto, alla situazione corrispondente a quella attuale. Generalmente l'operatore che esegue l'aggiornamento osserva allo strumento restitutore la situazione quale appare sulle fotografie aeree e la confronta con quella che appare dall'elaborato grafico che rappresenta la cartografia da aggiornare. Questa operazione è estremamente lunga, perché, se viene fatta correttamente, obbliga l'operatore ad un continuo confronto che implica una continua alternanza fra l'atto di osservare l'immagine stereoscopica nel restitutore e l'osservare il prodotto cartaceo sul tavolo di restituzione. Durante l'esecuzione di questa operazione che è lunga e faticosa, è inevitabile che l'operatore possa incorrere in omissioni, perché egli non ha mai la possibilità di vedere sovrapposta l'immagine stereoscopica, quale appare sulle fotografie aeree, con l'immagine cartografica. L'aspetto peculiare dell'aggiornamento nel caso della cartografia numerica è invece dato dal fatto che utilizzando i dispositivi di superimposizione si può facilitare enormemente l'operazione di aggiornamento, rendendola nel contempo più attendibile e sicura. I metodi di superimposizione attualmente disponibili sul mercato sono basati su due principi differenti. Il primo principio consiste nell'introdurre nel percorso ottico, che va dall'occhio dell'osservatore all'immagine fotografica, una immagine che rappresenta il disegno della cartografia esistente. La cosa può essere fatta o su un solo percorso ottico o su entrambi; in un caso si avrà la superimposizione non stereoscopica, nell'altro caso la superimposizione stereoscopica. Il secondo principio prevede che venga rasterizzata una delle due immagini che concorrono a formare il modello stereoscopico, che questa immagine rasterizzata venga presentata sul video Capitolo IX - Cartografia numerica pagina 311 R.Galetto A.Spalla - Lezioni di Topografia grafico che è collegato allo strumento restitutore e che sullo stesso video-grafico venga riprodotta l'immagine vettorializzata della cartografia numerica esistente. Mentre nel primo metodo, se si attua la superimposizione stereoscopica occorre deformare la cartografia esistente prospettivizzandola su entrambi i fotogrammi, nel secondo caso la prospettivizzazione della cartografia esistente deve essere effettuata unicamente per il fotogramma che viene presentato rasterizzato sul video grafico come sfondo della cartografia vettoriale. Con questi metodi di superimposizione l'operatore può direttamente confrontare la situazione cartografica sovrapposta alla nuova situazione del territorio quale appare dall'immagine fotografica. Si ha un'enorme velocizzazione dell'operazione di aggiornamento e un più alto grado di affidabilità perché questa coesistenza di sovrapposizione diretta tra la cartografia esistente e l'immagine, che è alla base dell'aggiornamento, elimina quasi completamente il rischio di errori di omissione. Al di fuori di questo aspetto peculiare, i problemi di aggiornamento della cartografia numerica possono essere dal punto di vista concettuale ricondotti a quelli di una cartografia tradizionale. Dal punto di vista operativo differiranno nelle stesse fasi di realizzazione che differenziano la cartografia numerica dalla cartografia tradizionale e che sono già state ai paragrafi precedenti; in particolare dopo l'operazione di restituzione, dovranno essere applicate quelle stesse operazioni di editing e di completamento della cartografia che riguardano la realizzazione exnovo della cartografia numerica. 5 Organizzazione dei dati e loro trasferimento 5.1 Struttura dei dati Nei limiti della trattazione di questo testo non c'è spazio per un esame comparativo dei metodi di organizzazione dei dati che sono adottati negli strumenti di realizzazione e di gestione della cartografia numerica in ambito di SIT. E' comunque opportuno richiamare brevemente i due modi con cui, al di là dell'aspetto formale, possono essere nella sostanza strutturati i dati cartografici. Le due tipologie di strutturazione dei dati, che possono poi venir tradotte in varie forme di organizzazione materiale dei medesimi, sono quella topologica e quella geometrica; in realtà la qualifica di geometrica non è altrettanto semanticamente corretta quanto quella di topologica e sarebbe più corretta sostituirla con quella di non topologica; sia chiaro quindi che nel seguito con questo significato verrà usata. Nel trattare l'argomento useremo la seguente terminologia: • • • oggetto: è un elemento naturale o artificiale del terreno che non è ulteriormente divisibile in elementi del suo stesso genere. Ad esempio: un lago, una casa, un muro, ecc.; entità: è la rappresentazione nella cartografia numerica di un oggetto o di parte di esso; gli elementi descrittivi di un'entità sono: la codifica e una primitiva geometrica; primitive geometriche: sono i punti e le spezzate. Capitolo IX - Cartografia numerica pagina 312 R.Galetto A.Spalla - Lezioni di Topografia Una strutturazione geometrica ha, in linea generale, le seguenti caratteristiche: • • • ogni oggetto è rappresentato da una sola entità; ogni entità è in genere descritta da una sola primitiva geometrica; si fa ricorso a più primitive geometriche solo quando l'entità è costituita da un poligono complesso (ad esempio casa con cortile interno); le primitive geometriche che servono alla descrizione di un'entità non sono condivise con nessuna altra entità; ne consegue che la cancellazione della o delle primitive geometriche che servono alla descrizione di un'entità non pregiudica la descrivibilità di nessun altra entità. Una strutturazione topologica ha, in generale, le seguenti caratteristiche: • • • non esistono primitive geometriche dello stesso tipo, parzialmente o totalmente sovrapposte; una stessa primitiva geometrica può essere utilizzata come elemento descrittivo di più entità; dalle due caratteristiche precedenti ne deriva che in genere gli oggetti sono rappresentati da più entità. Consideriamo l'esempio di figura 6 che rappresenta due case A e B; la casa A ha un lato che costituisce parte di un lato della casa B. Nella realtà abbiamo due case, quindi due oggetti. In una strutturazione topologica nella cartografia numerica esisteranno tre primitive geometriche, corrispondenti ai tre tratti di perimetro in cui è scomponibile l'insieme delle due case; la spezzata 1 e la spezzata 3 serviranno alla descrizione delle due entità tratto di perimetro della casa A e tratto di perimetro della casa B, rispettivamente; la spezzata 2 servirà alla descrizione di due entità: tratto del perimetro della casa A e tratto di perimetro della casa B. La geometria della spezzata 2 è condivisa da due entità. Nella cartografia numerica devono esistere gli elementi di informazione sufficienti a indicare l'esistenza dei due oggetti A e B, quali sono le entità attraverso le quali vengono rappresentati nella cartografia numerica e quali sono le primitive geometriche che descrivono le entità. B B A a) 1 2 b) 3 A c) figura 6 - Gli edifici A e B possono essere descritti o mediante 3 primitive grafiche in una struttura topologica (b) o mediante 2 oggetti grafici autoconsistenti (c) in una struttura non topologica. Capitolo IX - Cartografia numerica pagina 313 R.Galetto A.Spalla - Lezioni di Topografia In una strutturazione geometrica nella cartografia numerica esisteranno due entità, una che corrisponde alla casa A e una che corrisponde alla casa B; le due entità saranno descritte da due primitive geometriche, costituite da due spezzate chiuse. La descrizione geometrica di ognuna delle due entità è quindi autoconsistente. La strutturazione topologica ripete, in un certo senso il disegno tradizionale; e cioè, in una carta tradizionale il disegnatore non disegna due volte il tratto in comune alle due case, ma lo traccia o nel disegnare la casa A o nel disegnare la casa B. Ciò corrisponde a quanto prima detto, e cioè che nella struttura topologica non ci sono primitive geometriche totalmente o parzialmente sovrapposte. Con la struttura topologica la cartografia numerica è già ottimizzata per il disegno, tant'è vero che, quando la struttura è topologica le primitive geometriche vengono anche indicate col termine di primitive grafiche. La struttura geometrica traduce invece più da vicino il modo con cui un operatore umano interpreta la realtà dall'osservazione della carta; e cioè chi osserva una carta tradizionale vede le due case come nel caso c) della figura 6, cioè come superfici delimitate da due spezzate chiuse e non come due superfici delimitate dalle spezzate aperte rappresentate come nel caso b) della figura 6. Lo scegliere la struttura topologica anziché la struttura non topologica ha comunque importanti risvolti nella organizzazione dei dati. Per esempio scegliendo di strutturare i dati in maniera non topologica e cioè scegliendo di rappresentare gli oggetti cartografici in maniera autoconsistente, occorre risolvere il problema di come organizzare i dati che riguardano entità di tipo superficie assimilabili a poligoni complessi. Per descrivere entità assimilabili a poligoni complessi è necessario numerizzare l'oggetto topografico come un'entità formata da un perimetro esterno a cui occorre associare linee di esclusione. figura 7 - Uso del metodo del taglio fittizio per memorizzare un oggetto cartografico a), la cui proiezione in pianta è assimilabile ad un poligono complesso b), mediante un'unica entità c). A chiarimento di quanto esposto si consideri l'esempio riportato in figura 7 dove e' rappresentato un edificio che ha, al suo interno, una superficie di esclusione rappresentata da un cortile. Per numerizzare l'oggetto grafico che descrive, in maniera autoconsistente, l'edificio Capitolo IX - Cartografia numerica pagina 314 R.Galetto A.Spalla - Lezioni di Topografia dovrà essere rappresentato da un'unica spezzata chiusa, formata dal perimetro esterno collegato al perimetro della superficie di esclusione da un taglio fittizio; tale taglio fittizio si può realizzare mediante due segmenti memorizzati a penna su, cioè non visibili nelle visualizzazioni della cartografia numerica. Nella figura 7 il disegno c) evidenzia meglio il concetto di taglio fittizio ed il modo con cui i vertici della spezzata devono susseguirsi, partendo da un punto (vertice 1 in figura) per ritornare sul medesimo punto dopo aver percorso tutto il perimetro. Le coordinate dei vertici 1, 11, 7 dovranno essere coincidenti; cosi' pure quelle del vertice 2 dovranno coincidere con quelle del vertice 6. La tecnica del taglio fittizio può essere applicata anche in presenza di più aree di esclusione all'interno di una stessa superficie. Essa può inoltre essere adottata non solo per gli edifici, ma per ogni altra entità di tipo superficie che abbia superfici di esclusione al suo interno; ad esempio per rappresentare uno specchio d'acqua in cui vi sia un'isola. Comunque in questa sede non si vuole entrare nel dettaglio dei due tipi di strutturazione, né farne un elenco dei rispettivi vantaggi o svantaggi; ci sono però due considerazioni da fare: • • quasi tutti i software di gestione di cartografia degli utenti, (da non confondersi con quelli che le Ditte usano per la produzione della cartografia numerica!) sono basati su una strutturazione topologica della cartografia e hanno al loro interno dei traduttori che sanno trasformare una cartografia data in strutturazione geometrica in una cartografia strutturata topologicamente nel modo che è compatibile al Sistema di cui fanno parte; quindi, a meno di non fornire la cartografia numerica proprio nella strutturazione topologica che serve all'utente, può risultare più conveniente all'utenza che essa sia fornita strutturata geometricamente. i software basati su struttura topologica non hanno problemi se usati per gestire una carta numerica planimetrica, o con planimetria e altimetria; possono averne se la carta è tridimensionale. Infatti la struttura topologica non prevede la possibilità di trattare geometrie che si sovrappongono in planimetria, ma che sono a quote diverse; così pure i nodi, cioè i punti in cui convergono le spezzate, sono visti principalmente come posizione planimetrica, e comunque non ne è prevista da nessun sistema topologico una doppia quota, di cui invece vi sarebbe necessità in molti casi nella cartografia tridimensionale. Non è questa la sede per entrare nel merito di quale sistema di strutturazione convenga usare nei sistemi utente; si ritiene invece che nei software di produzione, potrebbe essere più conveniente usare una strutturazione di tipo geometrico; a prescindere da ogni considerazione di tipo informatico, essa, con quel suo ritornare agli oggetti, con quel suo dar valore ad ogni cosa in sé e per sé, una alla volta, aiuta gli operatori a tradurre la realtà del territorio e a darle ordine nella realtà stilizzata della cartografia. 5.2 Formato di trasferimento della cartografia numerica Il costante aumento della produzione della cartografia numerica e la sua utilizzazione sempre più diffusa per la conoscenza del Territorio, hanno messo in evidenza il problema della Capitolo IX - Cartografia numerica pagina 315 R.Galetto A.Spalla - Lezioni di Topografia definizione e della progettazione di standard per il contenuto informativo e per le modalità di trasferimento di dati cartografici. Tale problema è di attualità per tutti gli Enti di Governo del Territorio che mostrano particolare interesse ad acquisire la cartografia numerica realizzata per il territorio di propria competenza da altri Enti. Si pensi, ad esempio, alle Regioni che potrebbero acquisire le cartografie prodotte dai Comuni, dalle Provincie per approfondire il grado di dettaglio delle proprie carte tecniche; o ai Comuni stessi che potrebbero acquisire la cartografia catastale sia come dato tematico da inserire in sistemi informativi territoriali che già gestiscono cartografie numeriche redatte ad hoc, sia come dato cartografico d'impianto dove queste cartografie non siano ancora state prodotte. Da un punto di vista del tutto generale si possono fare le considerazioni nel seguito riportate. La necessità di definire degli standard prende origine dal fatto che i dati di cartografia numerica vengono prodotti e gestiti con strumentazioni differenti e sono generalmente articolati secondo strutture logiche diverse, proprie dei diversi sistemi hardware e software utilizzati. Perché i dati di cartografia numerica possano essere utilizzati da un maggior numero possibile di utilizzatori, deve essere garantita la trasferibilità dei dati fra i diversi sistemi di gestione esistenti sul mercato e in dotazione presso i diversi enti. Questa trasferibilità è possibile : • • se sono definiti degli standard di contenuto informativo e di formato dei dati se ogni sistema di produzione e gestione di dati cartografici garantisce la riconducibilità dei propri dati alle articolazioni logiche e ai formati di dati suggeriti come standard. Si intende con questo che un sistema di gestione di cartografia numerica deve: • poter acquisire dati secondo degli standard informativi e di formato-dati, e tradurre questi dati secondo la propria architettura di gestione, al fine di gestire le informazioni in essi contenuta secondo le proprie procedure ottimizzate, e deve inoltre: • poter convertire i propri dati, che sono organizzati in maniera funzionale alla propria struttura, nel sistema standard base per renderli utilizzabili dal mondo esterno e cioè da sistemi impostati su logiche e strutture differenti. Gli standard che si ricercano non hanno quindi lo scopo di essere standard generalizzati di gestione, definiti secondo logiche di utilizzo, ma devono essere, più semplicemente, regole di trasferimento, definite in modo tale da rendere possibile il trasporto dei dati fra sistemi, filtrando eventualmente il contenuto informativo nel passaggio dal dato originario al dato trasportato, secondo criteri di opportunità e convenienza. Per chiarire quali problemi si debbano affrontare nel trasferimento di dati cartografici, supponiamo di dover trasferire dati cartografici fra due sistemi che, per brevità definiremo sistema sorgente e sistema ricevente. Per compiere questa operazione è necessario: a) conoscere l'organizzazione dei dati nei due sistemi, b) recuperare le informazioni necessarie al sistema ricevente dalla struttura del sistema sorgente, c) organizzare le informazioni secondo l'architettura del sistema ricevente. Capitolo IX - Cartografia numerica pagina 316 R.Galetto A.Spalla - Lezioni di Topografia Non è detto che sia sempre possibile conoscere le architetture dei sistemi considerati in maniera così dettagliata da realizzare le operazione di cui in b) e c); le architetture dei dati possono infatti essere soggette a vincoli di riservatezza industriale; generalmente un utilizzatore evoluto di un sistema conosce la struttura dati del sistema su cui opera. Ma anche ipotizzando che la condizione a) sia verificata, nella realizzazione delle fasi b) e c) è possibile che si verifichi un decadimento del contenuto informativo, causato principalmente dal fatto che i sistemi di acquisizione, e/o di gestione, possono essere realizzati a partire da impostazioni di principio sostanzialmente differenti. Se infatti i dati del sistema sorgente sono organizzati secondo logiche non completamente ricostruibili nell'organizzazione del sistema ricevente, molte informazioni dei dati originari possono andare irrimediabilmente perdute. Ad esempio, nel passaggio di dati fra sistemi puramente topologici e sistemi topografici, sono difficilmente trasferibili le connessioni logiche tra entità. Con la definizione di standard di trasferimento si cerca di ovviare agli inconvenienti sopra descritti. Perché l'utilizzatore di un sistema possa fruire di dati acquisiti, o già gestiti, da altri sistemi, non è necessario che conosca, e in modo approfondito, tutti i sistemi da cui vuole attingere dati, basta che conosca il proprio sistema in modo da inserire in esso dati, che gli giungono organizzati secondo le convenzioni standardizzate. E, viceversa, semplicemente conoscendo le procedure necessarie a tradurre i propri dati secondo gli stessi standard, può trasferire i propri archivi ad altri utilizzatori. Ogni sistema è cioè aperto al mondo degli altri sistemi attraverso i media degli standard. Non è però operazione semplice definire degli standard che devono già ora non essere in contrasto con i criteri di impostazione concettuale dei principali database cartografici esistenti sul mercato e che devono inoltre essere aperti a possibili e anche sostanziali innovazioni che potranno imporre esigenze future. La struttura dei dati cartografici si presenta oggi, in Italia, molto diversificata. Vi sono cartografie numeriche che vengono prodotte e consegnate alla Committenza strutturate in forma topografica; tali cartografie contengono i dati qualitativi e metrici che erano caratteristici della cartografia disegnata tradizionale. In altri casi la cartografia numerica viene prodotta e strutturata secondo i criteri topologici che sono richiesti in generale dai software più diffusi per la gestione dei sistemi informativi territoriali In generale gli standard di trasferimento offrono differenti possibili articolazioni dei dati e consentono di trasferire dati di complessità diversa; tuttavia questa flessibilità dei sistemi di trasferimento, questa possibilità di accogliere dati che vanno da strutture estremamente semplici a strutture più complesse, viene pagata con una dilatazione della mole dei dati da trasferire che impiega quantità di memoria di massa anche rilevanti. La possibilità di poter ospitare dati di complessità diversa è risolta sia strutturando il sistema di trasferimento su più livelli, in modo da essere flessibile nei riguardi della complessità dei dati che devono essere trasferiti, sia nel rendere il sistema di trasferimento autodocumentato e quindi estremamente ricco di informazioni che consentono di ricostruire il significato dei dati, la loro qualità e le relative modalità di ricostruzione. Capitolo IX - Cartografia numerica pagina 317 R.Galetto A.Spalla - Lezioni di Topografia In Italia non sono stati prodotti sistemi di trasferimento codificati, universalmente accettati o comunque certificati a livello nazionale. Si osserva, a questo proposito, che un sistema di trasferimento perché sia valido deve essere inteso non come un'opera pregevole da realizzare una volta per tutte, ma deve essere considerato come un prodotto dinamico, da modificare in funzione di esigenze che le innovazioni tecnologiche e le richieste dell'utenza suggeriscono. Un sistema di questo tipo deve essere gestito da un apposito Ente che lo tenga costantemente aggiornato, così da sopperire alle eventuali necessità che si vengono a manifestare e che diffonda le evoluzioni del sistema di trasferimento certificandole nelle sedi riconosciute delle varie Nazioni. In Italia non è stato realizzato nulla di simile. Enti con giurisdizione territoriale, che hanno affrontato il problema del trasferimento dei dati di natura cartografica, hanno condotto studi comparati sui sistemi realizzati negli Stati Uniti, in Canada, in Inghilterra, al fine di individuare il sistema più adatto alle loro esigenze per adottarlo come proprio standard, in mancanza di uno standard nazionale italiano. L'IGMI ha adottato come proprio sistema di trasferimento il DIGEST che è stato elaborato a livello europeo dal DGIWG (Digital Geographic Information Working Group). E' questo un sistema che nasce in ambiente militare ed ha per scopo lo scambio di informazioni geografiche, raster e vettoriali, provenienti sia dalla grande che dalla media scala. La Direzione Generale del Catasto e alcune Regioni hanno adottato quale proprio sistema standard di trasferimento il sistema britannico NTF (National Transfer Format). La scelta attuata dalla Direzione Generale del Catasto e il fatto che una gran mole di dati del Catasto numerico sia già disponibile in tale formato, rende di fatto l'NTF il sistema di trasferimento attualmente più diffuso in Italia. 6 La cartografia numerica e i sistemi informativi territoriali (SIT) Nella sua accezione più generale un Sistema Informativo può essere inteso come una struttura la cui funzione è quella di governare, attraverso tecniche informatiche, un processo produttivo avente lo scopo di acquisire, sistematizzare, aggiornare ed elaborare dati per trasformarli in informazioni finalizzate ad essere di supporto a decisioni che devono essere prese nell'ambito di un'attività di programmazione, di progettazione e di gestione. I dati, che devono essere memorizzati e organizzati su supporti elaborabili da calcolatore elettronico (Banche di Dati), hanno la caratteristica di presentarsi, già alla fonte, in forma numerica o alfanumerica; ugualmente le informazioni vengono prodotte in forma numerica (tabelle, ecc.) o, talvolta, in forma diagrammatica. La caratteristica di un Sistema Informativo Territoriale è invece quella di gestire dati che si presentano in forma cartografica e di produrre informazioni che acquistano pienezza di significato quando associano il loro contenuto qualitativo alla corrispondente collocazione spaziale. Capitolo IX - Cartografia numerica pagina 318 R.Galetto A.Spalla - Lezioni di Topografia Il riferimento spaziale dei dati e delle informazioni può essere di rilevante aiuto non solo in un'attività che riguarda il governo del territorio da un punto di vista tecnico, ma anche quella volta all'emanazione di leggi e norme e al controllo del loro rispetto. Parlando di SIT si intende implicitamente: • • • • • che esiste un Ente che ha giurisdizione territoriale, con compiti o di pianificazione o di programmazione o di gestione (tecnica, amministrativa, fiscale, ecc.) che riguardano il territorio, quest'ultimo inteso come tutto ciò che esiste ed interagisce in una determinata area (elementi naturali, strutture artificiali, popolazione, attività, servizi, normativa, ecc.); che a questo scopo acquisisce dei dati, dei quali la parte di gran lunga preponderante, ha come caratteristica fondamentale quella di avere un riferimento topografico; che elabora questi dati con procedura ben definita, dove con procedura si intende un complesso di personale, strumenti, metodi di elaborazione e tipi di informazione prodotti; che attua un costante aggiornamento dei dati; che prevedi scambi di dati e informazioni, sia con Enti ad esso affini per compiti istituzionali, ma che operano a livello inferiore o superiore per estensione territoriale, sia con Enti che operano con finalità complementari. Questa dettagliata definizione di SIT non significa che esso sia nella realtà così ben definito nell'ambito delle pubbliche amministrazioni; anzi sono rari i casi dove esiste un settore operativo con tale specifica denominazione; esso si configura quindi in generale più come un complesso di attività che come una struttura. Talvolta esistono dei poli di agglomerazione che, a seconda dell'ente, possono essere o un ufficio cartografico, o l'assessorato all'Urbanistica, o un ufficio di pianificazione e così via; ma in generale le persone che si occupano dell'acquisizione e della elaborazione dei dati hanno spesso anche altre mansioni e i dati e gli strumenti per la loro elaborazione sono dislocati in luoghi differenti. Una visione più realistica della situazione attuale sposterebbe quindi i termini del problema e porterebbe a considerare l'introduzione dell'Informatica nei SIT non solo come un momento tecnico di potenziamento della capacità di trattamento dei dati e di riorganizzazione e razionalizzazione dei flussi di informazione, ma anche come momento politico nel quale ridefinire le funzioni del SIT nell'ambito delle Amministrazioni e darne una configurazione più precisa dal punto di vista strutturale. Si può comprendere quindi come sia difficile ritrovare delle linee generali di funzionamento di un organismo così proteiforme e cercare di individuarne le varie tipologie in modo da poter sistematizzare l'argomento da trattare. Senza entrare nel merito del discorso con una discussione approfondita, diremo che i SIT possono essere suddivisi, dal punto di vista della finalità a cui sono diretti, in due categorie: quelli a carattere prevalentemente descrittivo e quelli a carattere prevalentemente gestionale. I primi sono propri degli enti che svolgono attività di programmazione o di pianificazione del territorio ed il loro obbiettivo principale è quello di fornire informazioni utili ad orientare le decisioni che devono venir prese per attuare una politica di governo; per essi si potrebbe Capitolo IX - Cartografia numerica pagina 319 R.Galetto A.Spalla - Lezioni di Topografia adottare la terminologia anglosassone di decision support system, cioè sistemi a supporto delle decisioni. I dati trattati in questo tipo di SIT provengono in generale dall'esterno dell'ente cui il SIT appartiene, e l'attività svolta ad acquisirli e ad organizzarli può, in certi casi, essere prevalente rispetto a quella di effettuarne l'elaborazione finalizzata allo studio delle interazioni e delle correlazioni dei fenomeni che coesistono sul territorio. Rientrano in questa categoria, ad esempio, i SIT regionali. I SIT di tipo gestionale sono propri di quegli enti che svolgono un servizio, e la loro funzione principale è quella di organizzare e gestire dati che in buona parte sono interni all'ente cui il SIT appartiene e per la parte restante danno una conoscenza del territorio in uno spettro molto ristretto delle sue componenti, il quale risulta facilmente definito dal compito istituzionale dell'ente. Tipici SIT di questa categoria sono quelli delle Aziende municipalizzate che gestiscono reti di distribuzione (acqua, gas, ecc.) e per le quali l'informazione è intesa generalmente non come supporto a decisioni che riguardano scelte strategiche di sviluppo, bensì allo svolgimento dei compiti della gestione ordinaria. Diversi fattori concorrono a rendere più complessi e di più difficile realizzazione i SIT di tipo descrittivo rispetto a quelli gestionali. Innanzitutto nei primi è difficile prevedere, in fase di progetto, quali saranno le esigenze di conoscenza del territorio ai fini del lavoro di programmazione o di pianificazione e questo tende a farne prendere in considerazione una grande quantità di aspetti fino a dare al SIT quel carattere omnicomprensivo che ne è uno dei maggiori fattori di rischio. In secondo luogo la molteplicità delle fonti da cui provengono i dati, il loro diverso grado di aggregazione e di attendibilità , oltre a richiedere un pesante lavoro di omogeneizzazione e sistematizzazione, pone serie difficoltà al problema del loro aggiornamento. Infine il tipo di informazioni che devono essere prodotte deve coprire un arco molto esteso di esigenze: esse devono cioè essere a basso livello di dettaglio per fornire valori di sintesi su aree molto estese, quando sono prodotte a supporto di decisioni che riguardano la pianificazione territoriale; mentre devono avere la caratteristica di informazioni puntuali quando sono a supporto di decisioni che riguardano politiche urbanistiche a livello locale. Nei SIT gestionali invece gli obbiettivi sono ben individuabili e questo comporta la possibilità di definire con buona approssimazione quali dati debbano alimentare il flusso delle informazioni; inoltre il loro aggiornamento dipende in larga misura da strutture che sono interne all'ente cui il SIT appartiene; ed infine anche le informazioni sono destinate ad una utenza interna o comunque che interagisce con il SIT per linee orizzontali. Oltre a questi due tipi di SIT se ne può prendere in considerazione un terzo, che possiamo definire progettuale: esso si pone in posizione intermedia tra i due precedenti e cioè tende a fornire elementi descrittivi, ma per scopi che si realizzano a breve termine; inoltre, pur non essendo finalizzato all'espletamento di un servizio, è orientato a soddisfare esigenze molto ben definite. Indipendentemente dalla tipologia del SIT e dall'estensione del Territorio alla cui gestione o descrizione esso è finalizzato, è chiaro che la cartografia numerica costituisce uno dei suoi archivi fondamentali. Le funzioni della cartografia numerica nell'ambito di un SIT sono le seguenti: Capitolo IX - Cartografia numerica pagina 320 R.Galetto A.Spalla - Lezioni di Topografia • • • • • dare una rappresentazione della geometria del Territorio e cioè deve contenere tutti gli elementi qualitativi e metrici la cui conoscenza è indispensabile per pianificare e progettare i tipi di intervento che sono istituzionalmente previsti dall'ente che gestisce il SIT; costituire il supporto sul quale vengono riportati i progetti che costituiscono il risultato della pianificazione e della progettazione; opportunamente semplificata fornire la base topografica per la costruzione delle carte tematiche; costituire l'ossatura portante, perchè consente di collegare ogni tipo di informazione ad un sistema di riferimento spaziale; in tal modo, dati di natura molto diversa, in quanto relativi alle diverse componenti del Territorio, trovano, nel riferimento topografico, quell'anello di saldatura che conferisce loro una pienezza di significato che altrimenti non avrebbero, e che permette di mettere in evidenza e di analizzare le correlazioni e le interazioni dei fenomeni che avvengono sul territorio; favorire il collegamento sia in senso orizzontale che verticale con altri SIT con i quali possano essere scambiati in input o in output dati o loro elaborazioni. In definitiva la cartografia numerica fornisce per ogni punto del Territorio una connotazione precisa nel contesto generale consentendo di associare ad ogni informazione delle coordinate spaziali che, come un'impronta digitale, le conferiscano individualità ed individuabilità nel contesto del SIT. Capitolo IX - Cartografia numerica pagina 321 R.Galetto A.Spalla - Lezioni di Topografia APPENDICI 1. Sistemi di misura degli angoli. Nel sistema sessagesimale l'unità di misura, chiamata grado sessagesimale, è la 360ma parte dell'angolo giro. I sottomultipli sono il primo ed il secondo sessagesimale, ottenuti rispettivamente come la 60ma parte del grado e del primo. Un generico angolo risulta espresso in tale sistema nel modo che segue: 36° 51' 25". Il sistema centesimale ha come unità di misura il grado centesimale, che è la 400ma parte dell'angolo giro. I sottomultipli sono il primo centesimale, ottenuto come la 100ma parte del grado ed il secondo centesimale che è la 100ma parte del primo. Un generico angolo sarà: 57g, 41c, 87 cc , oppure, più semplicemente: 57,4187. Come si può notare, il sistema centesimale presenta il vantaggio della divisione centesimale del grado. Ad esempio la somma dei due angoli: α= 127 g,3849 β= 54 g,0348 127 g,3849 54 g,0348 181 g,4197 risulta Considerando inoltre, che la quasi totalità delle operazioni di calcolo prevede oggi l'impiego di strumenti di calcolo, per i quali la divisione decimale del grado rimane molto comoda, si comprende come il sistema centesimale, che pure è di più recente introduzione, prevalga ormai nei confronti di quello sessagesimale. Gli strumenti impiegati per la misura degli angoli hanno comunque i cerchi adibiti allo scopo di essere indifferentemente a graduazione sessagesimale o centesimale. In altre parole, lo stesso tipo di strumento viene fornito dalla Casa costruttrice, con il tipo di graduazione richiesto dall'acquirente. Quanto affermato nelle righe precedenti riguarda le misure degli angoli; a volte però gli angoli misurati devono essere convertiti in radianti, per poter valutare l'errore planimetrico che deriva da un errore angolare. S R α αr = S R Nel sistema analitico, il valore di un angolo in radianti è dato dal rapporto tra l'arco di cerchio che sottende l'angolo ed il corrispondente raggio del cerchio. Appendici pagina 322 R.Galetto A.Spalla - Lezioni di Topografia I sottomultipli del radiante sono il decimo, il centesimo, il millesimo, ecc. di radiante; un generico angolo in tale sistema risulta espresso così: 2r,316. Per trasformare gli angoli da gradi centesimali in radianti e viceversa, si imposta la proporzione: αr αg = 2π 400 ⇒ 1 radiante = 63g,6619772 Quindi per passare da un angolo espresso in gradi centesimali allo stesso angolo espresso in radianti, bisogna dividere per 63,6619772. È importante, inoltre, ricordare quanto valgono, in radianti, un primo o un secondo centesimale. 1 1 c cc 1 = 6.360 1 = 636.600 Per calcoli approssimati sarà sufficiente utilizzare valori approssimati, e cioè: 1 1 1c = 6.000 1cc = 600.000 Accenniamo ancora, prima di concludere l'argomento, al passaggio dal sistema sessagesimale al sistema analitico e viceversa che si realizza impostando una proporzione, in modo analogo a quanto visto per il precedente passaggio. In particolare ricordiamo i valori, espressi in radianti, del primo e del secondo sessagesimale: 1 1 ” 1’ = 3437 1 = . 206.265 ed i rispettivi valori approssimati: 1 1 = 3000 . ’ 2. 1 1 = 200.000 ” Angoli di direzione. Molte operazioni topografiche richiedono il calcolo delle coordinate di un punto P avendo eseguito le seguenti misure: • distanza d da un punto A di coordinate NA, EA note; • angolo che la congiungente AP forma con la direzione individuata dal individuata dal punto A e da un secondo punto B di coordinate NB, EB note. N B P A E Appendici pagina 323 R.Galetto A.Spalla - Lezioni di Topografia Per evitare ambiguità si è convenuto che tutti gli angoli misurati vadano sempre in senso orario dalla direzione nota a quella incognita; nel nostro caso quindi da AB ad AP (come indicato in figura). Per facilitare il calcolo delle coordinate di P, o più esattamente per permettere di eseguire il calcolo senza dover far ricorso a schemi grafici, si è introdotto un elemento geometrico che prende il nome di angolo di direzione. 2.1 Definizioni e convenzioni Un angolo di direzione viene definito da due soli punti. E cioè, dati due generici punti A e B si intende come angolo di direzione (AB), l'angolo che la parallela all'asse N passante per A forma con la congiungente AB. L'angolo di direzione può variare da 0 a 2π a seconda della posizione di B rispetto ad A. Esso infatti si computa sempre in senso orario dalla parallela all'asse N alla direzione AB (vedi figure). N N N N B (AB) A (AB) B A E B A E B A (AB) (AB) E E Si noti inoltre che l'angolo di direzione (AB) non è uguale all'angolo di direzione (BA): N N (AB) A B B E A (BA) E I due angoli sono però fra loro legati dalla relazione: (BA) = (AB) + π (- 2π ) Questa relazione va intesa così: si somma ad (AB) l'angolo π; se il risultato è minore di 2π, l'angolo ottenuto è l'angolo di direzione (BA); se il risultato supera 2π, per ottenere l'angolo (BA) occorre togliere alla somma (AB)+π, l'angolo 2π. Come si vede, il calcolo di (BA), in funzione di (AB), può essere facilmente eseguito anche in un programma di calcolo, cioè senza ricorso a schemi: PIGR = 3,1417... PIGR2 = 2* PIGR READ AB Appendici pagina 324 R.Galetto A.Spalla - Lezioni di Topografia BA = AB + PIGR IF (BA.LT.PIGR2) GO TO 1 BA = BA - PIGR2 1 CONTINUE Riportiamo per chiarire i due casi: N N B (AB) B (AB) A π π (BA) (AB) A (BA) (BA)=(AB)+ π (AB)=(BA)+ π−2π E (AB) E L'angolo di direzione tra due punti A e B può essere calcolato (si noti: calcolato, in quanto un angolo di direzione non può essere misurato, perché sul terreno non è nota la direzione parallela all'asse N) tenendo conto che: ∆E EB − EA tg( AB) = = ∆N N B − N A Risulta quindi: N ∆Ε B ∆Ν (AB) A E ( AB) = arctg ∆E E − EA = B ∆N N B − N A Per riconoscere però se la relazione su scritta ci dà l'esatto valore di (AB) occorre procedere a dei test sul segno di ∆E e ∆N. Infatti nel seguente caso (ad es.) la relazione ci darebbe un risultato non giusto: N A ∆Ν (AB) α ∆Ε B E Appendici pagina 325 R.Galetto A.Spalla - Lezioni di Topografia e cioè anziché l'angolo (AB) otterremo l'angolo α con segno negativo (tra l'altro un angolo di direzione è sempre positivo). I test da fare sono quindi i seguenti. N (AB) B A E se: ∆E > 0 e ∆N > 0 (AB) = arctg ∆E ∆N se: ∆E < 0 e ∆N > 0 (AB) = arctg ∆E + 2π ∆N se: ∆E > 0 e (AB) = arctg ∆E +π ∆N se: ∆E < 0 e N B A (AB) E N (AB) A B E ∆N < 0 N B A (AB) E ∆N < 0 (AB) = arctg ∆E +π ∆N Come si vede, date le coordinate di A e di B, si può fare un semplice programmino per il calcolo dell'angolo di direzione, senza che occorra ricorrere a schemi grafici: P = 3.1417.... ATAN = DE/DN IF (DE.GT.0.AND.DN.GT.0) GO TO 50 IF (DE.LT.0.AND.DN.GT.0) GO TO 40 ATAN = ATAN + P GO TO 50 Appendici pagina 326 R.Galetto A.Spalla - Lezioni di Topografia 40 ATAN = ATAN + 2 * P 50 RETURN 2.2 L’angolo di direzione nel calcolo delle coordinate di un punto Ritorniamo ora al problema dal quale eravamo partiti, e cioè il calcolo delle coordinate di un punto P avendo misurato la distanza da esso di un punto A di coordinate note, e l'angolo che la direzione AP forma con la direzione congiungente A con un secondo punto noto B. N B α P d A E Si calcola innanzitutto l'angolo di direzione (AB); come indicato al paragrafo precedente. Quindi si calcola l'angolo di direzione (AP) con la relazione: (AP) = (AB) +α (- 2π ) N B P α d A E Anche qui il (-2π ) sta ad indicare che, se la somma (AB) + α risulta superiore a 2π occorre togliere a tale somma 2π per ottenere il corretto valore di (AP). Una volta noto l'angolo (AP) si hanno le coordinate di P dalle relazioni: NP = NA + d cos (AP) EP = EA + d sen (AP) Queste relazioni sono molto comode poiché non occorre schema grafico per vedere se le quantità di cos(AP) e di sen(AP) vanno sommate o sottratte a NA e EA rispettivamente per ottenere NP e EP; infatti l'angolo di direzione (AP) varia da 0 a 2π e conseguentemente il suo Appendici pagina 327 R.Galetto A.Spalla - Lezioni di Topografia coseno ed il suo seno assumono valori positivi o negativi, in modo da sommarsi o sottrarsi come dovuto a NA e EA, anche se nella relazione si scrive sempre il segno + davanti a d cos (AP) ed a d sen (AP). Consideriamo il seguente esempio: B N α A d P E Essendo (AP) compreso tra π/2 e π risulterà: cos (AP) < 0 sen (AP) > 0 e quindi si avrà: d cos (AP) < 0 d sen (AP) > 0 e risulterà quindi automaticamente che NP < NA e EP > EA come deve essere. Abbiamo trattato questo argomento un po' a lungo per due motivi. In primo luogo perché in tutti i calcoli topografici si fa riferimento al concetto di angolo di direzione e quindi, essendo uno strumento di calcolo usuale, è bene che esso sia ben conosciuto. In secondo luogo è abbastanza istruttivo vedere come deve essere impostato un qualsiasi calcolo topografico che debba essere tradotto in un programma di calcolo elaborato da un calcolatore elettronico. L'impostazione del calcolo deve cioè soddisfare i seguenti requisiti: • fissare esattamente le convenzioni con le quali debbono essere forniti i dati relativi alle misure eseguite sul terreno; • non deve essere necessario ricorrere a schemi grafici; • il risultato finale deve essere univoco. Appendici pagina 328