caricato da
common.user10365
Area di Figure Irregolari: Esercitazione di Misura e Calcolo

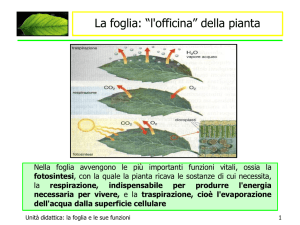
ESERCITAZIONE SUL CALCOLO DELL’ AREA DI UNA FIGURA IRREGOLARE Supponiamo di avere una figura irregolare di forma qualsiasi come una foglia e di rappresentarla su un classico foglio a quadretti la cui area di un quadretto sappiamo essere 0.25 cm 2 oppure su carta millimetrata Se consideriamo come unità di misura il quadrato di area 1 cm 2 potremmo andare a determinare L’Area Interna e L’Area Esterna della foglia ,ottenendo due valori approssimati per difetto e per eccesso. AREA INTERNA = 16 quadretti = 16 cm2 AREA ESTERNA = 42 quadretti = 50 cm2 Per ottenere un valore più preciso dell’ Area della foglia potrei fare una media tra le due aree ricavate , trovando un valore di area anch’esso approssimato ma sicuramente più attendibile. Per avvicinarsi al valore effettivo dell’ Area della foglia conviene considerare come unità di misura di riferimento invece che 1 cm2 il valore di 0,25 cm2 (Come si può notare i quadrati interni tendono a ricoprire meglio la superficie della foglia mentre quelli esterni tendono a delinearne piu in dettaglio il profilo AREA INTERNA = 88 quadretti = 22 cm2 AREA ESTERNA = 144 quadretti = 36 cm2 Per ottenere un valore più preciso dell’ Area della foglia potrei fare una media tra le due aree ricavate , trovando un valore di area anch’esso approssimato ma sicuramente più attendibile. Se adesso prendessimo in considerazione come unità di misura di riferimento invece che 1 cm 2 o 0,25 cm2 il valore di 1 mm2 e andassimo a calcolare L’Area interna tutti quadratini da 1mm2 interamente ricompresi nel perimetro della foglia e per l’Area Esterna i quadratini da 1 mm2 contenuti almeno in parte nel perimetro della foglia , si otterà un valore sempre approssimato dell’ area della foglia ma con un errore accettabile poiché molto piccolo e rientrante nella tolleranza. ire meglio la superficie della foglia mentre quelli esterni tendono a delinearne piu in dettaglio il profilo ESERCITAZIONE SUL CALCOLO DELL’ AREA DI UNA FIGURA IRREGOLARE 2° METODO Supponiamo di avere una figura irregolare di forma qualsiasi come una foglia e di rappresentarla su un classico foglio a quadretti la cui area di un quadretto sappiamo essere 0.25 cm 2 oppure su carta millimetrata Come possiamo notare il contorno della foglia non segue i bordi dei singoli quadrati. Caso 1 : Se contassimo tutti i quadrati parzialmente coperti come se lo fossero interamente, otterremmo una misura affetta da un errore sistematico per eccesso. Caso 2 : Se non li contassimo mai, la misura sarebbe affetta da un errore sistematico per difetto. Criterio Ideale : Un criterio possibile per decidere quali quadrati contare e quali no è il seguente: Contiamo solamente i quadrati il cui punto centrale cade dentro al contorno della mano, mentre non lo contiamo se il suo centro cade fuori. In questo modo l’errore commesso sarà del tutto casuale, e gli errori per eccesso e quelli per difetto tenderanno a compensarsi. Se contiamo i quadrati ricadenti dentro la foglia otteniamo 39 quadrati ovvero 39 cm 2 CALCOLO ERRORE ASSOLUTO Supponiamo di aver eseguito 4 misure di area della foglia disegnata in varie posizioni e di aver riportato il tutto dentro una tabella come questa: NUMERO MISURA AREA FOGLIA (cm2) Foglia n. 1 36 Foglia n. 2 39 Foglia n. 3 38 Foglia n. 4 36 IL VALORE MEDIO DELL’ AREA DELLA FOGLIA è detta anche misura più attendibile in quanto tiene conto della somma di tutte le misurazioni in eccesso ed in difetto , diviso il numero delle misurazioni eseguite; L’ERRORE ASSOLUTO o ERRORE MASSIMO COMMESSO SUL CALCOLO DELLL’AREA invece stima l’incertezza della misurazione eseguita o l’intono entro il quale si aggira il valore reale della misurazione eseguita , ovvero ci dice l’Errore massimo commesso nella misurazione in eccesso o in difetto . INTERVALLO IN CUI RICADE IL VALORE REALE DELL’ AREA DELL FOGLIO L’ERRORE RELATIVO PERCENTUALE invece da indicazione sulla qualità della misura eseguita , e sullo strumento utilizzato per la misurazione e si determina come rapporto fra (ERRORE ASSOLUTO / VALORE MEDIO) * 100 ESERCITAZIONE SUL CALCOLO DELL’ AREA DI UNA FIGURA IRREGOLARE USANDO L 1° METODO Consideriamo come unità di misura il quadrato di area 0,25 cm 2 e andiamo a determinare L’Area Interna e L’Area Esterna della foglia ottenendo due valori approssimati per difetto e per eccesso. AREA INTERNA = 123 quadretti = 30,75 cm2 AREA ESTERNA = 180 quadretti = 45,00 cm2 Per ottenere un valore più preciso dell’ Area della foglia potrei fare una media tra le due aree ricavate , trovando un valore di area anch’esso approssimato ma sicuramente più attendibile. ire meglio la superficie della foglia mentre quelli esterni tendono a delinearne piu in dettaglio il profilo