ENERGIA E TRASFORMAZIONE

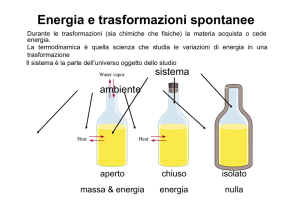
Energia e Spontaneità delle
Trasformazioni
Trasformazioni ed Energia
Durante le trasformazioni (sia chimiche che fisiche) la materia acquista o cede energia.
La termodinamica è quella scienza che studia le variazioni di energia in una trasformazione
Sistema: è la parte dell’universo
oggetto dello studio
Intorno del sistema o ambiente: è
la parte dell’universo esterna al
sistema in cui le interazioni sono
rilevabili
Sistema aperto
Sistema chiuso
Sistema isolato
massa & energia
energia
nulla
Trasformazioni ed Energia
L’interazione fra il sistema e l’ambiente può avvenire attraverso lo scambio di
calore e lavoro
-calore Q: energia trasferita tra il sistema e l’ambiente in conseguenza di una
differenza di temperatura
Q  m  c p  (Tfin  Tiniz )
cal o J ( 1cal = 4,186 J)
m è la quantità di sostanza coinvolta ;
Cp rappresenta la capacità termica specifica o calore specifico (cal (J) g-1 °C-1) della sostanza
Tfin e Tiniz rappresentano rispettivamente la temperatura finale e iniziale della sostanza
- Lavoro L:
forma di trasferimento dell’energia che può essere di tipo
meccanico, elettrico,……..
Trasformazioni ed Energia
Il trasferimento di energia durante una trasformazione (calore e/o
lavoro) richiedono da parte del sistema una variazione della sua
energia, definita energia interna U
U rappresenta l’energia totale del sistema ovvero la somma dell’energia
cinetica (traslazionale, rotazionale, vibrazionale), e dell’energia potenziale
(l’energia dei legami chimici , delle interazioni intermolecolari , delle forze di
attrazione nucleo – elettroni e l’energia dei protoni e neutroni nel nucleo.)
U  E cin  E pot
U è una funzione di stato ovvero dipende solo dallo stato in cui si
trova il sistema, ovvero temperatura, pressione, volume, tipo e
quantità di sostanza, e non dal “percorso” fatto per raggiungerlo.
2H2(g) + O2(g)
d=0,99820 g/ml
CuSO4 * 5H2O
H2O
T= 298,15 K
P= 1atm
La densità rimane costante
indipendentemente da come si
sia arrivato ad un dato stato del
sistema
quindi è una funzione di stato
Trasformazioni ed Energia
L’ energia interna di un sistema non è facilmente stimabile, ma per una
trasformazione fra uno stato 1 e uno stato 2 si può conoscere DU che
sarà sempre costante
Poiché U ha un valore unico in
ogni stato anche DU dovrà avere
un valore unico
DUtotale = U2-U1+U1-U2 = 0
Trasformazioni ed Energia
Principio di conservazione dell’energia: L’energia non può essere creata né
distrutta ma solo trasformata.
Se consideriamo la trasformazione da uno stato 1 (stato iniziale) ad uno stato 2
(stato finale) di un sistema chiuso.
DU  U2  U1  Q  L
I° principio della termodinamica
Per convenzione:
•Q assorbito dal sistema dall’ambiente ha segno positivo (+Q). La trasformazione si dice ENDOTERMICA
•Q ceduto dal sistema all’ambiente ha segno negativo (-Q). La trasformazione si dice ESOTERMICA
•L compiuto dal sistema vs l’ambiente ha segno positivo (+L)
•L compiuto dall’ambiente sul sistema ha segno negativo (-L)
Se consideriamo la trasformazione da uno stato 1 ad uno stato 2 di un sistema
isolato.
ΔU  0
ovvero l’energia totale è costante
Trasformazioni ed Energia
Sebbene U sia una funzione di stato Q e L non lo sono e il loro valore dipende dal
percorso seguito quando un sistema subisce una variazione.
Consideriamo
una
trasformazione isoterma di 0,1
moli di He alla T di 298,15 K
da uno stato 1 (P1= 2,40 atm)
ad uno stato 2 (P2 = 1,30 atm).
L = F∙s = Pest∙A∙h= PDV = Pest (Vfin-Viniz)
nRT
Viniz 
 1,02  L
Piniz
nRT
Vfin 
 1,88  L
Pfin
 J 
L  1,30 (atm)  (1,88  1,02 )( L) 101
  110  J
 L  atm 
Trasformazioni ed Energia
Realizziamo la medesima trasformazione introducendo uno stato intermedio
2
1
Viniz  1,02  L
Vint erm  1,36  L
Vfin  1,88  L
L  L1  L 2  1,80  1,36  1,02   1,30  1,88  1,36 101  130  J
Poiché DU= Q-L deve essere costante è evidente che l’aumento di L determina un
aumento di Q
Trasformazioni ed Energia
Per una trasformazione che avviene a P costante la principale forma di lavoro può
essere di contrazione (-L) o espansione (+L)
L = PDV
DU  Q  PDV
Se la trasformazione avviene invece a volume costante (recipiente ermeticamente
chiuso)
PDV  0
DU  Q v
La variazione di energia interna corrisponde
alla quantità di calore scambiata a volume
costante
Trasformazioni ed Energia
Per una trasformazione a P costante si definisce entalpia H del sistema la somma
dell’energia interna U e l’energia meccanica PV
Come U anche H è una funzione di stato di cui non
si conosce il valore assoluto
H  U  PV
Per una trasformazione da uno stato 1 (stato iniziale) ad uno stato 2 (stato finale) che
avviene a P costante (generalità dei casi)
DH  H 2  H1  (U 2  PV2 )  (U1  PV1 )  DU  PDV
Poiché dal I° principio della temodinamica
DU  PDV  Q p
DH  Q p
La variazione di entalpia
corrisponde alla quantità
di calore scambiata a
pressione costante
Quando a P costante la trasformazione avviene
senza variazione di volume
DH  DU  PDV
Qp  Qv
Trasformazioni ed Energia
Trasformazioni che avvengono senza variazione di volume:
H2(g) + I2(g)→2HI(g)
N2(g) + O2(g)→2NO (g)
Trasformazioni che avvengono con variazione di volume:
•2H2(g) + O2(g)→2H2O (l)
•CaCO3(s) →CaO(s) + CO2(g)
•H2O(l) →H2O(g)
•I2(s)→I2(g)
Trasformazioni ed energia
DU  Q v DH  Q p
Q  m  c p  (Tfin  Tiniz )
Bomba calorimetrica
Nella bomba calorimetrica si possono misurare
solo Qv poichè le trasformazioni sono condotte
in recipienti a V costante
Qv +Qass(ceduto )H2O + Qass(ceduto)bomba=0
Esempio:
1,85 g di grafite vengono bruciati con eccesso di O2 in una bomba calorimetrica di acciaio avente una
massa pari a 2,835 kg immersa in un recipiente perfettamente isolato contenete 3,20 kg di H2O. Un
termometro immerso nell’acqua indica, dopo la reazione di combustione, un aumento di temperatura di
4,12 °C.
Calcolare il DU e il DH della reazione di combustione in kcal.
(cpacciaio= 0,114 cal g-1 °C-1; cpH2O(l) = 1,00 cal g-1 °C-1 )
C(s) + O2(g)
CO2(g)
La reazione è esotermica (-Q) come dimostra l’aumento di temperatura misurata nell’acqua
per effetto del trasferimento del calore sviluppato nella reazione
Qv +Qass(ceduto )H2O + Qass(ceduto)bomba=0
Qv = -QassorbitoH2O - Qassorbito bomba
Q assorbitoH2O  m ( H 2O )  c p ( H 2O )  (Tfin  Tiniz )
Q assorbitobomba  m ( bomba )  c p ( bomba )  (Tfin  Tiniz )
 
 

 kcal 
 kcal 
  4,12(C)    2.835(kg)  0,114
  4,12(C)   14,5kcal
Q v    3,20(kg) 1,00
 kg  C 
 kg  C 
 

 
DU  Q v  14,5kcal
DH  DU  PDV
C(s) + O2(g)
CO2(g)
Il lavoro PDV che il sistema può compiere è legato alla formazione e alla scomparsa delle
specie gassose
DH  DU  DnRT
dove Dn = (ngas prodotto-ngas reagente)
Poichè Dn = (nCO2-nO2) =0
DH  DU  14,5kcal
Esempio:
Nella combustione del propano in una bomba calorimetrica DU =-2200kJ per mole di propano bruciato.
Calcolare il DH della reazione di combustione alla temperatura di 25 °C e alla P = 1 atm.
C3H8(l) + 5O2(g)
3CO2(g) + 4H2O(l)
DH  DU  PDV
DH  DU  DnRT
Se la reazione venisse effettuata in un recipiente aperto il lavoro possibile è un lavoro di
compressione
poichè Dn = (nCO2-nO2) =3-5 =-2
J
 L  atm 
 J 
R  0,0821
 101
  8,31
mole  K
 mole  K 
 L  atm 

8,31  kJ 
kJ
 kcal  
DH  2200
    2(moli ) 

  298,15(K )   2205
1000  mole  K 
mole
 mole  

Spontaneità delle trasformazioni
Il primo principio della termodinamica non pone limitazioni ai
trasferimenti di energia purché sia rispettato il principio di
conservazione.
Pertanto non è possibile prevedere, con il principio di conservazione
di energia, la direzione in cui una trasformazione chimica o fisica
avviene spontaneamente ovvero senza alcun intervento esterno.
Una trasformazione spontanea è anche irreversibile
Le Transizioni di stato- Spontaneità
Condensazione o
liquefazione
solidificazione
brinamento
DHfus >0
→
DHsolidif <0
←
DHevaporazione >0
→
DHcondensaz <0
←
Cosa causa l’espansione di un gas a T costante?
Q0
DU  D(PV )
Espansione isoterma
Pa Va  Pb Vb
3
Pa Va  kT
2
L’espansione non è causata dal passaggio
del sistema ad uno stato di minore energia
Una descrizione più funzionale della causa
determinate l’espansione è che per la stessa
energia totale sono disponibili, nel maggior
volume più livelli di energia traslazionale nei
quali possono distribuirsi le molecole del gas.
3
Pb Vb  kT
2
D(PV )  0
DU  0
DH  0
Processi reversibili e irreversibili
Processo reversibile quando le variabili di stato del sistema (volume,
pressione) variano solo di una quantità infinitesima.
Es: espansione reversibile di un gas
Pi=Pest +dP
Un processo reversibile può essere invertito in ogni momento tramite un
cambiamento infinitesimo delle proprietà dell’ambiente.
Processo irreversibile quando le variabili di stato del sistema variano di una
quantità finita.
Es: espansione irreversibile di un gas
Pi=Pest +DP
Un processo irreversibile non può essere invertito o arrestato e procede
spontaneamente in una direzione.
Processi reversibili e irreversibili
Lavoro in un processo reversibile:
Es: espansione reversibile di un gas
Pi=Pest +dP
dLrev = Pest ∙dV
V2
L rev   Pest dV
Lrev
V1
Poichè
Pi ~ Pest
V2
L rev
L rev
V2
V2
nRT
dV
  Pi  dV  
 dV  nRT 
V
V1
V1
V1 V
V2
 nRT ln
V1
Processi reversibili e irreversibili
Lavoro in un processo irreversibile:
Es: espansione irreversibile di un gas
Pi=Pest +DP
Lirrev
V2
V2
V1
V1
L irrev   Pest  dV   P2  dV  P2 (V2  V1 )
Lrev > Lirrev
Processi reversibili e irreversibili
Calore in un processo reversibile e irreversibile:
Processo reversibile
Processo irreversibile
Qirrev =DU+ Lirrev
Qrev =DU+ Lrev
Qrev - Qirrev = Lrev - Lirrev
Poichè
Lrev-Lirrev >0
Qrev-Qirrev >0
Qrev > Qirrev
Entropia- Spontaneità
La proprietà termodinamica collegata al modo in cui l’energia interna di un
sistema è distribuita su livelli di energia microscopici è detta entropia
Maggiore è il numero di configurazioni delle particelle
microscopiche (atomi, ioni, molecole) tra i livelli di energia di un
particolare sistema e maggiore è l’entropia del sistema
Stato di
disordine
maggiore
probabilità
Stato di
ordine
minore probabilità
La funzione di stato entropia S descrive quantitativamente la tendenza al
disordine (maggiore probabilità di stato) di un sistema e un aumento di
entropia accompagna i processi spontanei
Equazione di Boltzmann per l’ Entropia
L’entropia è correlata al numero di stati microscopici che lo descrivono
secondo l’equazione:
S = K ln W
dove
K è la costante di Boltzman (1,3807 10-23 J/K)
W è il numero di stati microscopici del sistema.
MAGGIORE E’ IL NUMERO DI STATI MICROSCOPICI MAGGIORE E’ LA
PROBABILITA’ D’ ESISTENZA DEL SISTEMA STESSO
L’entropia è una funzione di stato
Previsioni qualitative delle variazioni di entropia
E’ inoltre prevedibile una variazione anche per le trasformazioni chimiche;
2NH4NO3(s)
2SO2(g) + O2(g)
CO(g) + H2O(g)
2N2(g) + 4 H2O(g) + O2 (g)
2SO3(g)
CO2(g) + H2(g)
DS=Sprodotti- S reagenti >0
DS=Sprodotti- S reagenti <0
DS= incerta
Entropia di un sistema
Se un sistema subisce una trasformazione isoterma, reversibile e infinitesima
durante la quale scambia la quantità di calore dQrev con l’ambiente
H2O(l) (0°C, 1 atm)
H2O(s) (0°C, 1atm)
il suo contenuto di entropia varia di una quantità infinitesima pari a :
dQrev
dS 
T
Per una trasformazione tra lo stato 1 e lo stato 2 la variazione finita di entropia
sarà:
dQrev Qrev
DS  S 2  S1   dS  

T
1
1 T
2
2
cal K-1
Entropia di un sistema
Se un sistema subisce una trasformazione irreversibile
H2O(l) (0°C, 1 atm)
H2O(s) (0°C, 1atm)
Q irrev
Q rev  Q irrev
Q rev
Q irrev
DS 

T
T
Disuguaglianza di Clausius
In base a questi risultati in una trasformazione irreversibile si otterrebbe una quantità
più piccola delle effettiva variazione di entropia del sistema
Se il sistema si evolve attraverso una trasformazione irreversibile la variazione di
entropia che esso subisce si calcola lungo il cammino di una qualunque
trasformazione reversibile arbitrariamente scelta che consideri i medesimi stato
iniziale e finale
II° principio della termodinamica: Tutti i processi
spontanei e irreversibili producono un aumento di
entropia dell’universo
DStotale= DS+DSamb>0
DS>0
DS<0
DS>0
DS<0
Stato iniziale
Stato finale
T 0< T
T
Per il sistema
Sf < Si
Per l’ambiente
Sambf > Sambi
Supponendo che Q scambiato non faccia variare T0
DS  Q / T
DS totale
DSamb  Q / To
 1
Q
Q
1


 Q  
   0
T To
T
 To
Tanto più grande è T-T0 ossia tanto più ci si scosta dalle condizioni di reversibilità tanto maggiore
è l’aumento di entropia;
Se invece T-T0 tende a zero (trasformazione reversibile) la somma delle variazioni di entropia fra
sistema e ambiente è zero
Pertanto per valutare se un processo è spontaneo occorre valutare:
- La variazione entropica del sistema
- La variazione entropica dell’ambiente
- La somma delle due
Una semplificazione del problema si ottiene definendo una nuova funzione di
stato “ENERGIA LIBERA” che ci permette di valutare:
-Se un processo è spontaneo
-Come un cambiamento di temperatura possa condizionare il carattere
spontaneo di un processo
Energia Libera di Gibbs
Per un processo che avviene a T e P costante
DStotale  DS  DSamb
Q
DS totale  DS  rev
T
TDStotale  TDS  Q rev
TDStotale  TDS  DH
TDStotale  DH  TDS
Q rev  DH
Definita l’ Energia libera di Gibbs G come:
G= H-TS
G è una funzione di stato
DG = DH-TDS
DStotale >0 DG <0
DG= -TDStotale
DStotale =0 DG =0
DStotale <0 DG >0
Trasformazione
irreversibile o spontanea
Trasformazione reversibile
o all’equilibrio
Trasformazione non
spontanea
Spontaneità ed effetto della Temperatura
DG = DH-TDS
DH>0 e DS>0
Solido
DH< 0 e DS<0
spontanei ad alta temperatura
Liquido
Vapore o
gas
spontanei a bassa temperatura