1 Fattore di trasmissione e riflessione

1
1. FATTORE DI TRASMISSIONE E RIFLESSIONE
1
Fattore di trasmissione e riflessione
Riassunto
Consideriamo un moto unidimensionale per una particella di massa m in presenza di
un potenziale V (x). Dall’analisi svolta in classe discende che il processo in cui una
particella di impulso p urta, da sinistra, la zona in cui è presente il potenziale V , è
descritto da una soluzione stazionaria ψ(x) che ha come comportamento asinotico
(
x → −∞ eikx + R e−ikx
ψ(x) →
(1.1)
x → +∞ T eikx
con ~k = p/m. L’aspressione generale per la corrente per una funzione d’onda della
forma
ψ(x) = A eikx + Be−ikx
è
~
~k
(ψ ∗ ∂x ψ(x) − ψ(x)∂x ψ ∗ (x)) =
|A|2 − |B|2
2mi
m
Dalla conservazione della corrente segue
j=
|R|2 + |T |2 = 1
(1.2)
(1.3)
In queste formule è supposto che V (x) → 0 per x → ±∞. I coefficienti R e T si
trovano risolvendo l’equazione di Schrödinger
−
1.1
~2 00
ψ (x) + V (x)ψ(x) = E ψ(x) ;
2m
E=
~2 k 2
2m
(1.4)
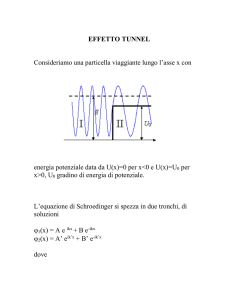
Gradino di potenziale
In una situazione come quella indicata in figura
V0
la soluzione asintotica (qui esatta) è
(
x → −∞
ψ(x) →
x → +∞
con
E=
~2 k 2
;
2m
eikx + R e−ikx
T eiqx
~2 q 2
= E − V0
2m
(1.5)
2
La conservazione della corrente in questo caso implica
k(1 − |R|2 ) = q |T |2 .
La condizione di continuità in x = 0 per ψ e la sua derivata prima fornisce

1 − kq
k−q

(

=
R
=

1+R=T
1 + kq
k+q
⇒
2k
2

ik(1 − R) = iqT

=
 T =
1 + kq
k+q
La soluzione verifica l’equazione di continuità.
1.2
Calcolo perturbativo
Vogliamo analizzare il caso istruttivo in cui il potenziale è “piccolo” rispetto all’energia
cinetica. L’equazione da risolvere è
ψ 00 + k 2 ψ =
2m
V (x)ψ(x)
~2
(1.6)
con E = ~2 k 2 /2m. Si suppone che V vada a zero all’infinito in modo sufficientemente
rapido.
In assenza di potenziale la soluzione che corrisponde ad un’onda incidente (da
sinistra) è
ψ(x) = eikx .
L’idea è quella di trovare la soluzione nella forma di sviluppo in serie della forma
ψ = ψ (0) + ψ (1) + . . . ;
ψ (n) ∼ V n
(1.7)
All’ordine più basso
ψ (0) = eikx
(1.8)
Sostituendo nella (1.6) si ricava, al primo ordine
d2 (1)
2m
ψ + k 2 ψ (1) = 2 V (x)ψ (0) (x)
dx2
~
(1.9)
cioè un’equazione d’onda non omogenea.
Equazione inomogenea
Per risolvere un’equazione del secondo ordine del tipo
d2
f (x) + k 2 f (x) = ρ(x)
dx2
(1.10)
è necessario fissare delle condizioni iniziali, o delle condizioni al contorno. Per capire il
problema e la sua soluzione conviene avere un’interpretazione intuitiva dell’equazione
stessa. Generalizzando l’analoga situazione elettrostatica si può immaginare ρ come
1. FATTORE DI TRASMISSIONE E RIFLESSIONE
3
una sorgente, di onde. La linearità dell’equazione permette di impostare il problema a
partire da una sorgente elementare, puntiforme, del tipo
ρ = δ(x − y)
che rappresenta una sorgente localizzata in x = y. Detta G(x, y) la soluzione per una
sorgente elementare:
d2
G(x, y) + k 2 G(x, y) = δ(x − y)
dx2
la soluzione dell’equazione generale (1.10) è immediata:
Z
f (x) =
dy G(x, y) ρ(y)
(1.11)
(1.12)
Ci aspettiamo che una sorgente elementare generi un’onda “di espansione” che
propaghi l’effetto della sorgente nello spazio al passare del tempo. In una dimensione
un’onda divergente è rappresentata, asintoticamente, da
f ∼ eikx ;
x→∞
f
∼
x→−∞
e−ikx ;
Di questo ci si convince immediatamente considerando la (sottintesa) dipendenza temporale exp(−iωt) e considerando il moto dei piani di fase. Per una sorgente puntifome
collocata nel’origine (y = 0) quindi ci si aspetta
f (x) = A exp ik|x|
La costante A di normalizzazione si determina imponendo l’equazione (1.11) ed usando le note relazioni
∂x |x| = (x) ;
∂x (x) = 2δ(x)
(x) è la funzione segno
(x) =
+1 ,
−1 ,
x>0
x<0
da cui
∂x Aeik|x| = A(ik)(x)eik|x| ;
∂x2 Aeik|x| = A(−k 2 )(x)2 eik|x| + A(ik)(2δ(x))eik|x| = −k 2 Aeik|x| + (2ikA)δ(x)
Generalizzando la soluzione usando l’invarianza per traslazioni si ottiene quindi la
funzione di Green nella forma
G(x, y) =
1
exp(ik|x − y|)
2ik
(1.13)
La sostituzione nella (1.12) fornisce la soluzione dell’equazione inomogenea (1.10):
Z
1
f (x) =
dy eik|x−y| ρ(y)
(1.14)
2ik
4
Coefficienti di riflessione e trasmissione perturbativi
La formula generale (1.14) applicata alla (1.9) fornisce
Z
2m 1
dy eik|x−y| V (y)eiky
ψ (2) (x) = 2
~ 2ik
(1.15)
Se V (y) ha supporto limitato, o comunque decresce in modo abbastanza rapido all’infinito, i valori di y che contribuiscono all’integrale sono quelli in una certa regione
|y| ≤ a, che caratterizza la zona in cui V è rilevante. Se |x| è grande possiamo quindi
sempre supporre che |y| < |x| nella zona asintotica. Si ha quindi
|x − y|
∼
x→−∞
−(x − y) ;
|x − y|
∼ (x − y) .
x→+∞
Il comportamento asintotico della soluzione è quindi

R
m
 eikx + i k~
dyV (y)e2iky e−ikx ; x → −∞
2
(1)
(2)
ψ(x) ' ψ (x) + ψ (x) =
 eikx + m R dyV (y)eikx ;
x → +∞
i k~2
da cui al primo ordine in V
Z
m
R=
dyV (y)e2iky ;
i k~2
T =1+
m
i k~2
Z
dyV (y)
(1.16)
Notiamo che |R|2 +|T |2 = 1+O(V 2 ), quindi la relazione di unitarietà (conservazione
della corrente) è soddisfatta.
2
Osservazioni sulla funzione di Green
Questa parte della teoria non è strettamente richiesta per lo svolgimento del corso, è
qui introdotta per gli studenti interessati ad approfondire l’argomento.
La forma della funzione di Green può anche essere derivata in modo più “costruttivo” e questo è utile per capire alcune tecniche standard in uso nella teoria.
Definendo la trasformata di Fourier
Z
dq
G(x) =
G̃(q)eiqx
(2.1)
2π
la trasformata di Fourier della (1.11) assume la forma
−q 2 G̃(q) + k 2 G̃(q) = 1
⇒
G̃(q) = −
1
q2 − k2
(2.2)
e quindi il problema sembra banale. In verità la sorgente che compare nella (1.11)
è una distribuzione, non una funzione regolare, e corrispondentemente la soluzione è
anch’essa una distribuzione. La singolarità è apparente dalla circostanza che la soluzione (2.2) dà luogo ad un integrale divergente quando è introdotta nella trasformata di
2. OSSERVAZIONI SULLA FUNZIONE DI GREEN
5
Fourier, presentando due poli sull’asse reale per q = ±k (ricordiamo che nella nostra
convenzione stiamo assumendo k > 0 ).
Il modo corretto per definire la trasformata di Fourier è quello di operare un passaggio al limite, come sempre nella definizione delle distribuzioni. Il modo più intuitivo
per capire la procedura è di pensare l’integrale in q nel campo complesso, deformando
leggermente il cammino in prossimità dei poli, o, equivalentemente, spostando i poli
dall’asse reale con l’aggiunta di una piccola parte immaginaria (che alla fine del calcolo
viene mandata a zero).
Adottiamo questa seconda procedura scrivendo
q 2 − k 2 → q 2 − k 2 − iε ;
(ε > 0)
I due poli sono ora situati in
p
q = ± k 2 + iε ' ±(k + iε) .
Torniamo ora all’integrale di Fourier (2.1). Nel campo complesso si può applicare il
lemma di Jordan. Per x > 0 l’integrale va chiuso nel semipiano complesso superiore
Im[q] > 0 (in verso antiorario), in modo da avere il comportamento esponenziale
decrescente all’infinito, mentre per x < 0 l’integrale va chiuso nel semipiano inferiore,
Im[q] < 0 (in verso orario). In questo modo applicando il metodo dei residui, per
x > 0 contribuisce solo il polo a q = +k mentre per x < 0 solo il polo a q = −k e si
ha
Z
dq
eiqx
x>0:
G(x) = −
2π (q − (k + iε))(q + (k + iε))
1
1 ikx
1 ikx
e
=
e
= (2πi) −
2π 2k
2ik
Z
dq
eiqx
x<0:
G(x) = −
2π (q − (k + iε))(q + (k + iε))
1
1 ikx
1 −ikx
1 ik|x|
= (−2πi) −
e
=
e
=
e
2π −2k
2ik
2ik
ovvero
G(x) =
1 ik|x|
e
2ik
(2.3)
6
Notiamo ora che la scelta col segno opposto per la parte immaginaria, k 2 → k 2 −
iε avrebbe dato luogo a funzioni di Green che descrivono onde convergenti, come è
immediato verificare.
Le altre due scelte possibili, corrispondenti come è facile convincersi, a due poli
con lo stesso segno della parte immaginaria, corrispondono a q 2 − k 2 → q 2 − k 2 ± iqε
e rompono la simmetria x → −x, dando luogo a funzioni non nulle solo nel semispazio
x > 0 o x < 0.
Un’applicazione interessante delle onde convergenti sarà data più avanti.
Esercizio proposto
Si dimostri, con le due procedure precedenti (calcolo diretto o trasformata di Fourier)
che in tre dimensioni la funzione di Green che soddisfa a
∇2 G + k 2 G = δ (3) (x)
è
1 eikr
4π r
Applicare questa formula per intepretare l’approssimazione di Kirkoff per la diffrazione da un foro circolare.
G=−
3
Operatore di transfert (Ω)
Per questo argomento e per un esempio esplicito costruito con un potenziale a δ si veda
il file: Appunti-4.pdf
4
Calcolo della normalizzazione nello spettro continuo
L’idea è esposta, ad esempio, nel volume 3 del corso di Landau-Lifchitz, sez.21 nell’edizione italiana. La riportiamo qui in forma semplificata e fornendo alcuni esempi.
Consideriamo delle funzioni ψk (x) appartenenti allo spettro continuo. Se le funzioni appartengono ad autovalori diversi dell’Hamiltoniana sono ortogonali per ragioni
generali (H è autoaggiunto). Se appartengono allo stesso autovalore la norma è infinita,
perchè appartengono allo spettro continuo. Diciamo per fissare le idee che
Z
dxψ2∗ (x)ψ1 (x) ∝ δ(E1 − E2 )
(4.1)
La δ dell’energia può spesso, convenientemente, essere espressa in δ degli impulsi o
del numero d’onda con un cambio di variabili.
Ad esempio per onde piane è usuale assumere la normalizzazione ψk (x) = exp(ikx),
e corrispondentemente
Z
dxψk∗0 (x)ψk (x) = (2π)δ(k − k 0 )
(4.2)
4. CALCOLO DELLA NORMALIZZAZIONE NELLO SPETTRO CONTINUO
7
Qui E = ~2 k 2 /2m. Dalla definizione di δ
1
m
δ(E − E 0 ) = ∂E δ(k − k 0 ) = 2 δ(k − k 0 )
~ k
∂k
e quindi se si vogliono normalizzare le onde piane alla δ dell’energia occorre usare
r
m ikx
ψE (x) =
e .
~2 k
L’idea per il calcolo esplicito del fattore di normalizzazione sta nel fatto che per
E1 = E2 il prodotto scalare (4.1) è divergente e questa divergenza può provenire solo
dal comportamento all’infinito della funzione d’onda, quindi la conoscenza del comportamento asintotico di ψ fissa la normalizzazione, indipendentemente dai dettagli
della funzione al finito, e questa è una semplificazione enorme.
Supponiamo che V vada a zero abbastanza rapidamente all’infinito, in questo caso
il comportamento asintotico è del tipo exp(±ikx), quindi basta saper calcolare gli
integrali, asintotici, di prodotti di esponenziali.
Se immaginiamo il sistema immerso in una scatola di lunghezza L, gli integrali
oscillanti, del tipo exp(iqx) mediano a zero, mentre gli esponenziali in cui le fasi
si cancellano danno un contributo proporzionale ad L. Si tratta quindi di trovare la
corrispondenza fra L e le funzioni δ. Ma questo è facilmente dedotto dalla (4.2): se
k = k 0 l’integrale vale L quindi la regola di corrispondenza è
L → 2π δ(k − k 0 ) .
(4.3)
Un esempio può aiutare a capire la procedura. Consideriamo lo scattering da un
potenziale V , con coefficienti di riflessione e trasmissione R, T . Il comportamento
asintotico per una soluzione esatta ψ1 (x) è, come è noto
x → −∞ :
eikx + Re−ikx ;
T eikx
x → +∞ :
Effettuiamo l’integrale di ψ1∗ ψ1 separando la parte sinistra e la parte destra (con intervalli di lunghezza L/2 naturalmente).
A sinistra, asintoticamente, l’integrale vale (mettiamo direttamente a zero i termini
oscillanti):
Z
Z
∗
ψ1 ψ1 →
dx (e−ikx + R∗ eikx )(eikx + Re−ikx ) →
x<0
x<0
Z
L
1 + |R|2
dx 1 + |R|2 =
2
x<0
a destra si ha immediatamente
Z
Z
∗
ψ1 ψ 1 →
x>0
dx T ∗ e−ikx T ∗ eikx →
x>0
L 2
|T |
2
Quindi in totale (usando la relazione di unitarietà):
L
(1 + |R|2 + |T |2 ) = L → 2π δ(k − k 0 )
2
8
Quindi le soluzioni“right-movers” (ψ1 ) sono normalizzate con
Z
dx ψ1∗ (k 0 , x) ψ1 (k, x) = 2π δ(k − k 0 )
Accanto alle soluzioni ψ1 esistono delle soluzioni ψ2 che corrispondono a onde
incidenti da sinistra, vedi Appunti-4.pdf:
(
T e−ikx
x → −∞
ψ2 (k, x) →
R∗ T ikx
−ikx
e
− ∗ e
x → +∞
T
Verifichiamo che le due soluzioni sono ortogonali
Z
Z
L
ψ2∗ ψ1 →
T ∗ eikx (eikx + Re−ikx ) → T ∗ R
2
x<0
x<0
Z
Z
∗
RT
L
ψ2∗ ψ1 →
eikx −
e−ikx T eikx → − RT ∗
T
2
x>0
x>0
la somma dei due termini dà effettivamente 0.
5
Osservazioni sulla matrice S
Questa parte della teoria non è strettamente richiesta per lo svolgimento del corso, è
qui introdotta per gli studenti interessati ad approfondire l’argomento.
Nel file Appunti-4.pdf sono state introdotte le due soluzioni linearmente indipendenti
( ikx
e + R e−ikx x → −∞
ψ1 (k, x) →
(5.1)
T eiqx
x → +∞

x → −∞
 T e−ikx
∗
ψ2 (k, x) →
(5.2)
 e−ikx − R T eikx x → +∞
∗
T
corrispondenti rispettivamente a soluzioni che per t → −∞ rappresentano un’onda
incidente da sinistra e destra rispettivamente.
Si è inoltre definta la matrice S come la matrice i cui elementi rappresentavano
le ampiezze di probabilità di trovare a +∞ uno stato con una particella con impulso
positivo o negativo (right e left movers). Avevamo calcolato la matrice in termini dei
coefficienti di riflessione e trasmissione


T
R

S =  R∗ T
(5.3)
− ∗
T
T
Vogliamo qui precisare meglio questa nozione.
Innanzitutto consideriamo le soluzioni ψ1 , ψ2 . Per come sono state costruite queste corrispondono all’assegnazione di uno stato con un dato impulso iniziale (±k) che
5. OSSERVAZIONI SULLA MATRICE S
9
evolve, fino al tempo t negli stati considerati. Asintoticamente questi stati rappresentano una sovapposizione di un’onda piana con un’onda sferica “divergente”, generata
dallo scatering. Consideriamo ad esempio ψ1 . Per grandi t, osservando al solito la fase
stazionaria, vediamo che sono presenti un’onda verso sinistra, di ampiezza R e, verso
destra, un’onda piana (di ampiezza 1) sovrapposta alla parte destra di un’onda divergente, di ampiezza T − 1. Questa decomposizione è naturale,in quanto in assenza di
scattering si avrebbe T = 1, e la parte “in espansione” dell’onda rappresenta appunto
il contributo della diffusione dal bersaglio.
In tre dimensioni la situazione corrispondente è più chiara perchè la parte asintotica “destra” e “sinistra” non sono più sconnesse, e la soluzione di scattering cercata
avrebbe il comportamento asintotico
1 ikr
e
(5.4)
r
Introducendo la dipendenza temporale, con fase −iωt, è ovvio che per t → −∞ la
fase temporale non può cancellare la fase positiva ikr, quindi nel passato solo l’onda
piana corrispondente alla particella incidente sopravvive, mentre per t → +∞ c’è sia il
contributo dell’onda piana che quello dell’onda sferica divergente. In una dimensione
la situazione è analoga, ma gli unici angoli possibili sono 0 e π, quindi la funzione si
decompone in due termini distinti.
Le soluzioni sono definite a partire da uno stato iniziale e ricavate come evoluzione
“nel futuro” della preparazione di questo stato. Per sottolineare questo fatto le soluzioni
di questo tipo si scrivono anche (usiamo la notazione tridimensionale)
ψ → eikx + f
ψ (+) (k, x)
Tralasciando per il momento la complicazione dovuta a possibili stati legati (supponiamo ad esempio il potenziale repulsivo) notiamo che le funzioni ψ (+) (k, x) sono un
insieme completo, descrivendo tutte le possibili preparazioni del sistema, cioè
Z
ψ (+) (k, x) (ψ (+) (k, y))∗ = δ(x − y)
(5.5)
k
Supponiamo di fare un esperimento di scattering, in meccanica quantistica la domanda corretta che si può fare è: preparato uno stato, nel passato, con impulso k
qual’è la probabilità di misurare, dopo lo scattering (nel futuro) una particella di impulso k0 ? Secondo le regole generali questa probabilità sarà data dal modulo quadro
dell’ampiezza, cioè del prodotto scalare, fra gli stati che descrivono le due situazioni.
Ora supponiamo di usare l’equazione di Schrödinger indipendente dal tempo. Abbiamo già discusso il fatto che le soluzioni trovate ψ (+) , corrispondono allo stato “preparato” a t = −∞, ma quali sono le funzioni che corrispondono ad uno stato “futuro”
di impulso k? In altre parole quale soluzione e quali condizioni al contorno dobbiamo
imporre all’equazione di Schrödinger per esprimere questa situazione fisica?
Se stiamo descrivendo la situazione al tempo t dobbiamo avere sicuramente un’onda piana ma sovrapposta ora ad un’onda sferica convergente che descrive appunto l’evoluzione all’indietro nel tempo di un dato stato. Se infatti abbiamo una funzione del
tipo
1
eikx + f e−ikr
r
10
vediamo che per t → +∞ la parte di onda sferica ha una fase
−ikr − iωt
che non può mai essere stazionaria (entrambi i termini hanno lo stesso segno, così come
le derivate), quindi il contributo di onda sferica sparisce e resta solo l’onda piana, che
è lo stato richiesto.
Le funzioni con “fisso” stato finale sono indicate con ψ (−) (k, x).
Per fortuna non c’è bisogno di risolvere nuovamente l’equazione di Schrödinger
per trovare queste soluzioni. Vediamo infatti che considerando il complesso coniugato
di una funzione ψ (+) si ottiene un’onda sferica convergente. In questo passaggio si
inverte però anche la fase dell’onda piana. Per mantenere l’impulso k basta cambiarne
il segno, in formule
ψ (−) (k, x) = (ψ (+) (−k, x))∗
(5.6)
Anche le funzioni ψ (−) sono un insieme completo: descrivono la situazione al tempo
t non attraverso i possibili stati iniziali ma attraverso i possibili risultati finali, diciamo
la risposta dei contatori di particelle1
Per quanto abbiamo detto è chiaro allora che l’ampiezza di probabilità (matrice S)
per il processo k → k0 è definita da
Z
S(k0 , k) = h−, k0 |+, ki = (ψ (−) (k0 , x))∗ ψ (+) (k, x)
(5.7)
Consideriamo in particolare il caso unidimensionale. Siccome l’energia nel processo d’urto è conservata l’eemento di matrice (5.7) è proporzionale a δ(E − E 0 ).
La costante di proporzionalità è una matrice nel sottospazio a energia fissa, in una
dimensione una matrice 2 × 2 (i due stati possibili left e right movers).
In una dimensione l’inversione dell’impulso corrisponde a scambiare gli stati ψ1
con gli stati ψ2 .
Come già visto in una sezione precedente (vedi sez.4) per il calcolo degli elementi di matrice è sufficiente conoscere lo sviluppo asintotico delle soluzioni. Scriviamo esplicitamente lo sviluppo asintotico delle soluzioni, nella forma compatta {x →
−∞; x → +∞}
(+)
ψ1
(+)
ψ2
(−)
ψ1
(−)
ψ2
= eikx + Re−ikx ; T eikx
R∗ T
= T e−ikx ; e−ikx − ∗ eikx
T
RT ∗ −ikx
(+)
= (ψ2 )∗ = T ∗ eikx ; eikx −
e
T
−ikx
(+) ∗
∗ ikx
= (ψ1 ) = e
+R e
; T ∗ e−ikx
(−)
Il lettore può facilmente verificare che effettivamente, ad esempio, ψ1 descrive per
t → +∞ un’onda piana nella zona x → +∞, senza aggiunta di onde sferiche.
1 Vedi
la nota storico-bibliografica alla fine della sezione.
5. OSSERVAZIONI SULLA MATRICE S
11
Per quanto riguarda la matrice S applicando la (5.7) si ritrova la (5.3). Ad esempio
Z
Z
Z
R∗ T
(−) ∗ (+)
−ikx
ikx
−ikx
S11 = dx (ψ1 ) ψ1 =
(T e
)(e + Re
)+
(e−ikx − ∗ eikx )T eikx
T
x<0
x>0
L
L
= T + T → T 2πδ(k − k 0 )
2
2
in accordo con la (5.3). Lo stesso procedimento può essere usato per gli altri elementi
di matrice.
Nota storica e indicazioni bibliografiche
La discussione sull’uso di soluzioni anticipate o ritardate delle equazioni d’onda (corrispondenti nel dominio spazio temporale alle onde sferiche divergenti e convergenti)
risale naturalmente alla discussione sulle soluzioni delle equazioni d’onda nel caso
elettromagnetico. Le onde divergenti, equipaggiate col fattore temporale, sono alla base dei noti potenziali ritardati. La possibilità di usare in modo del tutto equivalente i
potenziali anticipati è messa in luce da A.Einstein nell’articolo: On the present status
of the radiation problem (Zum gegenwärtingen Stand des Strahlungsproblems), Phys.
Zeit. 10, (1909), 185. Il ragionamento è analogo alla completezza sia degli stati ψ (+)
che degli stati ψ (−) .
La formulazione delle soluzioni con le corrette condizioni al contorno nell’equazione indipendente dal tempo, quindi la definizione degli stati ψ (±) , è dovuta a A.Sommerfeld.
Per un approfondimento sulle funzioni di Green si veda, ad esempio, K.Konishi,G.Paffuti:
Meccanica Quantistica: nuova introduzione, Ed. Plus, Cap.7, nello stesso volume nel
Cap.3 viene trattato in dettaglio il problema del potenziale a δ. Nel volume Meccanica
Quantistica: Applicazioni, Ed. Plus, Cap.7 l’argomento viene approfondito.
La trattazione degli stati ψ (±) in generale è abbastanza complessa. Il lettore può
trovare una discussione esauriente in A.Di Giacomo:Lezioni di Fisica Teorica, Edizioni ETS, Cap.4, questa lettura richiede una conoscenza delle basi della meccanica
quantistica e delle sue applicazioni elementari.